Group decision making method with hesitant fuzzy preference relations based on additive consistency and consensus

Abstract

To address the situation where the multi-criteria decision making (MCDM) has problems with hesitant fuzzy preference relations (HFPRs), this paper develops a group decision making method considering the additive consistency and consensus simultaneously. First, a new normalized method for HFPRs is developed to address the situation where the evaluation information has different number of elements. Second, for improving the unacceptable consistent HFPRs, an algorithm is designed to derive acceptable consistent HFPRs. The main characteristic of the design algorithm is that the values that need to be revised are identified first, and then design the local adjustment process. Third, an algorithm is developed to obtain a group of normalized HFPRs (NHFPRs), considering the additive consistency of HFPRs. Fourth, for improving the individual consistency and group consensus simultaneously, an algorithm is designed to obtain a group of HFPRs with acceptable consistency and consensus. Finally, the method of determining the decision makers’ weights and a procedure for MCDM problems with HFPRs are given. An illustrative example in conjunction with comparative analysis is used to demonstrate the proposed method which is feasible and efficient for practical MCDM problems.

Introduction

In multi-criteria decision making (MCDM) problems, we need to choose the best alternative according to several determined criteria from a set of alternatives [2]. Different approaches are developed from different perspectives, where preference relations (PRs) are one of the commonly used technologies. Its principle is to rank alternatives in view of the priority vector obtained from pairwise judgment [23]. According to the evaluation scale of the pairwise judgment, PRs can be derived into fuzzy PRs (FPRs) and multiplicative PRs (MPRs). The former used [0, 1] scale and the latter expressed the judgment with [1/9, 9]. In the process of developing PRs, consistency analysis is necessary to avoid the contradictory ranking. Tanino [27] developed two consistency concepts for FPRs, namely, additive consistent FPRs and multiplicative consistent FPRs. The former indicates the additive transitivity and the latter shows the multiplicative transitivity. As for MPRs, Saaty [24] defined the concept of multiplicative consistent MPRs, it indicates the multiplicative transitivity among three related judgements. Since then, MCDM approaches based on two types of PRs are proposed [1, 4, 9, 11, 28, 38].

Noticeably, FPRs and MPRs only employ an exact numeric value to denote the membership degree of pairwise judgment, which limits the applications owing to other types of information extensive exist in MCDM problems. It is very necessary to expend fuzzy information into other forms, such as, intuitionistic fuzzy [5, 15], Type-2 fuzzy [7, 21] and linguistic [6, 42]. To overcome the limitations of fuzzy sets when dealing with vague and imprecise information, Torra and Narukawa [29] developed the concept of hesitant fuzzy sets (HFSs). To be easily understood, Xia and Xu [35] expressed the HFSs as mathematical symbol and developed the concept of hesitant fuzzy elements (HFEs). Later, Xia and Xu [36] found the advantages of HFEs and introduced the concept of hesitant FPRs (HFPRs). The HFPRs can be considered as an effective tool to represent the preference information over alternatives for a group of decision makers, especially when anonymity is required to avoid influencing each other or protect decision makers’ privacy [45]. For instance, when providing the degree to which alternative $x_{1}$ is preferred to alternative $x_{2}$, the first expert provides 0.6, the second expert provides 0.7, and the third expert provides 0.8, then the degree to which $x_{1}$ is preferred to $x_{2}$ is denoted by HFE $\left\{ {0.7,0.8,0.9} \right\}$. It is more accurate than using a single value to express the evaluation information of experts.

Following the original work of Xia and Xu [36], many scholars dedicate themself to study the advanced of HFEs and lots of MCDM approaches based on HFPRs have been developed [8, 22, 30]. For example, MCDM approaches based on additive consistent HFPRs [12, 19, 39, 44], MCDM approaches based on multiplicative consistent HFPRs [10, 18, 31], while MCDM approaches based on multiplicative consistent hesitant MPRs (HMPRs) [46, 49, 50]. According to the principle of used the number of elements including in HFEs, these approaches can be classified into four categories [18]. A concise literature review of these approaches is presented as follows.

(1) Only considers one FPRs derived from HFPRs [25, 51, 52]. This method also named optimistic consistency, that is, a reduced FPR with the highest consistency degree is derived from HFPRs. The optimistic consistency method reflected the highest consistency degree of HFPRs, but it cannot reflect the hesitancy of decision makers. It leads to substantial information loss. (2) Based on ordered FPRs derived from normalized HFPRs [14, 47, 48]. This method also named normalized consistency. The normalized consistency requires that any two HFEs have an equal number of elements, if two HFEs have an unequal number of elements, a normalized process is needed. Therefore, to develop a reasonable and efficiency normalized method seems important if we execute this method. (3) Based on all possible FPRs including in HFPRs [44, 45]. This method defines the concept of consistent HFPRs seems too restricted. It is difficult for decision makers to provide such pairwise judgment in the actual decision making process. (4) Based on the derived FPRs for each value in HFEs [17, 26]. Compared to (3), this method only used some possible FPRs. It requires a FPR for each value including in HFPRs, in view of this, this method defines the concept of consistent HFPRs also seems too restricted, and the calculation burden is heavy in the priority vector deriving process.

Since the concept of HFPRs was introduced, many approaches for group decision making with HFPRs have been developed. Generally speaking, these approaches can be divided into four categories: (1) deriving the priority weights from several HFPRs [43]. In this category, to derive the priority weights of alternatives, by constructing the programming models considering the properties of HFPRs is a common method [43]. Unfortunately, this process ignored the consistency checking and improving. (2) Consistency checking and improving process [44, 45]. The consistency of the individual HFPRs is vital to judge whether the individual preferences are reasonable and logical or not. To guarantee the logicality and rationality of HFPRs, two parts are including, the defining of the consistency index and improving the consistency level. (3) Consensus checking and improving process [16, 34]. The consensus of the group is used to measure the agreement among the decision makers’ opinions. Similar to category (2), there are also two parts, including the defining of the consensus index and improving the consensus level of the group. (4) Consistency and consensus checking and improving processes simultaneously [18, 33]. Since the consistency of individual HFPRs and the consensus among the group are two important indexes, some scholars develop group decision making approaches with HFPRs considering the consistency and consensus simultaneously.

Although many approaches for group decision making with HFPRs are developed, there are still several issues need to be address. For example, (1) previous normalized approaches for HFPRs may result in loss of information [52], rely on decision makers’ risk preferences [41], normalization process is artificial [39], and practical significance is unclear [13]. (2) The optimization model-based method for improving the consistency/consensus level need to adjust all original evaluation information, and the original preferences evaluation has been greatly damaged in the new derived HFPRs [31, 34]. (3) Interactive-based method for improving the consistency/consensus level ignores the minimization adjustment, and some may adjustment many times which spend too much time [33]. (4) The method of deriving the priority weights from several HFPRs [43], the priority weights does not follow consistent/acceptable consistent HFPRs that may lead to unreasonable rankings [25].

To eliminate above mention defects and consider the effective of HFEs, this paper further studies group decision making method with HFPRs. The primary contributions of this study are summarized as follows:

• 1. To overcome the shortcoming of previous normalized approaches of HFPRs, a new normalized method is developed to address the situation where the evaluation information with different number of elements. The advantageous of this method is it helps the decision makers provide a proper optimized parameter and takes the consistency of HFPRs into account. Moreover, the constructed model is a linear programming. This reduces the amount of calculation and assures the existence of the optimal solution.

• 2. To overcome the optimization model-based method and interactive-based method for improving the consistency/consensus level, two algorithms are designed respectively to derive an acceptable consistent HFPR and obtained the consensus level. The main characteristic of the design algorithms is that the values need to be revised are identified first, and then design the local adjustment process.

• 3. To overcome the method of deriving priority weights from several HFPRs. This paper develops a group decision making method considering the additive consistency and consensus checking and improving process simultaneously. This ensures the reasonable outcomes and considers the discordant opinions among experts.

The remainder of the paper is organized as follows. In section “Preliminaries”, basic concepts and operations related to HFSs, HFPRs and several representative approaches of NHFPRs are reviewed. In section “A new normalized method for HFPRs”, a new normalized method for HFPRs is presented, and the consistency checking and improving process of HFPRs is introduced. In section “A framework of MCDM procedure with HFPRs”, an algorithm to integrate a group of HFPRs is designed, the method of consensus measuring and reaching process is showed, the method of determining the weights of decision makers is introduced, and the framework of MCDM procedure with HFPRs is proposed. In section “An illustrative example”, the proposed method is illustrated by an example, and a comparative analysis is provided. Finally, conclusions are presented in section “Conclusion”.

Preliminaries

In this section, some basic knowledge on the definitions of HFSs, HFPRs and several representative approaches of NHFPRs are introduced.

HFSs and HFPRs

To express hesitant preference information, Torra and Narukawa [29] introduced an effective tool which named HFSs.

Definition 1

[29]. Let $X$ be a fixed set. Accordingly, an HFS $E$ on $X$ is defined in terms of a function $h_{E} \left( x \right)$ that when applied to $X$ returns a finite subset of [0, 1].

To be easily understood, Xia and Xu [35] expressed the HFSs as the following mathematical symbol:

$$ E = \left\{ { < x,h_{E} \left( x \right) > \left| {x \in X} \right.} \right\}, $$

(1)

where $h_{E} \left( x \right)$ is a set of values in [0, 1] representing the possible membership degrees of element $x$ in $X$ to $E$, and $h_{E} \left( x \right)$ is named hesitant fuzzy element (HFE) and brevity denoted as $h = \left\{ {\gamma^{s} \left| {s = 1,2, \ldots ,{\#} h} \right.} \right\}$, ${\#} h$ is the number of elements including in $h$.

With the effective of HFE, Xia and Xu [36] developed the concept of HFPRs on the basis of HFSs and FPRs.

Definition 2

[36]. Let $X = \left\{ {x_{1} ,x_{2} , \ldots ,x_{n} } \right\}$ be a fixed set, HFPRs on $X$ is represented by a matrix $H = \left( {h_{ij} } \right)_{n \times n} \subset X \times X$, where $h_{ij} = \left\{ {\gamma_{ij}^{s} \left| {s = 1,2, \ldots ,{\#} h_{ij} } \right.} \right\}$ is an HFE indicating the possible preference degrees of alternative $x_{i}$ is preferred to alternative $x_{j}$. For all $i,j \in N$, $h_{ij}$ should satisfy:

$$ \left\{ \begin{gathered} \gamma_{ij}^{s} + \gamma_{ji}^{{{\#} h_{ij} - s + 1}} = 1 \hfill \\ \gamma_{ij}^{s} \le \gamma_{ij}^{s + 1} \hfill \\ \gamma_{ii}^{{}} = 0.5 \hfill \\ {\#} h_{ij} = {\#} h_{ji} \hfill \\ \end{gathered} \right., $$

(2)

where $\gamma_{ij}^{s}$ refers to the $s$th smallest element in $h_{ij}$.

In group decision making problems with HFPRs, the decision group can provide all possible preferences represented by HFEs, so HFEs often have different number of elements. To develop the distance measures and the priority methods of HFPRs, a normalization process becomes necessary to make HFEs have the same number of elements. Zhang et al. [47] developed the concept of additive consistent HFPRs based on normalized HFEs (NHFEs).

Definition 3

[47]. Let $H = \left( {h_{ij} } \right)_{n \times n}$ be an HFPR and $\mathop H\limits^{\_} = \left( \overline{h}_{i\!j} \right)_{n \times n}$ be its normalized HFPR (NHFPR), where $\overline{h}_{ij} = \left\{ {\overline{\gamma }_{ij}^{s} \left| {s = 1,2, \ldots ,{\#} \overline{h}_{ij} } \right.} \right\}$. For all $i,j \in N$, $i \ne j \ne k$, if $\mathop H\limits^{\_}$ satisfies the following condition:

$$ \overline{\gamma }_{ij}^{s} = \overline{\gamma }_{ik}^{s} + \overline{\gamma }_{kj}^{s} - 0.5,\;s = 1,2, \ldots ,{\#} \overline{h}_{ij} , $$

(3)

then $\mathop H\limits^{\_}$ is called additive consistent HFPR.

Summing both sides of Eq. (3) for all $k$, we have:

$$ \overline{\gamma }_{ij}^{s} = \frac{1}{n}\sum\limits_{k = 1}^{n} {\left( {\overline{\gamma }_{ik}^{s} + \overline{\gamma }_{kj}^{s} } \right)} - 0.5,\;s = 1,2, \ldots ,{\#} \overline{h}_{ij} . $$

(4)

If $\mathop H\limits^{\_}$ is consistency, then Eq. (4) is hold. Furthermore, the additive consistency index of $\mathop H\limits^{\_}$ is developed.

Definition 4

[47]. Let $H = \left( {h_{ij} } \right)_{n \times n} \subset X \times X$ be an HFPR and $\mathop H\limits^{\_} = \left( \overline{h}_{i\!j} \right)_{n \times n}$ be its NHFPR, where $\overline{h}_{ij} = \left\{ {\overline{\gamma }_{ij}^{s} \left| {s = 1,2, \ldots ,{\#} \overline{h}_{ij} } \right.} \right\}$. Then, the additive consistency index of $H$ is defined as follows:

$$ CI\left( H \right) = \frac{2}{{n\left( {n - 1} \right){\#} \overline{h}_{ij} }}\sum\limits_{i = 1}^{n - 1} {\sum\limits_{j = i + 1}^{n} {\sum\limits_{s = 1}^{{{\#} \overline{ h}_{ij} }} {\left| {\overline{\gamma }_{ij}^{s} + 0.5 - \frac{1}{n}\sum\limits_{k = 1}^{n} {\left( {\overline{\gamma }_{ik}^{s} + \overline{\gamma }_{kj}^{s} } \right)} } \right|} } } . $$

(5)

Several representative approaches of NHFPRs

This section introduces several representative approaches of NHFPRs, mainly including decision makers’ risk preferences-based method [41], optimization model-based method [52], consistency-based method [39], and least common multiple expansion-based method [13].

Decision makers’ risk preferences-based method

If two HFEs have different numbers of elements, to extend the shorter one, Xu and Xia [41] asserted that the best way is to add the same value several times. That is, the shorter one can be extended by adding any value in it. The selection of this value mainly depends on the decision makers’ risk preferences. Optimists anticipate desirable outcomes and may add the maximum value, while pessimists expect unfavorable outcomes and may add the minimum value. For example, let $h_{1} = \left\{ {0.2,0.3} \right\}$ and $h_{2} = \left\{ {0.2,0.3,0.4} \right\}$ be any two HFEs. Since ${\#} h_{1} < {\#} h_{2}$, to operate correctly, we should add some values to $h_{1}$ until it has the same length of $h_{2}$. The optimists may extend $h_{1}$ as $h_{1}^{o} = \left\{ {0.2,0.3,0.3} \right\}$ and the pessimists may extend it as $h_{1}^{p} = \left\{ {0.2,0.2,0.3} \right\}$. The advantageous of this method is it simple and easy to operate, and it takes into account the decision makers’ risk preferences. However, it can be easily found that the results may be different if we extend the shorter one by adding different values, and the decision makers’ risk preferences may directly influence the final decision. In other words, the shortcoming of this method is the normalized results seem subjective.

Optimization model-based method

To develop the normalized method, Zhu et al. [52] first introduced the add values with an optimized parameter, and then constructed an optimization model to determine the parameter value. The detailed process is showed in the following section.

Definition 5

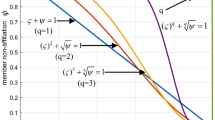
[52]. Let $h = \left\{ {\gamma_{i} \left| {i = 1,2, \ldots ,{\#} h} \right.} \right\}$ be an HFE, $\gamma^{ + }$ and $\gamma^{ - }$ be the maximum and minimum membership degrees in $h$, respectively, and $\varsigma$, $0 \le \varsigma \le 1$ be an optimized parameter. Thereafter, $\gamma = \varsigma \gamma^{ - } + \left( {1 - \varsigma } \right)\gamma^{ + }$ is called an added membership degree.

The parameter $\varsigma$ is the risk attitude of decision makers, whose different values reflect different risk preferences. If $\varsigma = 0$, then $\gamma = \gamma^{ + }$, which indicates that decision maker is risk-seeking; If $\varsigma = 1$, then $\gamma = \gamma^{ - }$, which indicates that decision maker is risk-averse; and if $\varsigma = 0.5$, then $\gamma = \frac{{\gamma^{ - } + \gamma^{ + } }}{2}$, which indicates that decision maker is risk-neutral. It can be easily found that when parameter $\varsigma$ set different values, the different normalized results will be derived, this is consistent with Xu and Xia [41]’s method. To obtain the highest consistency level and objective normalized result, Zhu et al. [52] developed an optimization model to determine the parameter $\varsigma$.

$$ \begin{gathered} \min \quad d\left( {H,\overline{H}} \right)\, = \sqrt {\frac{2}{{n\left( {n - 1} \right)}}\sum\limits_{j = 1}^{n - 1} {\sum\limits_{i = j + 1}^{n} {d\left( {h_{ij}^{N} ,\overline{h}_{ij}^{N} } \right)^{2} } } } , \hfill \\ {\text{s.t.}}\quad 0 \le \varsigma \le 1 \hfill \\ \end{gathered} $$

(6)

where $\left( {h_{ij}^{N} } \right)_{n \times n}$ is a NHFPR and $\left( {\overline{h}_{ij}^{N} } \right)_{n \times n}$ is its corresponding consistent HFPR both with parameter $\varsigma$. The advantageous of this method is it helps the decision makers provide a proper optimized parameter. However, it can be easily seen that Eq. (6) is a nonlinear programming model, it will increase the computational complexity and the model cannot ensure that a global optimal solution is obtained [3].

Consistency-based method

Xu et al. [39] believed that the added values should be based on some rules, and then introduced a consistency-based method. The procedure includes two steps: (1) establishes the elements that can be estimated in each iteration process. (2) estimation of a given unknown value, which calculating the average of all the estimate values using all the possible intermediate alternative using Eq. (8) presented in Xu et al. [39] as the final estimated value. The advantageous of this method is it can avoid adding the values randomly and consider the consistency of HFPRs. Furthermore, the proposed method can be used to normalize the incomplete HFPRs. However, this method claims that the elements are added after the existing values, this normalization process is artificial and the normalization results are not convincing.

Least common multiple expansion-method

To develop the NHFEs, Liu and Wang [13] proposed the concept of multiple HFSs based on the Least common multiple expansion principle.

Definition 6

[13]. Let $H = \left\{ {H_{1} ,H_{2} , \ldots ,H_{k} } \right\}$ be $k$ HFSs on $X = \left\{ {x_{1} ,x_{2} , \ldots ,x_{n} } \right\}$, for any $x_{i} \in X$, the possible membership of $x_{i} \in X$ to the set $H_{j}$ can be given as $H_{j} = \left\{ {h_{j}^{1} \left( {x_{i} } \right),h_{j}^{2} \left( {x_{i} } \right), \ldots ,h_{j}^{{{\#} H_{j} }} \left( {x_{i} } \right)} \right\}$, where ${\#} H_{j}$ represents the number of elements in $H_{j}$. Let $L\left( {H_{j} } \right)_{j = 1}^{k}$ be the least common multiple of ${\#} H_{1}$, ${\#} H_{2}$,$\ldots$, ${\#} H_{j}$ and $\mathop H\limits^{\_\_} = \left\{ {\overline {H}_{1} ,\overline {H}_{2} , \ldots ,\overline {H}_{k} } \right\}$ be the multiple HFSs. Then the HFE $h_{\overline{H}_{j} } \left( {x_{i} } \right)$ including in $\overline{H}_{j}$ can be defined as:

$$ h_{{\overline{H}_{j} }} \left( {x_{i} } \right) = \left\{ {\mathop {h_{j}^{1} \left( {x_{i} } \right), \ldots ,h_{j}^{1} \left( {x_{i} } \right)}\limits_{\begin{subarray}{l} \_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\\ \quad \quad \quad \quad n\left( {h_{j}^{1} \left( {x_{i} } \right)} \right) \end{subarray} } ,\mathop {h_{j}^{2} \left( {x_{i} } \right), \ldots ,h_{j}^{2} \left( {x_{i} } \right)}\limits_{\begin{subarray}{l} \_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\\ \quad \quad \quad \quad n\left( {h_{j}^{2} \left( {x_{i} } \right)} \right) \end{subarray} } , \ldots ,\mathop {h_{j}^{{{\#} H_{j} }} \left( {x_{i} } \right), \ldots ,h_{j}^{{{\#} H_{j} }} \left( {x_{i} } \right)}\limits_{\begin{subarray}{l} \_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\\ \quad \quad \quad \quad n\left( {h_{j}^{{{\#} H_{j} }} \left( {x_{i} } \right)} \right) \end{subarray} } } \right\}, $$

(7)

where $n\left( {h_{j}^{l} \left( {x_{i} } \right)} \right)$ is the number of $h_{{\overline{H}_{j} }} \left( {x_{i} } \right)$, which is determined by $\frac{{L\left( {H_{j} } \right)_{j = 1}^{k} }}{{L\left( {H_{j} } \right)}}$.

The advantageous of least common multiple expansion-method is it showed the added elements are included in the original HFEs which surmised the decision makers’ original information. However, this method does not combined with the background of the decision making problems, and its practical significance is unclear. Furthermore, there are too many multiple elements including in the NHFEs, the amount of calculation is increased when conducts this method in MCDM process.

To better demonstrate the above mention methods, an example presented in Zhu et al. [52] is showed as follows.

Example 1

[52]. Let $H$\ be an HFPR, which is showed as follows:

$$ H = \left( {\begin{array}{*{20}l} {\left\{ {0.5} \right\}} &\quad {\left\{ {0.2,0.3} \right\}} &\quad {\left\{ {0.4,0.5,0.6} \right\}} &\quad {\left\{ {0.8,0.9} \right\}} \\ {\left\{ {0.7,0.8} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.3,0.4} \right\}} \\ {\left\{ {0.4,0.5,0.6} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.5,0.6,0.7} \right\}} \\ {\left\{ {0.1,0.2} \right\}} &\quad {\left\{ {0.6,0.7} \right\}} &\quad {\left\{ {0.3,0.4,0.5} \right\}} &\quad {\left\{ {0.5} \right\}} \\ \end{array} } \right). $$

Decision makers’ risk preferences-based method

Suppose decision makers with optimistic preference, the maximum values are added in the shorter HFEs. Therefore, the NHFPR $H_{1}^{o}$ is:

$$ H_{1}^{o} = \left( {\begin{array}{*{20}l} {\left\{ {0.5} \right\}} &\quad {\left\{ {0.2,0.3,0.3} \right\}} &\quad {\left\{ {0.4,0.5,0.6} \right\}} &\quad {\left\{ {0.8,0.9,0.9} \right\}} \\ {\left\{ {0.7,0.8,0.8} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.5,0.5,0.5} \right\}} &\quad {\left\{ {0.3,0.4,0.4} \right\}} \\ {\left\{ {0.4,0.5,0.6} \right\}} &\quad {\left\{ {0.5,0.5,0.5} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.5,0.6,0.7} \right\}} \\ {\left\{ {0.1,0.2,0.2} \right\}} &\quad {\left\{ {0.6,0.7,0.7} \right\}} &\quad {\left\{ {0.3,0.4,0.5} \right\}} &\quad {\left\{ {0.5} \right\}} \\ \end{array} } \right). $$

Suppose decision makers with pessimistic preference, the minimum values are added in the shorter HFEs. Therefore, the NHFPR $H_{1}^{p}$ is:

$$ H_{1}^{p} = \left( {\begin{array}{*{20}l} {\left\{ {0.5} \right\}} &\quad {\left\{ {0.2,0.2,0.3} \right\}} &\quad {\left\{ {0.4,0.5,0.6} \right\}} &\quad {\left\{ {0.8,0.8,0.9} \right\}} \\ {\left\{ {0.7,0.7,0.8} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.5,0.5,0.5} \right\}} &\quad {\left\{ {0.3,0.3,0.4} \right\}} \\ {\left\{ {0.4,0.5,0.6} \right\}} &\quad {\left\{ {0.5,0.5,0.5} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.5,0.6,0.7} \right\}} \\ {\left\{ {0.1,0.1,0.2} \right\}} &\quad {\left\{ {0.6,0.6,0.7} \right\}} &\quad {\left\{ {0.3,0.4,0.5} \right\}} &\quad {\left\{ {0.5} \right\}} \\ \end{array} } \right). $$

Optimization model-based method

According to Algorithm 1 presented in Zhu et al. [52], the optimal parameter $\varsigma = 1$ is derived, the normalized HFPR is showed as follows (for the detailed calculation process, the readers turn to Zhu et al. [52]:

$$ H_{2} = \left( {\begin{array}{*{20}l} {\left\{ {0.5} \right\}} &\quad {\left\{ {0.2,0.2,0.3} \right\}} &\quad {\left\{ {0.4,0.5,0.6} \right\}} &\quad {\left\{ {0.8,0.8,0.9} \right\}} \\ {\left\{ {0.7,0.8,0.8} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.5,0.5,0.5} \right\}} &\quad {\left\{ {0.3,0.3,0.4} \right\}} \\ {\left\{ {0.4,0.5,0.6} \right\}} &\quad {\left\{ {0.5,0.5,0.5} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.5,0.6,0.7} \right\}} \\ {\left\{ {0.1,0.2,0.2} \right\}} &\quad {\left\{ {0.6,0.7,0.7} \right\}} &\quad {\left\{ {0.3,0.4,0.5} \right\}} &\quad {\left\{ {0.5} \right\}} \\ \end{array} } \right). $$

Consistency-based method

First, $H$ is transformed into three FPRs:

$H_{3}^{1} = \left( {\begin{array}{*{20}l} {\left\{ {0.5} \right\}} &\quad {\left\{ {0.2} \right\}} &\quad {\left\{ {0.4} \right\}} &\quad {\left\{ {0.8} \right\}} \\ {\left\{ {0.8} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.3} \right\}} \\ {\left\{ {0.6} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.5} \right\}} \\ {\left\{ {0.2} \right\}} &\quad {\left\{ {0.7} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.5} \right\}} \\ \end{array} } \right),$ $H_{3}^{2} = \left( {\begin{array}{*{20}l} {\left\{ {0.5} \right\}} &\quad {\left\{ {0.3} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.9} \right\}} \\ {\left\{ {0.7} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ x \right\}} &\quad {\left\{ {0.4} \right\}} \\ {\left\{ {0.5} \right\}} &\quad {\left\{ x \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.6} \right\}} \\ {\left\{ {0.1} \right\}} &\quad {\left\{ {0.6} \right\}} &\quad {\left\{ {0.4} \right\}} &\quad {\left\{ {0.5} \right\}} \\ \end{array} } \right)$ and $H_{3}^{3} = \left( {\begin{array}{*{20}l} {\left\{ {0.5} \right\}} &\quad {\left\{ x \right\}} &\quad {\left\{ {0.6} \right\}} &\quad {\left\{ x \right\}} \\ {\left\{ x \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ x \right\}} &\quad {\left\{ x \right\}} \\ {\left\{ {0.4} \right\}} &\quad {\left\{ x \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.7} \right\}} \\ {\left\{ x \right\}} &\quad {\left\{ x \right\}} &\quad {\left\{ {0.3} \right\}} &\quad {\left\{ {0.5} \right\}} \\ \end{array} } \right).$

Second, since $H_{3}^{2}$ and $H_{3}^{3}$ are incomplete FPRs. For $H_{3}^{2}$, according to Eq. (8) presented in Xu et al. [39], the complete FPRs is obtained as:

$$ H_{3}^{2} = \left( {\begin{array}{*{20}l} {\left\{ {0.5} \right\}} &\quad {\left\{ {0.3} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.9} \right\}} \\ {\left\{ {0.7} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.4} \right\}} \\ {\left\{ {0.5} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.6} \right\}} \\ {\left\{ {0.1} \right\}} &\quad {\left\{ {0.6} \right\}} &\quad {\left\{ {0.4} \right\}} &\quad {\left\{ {0.5} \right\}} \\ \end{array} } \right). $$

For $H_{3}^{3}$, since it is not an acceptable incomplete FPRs, to obtain an acceptable incomplete FPRs which each row and column has at least one known element, it is necessary to add some elements according to Definition 4 presented in Xu et al. [39]. For instance:

$$ H_{3}^{3} = \left( {\begin{array}{*{20}l} {\left\{ {0.5} \right\}} &\quad {\left\{ x \right\}} &\quad {\left\{ {0.6} \right\}} &\quad {\left\{ x \right\}} \\ {\left\{ x \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.6} \right\}} &\quad {\left\{ x \right\}} \\ {\left\{ {0.4} \right\}} &\quad {\left\{ {0.4} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.7} \right\}} \\ {\left\{ x \right\}} &\quad {\left\{ x \right\}} &\quad {\left\{ {0.3} \right\}} &\quad {\left\{ {0.5} \right\}} \\ \end{array} } \right). $$

Then, according to Eq. (8) presented in Xu et al. [39], the complete FPRs is obtained as:

$$ H_{3}^{3} = \left( {\begin{array}{*{20}l} {\left\{ {0.5} \right\}} &\quad {\left\{ {0.43} \right\}} &\quad {\left\{ {0.6} \right\}} &\quad {\left\{ {0.87} \right\}} \\ {\left\{ {0.57} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.6} \right\}} &\quad {\left\{ {0.99} \right\}} \\ {\left\{ {0.4} \right\}} &\quad {\left\{ {0.4} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.7} \right\}} \\ {\left\{ {0.13} \right\}} &\quad {\left\{ {0.01} \right\}} &\quad {\left\{ {0.3} \right\}} &\quad {\left\{ {0.5} \right\}} \\ \end{array} } \right). $$

Therefore, the NHFPR is:

$$ H_{3}^{{}} = \left( {\begin{array}{*{20}l} {\left\{ {0.5} \right\}} &\quad {\left\{ {0.2,0.3,0.43} \right\}} &\quad {\left\{ {0.4,0.5,0.6} \right\}} &\quad {\left\{ {0.8,0.9,0.87} \right\}} \\ {\left\{ {0.57,0.7,0.8} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.5,0.5,0.6} \right\}} &\quad {\left\{ {0.3,0.4,0.99} \right\}} \\ {\left\{ {0.4,0.5,0.6} \right\}} &\quad {\left\{ {0.4,0.5,0.5} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.5,0.6,0.7} \right\}} \\ {\left\{ {0.13,0.1,0.2} \right\}} &\quad {\left\{ {0.01,0.6,0.7} \right\}} &\quad {\left\{ {0.3,0.4,0.5} \right\}} &\quad {\left\{ {0.5} \right\}} \\ \end{array} } \right). $$

Least common multiple expansion-method

First, it can be easily found that the least common multiple of $H$ are six, then the NHFPR is determined according to Eq. (7) as follows:

$$ \begin{gathered} H_{4} = \hfill \\ \left( {\begin{array}{*{20}l} {\left\{ {0.5} \right\}} &\quad {\left\{ {0.2,0.2,0.2,0.3,0.3,0.3} \right\}} &\quad {\left\{ {0.4,0.4,0.5,0.5,0.6,0.6} \right\}} &\quad {\left\{ {0.8,0.8,0.8,0.9,0.9,0.9} \right\}} \\ {\left\{ {0.7,0.7,0.7,0.8,0.8,0.8} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.5,0.5,0.5,0.5,0.5,0.5} \right\}} &\quad {\left\{ {0.3,0.3,0.3,0.4,0.4,0.4} \right\}} \\ {\left\{ {0.4,0.4,0.5,0.5,0.6,0.6} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.5,0.5,0.5,0.5,0.5,0.5} \right\}} &\quad {\left\{ {0.5,0.5,0.6,0.6,0.7,0.7} \right\}} \\ {\left\{ {0.1,0.1,0.1,0.2,0.2,0.2} \right\}} &\quad {\left\{ {0.6,0.6,0.6,0.7,0.7,0.7} \right\}} &\quad {\left\{ {0.3,0.3,0.4,0.4,0.5,0.5} \right\}} &\quad {\left\{ {0.5} \right\}} \\ \end{array} } \right) \hfill \\ \end{gathered} $$

A new normalized method for HFPRs

In this section, we first introduce a new normalized method for HFPRs, and then the method of consistency checking is proposed. For the unacceptable HFPRs, an algorithm is presented for improving their consistency.

A new normalized method for HFPRs

To further consider optimization model-based method [52], the advantageous of it is helps the decision makers provide a proper optimized parameter. Furthermore, it takes into account the consistency of HFPRs. Unfortunately, the optimization model has a little complicated, and the model cannot derive a global optimal solution sometimes. To overcome these shortcomings, and considering the additive consistent HFPRs, a new normalized method for HFPRs is introduced in the following section. Let $H = \left( {h_{ij} } \right)_{n \times n}$ be an arbitrary HFPR and $\overline{H} = \left( {\overline{h}_{ij} } \right)_{n \times n}$, $\overline{h}_{ij} = \left\{ {\overline{\gamma }_{ij}^{s} \left| {s = 1,2, \ldots ,{\#} \overline{h}_{ij} } \right.} \right\}$ be its NHFPR with parameter $\varsigma$ derived from Definition 5. To derived the optimal parameter $\varsigma$, the optimization model is constructed as follows.

$$ \begin{aligned} &\min \quad z = \frac{2}{{n\left( {n - 1} \right){\#} \overline{h}_{ij} }}\\ &\quad \sum\nolimits_{i = 1}^{n - 1} {\sum\nolimits_{j = i + 1}^{n} {\sum\nolimits_{s = 1}^{{{\#} \left( \overline{h}_{i\!j} \right)_{n \times n} }} {\left| {\overline{\gamma }_{ij}^{s} + 0.5 - \frac{1}{n}\sum\nolimits_{k = 1}^{n} {\left( {\overline{\gamma }_{ik}^{s} + \overline{\gamma }_{kj}^{s} } \right)} } \right|} } } . \hfill \\ &\;{\text{s.t.}}\quad 0 \le \varsigma \le 1 \hfill \\ \end{aligned} $$

(8)

It can be been easily seen that Eq. (8) is an absolute value programming model, and there is only one constraint in the model, $\varsigma$ is the decision variable that needs to be determined. To simplify the objective function presents in (8), the following symbols are used. Let $\theta_{ij}^{s} = \overline{\gamma }_{ij}^{s} + 0.5 - \frac{1}{n}\sum\nolimits_{k = 1}^{n} {\left( {\overline{\gamma }_{ik}^{s} + \overline{\gamma }_{kj}^{s} } \right)}$ and $\vartheta_{ij}^{s} = \left| {\theta_{ij}^{s} } \right|$. Moreover, $\vartheta_{ij}^{s} = \left| {\theta_{ij}^{s} } \right|$ is equivalent to $\theta_{ij}^{s} \le \vartheta_{ij}^{s}$ and $- \theta_{ij}^{s} \le \vartheta_{ij}^{s}$, and the objective function is transformed into: $\min \quad z = \frac{2}{{n\left( {n - 1} \right){\#} \overline{h}_{ij} }}\sum\nolimits_{i = 1}^{n - 1} {\sum\nolimits_{j = i + 1}^{n} {\sum\nolimits_{s = 1}^{{{\#} \overline{h}_{ij} }} {\vartheta_{ij}^{s} } } }$. Furthermore, Eq. (8) can be equivalently transformed into the following programming model:

$$ \begin{gathered} \min \quad z = \frac{2}{{n\left( {n - 1} \right){\#} \overline{h}_{ij} }}\sum\limits_{i = 1}^{n - 1} {\sum\limits_{j = i + 1}^{n} {\sum\limits_{s = 1}^{{{\#} \overline{h}_{ij} }} {\vartheta_{ij}^{s} } } } \hfill \\ \;{\text{s.t.}}\quad \left\{ \begin{gathered} \overline{\gamma }_{ij}^{s} + 0.5 - \frac{1}{n}\sum\limits_{k = 1}^{n} {\left( {\overline{\gamma }_{ik}^{s} + \overline{\gamma }_{kj}^{s} } \right)} \le \vartheta_{ij}^{s} \hfill \\ - \overline{\gamma }_{ij}^{s} - 0.5 + \frac{1}{n}\sum\limits_{k = 1}^{n} {\left( {\overline{\gamma }_{ik}^{s} + \overline{\gamma }_{kj}^{s} } \right)} \le \vartheta_{ij}^{s} \hfill \\ i,j = 1,2, \ldots ,n;\quad i < j \hfill \\ s = 1,2, \ldots ,{\#} \overline{h}_{ij} ;\quad 0 \le \varsigma \le 1 \hfill \\ \end{gathered} \right.. \hfill \\ \end{gathered} $$

(9)

In Eq. (9), $\varsigma$ is the decision variable that including in the values $\overline{\gamma }_{ij}^{s}$, $i,j = 1,2, \ldots ,n;\;i < j$ and $s = 1,2, \ldots ,{\#} \overline{h}_{ij}$, and there are $\frac{{n\left( {n - 1} \right){\#} \overline{h}_{ij} }}{2}$ constraints in the model. It can be easily seen that Eq. (9) is a linear programming model. The optimal solution of it can be easily obtained by utilizing the programming software, such as LINGO, MATLAB and CPLEX, and so on.

Based on the above programming model, the following algorithm is designed to obtain the NHFPR which considering the additive consistency.

Algorithm 1

Input: An HFPR $H = \left( {h_{ij} } \right)_{n \times n}$.

Output: The optimal parameter $\varsigma$ and NHFPR $\overline{H} = \left( {\overline{h}_{ij} } \right)_{n \times n}$.

Step 1: According to Definition 5, its NHFPR is derived, denote as $\overline{H} = \left( {\overline{h}_{ij} } \right)_{n \times n}$, $\overline{h}_{ij} = \left\{ {\overline{\gamma }_{ij}^{s} \left| {s = 1,2, \ldots ,{\#} \overline{h}_{ij} } \right.} \right\}$.

Step 2: The additive consistent NHFPR is obtained according to Eq. (4).

Step 3: According to Eq. (9), the optimal parameter $\varsigma$ is derived.

Step 4: Return the value $\varsigma$ to $\overline{H}$, the NHFPR is obtained.

Step 5: End.

Example 2. The HFPR is the same as those given in Example 1.

Step 1: According to Definition 5, the NHFPR with optimal parameter $\varsigma$ is obtained as follows:

$$ \overline{H} = \left( {\begin{array}{*{20}l} {\left\{ {0.5} \right\}} &\quad {\left\{ {0.2,0.3 - 0.1\varsigma ,0.3} \right\}} &\quad {\left\{ {0.4,0.5,0.6} \right\}} &\quad {\left\{ {0.8,0.9 - 0.1\varsigma ,0.9} \right\}} \\ {\left\{ {0.7,0.7 + 0.1\varsigma ,0.8} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.5,0.5,0.5} \right\}} &\quad {\left\{ {0.3,0.4 - 0.1\varsigma ,0.4} \right\}} \\ {\left\{ {0.4,0.5,0.6} \right\}} &\quad {\left\{ {0.5,0.5,0.5} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.5,0.6,0.7} \right\}} \\ {\left\{ {0.1,0.1 + 0.1\varsigma ,0.2} \right\}} &\quad {\left\{ {0.6,0.6 + 0.1\varsigma ,0.7} \right\}} &\quad {\left\{ {0.3,0.4,0.5} \right\}} &\quad {\left\{ {0.5} \right\}} \\ \end{array} } \right). $$

Step 2: Based on Eq. (4), the additive consistent NHFPR is obtained as follows:

$$ \overline{H}^{N} = \left( {\begin{array}{*{20}l} {\left\{ {0.5} \right\}} &\quad {\left\{ {0.65,0.75,0.85} \right\}} &\quad {\left\{ {0.4,0.55 - 0.1\varsigma ,0.6} \right\}} &\quad {\left\{ {0.2,0.4 - 0.1\varsigma ,0.5} \right\}} \\ {\left\{ {0.15,0.25,0.35} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.35,0.5,0.65} \right\}} &\quad {\left\{ {0.75,0.85,0.95} \right\}} \\ {\left\{ {0.4,0.45 + 0.1\varsigma ,0.6} \right\}} &\quad {\left\{ {0.35,0.5,0.65} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.5,0.65 - 0.1\varsigma ,0.7} \right\}} \\ {\left\{ {0.5,0.6 + 0.1\varsigma ,0.8} \right\}} &\quad {\left\{ {0.05,0.15,0.25} \right\}} &\quad {\left\{ {0.3,0.35 + 0.1\varsigma ,0.5} \right\}} &\quad {\left\{ {0.5} \right\}} \\ \end{array} } \right). $$

Step 3: According to Eq. (9), the programming model is constructed as follows:

$$ \begin{gathered} \min \quad z = \frac{1}{18}\left( {\vartheta_{12}^{1} + \vartheta_{12}^{2} + \vartheta_{12}^{3} + \vartheta_{13}^{1} + \vartheta_{13}^{2} + \vartheta_{13}^{3} + \vartheta_{14}^{1} + \vartheta_{14}^{2} + \vartheta_{14}^{3} + \vartheta_{23}^{1} + \vartheta_{23}^{2} + \vartheta_{23}^{3} + \vartheta_{24}^{1} + \vartheta_{24}^{2} + \vartheta_{24}^{3} + \vartheta_{34}^{1} + \vartheta_{34}^{2} + \vartheta_{34}^{3} } \right) \hfill \\ \;{\text{s.t.}}\quad \left\{ \begin{gathered} \theta_{12}^{1} = 0.2 - 0.65;\quad \theta_{12}^{2} = 0.3 - 0.1\varsigma - 0.75;\quad \theta_{12}^{3} = 0.3 - 0.85; \hfill \\ \theta_{13}^{1} = 0.4 - 0.4;\quad \theta_{13}^{2} = 0.5 + 0.1\varsigma - 0.55;\quad \theta_{13}^{3} = 0.6 - 0.6; \hfill \\ \theta_{14}^{1} = 0.8 - 0.2;\quad \theta_{14}^{2} = 0.9 - 0.1\varsigma - 0.4 + 0.1\varsigma ;\quad \theta_{14}^{3} = 0.9 - 0.5; \hfill \\ \theta_{23}^{1} = 0.5 - 0.35;\quad \theta_{23}^{2} = 0.5 - 0.5;\quad \theta_{23}^{3} = 0.5 - 0.65; \hfill \\ \theta_{24}^{1} = 0.3 - 0.75;\quad \theta_{24}^{2} = 0.4 - 0.1\varsigma - 0.85;\quad \theta_{24}^{3} = 0.4 - 0.95; \hfill \\ \theta_{34}^{1} = 0.5 - 0.5;\quad \theta_{34}^{2} = 0.6 - 0.65 + 0.1\varsigma ;\quad \theta_{34}^{3} = 0.7 - 0.7; \hfill \\ \theta_{ij}^{s} \le \vartheta_{ij}^{s} ;\quad - \theta_{ij}^{s} \le \vartheta_{ij}^{s} ;\quad i,j = 1,2, \ldots ,4;\quad i < j;\quad s = 1,2,3 \hfill \\ 0 \le \varsigma \le 1 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} $$

Solving the above model by LINGO, we have the optimal parameter $\varsigma = 0.5$.

Step 4: Return the value $\varsigma = 0.5$ to $\mathop H\limits^{\_}$, the NHFPR is obtained as follows:

$$ \overline{H} = \left( {\begin{array}{*{20}l} {\left\{ {0.5} \right\}} &\quad {\left\{ {0.2,0.25,0.3} \right\}} &\quad {\left\{ {0.4,0.5,0.6} \right\}} &\quad {\left\{ {0.8,0.85,0.9} \right\}} \\ {\left\{ {0.7,0.75,0.8} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.5,0.5,0.5} \right\}} &\quad {\left\{ {0.3,0.35,0.4} \right\}} \\ {\left\{ {0.4,0.5,0.6} \right\}} &\quad {\left\{ {0.5,0.5,0.5} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.5,0.6,0.7} \right\}} \\ {\left\{ {0.1,0.15,0.2} \right\}} &\quad {\left\{ {0.6,0.65,0.7} \right\}} &\quad {\left\{ {0.3,0.4,0.5} \right\}} &\quad {\left\{ {0.5} \right\}} \\ \end{array} } \right) $$

Remark 1

Although the proposed method is similar to Zhu et al. [52]’s method, there are different in the type of model. It can be easily found that different normalization results are obtained from these two methods in the same example. This also confirms the effectiveness of the proposed method.

The consistency checking and improving process

Consistency of HFPRs is related to rationality. By comparison, inconsistent HFPRs often lead to misleading solutions. Therefore, developing some approaches to obtain the expected consistency level is necessary. The consistency level of NHFPRs is as small as possible when conducts algorithm 1. Unfortunately, the consistency level is still not met the requirements sometimes. In this case, the consistency checking and improving processes become necessary.

For the consistency checking of HFPRs, some scholars insist on calculating the distance between HFPRs and its consistent HFPRs [52], while some utilizing the consistency properties of HFPRs [31]. For the previous one, the construction of consistent HFPRs use their consistency properties, based on this, there is not much difference between these two methods. In this study, we use Eq. (5) to calculate the consistency level of HFPRs.

Remark 2

Although some scholars also asserted used Eq. (5) to calculate the consistency index of HFPRs, it can be easily seen that it will obtain different values when we derive different NHFPRs.

For the consistency improving of HFPRs, the existing research can be divided into two categories. One is the optimization model-based method [18], the other is iteration-based method [33]. The optimization model-based method obtains the new HFPRs by constructing the programming model, which takes into account the requirements of consistency level. This method is intuitive and easy to understand. Furthermore, it is easy to obtain the new HFPRs with the help of computer software. Unfortunately, the original evaluation information has been greatly damaged in the new derived HFPRs. The iteration-based method obtains the revised HFPRs first identifies the value that needs to be adjusted, and then obtains the adjusted value according to the iterative algorithm. This method can ensure the revised HFPRs retain the original evaluation information as much as possible, but the iterative process is relatively complex, which will consume a lot of time. To recognize these, it is necessary to develop a new consistency improving algorithm that both take into account the advantages of above approaches.

To this end, we first utilize the identification rule to find out the position of the element that needs to be adjusted. Then, an optimization model is constructed to obtain the optimal adjustment parameters.

Stage 1: Identification of the inconsistent evaluation elements.

The set of evaluation elements by HFPRs that greater than the threshold value of accept consistency level is identified as follows:

Step 1: Identify the decision makers whose consistency indexes at the HFPRs are greater than the threshold value $\alpha$ which provide in advance:

$$ {\text{DCI}} = \left\{ {\left. t \right|{\text{CI}}^{t} > \alpha } \right\}. $$

Step 2: Identify the alternatives under the $s$th evaluation values that need to be adjusted which satisfying the condition in Step 1. That is, the HFPRs’ consistency indexes at the alternative under the $s$th evaluation values are greater than the threshold value $\alpha$:

$$ {\text{ACI}} = \left\{ {\left. {\left( {t,i^{s} } \right)} \right|t \in {\text{DCI}} \wedge {\text{CI}}_{{i^{s} }}^{t} > \alpha \wedge s = 1,2, \ldots ,{\#} \overline{h}_{ij}^{t} } \right\}. $$

Step 3: Identify the evaluation elements that need to be adjusted for alternatives under the $s$th evaluation values satisfying the condition in Step 2. That is, the HFPRs’ consistency indexes at the $s$th evaluation values are greater than the threshold value $\alpha$:

$$ \begin{aligned} {\text{ECI}} &= \left\{ \left. {\left( {t,i^{s} ,j} \right)} \right|\left( {t,i^{s} } \right) \in {\text{ACI}} \wedge {\text{CI}}_{{i^{s} ,j}}^{t}\right.\\ &\qquad \left. > \alpha \wedge s = 1,2, \ldots ,{\#} \overline{h}_{ij}^{t} \wedge i \ne j \right\}.\end{aligned}$$

Stage 2: Derive the optimal adjustment parameter.

Let $H^{t} = \left( {h_{ij}^{t} } \right)_{n \times n}$ be an HFPR provided from decision makers $e^{t}$, and $\overline{H}^{t} = \left( {\overline{h}_{ij}^{t} } \right)_{n \times n}$, $\overline{h}_{ij}^{t} = \left\{ {\overline{\gamma }_{ij}^{s,t} \left| {s = 1,2, \ldots ,{\#} \overline{h}_{ij}^{t} } \right.} \right\}$ be its NHFPR, $\tau^{t} \in [0,1]$ is the adjustment parameter. If $\left( {t,i^{s} ,j} \right) \in \text{ECI}$, means the evaluation elements provided by the decision maker $e^{t}$ on alternative $a_{i}$ compare to alternative $a_{j}$ at the $s$th evaluation value needs to be adjusted. Then the adjusted elements $\tilde{\gamma }_{ij}^{s,t}$ can be represented as follows:

$$ \tilde{\gamma }_{ij}^{s,t} = \left( {1 - \tau^{t} } \right)\overline{\gamma }_{ij}^{s,t} + \tau^{t} \tilde{\gamma }_{ij}^{os,t} ,$$

(10)

where$\tilde{\gamma }_{ij}^{os,t}$ indicates its corresponding consistent value that is determined in Eq. (4), $\tau^{t}$ is the adjustment parameter that needs to be determined.

In Eq. (10), the adjustment parameter $\tau^{t} \in [0,1]$ indicates the damage degree of initial evaluation elements. In extreme cases, $\tau^{t} = 1$ means that initial evaluation elements have been completely replace with its corresponding consistent value, that is, the greatest extent of initial evaluation values are destroyed; and $\tau^{t} = 0$, indicates that the initial evaluation elements without any change. For the decision makers, it is expected that their evaluation values should be preserved to the largest degree. That is, the smaller the value $\tau^{t}$ is, the smaller the destroy degree. Then the following objective function can be constructed based on the minimum adjustment of initial evaluation values: $\min \quad z = \sum\nolimits_{{\left( {t,i^{s} ,j} \right) \in {\text{ECI}}}} {\left| {\tilde{\gamma }_{ij}^{s,t} - \overline{\gamma }_{ij}^{s,t} } \right|} = \tau^{t} \sum\nolimits_{{\left( {t,i^{s} ,j} \right) \in {\text{ECI}}}} {\left| {\overline{\gamma }_{ij}^{s,t} - \overline{\gamma }_{ij}^{os,t} } \right|}$. Furthermore, the optimal model is constructed as follows:

$$ \begin{gathered} \min \quad z = \tau ^{t} \sum\limits_{{\left( {t,i^{s} ,j} \right) \in \text{ECI}}} {\left| {\bar{\gamma }_{{ij}}^{{s,t}} - \bar{\gamma }_{{ij}}^{{os,t}} } \right|} \hfill \\ {\text{s.t.}}\;\left\{ \begin{gathered} \frac{2}{{n\left( {n - 1} \right){\#} \bar{h}_{{ij}}^{t} }}\sum\limits_{{i = 1}}^{{n - 1}} {\sum\limits_{{j = i + 1}}^{n} {\sum\limits_{{s = 1}}^{{{\#} \bar{h}_{{ij}}^{t} }} {\left| {\tilde{\gamma }_{{ij}}^{{s,t}} + 0.5 - \frac{1}{n}\sum\limits_{{k = 1}}^{n} {\left( {\tilde{\gamma }_{{ik}}^{{s,t}} + \tilde{\gamma }_{{kj}}^{{s,t}} } \right)} } \right|} } } \, \le \alpha \hfill \\ \tilde{\gamma }_{{ij}}^{{s,t}} = \left( {1 - \tau ^{t} } \right)\bar{\gamma }_{{ij}}^{{s,t}} + \tau ^{t} \bar{\gamma }_{{ij}}^{{os,t}} \quad \hfill \\ i,j = 1,2, \ldots ,n;\quad i < j;\quad s = 1,2, \ldots ,{\#} \bar{h}_{{ij}}^{t} \hfill \\ 0 \le \tau ^{t} \le 1 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} $$

(11)

In Eq. (11), the first constraint indicates that the consistency of HFPR meets the threshold value after multiple rounds of iterations, $\alpha$ is the threshold value which provides in advance and $\tau^{t}$ is the adjustment parameter that needs to be determined. To simplify the objective function presents in (11), the following symbols are used. Let $\pi_{ij}^{s,t} = \overline{\gamma }_{ij}^{s,t} - \overline{\gamma }_{ij}^{os,t}$ and $\sigma_{ij}^{s,t} = \left| {\pi_{ij}^{s,t} } \right|$. Moreover, $\sigma_{ij}^{s,t} = \left| {\pi_{ij}^{s,t} } \right|$ is equivalent to $\pi_{ij}^{s,t} \le \sigma_{ij}^{s,t}$ and $- \pi_{ij}^{s,t} \le \sigma_{ij}^{s,t}$, and the objective function is transformed into: $\min \quad z = \tau^{t} \sum\nolimits_{{\left( {t,i^{s} ,j} \right) \in \text{ECI}}} {\sigma_{ij}^{s,t} }$. In a similar way, the absolute value constraint in constraints condition can be further simplified. Let $\varsigma_{ij}^{s,t} = \tilde{\gamma }_{ij}^{s,t} + 0.5 - \frac{1}{n}\sum\nolimits_{k = 1}^{n} {\left( {\tilde{\gamma }_{ik}^{s,t} + \tilde{\gamma }_{kj}^{s,t} } \right)}$ and $\tau_{ij}^{s,t} = \left| {\varsigma_{ij}^{s,t} } \right|$. Moreover, $\tau_{ij}^{s,t} = \left| {\varsigma_{ij}^{s,t} } \right|$ is equivalent to $\varsigma_{ij}^{s,t} \le \tau_{ij}^{s,t}$ and $- \varsigma_{ij}^{s,t} \le \tau_{ij}^{s,t}$, and the absolute value constraint is transformed into: $\sum\nolimits_{i = 1}^{n - 1} {\sum\nolimits_{j = i + 1}^{n} {\sum\nolimits_{s = 1}^{{{\#} \overline{h}_{ij} }} {\tau_{ij}^{s,t} } } } \, \le \frac{{\alpha n\left( {n - 1} \right){\#} \overline{h}_{ij}^{t} }}{2}$. Furthermore, Eq. (11) can be equivalently transformed into the following programming model:

$$ \begin{gathered} \min \quad z = \tau^{t} \sum\limits_{{\left( {t,i^{s} ,j} \right) \in {\text{ECI}}}} {\sigma_{ij}^{s,t} } \hfill \\ {\text{s.t.}}\;\left\{ \begin{gathered} \sum\limits_{i = 1}^{n - 1} {\sum\limits_{j = i + 1}^{n} {\sum\limits_{s = 1}^{{{\#} \overline{h}_{ij}^{t} }} {\tau_{ij}^{s,t} } } } \, \le \frac{{\alpha n\left( {n - 1} \right){\#} \overline{h}_{ij}^{t} }}{2} \hfill \\ \overline{\gamma }_{ij}^{s,t} - \overline{\gamma }_{ij}^{os,t} \le \sigma_{ij}^{s,t} \hfill \\ - \overline{\gamma }_{ij}^{s,t} + \overline{\gamma }_{ij}^{os,t} \le \sigma_{ij}^{s,t} \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad . \hfill \\ \tilde{\gamma }_{ij}^{s,t} + 0.5 - \frac{1}{n}\sum\limits_{k = 1}^{n} {\left( {\tilde{\gamma }_{ik}^{s,t} + \tilde{\gamma }_{kj}^{s,t} } \right)} \le \tau_{ij}^{s,t} \hfill \\ - \tilde{\gamma }_{ij}^{s,t} - 0.5 + \frac{1}{n}\sum\limits_{k = 1}^{n} {\left( {\tilde{\gamma }_{ik}^{s,t} + \tilde{\gamma }_{kj}^{s,t} } \right)} \le \tau_{ij}^{s,t} \hfill \\ \tilde{\gamma }_{ij}^{s,t} = \left( {1 - \tau^{t} } \right)\overline{\gamma }_{ij}^{s,t} + \tau^{t} \overline{\gamma }_{ij}^{os,t} \hfill \\ i,j = 1,2, \ldots ,n;\quad i < j;\quad s = 1,2, \ldots ,{\#} \overline{h}_{ij}^{t} \hfill \\ 0 \le \tau^{t} \le 1 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} $$

(12)

It can be easily seen that Eq. (12) is a nonlinear programming model. The optimal solution of it can be easily obtained by utilizing the programming software.

Based on the above programming model, the following algorithm is designed to obtain the acceptable consistent HFPR which considering the additive consistency.

Algorithm 2

Input: An HFPR $H = \left( {h_{ij} } \right)_{n \times n}$.

Output: The acceptable consistent NHFPR $\tilde{H} = \left( {\tilde{h}_{ij} } \right)_{n \times n}$.

Step 1: According to algorithm 1, its NHFPR is derived, denote as $\overline{H} = \left( {\overline{h}_{ij} } \right)_{n \times n}$, $\overline{h}_{ij} = \left\{ {\overline{\gamma }_{ij}^{s} \left| {s = 1,2, \ldots ,{\#} \overline{h}_{ij} } \right.} \right\}$.

Step 2: With respect to Eq. (5), the additive consistency index of $\overline{H}$ is derived.

Step 3: If the consistency index ${\text{CI}} > \alpha$, then go to the next Step; Otherwise, go to Step 8.

Step 4: According to Eq. (4), the additive consistent NHFPR is obtained.

Step 5: Identification of the inconsistent evaluation elements with respect to stage 1 presents in section “The consistency checking and improving process”.

Step 6: Derive the optimal adjustment parameter according to Eq. (12).

Step 7: Return the optimal adjustment parameter value $\tau^{t}$ to $\tilde{H}$, the acceptable consistent NHFPR is obtained.

Step 8: End.

Example 3

The HFPR is the same as those given in Example 1.

Step 1: According to algorithm 1, its NHFPR is derived. For the detailed calculation process, the readers turn to Example 2.

Step 2: With respect to Eq. (5), the additive consistency index of $\overline{H}$ is derived as follows: ${\text{CI}}\left( H \right) = 0.1708$.

Step 3: Suppose the threshold value set $\alpha = 0.1$. It is obviously that ${\text{CI}}\left( H \right) > \alpha$, than $H$ is not an acceptable consistent HFPR. The consistency of it needs to be improved.

Step 4: According to Eq. (4), the additive consistent NHFPR is obtained as follows:

$$\overline{H}^{o} = \left( {\begin{array}{*{20}c} {\left\{ {0.5} \right\}} &\quad {\left\{ {0.48,0.56,0.65} \right\}} &\quad {\left\{ {0.4,0.5,0.6} \right\}} &\quad {\left\{ {0.5,0.6,0.7} \right\}} \\ {\left\{ {0.35,0.44,0.52} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.43,0.5,0.58} \right\}} &\quad {\left\{ {0.53,0.6,0.68} \right\}} \\ {\left\{ {0.4,0.5,0.6} \right\}} &\quad {\left\{ {0.42,0.5,0.57} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.38,0.48,0.55} \right\}} \\ {\left\{ {0.3,0.4,0.5} \right\}} &\quad {\left\{ {0.32,0.4,0.47} \right\}} &\quad {\left\{ {0.45,0.52,0.62} \right\}} &\quad {\left\{ {0.5} \right\}} \\ \end{array} } \right). $$

Step 5: Identification of the inconsistent evaluation elements with respect to stage 1.

The set of 3-tuples ${\text{ECI}}$ is identified under the threshold $\alpha = 0.1$ is:

$${\text{ECI}} = \left\{ \begin{gathered} \left( {1,1^{1} ,2} \right),\left( {1,1^{2} ,2} \right),\left( {1,1^{3} ,2} \right),\left( {1,1^{1} ,4} \right),\left( {1,1^{2} ,4} \right),\left( {1,1^{3} ,4} \right), \hfill \\ \left( {1,2^{1} ,4} \right),\left( {1,2^{2} ,4} \right),\left( {1,2^{3} ,4} \right),\left( {1,3^{1} ,4} \right),\left( {1,3^{2} ,4} \right),\left( {1,3^{3} ,4} \right) \hfill \\ \end{gathered} \right\}.$$

Step 6: Derive the optimal adjustment parameter according to Eq. (12).

Utilizing Eq. (12) to obtain the value of the optimal parameter: $\tau^{{1}} = 1$.

Step 7: Return the optimal adjustment parameter value $\tau^{1}$ to $\tilde{H}$, the acceptable consistent NHFPR is obtained.

It can be easily seen that the acceptable consistent NHFPR is the same as consistent NHFPR, that is $\tilde{H} = \overline{H}^{o}$.

Step 8: End.

A framework of MCDM procedure with HFPRs

In this section, a framework of MCDM procedure with HFPRs is introduced. Two main issues will be solved in the framework are: (1) to integrate the evaluation elements provided from a group of decision makers which has different number of elements including in different HFPRs. (2) to reach the consensus framework both considering the consistency of individual HFPRs and group consensus among a group of HFPRs. To address them, there are five subsection concerns, including the MCDM problems with HFPRs is described in section “The MCDM problems with HFPRs”. An algorithm to integrate a group of HFPRs is designed in section “An algorithm to integrate a group of HFPRs”. The method of consensus measuring and reaching process is showed in section “The method of consensus measuring and reaching processes”. In section “Calculate the weight vectors of decision makers”, a method of determining the weights of decision makers is introduced. Finally, the framework of MCDM procedure with HFPRs is proposed.

The MCDM problems with HFPRs

Hesitant MCDM problems involve $n$ alternatives denoted as $A = \left\{ {a_{1} ,a_{2} , \ldots ,a_{n} } \right\}$. Each alternative is assessed based on several feature criteria. Let $E = \left\{ {e_{1} ,e_{2} , \ldots ,e_{m} } \right\}$ be a set of decision makers and $\lambda = \left( {\lambda_{1} ,\lambda_{2} , \ldots ,\lambda_{m} } \right)$ be the decision makers’ weight vector. We assume that the weights of the decision makers are completely unknown. The evaluation of the alternative $a_{i}$, $i = 1,2, \ldots ,n$ with respect to the feature criterion is provided by decision maker $e^{t}$, $t = 1,2, \ldots ,m$, and denotes as $h^{t} = \left\{ {\gamma^{s,t} \left| {s = 1,2, \ldots ,{\#} h^{t} } \right.} \right\}$, which are HFPRs. This study focuses on integrating a group of HFPRs into a collective one, reaching consensus among a group of decision makers, and a best alternative is obtained by applying a framework of selection process.

An algorithm to integrate a group of HFPRs

For an HFPR, a normalized method is introduced in Sect. 3.1, but how to integrate a group of HFPRs which has different number of elements remains unsolved. To address this, our objective is to derive a new group of NHFPRs, which have acceptable additive consistency. An algorithm is designed as follows.

Algorithm 3

Input: A group of HFPRs $H^{t} = \left( {h_{ij}^{t} } \right)_{n \times n}$, $t = 1,2, \ldots ,m$.

Output: A group of acceptable consistent NHFPRs $\overline{H}^{t} = \left( {\overline{h}_{ij}^{t} } \right)_{n \times n}$, $t = 1,2, \ldots ,m$.

Step 1: According to algorithm 1, their NHFPRs are derived, denote as $\overline{H}^{t} = \left( {\overline{h}_{ij}^{t} } \right)_{n \times n}$, $\overline{h}_{ij}^{t} = \left\{ {\overline{\gamma }_{ij}^{s,t} \left| {s = 1,2, \ldots ,{\#} \overline{h}_{ij}^{t} } \right.} \right\}$.

Step 2: With respect to Eq. (5), the additive consistency indexes of $\overline{H}^{t}$ are calculated.

Step 3: If there is a consistency index ${\text{CI}}^{t} > \alpha$, then go to the next Step; Otherwise, go to Step 5.

Step 4: According to algorithm 2, the acceptable consistent NHFPRs $\tilde{H}^{t} = \left( {\tilde{h}_{ij}^{t} } \right)_{n \times n}$ are obtained.

Step 5: Identify the greatest number of elements among the group and denotes as $\tilde{H}^{o} = \left( {\tilde{h}_{ij}^{o} } \right)_{n \times n}$, that is:

$$ {\#} \overline{h}_{ij}^{o} {\text{ = max}}\left\{ {\overline{\gamma }_{ij}^{s,t} \left| {s = 1,2, \ldots ,{\#} \overline{h}_{ij}^{t} ;t = 1,2, \ldots ,m} \right.} \right\}. $$

(13)

Step 6: Make the group of HFPRs have the same number of elements.

To make the group of HFPRs have the same number of elements. The process is developed as follows:

Step 6.1: According to Definition 5, their NHFPRs with $\xi$ are derived, denote as $\overline{H}_{\xi }^{t} = \left( {\overline{h}_{ij,\xi }^{t} } \right)_{n \times n}$, $\overline{h}_{ij,\xi }^{t} = \left\{ {\overline{\gamma }_{ij,\xi }^{s,t} \left| {s = 1,2, \ldots ,{\#} \overline{h}_{ij,\xi }^{t} } \right.} \right\}$.

Step 6.2: Derive the optimal parameter $\xi$, a programming model is constructed as follows:

$$ \begin{gathered} \min \quad z = \frac{2}{{n\left( {n - 1} \right){\#} \overline{h}_{ij}^{t} }}\sum\limits_{i = 1}^{n - 1} {\sum\limits_{j = i + 1}^{n} {\sum\limits_{s = 1}^{{{\#} \overline{h}_{ij}^{t} }} {\left| {\overline{\gamma }_{ij}^{s,t} - \overline{\gamma }_{ij}^{s,o} } \right|} } } \, \hfill \\ {\text{s.t.}}\;\left\{ \begin{gathered} \frac{2}{{n\left( {n - 1} \right){\#} \overline{h}_{ij}^{t} }}\sum\limits_{i = 1}^{n - 1} {\sum\limits_{j = i + 1}^{n} {\sum\limits_{s = 1}^{{{\#} \overline{h}_{ij}^{t} }} {\left| {\overline{\gamma }_{ij}^{s,t} + 0.5 - \frac{1}{n}\sum\limits_{k = 1}^{n} {\left( {\overline{\gamma }_{ik}^{s,t} + \overline{\gamma }_{kj}^{s,t} } \right)} } \right|} } } \, \le \alpha \hfill \\ 0 \le \xi \le 1 \hfill \\ t = 1,2, \ldots ,m \hfill \\ t \ne o \hfill \\ \end{gathered} \right.. \hfill \\ \end{gathered} $$

(14)

In Eq. (14), the first constraint indicates that the consistency of HFPRs must meet the threshold value in the normalized results, $\alpha$ is the threshold value which provides in advance and $\xi$ is the optimized parameter that needs to be determined. To simplify the objective function presents in (14), the following symbols are used. Let $\phi_{ij}^{s,t} = \overline{\gamma }_{ij}^{s,t} - \overline{\gamma }_{ij}^{s,o}$ and $\delta_{ij}^{s,t} = \left| {\phi_{ij}^{s,t} } \right|$. Moreover, $\delta_{ij}^{s,t} = \left| {\phi_{ij}^{s,t} } \right|$ is equivalent to $\phi_{ij}^{s,t} \le \delta_{ij}^{s,t}$ and $- \phi_{ij}^{s,t} \le \delta_{ij}^{s,t}$, and the objective function is transformed into: $\min \quad z = \frac{2}{{n\left( {n - 1} \right){\#} \overline{h}_{ij}^{t} }}\sum\nolimits_{i = 1}^{n - 1} {\sum\nolimits_{j = i + 1}^{n} {\sum\nolimits_{s = 1}^{{{\#} \overline{h}_{ij}^{t} }} {\delta_{ij}^{s,t} } } }$. In a similar way, the absolute value constraint in constraints condition can be further simplified. Let $\varepsilon_{ij}^{s,t} = \overline{\gamma }_{ij}^{s,t} + 0.5 - \frac{1}{n}\sum\nolimits_{k = 1}^{n} {\left( {\overline{\gamma }_{ik}^{s,t} + \overline{\gamma }_{kj}^{s,t} } \right)}$ and $\gamma_{ij}^{s,t} = \left| {\varepsilon_{ij}^{s,t} } \right|$. Moreover, $\gamma_{ij}^{s,t} = \left| {\varepsilon_{ij}^{s,t} } \right|$ is equivalent to $\varepsilon_{ij}^{s,t} \le \gamma_{ij}^{s,t}$ and $- \varepsilon_{ij}^{s,t} \le \gamma_{ij}^{s,t}$, and the absolute value constraint is transformed into: $\sum\nolimits_{i = 1}^{n - 1} {\sum\nolimits_{j = i + 1}^{n} {\sum\nolimits_{s = 1}^{{{\#} \overline{h}_{ij} }} {\gamma_{ij}^{s,t} } } } \, \le \frac{{\alpha n\left( {n - 1} \right){\#} \overline{h}_{ij}^{t} }}{2}$. Furthermore, Eq. (14) can be equivalently transformed into the following programming model:

$$ \begin{gathered} \min \quad z = \frac{2}{{n\left( {n - 1} \right){\#} \overline{h}_{ij}^{t} }}\sum\limits_{i = 1}^{n - 1} {\sum\limits_{j = i + 1}^{n} {\sum\limits_{s = 1}^{{{\#} \overline{h}_{ij}^{t} }} {\delta_{ij}^{s,t} } } } \, \hfill \\ {\text{s.t.}}\;\left\{ \begin{gathered} \sum\limits_{i = 1}^{n - 1} {\sum\limits_{j = i + 1}^{n} {\sum\limits_{s = 1}^{{{\#} \overline{h}_{ij} }} {\gamma_{ij}^{s,t} } } } \, \le \frac{{\alpha n\left( {n - 1} \right){\#} \overline{h}_{ij}^{t} }}{2} \hfill \\ \overline{\gamma }_{ij}^{s,t} - \overline{\gamma }_{ij}^{s,o} \le \delta_{ij}^{s,t} ,\quad i,j = 1,2, \ldots ,n;\quad i < j;\quad s = 1,2, \ldots ,{\#} \overline{h}_{ij}^{t} \hfill \\ - \overline{\gamma }_{ij}^{s,t} + \overline{\gamma }_{ij}^{s,o} \le \delta_{ij}^{s,t} ,\quad i,j = 1,2, \ldots ,n;\quad i < j;\quad s = 1,2, \ldots ,{\#} \overline{h}_{ij}^{t} \quad \quad \quad \quad \quad \quad \quad \quad . \hfill \\ \overline{\gamma }_{ij}^{s,t} + 0.5 - \frac{1}{n}\sum\limits_{k = 1}^{n} {\left( {\overline{\gamma }_{ik}^{s,t} + \overline{\gamma }_{kj}^{s,t} } \right)} \le \gamma_{ij}^{s,t} ,\quad i,j = 1,2, \ldots ,n;\quad i < j;\quad s = 1,2, \ldots ,{\#} \overline{h}_{ij}^{t} \hfill \\ - \overline{\gamma }_{ij}^{s,t} - 0.5 + \frac{1}{n}\sum\limits_{k = 1}^{n} {\left( {\overline{\gamma }_{ik}^{s,t} + \overline{\gamma }_{kj}^{s,t} } \right)} \le \gamma_{ij}^{s,t} ,\quad i,j = 1,2, \ldots ,n;\quad i < j;\quad s = 1,2, \ldots ,{\#} \overline{h}_{ij}^{t} \hfill \\ 0 \le \xi \le 1 \hfill \\ t = 1,2, \ldots ,m \hfill \\ t \ne o \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} $$

(15)

It can be easily seen that Eq. (15) is a linear programming model. The optimal solution of it can be easily obtained by utilizing the programming software.

Step 7: Return the optimal adjustment parameter value $\xi$ to $\overline{H}^{t}$, then a group of acceptable consistent HFPRs are obtained.

Step 8: End.

Based on a group of acceptable consistent NHFPRs $\overline{H}^{t} = \left( {\overline{h}_{ij}^{t} } \right)_{n \times n}$, $t = 1,2, \cdots ,m$, the collective NHFPR $\overline{H}^{c} = \left( {\overline{h}_{ij}^{c} } \right)_{n \times n}$ is obtained with respective to following formula [35]:

$$ \overline{h}_{ij}^{c} = \sum\limits_{t = 1}^{n} {\lambda_{t} \overline{h}_{ij}^{t} ,} \;t = 1,2, \ldots ,m, $$

(16)

where $\lambda_{t}$ is the decision maker $e^{t}$’s weight vector.

The method of consensus measuring and reaching processes

Consensus level is used to measure the consensus status of all decision makers in the decision making process. With various skills, knowledge and experience, decision makers in decision making process may have different opinions. How to reach consensus and derive an acceptable alternative seems necessary. In this subsection, a consensus reaching framework with minimum adjustments is developed. The two main issues need to be solved in the process are: the consensus measuring and reaching processes.

For the consensus measuring process, some scholars insistent on calculating the proximity degrees between any two individual decision maker’s preferences, while some suggesting the proximity degree between the individual decision maker’s preference and group one. These two methods both use the deviation to measure the consensus, therefore they are essentially indistinguishable. In this study, we focus on the previous one. The higher the value of proximity degree is, the smaller the divergence of opinions in the group. Let $H^{t} = \left( {h_{ij}^{t} } \right)_{n \times n}$, $t = 1,2, \cdots ,m$ be a group of HFPRs, $\overline{H}^{t} = \left( {\overline{h}_{ij}^{t} } \right)_{n \times n}$ and $\overline{H}^{l} = \left( {\overline{h}_{ij}^{l} } \right)_{n \times n}$ be two NHFPRs obtained from algorithm 3, the consensus measuring of decision maker $e^{t}$ is developed as follows:

$$ {\text{GCI}}^{t} = 1 - \frac{1}{{n\left( {n - 1} \right)\left( {m - 1} \right){\#} \overline{h}_{ij}^{t} }}\sum\limits_{\begin{subarray}{l} l = 1 \\ l \ne t \end{subarray} }^{m} {\sum\limits_{i = 1}^{n} {\sum\limits_{\begin{subarray}{l} j = 1 \\ j \ne i \end{subarray} }^{n} {\sum\limits_{s = 1}^{{{\#} \overline{h}_{ij} }} {\left| {\overline{\gamma }_{ij}^{s,t} - \overline{\gamma }_{ij}^{s,l} } \right|} } } } \,. $$

(17)

For the consensus reaching process, we first utilize the identification rule to find out the position of the element that needs to be adjusted. Then, an optimization model is constructed to obtain the consensus reaching both considering the consistency and consensus.

Stage 1: Identification of the evaluation elements that do not reach consensus.

The set of evaluation elements by NHFPRs that less than the threshold value of accept consensus level is identified as follows:

Step 1: Identify the decision makers whose consensus indexes at the NHFPRs are smaller than the threshold value $\beta$ which provide in advance.

$$ {\text{DGCI}} = \left\{ {\left. t \right|{\text{GCI}}^{t} < \beta } \right\} $$

Step 2: Identify the alternatives that need to be adjusted which satisfying the condition in Step 1. That is, the NHFPRs’ consensus indexes at the alternative under the $s$th evaluation values are smaller than the threshold value $\beta$.

$$ {\text{AGCI}} = \left\{ {\left. {\left( {t,i^{s} } \right)} \right|t \in {\text{DGCI}} \wedge {\text{GCI}}_{{i^{s} }}^{t} < \beta \wedge s = 1,2, \ldots ,{\#} \overline{h}_{ij}^{t} } \right\} $$

Step 3: Identify the evaluation elements that need to be adjusted for alternatives satisfying the condition in Step 2. That is, the NHFPRs’ consensus indexes at the evaluation elements under the $s$th evaluation values are smaller than the threshold value $\beta$.

$$ \begin{aligned}{\text{EGCI}} = \left\{ \left. {\left( {t,i^{s} ,j} \right)} \right|\left( {t,i^{s} } \right) \in {\text{AGCI}} \wedge {\text{GCI}}_{{i^{s} ,j}}^{t} \right.\\ \left.< \beta \wedge s = 1,2, \ldots ,{\#} \overline{h}_{ij}^{t} \wedge i \ne j \right\}\end{aligned} $$

Stage 2: The method of consensus reaching process.

Let $H^{t} = \left( {h_{ij}^{t} } \right)_{n \times n}$ be a group of initial HFPRs provided from decision makers $e^{t}$, $t = 1,2, \cdots ,m$, and $\overline{H}^{t} = \left( {\overline{h}_{ij}^{t} } \right)_{n \times n}$, $\overline{h}_{ij}^{t} = \left\{ {\overline{\gamma }_{ij}^{s,t} \left| {s = 1,2, \ldots ,{\#} \overline{h}_{ij}^{t} } \right.} \right\}$ are their NHFPRs, $\tau \in [0,1]$ is the adjustment parameter. If $\left( {t,i^{s} ,j} \right) \in \text{EGCI}$, means the evaluation elements provide by the decision maker $e^{t}$ on the alternative $a_{i}$ compare to alternative $a_{j}$ under the $s$th evaluation values need to be adjusted. Then the adjusted evaluation elements $\tilde{\gamma }_{ij}^{s,t}$ can be represented as follows:

$$ \tilde{\gamma }_{ij}^{s,t} = \left( {1 - \tau } \right)\overline{\gamma }_{ij}^{s,t} + \tau \overline{\gamma }_{ij}^{s,c} , $$

(18)

where $\overline{\gamma }_{ij}^{s,c}$ indicates the collective NHFPR derived from Eq. (16). Accordingly, the remaining NHFPRs that do not require adjustment if $\left( {t,i^{s} ,j} \right) \notin {\text{EGCI}}$.

Similar to the discussion presents in Sect. 3.2, to derive the optimal adjustment parameter, the optimal model is constructed both considering the consistency and consensus:

$$ \begin{gathered} \min \quad z = \tau \sum\limits_{{\left( {t,i^{s} ,j} \right) \in EGCI}} {\left| {\overline{\gamma }_{ij}^{s,t} - \overline{\gamma }_{ij}^{s,c} } \right|} \hfill \\ {\text{s.t.}}\;\left\{ \begin{gathered} \tilde{\gamma }_{ij}^{s,c} = \sum\limits_{t = 1}^{n} {\lambda_{t} \tilde{\gamma }_{ij}^{s,t} } ,\quad i,j = 1,2, \ldots ,n;\quad i < j;\quad s = 1,2, \ldots ,{\#} \overline{h}_{ij}^{t} \hfill \\ \frac{2}{{n\left( {n - 1} \right){\#} \overline{h}_{ij}^{t} }}\sum\limits_{i = 1}^{n - 1} {\sum\limits_{j = i + 1}^{n} {\sum\limits_{s = 1}^{{{\#} \overline{h}_{ij}^{t} }} {\left| {\tilde{\gamma }_{ij}^{s,t} + 0.5 - \frac{1}{n}\sum\limits_{k = 1}^{n} {\left( {\tilde{\gamma }_{ik}^{s,t} + \tilde{\gamma }_{kj}^{s,t} } \right)} } \right|} } } \, \le \alpha ,\quad t \in {\text{EGCI}}\quad . \hfill \\ 1 - \frac{1}{{n\left( {n - 1} \right)\left( {m - 1} \right){\#} \overline{h}_{ij}^{t} }}\sum\limits_{\begin{subarray}{l} l = 1 \\ l \ne t \end{subarray} }^{m} {\sum\limits_{i = 1}^{n} {\sum\limits_{\begin{subarray}{l} j = 1 \\ j \ne i \end{subarray} }^{n} {\sum\limits_{s = 1}^{{{\#} \overline{h}_{ij} }} {\left| {\tilde{\gamma }_{ij}^{s,t} - \tilde{\gamma }_{ij}^{s,l} } \right|} } } } \ge \beta ,\quad t \in {\text{EGCI}} \hfill \\ 1 - \frac{1}{{n\left( {n - 1} \right)\left( {m - 1} \right){\#} \overline{h}_{ij}^{t} }}\sum\limits_{\begin{subarray}{l} l = 1 \\ l \ne t \end{subarray} }^{m} {\sum\limits_{i = 1}^{n} {\sum\limits_{\begin{subarray}{l} j = 1 \\ j \ne i \end{subarray} }^{n} {\sum\limits_{s = 1}^{{{\#} \overline{h}_{ij} }} {\left| {\overline{\gamma }_{ij}^{s,t} - \overline{\gamma }_{ij}^{s,l} } \right|} } } } \ge \beta ,\quad t \notin {\text{EGCI}} \hfill \\ \tilde{\gamma }_{ij}^{s,t} = \left( {1 - \tau } \right)\overline{\gamma }_{ij}^{s,t} + \tau \overline{\gamma }_{ij}^{s,c} ,\quad i,j = 1,2, \ldots ,n;\quad i < j;\quad s = 1,2, \ldots ,{\#} \overline{h}_{ij}^{t} \hfill \\ 0 \le \tau \le 1 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} $$

(19)

In Eq. (19), the second constraint indicates that the consistency of HFPRs can meet the threshold value $\alpha$, third and fourth constraints indicate that the group consensus level can meet the threshold value $\beta$, $\tau$ is the adjustment parameter that needs to be determined, $\lambda_{t}$ is the decision maker $e^{t}$’s weight vector which determines in advance. To simplify the objective function presents in (19), the following symbols are used. Let $\pi_{ij}^{s,t} = \overline{\gamma }_{ij}^{s,t} - \overline{\gamma }_{ij}^{s,c}$ and $\sigma_{ij}^{s,t} = \left| {\pi_{ij}^{s,t} } \right|$. Moreover, $\sigma_{ij}^{s,t} = \left| {\pi_{ij}^{s,t} } \right|$ is equivalent to $\pi_{ij}^{s,t} \le \sigma_{ij}^{s,t}$ and $- \pi_{ij}^{s,t} \le \sigma_{ij}^{s,t}$, and the objective function is transformed into: $\min \quad z = \tau \sum\nolimits_{{\left( {t,i^{s} ,j} \right) \in {\text{EGCI}}}} {\sigma_{ij}^{s,t} }$. In a similar way, the absolute value constraint in constraints condition can be further simplified. Let $\varsigma_{ij}^{s,t} = \tilde{\gamma }_{ij}^{s,t} + 0.5 - \frac{1}{n}\sum\nolimits_{k = 1}^{n} {\left( {\tilde{\gamma }_{ik}^{s,t} + \tilde{\gamma }_{kj}^{s,t} } \right)}$ and $\tau_{ij}^{s,t} = \left| {\varsigma_{ij}^{s,t} } \right|$. Moreover, $\tau_{ij}^{s,t} = \left| {\varsigma_{ij}^{s,t} } \right|$ is equivalent to $\varsigma_{ij}^{s,t} \le \tau_{ij}^{s,t}$ and $- \varsigma_{ij}^{s,t} \le \tau_{ij}^{s,t}$, and the absolute value constraint $\frac{2}{{n\left( {n - 1} \right){\#} \overline{h}_{ij}^{t} }}\sum\nolimits_{i = 1}^{n - 1} \sum\nolimits_{j = i + 1}^{n} \sum\nolimits_{s = 1}^{{{\#} \overline{h}_{ij}^{t} }} \left| {\tilde{\gamma }_{ij}^{s,t} + 0.5 -\break \frac{1}{n}\sum\nolimits_{k = 1}^{n} {\left( {\tilde{\gamma }_{ik}^{s,t} + \tilde{\gamma }_{kj}^{s,t} } \right)} } \right| \, \le \alpha$ is transformed into: $\sum\nolimits_{i = 1}^{n - 1} {\sum\nolimits_{j = i + 1}^{n} {\sum\nolimits_{s = 1}^{{{\#} \overline{h}_{ij} }} {\tau_{ij}^{s,t} } } } \, \le \frac{{\alpha n\left( {n - 1} \right){\#} \overline{h}_{ij}^{t} }}{2}$. Let $\mu_{ij}^{s,t} = \overline{\gamma }_{ij}^{s,t} - \overline{\gamma }_{ij}^{s,l}$ and $\nu_{ij}^{s,t} = \left| {\mu_{ij}^{s,t} } \right|$. Moreover, $\nu_{ij}^{s,t} = \left| {\mu_{ij}^{s,t} } \right|$ is equivalent to $\mu_{ij}^{s,t} \le \nu_{ij}^{s,t}$ and $- \mu_{ij}^{s,t} \le \nu_{ij}^{s,t}$, and the absolute value constraint $1 - \frac{1}{{n\left( {n - 1} \right)\left( {m - 1} \right){\#} \overline{h}_{ij}^{t} }}\sum\nolimits_{\begin{subarray}{l} l = 1 \\ l \ne t \end{subarray} }^{m} {\sum\limits_{i = 1}^{n} {\sum\nolimits_{\begin{subarray}{l} j = 1 \\ j \ne i \end{subarray} }^{n} {\sum\nolimits_{s = 1}^{{{\#} \overline{h}_{ij} }} {\left| {\overline{\gamma }_{ij}^{s,t} - \overline{\gamma }_{ij}^{s,l} } \right|} } } } \ge \beta$ is transformed into: $\sum\nolimits_{\begin{subarray}{l} l = 1 \\ l \ne t \end{subarray} }^{m} {\sum\nolimits_{i = 1}^{n} {\sum\nolimits_{\begin{subarray}{l} j = 1 \\ j \ne i \end{subarray} }^{n} {\sum\nolimits_{s = 1}^{{{\#} \overline{h}_{ij} }} {\nu_{ij}^{s,t} } } } } \le \left( {1 - \beta } \right)n\left( {n - 1} \right)\left( {m - 1} \right){\#} \overline{h}_{ij}^{t}$. In a similar way, the absolute value constraint $1 {-} \frac{1}{{n\left( {n - 1} \right)\left( {m - 1} \right){\#} \overline{h}_{ij}^{t} }}\sum\limits_{\begin{subarray}{l} l = 1 \\ l \ne t \end{subarray} }^{m} {\sum\limits_{i = 1}^{n} {\sum\limits_{\begin{subarray}{l} j = 1 \\ j \ne i \end{subarray} }^{n} {\sum\limits_{s = 1}^{{{\#} \overline{h}_{ij} }} {\left| {\tilde{\gamma }_{ij}^{s,t} {-} \tilde{\gamma }_{ij}^{s,l} } \right|} } } } {\ge} \beta$ is transformed into $\sum_{\begin{subarray}{l} l = 1 \\ l \ne t \end{subarray} }^{m} {\sum_{i = 1}^{n} {\sum_{\begin{subarray}{l} j = 1 \\ j \ne i \end{subarray} }^{n} {\sum\nolimits_{s = 1}^{{{\#} \overline{h}_{ij} }} {\tilde{\nu}_{ij}^{s,t} } } } } \le \left( {1 - \beta } \right)n\left( {n - 1} \right)\left( {m - 1} \right){\#} \overline{h}_{ij}^{t}$. Furthermore, Eq. (19) can be equivalently transformed into the following programming model:

$$ \begin{gathered} \min \quad z = \tau \sum\limits_{{\left( {t,i^{s} ,j} \right) \in {\text{EGCI}}}} {\sigma_{ij}^{s,t} } \hfill \\ {\text{s.t.}}\;\left\{ \begin{gathered} \tilde{\gamma }_{ij}^{s,c} = \sum\limits_{t = 1}^{n} {\lambda_{t} \tilde{\gamma }_{ij}^{s,t} } ,\quad i,j = 1,2, \ldots ,n;\quad i < j;\quad s = 1,2, \ldots ,{\#} \overline{h}_{ij}^{t} \hfill \\ \sum\limits_{i = 1}^{n - 1} {\sum\limits_{j = i + 1}^{n} {\sum\limits_{s = 1}^{{{\#} \overline{h}_{ij}^{t} }} {\tau_{ij}^{s,t} } } } \, \le \frac{{\alpha n\left( {n - 1} \right){\#} \overline{h}_{ij}^{t} }}{2},\quad t \in {\text{EGCI}} \hfill \\ \sum\limits_{\begin{subarray}{l} l = 1 \\ l \ne t \end{subarray} }^{m} {\sum\limits_{i = 1}^{n} {\sum\limits_{\begin{subarray}{l} j = 1 \\ j \ne i \end{subarray} }^{n} {\sum\limits_{s = 1}^{{{\#} \overline{h}_{ij} }} {\tilde{\nu}_{ij}^{s,t} } } } } \le \left( {1 - \beta } \right)n\left( {n - 1} \right)\left( {m - 1} \right){\#} \overline{h}_{ij}^{t} ,\quad t \in {\text{EGCI}} \hfill \\ \sum\limits_{\begin{subarray}{l} l = 1 \\ l \ne t \end{subarray} }^{m} {\sum\limits_{i = 1}^{n} {\sum\limits_{\begin{subarray}{l} j = 1 \\ j \ne i \end{subarray} }^{n} {\sum\limits_{s = 1}^{{{\#} \overline{h}_{ij} }} {\nu_{ij}^{s,t} } } } } \le \left( {1 - \beta } \right)n\left( {n - 1} \right)\left( {m - 1} \right){\#} \overline{h}_{ij}^{t} ,\quad t \notin {\text{EGCI}} \hfill \\ \overline{\gamma }_{ij}^{s,t} - \overline{\gamma }_{ij}^{s,c} \le \sigma_{ij}^{s,t} ,\quad i,j = 1,2, \ldots ,n;\quad i < j;\quad s = 1,2, \ldots ,{\#} \overline{h}_{ij}^{t} \hfill \\ - \overline{\gamma }_{ij}^{s,t} + \overline{\gamma }_{ij}^{s,c} \le \sigma_{ij}^{s,t} ,\quad i,j = 1,2, \ldots ,n;\quad i < j;\quad s = 1,2, \ldots ,{\#} \overline{h}_{ij}^{t} \hfill \\ \tilde{\gamma }_{ij}^{s,t} + 0.5 - \frac{1}{n}\sum\limits_{k = 1}^{n} {\left( {\tilde{\gamma }_{ik}^{s,t} + \tilde{\gamma }_{kj}^{s,t} } \right)} \le \tau_{ij}^{s,t} ,\quad i,j = 1,2, \ldots ,n;\quad i < j;\quad s = 1,2, \ldots ,{\#} \overline{h}_{ij}^{t} \hfill \\ - \tilde{\gamma }_{ij}^{s,t} - 0.5 + \frac{1}{n}\sum\limits_{k = 1}^{n} {\left( {\tilde{\gamma }_{ik}^{s,t} + \tilde{\gamma }_{kj}^{s,t} } \right)} \le \tau_{ij}^{s,t} ,\quad i,j = 1,2, \ldots ,n;\quad i < j;\quad s = 1,2, \ldots ,{\#} \overline{h}_{ij}^{t} \hfill \\ \overline{\gamma }_{ij}^{s,t} - \overline{\gamma }_{ij}^{s,l} \le \nu_{ij}^{s,t} ,\quad i,j = 1,2, \ldots ,n;\quad i < j;\quad s = 1,2, \ldots ,{\#} \overline{h}_{ij}^{t} \hfill \\ - \overline{\gamma }_{ij}^{s,t} + \overline{\gamma }_{ij}^{s,l} \le \nu_{ij}^{s,t} ,\quad i,j = 1,2, \ldots ,n;\quad i < j;\quad s = 1,2, \ldots ,{\#} \overline{h}_{ij}^{t} \hfill \\ \tilde{\gamma }_{ij}^{s,t} - \tilde{\gamma }_{ij}^{s,l} \le \tilde{\nu}_{ij}^{s,t} ,\quad i,j = 1,2, \ldots ,n;\quad i < j;\quad s = 1,2, \ldots ,{\#} \overline{h}_{ij}^{t} \hfill \\ - \tilde{\gamma }_{ij}^{s,t} + \tilde{\gamma }_{ij}^{s,l} \le \tilde{\nu}_{ij}^{s,t} ,\quad i,j = 1,2, \ldots ,n;\quad i < j;\quad s = 1,2, \ldots ,{\#} \overline{h}_{ij}^{t} \hfill \\ \tilde{\gamma }_{ij}^{s,t} = \left( {1 - \tau } \right)\overline{\gamma }_{ij}^{s,t} + \tau \overline{\gamma }_{ij}^{s,c} ,\quad i,j = 1,2, \ldots ,n;\quad i < j;\quad s = 1,2, \ldots ,{\#} \overline{h}_{ij}^{t} \hfill \\ 0 \le \tau \le 1 \hfill \\ \end{gathered} \right.. \hfill \\ \end{gathered} $$

(20)

It can be easily seen that Eq. (20) is a nonlinear programming model. The optimal solution of it can be easily obtained by utilizing the programming software.

Based on the above programming model, the following algorithm is developed to obtain a new group of NHFPRs which meets the individual consistency and group consensus level.

Algorithm 4

Input: A group of HFPRs $H^{t} = \left( {h_{ij}^{t} } \right)_{n \times n}$, $t = 1,2, \cdots ,m$.

Output: A new group of NHFPRs $\tilde{H}^{t} = \left( {\tilde{h}_{ij}^{t} } \right)_{n \times n}$, $t = 1,2, \ldots ,m$, which meet the individual consistency and group consensus level.

Step 1: According to algorithm 3, the acceptable consistent NHFPRs are derived, and denotes as $\overline{H}^{t} = \left( {\overline{h}_{ij}^{t} } \right)_{n \times n}$, $t = 1,2, \ldots ,m$.

Step 2: According to Eq. (16), the collective NHFPR $\overline{H}^{c} = \left( {\overline{h}_{ij}^{c} } \right)_{n \times n}$ is obtained.

Step 3: With respect to Eq. (17), the consensus indexes ${\text{GCI}}^{t}$ is derived.

Step 4: If there is at least one consensus index ${\text{GCI}}^{t} < \beta$, then go to the next Step; Otherwise, go to Step 8.

Step 5: Identify the evaluation elements that do not reach consensus with respect to stage 1 presents in section “An algorithm to integrate a group of HFPRs”.

Step 6: Derive the optimal adjustment parameter according to Eq. (20).

Step 7: Return the optimal adjustment parameter value $\tau$ to $\overline{H}^{t}$, a new group of NHFPRs is obtained, which meets the individual consistency and group consensus level.

Step 8: End.

Remark 3

The convergence of consensus reaching process presents in algorithm 4 can be easily obtained in a similar way that is provided in Wu et al. [32].

Calculate the weight vectors of decision makers

The influence of each decision maker in the consensus reaching process is different, and it could be quantified by the evaluation information they offered, based on which the weight of each decision maker can be assigned. This section provides a weight allocation method of decision makers through the analysis of consistency and consensus indexes.

First, as mentioned above, the HFPR with a lower consistency index indicates a more reasonable the evaluation elements he/she provides, and inconsistent preference relations usually result in unreasonable results. Therefore, the weight index of the decision maker $e^{t}$ based on the consistency level is defined as follows:

$$ \pi^{t} = \frac{{\varphi^{t} }}{{\sum\nolimits_{t = 1}^{m} {\varphi^{t} } }},\;t = 1,2, \ldots ,m, $$

(21)

where $\varphi^{t} = \frac{{1/{\text{CI}}^{t} }}{{\sum\nolimits_{t = 1}^{m} {1/{\text{CI}}^{t} } }}$, and ${\text{CI}}^{t}$ is the consistency level derived from Eq. (5).

Second, the HFPR with a higher consensus index indicates the evaluation elements he/she provides closer to the group’s opinion, and a more influence on the consensus reaching process. Therefore, the weight index of decision maker $e^{t}$ based on the consensus index is defined as follows:

$$ \vartheta^{t} = \frac{{{\text{GCI}}^{t} }}{{\sum\nolimits_{t = 1}^{m} {{\text{GCI}}^{t} } }},\;t = 1,2, \ldots ,m, $$

(22)

where ${\text{GCI}}^{t}$ is the consensus index derived from Eq. (17).

Finally, the final weight of individual decision maker could be obtained by aggregating the weight indexes of consistency and consensus through the linear weighting method:

$$ w^{t} = \delta \pi^{t} + \left( {1 - \delta } \right)\vartheta^{t} ,\;t = 1,2, \ldots ,m, $$

(23)

where $\delta \in \left[ {0,1} \right]$ be the linear weighting coefficient between $\pi^{t}$ and $\vartheta^{t}$. Furthermore, by the normalization of Eq. (23), the weight index of decision maker $e^{t}$ is obtained as follows:

$$ \lambda^{t} = \frac{{w^{t} }}{{\sum\nolimits_{t = 1}^{m} {w^{t} } }},\;t = 1,2, \ldots ,m. $$

(24)

A framework of MCDM procedure with HFPRs

The proposed decision making procedure is summarized in the following steps.

Step 1: Form individual HFPRs.

According to the determine criteria and alternatives, the decision makers respectively provide their judgment, and denotes as $H^{t} = \left( {h_{ij}^{t} } \right)_{m \times m}$, $t = 1,2, \ldots ,m$.

Step 2: Derive the individual NHFPRs.

The individual NHFPRs are obtained according to algorithm 1.

Step 3: Calculate the individual consistency indexes.

The individual consistency indexes are calculated with respective to Eq. (5).

Step 4: Determine the acceptable consistent NHFPRs.

If there is at least one individual consistency index ${\text{CI}}^{t} > \alpha$, then the acceptable consistent NHFPRs are determined according to algorithm 2.

Step 5: Derive a group of acceptable consistent NHFPRs.

If the NHFPRs have different number of elements, a group of acceptable consistent NHFPRs $\overline{H}^{t} = \left( {\overline{h}_{ij}^{t} } \right)_{n \times n}$, $t = 1,2, \cdots ,m$ are obtained with respective to algorithm 3. Otherwise, go to Step 6.

Step 6: Calculate the consensus indexes.

The consensus indexes are calculated with respective to Eq. (17).

Step 7: Improve the consensus level.

If there is at least one consensus index ${\text{GCI}}^{t} < \beta$, then the consensus level is improved according to algorithm 4.

Step 8: Determine the weights of decision makers.

The weights of decision makers are determined according to Eqs. (21)–(24).

Step 9: Obtain the collective NHFPR.

The collective NHFPR is derived with respective to Eq. (16).

Step 10: Calculate the score values of collective NHFPR.

The score values of collective NHFPR are determined by the following formula [37]:

$$ \vartheta_{i} = \frac{1}{{\left( {n - 1} \right){\#} \overline{h}_{ij}^{c} }}\sum\limits_{\begin{subarray}{l} j = 1 \\ j \ne i \end{subarray} }^{n} {\sum\limits_{s = 1}^{{{\#} \overline{h}_{ij}^{c} }} {\overline{\gamma }_{ij}^{s,c} } } ,\;i = 1,2, \ldots ,n. $$

(25)

Step 11: Rank the alternatives.

The ranking order of all alternatives is obtained by the value of collective optimal priority weight vector $\vartheta_{i}$, $i = 1,2, \ldots ,n$.

The proposed decision making procedure is depicted in Fig. 1.

Fig. 1

A framework of MCDM process with HFPRs

An illustrative example

In this section, the best graduate students selection for awarding scholarship (revised from Wan et al. [31]) is provided to illustrate the use of the proposed method, and conjunction with comparative analysis is conducted.

The descriptions of the illustrative example

To accelerate the internationalization of the graduate education, Jiangxi University of Finance and Economics plans to initiate an item that selects some outstanding graduate students for awarding scholarship to go to Boston University as exchange graduate students for a three-month study. The selecting process is divided into two stages, in the first stage, the students who want to apply for such a scholarship submit their application materials and obtain the qualification in his/her faculty before entering the final interview. In the final interview stage, the selected graduate students from different faculties are evaluated according to the application materials they provide, mainly including: English ability, scientific research ability and professional achievements.

After the first selection stage, four graduate students, denoted as $a_{1}$, $a_{2}$, $a_{3}$ and $a_{4}$ from college of statistics, college of finance, college of information technology and college of accounting are selected to enter the final interview. A committee consisted of three members $e^{t}$, $t$ = 1, 2, 3, which named three decision makers, are invited to evaluate the performances of these four graduate students. Because of the uncertainty of the criteria, it is difficult for the decision makers to use just one value to provide their evaluation values. To facilitate the elicitation of their evaluation values, HFPR is just an effective tool to deal with such situations, as demonstrated in matrices 1–3.

Take the evaluation value $a_{12}^{1}$ from decision maker $e^{1}$ for example. The decision maker $e^{1}$ is hesitant two possible values 0.3 and 0.5 when assesses the alternatives $a_{1}$ to $a_{2}$, and cannot determine which one is the best. In such case, the evaluation value can be modeled by a HFE $\left\{ {0.3,0.5} \right\}$. Other entries, that is, HFEs, in matrices 1–3 are similarly explained.

$$H^{1} = \left[ {\begin{array}{*{20}l} {\left\{ {0.5} \right\}} &\quad {\left\{ {0.3,0.5} \right\}} &\quad {\left\{ {0.5,0.6,0.7} \right\}} &\quad {\left\{ {0.4} \right\}} \\ {\left\{ {0.5,0.7} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.4,0.6} \right\}} &\quad {\left\{ {0.6,0.7} \right\}} \\ {\left\{ {0.3,0.4,0.5} \right\}} &\quad {\left\{ {0.4,0.6} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.6,0.8} \right\}} \\ {\left\{ {0.6} \right\}} &\quad {\left\{ {0.3,0.4} \right\}} &\quad {\left\{ {0.2,0.4} \right\}} &\quad {\left\{ {0.5} \right\}}, \\ \end{array} } \right]$$

$$H^{2} = \left[ {\begin{array}{*{20}l} {\left\{ {0.5} \right\}} &\quad {\left\{ {0.6,0.7} \right\}} &\quad {\left\{ {0.6,0.8} \right\}} &\quad {\left\{ {0.4,0.5} \right\}} \\ {\left\{ {0.3,0.4} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.5,0.7,0.8} \right\}} &\quad {\left\{ {0.2,0.4} \right\}} \\ {\left\{ {0.2,0.4} \right\}} &\quad {\left\{ {0.2,0.3,0.5} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.5,0.7} \right\}} \\ {\left\{ {0.5,0.6} \right\}} &\quad {\left\{ {0.6,0.8} \right\}} &\quad {\left\{ {0.3,0.5} \right\}} &\quad {\left\{ {0.5} \right\}} \\ \end{array} } \right],$$

and

$$H^{3} = \left[ {\begin{array}{*{20}l} {\left\{ {0.5} \right\}} &\quad {\left\{ {0.4,0.6,0.7} \right\}} &\quad {\left\{ {0.5,0.6,0.7} \right\}} &\quad {\left\{ {0.3,0.4} \right\}} \\ {\left\{ {0.3,0.4,0.6} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.3,0.5} \right\}} &\quad {\left\{ {0.6,0.8} \right\}} \\ {\left\{ {0.3,0.4,0.5} \right\}} &\quad {\left\{ {0.5,0.7} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.4,0.5,0.6} \right\}} \\ {\left\{ {0.6,0.7} \right\}} &\quad {\left\{ {0.2,0.4} \right\}} &\quad {\left\{ {0.4,0.5,0.6} \right\}} &\quad {\left\{ {0.5} \right\}} \\ \end{array} } \right]. $$

Illustration of the proposed method

The procedure for selecting the best graduate student for awarding scholarship using the proposed method is presented below.

Step 1: Form individual HFPRs.

All individual HFPR matrices have been provided, as demonstrated in matrices 1–3.

Step 2: Derive the individual NHFPRs.

According to algorithm 1, the process of deriving the individual NHFPRs is showed as follows:

Step 2.1: According to Definition 5, the NHFPRs of $H^{1}$, $H^{2}$ and $H^{3}$ with optimal parameter $\varsigma$ are obtained as follows:

$$\overline{H}^{1} = \left[ {\begin{array}{*{20}l} {\left\{ {0.5} \right\}} &\quad {\left\{ {0.3,0.5 - 0.2\varsigma_{1} ,0.5} \right\}} &\quad {\left\{ {0.5,0.6,0.7} \right\}} &\quad {\left\{ {0.4,0.4,0.4} \right\}} \\ {\left\{ {0.5,0.5 + 0.2\varsigma_{1} ,0.7} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.4,0.6 - 0.2\varsigma_{1} ,0.6} \right\}} &\quad {\left\{ {0.6,0.7 - 0.1\varsigma_{1} ,0.7} \right\}} \\ {\left\{ {0.3,0.4,0.5} \right\}} &\quad {\left\{ {0.4,0.4 + 0.2\varsigma_{1} ,0.6} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.6,0.8 - 0.2\varsigma_{1} ,0.8} \right\}} \\ {\left\{ {0.6,0.6,0.6} \right\}} &\quad {\left\{ {0.3,0.3 + 0.1\varsigma_{1} ,0.4} \right\}} &\quad {\left\{ {0.2,0.2 + 0.2\varsigma_{1} ,0.4} \right\}} &\quad {\left\{ {0.5} \right\}} \\ \end{array} } \right], $$

$$\overline{H}^{2} = \left[ {\begin{array}{*{20}l} {\left\{ {0.5} \right\}} &\quad {\left\{ {0.6,0.7 - 0.1\varsigma_{2} ,0.7} \right\}} &\quad {\left\{ {0.6,0.8 - 0.2\varsigma_{2} ,0.8} \right\}} &\quad {\left\{ {0.4,0.5 - 0.1\varsigma_{2} ,0.5} \right\}} \\ {\left\{ {0.3,0.3 + 0.1\varsigma_{2} ,0.4} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.5,0.7,0.8} \right\}} &\quad {\left\{ {0.2,0.4 - 0.2\varsigma_{2} ,0.4} \right\}} \\ {\left\{ {0.2,0.2 + 0.2\varsigma_{2} ,0.4} \right\}} &\quad {\left\{ {0.2,0.3,0.5} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.5,0.7 - 0.2\varsigma_{2} ,0.7} \right\}} \\ {\left\{ {0.5,0.5 + 0.1\varsigma_{2} ,0.6} \right\}} &\quad {\left\{ {0.6,0.6 + 0.2\varsigma_{2} ,0.8} \right\}} &\quad {\left\{ {0.3,0.3 + 0.2\varsigma_{2} ,0.5} \right\}} &\quad {\left\{ {0.5} \right\}} \\ \end{array} } \right], $$

and

$$\overline{H}^{3} = \left[ {\begin{array}{*{20}l} {\left\{ {0.5} \right\}} &\quad {\left\{ {0.4,0.6,0.7} \right\}} &\quad {\left\{ {0.5,0.6,0.7} \right\}} &\quad {\left\{ {0.3,0.4 - 0.1\varsigma_{3} ,0.4} \right\}} \\ {\left\{ {0.3,0.4,0.6} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.3,0.5 - 0.2\varsigma_{3} ,0.5} \right\}} &\quad {\left\{ {0.6,0.8 - 0.2\varsigma_{3} ,0.8} \right\}} \\ {\left\{ {0.3,0.4,0.5} \right\}} &\quad {\left\{ {0.5,0.5 + 0.2\varsigma_{3} ,0.7} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.4,0.5,0.6} \right\}} \\ {\left\{ {0.6,0.6 + 0.1\varsigma_{3} ,0.7} \right\}} &\quad {\left\{ {0.2,0.2 + 0.2\varsigma_{3} ,0.4} \right\}} &\quad {\left\{ {0.4,0.5,0.6} \right\}} &\quad {\left\{ {0.5} \right\}} \\ \end{array} } \right]. $$

Step 2.2: Based on Eq. (4), the additive consistent NHFPRs of $\overline{H}^{1}$, $\overline{H}^{2}$ and $\overline{H}^{3}$ are derived as follows:

$$\begin{gathered} \overline{H}^{N,1} = \hfill \\ \left[ {\begin{array}{*{20}l} {\left\{ {0.5} \right\}} &\quad {\left\{ {0.3,0.35 + 0.15\varsigma_{1} ,0.7} \right\}} &\quad {\left\{ {0.15,0.35 - 0.1\varsigma_{1} ,0.45} \right\}} &\quad {\left\{ {0.5,0.8 - 0.25\varsigma_{1} ,0.85} \right\}} \\ {\left\{ {0.3,0.65 - 0.15\varsigma_{1} ,0.7} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.4,0.5 + 0.15\varsigma_{1} ,0.75} \right\}} &\quad {\left\{ {0.45,0.65 - 0.1\varsigma_{1} ,0.75} \right\}} \\ {\left\{ {0.55,0.65 + 0.1\varsigma_{1} ,0.85} \right\}} &\quad {\left\{ {0.25,0.5 - 0.15\varsigma_{1} ,0.6} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.35,0.45 + 0.05\varsigma_{1} ,0.6} \right\}} \\ {\left\{ {0.15,0.2 + 0.25\varsigma_{1} ,0.5} \right\}} &\quad {\left\{ {0.25,0.35 + 0.1\varsigma_{1} ,0.55} \right\}} &\quad {\left\{ {0.4,0.55 - 0.05\varsigma_{1} ,0.65} \right\}} &\quad {\left\{ {0.5} \right\}} \\ \end{array} } \right], \hfill \\ \end{gathered}$$

$$\begin{gathered} \overline{H}^{N,2} = \hfill \\ \left[ {\begin{array}{*{20}l} {\left\{ {0.5} \right\}} &\quad {\left\{ {0.4,0.6 - 0.05\varsigma_{2} ,0.8} \right\}} &\quad {\left\{ {0.4,0.6,0.75} \right\}} &\quad {\left\{ {0.45,0.8 - 0.35\varsigma_{2} ,0.8} \right\}} \\ {\left\{ {0.2,0.4 + 0.05\varsigma_{2} ,0.4} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.2,0.4 - 0.05\varsigma_{2} ,0.55} \right\}} &\quad {\left\{ {0.35,0.6 - 0.1\varsigma_{2} ,0.7} \right\}} \\ {\left\{ {0.25,0.4,0.6} \right\}} &\quad {\left\{ {0.45,0.6 + 0.05\varsigma_{2} ,0.5} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.0,0.2 - 0.05\varsigma_{2} ,0.4} \right\}} \\ {\left\{ {0.2,0.2 + 0.35\varsigma_{2} ,0.55} \right\}} &\quad {\left\{ {0.3,0.4 + 0.1\varsigma_{2} ,0.65} \right\}} &\quad {\left\{ {0.6,0.8 + 0.05\varsigma_{2} ,1.0} \right\}} &\quad {\left\{ {0.5} \right\}} \\ \end{array} } \right], \hfill \\ \end{gathered}$$

and

$$\begin{gathered} \overline{H}^{N,3} = \hfill \\ \left[ {\begin{array}{*{20}l} {\left\{ {0.5} \right\}} &\quad {\left\{ {0.25,0.35 - 0.05\varsigma_{3} ,0.6} \right\}} &\quad {\left\{ {0.2,0.5 - 0.15\varsigma_{3} ,0.6} \right\}} &\quad {\left\{ {0.45,0.75 - 0.1\varsigma_{3} ,0.9} \right\}} \\ {\left\{ {0.4,0.35 + 0.05\varsigma_{3} ,0.75} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.4,0.65 - 0.1\varsigma_{3} ,0.85} \right\}} &\quad {\left\{ {0.15,0.4 - 0.15\varsigma_{3} ,0.55} \right\}} \\ {\left\{ {0.4,0.5 + 0.15\varsigma_{3} ,0.8} \right\}} &\quad {\left\{ {0.15,0.35 + 0.1\varsigma_{3} ,0.6} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.35,0.55 - 0.05\varsigma_{3} ,0.7} \right\}} \\ {\left\{ {0.1,0.25 + 0.1\varsigma_{3} ,0.55} \right\}} &\quad {\left\{ {0.45,0.6 + 0.15\varsigma_{3} ,0.85} \right\}} &\quad {\left\{ {0.3,0.45 + 0.05\varsigma_{3} ,0.65} \right\}} &\quad {\left\{ {0.5} \right\}} \\ \end{array} } \right]. \hfill \\ \end{gathered}$$

Step 2.3: Utilize Eq. (9) to obtain the value of the optimal parameters $\varsigma_{1} = 0.43$, $\varsigma_{2} = 1$ and $\varsigma_{3} = 0$.

Step 2.4: Return the values $\varsigma_{1} = 0.43$, $\varsigma_{2} = 1$ and $\varsigma_{3} = 0$ to $\overline{H}^{1}$, $\overline{H}^{2}$ and $\overline{H}^{3}$, the NHFPRs are obtained as follows:

$$\overline{H}^{1} = \left[ {\begin{array}{*{20}l} {\left\{ {0.50} \right\}} &\quad {\left\{ {0.30,0.41,0.50} \right\}} &\quad {\left\{ {0.50,0.60,0.70} \right\}} &\quad {\left\{ {0.40,0.40,0.40} \right\}} \\ {\left\{ {0.50,0.59,0.70} \right\}} &\quad {\left\{ {0.50} \right\}} &\quad {\left\{ {0.40,0.51,0.60} \right\}} &\quad {\left\{ {0.60,0.66,0.70} \right\}} \\ {\left\{ {0.30,0.40,0.50} \right\}} &\quad {\left\{ {0.40,0.49,0.60} \right\}} &\quad {\left\{ {0.50} \right\}} &\quad {\left\{ {0.60,0.71,0.80} \right\}} \\ {\left\{ {0.60,0.60,0.60} \right\}} &\quad {\left\{ {0.30,0.34,0.40} \right\}} &\quad {\left\{ {0.20,0.29,0.40} \right\}} &\quad {\left\{ {0.50} \right\}} \\ \end{array} } \right], $$

$$\overline{H}^{2} = \left[ {\begin{array}{*{20}l} {\left\{ {0.5} \right\}} &\quad {\left\{ {0.6,0.6,0.7} \right\}} &\quad {\left\{ {0.6,0.6,0.8} \right\}} &\quad {\left\{ {0.4,0.4,0.5} \right\}} \\ {\left\{ {0.3,0.4,0.4} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.5,0.7,0.8} \right\}} &\quad {\left\{ {0.2,0.2,0.4} \right\}} \\ {\left\{ {0.2,0.4,0.4} \right\}} &\quad {\left\{ {0.2,0.3,0.5} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.5,0.5,0.7} \right\}} \\ {\left\{ {0.5,0.6,0.6} \right\}} &\quad {\left\{ {0.6,0.8,0.8} \right\}} &\quad {\left\{ {0.3,0.5,0.5} \right\}} &\quad {\left\{ {0.5} \right\}} \\ \end{array} } \right], $$

and

$$\overline{H}^{3} = \left[ {\begin{array}{*{20}l} {\left\{ {0.5} \right\}} &\quad {\left\{ {0.4,0.6,0.7} \right\}} &\quad {\left\{ {0.5,0.6,0.7} \right\}} &\quad {\left\{ {0.3,0.4,0.4} \right\}} \\ {\left\{ {0.3,0.4,0.6} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.3,0.5,0.5} \right\}} &\quad {\left\{ {0.6,0.8,0.8} \right\}} \\ {\left\{ {0.3,0.4,0.5} \right\}} &\quad {\left\{ {0.5,0.5,0.7} \right\}} &\quad {\left\{ {0.5} \right\}} &\quad {\left\{ {0.4,0.5,0.6} \right\}} \\ {\left\{ {0.6,0.6,0.7} \right\}} &\quad {\left\{ {0.2,0.2,0.4} \right\}} &\quad {\left\{ {0.4,0.5,0.6} \right\}} &\quad {\left\{ {0.5} \right\}} \\ \end{array} } \right]. $$

Step 3: Calculate the individual consistency indexes.

According to Eq. (5), we have: ${\text{CI}}\left( {H^{1} } \right) = 0.16$, ${\text{CI}}\left( {H^{2} } \right) = 0.21$ and ${\text{CI}}\left( {H^{3} } \right) = 0.22$.

Step 4: Determine the acceptable consistent NHFPRs.

Set $\alpha { = 0}{\text{.1}}$, it is obvious that ${\text{CI}}\left( {H^{t} } \right) > \alpha$, $t = 1,2,3$. Then the consistency of $H^{1}$, $H^{2}$ and $H^{3}$ are unacceptable, the acceptable consistent NHFPRs are determined.

According to algorithm 2, first, the set of 3-tuples ${\text{ECI}}$ identified under the threshold $\alpha { = 0}{\text{.1}}$ are:

$${\text{ECI}} = \left\{ \begin{gathered} \left( {1,1^{1} ,3} \right),\left( {1,1^{2} ,3} \right),\left( {1,1^{3} ,3} \right),\left( {1,1^{2} ,4} \right),\left( {1,1^{3} ,4} \right),\left( {1,2^{3} ,3} \right),\left( {1,2^{1} ,4} \right),\left( {1,3^{1} ,4} \right),\left( {1,3^{2} ,4} \right),\left( {1,3^{3} ,4} \right),\left( {2,1^{1} ,2} \right), \hfill \\ \left( {2,1^{1} ,3} \right),\left( {2,1^{3} ,4} \right),\left( {2,2^{1} ,3} \right),\left( {2,2^{2} ,3} \right),\left( {1,2^{3} ,3} \right),\left( {2,2^{1} ,4} \right),\left( {2,2^{2} ,4} \right),\left( {1,2^{3} ,4} \right),\left( {2,3^{1} ,4} \right),\left( {2,3^{2} ,4} \right),\left( {1,3^{3} ,4} \right), \hfill \\ \left( {3,1^{1} ,2} \right),\left( {3,1^{2} ,2} \right),\left( {3,1^{1} ,3} \right),\left( {3,1^{1} ,4} \right),\left( {3,1^{2} ,4} \right),\left( {3,1^{3} ,4} \right),\left( {3,2^{2} ,3} \right),\left( {3,2^{3} ,3} \right),\left( {3,2^{1} ,4} \right),\left( {3,2^{2} ,4} \right),\left( {3,2^{3} ,4} \right) \hfill \\ \end{gathered} \right\}.$$

Second, utilize Eq. (12) to obtain the value of the optimal parameter: $\tau^{{1}} = 0.67$, $\tau^{{2}} = 0.35$ and $\tau^{{3}} = 0.28$, the acceptable consistent NHFPRs are obtained as follows:

$$\tilde{H}^{1} = \left[ {\begin{array}{*{20}l} {\left\{ {0.5{0}} \right\}} &\quad {\left\{ {0.30,0.41,0.50} \right\}} &\quad {\left\{ {0.27,0.41,0.53} \right\}} &\quad {\left\{ {0.40,0.59,0.70} \right\}} \\ {\left\{ {0.50,0.59,0.70} \right\}} &\quad {\left\{ {0.50} \right\}} &\quad {\left\{ {0.40,0.51,0.70} \right\}} &\quad {\left\{ {0.50,0.66,0.70} \right\}} \\ {\left\{ {0.47,0.59,0.73} \right\}} &\quad {\left\{ {0.30,0.49,0.60} \right\}} &\quad {\left\{ {0.50} \right\}} &\quad {\left\{ {0.43,055,0.67} \right\}} \\ {\left\{ {0.30,0.41,0.60} \right\}} &\quad {\left\{ {0.30,0.34,0.50} \right\}} &\quad {\left\{ {0.33,0.45,0.57} \right\}} &\quad {\left\{ {0.50} \right\}} \\ \end{array} } \right], $$

$$\tilde{H}^{2} = \left[ {\begin{array}{*{20}l} {\left\{ {0.50} \right\}} &\quad {\left\{ {0.53,0.60,0.70} \right\}} &\quad {\left\{ {0.53,0.60,0.80} \right\}} &\quad {\left\{ {0.40,0.40,0.61} \right\}} \\ {\left\{ {0.30,0.40,0.47} \right\}} &\quad {\left\{ {0.50} \right\}} &\quad {\left\{ {0.39,0.58,0.71} \right\}} &\quad {\left\{ {0.25,0.31,0.51} \right\}} \\ {\left\{ {0.20,0.40,0.47} \right\}} &\quad {\left\{ {0.29,0.42,0.61} \right\}} &\quad {\left\{ {0.50} \right\}} &\quad {\left\{ {0.33,0.38,0.60} \right\}} \\ {\left\{ {0.39,0.60,0.60} \right\}} &\quad {\left\{ {0.49,0.69,0.75} \right\}} &\quad {\left\{ {0.40,0.62,0.67} \right\}} &\quad {\left\{ {0.50} \right\}} \\ \end{array} } \right], $$

and

$$ \tilde{H}^{3} = \left[ {\begin{array}{*{20}l} {\left\{ {0.50} \right\}} &\quad {\left\{ {0.36,0.53,0.70} \right\}} &\quad {\left\{ {0.42,0.60,0.70} \right\}} &\quad {\left\{ {0.26,0.5,0.54} \right\}} \\ {\left\{ {0.30,0.47,0.64} \right\}} &\quad {\left\{ {0.50} \right\}} &\quad {\left\{ {0.30,0.54,0.60} \right\}} &\quad {\left\{ {0.47,0.69,0.73} \right\}} \\ {\left\{ {0.30,0.40,0.58} \right\}} &\quad {\left\{ {0.40,0.46,0.70} \right\}} &\quad {\left\{ {0.50} \right\}} &\quad {\left\{ {0.40,0.50,0.60} \right\}} \\ {\left\{ {0.46,0.50,0.74} \right\}} &\quad {\left\{ {0.27,0.31,0.53} \right\}} &\quad {\left\{ {0.40,0.50,0.60} \right\}} &\quad {\left\{ {0.50} \right\}} \\ \end{array} } \right].$$

Step 5: Derive a group of acceptable consistent NHFPRs.

Since $\tilde{H}^{1}$, $\tilde{H}^{2}$ and $\tilde{H}^{3}$ have the same number of elements, the normalized process is unnecessary, then go to next step.

Step 6: Calculate the consensus indexes.

The consensus indexes are calculated with respective to Eq. (17) as follows: ${\text{GCI}}^{1} = 0.88$, ${\text{GCI}}^{{2}} = 0.8{7}$ and ${\text{GCI}}^{{3}} = 0.{91}$.

Step 7: Improve the consensus level.

Set $\beta = 0.8$, since all the consensus indexes ${\text{GCI}}^{t} > \beta$, $t = 1,2,3$, then the consensus reaching process has been achieved.

Step 8: Determine the weights of decision makers.

The weights of decision makers are determined as follows:

According to Eq. (21), we have $\pi^{1} = 0.4$, $\pi^{2} = 0.31$ and $\pi^{3} = 0.29$.

With respective to Eq. (22), we have $\vartheta^{1} = 0.33$, $\vartheta^{2} = 0.33$ and $\vartheta^{3} = 0.34$.

Set $\delta = 0.5$, based on Eq. (23), we obtain: $w^{1} = 0.37$, $w^{2} = 0.32$ and $w^{3} = 0.32$.

Then, according to Eq. (24), we derive: $\lambda^{1} = 0.37$, $\lambda^{2} = 0.32$ and $\lambda^{3} = 0.32$.

Step 9: Obtain the collective NHFPR.

The collective NHFPR is derived with respective to Eq. (16) as follows:

$$H^{c} = \left[ {\begin{array}{*{20}l} {\left\{ {0.50} \right\}} & {\left\{ {0.40,0.52,0.64} \right\}} & {\left\{ {0.41,0.54,0.69} \right\}} & {\left\{ {0.36,0.51,0.63} \right\}} \\ {\left\{ {0.36,0.48,0.60} \right\}} & {\left\{ {0.50} \right\}} & {\left\{ {0.37,0.55,0.68} \right\}} & {\left\{ {0.42,0.59,0.66} \right\}} \\ {\left\{ {0.31,0.46,0.59} \right\}} & {\left\{ {0.32,0.45,0.63} \right\}} & {\left\{ {0.50} \right\}} & {\left\{ {0.39,0.49,0.63} \right\}} \\ {\left\{ {0.37,0.49,0.64} \right\}} & {\left\{ {0.34,0.41,0.58} \right\}} & {\left\{ {0.37,0.51,0.61} \right\}} & {\left\{ {0.50} \right\}} \\ \end{array} } \right].$$

Step 10: Calculate the score values of collective NHFPR.

The score values of collective NHFPR are determined according to Eq. (25) as follows:

$\vartheta_{1} = 0.42$, $\vartheta_{2} = 0.40$, $\vartheta_{3} = 0.36$ and $\vartheta_{4} = 0.35$.

Step 11: Rank the alternatives.

Since $\vartheta_{1} > \vartheta_{2} > \vartheta_{3} > \vartheta_{4}$, the ranking order of all alternatives is obtained as $a_{1} \succ a_{2} \succ a_{3} \succ a_{4}$. Thus, graduate student $a_{1}$ is ranking at number one for awarding scholarship.

Comparative analysis and discussion

To validate the feasibility of the proposed method, we conducted a comparative study with other method based on the same illustrative example.

Wan et al. [31] developed a new method for group decision making with HFPRs considering the multiplicative consistency and consensus simultaneously. Moreover, to improve the consistency and consensus simultaneously, a goal program is established to obtain a group of HFPRs with acceptable consistency and consensus. Finally, the final ranking is generated by the collective overall values of alternatives. To a better comparison, the results obtained by Wan et al. [31]’s method and the proposed method are summarized in Table 1.

Table 1 The ranking results of the different methods

As shown in Table 1, it can be seen that same ranking result is obtained from these two methods in the same illustrative example. This also confirms the effectiveness of the proposed method. The possibility reasons for the same ranking result are explained as follows. These methods both develop the methods to checking the consistency of HFPRs. For the unexpected consistency one, the algorithms are design to improve the consistency level. Moreover, in the consensus reaching process, the individual consistency of HFPRs and group consensus among the group HFPRs are considering simultaneously. In the selecting process, the final ranking both use the score function of the collective overall values of alternatives. Although these two methods derive the same ranking in the illustrative example, there are some differences between these methods. To check the consistency of the individual HFPRs, Wan et al.’s [31] method depends on the HFPR itself, while the proposed method constructs the completely additive consistent HFPRs. In the consistency and consensus improving process, Wan et al.’s [31] method utilize the minimum distance between revised HFPRs and original HFPRs, this may lead to the whole revised of original information, while the proposed method first identify the values that need to be revised, it is a local adjustment process. And the proposed method construct the linear programming models, while Wan et al.’s [31] method used goal programming models. Furthermore, the algorithm to obtain a group of NHFPRs are developed in the proposed method, which considering the consistency of HFPRs.

To verify the advantages of our approaches, we compare them with several representative models under the MCDM environment with HFPRs. Table 2 presents the performances of these approaches regarding several indexes.

• 1. Zhu et al. [52] and Xu et al. [40]: These approaches derived priority weights of alternatives based on a reduced FPR with the highest consistency degree derived from HFPR, and obtained the priority weights rely on only one stage strategy. Compared to Zhu et al. [52] and Xu et al. [40]’s approaches, the proposed method develops the concept of consistency based on NHFPR, to derive the priority weights focus on improving the consistency and consensus processes. Based on this fact, the proposed method has advantage in avoiding the loss of information and the priority weights deriving process seems more reasonable.

• 2. Zhang et al. [44] and Zhang et al. [45]. These approaches first defined the concepts of additive and multiplicative consistent HFPR, and then developed two programming models to derive the priority weights from HFPR based on additive and multiplicative consistency, respectively. Compared to Zhang et al. [44] and Zhang et al. [45]’s approaches, the proposed method defines the consistency and consensus indexes based on NHFPR, while Zhang et al. [44] and Zhang et al. [45]’s approaches based on all possible FPRs, this seems too restricted. For deriving the priority weights process, the proposed method focus on improving the consistency and consensus processes, while Zhang et al. [44] and Zhang et al. [45]’s approaches only considering the consistency process. The consensus reaching process considers the discordant opinions among experts. On account of these, the proposed method has advantage in avoiding the loss of information and the calculation seems simpler.

• 3. Meng et al. [18] and Meng et al. [20]. These approaches first defined the concepts of acceptably additive and multiplicative consistent HFPR, and then a series of optimization models to acquire acceptable consistent HFPR. Furthermore, an optimal model for reaching the consensus threshold is constructed. Finally, the priority weights are derived based on certain indexes. Compared to Meng et al. [18] and Meng et al. [20]’s approaches, the proposed method defines the consistency and consensus indexes based on NHFPR, while Meng et al. [18] and Meng et al. [20]’s approaches based on some possible FPRs, this seems too restricted. For improving the consistency and consensus processes, the proposed method using local adjustment method, while Meng et al. [18] and Meng et al. [20]’s approaches utilizing global adjustment method. It may lead to a great extent destroy the original evaluation information. In view of these, the proposed method has advantage in avoiding the loss of information and the calculation seems simpler.

Table 2 Comparisons of different MCDM approaches with HFPR

According to the comparison analysis, the method proposed in this study has the following advantages over other existing methods.

• 1. To improve the consistency of the individual HFPRs, the proposed method constructs the completely additive consistent HFPRs. This provides the direction of the decision makers to revise their evaluation values, and the consistency improving process is time-saving.

• 2. In the consistency and consensus improving processes, proposed method first identify the values that need to be revised, and design the local adjustment process. The proposed method can ensure the revised HFPRs retain the original evaluation information as much as possible. Furthermore, the proposed process constructs the linear programming models, there are more simple and the models can ensure that the global optimal solution is obtained [3].

• 3. The algorithm to obtain a group of NHFPRs are developed in the proposed method, which considering the consistency of HFPRs.

Conclusion

To address the situation where the MCDM problems with HFPRs, this paper develops a group decision making method considering the additive consistency and consensus simultaneously. First, a new normalized method for HFPRs is developed to address the situation where the evaluation information with different number of elements. Second, for improving the unacceptable consistent HFPR, an algorithm is designed to derive an acceptable consistent HFPR. Third, the algorithm to obtain a group of NHFPRs is developed. Fourth, to improve the individual consistency and group consensus simultaneously, an algorithm is designed to obtain a new group of HFPRs with acceptable consistency and consensus. Finally, a procedure for MCDM problems with HFPRs is given. An illustrative example in conjunction with comparative analysis is provided.

The present study provides several significant contributions for MCDM problems with HFPRs. They are summarized as follows: (1) a new normalized method for HFPRs is developed to address the situation where the evaluation information with different number of elements. The main characteristic of the design algorithm is that normalized model can ensure that the global optimal solution is obtained, and the normalized results seem more objective. (2) An algorithm is designed to derive an acceptable consistent HFPR. The main characteristic of the design algorithm is that the values need to be revised are identified first, and then design the local adjustment process. This can ensure the revised HFPRs retain the original evaluation information as much as possible. (3) An algorithm is designed to obtain a group of HFPRs with acceptable consistency and consensus, which can overcome the shortcoming that some studies only considering the consistency or consensus alone. In our future research, we will continue to conduct research on the consensus reaching process and propose a method that focuses on determining the adjustment parameter in a social networking environment. Moreover, we will extend the proposed consensus reaching process to other extensions of fuzzy sets, such as probabilistic hesitant fuzzy sets, dual hesitant fuzzy sets and so on. In addition, the application of the presented method in clustering analysis and solving other practical MCDM problems will be further studied.