Abstract
Grasp estimation is a fundamental technique crucial for robot manipulation tasks. In this work, we present a scene-oriented grasp estimation scheme taking constraints of the grasp pose imposed by the environment into consideration and training on samples satisfying the constraints. We formulate valid grasps for a parallel-jaw gripper as vectors in a two-dimensional (2D) image and detect them with a fully convolutional network that simultaneously estimates the vectors’ origins and directions. The detected vectors are then converted to 6 degree-of-freedom (6-DOF) grasps with a tailored strategy. As such, the network is able to detect multiple grasp candidates from a cluttered scene in one shot using only an RGB image as input. We evaluate our approach on the GraspNet-1Billion dataset and archived comparable performance as state-of-the-art while being efficient in runtime.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
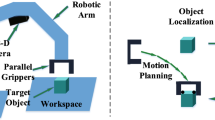
Grasping is an engaging and demanding skill for robots leveraged in industrial [1], home service [2], and logistic domains [3]. In these scenarios, the robot is often imposed with a diverse category of objects to grasp, whose appearance, precise three-dimensional (3D) models, and physical characters are unknown beforehand. Furthermore, the objects could be cluttered in a pile, making it even harder to distinguish them. Despite the difficulty of the grasping task, it is also required to be conducted at a high pace. For instance, in the logistics bin-picking scenario where the mean pick per hour (MPPH) metric is adopted to evaluate a robotic grasping system’s performance [4], an acceptable MPPH should exceed 600 to be considered as compatible with humans.
Due to robotic grasping’s wide applications and its fundamental role in robotic manipulation research, much literature has focused on the topic as detailed in section “Related work”. However, this problem is still considered open as it requires the grasping system to dynamically reason the potential interactions among the triplet—the robot, the object to grasp, and the environment they both belong to. In this sense, solely considering the object out of context is not enough for a successful grasp. The robot’s limited workspace may not encapsulate the ideal grasp pose; the collision in the scene may prevent particular trajectories from being executed; or, frequently, the grasping strategy may fail when the gripper is changed, or the environment is altered. These challenges essentially entail a comprehensive treatment for the triplet, wherein the constraints for generating grasps should be considered.
To be more specific, we categorize the grasp estimation approaches as object-oriented and scene-oriented. The first emphasizes object pose estimation, as if the model and the pose of the target object are known, one could transform predefined (by heuristic, analytic, or experimental methods) grasp poses adhered with the object model to the scene. Consequently, valid grasp poses could be filtered out from the candidates subject to the constraints. This kind of approach often relies on a database filled with complete 3D models of the objects, which helps the algorithm transfer to novel objects or provide key semantic/geometric landmarks for registering archived objects with those in the scene.
For object-oriented methods, its strength and weakness both arise from the heavy reliance on the database. The advantage is that it could produce a precise grasp, especially when the object in the scene is observed holistically and its reconstructed shape and texture are intact. However, building a large-scale 3D dataset is a non-trivial task, especially for the end-user of the grasping system who wants to add new objects at hand to the dataset but lacks the equipment and expertise. Moreover, the imaging in real-world scenarios could be highly affectable, resulting in a loss of crucial landmark features. Consequently, object-oriented methods relying on a static database could hardly scale to dynamic scenes and novel/deformable objects.
By contrast, scene-oriented approaches pursue an understanding of the whole scene. The same visual sensory criteria (viewing angle and distance, camera adopted, etc.) keep the input consistency for training and inferencing. Unlike object-oriented methods relying on predefined grasps of isolated objects, this spectrum of methods leverages a sampling procedure to produce grasp candidates on the fly. The sampling module could be a trained neural network estimating a grasp’s quality or directly regressing to coefficients composing a grasp. Although in the training phase, scene-oriented methods could also benefit from a large-scale dataset with predefined grasps, the distinctions are, first, the dataset is developed in an object agnostic manner where objects are free to be added, removed, or deformed, such that a generic sampling strategy could be learned; second, invalid grasps could be filtered out at the very beginning of generating training samples, instead of leaving that to the implementation. As a result, the robot–object–environment triplet’s kinematic and physical constraints could be considered early, eliminating unexpected behaviour (e.g., posing the gripper underneath the table), the error induced by registration, and unnecessary computation cost.
As explained above, the scene-oriented concept could potentially alleviate some most challenging damping factors in grasp estimation, such as clutter and imperfect imaging, and also save time during grasp estimation. However, there is a barrier to break, i.e., how to make the estimation generalizable. Specifically, this problem is two-fold. First, it should be compatible with different configurations regarding scenes, objects, grippers, sensors, viewing perspectives, etc. Second, it should make sure that the fine-tuning or re-training of the model is painless if the configurations changed drastically. For the first aspect, much research shows that leveraging a large-scale scene dataset could enhance the scalability of the model trained on them. We closely followed this idea and leveraged the GraspNet-1Billion [5] (for succinctness, we call it GraspNet afterwards) dataset to facilitate our scene-oriented grasp estimation approach. While for the second aspect, we highlight that the proposed Grasp Vector Detection Network (GraspVDN) could ease the training and fine-tuning confronted with changeable configurations since it directly estimates the grasp parameters in a minimum footprint with primary input (like RGB images), and is agnostic to the object or gripper type. The details of this approach are given in section “Methods”.
In a nutshell, this work’s core idea is using a large-scale scene dataset to endow a relatively simple network with the ability to generalize and adapt. Following this idea, we made three contributions in the grasp estimation domain:
-
1.
We proposed a learning-based method for grasp estimation that could take RGB, depth, or RGB-D images of the scene as input, estimating grasps for parallel-jaw grippers with concise parameters in an end-to-end fashion. In its simplest form, the parameters yield by GraspVDN includes the centre coordinates of the gripper and the open direction in the image plane.
-
2.
A strategy was proposed to convert the estimation of GraspVDN to an applicable grasp pose for the robot equipped with a parallel gripper to execute.
-
3.
We evaluated our model with the GraspNet test split and compared the performance with the state of the art. The results indicated that our approach is compatible with those counterparts in terms of average precision (AP) metric while being significantly efficient in and run time. A series of simulation experiments were also conducted to give insight into the performance of the method.
Related work
In this section, we review the related work of object-oriented and scene-oriented grasp estimations. In general, grasp estimation includes two related subproblems: perception and planning. The former deals with estimating the grasp pose of the gripper subject to the object to grasp and the collisions in the scene. The latter tackles how to reach that pose given the current configuration of the robot under environmental constraints. This review mainly focuses on the perception part, where whether considering the constraints in the environment could be a significant mark for distinguishing object-oriented and scene-oriented approaches.
Object-oriented methods
Object-oriented methods, in their canonical form, try to superpose a predefined rigid 3D model of the target object to its matching geometries in the perceived scene. The matching reveals the pose of the target object in the scene, which is then leveraged to derive corresponding grasp poses. Numerous studies utilizing distinct sensory data address the matching with various techniques for defining the 3D models and performing the registration [6].
Sun et al. [7] matched the segmented 3D point cloud with a primitive geometric model of the target to derive the registration. After a rough pose matching with RANSAC [8], the method refines the pose with the iterative closest point (ICP) algorithm. Its accuracy substantially depends on the matching quality of RANSAC yet is limited by the representativeness of primitive models. To tackle the inability of RANSAC-based methods to scale to large databases, a shape completion framework is proposed in [9] and simplified in [10] to enable grasp estimation. Since if the shape and texture of the perceived object are complete, the object-oriented method could be more accurate. A 3D convolutional neural network (CNN) was trained on a dataset of over 440,000 3D exemplars to learn to complete a segmented point cloud. The completion could generalize to new objects, allowing previously unseen items to be grasped. Yet, it still performs the grasp planning with GraspIt! [11] in an out of context manner, making it an object-oriented method.
Another research line for completing the perceived geometry and estimating its pose is via multi-view fusion [12]. This kind of methods is able to alleviate the damping factors of perception such as poor lighting conditions, clutter, and occlusions. Though, a precise estimation generally requires having an accurate computer-aided design (CAD) model [13] [14] for the target object.
The architecture of the GraspVDN. The input image is firstly processed by ResNet18, whose configurations are detailed in [15]. Then three deconvolution layers increase the spatial dimension of the extracted features. Finally, two branches, respectively, estimate a confidence heatmap and a two-layer scalarmap via \(1 \times 1\) convolution. Note that we apply tanh to the scalarmap branch to make the output values within \([-1,1]\) range
Scene oriented
Scene-oriented approaches pursue an understanding of the whole scene [16]. This kind of method can be generalized to new objects and environments, and dynamically reacts to the environment [17,18,19,20].
Grasping new objects in unknown (complex) scenes is a challenging problem in the field of robotics [21]. In recent years, end-to-end grasp estimation methods on this problem have thrived. These methods deal with the objects in context (the scene), which could be defined as scene-oriented grasp estimation. They take images or point clouds as input and produce viable grasp poses as output. This idea originated in the work of Saxena et al. [22], which enables the robot to grasp objects it has never seen before. The algorithm neither requires nor tries to build or complete a 3D model of the object. Instead, given two (or more) images of an object, it attempts to identify a few grasp points to locate the gripper with a supervised learned model. This set of sparse points is then triangulated to obtain a 3D location at which to attempt a grasp.
Subsequently, Zeng et al. [23] proposed to utilize multi-view RGB-D data self-monitoring and data-driven learning methods to obtain the grasping poses of objects. The system can estimate the object’s 6-DOF grasping poses reliably in a variety of scenes and adapts to the scene. Zapata-Impata et al. [24] proposed an optimal grasp estimation method for 3D point clouds based on the local perspective of unknown objects. This approach is flexible and stable to work with objects in ever-changing scenes but is limited to a non-cluttered environment. Mousavian et al. [25] introduced 6-DOF GraspNet for generating diverse grasps for unknown objects. The method leveraged a trained variational auto-encoder (VAE) to sample multiple grasps for an object. It also presented a scheme to move the gripper closer to a successful grasp pose. Wang et al. [26] proposed a method for robot grasping both rigid and soft objects. This method generates the grasping pose directly along its central axis without relying on a CAD model. An ambidextrous grasping framework is proposed in literature [4] as a significant extension of the previous versions of Dex-Net research. The approach learns strategies by training on a set of grippers using a domain randomized dataset and geometric analysis models. Wu et al. [27] proposed an end-to-end Grasp Proposal Network (GPNet) predicting a diverse set of 6-DOF grasp for an unseen object observed from a single and unknown camera view. GPNet builds on a crucial design for the grasp proposal module that defines anchors of grasp centres at discrete but regular 3D grid corners, being flexible to support either precise or diverse grasp predictions.
Chu et al. [28] presented a grasping detection system to predict grasp candidates for novel objects in RGB-D images. The system test on the Cornell grasping dataset as well as a self-collected multi-object multi-grasp dataset showed the effectiveness of the design. Ten Pas et al. [29] generated grasp hypotheses that do not require a precise segmentation of the object. They proposed incorporating prior knowledge about object categories to increase grasp classification accuracy. Since the algorithm does not segment the objects, it can detect grasps that treat multiple objects as a single atomic object. Liang et al. [30] proposed an end-to-end grasp evaluation model (PointNetGPD) to address the challenging problem of localizing robot grasp configurations directly from the point cloud. It is lightweight and can directly process the 3D point cloud locating within the gripper for grasp evaluation. In [31, 32], Generative Grasping Convolutional Neural Network (GG-CNN) was presented as a grasp synthesis model which directly generates grasp poses from a depth image on a pixel-wise basis, instead of sampling and classifying individual grasp candidates like other deep learning techniques.
Methods
This section first gives a comprehensive overview of the procedure using GraspVDN to generate grasp proposals for a robotic grasping system. Then we explain the architecture, training data generation, and optimization of GraspVDN in detail. Finally, we present the strategy for producing proper grasp poses with the output of GraspVDN and discuss the advantages and limitations of the proposed method.
Overview
As humans, we could grasp novel objects in a cluttered scene with our hands without being told the grasp affordances. We assume such capability partially comes from the perception and understanding of the possible interaction between the hand and the graspable regions that could be deduced from local geometry and visual appearance due to life-long practice (training) on grasping. Such assumption inspired us to start with simple visual input and biomimetic grasping modal, e.g., using RGB image as input and two-fingered parallel-jaw gripper, to deliver the perception and interaction aided by a learnable model.
Since the dynamic interaction between the gripper and the object could be complicated and intractable, we simplify it to a one-shot grasp parameterized by i) the 2D coordinates of the middle point (the projection of the palm centre \(\mathbf {m}\) on the image plane, referred as \(\mathbf {m}'\)Footnote 1) in the image I, along with ii) the opening direction from \(\mathbf {m}' \) to the open point (geometric centre \(\mathbf {o}\) of one of the two fingers projected on the image, referred as \(\mathbf {o} '\)). With \(\mathbf {m}'\) and \(\mathbf {o}'\), we formulate a vector label for a grasp analogue to the rectangle label in the grasp estimation context. The details are given in section “Training data generation”.
Essentially, such parameterization turned the grasp estimation into a 2D vector detection problem, as \(\overrightarrow{\mathbf {m}'\mathbf {o}'}\) naturally depict a vector. As such, it extends the application of the Vector Detection Network (VDN) [33] to this domain. To make a quick brief, VDNs derived the inspiration from human keypoints estimation and proposed detecting directions along with keypoints, where the common problem is to find semantically significant local keypoints in clutter. In this work, we further generalize the idea of vector detection from one category of objects (pointers of analog meters in the previous case) to arbitrary graspable objects.
Since only a minimum set of parameters representing the grasps is output by GraspVDN, they need to be converted to 6-DOF grasp poses by tailored strategies. Accordingly, we present the vertical grasping strategy, forcing the approaching direction to be vertical to the image plane. By this means, with the 3D position of the middle point \(\mathbf {m}\) derived from its 2D coordinates and camera parameters, we could determine the 6-DOF pose of the gripper in space based on \(\mathbf {m}\), the approaching direction, and the orthogonal \(\overrightarrow{\mathbf {m} '\mathbf {o}'}\) orientation. This scheme is remarkably straightforward for a camera-in-hand configuration and also applicable for a camera-over-shoulder setting.
Please note that our approach could generalize to multi-fingered grippers without enormous reversion by redefining the middle point and the open point in the gripper frame. Besides, it could also be enhanced by adding depth images as input, as depicted in section “Main results”.
Grasp vector detection network
Network architecture
The architecture (illustrated in Fig. 1) is a fully convolutional network (FCN) with dual outputs. GraspVDN takes a batch of RGB images (by default we used RGB images but it could be easy to switch to depth or RGB-D images) as input. It uses a ResNet backbone for feature extraction, followed by three deconvolutional layers for feature upscaling, whose output is separately processed by two branches of \(1 \times 1\) convolutional layers that generate a heatmap and a scalarmap, respectively. The 1-channel heatmap represents a dense estimation of a pixel’s likelihood corresponding to the grasp middle point. Its pixel values are in the range [0, 1] (converted to false colour in Fig. 1), where the higher the value, the more likely the pixel represents a valid grasp. Besides, the scalarmap has the same width and height as the heatmap, such that the pixels in the heatmap have a one-on-one coherence with those on the scalarmap. However, the scalarmap is a product of stacking two channels. In each channel, the pixel value represents one of the two scalar components of the resulting unit vector, whose scalar values’ quadratic sum numerically equals to 1. Notice that this only holds for middle point pixels and their adjacent regions. Otherwise, the pixel values would be set as zeros for both channels. As a result, we could perceive these infected regions as squares with solid colours in Fig. 1, where for each channel, the pixel values are in the \([-1,1]\) range and displayed with false colours. The network’s architecture and its training data are tailored to fulfil this value range. Consequently, a heatmap peak could query the 2-channel scalarmap with its coordinates and retrieve the unit vectors’ scalar components to yield the grasp.
Training data generation
We leveraged the GraspNet dataset for training and evaluating GraspVDN. This dataset is chosen because it provides a large-scale multi-object-multi-grasp grasp pose detection dataset with a unified evaluation system. The dataset contains 97,280 RGB-D images from 190 cluttered scenes with over one billion grasp poses. In each scene, two sets of RGB-D images are captured with an Intel RealSense 435 and a Kinect 4 Azure RGB-D camera, respectively, in a camera-in-hand fashion. This setting ideally meets the criteria of training GraspVDN because grasping along the same direction as perception raises the probability of the grasp being executed by the co-axis gripper compared with one detected in a different viewing point.
The training data of GraspVDN are images in the train split, together with the derivatives of corresponding grasp labels. GraspNet provides both 6-DOF grasp labels and rectangle labels. The meaning of the parameters denoting 6-DOF grasps is depicted in Fig. 2.
The rectangle labels provided by GraspNet ease the conversion from 6-DOF labels to vector labels. To convert 6-DOF labels to rectangle labels, first, \(\mathbf {a}_\text {grp}=\left( 1,0,0\right) ^\intercal \) is leveraged to represent the approaching vector in the gripper’s frame. Then for each positive 6-DOF grasp being feasible for the gripper and collision free, with the rotation matrix \(\mathbf {R} \in SO(3)\) given by the ground-truth label, one could transform \(\mathbf {a}_\text {grp}\) to the camera frame, deriving its coordinates \(\mathbf {a}\) as
By definition, \(\mathbf {a}_\text {cam}\) should be almost parallel with the Z-axis of the camera frame. The included angle \(\theta \) between the Z-axis and \(\mathbf {a}_\text {cam}\) is utilized to judge whether a grasp is valid for propagating to subsequential processes, where \(\theta \le 0.15\) radians is considered valid in our implementation. The 6-DOF grasp labels before and after the pruning are depicted in Fig. 3.
With the pruning scheme, we identified valid 6-DOF grasps and utilized the official API to convert them to rectangle labels \(\mathcal {R}\), each composed by
which is further converted to a vector label:
where \(\mathbf {u}'=(\alpha , \beta )\) is a unit vector having the same initial point and direction as \(\overrightarrow{\mathbf {m}'\mathbf {o}'}\); s is the score of the grasp; h is the height in Fig. 4. Notice that we ignored the half opening width \(\Vert \mathbf {m}'\mathbf {o}'\Vert \) and h, since they have no impact on the ground truths for training GraspVDN, and omitting them lets GraspVDN act in a pure gripper-agnostic and object-agnostic way.
Assume that \(\mathcal {G}_\mathcal {V}=\left\{ \mathcal {V}_1,\ldots ,\mathcal {V}_n \right\} \) is a set of n vector labels for an RGB image I, during the training phase, GraspVDN takes an affine transformed I as input (here we omit the batch for briefly), where the transform T is composed by random rotation and scaling. As a result, GraspVDN predicts a heatmap \(\hat{H}\) and a scalarmap \(\hat{S}\) to be regressed to the ground-truth heatmap H and scalarmap S, respectively.
For H, we initialize it with an empty map filled with zeros, and calculate the value for each pixel \(\mathbf {p}^*\) in H by applying a 2D Gaussian centered on \(\mathbf {m}_k^*\):
where \(\lambda \) is a constant shrink factor determined by the network architecture; \(\sigma \) is the standard deviation controlling the sharpness of the Gaussian; \(\eta \) is the number of selected grasps that build up H. Note that \(\eta \) could be different with the number of vector labels n; T is an affine transform with random rotation and scaling. In case that \(n \ge 20\), we select the best 20 labels according to their scores, and if \(n < 20\), then \(\eta = n\). In other words, GraspVDN regresses to top-20 grasps in a run, where 20 outnumbered the total object number in a GraspNet scene, enabling at least one grasp for an object. Please note that the top-20 labels are also induced to be from different objects to make the peaks sparse on the heatmap. This prevents grasps for one object dominate the ground truth. However, if two or more Gaussian regions do overlap, the pixel value \(H(\mathbf {p}^*)\) will be the maximum of the overlapped values.
For S, we respectively initialize its two channels \(S_\alpha \) and \(S_\beta \) with null maps of the same size as H, where \(\alpha \) and \(\beta \) mark the two scalar components of a vector. We derive the value of each pixel \(\mathbf {p}^*\) of them \(\forall k\in [1, \eta ]\) in a first-come-first-served way. Let
where \(S_{\alpha ,k}(\mathbf {p}^*)\) and \(S_{\beta ,k}(\mathbf {p}^*)\) are temporary maps respectively denoting the kth scalars contributed to the two channels of S at pixel \(\mathbf {p}^*\). Then for \(k \in [1, \eta ]\), we have
where \(\xi \) could be \(\alpha \) or \(\beta \).
From Eq. 7, we could tell that once the pixel value in \(S_\xi (\mathbf {p}^*)\) is manipulated, it will stay unchanged in subsequential processes as first-come-first-served. In other words, the areas touched formerly will not be overlapped by successors. Finally, S is derived by stacking \(S_\alpha \) and \(S_\beta \) along the channel dimension.
Optimization
GraspVDN minimizes the mean squared error (MSE) loss between the predicted maps and the ground truth maps. Let \(L(\hat{H},H)\) be the MSE loss between \(\hat{H}\) and H, and \(L(\hat{S},S)\) be the MSE loss between \(\hat{S}\) and S, the overall lose \(L_\epsilon \) for epoch \(\epsilon \) is
where \(\epsilon \in [0,\zeta -1]\) is the epoch index; \(\zeta \) is the total training epochs; \(\omega \) is a constant impending \(L(\hat{S},S)\) to dominate the early stage of training. The loss \(L(\hat{S},S)\) is specifically tackled as this because we observed that it converges slower than \(L(\hat{H},H)\). Without the treatment, GraspVDN will be prone to stuck in local maxima. From an empirical view, the reason for this phenomenon is that the semantic location of the middle point is significantly supported by underlying patterns than its semantic orientation, and the estimation of orientations would only be possible after having an accurate estimation of middle points.
6-DOF grasp conversion
The vertical grasping strategy is proposed to convert vector labels of grasps to 6-DOF labels. Formally, the 6-DOF label could be described as a set \(\mathcal {W}\):
where \(\mathbf {m} \in \mathbb {R}^3\) is the middle point’s 3D coordinates in the camera frame; \(\mathbf {R} \in SO(3)\) is the rotation matrix of the gripper frame subject to the camera frame; w is the half open width of the gripper for the grasp; d is the grasp depth as depicted in Fig. 2; s, h, and i follow the same definition as in Eqs. 2 and 3.
First, we highlight that \(\mathbf {m}\) could be derived with its 2D projection \(\mathbf {m}'\) by
where \(\mathbf {m}=(x_{\mathbf {m}},y_{\mathbf {m}},z_{\mathbf {m}})\); \(\mathbf {m}'=(x_{\mathbf {m}'},y_{\mathbf {m}'})\); \(f_x\) and \(f_y\) are the focal length of the camera in X- and Y-directions; \((c_x, c_y)\) is the principal point of the camera; z is the distance between \(\mathbf {m}\) and the camera origin, which could be queried from the depth image D registered to the image I.
To obtain \(\mathbf {m}'\), we turn to its estimation \(\hat{\mathbf {m}}'\) derived from the network output \(\hat{H}\). We apply the peak-local-max algorithm on \(\hat{H}\), and identify the detected peak as \(\hat{\mathbf {m}}^*\), which is then converted to \(\mathbf {m}'\) as
where \(T^\dagger \) denotes the inverse of the affine transform T.
For the rotation matrix \(\mathbf {R}\), recall that with \(\mathbf {m}'\) and \(\mathbf {u}'\) in Eq. 3, we could locate the 2D point \(\mathbf {p}'\), where \(\overrightarrow{\mathbf {m}'\mathbf {p}'}\) is parallel with \(\mathbf {u}'\). Using the same scheme as Eqs. 10–12 and let \(z=z_\mathbf {m}\), we get the 3D position of \(\mathbf {p}\). Then, with cross product, we get the 3D vector \(\overrightarrow{\mathbf {m}\mathbf {q}}\) orthogonal to \(\overrightarrow{\mathbf {m}\mathbf {p}}\). Finally, \(\overrightarrow{\mathbf {m}\mathbf {p}}\) and \(\overrightarrow{\mathbf {m}\mathbf {q}}\) are normalized to unit vectors \(\mathbf {\mathbf {p}}\) and \(\mathbf {\mathbf {q}}\), respectively, together with the unit translation vector \(\mathbf {\mathbf {m}}\) from the camera origin to the middle point, we have
To obtain \(\mathbf {u}'\), we simply query the two channels of the predicted scalarmap \(\hat{S}\) at \(\hat{\mathbf {m}}^*\) to obtain \(\mathbf {u}^*\), and then transfer it to \(\mathbf {u}'\):
We do not explicitly calculate w but assume it to be half of the maximum open width of the gripper leveraged in our implementation. Although this may induce collision in some scenarios and impede the grasp, it could be alleviated if using reactive force control or soft grippers. Yet, we leave the modification to future works. Meanwhile, h and d are fixed in the implementation according to the routine in the grasping estimation domain [32].
Experiments
Implementation details
We implemented GraspVDN with PyTorch and trained it on the train split of the GraspNet dataset. Specifically, the GraspVDN was separately trained on all 100 training scenes captured with the RealSense camera and the Kinect camera, where the only difference is the data source.
All three test splits, namely test-seen, test-similar, and test-novel were used for performance evaluation and ablation tests. The test-seen split was also utilized for determining when to save the best model subject to an accuracy metric detailed explained in section “Accracy metric”.
By default, the size of input images was set as \(384 \times 384\) pixels, and the output maps were set as \(96 \times 96\) pixels. Hence \(\lambda =0.25\) in Eq. 13. Unless otherwise noted, the backbone network was a ResNet18 initialized by the weights pre-trained on the ImageNet classification task [34]. During training, the base learning rate was 1e-3 initially and then dropped to 1e-4 and 1e-5 at the 160th and 180th epoch, respectively. We totally trained 200 epochs, taking approximately 15 hours with 16 samples per batch. \(\omega \) in Eq. 8 was set as 1 and \(\sigma \) in Eqs. 4–6 was set as 5. We kept other hyperparameters the same as [35].
The training and evaluations were conducted on a desktop with an AMD 3700X CPU, an NVIDIA GeForce 2070 GPU, and 32 GB RAM.
Accracy metric
During training, we need to figure out whether the model is improving or saturated regarding its performance of estimating positive grasps. A straightforward approach may be directly evaluating the intermediate model with GraspNet evaluation functions. However, such evaluation requires much computation and data I/O, hence not suitable for frequent invoking. Instead, we propose a light-weighted accuracy evaluation metric enabling fast yet reasonable judgment for the performance.
The basic idea behind this metric is that given the ground-truth and estimated middle point sets \(M^*=(m_1^*,\ldots ,m_j^*)\) and \(\hat{M}^*=(\hat{m}_1^*,\ldots ,\hat{m}_j^*)\), one could use the average distance between the matched points, plus the errors caused by non-matched outliers to depict how likely the estimation be similar to the ground-truth. The higher the similarity, the more likely the model performs better. Such problem has been investigated in [36]; however, the weighted Hausdorff distance (WHD) proposed in [36] relies on extra parameters, yet here we would like to keep the distance expression compact. Accordingly, we leverage the Hungarian algorithm [37] to match the point sets to find out the best match, deriving the mean distance \(\bar{d}_{\mathbf {m}^*} \in [0, 1)\) normalized by the map dimensions. Meanwhile, each outlier contributes a constant error (\(e_{\mathbf {m}^*}\) and \(e_{\hat{\mathbf {m}}^*}\) for the two sets, respectively) to the final metric. Thus, the total error E is
where \(\gamma \) and \(\delta \) are the outlier number in the two sets, respectively. In our implementation, we let \(e_{\mathbf {m}^*}=0\) and \(e_{\hat{\mathbf {m}}^*}=0.1\), i.e., we prefer under-estimation over over-estimation. Yet this configuration is not rigid but could be fine-tuned based on the circumstance.
With the total error E, we set a bar threshold \(T_E\), that for a batch of training output, the accuracy A is calculated as:
where B is the batch size; \(\phi (x)\) is a function deriving 1 when x is true, otherwise 0.
Please note that the validation loss is not used as the accuracy metric. The loss only evaluates the distinction between two maps but is unable to count the error induced by locating the peaks with the local maxima algorithm. In comparison, the metric proposed directly uses the peaks derived as maxima.
Qualitative results of GraspVDN tested on GraspNet. The detected grasps’ vector labels were transformed to 6-DOF labels as described in section “6-DOF grasp conversion” and displayed with the GraspNet visualization tool. The grasp handles in the image represent the grasp poses subject to the objects circumvented by them. The non-black colour of the handle indicates the robustness of grasping. The more the colour close to red, the more likely the grasp be feasible. Besides, the black colour indicates that the gripper is in collision with the scene
Main results
We report the performance of GraspVDN along with its variants and state-of-the-art in Table 1. To evaluate the performance of our method, we trained the model with default RGB input, and also made two variations by training with depth and RGB-D input. The trained models were then evaluated given corresponding input type in the test splits of GraspNet. The vector labels were converted to rectangle labels and finally to 6-DOF predictions following the scheme described in Sect 3.3. We dumped the 6-DOF labels into files, one for each image, and evaluated that with the GraspNet protocol. In general, the percentage of true positive grasps, i.e., Precision@k, was leveraged as the evaluation metric, which measures the precision of top-k ranked grasps. Hereby we let \(k=10\) instead of 50 in the GraspNet literature. Because our method detects relatively fewer grasps given the same scene than the method proposed in [5], the comparison would be unfair if k is too large.
In Table 1, the values denotes \(\text {AP}\) in percentage, i.e., the average Precision@k for k ranging from 1 to 10 given different friction \(\mu \) ranging from 0.2 to 1.0, with \(\Delta \mu =0.2\) as interval. Readers are suggested to refer to [5] for the details of the metric.
The results indicate three aspects. First, the proposed method struggles to catch up with methods using sophisticated networks and rich input data (e.g., point cloud) like [29, 30] as expected, as the point cloud provides fine-grained geometric details of the scene than RGB images. Nevertheless, it is compatible with the method that relies on depth image, and even better than that when also using depth information. Second, the proposed method shows comparable generalization performance across the three test splits of GraspNet, which drops at a similar ratio when more novel objects are added to the scene. Finally, opposite to others, the proposed method performs better on RealSense data. We witnessed that the images captured by the Kinect camera were taken in a longer shooting range, such that the objects are more concentrated in the image, which could cause heavy overlapping on the scalarmap and lower the accuracy of grasping orientation estimation. To alleviate that, adjusting the viewing distance could be helpful when implementing GraspVDN in real-world applications.
We show qualitative results, including failure cases of the grasps produced by our approach in Fig. 4. As illustrated, the major failure reason is the collision between the gripper and the objects/table as the gripper open width is set as the maxima. This issue could be reresolved by designing reactive behaviour for the hand and fingertip, by which the gripper will either move to avoid the contact, or cower its finger according to the contact force.
In terms of the model’s runtime performance, we make the comparisons in Table 2 by testing all the methods in GraspNet scenes. It suggested that the runtime for point cloud based methods could change drastically due to different input sizes. Whereas methods using image input, such as [31] and ours, could excel in runtime due to simple network architecture and also keep the performance consistent.
Simulation experiment setup and intermediate results. a A dual-arm mobile robot equipped with two Franka Emika arms and Robotiq 2F-85 grippers was used to grasp the objects on the table. In this setup, we only used the right arm. RGB and depth images captured by the simulated RealSense camera were depicted on the top left corner. b Given the scene in a, GraspVDN processed the input depth image and output vector labels marked with rays. c Heatmap and scalarmap output corresponding to b. d–g A full sequence of grasping given the estimation in b
Simulation experiment
We tested our algorithms in simulation with our developed collaborative dual-arm robot manipulator (named CURI) as shown in Fig. 5a. The upper body is formed by two arms, each of which is a 7-DOF Franka Emika panda robot, supported by a customized 3-DOF torso. The lower body is a Robotnik summit-XL steel omni-directional mobile platform. GraspVDN was utilized to aid CURI with Robotiq 2F-85 grippers to grasp GraspNet objects on a table. The setup implemented in Webots [38] and intermediate results are depicted in Fig. 5. A simulated RealSense camera was mounted along with the gripper in a camera-in-hand fashion. The camera carried by the gripper was initially facing downwards, whose optical axis was perpendicular with the table surface. For each trial, a pile composed of 5 randomly selected objects from the dataset were manually distributed underneath the camera, such that 1) they were all inside the camera frustum and 2) their poses allow at least one valid (decided heuristically) top-down grasp. We performed 20 trials in total to cover all 87 instances in the dataset, accumulating 100 individual grasps.
During each trial, the camera first took the image of the pile and sent it to the GraspVDN module. Then 6-DOF grasp candidates were generated as described in section “6-DOF grasp conversion”. Finally, the gripper moved to the first grasp pose given the estimated candidates, closed to exert predefined contact force, and then lifted the object in hand. We measured success as the object stay in hand for 3 seconds without falling. This process is looped until all 5 objects have been tackled, where failed objects (not graspable in 3 attempts) will be removed manually from the scene.
The results in Table 3 show that our models archived a higher success rate than tested on GraspNet’s seen split, even that the models were not fine-tuned in this scenario and the sim-to-real gap is huge. We ascribe this to the fact that the gripper could adjust the pose of the object in hand when a mild contact happened, such that it could still be gripped. However, a collision in GraspNet evaluation will directly result in a failure. The model with depth input could endure the gap better than the one with RGB input, and the one with RGB-D input archived the highest (yet not by a large margin) success rate. Typical failure cases include (1) inaccurate open point estimation leads to gripping along the wrong direction (usually orthogonal to the true direction). It would prevent the gripper to encompass the object inside the maximum gripping range. (2) The model failed to make the object legible in the heatmap, which leads to false-negative for estimating grasp middle points.
Conclusion
We have presented a scene-oriented grasping estimation approach predicting 6-DOF grasp poses for parallel-jaw grippers. The work shows that the grasp pose could be semantically represented as vector-like features in the 2D image plane. And by only using RGB, depth, or both images as input, the proposed method could reveal these vectors as projections of 6-DOF grasp poses in clutter without prior grasp sampling, archiving comparable performance in the GraspNet-1Billion dataset as state-of-the-art while being able to run in real-time.
Although in this work, GraspVDN was trained on the analytic ground-truths relied on a predefined 3D database to provide feasible grasps, it, on its own, is agnostic to the ground-truth source and could potentially be trained in a self-supervision manner. Specifically, one could first leverage GraspVDN to produce coarse labels for the scene and then use a robotic grasping system either in the real world or in simulation to verify the prediction. Such that positive grasps are distinguished and propagated to subsequential training of GraspVDN. Note that the perception with GraspVDN not only could happen in the initial glance of the scene but also proceed while approaching the target, in case that the camera is mounted on the gripper. This scheme is inexpensive because 2D vector labels could be generated at a high pace. Indeed, GraspVDN does not need dense annotation for each pixel on the image, yet sparse and stochastic annotations are enough.
In future work, we propose to utilize GraspVDN in dynamic and cluttered picking scenarios such as bin picking and waste sorting. Such applications not only require accuracy and success rate but also be tight on budget. To this end, GraspVDN could provide a low-cost solution since only RGB cameras are used. On the other hand, for applications demanding higher precision, we are about to further improve the performance of GraspVDN. Possible performance gain could be derived by integrating force control or visual servoing into the grasping system, as discussed in section “6-DOF grasp conversion”.
Data Availability Statement
Not applicable.
Notes
Throughout this paper, we use an apostrophe (’) to denote 2D points in the image space.
References
Stogl D, Zumkeller D, Navarro SE, Heilig A, Hein B (2017) Tracking, reconstruction and grasping of unknown rotationally symmetrical objects from a conveyor belt. In: 2017 22nd IEEE International Conference on Emerging Technologies and Factory Automation (ETFA) (IEEE), 1–8
Huang YL, Huang SP, Chen HT, Chen YH, Liu CY, Li THS (2017) A 3d vision based object grasping posture learning system for home service robots. In: 2017 IEEE International Conference on Systems, Man, and Cybernetics (SMC) (IEEE), pp 2690–2695
Fontanelli GA, Paduano G, Caccavale R, Arpenti P, Lippiello V, Villani L, Siciliano B (2020) A reconfigurable gripper for robotic autonomous depalletizing in supermarket logistics. IEEE Robot Autom Lett 5(3):4612. https://doi.org/10.1109/LRA.2020.3003283
Mahler J, Matl M, Satish V, Danielczuk M, DeRose B, McKinley S, Goldberg K (2019) Learning ambidextrous robot grasping policies. Sci Robot 4(26). https://doi.org/10.1126/scirobotics.aau4984
Fang HS, Wang C, Gou M, Lu C (2020) Graspnet-1billion: A large-scale benchmark for general object grasping. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) (2020)
Guo N, Zhang B, Zhou J, Zhan K, Lai S (2020) Pose estimation and adaptable grasp configuration with point cloud registration and geometry understanding for fruit grasp planning. Comput Electron Agric 179:105818. https://doi.org/10.1016/j.compag.2020.105818
Sun G, Lin H (2020) Robotic grasping using semantic segmentation and primitive geometric model based 3d pose estimation. In: 2020 IEEE/SICE International Symposium on System Integration (SII), pp 337–342. https://doi.org/10.1109/SII46433.2020.9026297
Fischler MA, Bolles RC (1981) Random sample consensus: a paradigm for model fitting with applications to image analysis and automated cartography. Commun ACM 24(6):381
Varley J, DeChant C, Richardson A, Ruales J, Allen P (2017) Shape completion enabled robotic grasping. In: 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), pp 2442–2447. https://doi.org/10.1109/IROS.2017.8206060
Lundell J, Verdoja F, Kyrki V (2019) Robust grasp planning over uncertain shape completions. In: 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS)
Miller AT, Allen PK (2004) Graspit! a versatile simulator for robotic grasping. IEEE Robot Autom Mag 11(4):110. https://doi.org/10.1109/MRA.2004.1371616
Wada K, Sucar E, James S, Lenton D, Davison AJ (2020) Morefusion: multi-object reasoning for 6d pose estimation from volumetric fusion. In: Proceedings of the IEEE/CVF conference on computer vision and pattern recognition
Gualtieri M, ten Pas A, Saenko K, Platt R (2016) High precision grasp pose detection in dense clutter. In: 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), pp 598–605. https://doi.org/10.1109/IROS.2016.7759114
Rink C, Kriegel S, Seth D, Denninger M, Marton ZC, Bodenmuller T (2016) Monte carlo registration and its application with autonomous robots. J Sens 2546819:28. https://doi.org/10.1155/2016/2546819
He K, Zhang X, Ren S, Sun J (2016) Deep residual learning for image recognition. In: Proceedings of the IEEE conference on computer vision and pattern recognition, pp 770–778
Yu H, Lai Q, Liang Y, Wang Y, Xiong R (2019) A cascaded deep learning framework for real-time and robust grasp planning. In: 2019 IEEE International Conference on Robotics and Biomimetics (ROBIO), pp 1380–1386. 10.1109/ROBIO49542.2019.8961531
Nikandrova E, Kyrki V (2015) Category-based task specific grasping. Robot Auton Syst 70:25. https://doi.org/10.1016/j.robot.2015.04.002
Tian H, Wang C, Manocha D, Zhang X (2019) Transferring grasp configurations using active learning and local replanning. In: 2019 International Conference on Robotics and Automation (ICRA) (IEEE), pp 1622–1628
Song S, Zeng A, Lee J, Funkhouser T (2020) Grasping in the wild: learning 6dof closed-loop grasping from low-cost demonstrations. IEEE Robot Autom Lett 5(3):4978. https://doi.org/10.1109/LRA.2020.3004787
Choi Y, Kee H, Lee K, Choy J, Min J, Lee S, Oh S (2020) Hierarchical 6-dof grasping with approaching direction selection. In: 2020 IEEE International Conference on Robotics and Automation (ICRA) (IEEE), pp 1553–1559
Bohg J, Kragic D (2010) Learning grasping points with shape context. Robot Auton Syst 58(4):362. https://doi.org/10.1016/j.robot.2009.10.003
Saxena A, Driemeyer J, Ng AY (2008) Robotic grasping of novel objects using vision. Int J Robot Res 27(2):157. https://doi.org/10.1177/0278364907087172
Zeng A, Yu K, Song S, Suo D, Walker E, Rodriguez A, Xiao J (2017) Multi-view self-supervised deep learning for 6d pose estimation in the amazon picking challenge. In: 2017 IEEE International Conference on Robotics and Automation (ICRA), pp 1386–1383. 10.1109/ICRA.2017.7989165
Zapata-Impata BS, Gil P, Pomares J, Torres F (2019) Fast geometry-based computation of grasping points on three-dimensional point clouds. Int J Adv Robot Syst 16(1):1729881419831846
Mousavian A, Eppner C, Fox D (2019) 6-dof graspnet: Variational grasp generation for object manipulation (Los Alamitos, CA, USA), pp 2901–10. https://doi.org/10.1109/ICCV.2019.00299
Wang X, Jiang X, Zhao J, Wang S, Liu Y (2020) Grasping objects mixed with towels. IEEE Access 8:129338. https://doi.org/10.1109/ACCESS.2020.3008763
Wu C, Chenv J, Cao Q, Zhang J, Tai Y, Sun L, Jia K (2020) Grasp proposal networks: An end-to-end solution for visual learning of robotic grasps. Preprint arXiv:2009.12606
Chu F, Xu R, Vela PA (2018) Real-world multiobject, multigrasp detection. IEEE Robot Autom Lett 3(4):3355. https://doi.org/10.1109/LRA.2018.2852777
Ten Pas A, Gualtieri M, Saenko K, Platt R (2017) Grasp pose detection in point clouds. Int J Robot Res
Liang H, Ma X, Li S, Görner M, Tang S, Fang B, Sun F, Zhang J (2019) Pointnetgpd: Detecting grasp configurations from point sets, in 2019 International Conference on Robotics and Automation (ICRA), pp. 3629–3635. 10.1109/ICRA.2019.8794435
Morrison D, Corke P, Leitner J (2018) Closing the loop for robotic grasping: A real-time, generative grasp synthesis approach. In: Proceedings of Robotics: Science and Systems (RSS)
Morrison D, Corke P, Leitner J (2020) Learning robust, real-time, reactive robotic grasping. Int J Robot Res 39(2–3):183. https://doi.org/10.1177/0278364919859066
Dong Z, Gao Y, Yan Y, Chen F (2021) Vector detection network: An application study on robots reading analog meters in the wild. Preprint arXiv:2105.14522
Deng J, Dong W, Socher R, Li LJ, Li K, Fei-Fei L (2009) Imagenet: A large-scale hierarchical image database. In: 2009 IEEE conference on computer vision and pattern recognition (Ieee), pp 248–255
Xiao B, Wu H, Wei Y (2018) Simple baselines for human pose estimation and tracking. In: Proceedings of the European conference on computer vision (ECCV), pp 466–481
Ribera J, Guera D, Chen Y, Delp EJ (2019) Locating objects without bounding boxes. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp 6479–6489
Kuhn HW (1955) The hungarian method for the assignment problem. Naval Res Logist Q 2(1–2):83
Michel O (2004) Cyberbotics ltd. webots\(^{{\rm TM}}\): professional mobile robot simulation. Int J Adv Robot Syst 1(1): 5
Funding
This work is supported by the National Natural Science Foundation of China (51805078) and the National Key Research and Development Program of China (2017YFB0304200).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Code availability
Not applicable.
Ethics approval
Not applicable.
Consent to participate
Not applicable.
Consent for publication
Not applicable.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Dong, Z., Tian, H., Bao, X. et al. GraspVDN: scene-oriented grasp estimation by learning vector representations of grasps. Complex Intell. Syst. 8, 2911–2922 (2022). https://doi.org/10.1007/s40747-021-00459-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40747-021-00459-x