Large-scale group decision-making based on Pythagorean linguistic preference relations using experts clustering and consensus measure with non-cooperative behavior analysis of clusters

Abstract

To represent qualitative aspect of uncertainty and imprecise information, linguistic preference relation (LPR) is a powerful tool for experts expressing their opinions in group decision-making (GDM) according to linguistic variables (LVs). Since for an LV, it generally means that membership degree is one, and non-membership and hesitation degrees of the experts cannot be expressed. Pythagorean linguistic numbers/values (PLNs/PLVs) are novel choice to address this issue. The aim of this paper which we propose a GDM problem involved a large number of the experts is called large-scale GDM (LSGDM) based on Pythagorean linguistic preference relation (PLPR) with a consensus model. Sometimes, the experts do not modify their opinions to achieve consensus. Therefore, the experts’ proper opinions’ management with their non-cooperative behaviors (NCBs) is necessary to establish a consensus model. At the same time, it is essential to ensure the proper adjustment of the credibility information. The proposed model using grey clustering method is divided with the experts’ similar evaluations into a subgroup. Then, we aggregate the experts’ evaluations in each cluster. A cluster consensus index (CCI) and a group consensus index (GCI) are presented to measure consensus level among the clusters. Then, we provide a mechanism for managing the NCBs of the clusters, which contain two parts: (1) NCB degree is defined using CCI and GCI for identifying the NCBs of the clusters; (2) implemented the weight punishment mechanism of the NCBs clusters to consensus improvement. Finally, an example is offered for usefulness of the proposed approach.

Introduction

The decision data provided by a huge number of decision-makers (DMs) or the experts are known as large-scale group decision-making (LSGDM) problem, which is a widespread human activity for the selection of the best option from a set of feasible alternatives. We solve real-life problems, some decision-making results related to the benefits of a large number of the experts. For example, emergency events often have a massive impact on public interest; emergency management usually requires the participation of many DMs from different professional backgrounds; the teachers’ appointment reformation system is in universities and so on. To date, we can see that the studies about LSGDM problem can be classified into three angles, i.e., clustering approaches [22, 57], consensus reaching process (CRP) [8, 41,42,43, 49,50,51, 55], the method of decision-making with various types of preferences [23, 32, 33, 49, 56]. These researches have contributed significantly to the development of LSGDM problems, but most of the cases DMs consider quantitative judgments. In [11,12,13,14], some scholars note that LSGDM problems might be too difficult to require the experts to deliver quantitative judgments. In this situation, Zadeh’s linguistic variables (LVs) [54] are appropriate tools that use DMs to represent quantitative judgment. However, Wang and Li [44] pointed out that the membership degree of a linguistic assessment value is one; the non-membership and hesitation degrees of DMs cannot be expressed. For example, if a DM compares two alternatives at a time and gives the opinion according to an LV such as “good”, but he/she cannot be entirely sure that this assessment results. Maybe, he/she has $75\%$ certain degree and $8\%$ degree of confusion. In this situation, Mandal et al. [38] proposed the new type of preference relation called Pythagorean linguistic preference relation (PLPR), which is addressed the preferred degree and non-preferred degree of LVs according to Yagers Pythagorean fuzzy sets (PFSs) [53]. We suggest for interested researchers to see the attractive studies in [4, 5, 9, 34, 37].

The existing studies on LSGDM problems mostly combine with the clustering method and CRP. The objective of the method of clustering is to divide a large number of the experts into a few subgroups. The CRP aims to reach a final decision which can satisfy most of the experts, instead of giving some of the experts impression that their opinions are considered lightly [12, 15, 48]. Till now, different consensus method has been proposed for LSGDM problems [6, 45,46,47]. In CRP, some researchers are effectively handling the behaviors of the experts or clusters. The behaviors of the experts or clusters addressing in CRP are different types such as:

• (1) non-cooperative behaviors discussed in [7, 8, 42, 43, 50];

• (2) self-confidence behaviors discussed in [27, 28, 30, 31];

• (3) overconfidence behaviors discussed in [29];

• (4) personal individual semantics behaviors discussed in [20, 21].

In this paper, in our proposed model, we consider non-cooperative behaviors of the experts or clusters where the experts use PLPR to express their opinions in LSGDM problems. The contributions of the proposed model in this paper are summarized as follows:

• (I) We develop a new clustering algorithm according to the grey clustering method based on a similarity degree between two experts, where the experts use PLPVs for comparing two alternatives at a time. The experts’ clustering method is shown in Algorithm 1.

• (II) According to the majority policy, we obtain the weight of each cluster and the weight of each expert in each cluster. We use the Pythagorean linguistic weighted averaging (PLWA) operator to aggregating the expert’s opinions in each cluster. Then, we obtain weight collective PLPR of all clusters PLPRs. We define a cluster consensus index (CCI) of each cluster using division measure between each cluster PLPR and weight collective PLPR of all clusters. Then, we obtain sum of the multiplication of CCI and weight of each cluster, which is called a group consensus index (GCI).

• (III) If we achieve acceptable consensus, so CRP is necessary. In CRP, here, we consider clusters behavior according to the non-cooperative behavior degree (NCBD) of each cluster, which is obtained from CCI of each cluster and GCI. The identification rule for identifying non-cooperative behavior clusters is designed, and then, feedback mechanisms are applied to these clusters. We control non-cooperative behavior clusters according to weight updating adjustment by the feedback parameter and the values of NCBD.

• (IV) We accept weight collective PLPR at the same time when we achieve acceptable consensus. Then, the selection process is applied to this accept weight collective PLPR. The selection process is done by row arithmetic values of weight collective PLPR and their lower index of expected values.

To do so, this paper is set out as follows: in the next section, we present notations and some basic concepts of linguistic set, Pythagorean linguistic set (PLS), and PLPR. In the following section, description of problem and proposed framework of consensus for the LSGDM problem based on PLPRs are discussed. In the next section, the consensus approach in the LSGDM with PLPRs: Method of expert clustering, Consensus measure of clusters, Non-cooperative behaviors managements mechanism, and Selection process are given. In the following section, one numerical example is presented to show the feasibility and validity of this study. This paper is concluded in the last section.

Preliminaries

In this section, offer some basic knowledge of the linguistic set, PLS, and PLPR are recalled.

Notations

To facilitate the comprehension of the paper, Table 1 summarizes some of the used notations, where $N=\{1,2,\dots , n\}$, $M=\{1,2,\dots , m\}$ and $Z=\{1,2,\dots , z\}$.

Table 1 List of the notations

Linguistic set

To represent the qualitative judgments, LVs [54] are a feasible and powerful tool of the experts. A linguistic term $s_{i} \in S$ is a possible value for a LV. In the following, we call up the basic operational laws on the linguistic term [12]:

• (1) the set is ordered: $s_{i}>s_{j}$ if and only if $i > j$;

• (2) negation operator: $neg(s_{i})=s_{-i}$.

Xu [52] defined the continuous linguistic term set denoted by $\overline{S}$, which is an extension of the above discrete linguistic term set S to process linguistic information. Let $s_{\alpha } \in \overline{S}$. If $s_{\alpha } \in S$, then it is called an original linguistic term. Otherwise, it is a virtual linguistic term [52].

In the following, we have operation laws [52] for any LVs $s_{\alpha }, s_{\beta } \in \overline{S}$ and $\lambda , \lambda _{1}, \lambda _{2} \in [0,1]$:

• (1) $s_{\alpha } \oplus s_{\beta }=s_{\alpha + \beta }$;

• (2) $\lambda s_{\alpha }=s_{\lambda \alpha }$;

• (3) $\lambda (s_{\alpha } \oplus s_{\beta })=\lambda s_{\alpha } \oplus \lambda s_{\beta }$;

• (4) $(\lambda _{1}+\lambda _{2})s_{\alpha }=\lambda _{1} s_{\alpha } \oplus \lambda _{2}s_{\alpha }$.

For any $s_{\alpha } \in \overline{S}$, the lower index $\alpha$ can be obtained in the following function:

$$\begin{aligned} I: \overline{S} \rightarrow [-\alpha ,\alpha ],~\text {and}~ I(s_{\alpha })=\alpha , \end{aligned}$$

(1)

for any $s_{\alpha }\in \overline{S}$.

PLS and PLPR

Definition 1

[38] A PLS P in X for $\overline{S}$ is defined as

$$\begin{aligned} P = \{x \mid \langle s_{\theta (x)}, (\mu _{P}(x),\nu _{P}(x)) \rangle \mid x \in X\}, \end{aligned}$$

(2)

where $\mu _{P}: X \rightarrow [0,1]$ and $\nu _{P}: X \rightarrow [0,1]$ represent the membership and non-membership degrees of the element x to $s_{\theta (x)} \in \overline{S}$, are, respectively, with the condition $0 \le \mu ^{2}_{P}(x) + \nu ^{2}_{P}(x) \le 1$, $\forall x \in X$. The hesitancy degree of x to $s_{\theta (x)}$ is represented by $\pi _{P}(x)=\sqrt{1 - \mu ^{2}_{P}(x) - \nu ^{2}_{P}(x)}$, $\forall x \in X$ for any PFS. In special case, if X be a singleton set, then PLS P is reduced to $\langle s_{\theta (x)}, (\mu _{P}(x),\nu _{P}(x)) \rangle$, which call it a Pythagorean linguistic value (PLV) or Pythagorean linguistic number (PLN). For convenience, a PLN is denoted by $p = \langle s_{\theta (p)}, (\mu (p), \nu (p))\rangle$, where $s_{\theta (p)} \in \overline{S}$ and $\mu (p)$, $\nu (p)$ $\in [0,1]$ with $0\le \mu ^{2}(p) + \nu ^{2}(p) \le 1$.

For example, let $p=\langle s_{3}, (0.9, 0.2) \rangle$ be a PLN, and from it, we clear that the membership degree of $s_{3}$ is 0.9 and the non-membership degree of $s_{3}$ is 0.2, and the degree of hesitancy is $\sqrt{0.15}$.

Definition 2

[38] The expected value of any PLN $p=\langle s_{\theta (p)}, (\mu (p),\nu (p))\rangle$ is denoted by $\mathcal {E}(p)$ and represented as follows:

$$\begin{aligned} \mathcal {E}(p)&= \frac{1}{2} \times (\mu ^{2}(p) + 1 - \nu ^{2}(p)) \times s_{\theta (p)}\nonumber \\&= s_{(\theta (p) \times (\mu ^{2}(p) + 1 - \nu ^{2}(p)))/2}, \end{aligned}$$

(3)

where $\mathcal {E}(p) \in [s_{-\theta (p)}, s_{\theta (p)}]$.

For example, let $p=\langle s_{3}, (0.9, 0.2)\rangle$ be a PLN, and then, the expected value $\mathcal {E}(p)$ of p can be calculated as follows:

$$\begin{aligned} \mathcal {E}(p)&= \frac{1}{2} \times ((0.9)^{2}+1-(0.2)^{2}) \times s_{3}\\&= s_{(3 \times ((0.9)^{2}+1-(0.2)^{2}))/2} = s_{2.655}. \end{aligned}$$

According to expression (1), the lower index of $\mathcal {E}(p)$ is $I(\mathcal {E}(p))=2.655$.

Definition 3

[38] The score function of any PLN $p=\langle s_{\theta (p)}, (\mu (p),\nu (p))\rangle$ is defined as

$$\begin{aligned} S(p) = I(\mathcal {E}(p)) \times (\mu ^{2}(p) - \nu ^{2}(p)), \end{aligned}$$

(4)

and that of accuracy function is defined as

$$\begin{aligned} H(p) = I(\mathcal {E}(p)) \times (\mu ^{2}(p) + \nu ^{2}(p)), \end{aligned}$$

(5)

where $I(\mathcal {E}(p))$ is the lower index of $\mathcal {E}(p)$ of the PLN p.

Definition 4

[38] For comparing any two PLNs $p=\langle s_{\theta (p)}, (\mu (p),\nu (p))\rangle$ and $q=\langle s_{\theta (q)}$, $(\mu (q)$, $\nu (q))\rangle$, then we have the following:

• (1) If $I(\mathcal {E}(p)) > I(\mathcal {E}(q))$, then $p \succ q$;

• (2) If $I(\mathcal {E}(p)) = (\mathcal {E}(q))$, then $S(p) > S(q)$, then $p \succ q$;

• (3) $I(\mathcal {E}(p)) = I(\mathcal {E}(q))$ and $S(p) = S(q)$, then if $H(p) > H(q)$, then $p \succ q$; if $H(p) = H(q)$, then $p = q$.

Theorem 1

[38] Let $p_{i}=\langle s_{\theta (p_{i})}, (\mu (p_{i}),\nu (p_{i}))\rangle$ $(i=1,2, \dots , n)$ be the collection of PLNs. Then, the aggregated value according to the PLWA operator is still a PLN and is given by

$$\begin{aligned}&PLWA(p_{1}, p_{2}, \dots , p_{n}) =\oplus _{i=1}^{n}w_{i}p_{i} \nonumber \\&=\left\langle s_{\sum _{i=1}^{n}w_{i}\theta (p_{i})}, \left( \sqrt{1-\prod _{i=1}^{n}(1-\mu ^{2}(p_{i}))^{w_{i}}},\right. \right. \nonumber \\&\left. \left. ~~~~~~\prod _{i=1}^{n}\nu ^{w_{i}}(p_{i}) \right) \right\rangle , \end{aligned}$$

(6)

where $w=(w_{1}, w_{2}, \dots , w_{n})^{T}$ is the weight vector of $p_{i}$ with $w_{i} > 0$ and $\sum _{i=1}^{n}w_{i}=1$.

Definition 5

[38] A PLPR P on the set X for the set $\overline{S}$ is defined as $P=(p_{ij})_{n \times n}$, where $p_{ij}=\langle s_{\theta _{ij}},(\mu _{ij},\nu _{ij})\rangle$ for all $i,j \in \{1$, 2, $\dots$, $n\}$, $\mu _{ij}$ and $\nu _{ij}$ are respective of the preferred and non-preferred degrees for the linguistic term $s_{\theta _{ij}} \in \overline{S}$ of the alternative $x_{i}$ over the alternative $x_{j}$ in the following conditions:

$$\begin{aligned} {\left\{ \begin{array}{ll} s_{-t} \le s_{\theta _{ij}} \le s_{t} &{} \forall i,j \in \{1,2,\dots , n\},\\ s_{\theta _{ij}} \oplus s_{\theta _{ji}}=s_{0} &{} \forall i,j \in \{1,2,\dots , n\},\\ s_{\theta _{ii}}=s_{0} &{} \forall i \in \{1,2,\dots , n\}, \end{array}\right. } \end{aligned}$$

(7)

and

$$\begin{aligned} {\left\{ \begin{array}{ll} 0\le \mu _{ij},\nu _{ij}\le 1 &{} \forall i,j \in \{1,2,\dots , n\},\\ \mu ^{2}_{ij}+\nu ^{2}_{ij}\le 1 &{} \forall i,j \in \{1,2,\dots , n\},\\ \mu _{ij}=\mu _{ji}, \nu _{ij}=\nu _{ji} &{} \forall i,j \in \{1,2,\dots , n\},\\ \mu _{ii}=1 &{} \forall i \in \{1,2,\dots , n\}. \end{array}\right. } \end{aligned}$$

(8)

In Definition 5, we say $p_{ij}=\langle s_{\theta _{ij}},(\mu _{ij},\nu _{ij})\rangle$ for all $i,j \in \{1$, 2, $\dots$, $n\}$ is a PLPV or a PLPN. In addition, $p_{ij}=\langle s_{\theta _{ij}},(\mu _{ij},\nu _{ij})\rangle$ denotes the Pythagorean linguistic preference of the alternative $x_{i}$ over the alternative $x_{j}$. Similar to fuzzy preference relation [40], the preferred and non-preferred degrees of the alternative $x_{j}$ over the alternative $x_{i}$ according to PLPV are denoted by $p_{ji}=\langle s_{\theta _{ji}},(\mu _{ji},\nu _{ji})\rangle =\langle s_{-\theta _{ij}},(\mu _{ij},\nu _{ij})\rangle$.

Theorem 2

[38] Let $P^{k}=(p^{k}_{ij})_{n \times n}$ $(k=1,2, \dots , m)$ be m PLPRs given by the experts $e_{k}$ $(k=1,2, \dots , m)$ and $\lambda _{k}=(\lambda _{1},\lambda _{2}, \dots , \lambda _{m})^{T}$ be the weight vector of the experts, where $p^{k}_{ij}=\langle s_{\theta _{ij}^{k}}$, $(\mu _{ij}^{k}$, $\nu _{ij}^{k})\rangle$, $\lambda _{k} > 0$, $k=1,2, \dots , m$, $\sum _{k=1}^{m}\lambda _{k}=1$, and then, the aggregation $P^{*}=(p^{*}_{ij})_{n \times n}$ of $P^{k}=(p^{k}_{ij})_{n \times n}$ $(k=1,2, \dots , m)$ is also a PLPR, where

$$\begin{aligned}&p^{*}_{ij}=\langle s_{\theta _{ij}^{*}},(\mu _{ij}^{*},\nu _{ij}^{*})\rangle , s_{\theta _{ij}^{*}}=s_{\sum _{k=1}^{m}\lambda _{k}\theta _{ij}^{k}},\nonumber \\&\mu _{ij}^{*}=\sum _{k=1}^{m}\lambda _{k}\mu _{ij}^{k}, \nu _{ij}^{*}=\sum _{k=1}^{m}\lambda _{k}\nu _{ij}^{k},\nonumber \\&s_{\theta _{ij}^{*}} \oplus s_{\theta _{ji}^{*}}=s_{0}, s_{\theta _{ii}^{*}}=s_{0},\nonumber \\&0 \le (\mu _{ij}^{*})^{2} + (\nu _{ij}^{*})^{2} \le 1, \mu _{ji}^{*}=\mu _{ij}^{*}, \nu _{ji}^{*}=\nu _{ij}^{*},\nonumber \\&\mu _{ii}=1, \end{aligned}$$

(9)

$\forall i,j=1,2,\dots , n$ and $k=1,2, \dots , m$.

Framework of consensus for the LSGDM problem based on PLPR

A framework is designed this section to solve the CRP for the LSGDM problem based on PLPRs.

Description of problem

Let $X=\{x_{1},x_{2}, \dots , x_{n}\}$ $(n\ge 2)$ be a finite set of objects. There are a large number of experts $E=\{e_{1},e_{2},\dots , e_{m}\}$, each of whom provides an opinion over alternatives in X. It is well known that preference relations are well-established tool to compare two alternatives at a time in the GDM problems. In this paper, the experts provide their decision over X using PLPR. The problem is addressed with a ranking of the alternatives or the selection of best options from the receivable information. Especially, the procedure for reaching a consensus the all individuals is analyzed in the following.

Proposed framework

It is necessary for a GDM problems before an optimal preference order can be analyzed: CRP and an appropriate selection process. In CRP, before making a decision, the DMs reach a mutual agreement with the expectation of gaining a more acceptable group solution. In the real LSGDM problem, the decision may affect entire groups or societies. Thus, in the LSGDM problem, DMs invite various professions from may be different countries, and hence, they are different interests. In this connection, the number of studies (discussed in Introduction) in the LSGDM problem is considered the experts behaviors. This paper is examined the non-cooperative behaviors of the experts or clusters in CRP. Non-cooperative behaviors may be classified in the following way: (i) a DM or an expert who demands that his/her evaluation is correct, but has no personal interests; (ii) an expert who realizes his/her assessment is accurate, where there may be own interests, and (iii) an independent expert demands that his/her evaluation is new. In this literature, we spotlight on the process of the first type of non-cooperative behavior. The other two types of non-cooperative behaviors are considered in the future. The existing studies [50] say that the non-cooperative behaviors handle two directions: one is weight punishment, i.e., weight modification where the experts’ weight decrease for a greater consensus and other is the adjustment of the experts’ opinion closure to the group evaluation.

Fig. 1

The proposed consensus framework in LSGDM based on PLPRs

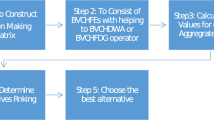
Our CRP is shown in Fig. 1 which contains four blocks: a method of cluster, consensus measures, detecting and managing non-cooperative behaviors, and a selection process.

• (1) The method of clustering displays in the first block. It is used to obtain clusters from the experts’ opinions, which is the main part of our proposed approach. Then, we manage the obtained cluster in the next block. The popular clustering algorithms are fuzzy clustering algorithm [2], fuzzy c-means algorithm [3], grey clustering algorithm [26], and K-means algorithm [36]. In the LSGDM problem [8, 55], the method of grey clustering is one of the effective methods and is broadly applied. In this paper, we apply this method for the experts’ clustering according to their importance. In “Method of the expert clustering”, we discuss this method (see Algorithm 1).

• (2) The measure of the classify clusters displays in the second block. After obtaining clusters, the weight of the clusters and the expert in a cluster are calculated. Then, we aggregate the experts’ opinion in each cluster and obtain the weight collective of all clusters. A division measure is defined over the PLPR, which is used to obtain the CCI for each cluster. Then, we find the GCI. The detail discussion is available of the second block in “Consensus measure of clusters” section.

• (3) The detection and management of non-cooperative behavior strategy is displayed in the third block. A non-cooperative behaviors detection and management strategy are handled through the changing of cluster weight. Detection rules and modification process are the techniques to use for management mechanism. In “Non-cooperative behavior managements mechanism” section, we discuss third block.

• (4) The selection process is displayed in fourth block. Once the final weight collective PLPR is obtained, the row arithmetic average values are calculated. Then, we find the lower index of each alternative from row arithmetic average values. The details process is discussed in “Selection process” section.

Proposed consensus approach

Since the CRP is iterative and which is the number of discussion rounds. The iteration-based approach is mainly concerned consensus measure and non-cooperative behaviors detection and management. In such an iterative process, the detection and management of the non-cooperative behaviors is an integral part, and this part is responsible for supervising and guiding the experts in a cluster through the iteration process. At first, we present the grey clustering method, and then, the consensus measures, non-cooperative behavior, and selection process are discussed.

Method of the expert clustering

Here, we consider the method of the experts’ clustering according to the experts’ opinions. It is a machine learning technique which is widely applied in data mining and machine learning communities [1]. Remarkable application is seen in information retrieval, segmentation of objects, recognition of object, etc. [10, 17]. Clustering aims to shrink a large number of decisions according to finding subgroups with the experts similar opinion to improve the efficiency of CRP in the LSGDM problems. Several types of clustering methods are considered in [16,17,18].

Since the method of grey clustering is one of the effective tools which is broadly applied in the LSGDM problems. It is based on similarity measure within the experts to perform opinion clustering. Let $SM=(e_{kh})_{m \times m}$ be a similarity matrix within the experts in E, where $e_{kh} \in [0,1]$ indicates the similarity degree between the experts $e_{k}$ and $e_{h}$ $(k, h \in M)$. In the grey clustering algorithm [26], there are two laws which are dependent on two parameters:

• (1) Let $\zeta \in [0,1]$ be a first parameter, which is used to find the neighbor of the experts, i.e., if $e_{kh} \ge \zeta$, then the expert $e_{k}$ is the direct neighbor of the expert $e_{h}$.

• (2) Let $\xi \in [0,1]$ be a second parameter, which is used to judge whether an expert belongs to a cluster or not. For a cluster $C_{\hat{z}}$ and an expert $e_{k}$ that needs to be classified, if the proportion of the neighbors of $e_{k}$ in $C_{\hat{z}}$ is larger than or equal to $\xi$, then $e_{k}$ can be classified into cluster $C_{\hat{z}}$.

In this paper, the expert clustering is done by grey clustering method.

In human decision-making, non-cooperative behaviors are leaded psychological factors, which a mental perception of the experts on their opinions. Various experts usually own different believe for their judgments. It is because there are several knowledge experiences, risk, or interests preferences among alliances or experts. Thus, in a few situations, the experts’ behaviors can be reflected in the process of decision-making and its essential impact on the obtained result [27]. Therefore, managing non-cooperative behaviors of the experts are crucial tools in the CRP for the LSGDM problem based on PLPR. For that reason, to achieve more consistent clustering results, we put forth to make the clustering of the experts by PLPVs similarity. Then, the associated definitions for the expert clustering based on PLPRs are defined as follows:

Definition 6

Let $P^{k}=(p_{ij}^{k})_{n \times n}$ and $P^{h}=(p_{ij}^{h})_{n \times n}$ be two PLPRs provided by the experts $e_{k}$ and $e_{h}$, respectively, where $p^{k}_{ij}=\langle s_{\theta _{ij}^{k}}$, $(\mu _{ij}^{k},\nu _{ij}^{k})\rangle$ and $p^{h}_{ij}=\langle s_{\theta _{ij}^{h}},(\mu _{ij}^{h},\nu _{ij}^{h})\rangle$. Then, the deviation measure between $P^{k}=(p_{ij}^{k})_{n \times n}$ and $P^{h}=(p_{ij}^{h})_{n \times n}$ is defined as:

$$\begin{aligned} d(P^{k},P^{h})&= \frac{1}{2g+1} \bigg (\frac{2}{n(n-1)}\sum _{i=1}^{n-1} \sum _{j=i+1}^{n} \nonumber \\&\quad \quad \left( I(\mathcal {E}(p_{ij}^{k})) - I(\mathcal {E}(p_{ij}^{h}))\right) ^{2} \bigg )^{\frac{1}{2}}. \end{aligned}$$

(10)

Definition 7

Let $P^{k}=(p_{ij}^{k})_{n \times n}$ and $P^{h}=(p_{ij}^{h})_{n \times n}$ be two PLPRs provided by the experts $e_{k}$ and $e_{h}$, and then, their degree of similarity is defined as

$$\begin{aligned} \rho _{kh}=1- d(P^{k},P^{h}). \end{aligned}$$

(11)

Obviously, $0 \le \rho _{kh} \le [0,1]$. The closer $\rho _{kh}$ is to 1, the more similar $P^{k}$ is to $P^{h}$, while the closer $\rho _{kh}$ is to 0, the more distance $P^{k}$ is from $P^{h}$.

The detailed experts clustering for the LSGDM based on PLPR is described in Algorithm 1.

Consensus measure of clusters

A large number of the experts are classified according to Algorithm 1, so we adopt in the following facts:

• (1) All the experts in the same cluster have similar preference information, so their weights are allotted equally.

• (2) According to majority policy, the clusters have contained a large number of experts which should be allowed higher weights.

We give the following two formulas for calculating the weights of the cluster $C_{\hat{z}}$ and the expert $e_{k} \in C_{\hat{z}}$:

$$\begin{aligned} w_{\hat{z}}&=\frac{o_{\hat{z}}}{\sum _{{\hat{z}}=1}^{z}o_{\hat{z}}}, \end{aligned}$$

(12)

$$\begin{aligned}&\varphi _{k}=\frac{1}{o_{\hat{z}}}. \end{aligned}$$

(13)

For aggregating the PLPRs given by the experts in the cluster $C_{\hat{z}}$, we use Theorem 1 and the expression (13). Therefore, the aggregated PLPR $P_{\hat{z}}=(p_{ij,\hat{z}})_{n \times n}$ of the cluster $C_{\hat{z}}$ can be obtained as:

$$\begin{aligned} p_{ij,\hat{z}}&=\left\langle s_{\sum _{k=1}^{o_{\hat{z}}}\varphi _{k}\theta _{ij}^{k}}, \left( \sqrt{1-\prod _{k=1}^{o_{\hat{z}}}(1-(\mu _{ij}^{k})^{2})^{\varphi _{k}}},\right. \right. \nonumber \\&\quad \quad \left. \left. \prod _{k=1}^{o_{\hat{z}}} (\nu _{ij}^{k})^{\varphi _{k}}\right) \right\rangle =\bigg \langle s_{\theta _{ij,\hat{z}}},\bigg (\mu _{ij,\hat{z}},\nu _{ij,\hat{z}}\bigg )\bigg \rangle . \end{aligned}$$

(14)

Similarly, we now use Theorem 2 and expression (14) for collect all clusters PLPRs, which is called weight collective PLPR, denoted by $P_{c}=(p_{ij,c})_{n \times n}$, where

$$\begin{aligned} p_{ij,c}&=\left\langle s_{\sum _{\hat{z}=1}^{z}w_{\hat{z}}\theta _{ij,\hat{z}}}, \left( \sum _{\hat{z}=1}^{z}w_{\hat{z}}\mu _{ij,\hat{z}},\right. \right. \left. \left. \sum _{\hat{z}=1}^{z}w_{\hat{z}}\nu _{ij,\hat{z}}\right) \right\rangle \nonumber \\&=\bigg \langle s_{\theta _{ij,c}},\bigg (\mu _{ij,\hat{z}},\nu _{ij,c}\bigg )\bigg \rangle . \end{aligned}$$

(15)

We provide the following definition to find the GCI of the LSGDM based on PLPR.

Definition 8

Let $P_{\hat{z}}=(p_{ij,\hat{z}})_{n \times n}$ be the PLPR of a cluster $C_{\hat{z}}$, and $P_{c}=(p_{ij,c})_{n \times n}$ be the weight collective PLPR. Then, the deviation measure between $C_{\hat{z}}$ and $P_{c}$ is denoted by $\varrho$ and defined as:

$$\begin{aligned} \varrho (P_{\hat{z}},P_{c})&=\bigg ( \frac{1}{2g+1} \frac{2}{n(n-1)}\sum _{i=1}^{n-1} \sum _{j=i+1}^{n} \nonumber \\&(I(\mathcal {E}(p_{ij,\hat{z}})) - I(\mathcal {E}(p_{ij,c})))^{2}\bigg )^{\frac{1}{2}}. \end{aligned}$$

(16)

Definition 9

Let $\varrho (P_{\hat{z}},P_{c})$ be the deviation measure between the cluster $C_{\hat{z}}$ and the weight collective $P_{c}$, and then, the cluster consensus index (CCI) of $C_{\hat{z}}$ is defined as

$$\begin{aligned} CCI(C_{\hat{z}})=1-\varrho (P_{\hat{z}},P_{c}). \end{aligned}$$

(17)

Using expression (17), the GCI can be calculated as

$$\begin{aligned} GCI=\sum _{\hat{z}=1}^{z}w_{\hat{z}} \times CCI(C_{\hat{z}}). \end{aligned}$$

(18)

Obviously, $0 \le GCI \le 1$. If $GCI = 1$, then there is no deviation between clusters evaluations. Moreover, the consensus degree among the clusters is higher if GCI is to closure 1. When an adequate consensus degree is achieved or not among the experts, a consensus threshold $\sigma \in [0,1]$ is usually predefined to measure this. In this paper, we consider that if $GCI \ge \sigma$ for an acceptable consensus. Otherwise, we activate a feedback mechanism for an acceptable consensus.

Non-cooperative behavior managements mechanism

After shrinking a large number of the experts opinions, i.e., clustering the experts, it is natural phenomena toward opinion adjustment some clusters behave non-cooperative attitude. It is challenged to manage; however, the decision result is obtained by CRP. Motivated by the studied in [42, 50], here, we discuss three facts such as identification rule, discussion and interaction, and proper adjustment for handling non-cooperative behavior of clusters.

Non-cooperative behavior clusters identification

It is difficult to guarantee that each expert can express their evaluation by similar PLPVs completely in the LSGDM problems based on PLPR. For that, why a significant number of the experts are required, and each expert has various knowledge experiences or preferences interest. Thus, we offer to identify non-cooperative behavior cluster $C_{\hat{z}}$ by measuring their NCBDs. For that, the measure of NCBD of cluster $C_{\hat{z}}$ is defined as:

Definition 10

Let $CCI(C_{\hat{z}})$ be the CCI of the cluster $C_{\hat{z}}$ and the group consensus index of the LSGDM based on PLPR be GCI. Then, the NCBD of $C_{\hat{z}}$ is defined as

$$\begin{aligned} NCBD(C_{\hat{z}})=1-\frac{CCI(C_{\hat{z}})}{GCI}. \end{aligned}$$

(19)

As per Definition 10, the higher value of NCBD $(C_{\hat{z}})$ is the higher degree of non-cooperative behavior cluster $C_{\hat{z}}$ will be.

Interaction and discussion

If a non-cooperative behavior cluster $C_{\hat{z}}$ is confirmed, then in-depth more analysis can be carried out between $C_{\hat{z}}$ and the other clusters. We have two outlines:

• (1) The weights of non-cooperative behavior clusters are reduced. If a cluster $C_{\hat{z}}$ is identified according to the non-cooperative behavior, then should be reduced weight $C_{\hat{z}}$ for adverse effect on the final decision.

• (2) The non-cooperative behavior degree is high of the cluster $C_{\hat{z}}$, the more the weights should be reduced. It is because the non-cooperative behavior hurts the LSGDM based on PLPR.

Proper adjustment

In the following, we give the rule to update the weight of cluster $C_{\hat{z}}$ according to the Definition 10

$$\begin{aligned} w_{\hat{z}}^{(\tau +1)}=w_{\hat{z}}^{(\tau )}(1-NCBD^{(\tau )} (C_{\hat{z}}))^{\delta }, \end{aligned}$$

(20)

where $\delta \in [0,1]$ is a feedback parameter to control the NCBD of cluster $C_{\hat{z}}$ on its weight. If the value of $\delta \in [0,1]$ be larger, then the adjustment of the cluster weight will be smaller.

In the following, the assessment information adjustment is to propose of non-cooperative behavior clusters, while we update their weights to improve CRP.

Find the position, $i_{\varsigma }$ and $j_{\varsigma }$ of the maximal elements $\tilde{x}^{(\tau )}_{i_{\varsigma }j_{\varsigma }}$ for $C_{\hat{z}}$, where

$\tilde{x}^{(\tau )}_{i_{\varsigma }j_{\varsigma }}=max(|I(\mathcal {E} (p^{(\tau )}_{ij,\hat{z}})) - I(\mathcal {E}(p^{(\tau )}_{ij,c}))|)$. Then, return $P_{\hat{z}}$ to cluster $C_{\hat{z}}$ to construct a new PLPR $P_{\hat{z}}^{(\tau +1)}= (p_{ij,\hat{z}}^{(\tau +1)})_{n\times n}$, and adjust the corresponding non-cooperative behavior levels:

$$\begin{aligned} p_{ij,\hat{z}}^{(\tau +1)} = {\left\{ \begin{array}{ll} p_{ij,c}^{(\tau )}, ~ &{} \text {if}~i=i_{\varsigma },~j=j_{\varsigma }\\ p_{ij,\hat{z}}^{(\tau )}, ~ &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

(21)

If the preference values of two elements are equal, i.e., $I(\mathcal {E}(p_{i_{\varsigma }j_{\varsigma },\hat{z}}^{(\tau )})) =I(\mathcal {E}(p_{i^{\prime }_{\varsigma }j^{\prime }_{\varsigma }, \hat{z}}^{(\tau )}))$, then we find the adjustment rules for these two preference values are given below:

• (1) If $|I(\mathcal {E}(p_{ij,\hat{z}}^{(\tau )})) \, - \, I(\mathcal {E}(p_{ij,c}^{(\tau )}))|\, < \, |I(\mathcal {E}(p_{i^{\prime }_{\varsigma }j^{\prime }_{\varsigma },\hat{z}}^{(\tau )})) - I(\mathcal {E}(p_{ij,c}^{(\tau )}))|$, then $p_{i^{\prime }_{\varsigma }j^{\prime }_{\varsigma },\hat{z}}^{(\tau )}$ to be modified in cluster $C_{\hat{z}}$;

• (2) If $|I(\mathcal {E}(p_{ij,\hat{z}}^{(\tau )})) {-} I(\mathcal {E}(p_{ij,c}^{(\tau )}))| > |I(\mathcal {E}(p_{i^{\prime }_{\varsigma }j^{\prime }_{\varsigma },\hat{z}}^{(\tau )})) - I(\mathcal {E}(p_{ij,c}^{(\tau )}))|$, then $p_{i_{\varsigma }j_{\varsigma },\hat{z}}^{(\tau )}$ to be modified in cluster $C_{\hat{z}}$;

• (3) $|I(\mathcal {E}(p_{ij,\hat{z}}^{(\tau )})) - I(\mathcal {E}(p_{ij,c}^{(\tau )}))|= |I(\mathcal {E}(p_{i^{\prime }_{\varsigma }j^{\prime }_{\varsigma },\hat{z}}^{(\tau )})) - I(\mathcal {E}(p_{ij,c}^{(\tau )}))|$, then randomly choose either $p_{i_{\varsigma }j_{\varsigma },\hat{z}}^{(\tau )}$ or $p_{i^{\prime }_{\varsigma }j^{\prime }_{\varsigma },\hat{z}}^{(\tau )}$ for modification in cluster $C_{\hat{z}}$.

Selection process

When we obtain acceptable consensus, then we now ready for ranking of the alternatives. For that, we first obtain the row arithmetical average values of the weight collective PLPR $P_{c}=(p_{ij,c})_{n \times n}$ in the following way:

$$\begin{aligned} p_{i,c}&=\left<s_{\frac{1}{n}\sum _{j=1}^{n}\theta _{ij,c}}, \left( \frac{1}{n}\sum _{j=1}^{n}\mu _{ij,c}, \frac{1}{n}\sum _{j=1}^{n}\nu _{ij,c}\right) \right>\nonumber \\&=\left<s_{\theta _{p_{i,c}}},\left( \mu _{p_{i,c}},\nu _{p_{i,c}} \right) \right>. \end{aligned}$$

(22)

From expression (22), we give the following definition for choosing the best alternatives.

Definition 11

Let $X=\{x_{1},x_{2}, \dots , x_{n}\}$ be the set of alternatives and $P_{c}=(p_{ij,c})_{n \times n}$ be the weight collective PLPR of the LSGDM based on PLPR, and then, the lower index $I(x_{i})$ of $P_{c}=(p_{ij,c})_{n \times n}$ for each alternative $x_{i}$ is defined as

$$\begin{aligned} I(x_{i})&=I(\mathcal {E}(p_{i,c}))\nonumber \\&=\frac{(\mu _{p_{i,c}}^{2}+1-\nu _{p_{i,c}}^{2}) \times s_{\theta _{p_{i,c}}}}{2}, \end{aligned}$$

(23)

$i\in \{1,2,\dots ,n\}$.

The detailed process of the ranking of alternatives LSGDM based on PLPR is depicted in Algorithm 2.

An illustrative numerical example and comparative analysis

In this section, we offer a numerical example to show the validity of the proposed consensus model for the LSGDM based on PLPR and compare with existing studies.

An example

Let $X=\{x_{1}$, $x_{2}$, $\dots$, $x_{5}\}$ be a set of alternatives and $E=\{e_{1}$, $e_{2}$, $\dots$, $e_{20}\}$ be the set of 20 experts are invited to make decisions. All the 20 experts individually make a pairwise comparison for the alternatives in X, and then give their opinion using PLPVs $p_{ij}^{k}=\langle s_{\theta _{ij}^{k}}, (\mu _{ij}^{k},\nu _{ij}^{k})\rangle$ $(1\le k \le 20)$ for the predefined linguistic term set $s=\{s_{-5}:$ extremely bad; $s_{-4}:$ very bad; $s_{-3}:$ bad; $s_{-2}:$ relatively bad; $s_{-1}:$ a little bad; $s_{0}:$ fair; $s_{1}:$ a little good; $s_{2}:$ relatively good; $s_{3}:$ good; $s_{4}:$ very good; $s_{5}:$ extremely good $\}$. The detailed preference information is shown in Table 2.

Table 2 Individual PLPRs given by each expert $e_{k}$ $(k=1,2,\dots ,20)$

According to proposed Algorithm 2, we have the following steps:

Step 1: In this step, we apply Algorithm 1 for the experts clustering. For this, let us assume that two parameter $\varsigma =0.86$, which is the similarity degree threshold value among the experts and $\xi =0.7$, which is the similarity degree threshold value between the expert and cluster. The results of clustering are shown in Table 3.

Step 2: Using expressions (12) and (13), we compute the weight of each cluster $C_{\hat{z}}$ $(\hat{z}=\{1,2,\dots , 5\})$ and the weight of each expert in $C_{\hat{z}}$ $(\hat{z}=\{1,2,\dots , 5\})$. The detailed results are shown in Table 4.

Step 3: Set $\tau = 0$. Using expression (14), we obtain $P_{\hat{z}}^{(0)}=(p_{ij,\hat{z}}^{(0)})_{5 \times 5}$ and the results are shown in Table 4. Using expression (15) and from Table 4, we compute the weight collective PLPR $P_{c}=(p_{ij,c})_{5 \times 5}$ given in expression (24). Using expressions (16) and (17), we calculate the deviation measure $\varrho (P_{\hat{z}},P_{c})$ and cluster consistency index $CCI(C_{\hat{z}})$. The detailed results are shown in Table 5.

$$\begin{aligned}&P_{c} = \left[ \begin{matrix} \langle s_{0},(1,0)\rangle &{} \langle s_{2},(0.639,0.386)\rangle &{} \langle s_{1},(0.739,0.309)\rangle \\ \langle s_{-2},(0.639,0.386)\rangle &{} \langle s_{0},(1,0)\rangle &{}\langle s_{0.35},(0.657, 0.331)\rangle \\ \langle s_{-1},(0.739,0.309)\rangle &{} \langle s_{-0.35},(0.657,0.331)\rangle &{} \langle s_{0},(1,0)\rangle \\ \langle s_{0.1},(0.625, 0.201)\rangle &{} \langle s_{-1.7},(0.612, 0.303)\rangle &{}\langle s_{-0.4},(0.699,0.159)\rangle \\ \langle s_{-2.95},(0.66,0.281)\rangle &{}\langle s_{-1.05},(0.599,0.342)\rangle &{}\langle s_{-0.7},(0.634,0.18)\rangle \\ \end{matrix} \begin{matrix} \langle s_{-0.1},(0.625,0.201)\rangle &{} \langle s_{2.95}(0.66,0.281)\rangle \\ \langle s_{1.7},(0.612, 0.303)\rangle &{} \langle s_{1.05},(0.599, 0.342)\rangle \\ \langle s_{0.4},(0.699, 0.159)\rangle &{} \langle s_{0.7},(0.634,0.18)\rangle \\ \langle s_{0},(1,0)\rangle &{} \langle s_{0.45},(0.682, 0.324)\rangle \\ \langle s_{-0.45},(0.682,0.324)\rangle &{} \langle s_{0},(1,0)\rangle \\ \end{matrix}\right] . \end{aligned}$$

(24)

Using expression (18) and Tables 4 and 5, we get $GCI^{(0)}=0.912$.

Step 4: Let us assume that the predefined acceptable consensus threshold $\sigma =0.975$ and the feedback parameter are $\delta =0.5$. Since $GCI^{(0)}=0.912<0.975$.

Steps 5, 6 & 7: Using expression (19), we compute the NCBD of each cluster $C_{\hat{z}}^{(0)}$, and we get $NCBD(C_{1}^{(0)})=0.091$, $NCBD(C_{2}^{(0)})=0.072$, $NCBD(C_{3}^{(0)})=0.075$, $NCBD(C_{4}^{(0)})=-0.043$, $NCBD(C_{5}^{(0)})=0.037$. Since $max\{NCBD$ $( C_{\hat{z}}^{(0)})$ $\mid \hat{z} = 1, 2, 3, 4, 5\} = 0.091 = NCBD(C_{1}^{(0)})$, i.e., $C_{1}^{(0)}$ is the non-cooperative behavior cluster. Therefore, the first consensus iteration should be implemented on the cluster $C_{1}^{(0)}$. The detailed consensus round results are shown in Table 6. The trend chart of GCI and the feedback parameter for each round is shown in Fig. 2, when $\sigma =0.975$. In Fig. 1, we also display the corresponding updating the weights and the trend of NCBD of clusters of different rounds, when $\sigma =0.975$.

Step 8: From Table 6, we see that after 18th round iteration, the GCI is acceptable. Thus, using expression (15), we calculate the weight collective PLPR $P_{c}^{(18)}$, which is shown in expression (25):

$$\begin{aligned}&P_{c}^{(18)} = \left[ \begin{matrix} \langle s_{0},(1,0)\rangle &{} \quad \langle s_{3.131},(0.684,0.321)\rangle &{} \quad \langle s_{1.242},(0.729,0.285)\rangle \\ \langle s_{-3.131},(0.684,0.321)\rangle &{} \quad \langle s_{0},(1,0)\rangle &{} \quad \langle s_{0.35},(0.663,0.331)\rangle \\ \langle s_{-1.242},(0.729,0.285)\rangle &{} \quad \langle s_{-0.35},(0.663,0.331)\rangle &{} \quad \langle s_{0},(1,0)\rangle \\ \langle s_{-0.254},(0.635,0.11)\rangle &{} \quad \langle s_{-1.825},(0.619,0.291)\rangle &{} \quad \langle s_{-1.171},(0.722,0.059)\rangle \\ \langle s_{-2.759},(0.669,0.253)\rangle &{} \quad \langle s_{-0.757},(0.599,0.295)\rangle &{}\ \quad \langle s_{-0.985},(0.651,0.115)\rangle \\ \end{matrix}\begin{matrix} \langle s_{0.254},(0.635,0.11)\rangle &{} \quad \langle s_{2.759}, (0.669,0.253)\rangle \\ \langle s_{1.825},(0.619, 0.291)\rangle &{} \quad \langle s_{0.757},(0.599, 0.295)\rangle \\ \langle s_{1.171},(0.722, 0.059)\rangle &{} \quad \langle s_{0.985},(0.651,0.115)\rangle \\ \langle s_{0},(1,0)\rangle &{}\quad \langle s_{1.615},(0.678, 0.275)\rangle \\ \langle s_{-1.615},(0.678,0.275)\rangle &{} \quad \langle s_{0},(1,0)\rangle \\ \end{matrix}\right] . \end{aligned}$$

(25)

Steps 9, 10 & 11: We obtain the row arithmetical average values of the weight collective PLPR $P_{c}^{(18)}=(p_{ij,c}^{(18)})_{5 \times 5}$ and the lower index of each alternative $I(x_{i})$ of $P_{c}^{(18)}=(p_{ij,c}^{(18)})_{5 \times 5}$ using expressions (22) and (23), are respectively. The detailed results are shown in Table 7. From Table 7 and the Definition 5, the alternative ranking is $x_{1} \succ x_{3} \succ x_{2} \succ x_{4} \succ x_{5}$. Thus, the best option for this LSGDM problem based on PLPR is $x_{1}$. The trend chart of $I(x_{i})$ of the alternatives $x_{i}$ $(1\le i \le 5)$ for various rounds when the acceptable consensus threshold value $\sigma =0.975$ is shown in Fig. 3.

Table 3 Experts clustering results with $\varsigma =0.86$ and $\xi =0.7$

Table 4 Aggregating results of cluster $C_{\hat{z}}$

Discussion with comparative analysis

In general, comparative analysis is done by two points of view such as: the comparison of the GDM technique with numerical example and characteristics comparison of the GDM technique. PLPR is a new type preference relation, and so, there is no previous study about decision-making with the LSGDM problem based on PLPR. Therefore, no comparison is made here for GDM technique with numerical example. We only provide the characteristics comparison with intuitionistic linguistic sets (ILSs) [44], intuitionistic linguistic preference relations (ILPRs) [39], PLS [35, 38], and PLPR [38], which is shown in Table 8.

Table 5 The results of $\varrho (P_{\hat{z}},P_{c})$ and $CCI(C_{\hat{z}})$

Table 6 The detailed consensus iteration results

Fig. 2

The trend chart of the GCI and the feedback parameter for different rounds when $\sigma =0.975$

Table 7 The results of $p_{i,c}$ and $I(x_{i})$

Fig. 3

The trend chart of updating the weights and the NCBD of clusters for different rounds when $\sigma =0.975$

Fig. 4

The $I(x_{i})$ of the alternatives $x_{i}$ $(1\le i \le 5)$ for different rounds when $\sigma =0.975$

Table 8 Comparison with existing studies

Conclusions

In this paper, we have studied the LSGDM problem in the fuzzified linguistic context, that is proposed an approach the LSGDM problem based on PLPR. We focus on non-cooperative behavior-based CRP with the degree of the non-cooperative behavior of clusters and feedback process for the LSGDM problem base on PLPR. We allow all the experts to use PLPR who express their opinion. In CRP, clusters are dynamically adjusted their non-cooperative behavior degrees while revising preferences values. Consequently, all clusters achieve a consensus level. In CRP, the determination of non-cooperative behavior degree is utilized to assign the weights of clusters, and then, cluster modification is done by the feedback process. An example is offered to demonstrate the effectiveness of the proposed method. Incomplete PLPR is not considered in this LSGDM problem, which will be studied in future.