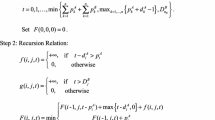Introduction

Multitasking means that there are a set of tasks processed at the same time or within a limited time interval for a person or a machine (a computer, a team, a center). Multitasking phenomenon has been discussed in many disciplines, for example, behavioral psychology [39], cognitive science [6], community pharmacy [25], experimental psychology [33, 34], healthcare operations management [20], managerial behavior [42], chemical engineering [23], computer science (embedded systems, distribution system and parallel computing), Noguera and Badia [31], Appasami and Suresh Joseph [4], Kardos et al. [19], Lai et al. [24], and so on.

There are two models of multitasking [9, 38,46]. One is the concurrent mode, i.e. to perform two or more tasks at the same time, for example, media multitasking [40] and [32]. The other is the sequential mode, i.e. to perform tasks by interleaving and switching from one task to other tasks [29]. The two types of multitasking are also seen in embedded computing system design employed in system-on-chip platforms [31].

In job scheduling domain or manufacturing field, several possible applications of multitasking were observed in, for example, administration processing [12], manufacturing [50]. In this paper, we study the sequential model of multitasking for job scheduling problem, i.e. a ‘machine’ (a team, a service center, and so on) processes a sequence of jobs (tasks) by interleaving and switching from one job to another during an interval of time. The operations for classical scheduling problem are to finish one job at one time then process another job, until all the required jobs are finished. The operations for multitasking scheduling problem (MSP) are also to perform a predetermined job (called a primary job) on a job sequence at one time, however, before the primary job to be fully finished, due to a certain reason, operations switch to process all the unfinished jobs (or called waiting jobs) by interleaving to finish a proportion of each waiting job, afterwards, the primary job is finished completely. Hall et al. [12,13], launched the multitasking research in the scheduling problem area, carried on by Sum and Ho [43], Zhu et al. [57, 58], Liu et al. [27], Ho and Sum [14], Li and Chong [26], and Ji et al. [18]. More recently, Zhu et al. [60] proposed optimal solution algorithms for multitasking scheduling with multiple rate-modifying activities and analyzed some special cases of them. Xiong et al. [48] applied an exact branch‐and‐price algorithm to solve an unrelated parallel-machine multitasking scheduling problem.

Hall et al. [12] constructed a mathematical model incorporated the multitasking into the traditional single-machine scheduling problem, and provided a summary of five motivations for multitasking. The objective criteria investigated were maximum lateness, the total weighted completion time, and total number of late jobs. Hall et al. [13] studied two models to accommodate two features that are possible happened on multitasking scheduling environment for human workers. One model employed “alternate period processing” for a disruption (and have to perform multitasks) owing to workers’ tiredness situation and the other model employed “shared processing” for a distraction (and have to perform multitasks) owing to routine tasks situation. The studied criteria were the maximum lateness, the total completion time, and the number of late jobs. They discussed the complexity of models and then developed algorithms to resolve the considered problems.

Following the considered problem by Hall et al. [13], Sum and Ho [43] derived the expected total (weighted) completion time and provided statistical analysis on the performance of multitasking for a human worker under the assumptions that the switching cost is constant and the amount of each interruption is proportional to the remaining processing time of the waiting job. They gave an advice “that multitasking should be avoided in a work place”. Ho and Sum [14] investigated the MSP with asymmetric switch cost functions and demonstrated that and the problem is unary NP-hard for minimization of the total completion time or a common due date assignment problem, and the problem is binary NP-hard for the makespan. They also showed that if a cost function has a special structure then the study problem can be solved in polynomial time for three common adopted criteria. Zhu et al. [57,58], explored the MSP with a (or multiply) rate-modifying activity (activities), respectively. They formulated models and developed algorithms to solve the MSP for criteria including the makespan, the total completion time, the lateness, and a multi-criteria that combines several criterions related to a common due date assignment. Zhu [57] put forward several optimal algorithms to solve the MSP with a deterioration effect to minimize the makespan and the total absolute differences in completion times. Liu et al. [27] added a common due date required for jobs into the multitasking scheduling formulation investigated by Hall et al. [12]. The objective function was a linear combination of the total earliness, the total tardiness, and a common due date assignment. They provided some theoretical results and developed an algorithm to solve the problem with linear interruption functions. Moreover, they suggested several future research topics for the MSP. Li and Chong [26] developed a single-machine multitasking scheduling model to management the progress on the processing jobs which can be split into subtasks to be processed, and also considered to check the progress at different milestones (time points). The main concern is to monitor or to control the amount of jobs been processed. Ji et al. [18], motivated from the service industry (internet service, medical service), investigated the MSP under parallel-machine setting with machine-dependent slack due window scenario. The objective was to minimize a total cost function which is a combination of criteria of the earliness, the tardiness and the time related to slack due window assignment. The main contribution of them was to represent the interruption function as a more general form that can reflect real service or manufacturing situations.

On the other hand, two-agent or multi-agent scheduling problem has been studied in the recent about 20 years. For example, Baker and Smith [5] and Agnetis et al. [1] are among the pioneers on this topic. In a two-agent single machine scheduling problem, different agents share one processing resource (machine) and each agent demands to optimize its own optimality criterion concerning to its own set of jobs. As the agents have its own optimality criterion, in general, they have to compete for sharing a collaborative resource to make the best their own criterion. Baker and Smith [5] investigated the problems of minimizing an aggregate of different optimality criteria adopted by two agents, in which the optimality criteria considered were the total weighted completion time, the maximum lateness, and the makespan. Depending on the optimality criterion of each agent and on the processing environment (single machine or job shop), Agnetis et al. [1] addressed a constrained optimization problem, in which one agent have to optimize its optimality criterion with respect to its own jobs subject to a constraint on the other agent’s objective function. Since then, study on the multi-agent job sequencing problem has been developed in the area of scheduling. For more discussing on two-agent or multi-agent scheduling research, the reader may refer, Mor and Mosheiov [30], Gerstl and Mosheiov [10], Kovalyovet al. [22], Yin et al. [51, 52, 53, 54], Li et al. [28], Zhang and Wang [56], Ahmadi-Darani et al. [3] a review paper by Perez-Gonzalez and Framinan [35], and the book by Agnetis et al. [2]. More recently, Yang et al. [49] introduced due date assignment into a two-agent scheduling problem to minimize the completion times of given jobs. Wang et al. [45] studied several multitasking scheduling models with multiple agents in which the objective functions were included the maximum of a regular function (associated with each task), the total completion time, and the weighted number of late jobs.

To the best of authors’ knowledge, there is no research on the machine multitasking scheduling problem (MSP) together with two (or more) agents. This study tries to bridge the gap, and also responds to one of the further research problems—“Second, the classical scheduling literature contains a large number of problems that remain to be studied in the presence of multitasking.” mentioned in Hall et al. [12]. Moreover, one of the future research directions in Agnetis et al. [1], in a multi-agent scheduling problems environment, is to “Extension to different resource usage modes (concurrent usage, preemption, etc.) and/or different system structure (e.g. parallel machines).” Therefore, we study the alliance of these two emerging topics in the scheduling problem area. The objective is to minimize the total tardiness of first agent’s jobs subject to an upper bound constraint on the total completion time of the second agent’s jobs.

The rest of this paper is organized as follows. The problem statement is given in “Problem statement”. In “Properties and a lower bound”, we derive several dominance properties and a lower bound for the study problem. In “Metaheuristics GA, SA, and CSA”, three commonly used metaheuristics [cloud simulated annealing algorithm (CSA), genetic algorithm (GA), simulated annealing algorithm (SA)] are adapted as tools to search (approximate) optimal solutions. “Data simulation analysis” is analysis of experimental simulation data, and conclusion and suggestions are in “Conclusion and suggestions”.

Problem statement

The proposed multitasking scheduling problem (MSP) in this study is formulated as follows. Consider a set of n jobs, \(\left\{{J}_{1},{J}_{2},\ldots ,{J}_{n}\right\}\), to be processed by a machine. For convenient explanations, sometimes we use the job i or i to represent \({J}_{i}\). The machine can operate at most one job at a time. Suppose that there are two competing agents denoted, respectively, by agents \(A\) and \(B\). Besides, let \(X\in \left\{A, B\right\}\) be the agent code. The jobs belong to agent \(X\) are presented as \(X\)-jobs. Let \({J}_{A}\) and \({J}_{B}\) denote the sets of jobs from agent A (or A-jobs) and jobs from agent B (or B-jobs), respectively, meanwhile let \({N}_{a}\) and \({N}_{b}\) denote the number of A-jobs in \({J}_{A}\) and B-jobs in \({J}_{B}\). That is \({J}_{A}= \left\{{J}_{1}^{A},{J}_{2}^{A},\ldots ,{J}_{{N}_{a}}^{A}\right\}\), \({J}_{B}= \left\{{J}_{1}^{B},{J}_{2}^{B},\ldots ,{J}_{{N}_{b}}^{B}\right\}\), and \({J}_{A}\cup {J}_{B}=\left\{{J}_{1},{J}_{2},\ldots ,{J}_{n}\right\}\). Both of jobs in the set \(\left\{A, B\right\}\) are available at the begin of operation (time zero). Both of the processing time (\({t}_{j}^{X}\)) and due date (\({d}_{j}^{X}\)) for a job \({J}_{j}^{X}\) are nonnegative integers. For a job schedules \(\sigma\), let \({C}_{j}^{X}(\sigma )\), or \({C}_{j}^{X}\), be the completion time of job \({J}_{j}\), and \({T}_{j}^{X}=\mathrm{max}\{ {C}_{j}^{X}\left(\sigma \right)-{ d}_{j}^{X}, 0\}\) be the tardiness of job j as in the job sequence \(\sigma\).

The serial (sequential) multitasking environment means that when a job is being processed, it is fractured by other unfinished jobs that are waiting for processing. Every job is assigned at any time point is represented as the primary job, while the jobs that are ready and not fully processed are denoted as waiting jobs. Under the multitasking situation, as a primary job is being processed, it is interrupted by all the waiting jobs. Two more assumptions are required to model the process on which the waiting jobs interrupt the primary jobs. One is called “interruption time” that is the time during which a waiting job interrupts the primary job, which is independent of the characteristics of the primary job. Let \(t_{i}^{X\prime }\) be the not yet finished processing time of a waiting job i at the beginning of a time point when job j is scheduled as a primary job. In this study, the amount of time for which job i interrupts job j is given by \(g(t_{i}^{X\prime } ) = Dt_{i}^{X\prime }\) as in Hall et al. (12), where D is a ratio of interruption (time) cost with \(0 < D < 1\). The other assumption is called “switching time” that is the amount of time prepared to deal with the primary job is scheduled, which depends only on the number of waiting jobs. Let \({S}_{j}\) be the set of waiting jobs when j is assigned to be the primary job and \(f(\left|{S}_{j}\right|)\) be the amount of switching time for processing the interrupting jobs. In this study, the switching time is adopted as \(f\left(\left|{S}_{j}\right|\right)=|{S}_{j}|\), which depends only on the number of waiting jobs. The objective function of this study is to minimize the total tardiness of all the jobs of the agent A subject to an upper bound, say Q, required on the total completion time of jobs of agent B. The three-field notation for this problem in scheduling domain can be denoted as \(1/{\text{`mt'}}/\sum T_{j}^{A} :\sum C_{j}^{B} \le Q\), where ‘mt’ represents multitasking.

Properties and a lower bound

The proposed problem is NP-hard, since the classical problem without agent concept or multitasking phenomenon is NP-hard (Pinedo 36). To efficiently deal with this problem, a branch-and-bound (B&B) algorithm is devised to find the optimal solutions for small-size instances and three metaheuristics are then utilized to quickly find the approximate solutions for relatively large-size instances. It is noted that the dominance properties act a considerable role in a B&B algorithm for searching an exact solution (schedule) because many lower nodes of the instances can be cut down by applying these dominant properties. To help speeding up the search process of the B&B, several dominance properties are established in this section. Let \(\upsigma =({\pi }_{1},i,j,{\pi }_{2})\) and \({\sigma }^{^{\prime}}=({\pi }_{1},j,i,{\pi }_{2})\) be two job sequences (schedules) in which \({\pi }_{1}\) and \({\pi }_{2}\) are two parts of subsequences with k jobs and (n-k-2) jobs, respectively. The switching cost function is \(f\left(\left|\left\{i,j,{\pi }_{2}\right\}\right|\right)=n-k\), k = n − 1, n − 2, …, 1, and s denote the staring time of job i in \(\upsigma =({\pi }_{1},i,j,{\pi }_{2})\) and job j in \({\sigma }^{^{\prime}}=({\pi }_{1},j,i,{\pi }_{2})\). D denotes the ratio of interruption cost, where \(t_{i}^{X\prime } = D \times t_{i}^{X}\). To show that \(\upsigma\) dominates \({\sigma }^{^{\prime}}\), the following suffices: \(\mathrm{max}\left\{{C}_{i}^{A}\left(\upsigma \right)-{d}_{i}^{A},0\right\}+\mathrm{max}\left\{{C}_{j}^{A}\left(\upsigma \right)-{d}_{j}^{A},0\right\}<\mathrm{max}\left\{{C}_{j}^{A}\left({\sigma }^{^{\prime}}\right)-{d}_{j}^{A},0\right\}+\mathrm{max}\left\{{C}_{i}^{A}\left({\sigma }^{^{\prime}}\right)-{d}_{i}^{A},0\right\},\) and \({C}_{j}^{A}\left(\upsigma \right)\) < \({C}_{i}^{A}\left({\sigma }^{^{\prime}}\right)\), where\({C}_{j}^{X}\left(\sigma \right)=s+{(1-D)}^{k-1}{t}_{j}^{X}+f\left(k\right)+\sum_{v\in {\pi }_{2}\bigcup \{j\}}D{(1-D)}^{k-1}{t}_{v}^{X}\). The proofs of following properties are left out because they can be proved by applying a pairwise interchange method.

Property 1

If \(s + (1 - D)^{k - 1} t_{i}^{A} + f(k) + \sum\nolimits_{{v \in \pi_{2} \cup \{ j^{A} \} }} {D(1 - D)^{k - 1} t_{v}^{X} } < d_{i}^{A}\) \(< s + (1 - D)^{k - 1} t_{j}^{A} + f(k) + \sum\nolimits_{{v \in \pi_{2} \cup \{ i^{A} \} }} {D(1 - D)^{k - 1} t_{v}^{X} } + (1 - D)^{k} t_{i}^{A} + f(k + 1) + \sum\nolimits_{{v \in \pi_{2} }} {D(1 - D)^{k} t_{v}^{X} }\) and \(\max \{ s + (1 - D)^{k - 1} t_{j}^{A} + f(k) + \sum\nolimits_{{v \in \pi_{2} \cup \{ i^{A} \} }} {D(1 - D)^{k - 1} t_{v}^{X} } ,s + (1 - D)^{k - 1} t_{i}^{A} + f(k)\) \(+ \sum\nolimits_{{v \in \pi_{2} \cup \{ j^{A} \} }} {D(1 - D)^{k - 1} t_{v}^{X} } + (1 - D)^{k} t_{j}^{A} + f(k + 1) + \sum\nolimits_{{v \in \pi_{2} }} {D(1 - D)^{k} t_{v}^{X} } \} < d_{j}^{A}\), then \(\sigma\) dominates \(\sigma^{\prime}\).

Property 2

If \(s + (1 - D)^{k - 1} t_{i}^{A} + f(k) + \sum\nolimits_{{v \in \pi_{2} \cup \{ j^{A} \} }} {D(1 - D)^{k - 1} t_{v}^{X} } > d_{i}^{A}\) and \(s + (1 - D)^{k - 1} t_{i}^{X} + f(k) + \sum\nolimits_{{v \in \pi_{2} \cup \{ j^{A} \} }} {D(1 - D)^{k - 1} t_{v}^{X} } + (1 - D)^{k} t_{j}^{A} + f(k + 1) + \sum\nolimits_{{v \in \pi_{2} }} {D(1 - D)^{k} t_{v}^{X} } \le d_{j}^{A}\), then \(\sigma\) dominates \(\sigma^{\prime}\).

Property 3

If \(s + (1 - D)^{k - 1} t_{i}^{A} + f(k) + \sum\nolimits_{{v \in \pi_{2} \cup \{ j^{A} \} }} {D(1 - D)^{k - 1} t_{v}^{X} } > d_{i}^{A}\), \(s + (1 - D)^{k - 1} t_{j}^{A} + f(k) + \sum\nolimits_{{v \in \pi_{2} \cup \{ i^{A} \} }} {D(1 - D)^{k - 1} t_{v}^{X} } > d_{j}^{A}\), \({d}_{i}^{A}<{d}_{j}^{A}\), and, \({d}_{j}^{A}-{d}_{i}^{A}<{t}_{j}^{A}-{t}_{i}^{A}\), then \(\sigma\) dominates \(\sigma^{\prime}\).

For any uncompleted node (PS, US) in which PS is already assigned partial sequence with k jobs and US is an undecided subset of jobs with (n-k) jobs, the following two properties hold.

Property 4

Let \({C}_{[l]}^{B}\) be the completion time of the last job in PS. If \({C}_{[l]}^{B}>Q\), then node (PS, US) should be an infeasible schedule.

Property 5

Let \({C}_{[k]}\) be the completion time of the last job in PS. If there is any B job in US and \({C}_{[k]}+{(1-D)}^{k-1}{t}_{j}^{B}+f\left(k\right)+\sum_{v\in US\backslash \{{j}^{B}\}}{D(1-D)}^{k-1}{t}_{v}^{X}>Q\), then node (PS, US) should be eliminated.

The performance of the B&B algorithm is also related to a good lower bound. In what follows, a simple lower bound will be presented. Assume that PS is a partial sequence in which the order of the first k jobs is determined and US be the unscheduled part with (\(n-k\)) jobs. Furthermore, let \(n-k={n}_{A}+{n}_{B},\) where \({n}_{A}\) denote the number of A-jobs while \({n}_{B}\) denote the number of B-jobs in US. Let \(\sigma\mathrm{dnote}\) a complete sequence obtained from PS. The completion time for the (k + 1)th job to the (k + \({n}_{A}\))th position in a \(\upsigma =(\mathrm{PS},\mathrm{US})\), if the \({n}_{A}\) A-jobs schedule on the first \({n}_{A}\) positions in US, is given by

$$C_{[k + 1]}^{A} (\sigma ) = s + (1 - D)^{k} t_{[k + 1]}^{A} + f(k + 1) + \sum\limits_{{v \in {\text{US}}\backslash \{ j_{[k + 1]} \} }} {D(1 - D)^{k} t_{v}^{X} } ,$$
$$\begin{aligned} C_{[k + 2]}^{A} (\sigma ) & = s + (1 - D)^{k} t_{[k + 1]}^{A} + f(k + 1) + \sum\limits_{{v \in {\text{US}}\backslash \{ j_{[k + 1]}^{A} \} }} {D(1 - D)^{k} t_{v}^{X} } \\ & \quad + (1 - D)^{k + 1} t_{[k + 2]}^{A} + f(k + 2) + \sum\limits_{{v \in {\text{US}}\backslash \{ j_{[k + 1]}^{A} ,j_{[k + 2]}^{A} \} }} {D(1 - D)^{k + 1} t_{v}^{X} } . \\ \end{aligned}$$

In a similar way, we have

$$\begin{aligned} C_{{[k + n_{A} ]}}^{A} (\sigma ) & = s + (1 - D)^{k} t_{[k + 1]}^{A} + f(k + 1) + \sum\limits_{{v \in {\text{US}}\backslash \{ j_{[k + 1]}^{A} \} }} {D(1 - D)^{k} t_{v}^{X} } \\ & \quad + (1 - D)^{k + 1} t_{[k + 2]}^{A} + f(k + 2) + \sum\limits_{{v \in {\text{US}}\backslash \{ j_{[k + 1]}^{A} ,j_{[k + 2]}^{A} \} }} {D(1 - D)^{k + 1} t_{v}^{X} } \\ & \quad \cdots \\ & \quad + (1 - D)^{{k + n_{A} }} t_{{[k + n_{A} ]}}^{A} + f(k + n_{A} ) + \sum\limits_{{v \in {\text{US}}\backslash \{ j_{[k + 1]}^{A} ,j_{[k + 2]}^{A} ,...,j_{{[k + n_{A} ]}}^{A} \} }} {D(1 - D)^{{k + n_{A} - 1}} t_{v}^{X} } . \\ \end{aligned}$$

According to the above definitions, those \({n}_{A}\) are arranged in a non-decreasing order to obtain the least amount of the completion times from \({n}_{A}\) A-jobs in US. Next problem is to find the maximum due date (say dM) from \({n}_{A}\) A-jobs in US and assign dM to be the due date for each A-job in US to yield the least amount of tardiness for the unscheduled part. It can be simplified as follows:

$${\text{LB}}\, = \,\mathop \sum \limits_{{i \in {\text{PS}}}} {\text{max}}\left\{ {0,C_{\left[ i \right]}^{A} \left( \sigma \right) - d_{\left[ i \right]}^{A} } \right\} + \mathop \sum \limits_{i = 1}^{{n_{A} }} {\text{max}}\left\{ {0,C_{{\left( {k + i} \right)}}^{A} \left( \sigma \right) - d_{{\text{M}}} } \right\},$$

where \({C}_{\left(k+i\right)}^{A}\left(\sigma \right)=s+{(1-D)}^{k}{t}_{(k+1)}^{A}+f\left(k+1\right)+\sum_{v\in \mathrm{US}\backslash \left\{{j}_{[k+1]}^{A}\right\}}D{(1-D)}^{k}{t}_{v}^{X}\)

$$+{(1-D)}^{k+1}{t}_{(k+2)}^{A}+f\left(k+2\right)+\sum_{v\in \mathrm{US}\backslash \left\{{j}_{\left[k+1\right],}^{A}{j}_{\left[k+2\right]}^{A}\right\}}D{(1-D)}^{k+1}{t}_{v}^{X}$$
$$+\cdots +{\left(1-D\right)}^{k+i}{t}_{\left(k+i\right)}^{A}+f\left(k+i\right)+\sum_{v\in \mathrm{US}\backslash \left\{{j}_{\left[k+1\right],}^{A}{j}_{\left[k+2\right], \cdots ,}^{A}{j}_{\left[k+i\right]}^{A}\right\}}D{\left(1-D\right)}^{k+i}{t}_{v}^{X}.$$

Metaheuristics GA, SA, and CSA

It is commonly known that the computation load can be much saved by utilizing a heuristic or metaheuristic (to quickly search a near optimal solution) to lay an (upper or lower) bound on a scheduling problem proceeding to execute a B&B (branch-and-bound) method. Thus, many research paid more attention on developing and analysis of heuristic or metaheuristic algorithms for finding optimal solutions for scheduling problems. Moreover, it is noted that the search for optimal solutions for large-size jobs is required much CPU time. However, an effective heuristic or metaheuristic can yield a good-quality approximate solution with a small margin of error and least amount of CPU time. In light of these observations, this study utilizes three metaheuristics, including the genetic algorithm (GA), the simulated annealing algorithm (SA), and the cloud simulated algorithm (CSA), to solve the study problem. These metaheuristics GA, SA, and CSA have been successfully used to deal with a wide variety of discrete combinatorial optimization problems. The main steps of GA are to start with a set of feasible population and iteratively to replace the current population by a new population throughout encode, reproduction mechanism, a crossover operator, a mutation operator, and decode (see [8, 11, 15, 41]). The details of the GA are given below.

figure a

The SA algorithm by Kirkpatrick et al. [21] is the most commonly utilized metaheuristic algorithm for solving problems from combinatorial optimization. The major steps of SA are provided below.

figure b

The cloud simulated algorithm (CSA) put forward by Torabzadeh and Zandieh [44] is also used to resolve the study problem. The key parameters of CSA are including the start (initial) temperature \({T}_{\mathrm{i}}\), stop temperature \({T}_{\mathrm{f}}\), and the decay (cooling) factor λ. The major details of CSA are provided below.

figure c

Note that TT(\({\sigma }_{1}\)) and TT(\({\sigma }_{0}\)) denote the total tardiness of \({\sigma }_{1}\) and \({\sigma }_{0}\), respectively, while \(\Delta = (TT(\sigma_{1} ) - TT(\sigma_{0} ))/TT(\sigma_{0} )\). To further improve the quality of the initial solutions (seeds) used in GA, SA, and CSA, three local searches were applied to improve each of the initial solutions in GA, SA, and CSA. During generating an initial solution process, those B-jobs are first generated and then A-jobs were generated and appended after B-jobs to form as a feasible initial solution. To get a good quality of solution, this initial solution is separately employed three local search methods to improve it. Those operations are the pairwise interchange (PI), extraction and backward-shifted reinsertion (EBSR), and extraction and forward-shifted reinsertion (EFSR), refer Della Croce et al. [7]. The initial solutions improved by the PI, EBSR, and EFSR are recorded as GA_p, GA_b, GA_f in GA, as SA_p, SA_b, SA_f in SA, and as CSA_p, CSA_b, CSA_f in CSA, respectively. Thus, three variants of each SA, GA and CSA are utilized in this study. Additionally, following the scheme of Wu et al. [47], the proposed properties, a lower bound, and the best solution among all proposed approximate solutions are utilized in a branch-and-bound method (B&B).

For further testing, all parameters in proposed nine algorithms, we examined parameters including the initial temperature (\({T}_{\mathrm{i}}\)), cooling factor (Cf), and number of improvement (\({N}_{\mathrm{r}}\)) in three SAs, three parameters including the initial temperature (\({T}_{\mathrm{i}}\)), annealing index (\(\lambda\)) and number of improvement (\({N}_{\mathrm{r}}\)) in three CSAs, and the number of parents (Nsize), genetic generation (Gsize) and mutation rate (P) in three GAs, respectively. When fixed n = 12, we randomly generated 100 instances and utilized all nine algorithms and a B&B method equipped with the dominance properties derived in “Properties and a lower bound” to solve them, and calculated the average error percentage (AEP) for the differences between the results yielded from nine algorithms and those yielded from the B&B method for determining appropriate parameters.

In our pretests, we found that the larger values of tardiness factor (\(\tau )\), due date range (\(\rho )\), number of B-jobs \({(N}_{B})\) are important factors that affected the algorithms to find a feasible schedule. The smaller value of interruption factor D and a control variable, Qlevel (refer “Data simulation analysis”), for bound above total completion time of B-jobs also had effects on finding a feasible solution. In view of this observation, the initial tested instances are generated by setting a design at n \(=12\), \({N}_{B}=10, D=0.001,\rho =0.75\), \(\tau =0.50\) and Qlevel = \(1.6\). After parameters tuning process, the (Ti, Cf, \({N}_{\mathrm{r}}\)) is adopted as (0.85, 0.4, 20) in three SAs, the (Ti, \(\lambda\), \({N}_{\mathrm{r}}\)) as (0.65, 0.3, 30) in three CSAs, the (Nsize, Gsize, P) as (32, 140, 0.09) in three GAs, in the later experimental tests.

Data simulation analysis

The processing times of A-jobs, \({t}_{j}^{A}\), or B-jobs, \({t}_{j}^{B}\), on a machine are generated randomly from uniformly distributed on integers between 1 and 100. The due date for each A-job is randomly generated from uniform distributions \({T}_{A}\times U\left(1-\tau -\frac{\rho }{2},1-\tau +\frac{\rho }{2}\right)\), where \({T}_{A}=\sum_{j\in {J}_{A}}{t}_{j}^{A}\), the control parameters of the due dates are tardiness factor \(\tau\) and range of due dates \(\rho\). In particular, \(\tau\) is set to 0.25 and 0.50, and \(\rho\) is set to 0.25, 0.50, and 0.75. Regarding the setting of the upper bound for the B-jobs, we designate \(Q=\mathrm{Qlevel}\times \sum_{j\in {J}_{B}}{t}_{j}^{B}\), in which the control parameters are Qlevel. Another parameter relevant to two-agent scenario is the number of B-jobs, \({N}_{B}\). In this study for small number of jobs, fixed n = 12, three types of Qlevel is set at 1.6, 1.7, and 1.8, while \({N}_{B}\) is set to be 2, 4, 6, 8 and 10, and the levels of the interruption factor D are set at 0.1, 0.01, and 0.001. In total, there are 270 (\(D\times \tau \times \rho \times \mathrm{Qlevel}\times {N}_{B}=\) 3 × 2 × 3 × 3 × 5) cases of test combinations and 100 instances are generated for each case. Note that if the number of nodes in B&B algorithm exceeds \({10}^{8}\), it is considered as a failure and turns to next instance, otherwise, it is recorded as a feasible case. The performances of the branch-and-bound method and the proposed nine algorithms over different parameters are summarized in Tables 1, 2, and 3.

Table 1 Performances of B&B over different parameters (n = 12)
Full size table
Table 2 Performances of B&B over four parameters (n = 12)
Full size table
Table 3 Performances of AEP of algorithms for parameters as n = 12
Full size table

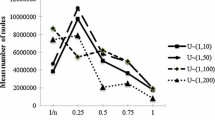
As shown in Table 2, it can be seen that B&B algorithm consumes fewer nodes as the interruption factor, D, is at higher value (D = 0.1). As for the impact of parameters \(\tau\) and \(\rho\), Table 2 shows that, on average, B&B method takes fewer nodes or run less CPU time at the big value of \(\tau\) or at a small value of \(\rho\). Regarding the impact of \({N}_{B}\) over different size, it can be seen in Table 2 that the average numbers of nodes have significant changes, this is possibly, because based on the fact that B-jobs have an upper limit constraint, the size of the searching space directly shrinks as the big number of \({N}_{B}\), say at 10. In other words, a smaller number of A-jobs reduce the search difficulty, so the B&B algorithm can complete the search process in fewer nodes. In contrast, as the values of Qlevel increases, the average number of nodes is gradually decreased, but the range of fluctuation affected by Qlevel is less than that affected by Nb.

Regarding the performance of all proposed nine algorithms, as show in Table 3, Figs. 1, 2, and 3, all nine algorithms performed better at a big value of D or \(\tau\) than those at a small value of D or \(\tau\). For the value of D at 0.1, it not only has better AEP performance, but also has a smaller variance on AEP than those of D at 0.01 and 0.001. All nine algorithms performed better at a small value of \(\rho\) than those at a big value of \(\rho\).

Fig. 1
figure 1

Impact of D on the AEPs of nine algorithms

Full size image
Fig. 2
figure 2

Impact of τ on the AEPs of nine algorithms

Full size image
Fig. 3
figure 3

Impact of ρ on the AEPs of nine algorithms

Full size image

Over all, \(\mathrm{GA}\_\mathrm{f}, \mathrm{GA}\_\mathrm{b}\), and \(\mathrm{GA}\_\mathrm{p}\) performed worse on average AEP than the rest of the algorithms did.

Regarding the effect of parameters Qlevel and \({N}_{b}\) on the AEP, it can be seen from the box plots in Fig. 4 that for different levels of Qlevel the dispersions on the AEP is not too large, meaning that the search ability for (near-) optimal solutions were about the same for all 9 algorithms. Meanwhile, as shown in Fig. 5, the impact on AEP for different \({N}_{b}\), there are two trends occurred in three GAs, where median and IQR of AEPs increase significantly as Nb increases from 2 to 8, but AEP declines sharply as \({N}_{b}\) is up to 10. The other trend occurred in three SAs and three CSAs, where the median of AEPs is about 1–3%, and the variances is in general less than that of GAs. This is due to the characteristic that GA is more sensitive to the initial solutions. As the value of \({N}_{b}\) is close to 6, the search space for A-jobs is wider than the other values of \({N}_{b}\). Therefore, that only using simple pairwise, forward or backward two-point interchange methods cannot provide good initial solutions, resulting in poor GA performance on the AEPs.

Fig. 4
figure 4

AEP of nine algorithms over different levels of Qlevel

Full size image
Fig. 5
figure 5

AEP of nine algorithmsover different values of \({N}_{b}\)

Full size image

As shown in Table 3 and Fig. 6, \(\mathrm{GA}\_\mathrm{f},\mathrm{GA}\_\mathrm{b}\), and \(\mathrm{GA}\_\mathrm{p}\) generally have larger IQR and three CSAs perform better on average AEP than other six algorithms do.

Fig. 6
figure 6

Boxplots of AEP for nine algorithms

Full size image

To examine whether the difference between nine algorithms is statistically significant or not, we used the analysis of variance (ANOVA) on AEPs and found that the observations from the experiments are not followed normal distributions. Thus, we performed the Kruskal–Wallis test (a nonparametric statistical method) to examine the statistical differences. The third column of Table 4 showed the mean rank of AEPs for 9 algorithms. The p value was < 0.001 (and the value of test statistic, Chi-Square distribution, was 198.6 with 8 degrees of freedom) of the Kruskal–Wallis (K–W) test, thus the differences among the performances of the nine algorithms are statistically significant.

Table 4 Mean ranks of algorithms in K–W test for small and large size jobs
Full size table

For further multiple comparison the performances among the 9 algorithms, the DSCF method (the Dwass–Steel–Critchlow–Fligner procedure, Holland [15]) was employed and the algorithms were grouped (run on SAS 9.4). As shown in Table 5, it can be seen that the three initial solutions used in GA, SA or CSA have no significant difference on AEP, but AEPs of GA and SA are significantly different with that of CSA. The CSAs did the best performance in term of the mean of AEP.

Table 5 DSCF for nine algorithms
Full size table

For the large number of jobs, fixed n = 60, three levels of D is set at 0.1, 0.01, and 0.001, three types of Qlevel is set at 1.6, 1.7, and 1.8, while \({N}_{b}\) is set at 10, 20, 30, 40, and 50. In total, there are 270 test combinations and 100 instances are generated for each combination. The results were summarized in Table 6.

Table 6 Performances of RPD of algorithms for parameters as n = 60
Full size table

It can be observed from Table 6 that the three initial solutions used in GA, SA or CSA have no significant difference on the RPD. The CSA seems have differences from both GA and SA; the CSAs did the best performance in term of the average of RPD.

As shown in Table 6 and Fig. 7, it can be seen that when the level of interruption factor is at high level (i.e. D = 0.1), all nine algorithms have smaller RPDs and smaller dispersions. It means that for a bigger value of D, proposed algorithms not only have a better RPD performance, but also have a lower degree of variation on the values of RPD. As D becomes smaller, the average RPDs and variances of RPDs became larger for the nine algorithms, in particular, for the three GAs.

Fig. 7
figure 7

RPD of nine algorithms over different levels of D

Full size image

Regarding the effects of τ, and ρ on the performance of each algorithm, as shown in Table 6, all nine algorithms performed at τ = 0.5 better than they did at τ = 0.25. As ρ increased the RPD of all three GAs increased, as seen in Table 6, but there is no such pattern for three SAs and three CSAs.

Regarding the impacts of Qlevel, and \({N}_{b}\) on the performance of each algorithm, it can be observed in Table 6 that the differences of RPD between three GAs or three SAs or three CSAs are very slight. It means that these nine algorithms can effectively solve instances, not affecting by the values of Qlevel. The RPDs of the nine algorithms increased as \({N}_{b}\) increased, as shown in Table 6.

To examine whether the difference between the nine algorithms is statistically significant for the large size jobs, we performed the K–W test to examine the statistical differences among the nine algorithms. The fifth column of Table 4 showed the mean rank of the nine algorithms. The p value was < 0.001 (and the value of test statistic, Chi-square distribution, was 813.9 with 8 degrees of freedom) of the Kruskal–Wallis test, thus there are significant differences among the performances of the nine algorithms.

The boxplot of RPDs for nine algorithms in Fig. 8 shows that the RPD of CSA seems have difference from those of GA and SA, the CSA did the best performance.

Fig. 8
figure 8

Boxplots of RPD for nine algorithms

Full size image

To examine the statistical difference among these nine algorithms, we performed multiple comparisons and groupings for algorithms using DSCF test. The result shows that CSAs is the best one, SAs next, and GAs is the worst; the group difference among GA, SA and CSA is very clearly (also refer Fig. 8); CSA_f performed the best among all proposed algorithms.

Regarding the CPU times, as showed in Fig. 9, GAs costs the most, SAs next, and the CSAs the least, but all were less one second.

Fig. 9
figure 9

CPU time for nine algorithms for large-size instances

Full size image

Conclusion and suggestions

In this paper, we study the sequential mode of multitasking for job scheduling together with two agents to minimize the total tardiness of A-agent’s jobs subject to a restriction (upper bound) on the total completion time of the B-agent’s jobs. The study issue belongs to the NP-hard set, thus, we derived five properties and a lower bound to embed in a B&B method to search optimal job sequences for small-sized jobs. Three variants of each of metaheuristics, GA, SA, and CSA, i.e., nine algorithms are employed to search optimal or approximate job sequences for large-sized jobs. Experimental results show that the CSAs performed best among these algorithms. For the future study, the complexity of multitasking scheduling problem with two (or more)-agents together with other criteria, for example the weighted number of lateness for one of agents, would be an interesting topic. Also, one can address the development of efficient optimization algorithm and heuristics for those hard problems.