Abstract
The linguistic Pythagorean fuzzy sets (LPFSs), which employ linguistic terms to express membership and non-membership degrees, can effectively deal with decision makers’ complicated evaluation values in the process of multiple attribute group decision-making (MAGDM). To improve the ability of LPFSs in depicting fuzzy information, this paper generalized LPFSs to cubic LPFSs (CLPFSs) and studied CLPFSs-based MAGDM method. First, the definition, operational rules, comparison method and distance measure of CLPFSs are investigated. The CLPFSs fully adsorb the advantages of LPFSs and cubic fuzzy sets and hence they are suitable and flexible to depict attribute values in fuzzy and complicated decision-making environments. Second, based on the extension of power Hamy mean operator in CLPFSs, the cubic linguistic Pythagorean fuzzy power average operator, the cubic linguistic Pythagorean fuzzy power Hamy mean operator as well as their weighted forms were introduced. These aggregation operators can effectively and comprehensively aggregate attribute values in MAGDM problems. Besides, some important properties of these operators were studied. Finally, we presented a new MAGDM method based on CLPFSs and their aggregation operators. Illustrative examples and comparative analysis are provided to show the effectiveness and advantages of our proposed decision-making method.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
In modern economic and social management activities, we have to face quite a few multi-attribute group decision-making (MAGDM) problems. In the field of operational research and decision sciences, MAGDM theories and methods have gained great interests and numerous achievements have been reported [1,2,3,4,5,6,7,8,9,10]. Considering the fact that the real world is full of uncertain information, MAGDM problems with uncertainties instead of certain information are prominent. In [11], the author proposed a new theory, called intuitionistic fuzzy sets (IFSs), which describe fuzzy information and uncertainties through both membership degrees (MDs) and non-membership degrees (MDs). Existing publications of IFSs-based MAGDM methods have illustrated the efficiency and good performance of IFSs in dealing with complicated evaluation values that provided by decision makers (DMs) [12,13,14,15,16]. In 2014, a new extension of IFSs, called Pythagorean fuzzy sets (PFSs), were proposed by Yager [17]. As it is known, the constraint of IFSs is that the sum of MDs and NMD should be less than or equal to one and PFSs should satisfy the condition that the square sum of MD and NMD should not be greater than one. Obviously, PFSs can descript wider information range than IFSs and PFS-based MAGDM methods have soon become a novel and active research field [18,19,20,21,22].
It should be noted that both IFSs and PFSs still have drawbacks, although they have been proven to be effective when dealing with complicated fuzzy information in some realistic situations. One of the main shortcomings of IFSs and PFSs is that they use crisp numbers to denote the MDs and NMDs. It should be pointed out that in quite a few actual-life MAGDM problems, DMs prefer to use some more flexible manners to express their opinions over MDs and NMDs. As it is widely known, linguistic terms, which are similar to natural language, are suitable to express DMs’ evaluation values. Hence, in [23] Chen et al. applied linguistic terms to denote the MDs and NMDs of IFSs and proposed the concept of linguistic intuitionistic fuzzy sets (LIFSs). Due to this reason, LIFSs are more powerful and appropriate to denote DMs’ evaluation values. After the appearance of LIFSs, Qu et al. [24] introduced a LIFSs-based TOPSIS method and applied it in enterprise resource plan systems selection. Yuan et al. [25] proposed a series of linguistic intuitionistic fuzzy (LIF) aggregation operators (AOs) and investigated their applications in MAGDM with unknown weights information. Liu and Qin [26] proposed a collection of LIF power average AOs, which capture more information from the aggregated LIF numbers (LIFNs). Liu and Qin [27] introduced LIF Maclaurin symmetric mean operators to deal with MAGDM, wherein attributes are interrelated under LIFSs. Liu et al. [28] soon introduced LIF partitioned Heronian mean to handle heterogeneous interrelationship among LIFNs. Similarly, Liu and Liu [29] introduced LIF partitioned Bonferroni mean to reflect the heterogeneous interrelationship among aggregated LIFNs. Liu and You [30] continued to study AOs for LIFNs based on Einstein t-norm and t-conorm. Garg and Kumar [31] investigated novel LIF power AOs based on set pair analysis. These aforementioned MAGDM methods reveal the powerfulness and capability of LIFSs in dealing with practical MAGDM problems; however, LIFSs still have drawbacks when expressing DMs’ evaluation values. Let \(\tilde{S} = \left\{ {s_{\alpha } \left| {s_{0} \le s_{\alpha } \le s_{t} ,\alpha \in \left[ {0,t} \right]} \right.} \right\}\) be a continuous linguistic term set, then a LIFS defined on \(\tilde{S}\) can be expressed as \(A = \left\{ {\left( {x,s_{\theta } \left( x \right),s_{\sigma } \left( x \right)} \right)\left| {x \in X} \right.} \right\}\), with the constraint that \(\theta + \sigma \le t\). It should be noted that this constraint cannot be always satisfied, which implies that LIFSs still have limitations in representing fuzzy decision information. For instance, a DM uses a linguistic intuitionistic fuzzy number \(\left( {s_{2} ,s_{5} } \right)\) to express his/her evaluation value, wherein \(s_{h}\) is a linguistic term and \(h \in \left[ {0,6} \right]\). It is easy to notice that the evaluation \(\left( {s_{2} ,s_{5} } \right)\) cannot be handled by LIFSs, as 2 + 5 \(\le\) 6. To operate and handle these cases effectively, Garg [32] proposed a new powerful fuzzy information representation tool, viz. linguistic Pythagorean fuzzy sets (LPFSs), satisfying the condition that \(\theta^{2} + \sigma^{2} \le t^{2}\). From the definition of LPFSs, it is evident that LPFSs are more flexible than LIFSs and can cope with more complicated decision-making situations and accurately depict DMs’ evaluation information. After that, Liu et al. [33] introduced a new MAGDM method with linguistic Pythagorean fuzzy values based on t-norm and t-conorm. Lin et al. [34] continued to investigate linguistic Pythagorean fuzzy MAGDM method based on interactive operational rules and partitioned Bonferroni mean.
Cubic fuzzy sets (CFSs), originated by Jun et al. [35] are a powerful theory to describe fuzzy information and they have two obvious advantages. First, CFSs effectively handle possible disagrees of the agreed interval values and vice versa. Second, they have the capability of taking two separate time zones simultaneously in one CFS, making they more capable and efficient to describe fuzzy decision-making information accurately. Nevertheless, the shortcomings of CFSs is also prominent, i.e., they can only deal with membership degrees, but fail to depict fuzzy information comprehensively. Hence, Kaur and Garg [36,37] generalized CFSs into cubic intuitionistic fuzzy sets (CIFSs), which are obviously more powerful and flexible, as they describe fuzzy data and information from both positive and negative aspects. Afterwards, CIFSs-based MAGDM methods have soon become an active research filed and quite a few new achievements have been published. For example, Muneeza and Abdullah [38] introduced some cubic intuitionistic fuzzy (CIF) AOs and presented a CIF-VIKOR method to deal with MAGDM problems. Muneeza et al. [39] proposed a novel MAGDM method under CIFSs based on Hamacher t-norm and t-conorm and, applied it in small hydropower plant locations selection. Kaur and Garg [40] put forward an Archimedean t-norm and t-conorm MAGDM method with CIF information. Garg and Kaur [41,42] continued to investigate CIF-TOPSIS based MAGDM methods and their application in practice. In addition, to accommodate different decision-making environments, scholars proposed different extensions of CFSs, such as linguistic cubic sets [43], cubic uncertain linguistic sets [44], neutrosophic cubic sets [45], cubic hesitant fuzzy sets [46], trapezoidal cubic hesitant fuzzy sets [47], triangular cubic linguistic hesitant fuzzy sets [48], cubic hesitant neutrosophic sets [49], cubic Pythagorean fuzzy sets (CPFSs) [50], cubic q-rung orthopair fuzzy sets [51], etc. These extensions of CFSs have been proved to be effective to handle DMs’ evaluation values in MAGDM problems in practice.
The above-mentioned references reveal the necessity and significance of extension of CFSs into classical fuzzy set theories. However, up to present, we have never witnessed the development of CFSs under linguistic Pythagorean fuzzy decision-making situations. Existing researches arouse our interests in studying extension of CFSs in LPFSs to propose a totally novel information representation, which is the first motivation of this paper. What is more, the application of the new information tool in MAGDM problems can provide us a valuable manner to determine the optimal alternative, which is the second motivation of our study. Based on the analysis, we first propose the notion of cubic linguistic Pythagorean fuzzy sets (CLPFSs) by extending CFSs to LPFSs. CLPFSs are constructed by LPFSs and uncertain linguistic Pythagorean fuzzy sets (ULPFSs), which absorb the advantages of both CFSs, LPFSs and ULPFSs, making them more suitable and powerful to describe inherent fuzziness and uncertainties in data and information. In addition, DMs prefer to use linguistic terms to express their evaluation values, and thus, the proposed CLPFSs are consistent with the reality. For the usage of CLPFSs in practical MAGDM problems, we further give basic operational rules of CLPFSs and based on which, a series of cubic linguistic Pythagorean fuzzy AOs are proposed. In addition, a new manner to solve MAGDM problems based on the new AOs is established and illustrative examples are further provided to show the performance of our decision-making method.
The rest of this manuscript is introduced as follows. The next section “Basic concepts” introduces the notion of CLPFSs along with their corresponding concepts, such as operational laws, ranking method and distance measure. “Some AOs for CLPFVs and their desirable properties” puts forward a collection of cubic linguistic Pythagorean fuzzy AOs and studies their properties. “A novel approach to MAGDM based on the proposed operators” proposes a novel MAGDM method with aid of CLPFSs. ”A practical example” uses numerical examples to prove the effectiveness, sensitivity and advantages of our proposed novel decision method. “Conclusions” The final section summarizes the paper.
Basic concepts
In this section, we introduce some basic concepts, including LPFSs, ULPFSs, CLPFSs and some basic operators.
LPFS and ULPFS
Definition 1
[32]. Let X be a finite universe of discourse and \(\widetilde{S} = \left\{ {s_{\beta } \left| {s_{0} \le s_{\beta } \le s_{t} ,\beta \in \left[ {0,t} \right]} \right.} \right\}\) be a continuous linguistic term set. A linguistic Pythagorean fuzzy set (LPFS) A defined on X is expressed as:
where \(s_{\theta } \left( x \right),s_{\sigma } \left( x \right) \in \widetilde{S}\) represent the linguistic membership degree (MD) and the linguistic non-membership degree(NMD) of the element \(x \in X\) to A, such that \(\theta^{2} + \sigma^{2} \le t^{2}\). For convenience, we call the ordered pair \(\left( {s_{\theta } \left( x \right),s_{\sigma } \left( x \right)} \right)\) a linguistic Pythagorean fuzzy value (LPFV), which can be denoted as \(\left( {s_{\theta } ,s_{\sigma } } \right)\) for simplicity.
To propose the notion of CLPFSs, in the following, we first extend LPFSs to ULPFSs, which employ uncertain linguistic variables (ULVs) to denote the MDs and NMDs.
Definition 2
Let X be a finite universe of discourse and \(\widetilde{S} = \left\{ {s_{\beta } \left| {s_{0} \le s_{\beta } \le s_{t} ,\beta \in \left[ {0,t} \right]} \right.} \right\}\) be a continuous linguistic term set. An uncertain linguistic Pythagorean fuzzy set (ULPFS) A defined on X is expressed as
where \(\left[ {s_{\theta } \left( x \right),s_{\tau } \left( x \right)} \right]\), \(\left[ {s_{\sigma } \left( x \right),s_{\varepsilon } \left( x \right)} \right] \in \widetilde{S}\) are two ULVs, representing the uncertain linguistic MD and the uncertain linguistic NMD of the \(x \in X\) to A respectively, such that \(\theta \le \tau\),\(\sigma \le \varepsilon\) and \(\tau^{2} + \varepsilon^{2} \le t^{2}\). For convenience, we call the ordered pair \(\left( {\left[ {s_{\theta } \left( x \right),s_{\tau } \left( x \right)} \right],\left[ {s_{\sigma } \left( x \right),s_{\varepsilon } \left( x \right)} \right]} \right)\) an uncertain linguistic Pythagorean fuzzy value (ULPFV), which can be denoted as \(\left( {\left[ {s_{\theta } ,s_{\tau } } \right],\left[ {s_{\sigma } ,s_{\varepsilon } } \right]} \right)\) for simplicity.
From Definition 2, it is easy seen that ULPFSs are more powerful than LPFSs, as they contain more information and give DMs more freedom. Particularly, if \(s_{\theta } \left( x \right) = s_{\tau } \left( x \right)\) and \(s_{\sigma } \left( x \right) = s_{\varepsilon } \left( x \right)\), then, the ULPFS A reduces to a LPFS. In addition, based on the operations of LPFVs, we can obtain the basic operational rules of ULPFVs, which are presented as follows.
Definition 3
Let \(\alpha_{1} = \left( {\left[ {s_{{\theta_{1} }} ,s_{{\tau_{1} }} } \right],\left[ {s_{{\sigma_{1} }} ,s_{{\varepsilon_{1} }} } \right]} \right)\), \(\alpha_{2} = \left( {\left[ {s_{{\theta_{2} }} ,s_{{\tau_{2} }} } \right],\left[ {s_{{\sigma_{2} }} ,s_{{\varepsilon_{2} }} } \right]} \right)\) and \(\alpha = \left( {\left[ {s_{\theta } ,s_{\tau } } \right],\left[ {s_{\sigma } ,s_{\varepsilon } } \right]} \right)\) be any three ULPFVs defined on a continuous linguistic term set \(\widetilde{S} = \left\{ {s_{\beta } \left| {s_{0} \le s_{\beta } \le s_{t} ,\beta \in \left[ {0,t} \right]} \right.} \right\}\), and \(\lambda\) be a positive real number, then:
(1) \(\alpha_{1} \oplus \alpha_{2} = \left( {\left[ {s_{{t\sqrt {{{\theta_{1}^{2} } \mathord{\left/ {\vphantom {{\theta_{1}^{2} } {t^{2} }}} \right. \kern-\nulldelimiterspace} {t^{2} }} + {{\theta_{2}^{2} } \mathord{\left/ {\vphantom {{\theta_{2}^{2} } {t^{2} }}} \right. \kern-\nulldelimiterspace} {t^{2} }} - \theta_{1}^{2} {{\theta_{2}^{2} } \mathord{\left/ {\vphantom {{\theta_{2}^{2} } {t^{4} }}} \right. \kern-\nulldelimiterspace} {t^{4} }}} }} ,s_{{t\sqrt {{{\tau_{1}^{2} } \mathord{\left/ {\vphantom {{\tau_{1}^{2} } {t^{2} }}} \right. \kern-\nulldelimiterspace} {t^{2} }} + {{\tau_{2}^{2} } \mathord{\left/ {\vphantom {{\tau_{2}^{2} } {t^{2} }}} \right. \kern-\nulldelimiterspace} {t^{2} }} - \tau_{1}^{2} {{\tau_{2}^{2} } \mathord{\left/ {\vphantom {{\tau_{2}^{2} } {t^{4} }}} \right. \kern-\nulldelimiterspace} {t^{4} }}} }} } \right],} \right.\left. {\left[ {s_{{t\left( {{{\sigma_{1} \sigma_{2} } \mathord{\left/ {\vphantom {{\sigma_{1} \sigma_{2} } {t^{2} }}} \right. \kern-\nulldelimiterspace} {t^{2} }}} \right)}} ,s_{{t\left( {{{\varepsilon_{1} \varepsilon_{2} } \mathord{\left/ {\vphantom {{\varepsilon_{1} \varepsilon_{2} } {t^{2} }}} \right. \kern-\nulldelimiterspace} {t^{2} }}} \right)}} } \right]} \right);\)
(2) \(\alpha_{1} \otimes \alpha_{2} = \left( {\left[ {s_{{t\left( {{{\theta_{1} \theta_{2} } \mathord{\left/ {\vphantom {{\theta_{1} \theta_{2} } {t^{2} }}} \right. \kern-\nulldelimiterspace} {t^{2} }}} \right)}} ,s_{{t\left( {{{\tau_{1} \tau_{2} } \mathord{\left/ {\vphantom {{\tau_{1} \tau_{2} } {t^{2} }}} \right. \kern-\nulldelimiterspace} {t^{2} }}} \right)}} } \right],} \right.\left. {\left[ {s_{{t\sqrt {{{\sigma_{1}^{2} } \mathord{\left/ {\vphantom {{\sigma_{1}^{2} } {t^{2} }}} \right. \kern-\nulldelimiterspace} {t^{2} }} + {{\sigma_{2}^{2} } \mathord{\left/ {\vphantom {{\sigma_{2}^{2} } {t^{2} }}} \right. \kern-\nulldelimiterspace} {t^{2} }} - \sigma_{1}^{2} {{\sigma_{2}^{2} } \mathord{\left/ {\vphantom {{\sigma_{2}^{2} } {t^{4} }}} \right. \kern-\nulldelimiterspace} {t^{4} }}} }} ,s_{{t\sqrt {{{\varepsilon_{1}^{2} } \mathord{\left/ {\vphantom {{\varepsilon_{1}^{2} } {t^{2} }}} \right. \kern-\nulldelimiterspace} {t^{2} }} + {{\varepsilon_{2}^{2} } \mathord{\left/ {\vphantom {{\varepsilon_{2}^{2} } {t^{2} }}} \right. \kern-\nulldelimiterspace} {t^{2} }} - \varepsilon_{1}^{2} {{\varepsilon_{2}^{2} } \mathord{\left/ {\vphantom {{\varepsilon_{2}^{2} } {t^{4} }}} \right. \kern-\nulldelimiterspace} {t^{4} }}} }} } \right]} \right);\)
(3) \(\lambda \alpha = \left( {\left[ {s_{{t\sqrt {1 - \left( {1 - {{\theta^{2} } \mathord{\left/ {\vphantom {{\theta^{2} } {t^{2} }}} \right. \kern-\nulldelimiterspace} {t^{2} }}} \right)^{\lambda } } }} ,s_{{t\sqrt {1 - \left( {1 - {{\tau^{2} } \mathord{\left/ {\vphantom {{\tau^{2} } {t^{2} }}} \right. \kern-\nulldelimiterspace} {t^{2} }}} \right)^{\lambda } } }} } \right],\left[ {s_{{t\left( {{\sigma \mathord{\left/ {\vphantom {\sigma t}} \right. \kern-\nulldelimiterspace} t}} \right)^{\lambda } }} ,s_{{t\left( {{\varepsilon \mathord{\left/ {\vphantom {\varepsilon t}} \right. \kern-\nulldelimiterspace} t}} \right)^{\lambda } }} } \right]} \right),\lambda > 0;\)
(4) \(\alpha^{\lambda } = \left( {\left[ {s_{{t\left( {{\theta \mathord{\left/ {\vphantom {\theta t}} \right. \kern-\nulldelimiterspace} t}} \right)^{\lambda } }} ,s_{{t\left( {{\tau \mathord{\left/ {\vphantom {\tau t}} \right. \kern-\nulldelimiterspace} t}} \right)^{\lambda } }} } \right],\left[ {s_{{t\sqrt {1 - \left( {1 - {{\sigma^{2} } \mathord{\left/ {\vphantom {{\sigma^{2} } {t^{2} }}} \right. \kern-\nulldelimiterspace} {t^{2} }}} \right)^{\lambda } } }} ,s_{{t\sqrt {1 - \left( {1 - {{\varepsilon^{2} } \mathord{\left/ {\vphantom {{\varepsilon^{2} } {t^{2} }}} \right. \kern-\nulldelimiterspace} {t^{2} }}} \right)^{\lambda } } }} } \right]} \right),\lambda > 0.\)
We provide the following comparison method to rank any two ULPFVs.
Definition 4
Let \(\alpha = \left( {\left[ {s_{\theta } ,s_{\tau } } \right],\left[ {s_{\sigma } ,s_{\varepsilon } } \right]} \right)\) be an ULPFV defined on the linguistic term set \(\widetilde{S} = \left\{ {s_{\beta } \left| {s_{0} \le s_{\beta } \le s_{t} ,\beta \in \left[ {0,t} \right]} \right.} \right\}\), the score function of \(\alpha\) is defined as
and the accuracy function of \(\alpha\) is defined as
For any two ULPFVs \(\alpha_{1}\) and \(\alpha_{2}\),
(1) If \(S\left( {\alpha_{1} } \right) > S\left( {\alpha_{2} } \right)\), then \(\alpha_{1} > \alpha_{2}\);
(2) If \(S\left( {\alpha_{1} } \right) = S\left( {\alpha_{2} } \right)\), then.
If \(H\left( {\alpha_{1} } \right) > H\left( {\alpha_{2} } \right)\), then \(\alpha_{1} > \alpha_{2}\);
If \(H\left( {\alpha_{1} } \right) = H\left( {\alpha_{2} } \right)\), then \(\alpha_{1} = \alpha_{2}\).
The CLPFSs
By combining LPFSs with ULPFSs, in the following we first propose the notion of CLPFSs. Some other concepts, such as basic operational rules, score function, accuracy function, comparison method and distance measure are also proposed. Examples are provided to better illustrate these concepts.
Definition 5
Let X be a finite universe of discourse and \(\widetilde{S} = \left\{ {s_{\beta } \left| {s_{0} \le s_{\beta } \le s_{t} ,\beta \in \left[ {0,t} \right]} \right.} \right\}\) be a continuous linguistic term set. A cubic linguistic Pythagorean fuzzy set (CLPFS) A defined on X is expressed as
where \(\left( {\left[ {s_{\theta } \left( x \right),s_{\tau } \left( x \right)} \right],\left[ {s_{\sigma } \left( x \right),s_{\varepsilon } \left( x \right)} \right]} \right)\) is a ULPFV and \(\left( {s_{\delta } \left( x \right),s_{\zeta } \left( x \right)} \right)\) is an LPFV. For convenience, \(\left\langle {\left( {\left[ {s_{\theta } \left( x \right),s_{\tau } \left( x \right)} \right],\left[ {s_{\sigma } \left( x \right),s_{\varepsilon } \left( x \right)} \right]} \right),\left( {s_{\delta } \left( x \right),s_{\zeta } \left( x \right)} \right)} \right\rangle\) is called a cubic linguistic Pythagorean fuzzy value (CLPFV), which can be denoted as \(\eta = \left\langle {\left( {\left[ {s_{\theta } ,s_{\tau } } \right],\left[ {s_{\sigma } ,s_{\varepsilon } } \right]} \right),\left( {s_{\delta } ,s_{\zeta } } \right)} \right\rangle\) for simplicity.
Definition 6
Let \(\eta_{1} = \left\langle {\left( {\left[ {s_{{\theta_{1} }} ,s_{{\tau_{1} }} } \right],\left[ {s_{{\sigma_{1} }} ,s_{{\varepsilon_{1} }} } \right]} \right),\left( {s_{{\delta_{1} }} ,s_{{\zeta_{1} }} } \right)} \right\rangle\), \(\eta_{2} = \left\langle {\left( {\left[ {s_{{\theta_{2} }} ,s_{{\tau_{2} }} } \right],\left[ {s_{{\sigma_{2} }} ,s_{{\varepsilon_{2} }} } \right]} \right),\left( {s_{{\delta_{2} }} ,s_{{\zeta_{2} }} } \right)} \right\rangle\) and \(\eta = \left\langle {\left( {\left[ {s_{\theta } ,s_{\tau } } \right],\left[ {s_{\sigma } ,s_{\varepsilon } } \right]} \right),\left( {s_{\delta } ,s_{\zeta } } \right)} \right\rangle\) be any three CLPFVs defined on the linguistic term set \(\widetilde{S} = \left\{ {s_{\beta } \left| {s_{0} \le s_{\beta } \le s_{t} ,\beta \in \left[ {0,t} \right]} \right.} \right\}\), and \(\lambda\) be positive real number
(1) \(\eta_{1} \oplus \eta_{2} = \left\langle {\left( {\left[ {s_{{t\sqrt {{{\theta_{1}^{2} } \mathord{\left/ {\vphantom {{\theta_{1}^{2} } {t^{2} }}} \right. \kern-\nulldelimiterspace} {t^{2} }} + {{\theta_{2}^{2} } \mathord{\left/ {\vphantom {{\theta_{2}^{2} } {t^{2} }}} \right. \kern-\nulldelimiterspace} {t^{2} }} - \theta_{1}^{2} {{\theta_{2}^{2} } \mathord{\left/ {\vphantom {{\theta_{2}^{2} } {t^{4} }}} \right. \kern-\nulldelimiterspace} {t^{4} }}} }} ,s_{{t\sqrt {{{\tau_{1}^{2} } \mathord{\left/ {\vphantom {{\tau_{1}^{2} } {t^{2} }}} \right. \kern-\nulldelimiterspace} {t^{2} }} + {{\tau_{2}^{2} } \mathord{\left/ {\vphantom {{\tau_{2}^{2} } {t^{2} }}} \right. \kern-\nulldelimiterspace} {t^{2} }} - \tau_{1}^{2} {{\tau_{2}^{2} } \mathord{\left/ {\vphantom {{\tau_{2}^{2} } {t^{4} }}} \right. \kern-\nulldelimiterspace} {t^{4} }}} }} } \right],} \right.} \right.\left. {\left. {\left[ {s_{{t\left( {{{\sigma_{1} \sigma_{2} } \mathord{\left/ {\vphantom {{\sigma_{1} \sigma_{2} } {t^{2} }}} \right. \kern-\nulldelimiterspace} {t^{2} }}} \right)}} ,s_{{t\left( {{{\varepsilon_{1} \varepsilon_{2} } \mathord{\left/ {\vphantom {{\varepsilon_{1} \varepsilon_{2} } {t^{2} }}} \right. \kern-\nulldelimiterspace} {t^{2} }}} \right)}} } \right]} \right),\left( {s_{{t\sqrt {{{\delta_{1}^{2} } \mathord{\left/ {\vphantom {{\delta_{1}^{2} } {t^{2} }}} \right. \kern-\nulldelimiterspace} {t^{2} }} + {{\delta_{2}^{2} } \mathord{\left/ {\vphantom {{\delta_{2}^{2} } {t^{2} }}} \right. \kern-\nulldelimiterspace} {t^{2} }} - \delta_{1}^{2} {{\delta_{2}^{2} } \mathord{\left/ {\vphantom {{\delta_{2}^{2} } {t^{4} }}} \right. \kern-\nulldelimiterspace} {t^{4} }}} }} ,s_{{t\left( {{{\zeta_{1} \zeta_{2} } \mathord{\left/ {\vphantom {{\zeta_{1} \zeta_{2} } {t^{2} }}} \right. \kern-\nulldelimiterspace} {t^{2} }}} \right)}} } \right)} \right\rangle\)
(2) \(\eta_{1} \otimes \eta_{2} = \left\langle {\left( {\left[ {s_{{t\left( {{{\theta_{1} \theta_{2} } \mathord{\left/ {\vphantom {{\theta_{1} \theta_{2} } {t^{2} }}} \right. \kern-\nulldelimiterspace} {t^{2} }}} \right)}} ,s_{{t\left( {{{\tau_{1} \tau_{2} } \mathord{\left/ {\vphantom {{\tau_{1} \tau_{2} } {t^{2} }}} \right. \kern-\nulldelimiterspace} {t^{2} }}} \right)}} } \right],} \right.} \right.\left. {\left[ {s_{{t\sqrt {{{\sigma_{1}^{2} } \mathord{\left/ {\vphantom {{\sigma_{1}^{2} } {t^{2} }}} \right. \kern-\nulldelimiterspace} {t^{2} }} + {{\sigma_{2}^{2} } \mathord{\left/ {\vphantom {{\sigma_{2}^{2} } {t^{2} }}} \right. \kern-\nulldelimiterspace} {t^{2} }} - \sigma_{1}^{2} {{\sigma_{2}^{2} } \mathord{\left/ {\vphantom {{\sigma_{2}^{2} } {t^{4} }}} \right. \kern-\nulldelimiterspace} {t^{4} }}} }} ,s_{{t\sqrt {{{\varepsilon_{1}^{2} } \mathord{\left/ {\vphantom {{\varepsilon_{1}^{2} } {t^{2} }}} \right. \kern-\nulldelimiterspace} {t^{2} }} + {{\varepsilon_{2}^{2} } \mathord{\left/ {\vphantom {{\varepsilon_{2}^{2} } {t^{2} }}} \right. \kern-\nulldelimiterspace} {t^{2} }} - \varepsilon_{1}^{2} {{\varepsilon_{2}^{2} } \mathord{\left/ {\vphantom {{\varepsilon_{2}^{2} } {t^{4} }}} \right. \kern-\nulldelimiterspace} {t^{4} }}} }} } \right]} \right),\left. {\left( {s_{{t\left( {{{\delta_{1} \delta_{2} } \mathord{\left/ {\vphantom {{\delta_{1} \delta_{2} } {t^{2} }}} \right. \kern-\nulldelimiterspace} {t^{2} }}} \right)}} ,s_{{t\sqrt {{{\zeta_{1}^{2} } \mathord{\left/ {\vphantom {{\zeta_{1}^{2} } {t^{2} }}} \right. \kern-\nulldelimiterspace} {t^{2} }} + {{\zeta_{2}^{2} } \mathord{\left/ {\vphantom {{\zeta_{2}^{2} } {t^{2} }}} \right. \kern-\nulldelimiterspace} {t^{2} }} - \zeta_{1}^{2} {{\zeta_{2}^{2} } \mathord{\left/ {\vphantom {{\zeta_{2}^{2} } {t^{4} }}} \right. \kern-\nulldelimiterspace} {t^{4} }}} }} } \right)} \right\rangle\)
(3) \(\lambda \eta = \left\langle {\left( {\left[ {s_{{t\sqrt {1 - \left( {1 - {{\theta^{2} } \mathord{\left/ {\vphantom {{\theta^{2} } {t^{2} }}} \right. \kern-\nulldelimiterspace} {t^{2} }}} \right)^{\lambda } } }} ,s_{{t\sqrt {1 - \left( {1 - {{\tau^{2} } \mathord{\left/ {\vphantom {{\tau^{2} } {t^{2} }}} \right. \kern-\nulldelimiterspace} {t^{2} }}} \right)^{\lambda } } }} } \right],\left[ {s_{{t\left( {{\sigma \mathord{\left/ {\vphantom {\sigma t}} \right. \kern-\nulldelimiterspace} t}} \right)^{\lambda } }} ,s_{{t\left( {{\varepsilon \mathord{\left/ {\vphantom {\varepsilon t}} \right. \kern-\nulldelimiterspace} t}} \right)^{\lambda } }} } \right]} \right)} \right.,\left. {\left( {s_{{t\sqrt {1 - \left( {1 - {{\delta^{2} } \mathord{\left/ {\vphantom {{\delta^{2} } {t^{2} }}} \right. \kern-\nulldelimiterspace} {t^{2} }}} \right)^{\lambda } } }} ,s_{{t\left( {{\zeta \mathord{\left/ {\vphantom {\zeta t}} \right. \kern-\nulldelimiterspace} t}} \right)^{\lambda } }} } \right)} \right\rangle\)
(4) \(\alpha^{\lambda } = \left\langle {\left( {\left[ {s_{{t\left( {{\theta \mathord{\left/ {\vphantom {\theta t}} \right. \kern-\nulldelimiterspace} t}} \right)^{\lambda } }} ,s_{{t\left( {{\tau \mathord{\left/ {\vphantom {\tau t}} \right. \kern-\nulldelimiterspace} t}} \right)^{\lambda } }} } \right],\left[ {s_{{t\sqrt {1 - \left( {1 - {{\sigma^{2} } \mathord{\left/ {\vphantom {{\sigma^{2} } {t^{2} }}} \right. \kern-\nulldelimiterspace} {t^{2} }}} \right)^{\lambda } } }} ,s_{{t\sqrt {1 - \left( {1 - {{\varepsilon^{2} } \mathord{\left/ {\vphantom {{\varepsilon^{2} } {t^{2} }}} \right. \kern-\nulldelimiterspace} {t^{2} }}} \right)^{\lambda } } }} } \right]} \right)} \right.,\left. {\left( {s_{{t\left( {{\delta \mathord{\left/ {\vphantom {\delta t}} \right. \kern-\nulldelimiterspace} t}} \right)^{\lambda } }} ,s_{{t\sqrt {1 - \left( {1 - {{\zeta^{2} } \mathord{\left/ {\vphantom {{\zeta^{2} } {t^{2} }}} \right. \kern-\nulldelimiterspace} {t^{2} }}} \right)^{\lambda } } }} } \right)} \right\rangle\)
Example 1
Let \(\widetilde{S} = \left\{ {s_{\beta } \left| {s_{0} \le s_{\beta } \le s_{6} ,\beta \in \left[ {0,6} \right]} \right.} \right\}\) be a continuous linguistic term set, and \(\eta = \left\langle {\left( {\left[ {s_{2} ,s_{3} } \right],\left[ {s_{3} ,s_{5} } \right]} \right),\left( {s_{5} ,s_{2} } \right)} \right\rangle\), \(\eta_{1} = \left\langle {\left( {\left[ {s_{4} ,s_{5} } \right],\left[ {s_{1} ,s_{2} } \right]} \right),\left( {s_{3} ,s_{5} } \right)} \right\rangle\), and \(\eta_{2} = \left\langle {\left( {\left[ {s_{1} ,s_{3} } \right],\left[ {s_{4} ,s_{5} } \right]} \right),\left( {s_{3} ,s_{4} } \right)} \right\rangle\) be three CLPFVs defined on \(\widetilde{S}\). Suppose \(\lambda = 2\), then
(1) \(\begin{gathered} \eta_{1} \oplus \eta_{2} = \left\langle {\left( {\left[ {s_{{6\sqrt {{{4^{2} } \mathord{\left/ {\vphantom {{4^{2} } {6^{2} }}} \right. \kern-\nulldelimiterspace} {6^{2} }} + {{1^{2} } \mathord{\left/ {\vphantom {{1^{2} } {6^{2} }}} \right. \kern-\nulldelimiterspace} {6^{2} }} - {{4^{2} 1^{2} } \mathord{\left/ {\vphantom {{4^{2} 1^{2} } {6^{4} }}} \right. \kern-\nulldelimiterspace} {6^{4} }}} }} ,s_{{6\sqrt {{{5^{2} } \mathord{\left/ {\vphantom {{5^{2} } {6^{2} }}} \right. \kern-\nulldelimiterspace} {6^{2} }} + {{3^{2} } \mathord{\left/ {\vphantom {{3^{2} } {6^{2} }}} \right. \kern-\nulldelimiterspace} {6^{2} }} - {{5^{2} 3^{2} } \mathord{\left/ {\vphantom {{5^{2} 3^{2} } {6^{4} }}} \right. \kern-\nulldelimiterspace} {6^{4} }}} }} } \right],} \right.} \right.\left. {\left. {\left[ {s_{{6\left( {{{\left( {1 \times 4} \right)} \mathord{\left/ {\vphantom {{\left( {1 \times 4} \right)} {6^{2} }}} \right. \kern-\nulldelimiterspace} {6^{2} }}} \right)}} ,s_{{6\left( {{{\left( {2 \times 5} \right)} \mathord{\left/ {\vphantom {{\left( {2 \times 5} \right)} {6^{2} }}} \right. \kern-\nulldelimiterspace} {6^{2} }}} \right)}} } \right]} \right),\left( {s_{{6\sqrt {{{3^{2} } \mathord{\left/ {\vphantom {{3^{2} } {6^{2} }}} \right. \kern-\nulldelimiterspace} {6^{2} }} + {{3^{2} } \mathord{\left/ {\vphantom {{3^{2} } {6^{2} }}} \right. \kern-\nulldelimiterspace} {6^{2} }} - {{3^{2} 3^{2} } \mathord{\left/ {\vphantom {{3^{2} 3^{2} } {6^{4} }}} \right. \kern-\nulldelimiterspace} {6^{4} }}} }} ,s_{{6\left( {{{\left( {4 \times 5} \right)} \mathord{\left/ {\vphantom {{\left( {4 \times 5} \right)} {6^{2} }}} \right. \kern-\nulldelimiterspace} {6^{2} }}} \right)}} } \right)} \right\rangle \hfill \\ = \left\langle {\left( {\left[ {s_{4.0689} ,s_{5.2678} } \right],} \right.} \right.\left. {\left. {\left[ {s_{0.6667} ,s_{1.6667} } \right]} \right),\left( {s_{3.9686} ,s_{3.3334} } \right)} \right\rangle \hfill \\ \end{gathered}\)
(2) \(\begin{gathered} \eta_{1} \otimes \eta_{2} = \left\langle {\left( {\left[ {s_{{6\left( {{{\left( {4 \times 1} \right)} \mathord{\left/ {\vphantom {{\left( {4 \times 1} \right)} {6^{2} }}} \right. \kern-\nulldelimiterspace} {6^{2} }}} \right)}} ,s_{{6\left( {{{\left( {5 \times 3} \right)} \mathord{\left/ {\vphantom {{\left( {5 \times 3} \right)} {6^{2} }}} \right. \kern-\nulldelimiterspace} {6^{2} }}} \right)}} } \right],} \right.} \right.\left. {\left[ {s_{{6\sqrt {{{1^{2} } \mathord{\left/ {\vphantom {{1^{2} } {6^{2} }}} \right. \kern-\nulldelimiterspace} {6^{2} }} + {{4^{2} } \mathord{\left/ {\vphantom {{4^{2} } {6^{2} }}} \right. \kern-\nulldelimiterspace} {6^{2} }} - 1^{2} {{4^{2} } \mathord{\left/ {\vphantom {{4^{2} } {6^{4} }}} \right. \kern-\nulldelimiterspace} {6^{4} }}} }} ,s_{{6\sqrt {{{2^{2} } \mathord{\left/ {\vphantom {{2^{2} } {6^{2} }}} \right. \kern-\nulldelimiterspace} {6^{2} }} + {{5^{2} } \mathord{\left/ {\vphantom {{5^{2} } {6^{2} }}} \right. \kern-\nulldelimiterspace} {6^{2} }} - 2^{2} {{5^{2} } \mathord{\left/ {\vphantom {{5^{2} } {6^{4} }}} \right. \kern-\nulldelimiterspace} {6^{4} }}} }} } \right]} \right),\left. {\left( {s_{{6\left( {{{\left( {3 \times 3} \right)} \mathord{\left/ {\vphantom {{\left( {3 \times 3} \right)} {6^{2} }}} \right. \kern-\nulldelimiterspace} {6^{2} }}} \right)}} ,s_{{6\sqrt {{{5^{2} } \mathord{\left/ {\vphantom {{5^{2} } {6^{2} }}} \right. \kern-\nulldelimiterspace} {6^{2} }} + {{4^{2} } \mathord{\left/ {\vphantom {{4^{2} } {6^{2} }}} \right. \kern-\nulldelimiterspace} {6^{2} }} - {{5^{2} 4^{2} } \mathord{\left/ {\vphantom {{5^{2} 4^{2} } {6^{4} }}} \right. \kern-\nulldelimiterspace} {6^{4} }}} }} } \right)} \right\rangle \hfill \\ = \left\langle {\left( {\left[ {s_{0.6667} ,s_{2.5000} } \right],} \right.} \right.\left. {\left. {\left[ {s_{4.0689} ,s_{5.1208} } \right]} \right),\left( {s_{1.5000} ,s_{6.1824} } \right)} \right\rangle \hfill \\ \end{gathered}\)
(3) \(\begin{gathered} \lambda \eta = \left\langle {\left( {\left[ {s_{{6\sqrt {1 - \left( {1 - {{2^{2} } \mathord{\left/ {\vphantom {{2^{2} } {6^{2} }}} \right. \kern-\nulldelimiterspace} {6^{2} }}} \right)^{2} } }} ,s_{{6\sqrt {1 - \left( {1 - {{3^{2} } \mathord{\left/ {\vphantom {{3^{2} } {6^{2} }}} \right. \kern-\nulldelimiterspace} {6^{2} }}} \right)^{2} } }} } \right],\left[ {s_{{6\left( {{3 \mathord{\left/ {\vphantom {3 6}} \right. \kern-\nulldelimiterspace} 6}} \right)^{2} }} ,s_{{6\left( {{5 \mathord{\left/ {\vphantom {5 6}} \right. \kern-\nulldelimiterspace} 6}} \right)^{2} }} } \right]} \right),\left( {s_{{6\sqrt {1 - \left( {1 - {{5^{2} } \mathord{\left/ {\vphantom {{5^{2} } {6^{2} }}} \right. \kern-\nulldelimiterspace} {6^{2} }}} \right)^{2} } }} ,s_{{6\left( {{2 \mathord{\left/ {\vphantom {2 6}} \right. \kern-\nulldelimiterspace} 6}} \right)^{2} }} } \right)} \right\rangle \hfill \\ = \left\langle {\left( {\left[ {s_{2.7487} ,s_{3.9686} } \right],\left[ {s_{1.5000} ,s_{4.1667} } \right]} \right)} \right.,\left. {\left( {s_{5.7130} ,s_{0.6667} } \right)} \right\rangle \hfill \\ \end{gathered}\)
(4) \(\begin{gathered} \alpha^{\lambda } = \left\langle {\left( {\left[ {s_{{6\left( {{2 \mathord{\left/ {\vphantom {2 6}} \right. \kern-\nulldelimiterspace} 6}} \right)^{2} }} ,s_{{6\left( {{3 \mathord{\left/ {\vphantom {3 6}} \right. \kern-\nulldelimiterspace} 6}} \right)^{2} }} } \right],\left[ {s_{{6\sqrt {1 - \left( {1 - {{3^{2} } \mathord{\left/ {\vphantom {{3^{2} } {6^{2} }}} \right. \kern-\nulldelimiterspace} {6^{2} }}} \right)^{2} } }} ,s_{{6\sqrt {1 - \left( {1 - {{5^{2} } \mathord{\left/ {\vphantom {{5^{2} } {6^{2} }}} \right. \kern-\nulldelimiterspace} {6^{2} }}} \right)^{2} } }} } \right]} \right)} \right.,\left. {\left( {s_{{6\left( {{5 \mathord{\left/ {\vphantom {5 6}} \right. \kern-\nulldelimiterspace} 6}} \right)^{2} }} ,s_{{6\sqrt {1 - \left( {1 - {{2^{2} } \mathord{\left/ {\vphantom {{2^{2} } {6^{2} }}} \right. \kern-\nulldelimiterspace} {6^{2} }}} \right)^{2} } }} } \right)} \right\rangle \hfill \\ = \left\langle {\left( {\left[ {s_{0.6667} ,s_{1.5000} } \right],\left[ {s_{3.9686} ,s_{5.7130} } \right]} \right)} \right.,\left. {\left( {s_{4.1667} ,s_{2.7487} } \right)} \right\rangle . \hfill \\ \end{gathered}\)
It is easy to prove the following theorem according to Definition 6.
Theorem 1
Let \(\eta\), \(\eta_{1}\) and \(\eta_{2}\) be any three CLPFVs and \(\lambda_{1} ,\lambda_{2} ,\lambda_{3} > 0\), then
-
(1)
\(\eta_{1} \oplus \eta_{2} = \eta_{2} \oplus \eta_{1}\)
-
(2)
\(\eta_{1} \otimes \eta_{2} = \eta_{2} \otimes \eta_{1}\)
-
(3)
\(\lambda \left( {\eta_{1} \oplus \eta_{2} } \right) = \lambda \eta_{2} \oplus \lambda \eta_{1}\)
-
(4)
\(\lambda_{1} \eta \oplus \lambda_{2} \eta = \left( {\lambda_{1} + \lambda_{2} } \right)\eta\)
-
(5)
\(\eta^{{\lambda_{1} }} \otimes \eta^{{\lambda_{2} }} = \eta^{{\lambda_{1} + \lambda_{2} }}\)
-
(6)
\(\eta_{1}^{\lambda } \otimes \eta_{2}^{\lambda } = \left( {\eta_{1} \otimes \eta_{2} } \right)^{\lambda } .\)
To rank any two CLPFVs, we provide the following comparison method for CLPFVs.
Definition 7
Let \(\eta = \left\langle {\left( {\left[ {s_{\theta } ,s_{\tau } } \right],\left[ {s_{\sigma } ,s_{\varepsilon } } \right]} \right),\left( {s_{\delta } ,s_{\zeta } } \right)} \right\rangle\) be a CLPFV defined on the linguistic term set \(\widetilde{S} = \left\{ {s_{\beta } \left| {s_{0} \le s_{\beta } \le s_{t} ,\beta \in \left[ {0,t} \right]} \right.} \right\}\), then the score function of \(\eta\) is expressed as
and the accuracy function of \(\eta\) is expressed as
Let \(\eta_{1} = \left\langle {\left( {\left[ {s_{{\theta_{1} }} ,s_{{\tau_{1} }} } \right],\left[ {s_{{\sigma_{1} }} ,s_{{\varepsilon_{1} }} } \right]} \right),\left( {s_{{\delta_{1} }} ,s_{{\zeta_{1} }} } \right)} \right\rangle\) and \(\eta_{2} = \left\langle {\left( {\left[ {s_{{\theta_{2} }} ,s_{{\tau_{2} }} } \right],\left[ {s_{{\sigma_{2} }} ,s_{{\varepsilon_{2} }} } \right]} \right),\left( {s_{{\delta_{2} }} ,s_{{\zeta_{2} }} } \right)} \right\rangle\) be any two CLPFVs,
(1) If \(S\left( {\eta_{1} } \right) > S\left( {\eta_{2} } \right)\), then \(\eta_{1} > \eta_{2}\);
(2) If \(S\left( {\eta_{1} } \right) = S\left( {\eta_{2} } \right)\), then.
if \(H\left( {\eta_{1} } \right) > H\left( {\eta_{2} } \right)\), then \(\eta_{1} > \eta_{2}\);
if \(H\left( {\eta_{1} } \right) = H\left( {\eta_{2} } \right)\), then \(\eta_{1} = \eta_{2}\).
Example 2
Let \(\eta_{1} = \left\langle {\left( {\left[ {s_{4} ,s_{5} } \right],\left[ {s_{1} ,s_{2} } \right]} \right),\left( {s_{3} ,s_{5} } \right)} \right\rangle\), \(\eta_{2} = \left\langle {\left( {\left[ {s_{1} ,s_{3} } \right],\left[ {s_{4} ,s_{5} } \right]} \right),\left( {s_{3} ,s_{4} } \right)} \right\rangle\) be two CLPFVs defined on the continuous linguistic term set \(\widetilde{S} = \left\{ {s_{\beta } \left| {s_{0} \le s_{\beta } \le s_{6} ,\beta \in \left[ {0,6} \right]} \right.} \right\}\), then, according to Definition 7,
Because \(s_{4.1792} > s_{3.4379}\), that is \(S\left( {\eta_{1} } \right) > S\left( {\eta_{2} } \right)\), we can get \(\eta_{1} > \eta_{2}\).
The distance between any two CLPFVs is expressed as follows.
Definition 8
Let \(\eta_{1} = \left\langle {\left( {\left[ {s_{{\theta_{1} }} ,s_{{\tau_{1} }} } \right],\left[ {s_{{\sigma_{1} }} ,s_{{\varepsilon_{1} }} } \right]} \right),\left( {s_{{\delta_{1} }} ,s_{{\zeta_{1} }} } \right)} \right\rangle\) and \(\eta_{2} = \left\langle {\left( {\left[ {s_{{\theta_{2} }} ,s_{{\tau_{2} }} } \right],\left[ {s_{{\sigma_{2} }} ,s_{{\varepsilon_{2} }} } \right]} \right),\left( {s_{{\delta_{2} }} ,s_{{\zeta_{2} }} } \right)} \right\rangle\) be any two CLPFVs defined on the linguistic term set \(\widetilde{S} = \left\{ {s_{\beta } \left| {s_{0} \le s_{\beta } \le s_{t} ,\beta \in \left[ {0,t} \right]} \right.} \right\}\), then the distance between \(\eta_{1}\) and \(\eta_{2}\) is expressed as:
Example 3
Let \(\eta_{1} = \left\langle {\left( {\left[ {s_{4} ,s_{5} } \right],\left[ {s_{1} ,s_{2} } \right]} \right),\left( {s_{3} ,s_{5} } \right)} \right\rangle\) and \(\eta_{2} = \left\langle {\left( {\left[ {s_{1} ,s_{3} } \right],\left[ {s_{4} ,s_{5} } \right]} \right),\left( {s_{3} ,s_{4} } \right)} \right\rangle\) be two CLPFVs defined on the continuous linguistic term set \(\widetilde{S} = \left\{ {s_{\beta } \left| {s_{0} \le s_{\beta } \le s_{6} ,\beta \in \left[ {0,6} \right]} \right.} \right\}\), then we can calculate the distance between \(\eta_{1}\) and \(\eta_{2}\),
Some basic AOs
Definition 9
[52]. Let \(a_{i} \left( {i = 1,2,...,n} \right)\) be n crisp numbers and \(k = 1,2,...,n\), if
then \({\text{HM}}^{\left( k \right)}\) is called the Hamy mean (HM) operator, where \(C_{n}^{k}\) is the binomial coefficient.
Definition 10
[53]. Let \(a_{i} \left( {i = 1,2,...,n} \right)\) be n crisp numbers, the power average (PA) operator is expressed as
where \(T\left( {a_{i} } \right) = \sum\nolimits_{j = 1;j \ne i}^{n} {{\text{Sup}}\left( {a_{i} ,a_{j} } \right)}\), \({\text{Sup}}\left( {a_{i} ,a_{j} } \right)\) denotes the support for \(a_{i}\) from \(a_{j}\), satisfying the conditions
(1) \(0 \le {\text{Sup}}\left( {a_{i} ,a_{j} } \right) \le 1\)
(2) \({\text{Sup}}\left( {a_{i} ,a_{j} } \right) = {\text{Sup}}\left( {a_{j} ,a_{i} } \right)\);
(3) \({\text{Sup}}\left( {a,b} \right) \le {\text{Sup}}\left( {c,d} \right)\), if \(\left| {a,b} \right| \ge \left| {c,d} \right|\).
Recently, Liu et al. [54] combined PA with HM and introduced the power Hamy mean (PHM) operator, which is defined as follows.
Definition 11
[54]. Let \(a_{i} \left( {i = 1,2,...,n} \right)\) be n crisp numbers and \(k = 1,2,...,n\), the power Hamy mean operator is expressed:
where \(T\left( {a_{i} } \right) = \sum\nolimits_{j = 1;j \ne i}^{n} {{\text{Sup}}\left( {a_{i} ,a_{j} } \right)}\), \({\text{Sup}}\left( {a_{i} ,a_{j} } \right)\) denotes the support for \(a_{i}\) from \(a_{j}\), satisfying the properties presented in Definition 10.
Some AOs for CLPFVs and their desirable properties
In this section, we shall extend the PA operator and the PHM operator to cubic linguistic Pythagorean fuzzy sets and propose some new cubic linguistic Pythagorean fuzzy AOs. Additionally, important properties and special cases of these new AOs are also studied.
The cubic linguistic Pythagorean fuzzy power average operator
Definition 12
Let \(\eta_{i} \left( {i = 1,2,...,n} \right)\) be a collection of CLPFVs, then the cubic linguistic Pythagorean fuzzy power average (CLPFPA) operator is defined as
where \(T\left( {\eta_{i} } \right) = \sum\nolimits_{j = 1;j \ne i}^{n} {{\text{Sup}}\left( {\eta_{i} ,\eta_{j} } \right)}\),\({\text{Sup}}\left( {\eta_{i} ,\eta_{j} } \right)\) denotes the support for \(\eta_{i}\) from \(\eta_{j}\), satisfying the conditions.
(1) \(0 \le {\text{Sup}}\left( {\eta_{i} ,\eta_{j} } \right) \le 1\);
(2) \({\text{Sup}}\left( {\eta_{i} ,\eta_{j} } \right) = {\text{Sup}}\left( {\eta_{j} ,\eta_{i} } \right)\);
(3)\({\text{Sup}}\left( {\eta_{1} ,\eta_{2} } \right) \le {\text{Sup}}\left( {\eta_{3} ,\eta_{4} } \right)\), if \(d\left( {\eta_{1} ,\eta_{2} } \right) \ge d\left( {\eta_{3} ,\eta_{4} } \right)\).
Theorem 2
Let \(\eta_{i} = \left\langle {\left( {\left[ {s_{{\theta_{i} }} ,s_{{\tau_{i} }} } \right],\left[ {s_{{\sigma_{i} }} ,s_{{\varepsilon_{i} }} } \right]} \right),\left( {s_{{\delta_{i} }} ,s_{{\zeta_{i} }} } \right)} \right\rangle\) \(\left( {i = 1,2,...,n} \right)\) be a collection of CLPFVs defined on the linguistic term set \(\widetilde{S} = \left\{ {s_{\beta } \left| {s_{0} \le s_{\beta } \le s_{t} ,\beta \in \left[ {0,t} \right]} \right.} \right\}\), then the aggregated value by the CLPFPA operator is still a CLPFV and
The proof of the theorem 2 is easy, so we omit it here to save space. In addition, it is obvious that the CLPFPA operator provides the properties of idempotency and boundedness.
Theorem 3
(Idempotency). Let \(\eta_{i} \left( {i = 1,2,...,n} \right)\) be a collection of CLPFVs, if \(\eta_{i} = \eta = \left\langle {\left( {\left[ {s_{\theta } ,s_{\tau } } \right],\left[ {s_{\sigma } ,s_{\varepsilon } } \right]} \right),\left( {s_{\delta } ,s_{\zeta } } \right)} \right\rangle\) holds for all i, then,
Theorem 4
(Boundedness). Let \(\eta_{i} \left( {i = 1,2,...,n} \right)\) be a collection of CLPFVs, then
where
and
The cubic linguistic Pythagorean fuzzy power weighted average operator
If the weight information of corresponding aggregated CLPFVs is taken into account in the CLPFPA operator, then its weighted form can be obtained.
Definition 13
Let \(\eta_{i} \left( {i = 1,2,...,n} \right)\) be a collection of CLPFVs and \(w = \left( {w_{1} ,w_{2} ,...,w_{n} } \right)^{{\text{T}}}\) be the corresponding weight vector, such that \(0 \le w_{i} \le 1\) and \(\sum\nolimits_{i = 1}^{n} {w_{i} } = 1\). The cubic linguistic Pythagorean fuzzy power weighted average (CLPFPWA) operator is expressed as
where \(T\left( {\alpha_{i} } \right) = \sum\nolimits_{j = 1;j \ne i}^{n} {{\text{Sup}}\left( {\alpha_{i} ,\alpha_{j} } \right)}\), \({\text{Sup}}\left( {\alpha_{i} ,\alpha_{j} } \right)\) denotes the support for \(\alpha_{i}\) from \(\alpha_{j}\), satisfying the properties presented in Definition 12.
Theorem 5
Let \(\eta_{i} = \left\langle {\left( {\left[ {s_{{\theta_{i} }} ,s_{{\tau_{i} }} } \right],\left[ {s_{{\sigma_{i} }} ,s_{{\varepsilon_{i} }} } \right]} \right),\left( {s_{{\delta_{i} }} ,s_{{\zeta_{i} }} } \right)} \right\rangle\) \(\left( {i = 1,2,...,n} \right)\) be a collection of CLPFVs defined on the linguistic term set \(\widetilde{S} = \left\{ {s_{\beta } \left| {s_{0} \le s_{\beta } \le s_{t} ,\beta \in \left[ {0,t} \right]} \right.} \right\}\), then the aggregated value by the CLPFPWA operator is also a CLPFV and
Similar to the CLPFPA operator, the CLPFPWA operator has also the properties of idempotency and boundedness.
Example 4
Let \(\eta_{1} = \left\langle {\left( {\left[ {s_{4} ,s_{5} } \right],\left[ {s_{1} ,s_{2} } \right]} \right),\left( {s_{3} ,s_{5} } \right)} \right\rangle\), \(\eta_{2} = \left\langle {\left( {\left[ {s_{1} ,s_{3} } \right],\left[ {s_{4} ,s_{5} } \right]} \right),\left( {s_{3} ,s_{4} } \right)} \right\rangle\) and \(\eta_{3} = \left\langle {\left( {\left[ {s_{2} ,s_{3} } \right],\left[ {s_{3} ,s_{5} } \right]} \right),\left( {s_{5} ,s_{2} } \right)} \right\rangle\) be three CLPFVs defined on the continuous linguistic term set \(\widetilde{S} = \left\{ {s_{\beta } \left| {s_{0} \le s_{\beta } \le s_{6} ,\beta \in \left[ {0,6} \right]} \right.} \right\}\), and let \(w = \left( {0.3,0.4,0.3} \right)^{T}\) be the weight vector of \(\eta_{i}\). Then, we utilize the CLPFPWA to aggregate them
Step 1. Compute the support \({\text{Sup}}\left( {\eta_{i} ,\eta_{j} } \right)\left( {i,j = 1,2,3} \right)\). As \({\text{Sup}}\left( {\eta_{i} ,\eta_{j} } \right) = 1 - d\left( {\eta_{i} ,\eta_{j} } \right)\), we can get
Step 2. Compute the overall support according to the equation \(T\left( {\eta_{i} } \right) = \sum\nolimits_{j = 1;j \ne i}^{n} {{\text{Sup}}\left( {\eta_{i} ,\eta_{j} } \right)}\). We have
Step 2. Calculate the power weight \(\omega_{i}\), where \(\omega_{i} = \frac{{w_{i} \left( {1 + T\left( {\alpha_{i} } \right)} \right)}}{{\sum\nolimits_{i = 1}^{n} {w_{i} \left( {1 + T\left( {\alpha_{i} } \right)} \right)} }}\). Then, we can obtain:
Similarly, \(\omega_{2} = 0.4102\), \(\omega_{3} = 0.3093\) can be obtained.
Step 3. Calculate the comprehensive value \(\eta = \left\langle {\left( {\left[ {s_{\theta } ,s_{\tau } } \right],\left[ {s_{\sigma } ,s_{\varepsilon } } \right]} \right),\left( {s_{\delta } ,s_{\zeta } } \right)} \right\rangle\) by the CLPFPWA operator, i.e., \(\eta = {\text{CLPFPWA}}\left( {\eta_{1} ,\eta_{2} ,\eta_{3} } \right)\).
According to Theorem 5, \(s_{\theta } = s_{{t\sqrt {1 - \prod\nolimits_{i = 1}^{n} {\left( {1 - \frac{{\theta_{i}^{2} }}{{t^{2} }}} \right)^{{\frac{{w_{i} \left( {1 + T\left( {\eta_{i} } \right)} \right)}}{{\sum\nolimits_{i = 1}^{n} {w_{i} \left( {1 + T\left( {\eta_{i} } \right)} \right)} }}}} } } }}\), where \(\frac{{w_{i} \left( {1 + T\left( {\alpha_{i} } \right)} \right)}}{{\sum\nolimits_{i = 1}^{n} {w_{i} \left( {1 + T\left( {\alpha_{i} } \right)} \right)} }}\) is the power weight \(\omega_{i}\) calculated in Step 2. So, we have
Similarly, \(s_{\tau } = s_{4.6744}\), \(s_{\sigma } = s_{1.4752}\), \(s_{\varepsilon } = s_{2.9316}\), \(s_{\delta } = s_{3.6737}\), and \(s_{\zeta } = s_{2.3619}\). Thus, the aggregated result is
The cubic linguistic Pythagorean fuzzy power Hamy mean operator
It is noted that the CLPFPA and CLPFPWA operators have the ability of reducing the negative influence of unreasonable CLPFVs on the final results. However, they fail to consider the interrelationship among aggregated CLPFVs. Hence, this subsection proposes some hybrid AOs for CLPFVs.
Definition 14
Let \(\eta_{i} \left( {i = 1,2,...,n} \right)\) be a collection of CLPFVs and \(k = 1,2,...,n\), then the cubic linguistic Pythagorean fuzzy power Hamy mean (CLPFPHM) operator is expressed as
where \(T\left( {\eta_{i} } \right) = \sum\nolimits_{j = 1;j \ne i}^{n} {{\text{Sup}}\left( {\eta_{i} ,\eta_{j} } \right)}\), \({\text{Sup}}\left( {\eta_{i} ,\eta_{j} } \right)\) denotes the support for \(\alpha_{i}\) from \(\alpha_{j}\), satisfying the properties presented in Definition 12. To simplify Eq. (22), we assume
then Eq. (21) can be written as
where \(0 \le r_{i} \le 1\) and \(\sum\nolimits_{i = 1}^{n} {r_{i} } = 1\).
Theorem 6
Let \(\eta_{i} = \left\langle {\left( {\left[ {s_{{\theta_{i} }} ,s_{{\tau_{i} }} } \right],\left[ {s_{{\sigma_{i} }} ,s_{{\varepsilon_{i} }} } \right]} \right),\left( {s_{{\delta_{i} }} ,s_{{\zeta_{i} }} } \right)} \right\rangle \left( {i = 1,2,...,n} \right)\) be a collection of CLPFVs defined on the continuous linguistic term set \(\widetilde{S} = \left\{ {s_{\beta } \left| {s_{0} \le s_{\beta } \le s_{t} ,\beta \in \left[ {0,t} \right]} \right.} \right\}\), then the aggregated value by the CLPFPHM operator is still a CLPFV and
Proof.
According to Definitions 6 and 13, we have
and
Then,
Furthermore,
Finally, we have
In addition, the CLPFPHM operator has the following properties.
Theorem 7
(Idempotency). Let \(\eta_{i} \left( {i = 1,2,...,n} \right)\) be a collection of CLPFVs, if \(\eta_{i} = \eta = \left\langle {\left( {\left[ {s_{\theta } ,s_{\tau } } \right],\left[ {s_{\sigma } ,s_{\varepsilon } } \right]} \right),\left( {s_{\delta } ,s_{\zeta } } \right)} \right\rangle\) for all i, then
Proof.
Since \(\eta_{i} = \eta = \left\langle {\left( {\left[ {s_{\theta } ,s_{\tau } } \right],\left[ {s_{\sigma } ,s_{\varepsilon } } \right]} \right),\left( {s_{\delta } ,s_{\zeta } } \right)} \right\rangle\) holds for \(i = 1,2,...,n\), we can get \({\text{Sup}}\left( {\eta_{i} ,\eta_{j} } \right) = 1\) for \(i,j = 1,2,...,n\). Then \(r_{i} = \frac{1}{n}\left( {i = 1,2,...,n} \right)\). According to Theorem 6, we can get
Theorem 8
(Boundedness). Let \(\eta_{i} = \left\langle {\left( {\left[ {s_{{\theta_{i} }} ,s_{{\tau_{i} }} } \right],\left[ {s_{{\sigma_{i} }} ,s_{{\varepsilon_{i} }} } \right]} \right),\left( {s_{{\delta_{i} }} ,s_{{\zeta_{i} }} } \right)} \right\rangle \left( {i = 1,2,...,n} \right)\) be a collection of CLPFVs, then
where
and
Proof
According to Theorem 6, we have
Similarly, we can get
and
According to Definition 7, \({\text{CLPFPHM}}^{\left( k \right)} \left( {\eta_{1} ,\eta_{2} ,...,\eta_{n} } \right) \le \eta^{ + }\) can be obtained. Similarly, we can get \(\eta^{ - } \le {\text{CLPFPHM}}^{\left( k \right)} \left( {\eta_{1} ,\eta_{2} ,...,\eta_{n} } \right)\). Thus, according to Theorem 7, \({\text{CLPFPHM}}^{\left( k \right)} \left( {\eta^{ + } ,\eta^{ + } ,...,\eta^{ + } } \right) \ge {\text{CLPFPHM}}^{\left( k \right)} \left( {\eta_{1} ,\eta_{2} ,...,\eta_{n} } \right)\) \(\ge\) \({\text{CLPFPHM}}^{\left( k \right)} \left( {\eta^{ - } ,\eta^{ - } ,...,\eta^{ - } } \right)\) is proved.
In the following, we further study special cases of the CLPFPHM operator with respect to the parameter k.
Case 1. If \(k = 1\), then the CLPFPHM operator reduces to the cubic linguistic Pythagorean fuzzy power average (CLPFPA) operator, that is
In this case, if \({\text{Sup}}\left( {\eta_{i} ,\eta_{j} } \right) = d\left( {d > 0} \right)\) for \(i,j = 1,2,...,n\left( {i \ne j} \right)\), then the CLPFPHM operator reduces to the cubic linguistic Pythagorean fuzzy average (CLPFA) operator, that is
Case 2. If \(k = n\), then the CLPFPHM operator reduces to the following:
In this case, if \({\text{Sup}}\left( {\eta_{i} ,\eta_{j} } \right) = d\left( {d > 0} \right)\) for \(i,j = 1,2,...,n\left( {i \ne j} \right)\), then the CLPFPHM operator reduces to the cubic linguistic Pythagorean fuzzy geometric (CLPFG) operator, that is
The cubic linguistic Pythagorean fuzzy power weighted Hamy mean operator
Definition 15
Let \(\eta_{i} \left( {i = 1,2,...,n} \right)\) be a collection of CLPFVs and \(k = 1,2,...,n\). Let \(w = \left( {w_{1} ,w_{2} ,...,w_{n} } \right)^{{\text{T}}}\) be the corresponding weight vector, such that \(0 \le w_{i} \le 1\) and \(\sum\nolimits_{i = 1}^{n} {w_{i} } = 1\). The cubic linguistic Pythagorean fuzzy power weighted Hamy mean (CLPFPWHM) operator is expressed as
where \(T\left( {\eta_{i} } \right) = \sum\nolimits_{j = 1;j \ne i}^{n} {{\text{Sup}}\left( {\eta_{i} ,\eta_{j} } \right)}\), \({\text{Sup}}\left( {\eta_{i} ,\eta_{j} } \right)\) denotes the support for \(\eta_{i}\) from \(\eta_{j}\), satisfying the properties presented in Definition 12. To simplify Eq. (32), we assume
then Eq. (32) can be written as
where \(0 \le g_{i} \le 1\) and \(\sum\nolimits_{i = 1}^{n} {g_{i} } = 1\).
Theorem 9
Let \(\eta_{i} = \left\langle {\left( {\left[ {s_{{\theta_{i} }} ,s_{{\tau_{i} }} } \right],\left[ {s_{{\sigma_{i} }} ,s_{{\varepsilon_{i} }} } \right]} \right),\left( {s_{{\delta_{i} }} ,s_{{\zeta_{i} }} } \right)} \right\rangle \left( {i = 1,2,...,n} \right)\) be a collection of CLPFVs defined on the continuous linguistic term set \(\widetilde{S} = \left\{ {s_{\beta } \left| {s_{0} \le s_{\beta } \le s_{t} ,\beta \in \left[ {0,t} \right]} \right.} \right\}\), then the aggregated value by the CLPFPWHM operator is still a CLPFV and
The proof of Theorem 9 is parallel to that of Theorem 6, so we omit it here. Meanwhile, the CLPFPWHM also has the following properties.
Theorem 10
(Boundedness). Let \(\eta_{i} = \left\langle {\left( {\left[ {s_{{\theta_{i} }} ,s_{{\tau_{i} }} } \right],\left[ {s_{{\sigma_{i} }} ,s_{{\varepsilon_{i} }} } \right]} \right),\left( {s_{{\delta_{i} }} ,s_{{\zeta_{i} }} } \right)} \right\rangle \left( {i = 1,2,...,n} \right)\) be a collection of CLPFVs, then
where
and
A novel approach to MAGDM based on the proposed operators
In this section, we present a novel method to MAGDM based on the proposed CLPFPWA and CLPFPWHM operators. Let \(A = \left\{ {A_{1} ,A_{2} ,...,A_{m} } \right\}\) be a collection of alternatives, \(C = \left\{ {C_{1} ,C_{2} ,...,C_{n} } \right\}\) be a set of attributes, and \(D = \left\{ {D_{1} ,D_{2} ,...,D_{l} } \right\}\) be a collection of DMs. For attribute \(C_{j} \left( {j = 1,2,...,n} \right)\) of alternative \(A_{i} \left( {i = 1,2,...,m} \right)\), the DM \(D_{h} \left( {h = 1,2,...,l} \right)\) expresses his/her assessment by \(\eta_{ij}^{h} = \left\langle {\left( {\left[ {s_{{\theta_{ij}^{h} }} ,s_{{\tau_{ij}^{h} }} } \right],\left[ {s_{{\sigma_{ij}^{h} }} ,s_{{\varepsilon_{ij}^{h} }} } \right]} \right),\left( {s_{{\delta_{ij}^{h} }} ,s_{{\zeta_{ij}^{h} }} } \right)} \right\rangle\), which is a CLPFV defined on the continuous linguistic term set \(\widetilde{S} = \left\{ {s_{\beta } \left| {s_{0} \le s_{\beta } \le s_{t} ,\beta \in \left[ {0,t} \right]} \right.} \right\}\). Thus, for each DM an individual cubic linguistic Pythagorean fuzzy decision matrix can be derived, which can be denoted as \(R^{h} = \left( {\eta_{ij}^{h} } \right)_{m \times n}\). Let \(\lambda = \left( {\lambda_{1} ,\lambda_{2} ,...,\lambda_{l} } \right)\) is the weight vector of DMs, satisfying \(\lambda_{h} \in \left[ {0,1} \right]\) and \(\sum\nolimits_{h = 1}^{l} {\lambda_{h} } = 1\). Let \(w = \left( {w_{1} ,w_{2} ,...,w_{n} } \right)\) be the weight of attributes, such that \(w_{j} \in \left[ {0,1} \right]\) and \(\sum\nolimits_{j = 1}^{n} {w_{j} } = 1\). In the followings, the main steps of solving the cubic linguistic Pythagorean fuzzy MAGDM problem are introduced.
Step 1. Standardize the original decision matrices. In real decision-making problems, there exists two kinds of attributes: benefit attributes (\(I_{1}\)) and cost attributes (\(I_{2}\)). The original decision matrices should be normalized using the following formula:
Step 2. Compute \({\text{Sup}}\left( {\eta_{ij}^{h} ,\eta_{ij}^{z} } \right)\) according to the following formula
where \(d\left( {\eta_{ij}^{h} ,\eta_{ij}^{z} } \right)\) is the distance between \(\eta_{ij}^{h}\) and \(\eta_{ij}^{z}\) described in Definition 8.
Step 3. Compute the overall supports \(T\left( {\eta_{ij}^{h} } \right)\) by
Step 4. Compute the power weight of \(\eta_{ij}^{h}\) provided by DM \(D_{h}\) by the following equation:
Step 5. Use the CLPFPWA operator to aggregate individual decision matrices \(R^{h} = \left( {\eta_{ij}^{h} } \right)_{m \times n} \left( {h = 1,2,...,l} \right)\) to obtain the comprehensive decision matrix \(R = \left( {\eta_{ij} } \right)_{m \times n}\):
Step 6. Compute \({\text{Sup}}\left( {\eta_{ij} ,\eta_{is} } \right)\) by
Step 7. Compute the overall supports \(T\left( {\eta_{ij} } \right)\) by the following formula
Step 8. Compute the power weight of \(\eta_{ij}\) by
Step 9. Utilize the CLPFPWHM operator to aggregate attribute values
and an overall preference value \(\eta_{i} \left( {i = 1,2,...,m} \right)\) with respect to each alternative \(A_{i} \left( {i = 1,2,...,m} \right)\) can be obtained.
Step 10. Compute the score of \(\eta_{i} (i = 1,2,...,m)\) according to Definition 7.
Step 11. Rank the corresponding alternatives according to the order of scores and select the best alternative.
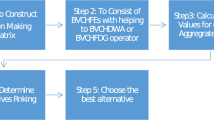
To better demonstrate the main decision-making steps, we provide the following flowchart, Fig. 1.
A practical example
In this section, the application of the new proposed method is illustrated by solving a practical MAGDM problem.
Example 5
Chronic diseases have become one of the main threats to human health these days. The World Health Organization reports that 71% of all deaths globally was caused by chronic diseases [55]. Hence, it is necessary to provides effective management service for chronic disease patients and high-risk groups. Generally, the objects of chronic diseases management (CDM) include three aspects [56]: health aspect (C1), which means disease risk factors, course of disease, complications and so forth; psychology aspect (C2), which refers to patients’ awareness of their diseases, psychological changes and behavior patterns after illness; social environment aspect (C3), which involves living environment, working environment, group environment, social status and so on. Medical administrators usually intervene patients’ condition from these three aspects in CDM. Noting that since diseases are long-term and may change at any time, while the treatment varies from person to person, CDM emphasizes the regular assessment of patients’ condition and the corresponding adjustment of treatment plan.
Suppose there are four patients Ai (i = 1, 2, 3, 4) who have been in the process of CDM for a while. The conditions of these four patients should be evaluated under the three factors: C1 (health aspect); C2 (psychology aspect); C3 (social environment aspect). The weight vector of these factors is \(w = \left( {0.40,0.35,0.25} \right)^{{\text{T}}}\). Three experts Dh (h = 1, 2, 3) are invited to give their assessments on the basis of linguistic term set S = {s0 = extremely poor, s1 = very poor, s2 = poor, s3 = slightly poor, s4 = general, s5 = slightly good, s6 = good, s7 = very good, s8 = extremely good}. The weight of these experts is \(\lambda = \left( {0.32,0.4,0.28} \right)^{{\text{T}}}\). The evaluation value of each attribute of each patient is in the form of CLPFV. In each CLPFV, the ULPFV represents the assessment of patient’s current situation, while the LPFV indicates the estimate of consistency as well as inconsistency of the patient status in the coming week. The assessment values given by the three experts for each attributes of each alternatives are summarized in the form of the decision matrix \(R^{h} = \left( {\eta_{ij}^{h} } \right)_{m \times n} \left( {h = 1,2,3} \right)\) presented in Tables 1, 2, and 3, respectively. Therefore, to identify the patients’ conditions in CDM, we utilize the proposed method to handle this issue.
The decision-making process
Step 1. The original decision matrices are normalized using Eq. (38). Since all attributes are benefit type, the three decision matrices remain unchanged here.
Step 2. The support between two CLPFVs \(\eta_{ij}^{h}\) and \(\eta_{ij}^{z}\) are computed according to Eq. (39), where \(h,z = 1,2,3\), \(h \ne z\) for all \(i = 1,2,3,4\) and \(j = 1,2,3\). For the sake of simplicity, we utilize \(S_{z}^{h}\) to represent the support for \(\eta_{ij}^{h}\) from \(\eta_{ij}^{z}\), and then,
Step 3. Equation (40) is conducted to calculate the overall supports \(T\left( {\eta_{ij}^{h} } \right)\), and we have
Step 4. Combining the weight of DM, the power weight of DM \(D_{h}\) relative to the CLPFV \(\eta_{ij}^{h}\) is obtained. Similarly, we denote the comprehensive power weights of DM \(D_{h}\) by \(\gamma^{h} \left( {h = 1,2,3} \right)\), and thus,
Step 5. The CLPFPWA operator is utilized to aggregate each individual decision matrix provided by DM \(D_{h}\) \(\left( {h = 1,2,3} \right)\). Thus, we can get the comprehensive decision matrix \(R = \left( {\eta_{ij} } \right)_{m \times n}\) (please see Table 4).
Step 6. Compute the support for \(\eta_{ij}\) from \(\eta_{is}\) \(\left( {i = 1,2,3,4;j,s = 1,2,3;j \ne s} \right)\), which can be denoted by \({\text{Sup}}_{s}^{j}\) for convenience, and thus,
Step 7. For each alternative, calculate the comprehensive support of each attribute from orthers, and we have
Step 8. Combine the weights of attributes to compute the power weights \(\omega_{ij}\) of the CLPFVs \(\eta_{ij}\)\(\left( {i = 1,2,3,4;j = 1,2,3} \right)\), and we can get
Step 9. Utilizing the CLPFPWHM operator to aggregate attribute values (set k = 3), and the comprehensive evaluation value of each alternative is obtained.
Step 10. Calculate the scores of comprehensive evaluation values, that is
Step 11. According to the scores, the order of alternatives is \(A_{4} \succ A_{1} \succ A_{3} \succ A_{2}\), where the symbol “\(\succ\)” means “superior to”. This reveals that in current CDM, the situation of patient A4 is the most optimistic, while that of \(A_{2}\) is the most urgent.
Sensitivity analysis
It is observed that the parameter k in the CLPFPWHM operator plays a significant role in the decision results. To investigate the influence of k, we assign different values to k, and calculate the corresponding scores and ranking results. We present the score values and ranking orders with different values of k in Table 5.
As can be seen from Table 5, the score of each alternative varies with k, which confirms that k has effect on score values. Specifically, the larger the value of k is, the smaller the score value of each alternative becomes. This reflects the risk preferences of DMs in actual decision context. In general, DMs can choose appropriate k according to their preferences. If \(k = \left[ {{n \mathord{\left/ {\vphantom {n 2}} \right. \kern-\nulldelimiterspace} 2}} \right]\), DMs are risk neutral, which also indicates that they have no special preference; if \(k < \left[ {{n \mathord{\left/ {\vphantom {n 2}} \right. \kern-\nulldelimiterspace} 2}} \right]\), DMs are risk aversion, and the smaller the k the greater the degree; if \(k > \left[ {{n \mathord{\left/ {\vphantom {n 2}} \right. \kern-\nulldelimiterspace} 2}} \right]\), DMs are risk preference, and the larger the k the greater the degree, where notation [] represents the round function, n is the number of attributes. In addition, it can be found that the ranking orders obtained by k = 1, 2 or 3 are slightly different. Noting that when k = 1 the relationship between attributes is not considered, when k = 2 the relationship between any two attributes is taken account of, and when k = 3 the interrelationship among all attributes can be considered, which indicates the flexibility and effectiveness of our proposed method.
Advantages of our method
In this subsection, we illustrate the advantages of our MAGDM method through comparative analysis.
The ability of expressing DMs’ evaluation values
As the extension of LPFSs introduced by Garg [32], the proposed CLPFSs contain more sufficient information and DMs can more comprehensively express their evaluation values. As mentioned in Introduction, CFSs have the ability of describing DMs’ evaluation information in two separate time zones. Hence, our proposed CLPFSs inherit the advantages of CFSs, i.e., they can depict decision-making related information in two separate time zones simultaneously, by using a LPFS and ULPFS in one evaluation element. This characteristic makes CLPFSs more powerful and flexible than Garg’s LPFSs [32]. In addition, in real MAGDM problems, to better depict evaluation values of alternatives’ performance, it is necessary to consider DMs’ assessment information in two separate zones, which can be described by CLPFSs. In Example 5, in the process of patients’ conditions identification, to comprehensively depict the attribute values, the DMs are allowed to provide their evaluation information in two separate time zone, and obviously our proposed CLPFSs can effectively deal with this situation.
The ability to reduce the negative impact of extreme evaluation values
In real decision-making problems, DMs may give some unreasonable or extreme evaluation values out of some reasons, usually resulting in negative impacts on the decision outcomes. There are many reasons, such as lack of expertise, time shortage and the inherent prejudice. To make a wise selection, such adverse effects should be eliminated during decision-making process. Our proposed method is based on the CLPFPWA and CLPFPWHM, which implies that our MAGDM method can effectively deal with DMs’ unreasonable or irrational bias, making the final decisions more reasonable. To better demonstrate this advantage, we provide the following example.
Example 6
Because of the high complexity of decision environment, it is impossible for DMs to know all the information about each alternative. As a result, DMs sometimes may provide some unreasonable evaluation values. In Example 5, affected by prejudices, DM D1provides some extreme values for alternative A3 and A4. The new CLPF decision matrix is presented in Table 6, and the evaluations of D2 and D3 are unchanged. We still use our new developed method to solve the problem.
We can recalculate the scores for these alternatives, that is, \(S\left( {\eta_{1} } \right) = s_{6.1540}\),\(S\left( {\eta_{2} } \right) = s_{5.8072}\), \(S\left( {\eta_{3} } \right) = s_{5.9391}\), \(S\left( {\eta_{4} } \right) = s_{6.1797}\), then the order is \(A_{4} \succ A_{1} \succ A_{3} \succ A_{2}\) (k = 3). Compared with the result of Example 5, the scores of A3 and A4 are changed due to D1s bias. However, the ranking order is still same. This reveals our method based on the PA operators can effectively balance the adverse effects of extreme or unreasonable evaluation values on the final ranking results and, shows the stability and reliability of the new method.
The ability to capture the interrelationship among attributes
As aforementioned, in our method, parameter k can control the number of related attributes. In real MAGDM problems, relationship among attributes is usually a significant factor for reasonable results, and thus, DMs can choose the appropriate value of k according to the actual needs. For example, in Example 5, the evaluation factors involve three aspects, i.e., physical (C1), psychological (C2) and social (C3). It is well known that the restrictive relation exists among the three attributes, which indicates the intervention on one aspect will be affected by the other two, so that we can set k equal to 3. This shows our proposed method is a powerful tool to process MAGDM.
Summarization
In this section, we will further compare our method based on CLPFPWA and CLPFPWHM operators with some state-of-the-art methods, including that introduced by Garg [32] based on LPFWA operator and that developed by Abbas et al. [50] based on CPFWA operator. We then summarize the superiority of the proposed method over these existing methods according to Table 7, which clearly displays the characteristics of different multi-attribute methods.
-
(1)
Firstly, Garg’s [32] method is based on LPFSs, where the MD and NMD is, respectively, denoted by a single linguistic variable (LV). Our method is based on CLPFSs which are constructed by combining LPFSs and ULPFSs, so that ULVs and LVs can be simultaneously used to represent DMs’ evaluation. It is obvious that the proposed CLPFSs can contain more effective information and can be adopted in more possible decision-making scenarios. Additionally, in Garg’s [32] method, linguistic Pythagorean fuzzy weight average (LPFWA) operator was developed to aggregate DM’s evaluation values. Garg’s [32] developed operator is derived by the basic weight average (WA) algorithm and has no additional functions. In comparison, the CLPFPHM operator in our method is based on PHM operator which enables these two practical functions, i.e., balancing the influence of extreme evaluation as well as capturing the interrelationship of input attributes. Therefore, our proposed method is superior to Garg’s as it provides more comprehensive information expression approach and more richer information fusion functions.
-
(2)
Secondly, Abbas et al.’s [50] method is based on CPFSs which also inherits the merit of CFSs. This characteristic is same as our method. However, CPFSs can only be used to depict quantitative information, but fail to describe qualitive linguistic information common in real-life decision scenarios. Furthermore, the AO in Abbas et al.’s [50] method, i.e., cubic Pythagorean fuzzy weight average (CPFWA), is still based on WA. As aforementioned, the WA is a basic approach and our proposed CLPFPHM is more powerful than it. Hence, compare with Abbas et al.’s [50] method, our method is stronger both in linguistic information expression and information aggregation.
Conclusions
In this paper, we introduced the CLPFSs, which are a new generalization of the existing fuzzy set theories, such as LIFS, LPFSs, CFSs and so forth, and have strong ability to express the uncertainty and hesitation of DMs in the MAGDM. Then, we put forward the fundamental operation law for CLPFVs. Based on this, a series of cubic linguistic Pythagorean fuzzy AOs, including the CLPFPA, CLPFPWA, CLPFPHM and CLPFPWHM operators, were developed by combining the powerful PA and HM operators in cubic linguistic Pythagorean fuzzy environment, and then some desirable properties of them were investigated. Furthermore, we proposed a new MAGDM method, and illustrated it with an application example of chronic disease management. Also, the sensitivity analysis showed that the parameter k enables great flexibility of the proposed method. Finally, the advantages of our method over some existing methods were explained, and hence the proposed method should be recommended to handle MAGDM problems. We plan to continue our researches from the following three aspects. First, we shall apply the novel proposed MAGDM method to more practical decision-making issues, such as supplier selection, talent evaluation, disease severity assessment etc. Second, we plan to investigate more AOs for CLPFSs and study their application in decision-making. Third, we will continue to investigate more novel extensions of CLPFSs, such as hesitant CLPFSs, probabilistic hesitant CLPFSs, etc.
References
Niu L, Li J, Li F, Wang Z (2020) Multi-criteria decision-making method with double risk parameters in interval-valued intuitionistic fuzzy environments. Syst, Complex Intell. https://doi.org/10.1007/s40747-020-00165-0
Wang J, Shang X, Feng X, Sun M (2020) A novel multiple attribute decision making method based on q-rung dual hesitant uncertain linguistic sets and Muirhead mean. Arch Control Sci 30(2):233–272
Garg H (2018) Hesitant Pythagorean fuzzy sets and their aggregation operators in multiple attribute decision-making. Int J Uncertain Quan 8(3):267–289
Li L, Zhang R, Wang J, Shang X (2018) Some q-rung orthopair linguistic Heronian mean operators with their application to multi-attribute group decision making. Arch Control Sci 28(4):551–583
Vakkas U, Irfan D, Mehmet S (2018) Intuitionistic trapezoidal fuzzy multi-numbers and its application to multi-criteria decision-making problems. Complex Intell Syst 5:65–78
Wang J, Zhang R, Zhu X, Shang X (2019) Some q-rung orthopair fuzzy Muirhead means with their application to multi-attribute group decision making. J Intell Fuzzy Syst 36(2):1599–1614
Garg H (2019) Special issue on “Pythagorean fuzzy set and its extensions in decision-making process.” Complex Intell Syst 5(2):91–92
Xu Y, Shang X, Wang J, Wu W (2018) Some q-rung dual hesitant fuzzy Heronian mean operators with their application to multiple attribute group decision-making. Symmetry 10(10):472
Abdullah L, Goh P (2019) Decision making method based on Pythagorean fuzzy sets and its application to solid waste management. Complex Intell Syst 5:185–198
Singh SP, Singh P (2018) A hybrid decision support model using axiomatic fuzzy set theory in AHP and TOPSIS for multicriteria route selection. Complex Intell Syst 4:133–143
Atanassov K (1986) Intuitionistic fuzzy sets. Fuzzy Sets Syst 20(1):87–96
Wang X, Peng H, Wang J (2018) Hesitant linguistic intuitionistic fuzzy sets and their application in multicriteria decision-making problems. Int J Uncertain Quan 8(4):321–341
Singh S, Sharma S, Lalotra S (2020) Generalized correlation coefficients of intuitionistic fuzzy sets with application to MAGDM and clustering analysis. Int J Fuzzy Syst 22:1582–1595
Rani D, Garg H (2017) Distance measures between the complex intuitionistic fuzzy sets and their applications to the decision-making process. Int J Uncertain Quan 7(5):423–439
Feng F, Xu Z, Fujita H, Liang M (2020) Enhancing PROMETHEE method with intuitionistic fuzzy soft sets. Int J Intell Syst 35(2):1–34
Liu P, Ali A, Rehman N, Shah S (2020) Another view on intuitionistic fuzzy preference relation-based aggregation operators and their applications. Int J Fuzzy Syst 8:1–15
Yager R, Abbasov A (2013) Pythagorean membership grades, complex numbers and decision making. Int J Intell Syst 28(5):436–452
Alk A (2020) A novel pythagorean fuzzy AHP and fuzzy TOPSIS methodology for green supplier selection in the industry 4.0 era. Soft Comput. https://doi.org/10.1007/s00500-020-05294-9
Ozgur Y, Yakup T, Nisa C, Cengiz K (2020) Interval-valued Pythagorean fuzzy EDAS method: an application to car selection problem. J Intell Fuzzy Syst 38(4):4061–4077
Akram M, Luquman A, Alcantud J (2020) Risk evaluation in failure modes and effects analysis: hybrid TOPSIS and ELECTRE I solutions with Pythagorean fuzzy information. Neural Comput Appl. https://doi.org/10.1007/s00521-020-05350-3
Guleria A, Bajaj R (2020) A robust decision making approach for hydrogen power plant site selection utilizing (R, S)-Norm Pythagorean Fuzzy information measures based on VIKOR and TOPSIS method. Int J Hydrog Energy 45(38):18802–18816
Li L, Zhang R, Wang J, Zhu X, Xing Y (2018) Pythagorean fuzzy power Muirhead mean operators with their application to multi-attribute decision making. J Intell Fuzzy Syst 35(2):2035–2050
Chen Z, Liu P, Pei Z (2015) An approach to multiple attribute group decision making based on linguistic intuitionistic fuzzy numbers. Int J Comput Int Syst 8(4):747–760
Ou Y, Yi L, Zou B, Zheng P (2018) The linguistic intuitionistic fuzzy set TOPSIS method for linguistic multi-criteria decision makings. Int J Comput Intell Syst 11(1):120–132
Yuan R, Tang J, Meng F (2019) Linguistic intuitionistic fuzzy group decision making based on aggregation operators. Int J Fuzzy Syst 21(2):407–420
Liu P, Qin X (2017) Power average operators of linguistic intuitionistic fuzzy numbers and their application to multiple-attribute decision making. J Intell Fuzzy Syst 32(1):1029–1043
Liu P, Qin X (2017) Maclaurin symmetric mean operators of linguistic intuitionistic fuzzy numbers and their application to multiple-attribute decision-making. J Exp Theor Artif Intell 29(6):1173–1202
Liu P, Liu J, Merigo J (2018) Partitioned Heronian means based on linguistic intuitionistic fuzzy numbers for dealing with multi-attribute group decision making. Appl Soft Comput 62:395–422
Liu P, Liu J (2020) A multiple attribute group decision-making method based on the partitioned Bonferroni mean of linguistic intuitionistic fuzzy numbers. Cogn Comput 12(1):49–70
Liu P, You X (2018) Some linguistic intuitionistic fuzzy Heronian mean operators based on Einstein T-norm and T-conorm and their application to decision-making. J Intell Fuzzy Syst 35(2):2433–2445
Garg H, Kumar K (2019) Multiattribute decision making based on power operators for linguistic intuitionistic fuzzy set using set pair analysis. Expert Syst 36(4):e12428
Garg H (2018) Linguistic Pythagorean fuzzy sets and its applications in multiattribute decision-making process. Int J Intell Syst 33(6):1234–1263
Liu Y, Qin Y, Xu L, Liu H, Liu J (2019) Multiattribute group decision-making approach with linguistic Pythagorean fuzzy information. IEEE Access. https://doi.org/10.1109/ACCESS.2019.2945005
Lin M, Wei J, Xu Z, Chen R (2018) Multiattribute group decision-making based on linguistic Pythagorean fuzzy interaction partitioned Bonferroni mean aggregation operators. Complexity 1–24
Jun Y, Kim C, Yang K (2012) Cubic sets. Ann Fuzzy Math Inform 4(1):83–98
Kaur G, Garg H (2018) Multi-attribute decision-making based on Bonferroni mean operators under cubic intuitionistic fuzzy set environment. Entropy 20(1):65
Kaur G, Garg H (2018) Cubic intuitionistic fuzzy aggregation operators. Int J Uncertain Quan 8(5):405–427
Muneeza AS (2020) Multicriteria group decision-making for supplier selection based on intuitionistic cubic fuzzy aggregation operators. Int J Fuzzy Syst 22:810–823
Abdullah S, Aslam M (2020) New multicriteria group decision support systems for small hydropower plant locations selection based on intuitionistic cubic fuzzy aggregation information. Int J Intell Syst 35(6):983
Kaur G, Garg H (2019) Generalized cubic intuitionistic fuzzy aggregation operators using t-norm operations and their applications to group decision-making process. Arab J Sci Eng 44(3):2775–2794
Garg H, Kaur G (2019) TOPSIS based on nonlinear-programming methodology for solving decision-making problems under cubic intuitionistic fuzzy set environment. Comput Appl Math 38(3):114
Garg H, Kaur G (2018) Extended TOPSIS method for multi-criteria group decision-making problems under cubic intuitionistic fuzzy environment. Sci Iran 27(1):396–410
Jan N, Zedam L, Mahmood T (2019) Multiple attribute decision making method under linguistic cubic information. J Intell Fuzzy Syst 36(1):253–269
Fahmi A, Abdullah S, Amin F (2019) Cubic uncertain linguistic powered Einstein aggregation operators and their application to multi-attribute group decision making. Math Sci 13(2):129–152
Liu P, Khan Q, Mahmood T (2020) Group decision making based on power Heronian aggregation operators under neutrosophic cubic environment. Soft Comput 24(3):1971–1997
Mahmood T, Mehmood F, Khan Q (2016) Cubic hesistant fuzzy sets and their applications to multi criteria decision making. Int J Algebra Stat 5:19–51
Amin F, Fahmi A, Abdullah S (2019) Dealer using a new trapezoidal cubic hesitant fuzzy TOPSIS method and application to group decision-making program. Soft Comput 23(14):5353–5366
Fahmi A, Abdullah S, Amin F, Ahmed R, Ali A (2018) Triangular cubic linguistic hesitant fuzzy aggregation operators and their application in group decision making. J Intell Fuzzy Syst 34(4):2401–2416
Fu J, Ye J (2020) Similarity measure with indeterminate parameters regarding cubic hesitant neutrosophic numbers and its risk grade assessment approach for prostate cancer patients. Appl Intell. https://doi.org/10.1007/s10489-020-01653-z
Abbas S, Khan M, Abdullah S, Sun H, Hussain F (2019) Cubic Pythagorean fuzzy sets and their application to multi-attribute decision making with unknown weight information. J Intell Fuzzy Syst 37(1):1529–1544
Wang J, Shang X, Bai K, Xu Y (2020) A new approach to cubic q-rung orthopair fuzzy multiple attribute group decision-making based on power Muirhead mean. Neural Comput Appl 32:1–26
Hara T, Uchiyama M, Takahasi S (1998) A second-class of various mean inequalities. J Inequal Appl 2:387–395
Yager R (2001) The power average operator. IEEE Trans Syst Man Cybern A 31:724–731
Liu P, Khan Q, Mahmood T (2019) Application of interval neutrosophic power Hamy mean operators in MAGDM. Informatica 30:293–325
World Health Organization (2018) Noncommunicable diseases. https://www.who.int/news-room/fact-sheets/detail/noncommunicabale-diseases. Accessed 18 July 2020
Zhou Y (2011) Discussing the targets and methods of chronic diseases management. Chin Health Serv Manag 28(10):788–790
Acknowledgements
This work was supported by National Natural Science Foundation of China (Grant number 61702023), Humanities and Social Science Foundation of Ministry of Education of China (Grant number 17YJC870015), and the Beijing Natural Science Foundation (Grant number 7192107).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
We declare that there is no conflict of interests.
Ethical approval
This paper does not contain any studies with human participants or animals.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Xu, W., Shang, X. & Wang, J. Multiple attribute group decision-making based on cubic linguistic Pythagorean fuzzy sets and power Hamy mean. Complex Intell. Syst. 7, 1673–1693 (2021). https://doi.org/10.1007/s40747-020-00255-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40747-020-00255-z