A comparative study of social group optimization with a few recent optimization algorithms

Abstract

From the past few decades, the popularity of meta-heuristic optimization algorithms is growing compared to deterministic search optimization algorithms in solving global optimization problems. This has led to the development of several optimization algorithms to solve complex optimization problems. But none of the algorithms can solve all optimization problems equally well. As a result, the researchers focus on either improving exiting meta-heuristic optimization algorithms or introducing new algorithms. The social group optimization (SGO) Algorithm is a meta-heuristic optimization algorithm that was proposed in the year 2016 for solving global optimization problems. In the literature, SGO is shown to perform well as compared to other optimization algorithms. This paper attempts to compare the performance of the SGO algorithm with other optimization algorithms proposed between 2017 and 2019. These algorithms are tested through several experiments, including multiple classical benchmark functions, CEC special session functions, and six classical engineering problems etc. Optimization results prove that the SGO algorithm is extremely competitive as compared to other algorithms.

Introduction

The meta-heuristic optimization algorithm is a practical approach for solving global optimization problems. It is mainly based on simulating nature and artificial intelligence tools, invokes exploration and exploitation search procedures to diversify the search all over the search space and intensify the search in some promising areas. Flexibility and gradient-free approaches are the two main characteristics that make meta-heuristic strategies exceedingly popular for optimization researchers. From 1960s till date, several meta-heuristic optimization algorithms have been proposed. According to no-free-lunch (NFL) [1] theorem for optimization, none of the algorithms could solve all classes of optimization problems. This motivated many researchers to design new algorithms or modify/hybridize existing algorithms to solve different problems or provide competitive results, as compared to the current algorithms.

Meta-heuristic algorithms can be classified into mainly four categories: (a) evolutionary-based algorithm, (b) swarm intelligence-based algorithm, (c) human-based algorithm, and (d) physics and chemistry-based algorithm. Evolutionary algorithms mimic concepts of evolution in nature. The genetic algorithm (GA) [2] is the best example of an evolutionary algorithm that simulates the concepts of Darwinian theory of evolution. After that several other evolutionary algorithms have been proposed such as evolutionary strategy (ES) [3], and evolutionary programming (EP) [4], gene expression programming (GEP) [5, 6], genetic programming (GP) [7], covariance matrix adaptation evolution strategy CMA-ES) [8], differential evolution (DE) [9], biogeography-based optimization (BBO) algorithm [10].

Swarm intelligence algorithms mimic the intelligence of swarms. Each swarm consists of a group of creatures. So, these algorithms originate from the collective behaviour of a group of creatures in the swarm. Many swarm intelligence algorithms are seen in the literature. These are particle swarm optimization (PSO) [11] inspired by bird flocking, ant colony optimization (ACO) [12] inspired by Ants behaviour while collecting food, artificial bee colony (ABC) [13] mimicked by Honey bee for collecting nectar, etc. Additionally, there are many more algorithms such as bacterial foraging(BF) [14], bat algorithm (BA) [15], firefly algorithm (FFA) [16], krill herb (KB) [17], cuckoo search (CS) [18], monkey search (MS) [19], bee colony optimization (BCO) [20], cat swarm [21], wolf search (WS) [22], ant lion optimizer (ALO) [23], grey wolf optimization (GWO) [24], whale-optimization algorithm (WOA) [25], crow search algorithm (CSA) [26], Salp swarm algorithm (SSA) [27], grasshopper optimization algorithm (GOA) [28], butterfly optimization algorithm (BOA) [29], squirrel search algorithm (SSA) [30], Harris Hawks optimization (HHO) [31].

Human based algorithms are mainly inspired by behaviors of human. Some of the popular algorithms are teaching–learning-based optimization (TLBO) [32], harmony search (HS) [33], Tabu (Taboo) search (TS) [34,35,36], group search optimizer (GSO) [37, 38], imperialist competitive algorithm (ICA) [39], league championship algorithm (LCA) [40], firework algorithm [41], colliding bodies optimization (CBO) [42], interior search algorithm (ISA) [43], mine blast algorithm (MBA) [44], soccer league competition (SLC) algorithm [45], seeker optimization algorithm (SOA) [46], social-based algorithm (SBA) [47], exchange market algorithm (EMA) [48], and group counselling optimization (GCO) algorithm [49, 50], social emotional optimization (SEO) [51], ideology algorithm (IA) [52], social learning optimization (SLO) [53], social group optimization (SGO) [54, 55], election algorithm (EA) [56], cultural evolution algorithm (CEA) [57], cohort intelligence (CI) [58], anarchic society optimization (ASO) [59], volleyball premier league algorithm (VPL) [60], socio evolution and learning optimization algorithm (SELO) [61].

Physical and chemical based algorithms are inspired by physical rules and chemical reactions of the universe. Some popular algorithms are simulated annealing (SA) [62], gravitational local search (GLSA) [63], big-bang big-crunch (BBBC) [64], gravitational search algorithm (GSA) [65], charged system search (CSS) [66], central force optimization (CFO) [67], artificial chemical reaction optimization algorithm (ACROA) [68], black hole (BH) algorithm [69], ray optimization (RO) [70] algorithm, small-world optimization algorithm (SWOA) [71], galaxy-based-search algorithm (GbSA) [72], curved space optimization (CSO) [73], water cycle algorithm(WCA) [74]. Spiral optimization (SO) [75], river formation dynamics (RFD) [76], sine cosine algorithm (SCA) [77], multi verse optimizer (MVO) [78], lightning attachment procedure optimization (LAPO) [79], golden ratio optimization method (GROM) [80].

Meta-heuristic algorithms are extensively recognized as effective approaches for solving large-scale optimization problems (LOPs). These algorithms provide effective tools with essential applications in business, engineering, economics, and science. Recently, many researchers of meta-heuristic algorithm have paid their attention to the solution of large-scale optimization problems [81]. However, the standard metaheuristic algorithms for solving LOPs suffer from a main deficiency which is the curse of dimensionality, i.e., the performance of algorithms deteriorates when dimension of problems increases. There are two major reasons for the performance deterioration of these algorithms: Firstly, increasing size of the problem dimension increases its landscape complexity and characteristic alteration. Secondly, the search space exponentially increases with the problem size; so, an optimization algorithm must be able to explore the entire search space efficiently; which is not a trivial task. It is motivating to consider these reasons and difficulties while proposing new approaches of tackling LOPs [82]. The existing algorithms for LOPs can be mainly classified into the following two categories [83]: (1) the cooperative coevolution methods for LOPs, (2) the methods with learning strategies for LOPs. Since several real-world applications are considered as optimization of a large number of variables, various meta-heuristic algorithms have been proposed to handle the large-scale optimization problems [84,85,86,87,88,89].

In the real world, it is common to face an optimization problem with more than three objectives. Such problems are called many-objective optimization problems (MaOPs) that pose great challenges to the area of evolutionary computation. The failure of conventional Pareto based multi-objective evolutionary algorithms in dealing with MaOPs motivates various new approaches. Deb et al. [90] suggest a reference-point-based many-objective evolutionary algorithm following NSGA-II framework that emphasizes population members that are nondominated, yet close to a set of supplied reference points. This approach is applied to several many-objective test problems and gets satisfactory results to all problems [90]. Lin et al. propose a balanceable fitness estimation method and a novel velocity update equation to compose a novel multi-objective particle swarm optimization algorithm to address the (MaOPs) [91]. Achieving a balance between convergence and diversity in many-objective optimization is a great challenge. Liu et al. suggest an evolutionary algorithm based on a region search strategy that enhances the diversity of the population without losing convergence [92]. A hybrid evolutionary algorithm based on knee points and reference vector adaptation strategies (KnRVEA) is proposed to improve the convergence of solution where a novel knee adaptation strategy is introduced to adjust the distribution of knee points [93]. A new differential evolution algorithm (NSDE-R) capable of efficiently solving many-objective optimization problems, where the algorithms make use of reference points evenly distributed through the objective function space to preserve diversity and aid in multi-criteria-decision making was thus proposed [94]. Generally, the methods proposed for solving MaOPs can be roughly classified into three categories [95]. These are (1) multi/many-objective optimization algorithms based on dominance relationships. (2) multi/many-objective optimization algorithms based on decomposition strategy and (3) indicator-based evolutionary algorithms. The application of many-objective optimization can be demonstrated in stormwater management project selection, encouraging decision-maker buy-in [96]. Additionally, the application can also be seen in mixed-model disassembly line balancing along with multi-robotic workstation [97].

Many real-world optimization problems are challenging because the evaluation of solutions is computationally expensive. For those expensive problems, there are three kinds of models utilized in the meta-heuristic algorithms, i.e., the global model, the local model, and the surrogate ensembles [98]. Surrogate-assisted evolutionary algorithms are promising approaches to tackle this kind of problems. They use efficient computational models, known as surrogates, for approximating the fitness function in evolutionary algorithms. These are found successful applications not only in solving computationally expensive single or multi-objective optimization problems but also in addressing dynamic optimization problems, constrained optimization problems, and multi-modal optimization problems. Surrogate models have shown to be effective in assisting meta-heuristic algorithms for solving computationally expensive complex optimization problems. Examples of some surrogate-assisted optimization algorithms for expensive optimization problems can be found in [99,100,101,102,103].

In the year 2017–2019, some of the popular meta-heuristic algorithms were proposed. Those are Salp swarm algorithm (SSA), grasshopper optimization algorithm (GOA), lightning attachment procedure optimization (LAPO), golden ratio optimization method (GROM), butterfly optimization algorithm (BOA), squirrel search optimization algorithm (SSOA), Harris Hawks optimization (HHO), volleyball premier league algorithm (VPL), socio evolution and learning optimization algorithm (SELO). SGO algorithm was proposed in the year of 2016 by Satapathy et.al. The SGO algorithm is based on the social behavior of humans for solving a global optimization problem. Applications of the SGO algorithm are discussed in papers [104,105,106,107,108,109]. In this work, the authors plan to have an exhaustive comparative analysis with SGO, their own proposed algorithm, and algorithms that were developed from 2017 to 2019. The GOA algorithm mimics the behavior of grasshopper swarms and their social interaction. Applications of the GOA algorithm are elaborated in papers [110,111,112,113,114,115]. The SSA algorithm is inspired by the swarming behavior of salps when navigating and foraging in oceans. In [116,117,118,119,120,121], applications of SSA are highlighted. The LAPO algorithm is based on the concepts of the lightning attachment procedure. The application of LAPO is seen in paper [122,123,124,125]. The GROM algorithm is inspired by the golden ratio of plant and animal growth. The BOA algorithm mimics the food search and mating behavior of butterflies. The SSOA algorithm imitates dynamic foraging behavior of southern flying squirrels and their efficient way of locomotion. The HHO algorithm is based on cooperative behavior and the chasing style of Harris’ hawks in nature. The VPL algorithm is inspired by competition and interaction among volleyball teams during a season. It also mimics the coaching process during a volleyball match. The SELO algorithm is inspired by the social learning behavior of humans organized as families in a societal setup.

In this paper, we have compared the performance of those nine algorithms developed between 2017 and 2019, to SGO, which exhibit similar characteristics. These algorithms are tested through several experiments using many classical benchmark functions, CEC special session functions, and six classical engineering design problems. The results of the experiments are tabulated, and inferences are drawn in conclusion.

The remaining paper is organized as follows: In "Preliminaries of SGO, SSA, GOA, LAPO, GROM, BOA, SSOA, VPL, HHO, and SELO", all algorithms are briefly summarized. In "Simulation and experimental results", simulation and experimental results are discussed, and the paper concludes with "Conclusion".

Preliminaries of SGO, SSA, GOA, LAPO, GROM, BOA, SSOA, VPL, HHO, and SELO

Social group optimization (SGO) algorithm

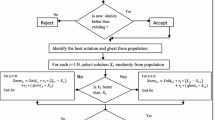
The SGO algorithm is based on the social behavior of human to solve complex problems. Each person represents a candidate solution empowered with some information (i.e., traits) and has an ability to solve a problem. The human traits represent the dimension of the person, which in turn represents the number of design variables of the problem. This optimization algorithm goes through two-phase: improving phase and acquiring phase. In the improving phase, an individual’s knowledge (solution) level is improved based on the best individual influence. In the acquiring phase, the individual’s knowledge (solution) level is improved by mutual interaction between individuals and the person who has the highest knowledge level, as well as the ability to solve the problem under consideration. However, for a detailed description of SGO, anyone's paper can be referred to [54, 55]. Algorithm 1 details the flow of SGO.

SSA, GOA, LAPO, GROM, BOA, SSOA, VPL, HHO and SELO algorithms

Preliminaries of the above-listed algorithms can be found in the literature. The SSA can be referred to in [27]; the basic of GOA is in [28], BOA is well described in [29]. The basic of SSOA is in [30]. The basic of HHO is in [31], and basic of VPL is in [60]. SELO, LAPO, and GROM can be followed in [61, 79, 80], respectively.

Simulation and experimental results

We have carried out an extensive comparison of SGO with the other nine algorithms. Individually, six experiments have been conducted batch-wise, on selecting a few algorithms out of nine algorithms; they are compared with SGO. Finally, in the last experiment, an overall comparison analysis is conducted with all nine algorithms with SGO. In the first experiment, the LAPO and GROM algorithms are compared with the SGO algorithm by considering twenty-nine benchmark functions in a combination of unimodal, multimodal, fixed dimensional and composite benchmark functions. In the second experiment, BOA is compared with the SGO algorithm using thirty classical benchmark functions. In the third experiment, SSOA is compared with the SGO algorithm using twenty-six classical benchmark functions, and seven functions are taken from the CEC 2014 special session. In the fourth experiment, VPL is compared with the SGO algorithm using twenty-three classical benchmark functions. In the fifth experiment, SELO is compared with the SGO algorithm using fifty classical benchmark functions. In the sixth experiment, HHO, SSA, and GOA algorithms are compared with the SGO algorithm using twenty-nine classical benchmark functions. The selections of the batch of algorithms are made based on the benchmark functions experiments which have been made by reference papers and the availability of results. In the seventh experiment, all algorithms are compared with each other by considering six classical engineering problems.

To compare the performance, the SGO algorithm is implemented by us and, the results of all other algorithms are taken from their respective papers (Fig. 1).

“For comparing the speed of the algorithms, the first thing we require is fair time measurement. The number of iterations or generations cannot be accepted as a time measure since the algorithms perform the different amount of works in their inner loops, and they have different population sizes (pop_sizes). Hence, we choose the number of fitness function evaluations (FEs) as a measure of computation time instead of generations or iterations” [54]. Since meta-heuristic algorithms are stochastic in nature, the results of two successive runs usually do not match. Hence, we have taken different independent runs (with different seeds of random number generator) of each algorithm and find out the best function value, mean function value, and standard deviation and put in tables in each experiment. For comparing the performance of algorithms, different tests have been conducted in experiments.

Fig. 1

Figure of benchmark functions

Experiment 1

In this experiment, LAPO and GROM algorithms are compared with the SGO algorithm. For comparison of the performance of algorithms, twenty-nine classical benchmark functions are considered. Out of which seven are unimodal benchmark-functions. The unimodal functions (F1–F7) are suitable for benchmarking the exploitation of algorithms since they have only one global optimum. Six are multimodal benchmark-functions and, ten are fixed-dimensional multimodal benchmark-functions. Each multimodal function from F8–F23 has massive numbers of local optima. These functions are considered to examine the exploration capability of algorithms. There are six composite benchmark functions. The composite benchmark-functions (F24–F29) are considered from CEC 2005 special session [126]. These benchmark functions are kept for judging the capability of the algorithm for the proper balance between exploration and exploitation search to avoid local optima and are described in Appendix A with illustrations in Fig. 2.

Fig. 2

a Schematic of the spring; b stress distribution evaluated at the optimum design; and c displacement distribution evaluated at the optimum design

In our experiment test functions are solved for two cases, low dimensional and high dimensional. SGO algorithm is implemented in MATLAB 2016a. Experiments are conducted on an Intel Core i5, 8 GB RAM, and Windows 10 environment. For the LAPO, results are taken from [79], and for the GROM algorithm, the results are taken from [80].

For low dimensional cases, the common control parameter such as pop_size is set to 40, maximum iteration is 500, and Max_FEs is set to 40,000. The other specific parameters for each algorithm are given below.

• SGO setting: For SGO, there is only one parameter C called a self-introspection factor. The value of C is empirically set to 0.2.

• LAPO settings: There is no such specific parameter to set value.

• GROM settings: There is no such specific parameter to set value.

For each benchmark function, algorithms are run 30 times with different randomly generated populations. Statistical results in terms of best value, mean value, and corresponding standard deviation are reported in tables. Table 1 is for unimodal benchmark-functions. Table 2 is for multimodal benchmark-functions. Table 3 is for fixed dimensional multimodal benchmark-functions and, Table 4 is for the composite benchmark.

Table 1 Unimodal benchmark function on 30 repetitions

Table 2 Multimodal benchmark function on 30 repetitions

Table 3 Fixed-dimensional multimodal benchmark function on 30 repetitions

Table 4 Composite benchmark function on 30 repetitions

For the high dimensional case, the 200-dimensional version of unimodal, multimodal functions are solved in two cases. In case 1, pop_size is taken as 200, and the maximum iteration is 2000, and the results are given in Table 5. In case 2, pop_size is taken as 40, and the maximum iteration is 500, and the results are given in Table 6. The idea is to see how the algorithms behave for high dimensions in a large population with more iteration, and relatively small populations with less iteration. For every benchmark function, the best results have been put in bold letters in the result table.

Table 5 Result 200 dimensional with population size 200 and 2000 iterations

Table 6 Result 200 dimensional with population size 40 and 500 iterations

Table 7 Overall algorithms comparison on Wilcoxon’s rank-sum test using Tables 1, 2, 3 and 4

Table 8 Overall algorithms comparison of Wilcoxon’s rank-sum test using Tables 5 and 6

To obtain statistically sound conclusions, Wilcoxon's rank-sum (WRS) test at a 0.05 significance level is conducted on experimental results, and the last three rows of each respective table summarize experimental results.

Discussion

The unimodal functions have only one global optimum. These functions allow evaluating the exploitation capability of the investigated meta-heuristic algorithms. As seen in Table 1, SGO has gained the best performance, and it has reached to first rank among other algorithms. SGO has shown excellent performance in exploitation capability and convergence characteristic. It has also successfully overcome to solve all the problems within this category except F5. It is clear from results that SGO achieves success in finding global optimum on F1, F2, F3, and F4 within 40,000 max_FEs. For F1, F2, F3, F4, F6, F7, the performance of SGO is better than LAPO and GROM algorithm, whereas, for F5, the performance of LAPO and GROM algorithm is far better than SGO. From Table 1, we find that out of seven unimodal test functions according to the WRS test, SGO performs superior to LAPO and GROM in six test functions and worse in one test function.

The multimodal functions test functions F8–F13 are beneficial, while the exploration capability of the optimization algorithm is considered. Form Table 2, results show that the SGO algorithm is eligible for solving problems with challenging search space. In this case, SGO has demonstrated excellent performance in comparison, and it has reached to first rank among algorithms. Table 2 shows that SGO has consistently performed better than other algorithms. SGO has an excellent performance in exploration, and it successfully overcomes to solve all the problems within this category. It is clear from table results that both SGO and GROM achieve success in finding global optimum on F9 and F11, and for F10, find equivalent results. From Table 2, we get that out of six multimodal test functions according to the WRS test, SGO performs superior to LAPO in all six test functions and superior to GROM in three test functions and equivalent in three test functions.

The fixed-dimensional multimodal functions are designed to have many local optimal where computation complexity increases drastically with the increase of the problem size. The results reported from Table 3 for functions F14-F23 indicate that SGO has an excellent exploration capability except for the shekel family (F21, F22, F23) that SGO has. It is clear from tabular results that the SGO algorithm achieves success in finding a global optimum on F14–F20. In contrast, GROM achieves success in F16–F19, F21–F23, and LAPO achieves success in F4, F16, F18, and F19 in finding a globally optimal solution. GROM achieves success in finding an optimum solution on the shekel family only. The results for LAPO on the shekel family are better than the SGO algorithm. From Table 3, as per WRS test, we find that out of ten fixed dimensional multimodal test functions, SGO performs superior to LAPO in two test functions, worse in three test functions, and equivalent with five tests functions. Again SGO performs superior to GROM in two test functions, worse in three test functions and equivalent with five test functions.

The composite functions are well enough to judge the ability to escape from local minima of a meta-heuristics optimization algorithm. Optimization of composite mathematical functions is a challenging task because only a proper balance between exploration and exploitation allows local optima to be avoided. The results in Table 4 show that none of the algorithms achieve success in finding the global optimal solution. However, LAPO and GROM find a superior solution than then SGO algorithm in solving F24, F25, and F28, whereas SGO finds superior solution then LAPO and GROM in solving F26, F27, and F29 benchmark functions. From Table 4, it is seen that out of six composite test functions according to the WRS test, SGO performs superior to LAPO and GROM in three test functions, worse in three test functions.

In Tables 5 and 6, seven unimodal and six multimodal functions are considered for judging high dimensional parameter optimizations among SGO, LAPO, and GROM algorithm by considering 200 dimensions. Table 5 is for the results of pop_size 200 and 2000 iteration, and Table 6 is for the results of pop_size 40 and iterations 500. It is clear from both tables that SGO achieves success in finding global optimum on F1, F2, F3, F4, F9, and F11 in both cases. GROM achieves success in finding global optimum on F9 and F11 in both cases. GROM and SGO find equivalent results on F10 for both cases. SGO algorithm finds better results than GROM on F1–F8, F12, and F13 in both cases. In the first case, the LAPO algorithm achieves success on finding global optimum for F9 and F11, it finds equivalent results as of SGO for F10, and worse results on F1–F8, F12 and F13 compared to SGO. However, SGO algorithm finds superior results compared to LAPO for all benchmark functions F1-F13 in the second case. Hence, from Table 5 we summarize that as per the WRS test, SGO performs superior to LAPO and GROM in ten test functions and equivalent on three tests out of thirteen test functions. And from the Table 6, as per the WRS test, SGO performs superior to LAPO in all thirteen test functions and superior to GROM in ten test functions and equivalent with three test functions out thirteen test functions.

Experiment 2

In this experiment, BOA (butterfly optimization algorithm) [29] is compared with the SGO algorithm. For comparison of the performance of algorithms, 30 classical benchmark functions are considered. These benchmark functions are described in appendix B. These functions are chosen from the benchmark set proposed in [127, 128] to determine various features of the algorithm, such as fast convergence, attainment of a large number of local minima points, ability to jump out of local optima and avoid premature convergence. BOA results are taken from paper [29], and for results of the SGO algorithm, the codes are implemented in MATLAB 2016a. Experiments are conducted on an Intel Core i5, 8 GB RAM, and Windows 10 environment.

For the BOA algorithm, according to parameter setting in its paper [29], the common control parameter such as pop_size and maximum iterations are 50 and 10,000, respectively. But for the SGO algorithm, we have taken the same pop_size, but maximum iteration is reduced to 500. This is due to our observation of the fast convergence characteristic of SGO. Max_FEs is set to 50,000 (2 $\times \hspace{0.17em}$50 $\times \hspace{0.17em}$500 = 50,000). It is due to two times fitness calculation in one iteration for one particle in population. In this experiment, we have done two tests. In one test, we have set common control parameters the same as above, and in other, we have set pop_size is ten and maximum iteration 500. So Max_FEs is set to 10,000 (2 $\times \hspace{0.17em}$10 $\times \hspace{0.17em}$500 = 10,000). The other specific parameters for each algorithm are given below.

• SGO setting: For SGO, there is only one parameter C called a self-introspection factor. The value of C is empirically set to 0.2.

• BOA settings: Modular modality c is 0.01, and power exponent a is increased from 0.1 to 0.3 throughout iterations, p = 0.8. These parameters are set as reported by authors in paper [29].

For each benchmark function, algorithms are run 30 times with different randomly generated populations. Statistical results in terms of mean value, standard-deviation value, the best value, median value, and worse value are reported in tables. Table 9 provides results for test 1 with 50,000 max_FEs, and Table 10 presents results for test 2 with 10,000 max_FEs. For every benchmark function, the best results are boldfaced.

Table 9 Comparison on BOA and SGO on 30 independent runs with 50,000 fitness function evaluations

Table 10 Comparison of BOA and SGO on 30 independent runs with 10,000 fitness function evaluations

To obtain statistically sound conclusions, Wilcoxon’s rank-sum test at a 0.05 significance level is conducted on experimental results of Tables 9, 10 and put in Table 11. The comparison results in terms of best value also are given in Table 11. The last three rows of Table 11 summarize experimental results.

Table 11 Wilcoxon rank test result and the comparison result on the best value between BOA and SGO

Discussion

In Tables 9 and 10, for the function F22, in the place of best value, worse value, and median value, we have put star ‘*’ because we think that these values are wrongly put in the paper [29]. For the function F28, the minimum function value is given as − 1500 [29]. But the BOA algorithm finds less than that − 1500 and hence a confusion arises on the minimum value. To avoid any conflicts, we have excluded this result and have put ‘*’ in Table 11. From Table 11, we see that except for the F5 function, both Tables 9 and 10 show equivalent results. From Tables 9 and 10, it is clear that SGO algorithm reaches global optimum for 22 benchmark functions such as F1–F4, F6, F8, F11–F13, F15–F24, F26, F27, F29 whereas BOA reaches to global optimum for 18 benchmark functions such as F1–F4, F6, F11–F13, F15–F17, F19, F21–F24, F27, F29. SGO also shows its dominating performance in most functions and satisfactory results in 10 functions such as F7, F8, F9, F10, F14, F18, F20, F25, F26, and F30. For function F26, i.e., shekel 4.5, the BOA algorithm finds superior results than the SGO algorithm. Special attention should be paid to the noisy (quartic) problems as these challenges frequently occur in real-world applications. SGO provided a significant performance boost on this noisy problem and gave an equivalent solution in comparison to BOA, but the best result is better than BOA’s best result. It is shown in Table 9. Besides optimization accuracy, convergence speed is quite essential to an optimizer. In this experiment, Table 9 provided the results on 50,000 max_FES with 500 iterations as the termination criterion. Table 10 provided the results on 10,000 max_FES with 500 iterations as the termination, whereas for BOA 10,000 iterations as the termination criterion.

For Test 1, i.e., from Tables 9 and 11, according to the WRS test, it is clear that the SGO algorithm finds better results than the BOA algorithm in nine functions and equivalent results in 19 functions out of 29 benchmark functions. So only in one case, SGO finds worse results than BOA. For test 2, i.e., from Tables 10 and 11, the SGO algorithm performs better than the BOA algorithm in nine functions and equivalent results in 18 functions out of 29 benchmark functions. So only in two cases, the SGO algorithm finds worse results than the BOA algorithm. Similarly, when we compare the results by considering the best results, we find that SGO performs best in ten functions and equally well for 18 functions than BOA in both tests.

From the above experiment and results in discussion, it is found that SGO outperformed than BOA, and the convergence is much fast as it is evident from the maximum numbers of FEs and iterations.

Experiment 3

In this experiment, SSOA (squirrel search optimization algorithm) [30] is compared with the SGO algorithm. For comparison of performances of both the algorithms, 33 benchmark functions are considered. Out of these, 26 functions are classical benchmark functions, and seven are taken from CEC 2014 special session [129]. These benchmark functions are described in Appendix C. These benchmark functions are also described in the paper [30] and taken from [130, 131]. Out of these 26 classical benchmark functions, four are unimodal separable benchmark functions, eight are unimodal non-separable benchmark functions, six are multimodal separable benchmark functions, and eight are multimodal non-separable benchmark functions.

We have directly derived results of SSOA from [30], and for results of the SGO algorithm, the codes are implemented in MATLAB 2016a. Experiments are conducted on Intel Core i5, 8 GB RAM, and Windows 10 environment.

According to parameter settings of SSOA in its respective paper [30], the common control parameter such as pop_size is 50, and the maximum iteration is 500. For seven CEC2014 benchmark functions, pop_size is 50, and the maximum iteration is 6000. So max_FEs is 300,000. So for the SGO algorithm, we have taken pop_size is 25, and the maximum iteration is 500. Hence max_FEs are 25,000(2 $\times \hspace{0.17em}$25 $\times \hspace{0.17em}$500 = 25,000, two is due to two-time fitness calculation in one iteration for one particle in population) for classical benchmark functions, and pop_size is 50, and maximum iteration is 3000. So max_FEs is 300,000 (2 $\times \hspace{0.17em}$50 $\times \hspace{0.17em}$3000 = 300,000) for CEC2014 benchmark functions.

The other specific parameters for each algorithm are given below.

• SGO setting: For SGO, there is only one parameter C called a self-introspection factor. The value of C is empirically set to 0.2.

SOA settings: nutritious food resources ${N}_{\mathrm{fs}}$ = 4, gliding constant ${G}_{\mathrm{c}}$ = 1.9 and predator presence probability ${P}_{\mathrm{dp}}$ = 0.1. Parameters are set as reported by authors in paper [30].

For each benchmark function, algorithms are run 30 times with different randomly generated populations. Statistical results in terms of mean value, corresponding standard-deviation, the best value, and worse value are reported in tables. Table 12 indicates the test results for unimodal separable benchmark functions. Table 13 reports the test results for unimodal non-separable benchmark functions. Table 14 reports the test results for multimodal separable benchmark functions. Table 15 reports the test results for multimodal non-separable benchmark functions, and Table 16 reports the test results for CEC2014 functions. For every benchmark function, the best results are boldfaced.

Table 12 Comparison on SSOA and SGO on 30 independent runs on unimodal separable benchmark functions

Table 13 Comparison on SSOA and SGO on 30 independent runs on unimodal nonseparable benchmark functions

Table 14 Comparison on SSOA and SGO on 30 independent runs on multimodal separable benchmark-functions

Table 15 Comparison on SSOA and SGO on 30 independent runs on multimodal nonseparable functions

Table 16 Comparison on SSOA and SGO on 30 independent runs on CEC 2014 benchmark-functions with 30 dimension

Table 17 Wilcoxon rank test result and comparison result on best value between SSOA and SGO

To obtain statistically sound conclusions, the WRS test at a 0.05 significance level is conducted on the experimental results of Tables 12, 13, 14, 15, 16 and reported in Table 17. A comparison of the best results obtained in Tables 12, 13, 14, 15, 16, also published in Table 17. The last three rows of Table 17 summarize experimental results.

Discussion

It is clear from Table 12 that the SGO achieves success in finding global optimum on unimodal separable functions F1, F2, and F3. For F1, the performance of the SSOA is found identical to the SGO. Only for F4, the SGO could not reach the global optimum region but find better results than the SSOA.

Table 13 provides results on unimodal non-separable functions. It is clear from the table that the SGO achieves success in finding global optimum on functions F5, F6, F7, F9, F10, F11, but the SSOA achieves success in finding global optimum only on F6. For F6 only, the performance of SSOA is found identical to the SGO. Only for F8 and F12, SGO could not reach the global optimum region. For the F8 function, SSOA finds a better result than SGO, and for F12 SGO, find a better result than SSOA.

It is clear from Table 14 that the SGO achieves success in finding global optimum on multimodal separable functions F13, F14, F15, F18, but SSOA achieves success in finding only on F13 and F15. For F13 and F15, the performance of SSOA is found identical to SGO. For F16 and F17, SGO could not reach the global optimum region but find better results than the SSOA.

It is clear from Table 15 results that the SGO achieves success in finding global optimum on multimodal non-separable functions F19, F20, F21, F22, F23, F25, but the SSOA achieves success in finding only on F20, F21, F22, and F23. Only for F24 and F26, SGO could not reach the global optimum region. For F24, SSOA finds better results, and for F26, SGO finds a better result.

It is clear from Table 16 that SGO finds a better solution in F27, F28, F29, then SSOA, whereas SSOA finds better in F30 and F31 then SGO, and in F32 and F33, both SGO and SSOA finds equivalent results.

From Table 17, according to the WRS test, we find that the SGO algorithm performs superior solutions in three cases, equivalent solution in one case out of four unimodal separable benchmark functions than the SSOA algorithm. Out of eight unimodal non-separable benchmark functions, the SGO algorithm performs superior solutions in six cases, equivalent solution in one case and worse solution in one case than the SSOA algorithm. Out of six multimodal separable benchmark functions, the SGO algorithm performs superior solutions in four cases, an equivalent solution in two cases than the SSOA algorithm. Out of eight multimodal non-separable benchmark functions, the SGO algorithm performs superior solutions in three cases, equivalent solution in four cases, worse solution in one case than the SSOA algorithm. Out of seven CEC2014 benchmark functions, the SGO algorithm performs superior solutions in three cases, equivalent solutions in two cases, and worse solutions in two cases than the SSOA algorithm.

While comparing in terms of best solution value between SGO and SSOA algorithm, then the SGO algorithm performs better in three cases and similar to SSOA algorithm in one case, out of four unimodal separable benchmark functions. The SGO algorithm is better performing in six cases, one case being similar, and one case giving worse solution than SSOA algorithm out of eight unimodal non-separable benchmark functions. The SGO algorithm is better in two cases and similar to the SSOA algorithm in four cases, out of six multimodal separable benchmark functions. The SGO algorithm is better in one case, similar in six cases and gives worse solution than SSOA algorithm in one case, out of eight multimodal non-separable benchmark function. The SGO algorithm is better in three cases and gives similar solution with SSOA algorithm in four cases, out of seven CEC2014 benchmark functions.

Experiment 4

In this experiment, the VPL (volleyball premier league) algorithm [60] is compared with the SGO algorithm. For performance comparison of algorithms, 23 classical benchmark-functions are considered. Out of which seven are unimodal benchmark-functions, six are multimodal benchmark-functions, ten are fixed-dimension multimodal benchmark-functions. These benchmark-functions are described in Appendix A.

We have directly derived results of the VPL algorithm from [60], and for results of the SGO algorithm, the codes are implemented in MATLAB 2016a. Experiments are conducted on an Intel Core i5, 8 GB memory laptop in Windows 10 environment.

According to parameter settings of the VPL algorithm in its respective paper [60], the common control parameter, such as max_FEs, is 100,000. So, for the SGO algorithm, common control parameters such as pop_size are set to 50, and maximum iteration is set to 1000. So max_FEs is 2 $\times$ 50 $\times$ 1000 = 100,000. The other specific parameters for each algorithm are given below.

• SGO setting: For SGO, there is only one parameter C called a self-introspection factor. The value of C is empirically set to 0.2.

• VPL setting: For VPL L = 60, PC = 0.5, rate of promoted ${\delta }_{\mathrm{Pr}} =0.05$, ${\delta }_{\mathrm{st}} =0.54$, N = 10, and $\beta=7$.

Parameters are set as reported by authors in paper [60].

For each benchmark-function, algorithms are run 30 times with different randomly generated populations. Statistical results in terms of mean value, corresponding standard-deviation, the best value, and worse value are reported in tables. Table 18 reports the test results for unimodal benchmark functions. The test results for multimodal benchmark functions are reported in Table 19. Table 20 reports the test result for fixed dimensional multimodal benchmark functions. For every benchmark function, the best results are boldfaced.

Table 18 Result of unimodal benchmark functions

Table 19 Result of multimodal benchmark functions

Table 20 Results on fixed-dimensional benchmark functions

To obtain statistically sound conclusions, the WRS test at a 0.05 significance level is conducted on the experimental results of Tables 18, 19, 20 and reported in their respective tables. Also, comparisons on the best results are obtained and are given in the respective table also. The last three rows of tables summarize experimental results.

According to Table 18, SGO has gained the best performance and consistently performed better than VPL algorithms. SGO has an excellent performance in exploitation and convergence then VPL, and it successfully overcomes to solve all the problems within this category. It is clear from the results that SGO achieves success in finding global optimum on F1–F4. For F5, F6, and F7, the performance of SGO is better than VPL.

From Table 18, we find that in all the cases of unimodal benchmark functions according to the WRS test, the SGO algorithm shows better performance than the VPL algorithm. Similarly, comparison on best results obtained by algorithms, we find that the SGO algorithm gets either the best result than the VPL algorithm or similar result with the VLP algorithm. From the table, it is evident that the SGO algorithm outperforms in solving unimodal benchmark functions in comparison to VPL algorithms.

In Table 19, there is ‘*’ mark in the first row with the result of the VPL algorithm to say that the result may be put wrongly as the minimum value of the F8 function is − 12,569.487. But we get less than that in the paper and hence a confusion arising on the minimum value. To avoid any conflicts, we have excluded this result and have put ‘*’ in Table 19. So, for comparison, we have considered only five multimodal functions. The multimodal functions are beneficial, while the exploration capability of the optimization algorithm is considered. Form Table 19, results show that the SGO algorithm is eligible for solving problems with challenging search space. The table shows that SGO has consistently performed better than VPL algorithms. SGO has an excellent performance in exploration and convergence, and it successfully overcomes to solve all the problems within this category. It is clear from table results that both SGO and VPL achieve success in finding global optimum on F9 and F1. For F10, both SGO and VPL get equivalent results. For F12 and F13, the SGO algorithm finds better results than the VPL algorithm. According to the WRS test from Table 19, we find that in two out of five cases, SGO algorithm shows better performance than the VPL algorithm and similar in three out of five cases with the VPL algorithm. Similarly, comparison on best results obtained by algorithms, we get that the SGO algorithm either gets the best result than the VPL algorithm or similar result to the VPL algorithm. Hence, we find that the SGO algorithm shows best performance in solving multimodal benchmark functions in comparison to VPL algorithms.

In Table 20, there is ‘*’ mark with the result of the VPL algorithm to say that there, the result might be put wrongly as the minimum value of the F15 function is 3.0749e−04. But we get different values in the paper and hence a confusion arising on minimum value. To avoid any conflicts, we have excluded this result and have put ‘*’ in Table 20. The fixed-dimensional multimodal functions are designed to have many local optimal where computation complexity increases drastically with the problem size. The results reported from Table 20 shows that the SGO algorithm achieves success in finding global optimum on F14, F15, F16, F17, F18, and F19.

In contrast, VPL reaches optimal solution only for F14, F16, F17, and F18. For shekel family, i.e., for F21, F22 and F23 VPL finds better result than SGO algorithm. From Table 20, according to the WRS, we find that out of ten cases, SGO algorithm shows better performance in three cases and similar performance in four cases than the VPL algorithm In contrast, the VPL algorithm shows its better performance in three cases out of ten than the SGO algorithm. Similarly, comparison on best results obtained by algorithms, we find that the SGO algorithm either gets the best result than the VPL algorithm or similar result with the VLP algorithm except for two cases. Hence, we can see that the VPL algorithm shows best performance in solving fixed dimensional multimodal benchmark functions in comparison to SGO algorithms.

Experiment 5

In this experiment, SELO (socio evolution and learning optimization) [61] algorithm is compared with the SGO algorithm. For comparison of the performance of algorithms, a set of 50 benchmark functions are considered. These set of test functions include problems of varying complexity levels, such as unimodal, multimodal, separable, and non-separable [132,133,134]. All benchmark test problems are divided into four categories, such as unimodal separable (US), multimodal separable (MS), unimodal non-separable (UN), and multimodal non-separable (MN). Also, the range, formulation, characteristics, and dimensions of these problems and listed in paper [61].

We have directly derived results of the SELO algorithm from [61], and for results of the SGO algorithm, the codes are implemented in MATLAB 2016a. Experiments are conducted on an Intel-Core-i5, 8 GB memory laptop in Windows 10 environment.

According to parameter settings of the SELO algorithm in its respective paper [61], the common control parameter, such as a maximum number of iterations, is 70,000. In this experiment for each function, the SGO algorithm is tested twice. So, in the first test, we have considered pop_size 50, and the maximum iteration is 250. Hence Max_FEs is (2 $\times$ 50 $\times$ 250 = 25,000), and in the second test, we have found pop_size is 20, and the maximum iteration is 50, so maximum Max_FEs is (2 $\times$ 20 $\times$ 50 = 2,000). The other specific parameters for each algorithm are given below.

• SGO setting: For SGO, there is only one parameter C called a self-introspection factor. The value of C is empirically set to 0.2.

• For SELO initial number of families created M = 03, number of parents in each family p = 02, number of children in each family = 03, parent_follow_probability ${r}_{\mathrm{p}}$= 0.999, follow_prob_ownparent = 0.999,peer_follow_probability ${r}_{\mathrm{k}}$ = 0.1, follow_prob_factor _otherkids = 0.9991 and sampling interval reduction factor r  = 0.95000 to 0.99995. Parameters are set as reported by authors in paper [61].

For each benchmark-function, algorithms are run 30 times with different randomly generated populations. Statistical results in terms of mean value, corresponding standard deviation, and best value are reported in Table 21. The table reports the results corresponding to SGO(1) with (2 × 50 × 250) Max_FEs and results corresponding to SGO(2) with (2 × 20 × 50) Max_FEs. In this experiment values below 1 ${\mathrm{E}}^{-16}$ are considered to be zero. For every benchmark function, the best results are boldfaced.

Table 21 Comparison on SELO and SGO on 30 repetitions

To obtain statistically sound conclusions, the WRS test at a 0.05 significance level is conducted on experimental results of Table 21 for both SGO(1) and SGO(2) and reported in the same table. The last three rows of the table summarize results.

Discussion

According Table 21, SGO algorithm achieves success in finding global optimum on F1, F5, F11, F14–F18, F25, F30, F33, F35, F36, F37, F38, F42–F47, F50 functions and near-global optimum for functions F2, F19, F20, F21, F26. For function F3, F4, F6, F12, F13, F14, F19, F21, F22, F27, F28, F29, F36, F37, F48, F49, SGO finds better results than SELO algorithm. For F23, F24, F31, F34, F39, F40, F41 function SELO finds better results than SGO algorithm.

In Table 21, there is ‘*’ mark with the result of the SELO algorithm for the function F14 and F26 to say that there the result might be put wrongly as the minimum value of F14 function is − 1, and minimum value for F26 is − 1.801303410098554. To avoid any conflicts, we have excluded this result and have put ‘*’ in Table 21. From Table 21, according to the WRS test, we find that in 19 cases out of 50 cases SGO(1) algorithm shows better performance than the SELO algorithm and similar to 24 cases out of 50 cases with the SELO algorithm. In contrast, the SELO algorithm shows its better performance in 7 cases out of 50 than the SGO (1) algorithm. Similarly, we find that in 19 cases out of 50 cases SGO (2) algorithm shows better performance than SELO algorithm and similar with 20 cases out of 50 cases with SELO algorithm. In contrast, the SELO algorithm shows its better performance in eleven cases out of 50 than the SGO (2) algorithm.

Hence, we find that the SGO algorithm shows superior performance than the SELO algorithm in this experiment. However, max_FEs for SGO is much less than max_FEs for SELO algorithm, i.e. (25,000 FEs in SGO(1) < 70,000 iterations) and (2000 FEs in SGO(2) < 70,000 iterations). So we can claim that the SGO algorithm outperformed than SELO algorithm in Experiment 5.

Experiment 6

In this experiment, HHO (Harris hawks optimization) [31], SSA (Salp swarm algorithm) [27], GOA (grasshopper optimisation algorithm) [28] and SGO (Social Group optimization) [54] algorithm are compared together. For comparison of the performance of algorithms, a set of 29 benchmark functions are considered. Details of these benchmark functions are given in experiment 1.

We have directly derived results of the HHO algorithm from [31], and the results of the SGO algorithm, SSA algorithm, and GOA algorithm, the codes are implemented in MATLAB 2016a. The source code for the SSA algorithm and GOA algorithm is taken from https://www.alimirjalili.com/SSA.html and https://www.alimirjalili.com/GOA.html, respectively. Experiments are conducted on an Intel-Core−i5, 8 GB memory laptop in Windows 10 environment.

According to parameter settings of the HHO algorithm in its respective paper [31], the common control parameter, such as a maximum number of iterations is 500, and Pop_size is 30. So, for the GOA algorithm and SSA algorithm, the maximum number of iteration and pop_size is set to 500 and 30, respectively. For the SGO algorithm, the maximum number iteration is set to 250.and pop_size is set 30. Hence max_FEs for SGO (2 × 30 × 250) are the same with other algorithms. The other specific parameters for each algorithm are given below.

• SGO setting: For SGO, there is only one parameter C called a self-introspection factor. The value of C is empirically set 0.2.

• SSA settings: For SSA, there is a parameter ${c}_{1}$ = 2 ×${\mathrm{e}}^{-{(\frac{4}{L})}^{2}}$, where L = max_iteration = 500 as in [27]

• GOA settings: For GOA, ${c}_{\mathrm{max}}$=1, ${c}_{\mathrm{min}}$ =0.00004 for finding value of c = ${c}_{\mathrm{max}}\hspace{0.17em}$− l × ((${c}_{\mathrm{max}}-\hspace{0.17em}{c}_{\mathrm{min}}$)/Max_iter), Max_iter = 500 as in [28]

• HHO setting: referred to paper [31].

In this experiment, all algorithms are utilized to tackle scalable unimodal and multimodal F1–F13 test cases with 30, 100, 500, and 1000 dimensions. For each benchmark-function, algorithms are run 30 times with different randomly generated populations. Statistical results in terms of mean value, corresponding standard-deviation are reported in tables. Table 22 reports the result for 30 dimensions. Table 23 reports the result for 100 dimensions. Table 24 reports the result for 500 dimensions. Table 25 reports the result for 1000 dimensions, and Table 26 reports the result for fixed dimensional multimodal and composite benchmark functions. For every benchmark function, the best results are boldfaced.

Table 22 Comparison result on HHO, SSA, GOA, and SGO on 3O repetitions on 30 dimension

Table 23 Comparison result on HHO, SSA, GOA and SGO on 3O repetitions on 100 dimension

Table 24 Comparison result on HHO, SSA, GOA and SGO on 3O repetitions on 500 dimension

Table 25 Comparison result on HHO, SSA, GOA, and SGO on 3O repetitions on 1000 dimension

Table 26 Comparison result on HHO, SSA, GOA and SGO on 3O repetitions on fixed-dimensional and composite benchmark functions

To obtain statistically sound conclusions, the WRS test at a 0.05 significance level is conducted on experimental results of Tables 22, 23, 24, 25 and 26 and reported in their respective tables. The last three rows of each respective table summarize experimental results.

Discussion

According to Tables 22, 23, 24 and 25, SGO has gained the best performance and consistently performed better than SSA and GOA algorithms. SGO has an excellent performance in exploitation as well as an exploration than SSA and GOA algorithms. It is clear from the results that SGO achieves success in finding global optimum on F1, F3, F9, and F11. HHO algorithm makes success in finding global optimum for the function F9 and F11. For F5, F6, F8, F12, F13, the performance of HHO is better than SSA, GOA, and SGO, whereas, for F1, F2, F3, F4, F7, the performance of SGO is better than HHO, SSA, and GOA. For F19, F10, and F11, both HHO and SGO find equivalent solutions.

From Table 22, according to the WRS test, we find that the SGO algorithm performs superior to the HHO algorithm in five cases, equivalent with four cases out of 13 in 30-dimensional functions. Similarly, the SGO algorithm performs superior to the SSA algorithm in 12 cases and from the GOA algorithm in 13 cases out of 13. In contrast, the HHO algorithm performs superior to the SGO algorithm in four cases, and the SSA algorithm performs superior to SGO in one case. Hence it is seen that the SGO algorithm is outperforming than HHO, SSA, and GOA algorithm in solving 30-dimensional benchmark functions. From Table 23, according to the WRS test, we find that the SGO algorithm performs superior to the HHO algorithm in five cases, equivalent with three cases out of 13 in 100-dimensional functions.

Similarly, the SGO algorithm performs superior to the SSA algorithm in 13 cases and from the GOA algorithm in 13 cases out of 13. In contrast, the HHO algorithm performs superior to the SGO algorithm in five cases. Hence it is seen that both SGO and HHO algorithms are performing equivalent performance, and both SGO and HHO algorithms are outperforming than SSA and GOA algorithm in solving 100-dimensional benchmark functions. From Table 24, according to the WRS test, we find that the SGO algorithm performs superior to the HHO algorithm in five cases, equivalent with three cases out of 13 in 500-dimensional functions. Similarly, the SGO algorithm performs superior to the SSA algorithm in 13 cases and from the GOA algorithm in 13 cases out of 13. In contrast, the HHO algorithm performs superior to the SGO algorithm in five cases. Hence it is seen that the SGO algorithm is performing equivalent performance with the HHO algorithm and outperforming than SSA and GOA algorithm in solving 500-dimensional benchmark functions. From Table 25, according to Wilcoxon’s rank-sum test, we find that the SGO algorithm performs superior to the HHO algorithm in five cases, equivalent with three cases out of 13 in 1000 dimensional functions. Similarly, the SGO algorithm performs superior to the SSA algorithm in 13 cases and from the GOA algorithm in 13 cases out of 13, whereas the HHO algorithm performs superior to the SGO algorithm in five cases. It is seen that the SGO algorithm is performing equivalent performance with the HHO algorithm and outperforming than SSA and GOA algorithm in solving 1000-dimensional benchmark functions.

The fixed-dimensional multimodal functions are designed to have many local optimal where computation complexity increases drastically with the problem size. The results reported from Table 26, it is clear that the SGO algorithm achieves success in finding an optimal solution for functions F14, F16, F17, F18, F19, and F20. Similarly, the GOA algorithm makes success in finding an optimal solution for functions F14, F16, F17, and F18. SSA algorithm finds success for function F16–F19. HHO algorithm finds success for function F14, F16–F20, F22–F23. For the shekel family, the HHO algorithm finds superior solutions than SSA, GOA, and SGO algorithm.

The composite functions are well enough to judge the ability to escape from local minima of meta-heuristics optimization algorithms. The results from Table 26, it is clear that the SSA algorithm finds a superior solution for F24, F25, F26, and F28, and for F27 and F29, GOA finds superior solution than other algorithms. The performance of the HHO algorithm for solving composite benchmark functions is worse than other algorithms.

From Table 26, according to the WRS test, we find that the SGO algorithm performs superior to the HHO algorithm in six cases, equivalent with seven cases out of 16 benchmark functions. Similarly, the SGO algorithm performs superior to the SSA algorithm in six cases, equivalent with five cases out of 16 benchmark functions. SGO algorithm performs superior to the GOA algorithm in ten cases, equivalent with four cases out of 16 benchmark functions. Whereas the HHO algorithm performs superior to the SGO algorithm in three cases, the SSA algorithm performs superior to SGO in five cases, and the GOA algorithm performs superior to SGO in two cases. Hence it is seen that the SGO algorithm is outperforming performance than HHO, SSA and GOA algorithm in solving ten fixed dimensional multimodal and six composite benchmark functions.

Experiment 7: on classical engineering problem

In this experiment, we have applied all the algorithms such as LAPO, GROM, BOA, SSA, VPL, HHO, SELO, SSOA, GOA, and SGO algorithm for solving classical engineering problems. Here we have considered six classical engineering problems. These are.

Tension/compression spring design problem

The objective of this test problem is to minimize the weight of tension/compression spring shown in Fig. 2 [135, 136]. The optimum design must satisfy constraints on shear stress, surge frequency, and deflection. There are three design variables: wire diameter (d), mean coil diameter (D), and many active coils (N). The formulated optimization problem is given in Appendix D.

The optimization result of all algorithms for the compression spring design problem is given in Table 27. The result of LAPO algorithm is reported from paper [79], for GROM the result is reported from [80], for BOA the result is reported from [29], for VPL the result is reported from [60], for HHO the result is reported from [31], for SSA the result is taken reported from [27] and result for SGO is found by us. “NA” stands for an experiment that is not conducted for that algorithm. The best result is represented in boldface. From the table, we find that the BOA algorithm outperforms than all other algorithms.

Table 27 Comparison of tension/compression spring design problem

The welded beam design problem

The objective of this test problem is to minimize the fabrication cost of the welded beam shown in Fig. 3 [137]. Optimization constraints are on shear stress (τ), and bending stress in the beam (θ), buckling load (Pc), end deflection of beam (δ). There are four optimization variables: the thickness of the weld (h), length of clamped bar (l), the height of the bar (t), and thickness of the bar (b). The formulated optimization problem is given in Appendix D.

Fig. 3

Welded beam design problem: a schematic of the weld; b stress distribution evaluated at the optimum design; c displacement distribution at the optimum design

The optimization result of all algorithms for Welded beam design problem is given in Table 28. The result of LAPO algorithm is reported from paper [79], for GROM the result is reported from [80], for BOA the result is reported from [29], for VPL the result is reported from [60], for HHO the result is reported from [31], for SSA the result is reported from [27]. The result for SGO is found by us. “NA” stands for an experiment that is not conducted for that algorithm. The best result is represented in boldface. From the table, we find that the SGO algorithm outperforms than all other algorithms.

Table 28 Comparison of Welded beam design problem

Pressure vessel design problem

This problem goal is to minimize the total cost (material, forming, and welding) of cylindrical pressure vessels shown in Fig. 4 [25]. Both ends of the vessel are capped while the head has a hemispherical shape. There are four optimization variables: the thickness of the shell (${T}_{\mathrm{s}}$), the thickness of the head (${T}_{\mathrm{h}}$), inner radius (R), length of the cylindrical section without considering head (L). The formulated optimization problem is given in Appendix D.

Fig. 4

Pressure vessel design problem: a schematic of the vessel; b stress distribution evaluated at the optimum design; and c displacement distribution evaluated at the optimum design

The optimization result of algorithms for the pressure vessel design problem is given in Table 29. The result of the LAPO algorithm is reported from paper [79], for the GROM the result is reported from [80], for the VPL the result is reported from [60], for HHO the result is reported from [31] and result for SGO is found by us. A “NA” stand for the experiment is not conducted for that algorithm. The best result is represented in boldface. From table, we find that the SGO algorithm outperforms all other algorithms.

Table 29 Comparison of pressure vessel design problem

Cantilever beam design problem

In this problem, the goal is to minimize the weight of a cantilever beam with hollow square blocks. There are five squares of which the first block is fixed, and the fifth one burdens a vertical load, box girders, and lengths of those girders are design parameters for this problem. This cantilever beam design is shown in Fig. 5 [78]. The formulated optimization problem is defined in Appendix D.

Fig.5

Cantilever beam design

The optimization result of algorithms for cantilever beam design problem is given in Table 30. The result of LAPO algorithm is reported from paper [79], for GROM the result is reported from [80], for VPL the result is taken from [60], for SSA the result is reported from [27], for GOA the result is reported from [28] and result for SGO is found by us. “NA” stands for the experiment are not conducted for that particular algorithm. The best result is represented in boldface. From the Table, we get that the SGO algorithm outperforms than all other algorithms.

Table 30 Results for cantilever beam design problem

Gear train design problem

The objective of Gear train design problem is to minimize gear ratio where gear ratio is calculated as by Eq. 1:

$$ {\text{Gear}}\;{\text{ratio}} = \frac{{\text{angular velocity of output shaft}}}{{\text{angular velocity of input shaft}}}. $$

(1)

This problem has four parameters. The parameters of this problem are discrete with an increment size of 1 since they define teeth of the gears $({n}_{\mathrm{A}},{n}_{\mathrm{B}},{n}_{\mathrm{C}},{n}_{\mathrm{D}})$. These constraints are only limited to the ranges of the variables. This Gear train design is shown in Fig. 6 [78]. The formulated optimization problem is defined in Appendix D.

Fig. 6

Gear train design

The optimization result of algorithms for the gear train design problem is given in Table 31. The result of the LAPO algorithm is reported from paper [79]. For GROM, the result is reported from [80], for BOA, the result is reported from [28], the result for SGO is found by us. “NA” stands for the experiment is not conducted for that particular algorithm. The best result is represented by boldface. From the table, we get that all the algorithms perform equally.

Table 31 Comparison results for gear train design problem

Three-bar truss design problem

Here the objective is to design a truss with a minimum weight that does not violate constraints. A most important issue in designing truss is constraints that include stress, deflection, and buckling constraints. Figure 7 [78] shows the structural parameters of this problem. The formulated design problem is given in Appendix D. We can see that the objective function is quite simple, but it is subject to several challenging constraints. This truss design problems are prevalent in the literature of meta-heuristics [138, 139]

Fig. 7

Three-bar-truss design

The optimization result of algorithms for the three-bar-truss design problem is given in Table 32. The result for the HHO algorithm is reported from paper [31], for SSA, the result is reported from [27], for GOA, the result is reported from [28], the result for SGO is found by us. “NA” stands for the experiment are not conducted for that algorithm. The best result is represented in boldface. From the Table, we get that the SGO algorithm outperforms than all other algorithms.

Table 32 Results of the three-bar truss design problem

Overall conclusion

This section applies all the algorithms such as LAPO, GROM, BOA, SSA, VPL, HHO, SELO, SSOA, GOA, and SGO algorithm for solving benchmark functions as well as classical engineering problems. From the above experiments, we conclude that the performance of the SGO algorithm is worse than other algorithms while solving Rosenbrock's benchmark function, shekel family benchmark function, i.e., shekel 2, shekel 5, and shekel 7. While solving composite benchmark functions, SSA (Salp swarm algorithm) is superior, and the HHO algorithm is worse than other algorithms. On solving high dimensional and classical engineering problems, the SGO algorithm is superior to other algorithms.

Conclusion

As we know, meta-heuristic optimization algorithms are more popular than deterministic search optimization algorithms in solving global optimization problems, and several optimization algorithms are proposed to solve global optimization problems. The exploration search and exploitation search are two important factors related to meta-heuristic optimization methods. These two factors are in contrast with each other. In other words, focusing too much on local search, i.e., exploitation may result in getting stuck in local optimum points, and too much focusing on global search, i.e., exploration, may cause the low quality of the final best answer. So an algorithm should be in the form that it can balance in between and find out an optimal solution to the problem. Free-Lunch theorem for optimization says that none of the optimization algorithms can solve all optimization problems and makes this area of research open. So, researchers improve/adapt the current algorithms for solving different problems or propose new algorithms for providing competitive results compared to the existing algorithms. As a result, a number of optimization algorithms have been proposed from a few decades to till date. It is difficult to compare all algorithms or challenging to say, which is the best because none of the algorithms can solve all optimization problems. In this paper, we have considered ten algorithms SGO, LAPO, GROM, BOA, SSOA, VPL, HHO, SELO, GOA, and SSA those are proposed in the year 2017–2019 except SGO as SGO is proposed in the year of 2016, and have conducted seven experiments by considering a different type of problems such as mathematical classical optimization problems, CEC global optimization problems, and six classical engineering design problems. We have seen that the SGO algorithm has shown its superior performance in comparison to all other algorithms in solving problems in each experiment. Still, while addressing Rosenbrock benchmark function and shekel family benchmark function, i.e., shekel 2, shekel 5, and shekel 7, the performance of SGO is not so well in comparison to other algorithms. One of the best things we see in SGO is that the performance does not deteriorate as the dimension of the problem increases, and at the same time, it can find an optimum result in less fitness evaluation. As further research, we improve the performance of the SGO algorithm by balancing between exploration and exploitation search so that it can find the optimal solution of benchmark function like shekel family and other. Also, we compare SGO performance with newly proposed optimization algorithms, solving the problem of large-scale optimizations and multi-objective optimizations.

Appendices

Appendix A

See Tables 33, 34, 35, and 36.

Table 33 Unimodal benchmark functions

Table 34 Multi-modal benchmark functions

Table 35 Fixed –dimensional multimodal benchmark functions

Table 36 Composite functions

Appendix B

See Tables 37.

Table 37 Benchmark functions used in butterfly optimization algorithm

Appendix C

See Tables 38, 39, 40, 41 and 42.

Table 38 Unimodal separable function

Table 39 Unimodal nonseparable function

Table 40 Multimodal separable function

Table 41 Multimodal nonseparable function

Table 42 Brief description of CEC 2014 benchmark functions

Appendix D

Welded beam design problem

Min $f\left({x}_{1},{x}_{2},{x}_{3},{x}_{4}\right)=1.10471{x}_{1}^{2}{x}_{2}+0.04811{x}_{3}{x}_{4}\left(14.0+{x}_{2}\right)$

Subject to:

$${g}_{1}\left(X\right)={x}_{1}-{x}_{4}\le 0$$

$${g}_{2}\left(X\right)=\delta -0.25\le 0$$

$${g}_{3}\left(X\right)=\tau -13600\le 0$$

$${g}_{4}\left(X\right)=\rho -30000\le 0$$

$${g}_{5}\left(X\right)=0.10471{x}_{1}^{2}+0.04811{x}_{3}{x}_{4}\left(14.0+{x}_{2}\right)-5\le 0$$

$${g}_{6}\left(X\right)=0.125-{x}_{1}\le 0$$

$${g}_{7}\left(X\right)=6000-F\le 0$$

where the variables satisfy 0.1 $\le {x}_{1}$, ${x}_{4}\le 2.0$ and 0.1 $\le {x}_{2}$, ${x}_{3}\le 10$.

$$\rho =50400/{x}_{3}^{2}{x}_{4}$$

Q = 6000(14 + ${x}_{2}/2)$

D = $\frac{1}{2}\sqrt{{x}_{2}^{2}+{\left({x}_{1}+{x}_{3}\right)}^{2}}\beta =\frac{QD}{J}$

J = $\sqrt{2}{ x}_{1}{x}_{2}$ (${x}_{2}^{2}/6$+${({x}_{1}+{x}_{3})}^{2}/2$)

$$\delta =65856/3000{x}_{3}^{3}{x}_{4}\alpha =6000/(\sqrt{2}{ x}_{1}{x}_{2})$$

$$\tau =\sqrt{{\alpha }^{2}+\frac{\alpha \beta {x}_{2}}{D}+{\beta }^{2}}$$

F = 0.61423 $\times {10}^{6}\frac{{x}_{4}^{3}{x}_{3}}{6}(1-\frac{{x}_{3}\sqrt{30/48}}{28})$

Pressure vessel design problem

Min $f\left({x}_{1},{x}_{2},{x}_{3},{x}_{4}\right)=0.6224{x}_{1}{x}_{2}{x}_{3}+1.7881{x}_{2}{x}_{3}^{2}$+3.1661 ${x}_{4}{x}_{1}^{2}$+19.84 ${x}_{3}{x}_{1}^{2}$

Subject to:

$${g}_{1}\left(X\right)=-{x}_{1}+0.0193{x}_{3}\le 0$$

$${g}_{2}\left(X\right)=-{x}_{2}+0.0954{x}_{3}\le 0$$

$${g}_{3}\left(X\right)=-{\pi {x}_{3}^{2}x}_{4}-\frac{4}{3}\pi {x}_{3}^{2}+1296000\le 0$$

$${g}_{4}\left(X\right)={x}_{4}-240\le 0$$

where the variables satisfy 0 $\le {x}_{1},{x}_{2}\le 100$ and 10 $\le {x}_{3},{x}_{4}\le 200$.

Tension/compression spring design problem

Min $f\left({x}_{1},{x}_{2},{x}_{3}\right)=({x}_{3}+2){x}_{1}^{2}{x}_{2}$

Subject to:

$${g}_{1}\left(X\right)=1-\frac{{x}_{2}^{2}{x}_{3}}{71785{x}_{1}^{4}}\le 0$$

$${g}_{2}\left(X\right)=\frac{{x}_{2}(4{x}_{2}-{x}_{1})}{12566{x}_{1}^{3}({x}_{2}-{x}_{1})}+\frac{1}{5108{x}_{1}^{2}}-1\le 0$$

$${g}_{3}\left(X\right)=1-\frac{140.45{x}_{1}}{{x}_{2}^{2}{x}_{3}}\le 0$$

$${g}_{4}\left(X\right)=\frac{2({x}_{2}+{x}_{1})}{3}-1\le 0$$

where the variables satisfy 0.05 $\le {x}_{1}\le$ 2, 0.25 $\le {x}_{2}\le$ 1.3 and

2 $\le {x}_{3}\le 15.$

Gear train design problem

Min $f\left({x}_{1},{x}_{2},{x}_{3},{x}_{4}\right)$=${(\frac{1}{6.931}-\frac{{x}_{3}{x}_{2}}{{x}_{1}{x}_{4}})}^{2}$

Variable range 12 $\le {x}_{1},{x}_{2},{x}_{3},{x}_{4}\le$ 60

Three-bar truss design problem

Min $f\left({x}_{1},{x}_{2}\right)=\left(2\sqrt{2}{x}_{1}+{x}_{2}\right)\times l$

Subject to:

$${g}_{1}\left(X\right)=\frac{\sqrt{2}{x}_{1}+{x}_{2}}{\sqrt{2}{x}_{1}^{2}+2{x}_{1}{x}_{2}}P-\sigma \le 0$$

$${g}_{2}\left(X\right)=\frac{{x}_{2}}{\sqrt{2}{x}_{1}^{2}+2{x}_{1}{x}_{2}}P-\sigma \le 0$$

$${g}_{3}\left(X\right)=\frac{1}{\sqrt{2}{x}_{1}^{2}+2{x}_{1}{x}_{2}}P-\sigma \le 0$$

Variable range 0 $\le {x}_{1},{x}_{2}\le$ 1

Where $l$ =100 cm. P = 2 KN/c${\mathrm{m}}^{2} \sigma =2 \mathrm{KN}/$c${\mathrm{m}}^{2}$

Cantilever beam design problem

Min $f\left({x}_{1},{x}_{2},{x}_{3},{x}_{4},{x}_{5}\right)=0.6224\left({x}_{1}+{x}_{2}+{x}_{3}+{x}_{4}+{x}_{5}\right)$

Subject to:

$${g}_{1}\left(X\right)=\frac{61}{{x}_{1}^{3}}+\frac{27}{{x}_{2}^{3}}+\frac{19}{{x}_{3}^{3}}+\frac{7}{{x}_{4}^{3}}+\frac{1}{{x}_{5}^{3}}-1\le 0$$

Variable range 0.$01\le {x}_{1},{x}_{2},{x}_{3},{x}_{4},{x}_{5}\le$ 100.