A robust system maturity model for complex systems utilizing system readiness level and Petri nets

Abstract

System development can be plagued with excessive cost and schedule delay. During the system development lifecycle process, the development team makes difficult decisions concerning where to allocate project resources. As systems become more complex, and budgets are more constrained, understanding how to make these decisions becomes more problematic. To assist in the system development lifecycle process, this research introduces a new system maturity model called Petri net system readiness level (PNSRL). PNSRL integrates the fundamentals of System Readiness Level (SRL) and Petri nets (PNs) to create a more robust system view that can be used to analyze and score the readiness of system-of-system architectures. Integrations between technologies are expanded using PN transitions, to offer integration relationships. System workflow can be visualized with PNSRL, which can lead to system model validation utilizing PN tokens. PNSRL expands SRL mathematical equations by including PN capacities, which are used to weight each sub-system’s importance based on the number of interconnections associated. This article will illustrate how to use the PNSRL model by creating a functional system view for system readiness calculations. PNSRL is graphically and mathematically compared to the latest SRL model, Incidence Matrix System Readiness Level (IMSRL), to show how PNSRL represents all system components when calculating system readiness and produces a more accurate readiness value. Guidelines for PNSRL token and capacity allocation are offered, to assist in the system validation process using reachability graphs. Project managers and systems engineers can use this model to accurately depict their system and more precisely calculate technology maturity through the system development lifecycle. This model can aid in the system resource allocation decision process and allows further understanding of how the system’s key components operate.

Introduction

The United States Government Accountability Office (GAO) states in the 2016 Selected Weapon Program Assessment that only 7% of programs began system development with completely mature technologies [1]. The GAO also states that, on average, programs that do not show fully mature technologies prior to development and do not conduct systems engineering reviews will carry unwanted risk into subsequent phases of acquisition that could result in cost growth or schedule delays [1]. With the introduction of the Technology Readiness Level (TRL), system maturity could be quantified to help generate helpful assessments and determine a system’s maturity before that system’s deployment in the operational environment [2]. TRL helped to provide the baseline of readiness level measurement, which is still used today. With systems becoming more complex, however, the older methods of readiness level measurement are inefficient and fall short [3].

Newer system assessment tools, such as System Readiness Level (SRL), utilize TRL and provide a more complete and accurate maturity assessment [4]. SRL provides a graphical and mathematical way to determine the maturity of a system, and its status within the system development lifecycle [4, 5]. Over the years, SRL has continued to grow into a powerful system management tool, allowing managers and systems engineers to assess system development in near real-time, and take proactive measures accordingly [5]. SRL has evolved from the original model developed by Systems Development and Maturity Laboratory (SD&ML) at Stevens Institute of Technology to the latest Incidence Matrix SRL (IMSRL) model created from the doctoral research of London et al. at George Washington University [3, 4].

SD&ML has described the use of SRL through different use cases, such as defining component rank using an importance measurement score, and strategic decision making using an optimized resource algorithm [6, 7]. Even though the importance of SRL has been proven, the fundamental foundation of the current SRL model could be further enhanced by expanding the underlining component structure. The research presented in this article will demonstrate how the inclusion of Petri nets (PNs) can enhance SRL to create a new system maturity model called Petri net system readiness level (PNSRL). PNSRL improves the depiction and use of integrations between components, and offers a better graphical representation of sub-system inner workings. Since SRL relies on graph theory, the improved functional graphical representation provides more accurate component information for the mathematical readiness calculations. Utilizing PNs, the PNSRL model can be validated using tokens in reachability graph analysis and can simulate system process workflow. Additionally, PNSRL offers a newer SRL equation utilizing PN capacities to weight component importance based on the number of integrations attached.

Current readiness level models

TRL is a method of measuring the maturity levels of Critical Technology Elements (CTEs) in a system [8]. TRL was originally created by NASA in the 1970s, and has evolved into a more useable system maturity assessment tool over the years [9]. It has been widely adopted since its conception. Generally, it consists of a scale from 1 to 9, from less mature to more mature, respectively [9]. However, research by SD&ML suggests that TRL does not properly identify the full system-level maturity [4, 9].

SD&ML originally developed SRL in 2006 to overcome the shortcomings of TRL [9]. SRL uses a combination of TRL and IRL to produce a new metric that determines system readiness [4]. SRL expanded upon TRL by adding integrations with associated integration readiness levels (IRLs), which act as a bridge between the CTEs and focus on the interfaces and interactions of the CTEs [4, 9]. IRLs provide a way to assess the risk of integration besides TRL, which only assesses the technologies themselves [4, 5, 9]. Similar to TRL, IRL uses a scale from 1 to 9, from less mature to more mature, respectively.

SRL is based on graph theory and uses a nodal diagram to express the TRL and IRL values [9]. Once constructed, mathematical equations can output integration technology readiness level (ITRL) for individual technologies and a composite SRL value for the entire system. This enables managers to evaluate system development in real time and take proactive measures by examining the status of all elements of the system simultaneously [5]. SRL uses a scale of values from 0.10 to 1.00, from less mature to more mature, respectively [3,4,5, 9]. Table 1 describes the SRL scale that maps the SRL values to acquisition phases in the system development lifecycle [4, 5, 9].

Table 1 SRL scale developed by SD&ML [4, 5, 9]

SRL has evolved over the years from the original SD&ML SRL (SSRL) model. Newer SRL models include Graph Theory SRL (GTSRL), Topical Algebra SRL (TASRL) and IMSRL. Each SRL model consists of a distinct system view and an SRL calculation methodology. Every SRL model builds off of its predecessor to continue to evolve SRL into a better tool. Table 2 describes the differences between the SRL models.

Table 2 SRL model comparison overview [3,4,5, 9,10,11]

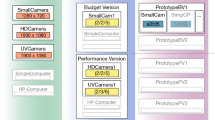
Each SRL model relies on a strictly defined system view. The PNSRL model further expands SRL by incorporating PNs into the development of the graphical representation. Figure 1 illustrates each SRL system view, including the research offered in this article.

Fig. 1

SRL model graphical representation comparison [3,4,5, 9,10,11]

Each system view represents a graphical enhancement to its predecessor. The SSRL model first created a basic node structure with circles representing technologies, and lines representing integrations [4]. The GTSRL model expands the SSRL model by incorporating direction into the integrations [10]. The TASRL model uses the same system view as GTSRL, but a different SRL equation [11]. IMSRL evolves the GTSRL system view by defining integrations using an incidence matrix and eigenvalues, enabling an unlimited number of integrations between technologies [3]. The PNSRL model, defined in this article, utilizes a PN to illustrate the system view, enabling integration relationships and system validation. The PNSRL graphical representation uses the classical definition of PNs. To understand the PNSRL model, PNs must be defined.

Petri nets

PNs were originally invented in 1962 by Dr. Carl Petri to describe chemical processes [12]. Over the years, researchers have found that PNs are powerful in modeling events graphically and mathematically [13]. A PN is a directed graph used to model events and states in a distributed system [12,13,14]. Graphically, PNs can provide a visual aid detailing system processes and flow [14]. Mathematically, PNs can provide the ability to set up state equations, algebraic equations, and other models governing the behavior of a system [14]. PNs are a powerful mechanism to bridge the gap between theory and practice [14]. In addition, there are many tools to help create and validate PNs, such as the Platform Independent Petri Net Editor (PIPE) [15].

PNs consist of places and transitions that are connected via arcs [12, 13]. A place symbolizes a condition with a finite capacity, and is graphically represented by a circle [12, 13]. Transitions are graphically illustrated by bars and represent events [12, 13]. The transitions show the interactions between the places [12, 13]. Arcs are directed arrows showing flow and are found between places and transitions or vice versa. However, arcs are never between two places or two transitions; places and transitions are disjointed [12, 13]. The arcs running from places to transitions are described as inputs and arcs running out from transitions to places are described as outputs [12,13,14]. Places and transitions can have zero or more inputs and zero or more outputs [12, 13].

The behavior of the system is defined by states [16]. States are represented by a snapshot in time of the system using tokens [16]. Tokens are small dots or marks of quantity k that signify that k resources are available [16]. Places contain a finite space and restrict the number of tokens that can be placed at any time [12,13,14]. Tokens cannot be put into places that have reached their maximum capacity [16]. Transitions can take the number of tokens equal to the weight of the inputs before firing [16]. The firing of a transition means that the transition is enabled and tokens flow through the transition from input places to supply tokens to connecting output places [16]. This process is non-interruptible and nondeterministic [16]. However, firing can be inhibited by transitions if the input places do not supply the minimum number of tokens equal to the input arc weights [16]. Once the k number of tokens at the input places satisfy the combined weight k of the input arcs, the transition can fire [16]. Once the transition is fired, k number of tokens are removed from the input places and transformed into the output of the transition [16]. The outputs of a transition utilize tokens corresponding to the weight of the output arcs and happen concurrently [12]. Input tokens and output tokens from a transition correspond to their arc weights, so the number of input tokens can change when they become output tokens [16]. A transition will also be delayed if a place connected to the transition’s output is at maximum capacity [16].

Petri net system readiness level (PNSRL) model

PNs allow a system to be treated similar to a workflow, which is typically how a system operates. In the current SRL models, integrations are created at a high level with a one-to-one methodology, but integrations between systems are not so simple. System integrations can occur synchronously or asynchronously, be halted or delayed by other interactions, and can show relationships with other integrations. However, current SRL models fail to offer these integration relationships. PNs can provide a detailed view of the inner workings of the system, and how the sub-systems communicate with each other. This research combines PNs and SRL to create PNSRL, which offers a more robust graphical view, the ability to validate the system model, and offers an SRL mathematical equation that utilizes PN capacities. First, the system view needs to be graphically represented using a PN.

PNSRL graphical representation

PNs and current SRL system views are both bipartite graphs. The distinct parts of the SRL view and PNs are comparable and can be seen as having a direct relationship to one another. SRL technologies and PN places are similar, as they represent the CTEs of the overall system. Moreover, the SRL integrations and PN transitions are similar, as they represent interconnections between the CTEs. However, the SRL view can only show an integration as a single connection between two technologies, suggesting only that some types of connection exist. They do not show relationships to more than two technologies, nor relationships to other integrations. PNs can enable more robust integrations using transitions, showing a deeper connection between technologies and integrations. PN transitions are split into two parts, inputs and outputs. Transitions are designed to take any number of associated inputs, and create any number of outputs. If applied to integrations, this could allow for a higher level of system understanding of how integrations can relate to each other.

PNSRL utilizes the places as the CTEs and the transition as a split of the IRL. For a basic integration with no relationship to other integrations, a single transition could be used with the same IRL value for both the transition input and output. For this type of integration, little benefit is seen by utilizing a transition. However, if an integration has relationships to other integrations, PNs offer the only way to recognize these associations and use this important information both graphically and mathematically. Figure 2 shows an example of a nuclear reactor system creating electricity, comparing the IMSRL and PNSRL model.

Fig. 2

Nuclear reactor example using IMSRL and PNSRL [18, 19]

A nuclear reactor operates by combining heat from a reactor with water from a condenser, which will produce steam for a turbine to generate electricity. In this example, the IMSRL graphical representation illustrates each CTE with integrations between them [3]. However, the IMSRL model fails to demonstrate how the system operates, which could affect how system maturity is calculated. By utilizing a PN, the nuclear reactor workflow can be visualized to offer a better graphical representation of the system inner-workings.

The main difference between the IMSRL system view and the PNSRL PN is the construction of the integrations. A transition displays all integrations as inputs and outputs, utilizing arcs [12,13,14]. The transition describes an event, where the input arcs collectively trigger an action that causes a change of state, and output arcs are the result of that action [20]. For example, the steam generator is one of the key components in the nuclear reactor. Steam generators require heat from the reactor and water from the condenser to produce steam. The steam generator can only operate when the reactor and the condenser function together. This means that both the reactor and the condenser have a relationship and the steam generator requires both technologies in order to run. In the IMSRL model, there are separate integrations from the reactor and condenser to the steam generator. Because each integration is separate, this offers the assumption that the steam generator could operate using only the reactor or only the condenser. The PNSRL model expands this relationship by creating a transition, illustrated as t3, which uses both the reactor and condenser integrations as input arcs, shown as $\varepsilon _{6}$ and $\varepsilon _{7}$. An output arc, shown as $\varepsilon _{9,}$ is generated using an IRL value equal to the average value of the input arcs’ IRL values. This method is used to show that the output arc could only reach full maturity once all input arcs reach full maturity. An input arc’s maturity can have a direct influence to output arc’s maturity.

In this example, the transition t3 has two output arcs. Output arc $\varepsilon _{9}$ was generated by the input arc’s relationship, and output arc $\varepsilon _{8}$ is a loopback arc to the control rods. This loopback arc shows that the control rods need to regulate the reactor after the system produces steam with the steam generator. Since an IRL value was already determined, the IRL value for $\varepsilon _{8}$ stays the same. The IRL value for $\varepsilon _{8}$ was originally determined independently from the input IRL values, but the PNSRL model shows that this integration should be affected by the maturity of the $\varepsilon _{6}$ and $\varepsilon _{7.}$ The PNSRL model offered in this article only distinguishes a basic level of integration relationship, seen as the average of all input arcs’ IRL values. Relationships between integrations have the potential of being more complex. Project managers and system engineers should take into account different types of relationships and distinguish the maturity of integrations according to their system. The PNSRL model offers a basic way to determine IRL values for indeterminate integration relationships.

Transition t6 describes a sink transition. A sink transition is a transition that can consume tokens but does not create them [14]. Transition t6 represents how the generator produces power for other systems. This type of transition is important for this example when producing a reachability graph for model validation.

Both the IMSRL and PNSRL graphical representation illustrate all system components. PNSRL offers a more robust functional graphical view that can illustrate system workflow and can be validated. To further enhance the graphical representation of the system, PNSRL can utilize PN tokens and place capacities.

PNSRL token and capacity assignment

Since PNSRL creates a PN, tokens can be used to step through the systems functionality, ensuring system completeness [16, 20]. Capacities are weighted values for places that distinguish how many tokens can reside at a place [16, 20]. These capacities can be used to show technology importance based on the number of integration arcs connected. PNs also offer weights to arcs, which can demonstrate integration importance. In the current PNSRL model, all transition arcs have a weight of one, meaning all transitions are equally important. Since PNSRL is a collection of technologies and integrations, rather than a workflow, it is difficult to gauge where to place starting tokens and how to assign capacities. Based on this research, the following rules are recommended to be used as guidelines when placing starting tokens and applying capacities for the PN described in this article.

• 1. Tokens exist at a place that has one or more input arcs to a transition, and no output arcs from other places. A place that has any self-looping transition, and no other output arcs, may receive tokens. The quantity of tokens is equal to the number of input arcs going from the token accepting place to transitions.

• 2. If there is an enclosed looping sub-system with no outside influence from output arcs, tokens can be assigned at the place with the largest capacity. The number of tokens assigned will equal to the capacity of that place. If all places have the same capacity, tokens can be assigned to any place in the self-looping sub-system.

• 3. The capacity of a place equals the number of output arcs connected to it. If no output arcs connect, the capacity of the place will be 1. If the place has starting tokens, the capacity of the place is equal to the number of assigned tokens or number of output arcs, whichever is greater.

• 4. Weight of all arcs is 1.

Figure 3 shows the nuclear reactor example in Fig. 2, using the token and capacity allocation rules outlined above.

Fig. 3

Nuclear reactor example PNSRL token and capacity allocation [2, 5, 6, 11, 13]

Capacities and tokens were allocated to the nuclear reactor, seen in Fig. 3. Capacities are assigned to each place equal to the number of output arcs connected, third rule stated above. For this example, all capacities are equal to 1, except the Condenser. Since the Condenser has multiple output arcs entering the technology, the capacity is increased to accommodate the additional token flows. Tokens are allocated to the Control Rods and Cooling Towers as they represent the initial state of the system. The Cooling towers have no output arcs from other places, and only contains the self-looping output arc. The Cooling Towers satisfy the first rule described above. The Control Rods have output arcs from other places, but the system it receives its tokens is an enclosed looping sub-system. This means that the control rods will only receive tokens from itself or the reactor, and all tokens produced by this sub-system are preserved. Using the second rule described above, a token could be assigned to the Control Rods or the Reactor, since both places have equal capacities. No other place satisfies the first two rules for token assignment, so no other tokens will exist at the initial state of the system.

The sink transition t6 represents a transition that consumes tokens but does not produce them [14]. When the Generator contains a token, t6 will fire and consume that token. This token is not preserved, allowing the Generator to acquire more tokens from the turbine. Without this sink transition, the PN would backup and fill all places with tokens very quickly. The nuclear reactor is a self-looping system that requires itself to continually run. Instead of a sink transition, the Generator place could have been allocated an unlimited capacity. However, based on how a generator operates, a sink transition was used to describe how the generator produces power rather than stores it.

After designating the tokens and assigning capacities to places, the system can be validated for correctness using a reachability graph [12, 13]. Using the basic rules of reachability graphs for PNs, the PN can be validated [12, 13]. Figure 4 shows the reachability graph for the nuclear reactor PNSRL example. Tools such as PIPE, will create a reachability graph and ensure all states have been reached, confirming validity of the PN [15]. Past models, like IMSRL, have no way to validate the graphical model to ensure that all technologies can be reached in the system.

Fig. 4

Nuclear reactor example reachability graph based on the PNSRL model, illustrated in PIPE [15]

In total, there are 72 reachable states, with no end states. The end state, called the tangible state, is a state where tokens can no longer flow through the PN. For the nuclear reactor example, there is a never-ending token flow where only vanishing states exist. Vanishing states are a finite set of unique states where tokens can continue to flow. The nuclear reactor is a self-looping system, meaning it continues to run and tokens never stop flowing. With the model validated using tokens and capacities, an ITRL and composite SRL value can be calculated.

Capacity PNSRL equation

As systems become larger and more intricate, the composite SRL and ITRL equations become more complex. The prior SRL models, from SSRL to IMSRL, rely on matrix math to calculate system readiness [3, 4, 10, 11]. SSRL and GTSRL utilize pairwise matrix multiplication, TASRL uses Min-Plus topical algebra, and IMSRL uses Min–Min topical algebra [3,4,5, 9,10,11]. In 2012, Kujawski proved that matrix multiplication of ordinal TRL and IRL data elements produces inaccurate computations of system readiness [17]. In doctoral research conducted by McConkie et al. in 2013, a solution was created by employing Min-Plus topical algebra instead of pairwise matrix multiplication [11]. To further enhance the SRL system view, doctoral research by London et al. employed an incidence matrix to allow for an infinite number of integrations [3]. This research calculated ITRL and a composite SRL using a Min–Min topical algebra approach [3]. The Min–Min topical algebra approach calculates SRL as the minimum IRL or TRL value contained in the system [3]. In a way, this can be seen as displaying the worst-case SRL scenario for the system. However, this approach creates a problem when the technologies and integrations begin to become more mature. Since Min–Min topical algebra calculates the lowest TRL or IRL score, the entire system is always reduced to the lowest value regardless of maturity of other components [3]. Using a weighted average to calculate ITRL and the composite SRL value can produce a better readiness value by allowing all system components to have an effect on the readiness values.

PNSRL utilizes the eigenvalue concept of Incidence Matrices, defined by the IMSRL model, to allow for an infinite number of integrations between technologies [3]. Instead of using a matrix for these values, PNSRL uses an array of arrays for IRL values. Each sub-array consists of all integration IRL values that exist for a specific technology. The length of each sub-array equals to the number of integrations attached to a specific technology and varies among each sub-array. Another array holds all the TRL values associated with each technology. Capacity for each place is defined in an additional array. Both the IRL and capacity array lengths equal to the length of the TRL array. Capacity is used to describe the weight of the technology associated with each integration.

Using the nuclear reactor example in Fig. 2, the IRL, TRL, and capacity arrays can be created.

$$\begin{aligned} \hbox {TRL}_{\mathrm{capacity}}= & {} (\hbox {TRL}_1, \hbox {TRL}_2,\hbox {TRL}_3,\hbox {TRL}_4, \hbox {TRL}_5,\hbox {TLR}_6,\hbox {TRL}_7)\\= & {} ({6, 8, 4, 2, 5, 3, 9})\\ \hbox {IRL}_{\mathrm{capacity}}= & {} [({\varepsilon _{1}}, \varepsilon _{8}),( {\varepsilon _{3}, \varepsilon _{4} }),( {\varepsilon _{2}, \varepsilon _{6} }),( {\varepsilon _{5}, \varepsilon _{7}, \varepsilon _{14} } ),\\&({\varepsilon _{3}, \varepsilon _{10} }), ( {\varepsilon _{11}, \varepsilon _{12}} ,\varepsilon _{14}),( {\varepsilon _{13}}, \varepsilon _{16})]\\= & {} [(3,5),( 5,3 ),( 3,4 ), ( 5,2,1 ), ( 3,4 ),\\&( 4,5,1 ),( 7,9)]\\ \hbox {Capacity}= & {} k=( {1, 1, 1, 2, 1, 1, 1} ). \end{aligned}$$

Each ITRL value can be calculated by taking the average of the weighted technology and every associated integration. For the PNSRL model defined in this article, all input and output integrations are weighted the same in the equation. The formula below offers a way to calculate the ITRL value for a specific technology, where n equals the number of IRL values for a given technology, and k equals the capacity of the technology.

$$\begin{aligned} \hbox {ITRL}_{\mathrm{capacity}} =\frac{\sum _{i=1}^n (( {k\times \mathrm{TRL}} )+\hbox {IRL}_i )/(c+1)}{n}. \end{aligned}$$

Table 3 shows all the ITRL values for the nuclear reactor.

Table 3 Capacity PNSRL ITRL calculations for the nuclear reactor example

The ITRL values produced from Table 3 need to be normalized to understand where they fall on the SRL scale. Table 4 shows the normalized ITRL values with the associated acquisition phase.

Table 4 Capacity PNSRL ITRL calculations for the nuclear reactor example normalized and compared to the SRL scale

From the normalized ITRL values, each technology falls somewhere in the system development lifecycle [5]. A project manager or systems engineer would use this information to make critical decisions during system development [5]. For example, the condenser has the lowest readiness from all the other technologies. Additional resources could be allocated to the development of this technology. On a regular basis, the ITRL values should be reassessed to ensure that technologies are maturing correctly [5]. Over time, all technologies should mature. However, additional factors, such as scope creep, could reduce the maturity of a technology. The PNSRL model can help in the process of decision management and help ensure critical technologies mature efficiently.

With the ITRL values, a composite SRL value can be calculated for the entire system. Capacity PNSRL uses the average of all ITRL values to calculate the composite SRL value. Below shows how to calculate a composite SRL value.

$$\begin{aligned} \hbox {SRL}_{\mathrm{capacity}}= & {} \frac{\sum _{m=1}^j [ {\mathrm{ITRL}_m }]}{j}\\ \hbox {SRL}_{\mathrm{capacity}}= & {} \left( {\frac{0.56+0.67+0.42+0.25+0.47+0.35+0.94}{7}}\right) \\= & {} 0.52. \end{aligned}$$

The composite SRL value, calculated from the Capacity PNSRL ITRL values above, details that the nuclear reactor is in the Technology Development acquisition phase. With this composite SRL value nearing the next acquisition phase, it would be expected for the total system development to go into the System Development and Demonstration acquisition phase soon.

Capacity PNSRL uses a similar mathematical approach to SSRL and GTSRL, without using matrices. The PNSRL model could also be used with the Min–Min topical algebra approach from the IMSRL model. However, capacities will be ignored with Min–Min topical algebra since the equation does not sufficiently support this information. Table 5 shows the ITRL values and the composite SRL values of the nuclear reactor using Capacity PNSRL and Min–Min topical algebra.

Table 5 PNSRL and IMSRL ITRL values compared using the nuclear reactor example

From Table 5, The Capacity PNSRL approach produces different ITRL and composite SRL values than the Min–Min Topical Algebra approach. The reason there are large discrepancies between the approaches is due to how Min–Min Topical algebra calculates SRL. Min–Min topical algebra calculates ITRL using the lowest TRL or IRL value associated with a technology [3]. The composite SRL value is then calculated using the lowest ITRL value [3]. The concern with this approach is that it generates a value based on the least mature component for ITRL, and lowest ITRL value for total system SRL. Additionally, Min–Min topical algebra does not distinguish if an ITRL value was calculated from a TRL or IRL value. Capacity PNSRL properly represents all components in the ITRL and SRL calculations, since they all contribute to the maturity of a system.

Benefits

The PNSRL model continues to expand SRL graphically and mathematically. Benefits of using the PNSRL model include:

• Integration expansion to allow for relationships to other integrations. This enhances the graphical view to create a robust system view to aid in a deeper understanding of the system. Since PNSRL is based on graph theory, the mathematical equation is positively affected by calculating a more accurate representation of ITRL and composite SRL.

• Capacity allocation creates weighted technologies, based on the number of associated integrations, for validation and ITRL calculations.

• Token allocation allows visualization of inner system workflow, system state traceability, and aids in the validation of the system model.

• Capacity PNSRL removes matrix calculations to simplify large calculations.

• Capacity PNSRL utilizes capacities allocated to technologies, to weight technologies against their associated integrations. This distinguishes the technology importance compared to the integrations.

• Capacity PNSRL represents all technologies and integrations when calculating ITRL and SRL values.

Limitations

Limitations of PNSRL include:

• Arcs are weighted the same, and are equal to a weight of 1. The current PNSRL model provides no method of assigning weights to arcs and does not include arc weights in the Capacity PNSRL equation.

• For a technology, input and output arcs connected are used to calculate ITRL the same regardless of direction in the ITRL calculations.

• PNSRL does not detail the interval length between readiness levels.

• Creating a PN for a system may be difficult due to the size and complexity of a system. It is recommended that subject matter experts help in the PN development process. Fortunately, PNSRL only requires to create one PN for system maturity analysis. However, PNs may change during the development lifecycle.

Conclusion

As this article has shown, PNSRL expands current SRL models to enable better readiness level calculations and to offer a more useable graphical representation. The enhanced integrations between technologies show a better relationship between the sub-systems in system-of-system architectures. Utilizing tokens and capacities, a system model can show system workflow, and can be validated for correctness. Capacities are essential to the validation of a PN, and detail how a technology is weighted for ITRL calculations. Capacity PNSRL reduces mathematical complexity of matrix calculations, while representing all technologies in the system for readiness level computations. Project managers and systems engineers can use PNSRL to monitor system maturity for decision management and resource allocation. Models like PNSRL will continue to evolve SRL, expanding functionality and flexibility. PNSRL enables the development of a more comprehensible model to calculate SRL and treats the system as a flow of interoperability.