Introduction

Commercial organizations should enhance their competitive edge through continuous improvement to survive in competitive markets [32]. The success of a firm can be assessed by accurate and appropriate performance indicators to reflect its competitiveness [27]. Evaluation of business performance excellence is one of the main points of learning and measurement process including employee involvement. Thus, it allows organizations to develop and strengthen the management systems and focus on improving their performance [23, 29].

Quality awards enhance awareness of performance excellence in a competitive environment and the chance of sharing successful performance strategies. The Union of Japanese Scientists and Engineers (JUSE) established the Deming Prize in 1951 to reward Japanese companies for excellence in quality improvement. MBNQA is the most commonly used excellence framework launched in United States in 1988. The award has increased the awareness of the importance of quality management systems and has helped achieving the goals established for customer satisfaction. The Australian Business Excellence Award was launched by Australian Quality Council (AQC) in 1988. The aim of the award is to increase the quality awareness in firms and to recognize the success in productivity improvement. Another award is the Canada Award for Excellence introduced by the Ministry of Industry in 1984 and it was revised in 1989 to consider the assessment criteria of Malcolm Baldrige Model.

In 1991, European Foundation for Quality Management (EFQM) launched the European Quality Award to promote total quality performance into practice and to share lessons learned from quality management practices. In 1994, the Singapore Quality Award (SQA) and UK Excellence Award were launched to award organizations to improve quality management systems and to enhance the competitiveness of firms.

There are several approaches to measure the performance of a firm, involving both tangible and intangible attributes. Therefore, performance measurement can be regarded as a multi-criteria decision-making (MCDM) problem. There are many multi-criteria methods to overcome these performance measurement problems. A widely used MCDM tool for solving performance measurement problem with qualitative and quantitative data is the Analytic Hierarchy Process (AHP) developed by Saaty [25]. AHP enables experts to structure a hierarchy to select the best one among various alternatives. AHP employs pairwise comparison matrices using the 1–9 scale to assess alternatives and criteria in the hierarchy.

In many MCDM problems, crisp data are generally unavailable and difficult to expose. Therefore, experts need linguistic expressions rather than crisp numerical values for the evaluation of criteria and alternatives. To deal with the vagueness and impreciseness in human thoughts, the fuzzy set theory was developed by Zadeh [38]. The fuzzy set theory has been widely used in the solutions of MCDM problems because of its ability to quantify the subjectivity in human thoughts.

Although the classical AHP method uses crisp judgments to assess criteria and alternatives, experts prefer making linguistic judgments such as close to equal importance and not more than medium importance. Hence, experts generally utilize linguistic variables and fuzzy numbers to express the incomplete and insufficient information related to the consider problem. Therefore, the fuzzy sets and classical AHP method were integrated to produce the Fuzzy AHP approaches by many researchers. Laarhoven and Pedrycz [15] performed the first study on fuzzy AHP using triangular membership functions to define fuzzy scores. Buckley [5] proposed a new fuzzy AHP method based on trapezoidal membership functions and criticized Laarhoven and Pedryzs’ method in many ways. Chang [6] developed the extent analysis method based on triangular fuzzy numbers for pairwise comparisons. This method has been criticized by many researchers later. Zeng et al. [39] brought forward a modified fuzzy AHP for the assessment of project risk based on a flexible scale including triangular fuzzy numbers, trapezoidal fuzzy numbers, interval numbers, and verbal expressions. Aydın and Kahraman [1] developed a new fuzzy AHP method using positive and negative fuzzy numbers. They illustrated its application for a supplier selection problem.

In classical AHP, we use the 1–9 scale to evaluate the criteria or alternatives in pairwise comparison matrices. The reciprocal value of an assigned score is the inverse of that score with respect to multiplication operator. It is relatively difficult to assign a score in pairwise comparisons when a score is less than 1.0. In many applications, it has been revealed that expert generally prefer assigning scores larger than 1.0, and then, the reciprocal values are automatically determined. The aim of this paper is to develop a new and more practical scale and an AHP method under fuzziness to assess the firms applying for MBNQA. Unlike the other fuzzy AHP methods in the literature, the paper aims at using simple arithmetic operations for calculating the priority weights of criteria and alternatives. We allow experts to use negative fuzzy numbers in pairwise comparison matrices and also modify the normalization method of the classical AHP using a simple normalization formula to get the priority weights.

The rest of this paper is organized as follows. Literature review is given in the next section followed by which MBNQA is briefly explained. The subsequent section gives the proposed method. Then the numerical illustration and sensitivity analysis are presented, respectively. Before the concluding section, a comparison with Buckley’s approach is presented. Finally, conclusions are given.

Literature review

There are many studies on business performance excellence in the literature. These studies employ single or multiple criteria decision-making methods under certainty or uncertainty. Yeh et al. [33] developed a fuzzy multi-criteria analysis approach to assess performance testing for bus companies. Kaplan and Norton [13] launched Balanced Scorecard (BSC) as a framework for performance measurement. This study enabled to translate an organization’s vision and strategy into quantitative objectives and measures. Kald and Nilsson [14] performed a survey of 236 Nordic firms. They claimed that performance measurement helps organizations to understand theirselves. Güven and Persentili [9] developed a linear programming for the testing performance of bank balance-sheet management. Tözüm [26] used the ratio analysis to evaluate banks according to their performance. Yurdakul and İç [37] used TOPSIS method for measuring the performance of the firms in the automotive industry. Maiga and Jacobs [20] studied the relation between benchmarking and organization performance.

Lin and Su [17] used Taiwan National Quality Award for the evaluation of firms that apply quality improvement programs. Liu et al. [19] constructed the collaboration networks of intercontractors using the electronic database of NQAPC. Their aim is to investigate the structural evolution of the collaborations between contractors in China construction industry. Guh et al. [8] established hierarchical structures for performance evaluation of ambiguous and humanistic complicated systems using a fuzzy relation-based cluster analysis. Yu and Lin [35] brought forward a DEA model to measure the performance of railways and data set was used from International Railway union. Wang et al. [30] used the fuzzy DEA to achieve performance assessment of eight manufacturing enterprises in China. Ertuğrul and Karakaşoğlu [7] evaluated the performance of Turkish cement firms in Istanbul Stock Exchange by employing fuzzy AHP and TOPSIS methods. Tseng et al. [27] used an integrated DEA and AHP methodology for measuring company’s business performance in Taiwan. Azadeh et al. [2] brought forward an adaptive neural network based meta-heuristic approach for performance assessment. Tseng [28] proposed an integrated approach involving ANP, fuzzy set theory, BSC methods for performance evaluation. Azadeh et al. [3] developed an integrated neutral network algorithm for performance assessment. Yu and Hu [36] developed an integrated approach composed of a voting method and a fuzzy TOPSIS method to assess the performance of manufacturing plants.

Peng and Prybutok [22] utilized the partial least squares to examine the relative effectiveness of each MBNQA category. Haffer [11] proposed a new Delphi method of business performance measurement system for organizational self assessment. Metaxas et al. [21] put forward a new integrated methodology integrating fuzzy AHP and TOPSIS for bench marking the sustainability of organizations. Ha et al. [10] proposed a new decision-making framework composed of AHP and Fuzzy TOPSIS for prioritizing port performance. Yoon et al. [34] developed a technology assessment named K-TOL for sustainable development of LNG terminals.

Malcolm Baldrige National Quality Award

MBNQA is the most known and most widely used national quality program for the evaluation of firms. The award was first launched in 1987 and originally used to recognize United States national firms for measuring the level of business excellence and quality achievement. In its first version, MBNQA considered only six criteria for assessment. In 1999, education and healthcare criterion were added as the seventh criterion [23]. Since the beginning of 2007, not only private sector but also government and nonprofit firms were evaluated for business excellence in USA. The aim of the award is to encourage US organizations for the progress in quality awareness and achievement and to improve customers’ satisfaction. MBNQA criteria have been modified over the years. They are the most widely known set of quality standards defining how an organization can establish an excellent quality management system [4].

The Baldrige criteria for performance excellence can be applied to manufacturing, service and small business. The requirements of the criteria are embodied in seven categories as follows (“As of 24 December, 2017 http://www.asq.org/index.html.”):

  • Criterion 1: Leadership (120 points): How upper management leads the organization, and how the organization leads within the community.

  • Criterion 2: Strategic planning (85 points): How the organization establishes and plans to carry out strategic directions.

  • Criterion 3: Customer focus (85 points): How the organization builds and maintains strong, lasting relationships with customers.

  • Criterion 4: Measurement, analysis and knowledge management (90 points): How the organization uses data to support key processes and manage performance.

  • Criterion 5: Workforce focus (85 points): How the organization empowers and involves its workforce.

  • Criterion 6: Process management (85 points): How the organization designs, manages and improves key processes.

  • Criterion 7: Results (450 points): How the organization performs in terms of customer satisfaction, finances, human resources, supplier and partner performance, operations, governance and social responsibility, and how the organization compares to its competitors.

55% of the criteria in MBNQA are related to how an organization should be run and the remaining 45% of the criteria focus on the achieved results. Criterion 1 through Criterion 6 (550 points) focuses on the approaches or systems of firms. The remaining 45% of the points belongs to Criterion 7.

The seven categories of MBNQA criteria are divided into 18 sub-items. Table 1 shows points of categories and items for performance excellence in Baldrige system. All these categories and items work as a unit of a system. In this system, first of all, customers’ wants and needs are determined. In Category 1, leadership determines company’s mission, values, and products. Then, the company determines its strategies, goals for improvement, and performance metrics in Category 2. In Category 4, achievement in Measurement, Analysis, and Knowledge Management are aimed. Later, the company designs systems and processes for its individuals (Category 5: Workforce Focus) and its customers (Category 3: Customer Focus), and its major work processes (Category 6: Process Management) [31]. All of these systems should cooperate to produce results (Category 7: Results) for the organization and customers.

Prybutok et al. [24] examine MBNQA 2002 criteria and their applicability to the government sector. They also address the need for performance metrics for government organizations.

Table 1 Criteria for performance excellence
Full size table

Proposed model

Implementing the proposed method is realized by seven steps:

Step 1: Structure hierarchy The criteria of MBNQA are used for the assessment of firms. Hence, 7 main criteria and 18 sub-criteria are used.

Step 2: Make pairwise comparisons for factors Experts are required to compare each factor with another in the hierarchy. Experts use the proposed fuzzy scale. Seven different scales are used to set up comparison matrices. In MBNQA system, there are six different point value items; these point values are 70 points, 50 points, 40 points, 45 points, 35 points, and 100 points, as shown in Table 1.

We developed new fuzzy scales to get an easy understanding of scoring in AHP. In these scales, negative values as the reciprocals of positive scores can be assigned. The scales have been developed based on the exponential importance function in the classical AHP. Table 2 is used for comparing main criteria (categories) and items; Table 3 for comparing alternatives regarding 70 points values items; Table 4 for comparing alternatives regarding 50 points values items; Table 5 for comparing alternatives regarding 40 points values items; Table 6 for comparing alternatives regarding 45 points values items; Table 7 for comparing alternatives regarding 35 points values items; and Table 8 for comparing alternatives regarding 100 points values items.

Experts use their experiences, perceptions, and knowledge to make comparisons between criteria. Because experts may have different points of view to a certain problem, they may use different linguistic variables in pairwise comparison matrices of AHP approach. The weights (c) of the experts are determined based on their knowledge and experience. Suppose that m experts exist in the group and the kth expert \(E_k\) is assigned an expert weight of \(c_k \), where \(c_k \in [0,1]\), \(c_1 +c_2 +\cdots +c_m =1.\)

Table 2 Triangular fuzzy conversion scale for categories comparison
Full size table
Table 3 Triangular fuzzy conversion scale for 70 points values items
Full size table
Table 4 Triangular fuzzy conversion scale for 50 points values items
Full size table
Table 5 Triangular fuzzy conversion scale for 40 points values items
Full size table
Table 6 Triangular fuzzy conversion scale for 45 points values items
Full size table
Table 7 Triangular fuzzy conversion scale for 35 points values items
Full size table
Table 8 Triangular fuzzy conversion scale for 100 points values items
Full size table

Step 3: Aggregate individual TFNs to group TFNs This step applies an aggregation operator to obtain a group preference from several individual preferences. We apply the fuzzy weighted triangular averaging operator, as given in Eq. (1):

$$\begin{aligned} {{\tilde{a}_{ij}}} ={{\tilde{a}_{ij_1 } }} \otimes c_1 \oplus {{\tilde{a}_{ij_2 } }} \otimes c_2 \oplus \cdots \oplus {\tilde{a}_{ij_m } } \otimes c_m, \end{aligned}$$
(1)

where \({{\tilde{a}_{ij} }} \) is the aggregated fuzzy score for \(A_i -A_j \) comparisons, \(i,j=1,2,\ldots ,n;{{\tilde{a}_{ij_1 } }},{{\tilde{a}_{ij_2 } }},\ldots ,{\tilde{a}_{ij_m } } \) are corresponding TFNs assigned by experts \(E_1,E_2,\ldots ,E_m \), respectively. \(\otimes \) and \(\oplus \) shows fuzzy operations for multiplication and addition, respectively.

Step 4: Convert negative fuzzy TFNs to positive TFNs We determine the corresponding exponential values of negative scores since the scale of the classical AHP is based on an exponential importance. This conversion is realized as follows: Eq. (2) for comparing main criteria (categories) and items; Eq. (3) for comparing the alternatives with respect to the items of 70 points in Table 1; Eq. (4) for comparing the alternatives with respect to the items of 50 points in Table 1; Eq. (5) for comparing the alternatives with respect to the items of 40 points in Table 1; Eq. (6) for comparing the alternatives with respect to the items of 45 points in Table 1; Eq. (7) for comparing the alternatives with respect to the items of 35 points in Table 1; and Eq. (8) for comparing the alternatives with respect to the items of 100 points, as shown in Table 1:

$$\begin{aligned} {\tilde{a}^{{*}}_{ij} }= & {} e^{({\tilde{a}}_{ij} /4)} \end{aligned}$$
(2)
$$\begin{aligned} {\tilde{a}^{{*}}_{ij} }= & {} e^{({\tilde{a}}_{ij} /32)} \end{aligned}$$
(3)
$$\begin{aligned} {\tilde{a}^{{*}}_{ij} }= & {} e^{({\tilde{a}}_{ij} /22.75)} \end{aligned}$$
(4)
$$\begin{aligned} {\tilde{a}^{{*}}_{ij} }= & {} e^{({\tilde{a}}_{ij} /18)} \end{aligned}$$
(5)
$$\begin{aligned} {\tilde{a}^{{*}}_{ij} }= & {} e^{({\tilde{a}}_{ij} /20.5)} \end{aligned}$$
(6)
$$\begin{aligned} {\tilde{a}^{{*}}_{ij} }= & {} e^{({\tilde{a}}_{ij} /16)} \end{aligned}$$
(7)
$$\begin{aligned} {\tilde{a}^{{*}}_{ij} }= & {} e^{({\tilde{a}}_{ij} /45.5)}. \end{aligned}$$
(8)

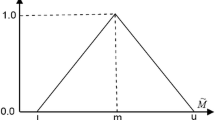
\({{\tilde{a}_{ij} }} =(l_{ij},m_{ij},u_{ij} )\) and \((l_{ij},m_{ij},u_{ij} )\) is a triangular fuzzy number.

Table 9 Comparison matrix of alternatives respect to senior leadership
Full size table
Table 10 \(a_{ij}\) values of Senior Leadership
Full size table

In this step, the consistency of each fuzzy pairwise comparison matrix is examined. To check the consistency of the fuzzy pairwise comparison matrices, the fuzzy consistency test with tolerance deviation model proposed by Leung and Cao [16] is used:

$$\begin{aligned}&\left( { {\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} 1&{} {r_{12} }&{} \ldots ,&{} {r_{1n} } \\ {r_{21} }&{} 1&{} \ldots ,&{} {r_{2n} } \\ .&{} .&{} \ldots ,&{} . \\ {r_{n1} }&{} {r_{n2} }&{} \ldots ,&{} 1 \\ \end{array} }} \right) r_{ij}\cdot r_{ji} =1 \end{aligned}$$
(9)
$$\begin{aligned}&{\tilde{r}}_{ik} \otimes {\tilde{r}}_{kj} \cong {\tilde{r}}_{ij},\quad i,j,k\in 1,\ldots ,n \end{aligned}$$
(10)
$$\begin{aligned}&s_\alpha =\Bigg \{w:L_{ij\alpha } \le w_i /w_j \le U_{ij\alpha } , i\ne j=1,\ldots ,n,\nonumber \\&\qquad \qquad \qquad \qquad w_j \ge 0,\ \sum _{j=1,\ldots ,n} {w_j =1} \Bigg \} \end{aligned}$$
(11)
$$\begin{aligned}&S_\alpha ^{\prime } =\left\{ {\begin{array}{l} w:(1-\delta )L_{ij\alpha } \le \frac{w_i }{w_j }\le (1+\delta )U_{ij\alpha },\ i\ne j=1,\ldots ,n, \\ w_j \ge 0,\ \sum _{j=1,\ldots ,n.} {w_j =1} \\ \end{array}} \right\} \end{aligned}$$
(12)
$$\begin{aligned}&\lambda _{\max } \le n+\sum _{\begin{array}{c} j=1,\ldots ,n \\ j\ne i \end{array}} {\delta _{ij} } \end{aligned}$$
(13)
$$\begin{aligned}&(\lambda _{\max } -n)/(n-1)\le \delta \end{aligned}$$
(14)
$$\begin{aligned}&\min \beta =\beta _1 +\beta _2 \nonumber \\&\hbox {s.t.}\quad \ln (1-\delta )L_{ij1} \le \ln w_i -\ln w_j +\beta _{1_{ij} } -\beta _{2_{ij} } \nonumber \\&\qquad \qquad \le \ln (1+\delta )U_{ij1}, i\ne j,1,\ldots ,n.\nonumber \\&\beta _1 \ge \beta _2,\quad \beta _2 -\beta _{2_{ij} },\quad \beta _{1ij} -\beta _{2_{ij} } \ge 0, \end{aligned}$$
(15)

where \(\ln w_i, \beta _{1_{ij} },\beta _{2_{ij} },\beta _1,\beta _2\) are decision variables.

If \( \beta =0\), the fuzzy pairwise comparison matrix is sufficiently consistent. If \( \beta >0\), it means that the fuzzy pairwise comparison matrix is not sufficiently consistent and it must be re-evaluated.

Step 5: Calculate the priority weights of factors Consider a triangular fuzzy comparison matrix expressed by

$$\begin{aligned}&\tilde{A} =({\tilde{a}}_{ij} )\nonumber \\&\quad \,\, =\left[ {{\begin{array}{cccc} {(1,1,1)}&{} {(l_{12},m_{12},u_{12} )}&{} \ldots &{} {(l_{1n},m_{1n} ,u_{1n} )} \\ {(l_{21},m_{21},u_{21} )}&{} {(1,1,1)}&{} \ldots &{} {(l_{2n},m_{2n} ,u_{2n} )} \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ {(l_{n1},m_{n1},u_{n1} )}&{} {(l_{n2},m_{n2},u_{n2} )}&{} \ldots &{} {(1,1,1)} \\ , \end{array} }} \right] \nonumber \\ \end{aligned}$$
(16)

where \({\tilde{a}}_{ij} = ({l_{ij}},{m_{ij}},{u_{ij}}) = {\tilde{a}_{ij}}^{ -1} = (1/{u_{ji}},1/{m_{ji}},1/{l_{ji}})\) for \(i,j=1,\ldots ,n\) and \(i\ne j.\)

Table 11 Final fuzzy importance weights of firms
Full size table
Table 12 Ranking of the firms
Full size table

Because our aim is to bring out a simplified fuzzy AHP, we avoid using a complicated normalization formula.

A normalized matrix \(\tilde{N}\) can be calculated as follows:

$$\begin{aligned}&\tilde{N} =\left[ {\tilde{n}_{ij}} \right] _{m\times n} \end{aligned}$$
(17)
$$\begin{aligned}&\tilde{n}_{ij} =\left( {\frac{l_{ij} }{u_j^{*} },\frac{m_{ij} }{u_j^{*} },\frac{u_{ij} }{u_j^{*} }} \right) . \end{aligned}$$
(18)

The normalization method clarified above is for preserving the property that the ranges of normalized triangular fuzzy numbers belong to [0, 1].

The importance weights of the factors can be calculated as follows:

$$\begin{aligned} W_i ^{{\prime }}=\frac{\sum _{j=1}^n {\tilde{n}_{ij} } }{\sum _{k=1}^n {\sum _{j=1}^n {n_{kj}}}}\quad k=1,2,\ldots ,n. \end{aligned}$$
(19)

Step 6: Calculate final weights In this step, the weights of alternatives and sub-criteria are aggregated to get local priority of each main criterion. The local priorities are then multiplied by the weights of the main criteria and the global priorities of alternatives are obtained.

Step7: Compare the weights using a ranking method In the last step, the obtained fuzzy numbers need to be ranked. To rank the fuzzy numbers the integral value method developed by Liou and Wang [18] is used.

Application

To show the usefulness of the proposed model here, an illustrative example is given. Three logistic firms are assessed according to the proposed model. A four levels hierarchy composed of MBNQA main and sub-criteria and three alternatives are used. In this study, three experts are utilized to test firms, and the experts’ weights are assigned according to their background, experiences, and knowledge. The assigned weights are 0.3, 0.3, and 0.4, respectively.

The experts test each factor of the hierarchy using the fuzzy scales, as given in Table 2 through Table 8. In the following sample, calculations are given.

Step 2 All factors in the hierarchy are tested by the experts. The comparison matrix of alternatives regarding senior leadership matrix is shown in Table 9.

Step 3 The aggregation of the obtained scores is calculated by Eq. (1) as follows;

$$\begin{aligned} {\tilde{a}}_{{13_{\mathrm{Senior\,Leadership}}}}= & {} 0.3\otimes (42,46,70)\oplus 0.3\otimes (28,42,56)\\&\oplus \, 0.4\otimes (28,42,56) \\= & {} (32.20, 46.20, 60.20). \end{aligned}$$

The other aggregated scores of the hierarchy are also obtained similarly.

To check the consistency of the fuzzy pairwise comparison matrices, we used the consistency test auxiliary linear programming mentioned in Eqs. (9) through (15).

For solving the linear problem, we used MATLAB programming tool. We found that all the fuzzy comparison matrices are consistent.

Step 4 In this step, the corresponding exponential values of negative scores are calculated using Eqs. (2) through (8). The results in Table 9 are calculated by Eq. (2):

$$\begin{aligned}&{\tilde{a}^{{*}}}_{{12_{\mathrm{seniorleadership}}}} =e^{(l_{12}, m_{12},u_{12} )/32}\\&{\tilde{a}}_{{12}_{\mathrm{seniorleadership}}} =e^{(28,42,56)/32}=(2.40, 3.72, 5.75). \end{aligned}$$

Other \(a_{ij}\) values of Senior Leadership are given in Table 10.

Step 5 Table 10 is normalized using Eqs. (17) and (18) as follows:

$$\begin{aligned} a_{12} =(2.40, 3.72, 5.75)/5.75=(0.42, 0.65,1.00). \end{aligned}$$

The other normalized \(a_{ij}\) values of Senior Leadership are also obtained similarly.

The importance weights of the alternatives under Senior Leadership are obtained using Eq. (19). Here, we have

$$\begin{aligned} W_{\mathrm{Firm}\,A}^{{\prime }}= & {} (0.39, 0.66, 1.10),\quad W_{\mathrm{Firm}\,B} ^{{\prime }}=(0.11, 0.21, 0.38), \\ W_{\mathrm{Firm}\,C}^{{\prime }}= & {} (0.08, 0.14,0.24). \end{aligned}$$

Step 6 All the priority values in the hierarchy are obtained and synthesized to determine the best firm, as shown in Table 11.

Step 7 After obtaining fuzzy priorities, the integral value method developed by Liou and Wang [18] is used to rank the fuzzy weights. The obtained results are given in Table 12.

By adopting the proposed method, Firm A is selected as the best firm among alternatives with the priority weight of (0.09, 0.28, 1.00). Firm C is the second one, and Firm B is the third one.

Sensitivity analysis

In this section, a sensitivity analysis is applied. Experts’ judgments are altered on some alternatives comparisons and are analyzed to see how much it will influence the final scores of alternatives. Figure 1 illustrates the results of sensitivity analysis. In case 1, the importance weights of alternatives regarding “Governance and Societal Responsibilities” under “Leadership” are altered like that: \(w_{A}^{\prime } =(0.11, 0.19, 0,32), w_{B}^{\prime } =(0.37, 0.66, 1.16), w_{C}^{\prime } =(0.07, 0.14, 0.28)\), and the importance weights of alternatives regarding “ Product Outcomes” under “Results” are altered like that: \(w_{A}^{\prime } =(0.05, 0.10, 0,18), w_{B}^{\prime } =(0.43, 0.72, 1.21), w_{C}^{\prime } =(0.09, 0.17, 0.32)\). Therefore, the final scores of alternatives are obtained as: \(w_{A}=(0.07, 0.22, 0,82), w_{B}=(0.07, 0.24, 0.87), w_{C}=(0.07, 0.22, 0.83)\). In case 2, the importance weights of alternatives regarding “Senior Leadership” under “Leadership” are altered like that: \(w_{A}^{\prime } =(0.06, 0.11, 0,19), w_{B}^{\prime } =(0.19, 0.36, 0.66), w_{C}^{\prime } =(0.28, 0.54, 1.01)\). The final scores of alternatives are obtained as: \(w_{A}=(0.08, 0.24, 0,84), w_{B}=(0.06, 0.21, 0.77), w_{C}=(0.07, 0.24, 0.97)\). The importance weights of alternatives regarding “Work Processes” under “Process Management” are altered like \(w_{A}^{\prime } =(0.07, 0.15, 0,29), w_{B}^{\prime } =(0.35, 0.62, 1.11), w_{C}^{\prime } =(0.12, 0.21, 0.36)\). Therefore, the final scores of alternatives are obtained as: \(w_{A}=(0.08, 0.27, 0,98), w_{B}=(0.07, 0.22, 0.81), w_{C}=(0.06, 0.20, 0.77)\).

Fig. 1
figure 1

Sensitivity analysis results

Full size image

Comparison with Buckley’s fuzzy AHP

In this section, the results obtained by the integrated method are compared with the results of Buckley’s [5] fuzzy AHP. Buckley incorporated fuzzy comparison ratios \(a_{ij}\) to Saaty’s AHP method. Buckley’s [5] approach is shown in the following steps.

Step 1 Consult the decision makers and obtain the comparison matrix a whose elements are \(\tilde{t}_{ij} =(a_{ij,} b_{ij,} c_{ij,} d_{ij} ),\) where all i and j are trapezoidal fuzzy numbers. Table 13 shows the linguistic scale for evaluation of alternatives.

Table 13 Interpretation of entities in a pairwise comparison matrix
Full size table

Step 2 The fuzzy weights \(w_i \) can be calculated as follows. The geometric mean for each row is determined:

$$\begin{aligned} \tilde{z}_{i} =\left[ {\prod _{j=1}^n {\tilde{{t_{ij} }} } } \right] ^{1/n},\quad \text {for all} i. \end{aligned}$$
(20)

The fuzzy weight \(w_i\) is given as

$$\begin{aligned} w_i = {\tilde{z}_i }\oplus \left[ {\sum _{j=1}^n {{\tilde{z}_j } } } \right] ^{-1}. \end{aligned}$$
(21)

In the following discussion, we will detail the derivation of fuzzy weight \(w_i \). Let the left leg and right legs of \(\tilde{t}_{ij}\) be, respectively, defined as

$$\begin{aligned} f_i (\alpha )= & {} \left[ {\prod _{j=1}^n {((b_{ij} -a_{ij} )\alpha +a_{ij} } } \right] ^{1/n},\quad \alpha \in \left[ {0,1} \right] \end{aligned}$$
(22)
$$\begin{aligned} g_i (\alpha )= & {} \left[ {\prod _{j=1}^n {((c_{ij} -d)\alpha +b_{ij} } } \right] ^{1/n},\quad \alpha \in \left[ {0,1} \right] . \end{aligned}$$
(23)

Furthermore, let

$$\begin{aligned} a_{ij}= & {} \left[ {\prod _{j=1}^n {(a_{ij} )} } \right] ^{1/n} \end{aligned}$$
(24)
$$\begin{aligned} a= & {} \sum _{i=1}^m {a_i }. \end{aligned}$$
(25)

Similarly, we can define \(b_i \) and b, \(c_i \) and c, and \(d_i \) and d. The fuzzy weight \(w_i\) is determined as

$$\begin{aligned} w_i =\left( {\frac{a_i }{d},\frac{b_i }{c},\frac{c_i }{b},\frac{d_i }{a}} \right) , \quad \forall i. \end{aligned}$$
(26)

The membership function \(\mu _{wi} (x)\) can be given, as shown in Table 14.

Table 14 Interpretation of entities in a pairwise comparison matrix
Full size table

When \(x\in \left[ {\frac{a_i }{d},\frac{b_i }{c}} \right] \)or \(x\in \left[ {\frac{c_i }{b},\frac{d_i }{a}} \right] \), x is calculated as

$$\begin{aligned} x=\left\{ {\begin{array}{ll} f_i (a)/g(a),\quad \hbox {if } x\in \left[ {a_i /d, b_{i } /c} \right] \\ g_i (a)/f(a),\quad \hbox {if } x\in \left[ {c_i /b, d_{i } /a} \right] \end{array}} \right\} \end{aligned}$$
(27)

where \(f(\alpha )=\sum _{i=1}^m {f_i (\alpha )\,\, ve }\,\, g(\alpha )=\sum _{i=1}^m {g_i (\alpha )}.\)

Step 2 is repeated for all the fuzzy performance scores.

Step 3 The fuzzy weights and fuzzy performance scores are aggregated. The fuzzy utilities \(U_i,\forall i,\) are obtained based on

$$\begin{aligned} U_i =\sum _{j=1}^n w_j r_{\imath j},\quad \forall i. \end{aligned}$$
(28)

Application of Buckley’s fuzzy AHP

Step 1 Decision makers compare the alternatives with respect to each criterion. In this step, only calculation of senior leadership is given for illustration. In this method, the compromised decision of decision makers is used.

Step 2 For the pairwise comparison matrix for senior leadership, the geometric mean is calculated as follows:

$$\begin{aligned} a_{1} = \left( {\prod \limits _{J=1}^3 {a_{1j} } } \right) ^{1/3}= & {} (a_{11} *a_{12} *a_{13} ) \\= & {} (1*2*6)^{1/3} \\= & {} 2.29 \\ a_{3} = \left( {\prod \limits _{J=1}^3 {a_{3j} } } \right) ^{1/3}= & {} (a_{31} *a_{32} *a_{33} ) \\= & {} (0.13*0.17/1)^{1/3} \\= & {} 0.28. \end{aligned}$$

Similarly, we get other \(a_{ij}\) values. Hence

$$\begin{aligned} a=\sum _{j01}^3 {a_i } =2.29+1.00+0.28=3.56. \end{aligned}$$

Similarly, we can get \(b_i \) and b, \(c_i \) and c, and \(d_i \) and d. They are summarized, as shown in Table 15.

Thus, \((a, b, c, d) = (3.56, 4.25, 4.25, 4.96).\)

Table 15 Geometric mean
Full size table

Then performance scores are obtained;

$$\begin{aligned} r_{11} =\left( {\frac{a_1 }{d},\frac{b_1 }{c},\frac{c_1 }{b},\frac{d_1 }{a}} \right) =(0.46,0.64,0.64,0.89). \end{aligned}$$

We repeat Step 2 on the other reciprocal matrices one by one. All the fuzzy performance scores of the factors and fuzzy weights in the hierarchy are calculated.

Step 3 The fuzzy weights and fuzzy performance scores are aggregated. So the fuzzy utilities \(U_i,\forall i,\) are obtained:

$$\begin{aligned} U_a= & {} \left( {0.13, 0.39, 0.39,1.17} \right) \\ U_b= & {} \left( {0.15,0.26,0.26,0.92} \right) \\ U_c= & {} \left( {0.16,0.31,0.31,0.90} \right) . \end{aligned}$$

To figure the rank of final fuzzy utilities, the area-based ranking method which was developed by Kahraman and Tolga [12] is used. Consequently, based on Buckley’s approach, the ranking of the alternatives in descending order are, Firm A, Firm C, and Firm B.

Conclusion

This study proposes an integrated approach for testing business performance of MBNQA with the proposed AHP. MBNQA is the most widely used performance excellence model. Its usage in organizations promotes the awareness of performance excellence in a competitive environment and enhances sharing information of performance strategies. The proposed approach creatively proposes a new fuzzy AHP framework for MBNQA. The proposed model enables experts to use linguistic judgments to measure the performance of firms according to MBNQA criteria. Not only positive fuzzy numbers but also negative fuzzy numbers can be used in comparison matrices. Thus, the approach presents more understandable scales for comparing alternatives.

This study also proves the applicability of the proposed model by a numerical example. First, the four levels hierarchy, comprising seven main criteria and 18 sub-criteria of MBNQA was established. Each expert used seven different triangular fuzzy scales for establishing comparison matrices. These scales were formed to show MBNQA scoring system. Then simple normalization formula was used to get the importance weights. The finals weight of the firms were calculated and ranked using the integral value method developed by Liou and Wang [18]. Therefore, Firm A was selected the most proper firm for MBNQA.

The fuzzy MBNQA process has been compared with Buckley’s fuzzy approach. The results justify that the proposed method produces meaningful outcomes. Our proposed method is based on simple arithmetic operations, and it requires less time when compared with Buckley’s approach. Both methodologies produced the same results in the application.

For further research, the obtained results of our paper can be compared by the results of other fuzzy multi-criteria methods like fuzzy TOPSIS, fuzzy ELECTRE, or fuzzy VIKOR. Alternatively, the new extensions of fuzzy sets such as intuitionistic fuzzy sets, hesitant fuzzy sets, and type-2 fuzzy sets can be used in this multi-criteria decision-making method.