1 Introduction

Tribocorrosion is the process of material degradation due to the combined action of mechanical, adhesive, abrasive, fretting and fatigue wear mechanisms and chemical ones such as uniform or localized corrosion [1]. Currently, the phenomenon is largely diffuse in industrial scenarios, particularly in the marine [2], automotive [3] and biological sector [4]. In fact, the economic and clinical effects of wear have prompted many researchers to investigate and analyse it [5,6,7]. Tribology, i.e., the science of friction, wear and body interaction [8], is thus coupled with the chemical field by reactions such as oxidation, protective layer formation and transpassive dissolution. These processes occur between the samples and the lubricant present in the coupling and act simultaneously to influence each other. Currently, tribocorrosive tests can be conducted by oscillatory or reciprocating tribometers connected to a potentiostat with 2- or 3-electrode configurations [9]. Examples of the main techniques adopted are open-circuit potential, potentiostatic and potentiodynamic tests and electrochemical impedance spectroscopy, where variables such as the friction coefficient, current and potential trend, material loss, oxide layer composition are commonly evaluated. Despite the great developments achieved during these years concerning the introduction of new biomaterials [10, 11], many doubts have been unsolved, mainly due to the complexity of the phenomena and to the notable number of factors involved from different engineering fields. One of them is certainly the effect of the composition of the biological medium. In that sense, Zhang et al.[12] analysed stainless steel 304 in different seawater corrosive media and noted that a lower pH promoted greater wear and that abrasive wear prevailed in all solutions. Mischler et al.[13], instead, evaluated DIN 34CrNiMo6 steel in aqueous solution by the passivity–total wear relationship. Concerning the biological environment and, in particular, the oral cavity, Mathew et al.[14] studied the effect of artificial saliva pH on commercial pure titanium (cP) and reported that the configuration with a pH equal to 6 was worse than the other two configurations with pH equal to 3 and 9 owing to the less stable protective layer. Titanium grade V, both realized conventionally and by additive manufacturing, was investigated by Hamza et al.[15] in artificial saliva and deionized water with chemical species added, such as calcium chloride, sodium fluoride and lactic acid, and the authors observed that the latter two significantly reduced the corrosion resistance of titanium. Espallargas et al.[16] investigated a carbon CoCrMo alloy in NaCl and a phosphate buffer solution with and without albumin, which increased the chromium and molybdenum concentrations for tribocorrosion tests but only increased the molybdenum concentration for corrosion trials. On the other hand, the modelling of tribocorrosive wear is still a critical issue. The current state of the art proposes diverse theories and applications, including both numerical and experimental models [17]. For instance, Gilbert and Zhu [18] presented a relationship for the prediction of current and voltage during fretting corrosion. Ramachandran et al.[19] adopted machine learning for forecasting tribocorrosion rates with accuracies greater than 90%. Jemmely et al.[20] focused on the kinetics of the repassivation of an iron–chromium alloy (AISI 430) in sulfuric acid due to the importance of the protective layer against tribocorrosive attack. Unfortunately, evident discrepancies occurred when the analytical results were compared with the experimental results because of the key role played by the pin geometry, the probable presence of a third body and other mechanical/tribological aspects. Cao et al.[21] tried to include lubrication by Hamrock–Dowson’s law in the effective force exchange between bodies. The total wear, in this case, was estimated as the sum of the mechanical and chemical–mechanical components (wear accelerated corrosion). The same approach was used by Pina et al.[22] for beta titanium immersed in phosphate-buffered saline solution. Yan et al.[23], instead, starting from a synergistic model, considered the volume loss as the sum of the mechanical, chemical and combined action in terms of both wear-accelerated corrosion and corrosion accelerated- wear. Papageorgiou et al.[24] correlated the wear at the end of tribocorrosion tests with the friction coefficient of a NiCrMo625 alloy in a 3.4 wt% NaCl aqueous solution. Last, other strategies may be driven to a more computational point of view, as described by Wang and Cai [25] by the finite element method (FEM), which involves elastic‒plastic mechanical deformation and galvanic corrosion, or by Feyzi et al.[26], who coupled the abrasion term with oxide film growth.

In this light the manuscript aims to interpret, from a tribological and biological perspective, the influence of a single chemical element on tribocorrosive material loss as much as on common variables like friction coefficient, potential and current since has not been extensively discussed in the literature, especially for titanium alloys and Ringer’s solutions. These factors provided the basis for synergistic wear analytical modelling that is still a critical aspect in tribocorrosion field and in which a general law has not yet been provided.

2 Materials and Methods

The coupling object of investigation was titanium grade V-alumina, which represents an example of a dental implant-abutment configuration [27, 28]. Titanium grade V alloy, composed of 90% Ti, 4% V, and 6% Al by weight, was chosen as the test sample due to its high corrosion resistance, mechanical performance and especially biocompatibility [29], making it very common in implantology [30]. The titanium disc has the following geometrical features: diameter of 25 mm, height of 6 mm and arithmetical roughness (Sa) of 0.68 \(\pm\) 0.2 μm. Alumina sphere (Al2O3-puriss. 98%\(\pm\) 1) of 10 mm and Sa equals 1.60 \(\pm\) 0.3 μm were adopted. The counterpart owns a rough surface, comparable to other tribocorrosive analyses [31,32,33], in order to evaluate also the effect of roughness on samples wear. The mean and maximum Hertzian pressures of the ball-on-flat configuration were 368 and 552 MPa, respectively, which are in the range of the stress diffused in dental implants [34]. The mechanical and chemical properties of the specimens are reported in Table 1. Before the tests, the samples were cleaned in an ethanol bath for 10 min and subsequently dried.

Table 1 Mechanical and chemical properties of the specimens
Full size table

Four Ringer’s solutions [35, 36] with different pH are shown in Table 2 in which the remaining part is attributed to water. The mediums also own specific compositions so that it is possible to evaluate the effect of the single weight of chemical elements on the tribocorrosive response of titanium alloys, which is highly relevant in the dental field [37]. For instance, the solution 1 has sodium bicarbonate, which is usually used in toothpastes, but not sodium and potassium chloride as the solution 3. The 2–3 are almost similar but have diverse calcium chloride dihydrate and sodium bicarbonate concentrations. Finally, the 4 is composed of sodium lactate and has the lowest pH.

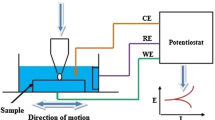
Table 2 Chemical composition of the four biological solutions
Full size table

The experimental tests were performed using a Ducom POD-4.0 modular reciprocating tribometer and an Ivium potentiostat (Fig. 1a–b). A three-electrode configuration was adopted [38], with silver chloride immersed in saturated KCl (E = 0.197 V) as the reference electrode (RE) and graphite as the counter electrode (CE). The working specimen (WE) was connected to the specimen by a metallic frame. Last, both the cup and the pin holder were in polyethylene since it is electrically insulating.

Fig. 1
figure 1

In situ experimental setup for tribocorrosion tests: lateral (a) and front (b) views

Full size image

Concerning the type of tests, the following techniques were used:

  1. 1.

    Dry tribological test for the estimation of the friction coefficient and mechanical wear

  2. 2.

    Open circuit potential (OCP) with no motion or current imposed for the evaluation of the free potential

  3. 3.

    Potentiodynamic test for the extrapolation of Tafel curves, corrosive current and passivation charge density

  4. 4.

    OCP trend during tribocorrosion test with no applied current for the calculation of the total wear

  5. 5.

    Potentiostatic test under OCP for analysing the evolution of tribocorrosive current

All the experiments were repeated three times to guarantee the repeatability of the results and were carried out at room temperature (25 \(\pm\) 2 °C). More specifically, the tribological tests were performed in accordance with the following input conditions: a load of 10 N, frequency of 2 Hz, stroke length of 5 mm, and sliding time and distance of 30 min and 36 m, respectively. 3600 cycles were therefore tested to simulate daily food activity by assuming two meals with a duration of 15 min and a masticatory frequency of 2 Hz.

The OCP test lasted an average of 3–4 h for complete stabilization of the oxide protective layer, and it ended when the potential changed by less than 50 mV per half an hour [39].

The potentiodynamic approach provided a constant scan rate of 1 mv/s in the interval \(\pm\) of 1 V vs. OCP [40], whereas the current was extrapolated by intersecting the anodic and cathodic curves at \(\pm\) 0.01 V vs. OCP and \(\pm\) 0.1 V vs. OCP.

The tribocorrosion tests were carried out according to this procedure:

  1. 1.

    10 min without sliding for OCP stabilization.

  2. 2.

    30 min of sliding to monitor the synergistic effect of wear and corrosion.

  3. 3.

    20 min with no sliding to analyse the OCP trend after tribocorrosion impact.

In conclusion, the tribocorrosive currents were evaluated via potentiostatic technique by imposing open-circuit potential in accordance with the same motion range of the tribocorrosion tests. The current was thus estimated as the arithmetical mean of the values measured during the sliding.

The total volume loss (VTOT) [mm3] was estimated by a synergistic approach and, in particular, as indicated in Eq. 1, as the sum of mechanical (VM) and wear-accelerated corrosion (VS) [41]. The former was calculated by Archard’s law (Eq. 2) via a dry tribological experiment which yielded the Archard’s constant (K) equal to 9.82*10–4 [42], as done in other investigations in literature [43,44,45]. Consequently, by not involving the fluid, it is possible to isolate and define rigorously the only mechanical contribution.

$$V_{TOT} = V_{M} + V_{S}$$
(1)
$$V_{M} = \frac{K}{H} \cdot F_{N} \cdot s$$
(2)

With H hardness, the FN normal load and s total sliding equal the testing time x frequency × 2 × stroke length.

On the other hand, the synergistic part was determined by subtracting the mechanical wear from the total. The latter was evaluated both by the weighing method via a scale of sensitivity of 0.1 mg and by optical profilometry achieved by a Sensofar interferometric/optical laser microscope equipped with a lens of 5x, 20 × and 50 × of magnification. The procedure adopted also high-performance MountainsLab Premium 9 software [46] to process the wear analysis, which was conducted coherently with the ISO 25178-2:2021 standard. More precisely, the procedure starts by first removing the outliers due to errors during profilometer acquisition and filling the nonmeasured or missing points by matching the neighboring values and then by applying a low-pass filter with a cut-off λc of 0.08 mm, levelling by least-mean-square and removing the shape effect by a second-grade polynomial. The volume of the wear track was finally calculated by integrating the area below the plane of the unworn material [47].

3 Results and Discussion

In this section, the results obtained by the experimental tests are discussed. In detail, the potentiodynamic curves, the evolution of the open-circuit potential, the current and friction coefficient during a tribocorrosion test, and the wear estimation, both in terms of volume loss and percentage contribution, were reported as much as the particle analysis. In addition, by analysing the experimental data, the synergistic action was analytically modelled. First, the pure corrosion behavior of titanium alloys in different solutions was investigated and the current and potential are shown in Table 3 and Fig. 2, in good agreement with literature results [48]. Chemically speaking, these variables are a function of the strength of the oxide film formed [49] on the surface of the specimens (TiO2). In that sense, solutions 1, 3 and 4 present a positive potential in contrast with the 2, which results in only one negative potential. On the other hand, the highest corrosion currents are attributed to solutions 2-3-4, which were almost comparable but certainly greater than that medium 1. This behavior can be explained by taking into account the presence of salts such as sodium chloride, sodium bicarbonate and sodium lactate in these solutions, which strongly influence the corrosive response of titanium [50]. Moreover, for cathodic potentials, fluctuations in all solutions, except for the 2, were found: in that region, the stable oxide layer is clearly unformed since the potentials are far lower than the corrosion potentials [51], triggering different chemical reactions in accordance with the composition of the medium. Overall, the polarization resistances of all the solutions, which are 2096 \(\pm\) 1, 35 \(\pm\) 2, 23 \(\pm\) 1, and 30 \(\pm\) 1.5 KΩ, confirm the good corrosive response of titanium, which is a passive metal and therefore suitable for orthopedics [52] and dental applications. Nevertheless, wear particles are even a critical issue for our oral cavity and, unfortunately, a likely finding, especially around the implants, in cells and bone [53] but also in distal organs because of migration via blood flow [54]. Indeed, it was demonstrated that the particles may lead to clinical complications such as inflammation [55] and consequential loss of implant functionality.

Table 3 OCP and current values of the four solutions tested
Full size table
Fig. 2
figure 2

Potentiodynamic curves of the four solutions tested

Full size image

Concerning the tribocorrosion tests, the OCP trend is highlighted (Fig. 3). After the initial stabilization of the potential, when sliding started, a drop was noted because of the rupture of the protective oxide layer [56] characterized by continuous oscillations with no complete repassivation in which several phenomena may occur such as hydrogen embrittlement phenomena [57]. The maximum drops were estimated to be 265 ± 13, 75 ± 3.5, 70 ± 3, and 80 ± 4 mV after a few seconds of motion inception (2–10 s). Successively, the potential increases slowly due to the partial reformation of the oxide coating, almost reaching the initial value when the sliding stopped. In this regard, the discrepancies between the starting and final values were approximately 5–6 \(\pm\) 0.5 mV for Solutions 1, 2, and 3 but equal to 46 \(\pm\) 1 mV for the latter. This can be explained by considering that the medium 4 is more aggressive since it contains sodium lactate [58], leading to major material loss, as will be indicated in the next section.

Fig. 3
figure 3

OCP trend during a tribocorrosion test of the four solutions tested

Full size image

Figure 4 shows the evolution of the friction coefficient (COF), including that of the dry tribotests, whereas Fig. 5 shows the mean values. After a sharp increase lasted 100–200 s depending on the solution used, a steady-state composed of small oscillations [59] occurred because of the formation and destruction of the passive film. In addition, the two figures below show that the dry configuration has a higher friction coefficient, justifying the lubricating properties of Ringer’s solution [60], with no fluid film regime but only boundary. Nevertheless, the lubricating film is responsible for tribocorrosion enhancement [61], promoting greater total wear. Focusing instead on the kind of solution, the 2 had the lowest COF (0.24 \(\pm\) 0.02). The other values for medium 1, 3 and 4 friction were 0.32 \(\pm\) 0.01, 0.35 \(\pm\) 0.03 and 0.36 \(\pm\) 0.02, respectively. Hence, in addition to tribological properties such as load or sliding speed [62], the chemical composition has a notable effect on friction, and in that sense, sodium bicarbonate and lactate had greater effects on the COF than sodium and potassium chloride.

Fig. 4
figure 4

COF evolution of tribocorrosive and dry tests

Full size image
Fig. 5
figure 5

Mean friction coefficient values

Full size image

By combining Figs. 3–4, it is almost evident that the OCP and COF follow the same trend [63]: when sliding started, the friction increased and the potential decreased, followed by the same oscillations caused by the mechanochemical interactions between the specimen, alumina ball and corrosive medium.

Figures 6–7 represent the current trend during the tribocorrosion tests, which was also compared with that obtained via the potentiodynamic test. In this way, the impact of sliding and, in particular, of the mechanical aspect can be easily observed. First, the evolution of the tribocorrosive current is shown in Fig. 6. Before and after the motion, the current is almost zero, indicating that no chemical reactions occur on the titanium sample. In contrast, when movement was imposed, an evident jump could be noted for all the solutions due to the galvanic coupling between the active and passive regions of the titanium alloy [64]. In addition, the mean outcomes are shown in Table 4. As expected, the values are approximately one order of magnitude greater than those of corrosive materials [65] as a consequence of mechanical wear-induced corrosion. However, some differences among the four solutions emerged: if the current of medium 1 was before much lower than the other, then it was comparable with the solutions 2–3 because of the counterpart action. This particular behavior can be observed in the medium 4, where the latter reached very high peaks due to the presence of lactic acid. In fact, during the tribocorrosion test, the removal of the protective layer by the alumina spheres facilitated acid attack with a considerable increase in titanium corrosion. Moreover, the repassivation time, estimated as the time requiring to the OCP to stabilize (fluctuations lower than 1 mV) after the motion stop, of this solution was approximately 250 s compared to 100–150 s for the other media.

Fig. 6
figure 6

Tribocorrosive current trend of the four solutions tested

Full size image
Fig. 7
figure 7

Tribocorrosive current and friction coefficient relationship for the four solutions tested

Full size image
Table 4 Corrosive and tribocorrosive currents mean values of the four solutions tested
Full size table

Finally, the current was investigated in comparison with the friction coefficient, as shown in Fig. 7. This relationship was the object of interest of other works in the literature, such as Stachowiak and Zwierzycki [66], who defined the total current as the sum of several currents originating from activated contact asperities, or experimentally by Sun and Rana [67]. When the counterpart passes over the titanium surface, the microjunctions formed in the coupling are destroyed by the asperities [68], which detach the oxide particles that protect the sample; these particles can act as third bodies if they are trapped in the coupling or are ejected from the wear track. In this phase, the friction and the current increase[69]. Immediately after, partial repassivation begins, leading to a reduction in both but not to the same extent since the velocity of the pin is far greater than that of the repassivation pin. At first glance, no correlations were found between the mean COF and current for the four solutions. To correctly describe this behavior, it is necessary to emphasize that both passivation phenomena and wear mechanisms should be considered. Since the alumina balls are rough, microcutting is likely to occur, the effectiveness of which depends on the tribochemical coupling formed during the tests. In that sense, if medium 2 is neglected, higher currents determine a greater friction coefficient [70] as a result of surface deformation and depassivation. This process occurs partially when medium 2 is adopted because the oxide layer is more stable with a constant friction coefficient shortly after 100 s.

3.1 Wear Analysis

The total volume loss of titanium alloy immersed in the four solutions was highest in the medium 4 and equal to 0.137 \(\pm\) 0.007 mm3. Consequently, considering that the mechanical wear is exactly the same, the difference between the outcomes is explained by the synergistic effect. In this regard, the effect of lactic acid, obtained by the chemical reaction between water and sodium lactate, also significantly impacts on the material loss when the protective layer is removed by the sliding of the counterpart. The other tests provided the following results: 0.121 \(\pm\) 0.006, 0.096 \(\pm\) 0.005 and 0.131 \(\pm\) 0.006 mm3 for solutions 1, 2 and 3, respectively, which are in agreement with those reported in the literature [71]. The wear rates were 3.36 \(\bullet\) 10–4, 2.67 \(\bullet\) 10–4, 3.64 \(\bullet\) 10–4 and 3.81 \(\bullet\) 10–4 mm3/Nm. The wear tracks are shown in Figs. 8–9, with maximum and average depths respectively equal to 25, 20, 35, 45 μm and 20, 16, 21 and 23 μm. The significant differences of the maximum depth can be explained by considering the effect of solution corrosivity, especially for the last two solutions, promoting thus the penetration of the alumina ball into titanium surface. On the other hand, the average ones are of the same magnitude and proportional to total material loss since their direct correlation proved in other experimental [72] and numerical tests [73]. By subtracting the mechanical wear from these values (Eq. 1), the following synergy wear can be easily obtained: 0.03, 0.005, 0.04 and 0.046 mm3. By correlating the chemical composition reported in Table 2 and the volume loss, COF (Fig. 5), corrosive and tribocorrosive currents (Table 4), it is possible to estimate the effect of a single chemical. Hence, the following comparisons were considered:

  • Solution 3 with respect to Solution 2: 1.9 g/L sodium bicarbonate but less than 0.07 g/L calcium chloride dihydrate;

  • Solution 3 with respect to Solution 1: 9 g/L sodium chloride and 0.4 g/L potassium chloride;

  • Solution 1 with respect to Solution 2: 0.9 g/L sodium bicarbonate in addition to 9 g/L sodium chloride and 0.07 g/L calcium chloride dihydrate;

  • For Solution 4 with respect to Solution 3, 5.42 g/L sodium lactate and 0.1 g/L calcium chloride dihydrate were used more, but 3 g/L sodium chloride and 2.1 g/L sodium bicarbonate less.

Fig. 8
figure 8

Wear tracks of titanium grade V immersed in solutions 1 (a) and 2 (b)

Full size image
Fig. 9
figure 9

Wear tracks of titanium grade V immersed in solutions 3 (c) and 4 (d)

Full size image

For the first comparison, all the outcomes increased, particularly the synergy volume, which was eight times greater (1.37 times greater the total wear), with the exception of the tribocorrosive current, which was almost comparable. This can be explained by considering the greater stability of oxide layer for solution 2 due to the major quantity of calcium chloride [74]. Indeed, the latter was characterized by less marked fluctuations of OCP (Fig. 3) and by lower friction coefficient (Fig. 4) underling the key role played by the oxide layer against both tribological and chemical wear. Concerning the second one, the major concentrations of potassium and sodium chloride again induced greater material loss but not to the extent of the previous case. Indeed, the synergy and the total wear were, respectively 1.33 and 1.08 greater in Solution 3 than in Solution 1. Analogously for the friction coefficient. On the other hand, the current was far greater, above all that of the corrosive tests. In that sense, these two salts enhanced the pure corrosion of titanium. The medium 3 provided an increase in material loss on the order of 6 and 1.26-fold for synergy and total wear, respectively, because of the presence of sodium bicarbonate (third comparison). In contrast, the current was lower than that of the other solutions [75]. Last, when sodium lactate is added, a slight increase in the COF and wear can be observed, whereas the tribocorrosive current becomes 15 times greater.

In summary, sodium and potassium chloride caused more corrosion, lactic acid had the highest wear and tribocorrosive current, calcium chloride had a more protective oxide layer, and sodium bicarbonate was also correlated with wear due to the susceptibility of titanium to hydrogen [76] as underlined in Fig. 10 with presence of microfractures [77].

Fig. 10
figure 10

Hydrogen embrittlement for solution 3 with presence of microfractures. Image obtained by the interferometric lens with 50 × of magnification

Full size image

The main mechanisms of tribocorrosive wear are abrasion, adhesion, fretting, fatigue and oxidation [78]. Considering the coupling of titanium and alumina as much as the difference in hardness, the dominant difference was the abrasive with ploughing grooves parallel to the sliding motion coupled with oxide patches [79] as shown in Fig. 11. By analysing the grooves generated by the plastic deformation of contacting asperities [80], larger and deeper sites are almost evidently affected by solution chemical attack in terms of localized pitting corrosion. In addition, as shown in Fig. 4, where the friction coefficient tends to stabilize or decrease, the presence of third bodies is probably removed [81]. In contrast, no wear tracks were found on the alumina balls where few metal transfers were observed [82] of approximately 0.05 mg, which is one order of magnitude lower than that of the titanium samples. Similar results, in terms of total wear rate and friction coefficient, can be appreciated when zirconia was adopted [83]. Borrás et al. instead evaluated the zirconia-yttria against titanium grade IV in artificial saliva [84]. In their investigation, no wear tracks were observed on the counterpart but titanium metal transfer at anodic potentials. Corne et al.[85] analysed different dental implant-abutment couplings in fretting-corrosion regime as titanium grade V against titanium grade V, titanium grade IV, yttria-tetragonal zirconia and titanium grade IV vs yttria-tetragonal zirconia in human saliva noting that the coupling titanium grade IV/Y-TZP produced the lowest volume loss whereas on the counterpart it was negligible. Sikora et al.[86] found out comparable trends for zirconia/Ti-6Al-4 V pair which, although suffered more mechanical impact than titanium/titanium, had the least wear thanks to zirconia corrosion resistance. Nevertheless, the latter was supposed to be transferred in titanium surface as result of OCP increase. Feyz et al.[87] studied the coupling zirconia-titanium grade V in PBS solution for diverse values of load and frequency. Both the variables highlighted complex interactions with the total material loss of titanium whereas the zirconia ball was not damaged.

Fig. 11
figure 11

Section of the wear track for solution 1 obtained by the interferometric lens with 50 × of magnification

Full size image

Moreover, a particle analysis was carried out to more deeply analyse the kind of wear debris in terms of roughness, texture direction, equivalent diameter, form factor, aspect ratio, roundness, orientation, and number of particles. Indeed, the impact of these particles on human tissues, from a biological point of view, is highly relevant. In this regard, the texture directions were evaluated by the three largest peaks but not considering the secondary peaks at less than 5° of an already detected peak. The equivalent diameter is the diameter of the disk whose area is equal to the area of the particle (Heywood diameter). The form factor (Eq. 3) describes the shape of the particle, the aspect ratio (Eq. 4) is the form of the particle if it is a disk or oblong, the roundness (Eq. 5) if the latter is circular, and the orientation is the angle between the largest axis of the particle and the x-axis. Finally, the number of particles evaluated by the watershed algorithm with pruning criteria, applied to the hill motifs, was merged if they covered less than 0.1% of the surface area. Tables 5, 6, 7 show the achieved outcomes.

$$Form\;Factor = \frac{4\pi Area}{{(perimeter)^{2} }}$$
(3)
$$Aspect\;Ratio = \frac{{D_{\max } }}{{D_{\min } }}$$
(4)
$$Roundness = \frac{4Area}{{\pi (D_{\max } )^{2} }}$$
(5)
Table 5 Roughness values of the four solutions tested
Full size table
Table 6 Texture directions of the four tested solutions
Full size table
Table 7 Particle parameters of the four solutions tested
Full size table

Table 5 represents the arithmetic roughness (Sa), the root mean square height (Sq), the skewness and (Ssk) kurtosis factor (Sku), all of which refer to the worn area. Before the tribocorrosive tests, the titanium surfaces showed the following values 0.70 μm, 0.88 μm, − 0.03, and 3.2. After the experimental trials, as expected and considering that the alumina spheres were not very smooth, the roughness strongly increased by more than one order of magnitude in the medium 4. In contrast, solution 2 showed the lowest values of Sa and Sq as a result of minor wear. Moreover, the surface distribution of the titanium surface was at the beginning almost normal and symmetrical around the mean plane. After the tests, the skewness values showed dissimilarities between the solutions 1-2-3 and the 4 since the former were below the mean plane whereas the latter above it (negative Ssk) presenting thus sharp valleys and round peaks [88] as a result of the material loss process induced. Besides, the solution 4 had the lowest value of kurtosis indicating low peaks and valleys and thus a smaller real contact area respect to the other threes. A lower kurtosis may also promote the corrosive attack of the medium due to the better attitude to form lubricating film [89]. In conclusion, the fewest kurtosis and skewness were correlated with the greatest friction coefficient, tribocorrosive wear and current.

Concerning the texture directions, the starting one was isotropic with a main direction near 80°, which, again, was strictly altered, as reported in Table 6. Finally, the number of particles was proportional to the tribocorrosive wear and was estimated for the four solutions to be 77, 34, 103, and 244 n°/mm2. In addition, if the orientations of the four wear tracks are comparable, the other parameters indicate that the solutions 1, 3, and 4 have different morphologies, in contrast to the 2, especially for roundness and aspect ratio. First, the form factor indicates that no track has a perfect circular shape (< 1), and the lowest value is attributed to medium 2, which also has the highest aspect ratio and equivalent diameter. This means that the lowest COF and wear induced fewer oblong particles along the sliding direction with larger diameters. In contrast, the remaining solutions have a more circular shape and smaller dimensions, especially in solution 4, where the increased number is due to more pronounced tribocorrosion.

3.2 Synergistic Wear

In this section, an attempt was made to better model the synergistic effect of tribocorrosive wear, which is the sum of the mechanical and synergistic effects (Eq. 1). The percentages of the four solutions (Fig. 12) of the former and the latter were 75.21–24.79% for medium 1, 94.79–5.21% for medium 2, 69.47–30.53% for medium 3 and 66.42–33.58% for medium 4. Hence, the combined action of mechanical and chemical wear was evaluated in the range of 5–35% [90], resulting in nonnegligible total wear. To analytically model it, the following relationship (Eq. 6) was considered[21, 91]:

$$V_{S} = \frac{{k_{c} \cdot Q_{P} \cdot MM \cdot s \cdot (F_{N} /H)^{0.5} }}{n \cdot F \cdot \rho }$$
(6)

where kc is the synergistic constant, MM is the molecular weight, n is the number of electrons exchanged and equals to 4, F is the Faraday constant equal to 96,485 C/mol and ρ is the density. QP is the charge density needed to form a passive film either from the bare metal or when it is removed [92], obtained by potentiodynamic tests in accordance with Eq. 7:

$$Q_{P} = \frac{{\int\limits_{{t_{1} }}^{{t_{2} }} {I(t)\;dt} }}{A}$$
(7)

where t1 and t2 are the two instants of time in which the potential shifts from cathodic to anodic, I(t) the current measure during the potentiodynamic test and A is the wear track surface. The obtained values were 1.17 \(\pm\) 0.06, 0.95 \(\pm\) 0.05, 1.53 \(\pm\) 0.04, and 1.39 \(\pm\) 0.07 C/m2 [22], respectively.

Fig. 12
figure 12

Wear contributions of the four solutions tested

Full size image

The latter was the last input for Eq. 6, which was successively compared with the experimental data, as shown in Fig. 13, where the synergistic wear rate (WS) was correlated with the mechanic-chemical parameters, such as the charge density expressed in C/m2, the normal load in N and the hardness H in MPa.

Fig. 13
figure 13

Correlations between the synergistic wear rate and mechanical-chemical parameters

Full size image

The determination coefficient (R2) was 0.83, confirming, in the limitation of the number of experiments, the comparability between the model and experimental results. By rewriting Eq. 6, it is also possible to evaluate the synergistic rate contribution (Eq. 8):

$$W_{S} = K_{S} \cdot Q_{P} \cdot (F_{N} /H)^{0.5}$$
(8)

where WS is the synergistic wear rate and KS indicated in Eq. 9:

$$K_{S} = \frac{{k_{c} \cdot MM \cdot v}}{n \cdot F \cdot \rho }$$
(9)

With v sliding velocity.

Nevertheless, one of the most critical issues is the real force exchanged by the asperities in contact [93], which involves both the lubrication regime and topography of the sample. An interesting recent idea was proposed by duo Cao-Mischler, who investigated the film thickness via the Hamrock and Dowson relationship and the Abbott-Firestone curve for the asperity profile [31]. Unfortunately, as stated before, lubrication is essentially boundary reason why another approach should be undertaken. In this light, a linear relationship was found between the friction coefficient and synergy (Eq. 10), with R2 equal to 0.92 (Fig. 14), which was also confirmed in our other work [94]. The latter provides the input for the correction of the normal load (Eq. 12) presented in Eq. 6 via a novel coefficient. Indeed, the tribological meaning of COFs is that microcontacts are formed between surface peaks [95] in which the lubricant cannot completely separate the asperities. Consequently, the greater the friction is, the greater the number of asperities in contact and the greater the load exchanged. By applying this concept, a better fit was noted, with the determination coefficient increasing from 0.83 (previous model, named Model 1) to 0.89 (new model, named Model 2), as underlined in Fig. 15.

$$y = 0.78x$$
(10)

where x is the value of the COF and y the synergy percentage. Equation 10 was formulated respecting the mathematical conditions reported in Eq. 11:

$$V_{S} (\% ) = 0\;\;if\;COF = 0$$
(11)
Fig. 14
figure 14

Synergy-COF linear relationship with a determination coefficient R.2 of 0.92

Full size image
Fig. 15
figure 15

Models 1 and 2 with their own determination coefficients. In the second case, the normal force is modified by the coefficient “y”

Full size image

This relation implies that there is no synergy when the friction is close to 0 (fluid-film lubrication). On the other hand, it is appropriate to take into account that the solutions are composed of corrosive elements such as salts that can cause corrosive wear. Nevertheless, in the case of titanium, it is absolutely negligible with respect to the mechanical effect, which is why this hypothesis is correct.

$$V_{S} = \frac{{k_{c} \cdot Q_{P} \cdot MM \cdot s \cdot (y \cdot F_{N} /H)^{0.5} }}{n \cdot F \cdot \rho }$$
(12)

in which y is the coefficient extrapolated by Eq. 10 and introduced for the normal load.

Overall, these trends were obtained for the coupled titanium-alumina alloy, and it is reasonable to believe that the model should be calibrated for different tribological pairs. In fact, the pin, the type of solution and the tribological-chemical conditions are relevant variables in the tribocorrosion environment.

4 Conclusions

Tribocorrosion is a common and impactful phenomenon in biomedical engineering and constitutes a relevant field of investigation. The main aim of the proposed work is to rigorously define the tribocorrosive behavior of typical dental implant materials for long-term survival of the prosthesis. In this regard, the manuscript evaluated the effect of the chemical composition of biological Ringer’s solutions on the tribocorrosive response of coupled titanium grade V-alumina. The analyses involved several approaches, such as open-circuit potential, potentiostatic and potentiodynamic techniques, dry and tribocorrosive experimental tests. In addition, an attempt was made to propose a novel adjustment of the theoretical models reported in the scientific literature for synergistic wear calculations. The experiments confirmed that the solution plays a key role in tribocorrosion, as confirmed by the following main results:

  1. 1.

    The solution containing sodium lactate induced the highest friction coefficient, tribocorrosive current and total wear.

  2. 2.

    Sodium and potassium chloride resulted in more pronounced corrosion

  3. 3.

    Sodium bicarbonate was also correlated with wear due to titanium susceptibility to hydrogen

  4. 4.

    Calcium chloride promoted the formation of a stronger oxide layer

  5. 5.

    The synergistic wear model was better specified for the normal load by introducing a new coefficient that originated from the linear relationship between the friction coefficient and synergy. In fact, by the comparison with experiments the determination coefficient (R2) increased from 0.83 to 0.89.

Overall, further experimental tests under other tribocorrosive conditions are necessary to confirm and validate the results proposed. The tests should involve different tribological conditions such as load, frequency, pin geometry, and chemical properties such as pH or other solution compositions.