1 Introduction

A good understanding of the wave conditions in the coastal area is fundamental for designs of coastal structures. There has been active activities at the Norwegian coast, such as the floating bridges planned to connect the Norwegian fjords along the E39 coastal highway (Ellevset 2012; Dunham 2016). A typical Norwegian fjord is characterised with deep water condition, fast-changing bathymetry and irregular coastlines. These conditions make the understanding of the coastal wave conditions a challenging task. So far, the most reliable source of wave information are the in-situ wave measurements. However, the number of deployable wave gauges is limited and thus wave information can only be collected at few discrete locations. As a result, the complicated wave transformation pattern in the fjords is very hard to be detected. Physical experiments have been a common practice to investigate wave conditions in coastal areas. However, to set up a physical model for the complicated Norwegian coast is financially demanding and time consuming. Physical wave basins are also usually less flexible to adapt to such a wide range of topographies and scenarios. For example, there are at least seven major fjord-crossings (Dunham 2016) along in the E39 project and wave conditions vary in each fjord. With the development of numerical techniques and improving computational facilities, numerical wave modelling is a good alternative to present the wave fields in the entire area with great time-efficiency and flexibility.

Phase-averaging spectral wave models have been used in the modelling of waves inside the fjords (Fergstad et al. 2018). In this approach, the free surface elevation and the wave phases are not resolved. Instead, the models solve the wave energy action balance equation and provide primarily knowledge on the wave energy distribution. Thus, these models are very computationally efficient. However, this type of models have limited capacity for strongly non-linear phenomena such as strong diffraction around large obstacles (Thomas and Dwarakish 2015). The islands and archipelagos, which are commonly found near the entries of fjords, tend to create strong diffraction. Fergstad et al. (2018) also reported that the significant wave height \(H_s\) inside the fjord predicted by the spectral wave model tend to be lower than measurements, which are most likely due to insufficient representation of wave diffraction. In addition, the spectral wave models do not provide time-domain information, which is needed for inhomogeneity and incoherence analysis of the wave fields as well as future fatigue analysis of the structures.

In contrast, phase-resolving wave models resolve the free surface elevation and the vertical information of the water column. They are able to represent nearly all wave transformations and provide time-domain information in the entire domain. However, the validity of many existing phase-resolving wave models is limited by the complex bathymetry, coastlines and the large domain of interest in the Norwegian fjords. The deep water condition and fast-varying bathymetry tend to exceed the validity of depth-averaged shallow water equation (SWE) based models such as the Boussinesq-type models (Madsen et al. 1991; Madsen and Sørensen 1992; Nwogu 1993) and mild-slope models (Demirbilek and Panchang 1998). Several efforts are made to improve the shallow-water equation based models to represent the deep water wave dispersion relation. For example, Madsen and Schäffer (1998) and Gobbi et al. (2000) achieved better representation of water waves in deeper water conditions by increasing the order of the Boussinesq terms. Wave simulations are made possible up to \(kh=39\) through the work from Madsen et al. (2002, 2003), k being the wave number, h being the water depth. However, this method tends to increase the complexity of the equation systems which increases the probability of numerical instability. The trough instability in the Boussinesq approach has been examined in detail by Madsen and Fuhrman (2020), where the applicable scenarios concerning Nyquist wavenumber and deepest trough are identified for different Boussinesq formulations and a remedy by including the exact linear dispersion relation is proposed for future researches. Multi-layer non-hydrostatic models (Lynett and Liu 2004; Stelling and Duinmeijer 2003; Zijlema and Stelling 2005) are able to represent deep water waves with an increasing number of vertical layers while sacrificing computational speed (Monteban 2016). A different type of non-hydrostatic model assumes a quadratic profile of the non-hydrostatic pressure (Jeschke et al. 2017; Wang et al. 2020b). However, the best performance of this approach is limited to up to a water depth to wave length ratio \(d/h=0.25\) (Wang et al. 2020b). In general, it remains challenging to improve shallow-water based models for deep water conditions in the fjords without sacrificing numerical performance.

Potential flow theory-based models are less restricted to water depth condition in comparison to SWE-based approach. Varying bathymetry can also be included in many potential flow models, such as the boundary element method (BEM) models (Grilli et al. 1994, 2001) and finite difference (FDM) fully nonlinear potential flow (FNPF) models (Li and Fleming 1997; Bingham and Zhang 2007; Engsig-Karup et al. 2009). With improved methods, the high-order spectra (HOS) wave models (Ducrozet et al. 2012; Bonnefoy et al. 2006) are also able to include varying sea floor in their simulations (Raoult et al. 2016; Yates and Benoit 2015). However, there are few efficient solutions to include irregular coastlines in a potential flow model. The finite difference model OceanWave3D (Engsig-Karup et al. 2009) uses a curvilinear grid system to adapt to the irregular coastline boundaries. This approach requires demanding case-dependent grid generation for complicated coastal geometries. With the archipelagos outside the Norwegian fjord that play important roles in wave propagation, an efficient way of including the coastline geometry and a reliable boundary condition treatment at the coastlines are still required.

Computational fluid dynamics (CFD) models provide the most detailed flow information with few assumptions on water depth or coastlines but have high demand on computational resources and computational time, especially when compared to the SWE and FNPF models. It was reported that the computational speed of the SWE and FNPF models are faster than the CFD models in the order of \(10^2\) to \(10^3\) for the same accuracy using the same numerical framework (Wang et al. 2020a). The spatial scale of Norwegian fjords is up to tens of kilometres in each horizontal dimensions, which makes the application of CFD in such situation nearly impossible with the currently available computational resources.

As a result, there are very few attempts of phase-resolved wave modelling in the Norwegian fjords. Wang et al. (2017) reported large-scale wave simulations in a Norwegian fjord with a CFD model. However, the reported calculation time to real time ratio is about 60 when using 320 processors on a supercomputer, meaning a standard 3-h simulation is expected to take nearly one week even with coarse grid. This confirms the limitation of the CFD application for wave propagation modelling in such situation.

In a recent development, a fully nonlinear potential flow model REEF3D::FNPF is developed at the Norwegian university of science and technology (Wang et al. 2022; Bihs et al. 2020). The model introduces a novel level-set method based coastline identification algorithm that captures the coastlines and applies the boundary conditions effectively over the entire domain. Equipped with the new coastline algorithm and the proven breaking wave algorithms, the model has been validated against benchmarks and experiments regarding breaking waves, irregular coastlines and different wave transformations (Wang et al. 2022). An effective procedure to produce extreme irregular sea state with different breaking wave scenarios was also presented (Wang et al. 2021a, b). The model is found to be around 1000 times faster than a CFD model for most hydrodynamic and free surface wave applications (Wang et al. 2020a). The computational efficiency of this potential flow solver enables large-scale phase-resolved simulations. As part of the open-source hydrodynamics framework REEF3D (Bihs et al. 2016), the model also inherits the high-order discretisation schemes and parallelised high performance computation capacity, which were previously presented in a wide range of applications related to ocean engineering problems (Alagan Chella et al. 2019; Aggarwal et al. 2020; Ahmad et al. 2020; Martin et al. 2021a, b). These numerical implementations enable accurate representations of complicated non-linear wave transformations and a great computational scalability for large-domain long duration simulations. As a result, the challenges of water depth conditions, nonlinear wave transformation, computational efficiency and the inclusion of irregular coastlines are all addressed with REEF3D::FNPF, making it an attractive tool for an accurate calculation of large-scale wave propagation at the Norwegian coast.

Previously, most wave environment analyses have been performed with field measurement (Cheng et al. 2019, 2021) and phase-averaging spectral wave models (Stefanakos et al. 2020). With the advance of the numerical model, the large-scale phase-resolving wave simulations are made possible at the Norwegian fjords featuring drastically varying bathymetry and coastlines. In this work, REEF3D::FNPF is used to simulate wave propagation and transformation at two different Norwegian fjords on the spatial scale of tens of kilometres in each horizontal dimension.

To the best knowledge of the authors, this is the first time that the phase-resolving modelling approach is used for design purpose and engineering analysis at the Norwegian fjords. The work will examine the wave fields in the fjords to offer new insights from different perspectives. This includes: 1) the comparison between the phase-averaging and the phase-resolving modelling approach in the complex coastal condition, 2) the inhomogeneity in the fjords due to the complex wave transformations and 3) the incoherence of waves along the bridge span at the potential fjord-crossing locations. Both wave field inhomogeneity and incoherence are of great significance to the moored floating bridge designs (Dai et al. 2020). Though wind-forcing and surface currents have significant influence on the wave fields in the fjords (Christakos et al. 2020, 2021; Christakos 2021), the presented work isolates the complex marine system and focuses on the swell wave propagation and transformation in the fjord, leaving the inclusion of other marine elements for further studies. With the presented analysis, the authors aim to demonstrate the potential of large-scale phase-resolved modelling for industry applications and the important information that can be extracted from such simulations and to offer valuable considerations for the floating bridge design and other coastal engineering perspectives.

2 Numerical model

2.1 Governing equations

The governing equation for the REEF3D::FNPF is the Laplace equation:

$$\begin{aligned} \frac{\partial ^2\phi }{\partial x^2}+\frac{\displaystyle \partial ^2\phi }{\displaystyle \partial y^2}+\frac{\displaystyle \partial ^2\phi }{\displaystyle \partial z^2}=0. \end{aligned}$$
(1)

In order to solve for the velocity potential \(\phi \), the free surface boundary conditions and the bottom boundary condition are required. The fluid particles at the free surface remain at the surface and the pressure in the fluid is equal to the atmospheric pressure. These conditions form the kinematic and dynamic free surface boundary conditions at \(z=\eta (x,y,t)\). In addition, the velocity component normal to the sea bed is zero, since the fluid particle cannot move through the solid boundary, which form the bottom boundary condition. These boundary conditions are summarised in the following:

$$\begin{aligned}&\frac{\partial \eta }{\partial t}=-\frac{\partial \eta }{\partial x}\frac{\partial \widetilde{\phi }}{\partial x}-\frac{\partial \eta }{\partial y}\frac{\partial \widetilde{\phi }}{\partial y} +{\widetilde{w}}\left( 1+\left( \frac{\partial \eta }{\partial x}\right) ^2+\left( \frac{\partial \eta }{\partial y}\right) ^2\right) , \end{aligned}$$
(2)
$$\begin{aligned}&\frac{\partial \widetilde{\phi }}{\partial t}=-\frac{1}{2}\left( \left( \frac{\displaystyle \partial \widetilde{\phi }}{\displaystyle \partial x}\right) ^2+\left( \frac{\displaystyle \partial \widetilde{\phi }}{\displaystyle \partial y}\right) ^2\right. \nonumber \\&\left. \quad -{\widetilde{w}}^2\left( 1+\left( \frac{\displaystyle \partial \eta }{\displaystyle \partial x}\right) ^2+\left( \frac{\displaystyle \partial \eta }{\displaystyle \partial y}\right) ^2\right) \right) -g\eta . \end{aligned}$$
(3)
$$\begin{aligned}&\frac{\partial \phi }{\partial z}+\frac{\partial h}{\partial x}\frac{\partial \phi }{\partial x}+\frac{\partial h}{\partial y}\frac{\partial \phi }{\partial y}=0, \;\;z=-h, \end{aligned}$$
(4)

where \(\eta \) is the free surface elevation, \(\widetilde{\phi }=\phi ({\textbf {x}},\eta , t)\) is the velocity potential at the free surface, \({\textbf {x}}=(x,y)\) represents the coordinates in the x–y plane, \(\widetilde{w}=\partial \widetilde{\phi }/\partial z |_{z=\eta }\) is the vertical velocity component at the free surface and \(h=h({\textbf {x}})\) is the water depth measured from the still water level to the bottom.

The Laplace equation together with the boundary conditions at the free surface and the bottom is solved on a \(\sigma \)-coordinate grid. The \(\sigma \)-coordinate grid follows the water depth variations and free surface evolutions. The transformation from a Cartesian coordinate to a \(\sigma \)-coordinate grid is achieved as follows:

$$\begin{aligned} \sigma =\frac{z+h\left( {\textbf {x}}\right) }{\eta ({\textbf {x}},t)+h({\textbf {x}})}. \end{aligned}$$
(5)

The velocity potential after the \(\sigma \)-coordinate grid transformation is denoted as \(\varPhi \). The boundary conditions and the governing equation in the \(\sigma \)-coordinate grid are written in the following format:

$$\begin{aligned}&\varPhi =\widetilde{\phi }\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; ,\sigma =1; \end{aligned}$$
(6)
$$\begin{aligned}&\frac{\partial ^2\varPhi }{\partial x^2}+\frac{\partial ^2\varPhi }{\partial y^2}+\left( \frac{\partial ^2\sigma }{\partial x^2}+\frac{\partial ^2\sigma }{\partial y^2}\right) \frac{\partial \varPhi }{\partial \sigma }+2\left( \frac{\partial \sigma }{\partial x}\frac{\partial }{\partial x}\left( \frac{\partial \varPhi }{\partial \sigma }\right) +\right. \nonumber \\&\quad \left. \frac{\partial \sigma }{\partial y}\frac{\partial }{\partial y}\left( \frac{\partial \varPhi }{\partial \sigma }\right) \right) +\left( \left( \frac{\partial \sigma }{\partial x}\right) ^2+\left( \frac{\partial \sigma }{\partial y}\right) ^2+\left( \frac{\partial \sigma }{\partial z}\right) ^2\right) \nonumber \\&\quad \frac{\partial ^2\varPhi }{\partial \sigma ^2}=0 \;\;\;,0\le \sigma <1; \end{aligned}$$
(7)
$$\begin{aligned}&\left( \frac{\partial \sigma }{\partial z}+\frac{\partial h}{\partial x}\frac{\partial \sigma }{\partial x}+\frac{\partial h}{\partial y}\frac{\partial \sigma }{\partial y}\right) \frac{\partial \varPhi }{\partial \sigma }+\frac{\partial h}{\partial x}\frac{\partial \varPhi }{\partial x}+\frac{\partial h}{\partial y}\frac{\partial \varPhi }{\partial y}=0 \nonumber \\&\qquad \sigma =0. \end{aligned}$$
(8)

When the velocity potential \(\varPhi \) is solved in the \(\sigma \)-coordinate grid, the fluid particle velocities are calculated as the following:

$$\begin{aligned}&u\left( {\textbf {x}},z\right) =\frac{\partial \varPhi \left( {\textbf {x}},z\right) }{\partial x}=\frac{\partial \varPhi \left( {\textbf {x}},\sigma \right) }{\partial x}+\frac{\partial \sigma }{\partial x}\frac{\partial \varPhi \left( {\textbf {x}},\sigma \right) }{\partial \sigma }, \end{aligned}$$
(9)
$$\begin{aligned}&v\left( {\textbf {x}},z\right) =\frac{\partial \varPhi \left( {\textbf {x}},z\right) }{\partial y}=\frac{\partial \varPhi \left( {\textbf {x}},\sigma \right) }{\partial y}+\frac{\partial \sigma }{\partial y}\frac{\partial \varPhi \left( {\textbf {x}},\sigma \right) }{\partial \sigma }, \end{aligned}$$
(10)
$$\begin{aligned}&w\left( {\textbf {x}},z\right) =\frac{\partial \varPhi \left( {\textbf {x}},z\right) }{\partial z}=\frac{\partial \sigma }{\partial z}\frac{\partial \varPhi \left( {\textbf {x}},\sigma \right) }{\partial \sigma }. \end{aligned}$$
(11)

The Laplace equation in the transformed domain is discretised using second-order central difference methods on a Cartesian grid in the horizontal xy-plane. It is then solved using a parallelised geometric multi-grid preconditioned conjugated gradient solver provided by hypre (van der Vorst 1992). The gradient terms of the free-surface boundary conditions are discretised with the 5th-order Hamilton-Jacobi weighted essentially non-oscillatory (WENO) scheme (Guang-Shan and Chi-Wang 1996). The time-dependent terms are treated with a 3rd-order accurate total variation diminishing (TVD) Runge–Kutta scheme (Shu and Osher 1988). Adaptive time stepping can be used by controlling a constant temporal factor that is equivalent to the Courant–Friedrichs–Lewy (CFL) condition:

$$\begin{aligned} \begin{aligned} c_u&= \frac{\textrm{d}x}{\left| max(u_{\textrm{max}}, 1.0\sqrt{9.81*h_{\textrm{max}}})\right| }, \\ c_v&= \frac{\textrm{d}x}{\left| max(v_{\textrm{max}}, 1.0\sqrt{9.81*h_{\textrm{max}}})\right| }, \\ c_{tot}&= min(c_u, c_v), \\ dt&=c_{tot}CFL, \end{aligned} \end{aligned}$$
(12)

where \(u_{\textrm{max}}, v_{\textrm{max}}\) are the maximum particle velocities in x and y directions at the free surface, \(h_{\textrm{max}}\) is the maximum water depth.

The model is fully parallelised following the domain decomposition strategy with ghost cells exchanging and updating information from the neighbouring processors via Message Passing Interface (MPI). The parallel computation greatly enhances the computational efficiency by utilising multiple processors for one simulation.

In the \(\sigma \)-grid arrangement, a stretching function is used for the vertical cell sizes to ensure a denser grid close to the free surface:

$$\begin{aligned} {\sigma _k} = \frac{\sinh \left( -\alpha \right) -\sinh \left( \alpha \left( \frac{k}{N_z} - 1\right) \right) }{\sinh \left( -\alpha \right) }, \end{aligned}$$
(13)

where \(\alpha \) is the stretching factor and k and \(N_z\) stand for the index of the grid point and the total number of cells in the vertical direction.

2.2 Wave generation, dissipation and breaking

In this study, the relaxation method (Mayer et al. 1998) is used for the wave generation. The following relaxation function is used in the numerical model:

$$\begin{aligned} \varGamma (\widetilde{x})=1-\frac{e^{(\widetilde{x}^{3.5})}-1}{e-1}\ for\ \widetilde{x}\in [0;1], \end{aligned}$$
(14)

where \(\widetilde{x}\) is scaled to the length of the relaxation zone. The free surface velocity potential \(\widetilde{\phi }\) and the surface elevation \(\eta \), are increased to the theoretical values in the wave generation zone:

$$\begin{aligned} \widetilde{\phi }(\widetilde{x})_\textrm{relaxed}&=\varGamma (\widetilde{x})\widetilde{\phi }_\textrm{analytical}+(1-\varGamma (\widetilde{x})) \widetilde{\phi }_\textrm{computational}, \end{aligned}$$
(15)
$$\begin{aligned} \eta (\widetilde{x})_\textrm{relaxed}&=\varGamma (\widetilde{x})\eta _\textrm{analytical}+(1-\varGamma (\widetilde{x})) \eta _\textrm{computational}. \end{aligned}$$
(16)

In the wave damping zone designed to eliminate undesired wave reflection, a similar but reverse process takes place, the free surface velocity potential \(\widetilde{\phi }\) and the surface elevation \(\eta \) are reduced to zero or initial still water values.

In the REEF3D:FNPF, the free surface is represented by a single value and thus the geometry of an over-turning wave breaker is not represented. However, correct energy dissipation during a wave-breaking process can be achieved together with effective breaking wave detection algorithms for both deep water and shallow water scenarios.

The depth-induced shallow water wave breaking is initialised when the vertical velocity component of the free surface exceeds a fraction of the shallow water celerity (The SWASH Team 2017):

$$\begin{aligned} \frac{\partial \eta }{\partial t}\ge \alpha _s\sqrt{gh}, \end{aligned}$$
(17)

where \(\alpha _s=0.6\) is recommended for most wave conditions.

The deepwater wave steepness-induced breaking is detected with a wave steepness criterion:

$$\begin{aligned} \frac{\partial \eta }{\partial x_i}\ge \beta . \end{aligned}$$
(18)

In the model, one method to dissipate wave energy is a geometric filtering method that smoothens the free surface to mimic energy dissipation (Jensen et al. 1999). Here, an explicit scheme is used and therefore there is no CFL constraint. Another method is the viscous damping method. Here, an artificial viscous term is inserted in the free surface boundary conditions (Baquet et al. 2017). During a wave breaking process, the free surface boundary conditions Eqs. 2 and  3 become:

$$\begin{aligned} \frac{\partial \eta }{\partial t}&=-\frac{\partial \eta }{\partial x}\frac{\partial \widetilde{\phi }}{\partial x}-\frac{\partial \eta }{\partial y}\frac{\partial \widetilde{\phi }}{\partial y} +{\widetilde{w}}\left( 1+\left( \frac{\partial \eta }{\partial x}\right) ^2+\left( \frac{\partial \eta }{\partial y}\right) ^2\right) \nonumber \\&\quad +\nu _b\left( \frac{\partial ^2\eta }{\partial x^2}+\frac{\partial ^2\eta }{\partial y^2}\right) , \end{aligned}$$
(19)
$$\begin{aligned} \frac{\partial \widetilde{\phi }}{\partial t}&=-\frac{1}{2}\left( \left( \frac{\displaystyle \partial \widetilde{\phi }}{\displaystyle \partial x}\right) ^2+\left( \frac{\displaystyle \partial \widetilde{\phi }}{\displaystyle \partial y}\right) ^2 \right. \nonumber \\&\left. \quad - {\widetilde{w}}^2\left( 1+\left( \frac{\displaystyle \partial \eta }{\displaystyle \partial x}\right) ^2+\left( \frac{\displaystyle \partial \eta }{\displaystyle \partial y}\right) ^2\right) \right) \nonumber \\&\quad -g\eta +\nu _b\left( \frac{\partial ^2\phi }{\partial x^2}+\frac{\partial ^2\phi }{\partial y^2}\right) , \end{aligned}$$
(20)

where \(\nu _b\) is the artificial turbulence viscosity. \(\nu _b\) is calibrated by the comparison against model test data and CFD simulations and a value of 1.86 is recommended for general practice (Baquet et al. 2017). In the new free surface boundary conditions Eqs. 19 and  20, the viscous term is treated with an implicit time scheme and the rest terms are treated with explicit time schemes. This way, there is no extra constraint on time step sizes. The two breaking wave methods are used in combination in the swash zone around the coastlines to ensure the effectiveness of the coastline algorithm which is to be discussed in the next section.

2.3 Coastline detection and treatment

It is challenging for many potential flow models to include complicated coastlines. The numerical model OceanWave3D (Engsig-Karup et al. 2009) generates curvilinear grid around the complex boundaries. However, this type of grid generation is case-dependent and can be time consuming. In addition, numerical instabilities may occur in the extremely shallow swash zone due to the derivatives of velocity potential over near infinitesimal water depth in Eq. 7. In the model REEF3D::FNPF, an innovative coastline algorithm is introduced to meet the challenge.

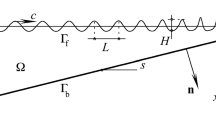
First, the identification of wet cells and dry cells is performed following a relative-depth criterion. The local water depth h is defined as a sum of still water level d and the free surface elevation \(\eta \):

$$\begin{aligned} h=\eta +d, \end{aligned}$$
(21)

where \(\eta \) is the surface elevation, d is the still water level measured from the bottom. The relationship among h, d and \(\eta \) is illustrated in Fig. 1.

Fig. 1
figure 1

Illustration of the still water level h, local water depth d, free surface elevation \(\eta \) and coastline detection algorithm

Full size image

If the local water depth h is smaller than a threshold \({\widehat{h}}\), then the local cell is identified as a dry cell:

$$\begin{aligned} \left\{ \begin{array}{lc}u=0,&{}if\;h<{{\widehat{h}}},\;\\ v=0,&{}if\;h<{{\widehat{h}}}.\;\end{array}\right. \end{aligned}$$
(22)

The velocities in the cell is set to be zero when a cell is identified as a dry cell. The threshold can be customised based on specific conditions. In this study, a small value of 0.00005 m is used to represent the coastlines as accurate as possible

After the wet and dry cell identification, the wet cells are assigned with a value \(+1\) and the dry cells are assigned with a value \(-1\). The level-set function of Osher and Sethian (1988) is then used to capture the exact location of the coastlines:

$$\begin{aligned} \phi (\textbf{x},t){\left\{ \begin{array}{ll} >0\ if\ \vec {x}\in wet \ cell, \\ =0\ if\ \vec {x}\in \varGamma ,\\ <0\ if\ \vec {x}\in dry \ cell, \\ \end{array}\right. } \end{aligned}$$
(23)

where \(\varGamma \) indicates the coastline. Using the same level-set function, the distances away from the coastlines can also be calculated.

In this way, the computational grid in the horizontal plane remains uniform and structured and no extra case-dependent grid generation is required. As a result, the inclusion of coastlines is universal and the numerical schemes in the horizontal plane is consistent. Wave damping zones are then applied along the wet side of the detected coastlines. As a result, the wave run-ups in the swash zones are eliminated and thus ensure the stability of the simulations. The coastal relaxation one convergence study presented by Wang et al. (2022) shows that only two cells of coastal relaxation zone width is sufficient to provide stable simulations. Two computational cells are often small enough not to influence the characteristics of the coastline geometry.

3 Irregular breaking waves at coastal conditions

Previously, extreme irregular sea states in deep water with different wave breaking scenarios have been reproduced using REEF3D::FNPF by Wang et al. (2021a). Regular wave breaking over varying bathymetry has also been validated against the experiment of Beji and Battjes (1993) using the numerical model (Wang et al. 2022). In this study, a further validation of irregular breaking wave over varying bathymetry is performed before the full-scale simulation of the Norwegian fjords. The irregular wave breaking experiment by Beji and Battjes (1994) is used for the validation.

The NWT setup closely follows that of the physical test, and the illustration of the 2D NWT is shown in Fig. 2. The test case with a significant wave height of 0.054 m and peak period of 2.5 s is used for the validation. The JONSWAP spectrum with the standard peak enhance parameter of 3.3 (DNV-GL 2011) is used as the input power spectrum. The flat bottom part of the NWT has a constant water depth of 0.4 m. The domain length in the x-direction is 40 m. The irregular waves are generated at the inlet boundary with a wave generation zone of 5 m, which roughly corresponds to a wave with 2.5 s period in the water depth condition. A numerical damping zone of two wavelength with a 2.5 s period is used at the outlet boundary to eliminate undesired wave reflection.

The submerged obstacle starts 6 m away from the end of the wave generation zone. The obstacle has a trapezoidal shape that starts with a weather side ramp with a slope of 1:20 until it reaches a plateau of 2 m in length and 0.3 m in height, which is followed by a lee side downwards ramp with a slope of 1:10. 8 wave gauges are located over the span of the submerged obstacle. The first two wave gauge are located at 6 m and 11 m from the wave generation zone. The x-coordinates of the rest wave gauges increase from that of the second gauge by an increment of 1 m. The narrow band frequency range between half and double peak frequency \([0.5f_p,2f_p]\) is used with 1024 discrete frequency components.

Fig. 2
figure 2

Numerical wave tank setup for the irregular wave propagation and breaking over a submerged obstacle

Full size image

All simulations use 10 vertical cells with a stretching factor of 1.25 for the intermediate water condition. Four horizontal cell sizes are used to conduct grid convergence study: \(\textrm{d}x=\) 0.02 m, 0.04 m, 0.08 m and 0.16 m. Wave decomposition takes place over the crest of the submerged obstacle together with wave breaking. In order to find an adequate cell size, the grid convergence property is investigated at both wave gauge 1 before the obstacle and wave gauge 8 after the obstacle. The reconstructed wave spectra with various cell sizes at the two wave gauges are compared in Fig. 3. The Fast Fourier Transform (FFT) method is used to produce the wave spectrum from the time series of the free surface elevation. A Gaussian smoothing algorithm is used with a smoothing factor of 0.03 to filter the noise in the spectrum and reveal the spectrum characteristics.

Fig. 3
figure 3

Grid convergence at wave gauge 1 and 8 in the simulation of irregular wave propagation and breaking over a submerged obstacle

Full size image

It is seen that the reproduced wave spectra at wave gauge 1 are very similar using the different grids. The peak frequency at 0.4 Hz is well represented in all cases and the secondary peak near 0.75 Hz are also captured in all simulations. However, cell sizes 0.08 m and 0.16 m lose large percentage of wave energy in the high frequency domain over 0.8 Hz at wave gauge 8. Cell sizes 0.04 m and 0.02 m produce similar wave spectra at the high frequency domain after the decomposition and breaking process at the last wave gauge. As a result, cell size of 0.04 m is used in the following validations against the experimental measurement.

In order to be more objectively comparable with the experiment data, the input wave is adjusted so that the \(H_s\) matches with the experiment at the first wave gauge. As a result, the actual input wave has \(H_s=0.0525\) m and \(T_p=2.5\) s. The \(H_s\) at all wave gauges calculated from 900 s simulations are compared to the experiment in Fig. 4.

Fig. 4
figure 4

Variation of \(H_s\) at different wave gauges during wave propagation and breaking over a submerged obstacle. Black circles are \(H_s\) calculated from the experimental measurements, red asterisks are the \(H_s\) from the simulated waves in the NWT (colour figure online)

Full size image

It is seen that the significant wave heights calculated from the simulation are very close to the experiment. The NWT produces the same \(H_s\) as the experiment at wave gauge 1, ensuring the correct wave energy input. The most significant breaking wave energy dissipation takes place between gauge 3 and 4, where a drastic reduction of \(H_s\) is observed. At wave gauge 7, the wave energy stabilises in the wake of the wave breaking events. To further investigate the flow detail, the wave spectra at the four critical wave gauges 1,3,4 and 7 are shown in Fig. 5. It is seen that the numerical wave spectrum at gauge 1 shows a higher peak but a lower high-frequency energy though a similar total wave energy is achieved. The wave spectra at wave gauge 3 and 4 are similar to the experiment across the entire frequency band. At wave gauge 7, the high-frequency waves share a larger proportion of the total energy and the numerical simulation slightly over-predicts the high-frequency energy. Despite these differences, an overall good agreement is achieved between the simulation and the experiment in the relevant frequency band.

Fig. 5
figure 5

Comparison between the simulated and experimental wave spectra at all wave gauges wave propagation and breaking over a submerged obstacle

Full size image
Fig. 6
figure 6

Locations of the sites in the study in the west coast of Norway (red boxes), their surrounding areas and the computational domain (yellow boxes). The upper right site is Sulafjord and the lower right is Bjørnafjord (colour figure online)

Full size image
Fig. 7
figure 7

Sulafjord and its adjacent areas: a satellite image, b topographic map (Statens kartverk 2020). The yellow box indicates the computational domain, which is further illustrate in Fig. 8 (colour figure online)

Full size image

4 Wave analysis at Norwegian fjords along the E39 coastal highway

The afore-presented validation further demonstrate the model’s capability for representing complex wave transformations as will take place in the fjords. Thus, detailed investigations on the wave environment are performed in this section at the two Norwegian fjords where floating bridges are proposed as permanent fjord-crossing means, replacing the current ferry-based crossing system along the E39 coastal highway. One of the fjords, Sulafjord, is exposed to the ocean swell, while the other, Bjørnafjord, is more sheltered from the ocean swell. The overview of the locations of the two fjords is shown in Fig. 6. In this work, only offshore ocean swell wave are considered, leaving the local wind-generated wave and the surface currents to future endeavours.

4.1 Wave analysis at Sulafjord

Sulafjord and its surrounding areas are further illustrated in Fig. 7. The fjord is exposed to the North Sea to the northwest direction. Sula and Harbeid are the two large islands at each side of the fjord. The ninth biggest city in Norway, Ålesund, is located in the northeast entry of the fjord. Consequently, there is constant marine traffic both at the exterior parts of the fjord as well as inside the fjord. The island Godøya is the only major obstacle that shelters the fjord from ocean swell. The red dashed lines in Fig. 7a are the possible fjord crossing locations for floating bridges. As can be seen in Fig. 7b, a deep water channel extends from the fjord towards offshore. This deep channel tends to lead ocean swell waves into the fjord, especially when the waves are coming from \(315^{\circ }\) north northwest. A typical wave condition near the Sulafjord is chosen for the study according to according to NORSOK (2007). The input wave has a significant wave height \(H_s=5.34\) m and peak period \(T_p=16.86\) s. A narrow band frequency range is chosen for the simulations. The low frequency limit is chosen to be 0.5\(f_p\), which only truncates off less than 0.5\(\%\) wave energy due to the skewness of the wave spectrum towards the low frequency range. Since high frequency waves have less capacity to diffract around larger obstacles and are therefore less likely to propagate inside the fjord, the high frequency limit is only up to 2\(f_p\). The JONSWAP spectrum (DNV-GL 2011) with the peak factor 3.3 is used to describe the wave energy distribution over frequency. 1024 discrete frequency components are used within the chosen frequency range based on an FFT analysis. As shown as a yellow box to the upper right corner in Fig. 6, the computational domain is chosen so that the inlet boundary corresponds to a swell coming from \(315^\circ \) north northwest, where the swell can enter the fjord with the least obstacles. The chosen domain is 25 km in the x-direction and 16 km wide in the y-direction with its maximum water depth of 500 m. The topography represented in the numerical wave tank (NWT) is shown in Fig. 8.

Fig. 8
figure 8

Topography of Sulafjord in the numerical wave tank. Positive values (warm colours) are water depth below the free surface, negative values (cold colours) are land elevation over the free surface (colour figure online)

Full size image

The configuration of the numerical wave tank is shown in Fig. 9. The red box to the left is the wave generation zone of one wavelength that the calculated based on the peak period. Three numerical damping zones of the same length are arranged at the other three boundaries, shown as yellow boxes. The ongoing field measurements are conducted at three locations D, A and B, as shown in Fig. 9. The coordinates of the three wave gauges in UTM 33 coordinate system are listed in Table 1.

Fig. 9
figure 9

Numerical configuration for the simulations of wave propagation into Sulafjord. The red box is the wave generation zone, the yellow boxes along the other three boundaries are numerical damping zone. The red lines show the coastlines and the yellow lines show the outer boundary of the coastal damping zone. The yellow dots are the wave gauges (colour figure online)

Full size image
Table 1 The coordinated in UTM 33 of the wave gauges at Sulafjord
Full size table

A grid convergence study is performed in a two-dimensional NWT with the same longitudinal domain length and a constant water depth of 500 m. The wave gauge at 10,000 m away from the wave generation zone is used for the analysis. Four different cell sizes are used and their spectra are compared in Fig. 10. All simulations are performed on 10 vertical cells with a stretching factor of 2.5 for the deep water condition.

Fig. 10
figure 10

Wave spectra reproduced with different cell sizes in the 2D convergence tests for the wave condition in Sulafjord

Full size image

It is seen that the wave spectrum preserves the shape and peak well with both 15 m and 7.5 m horizontal cell sizes. The high frequency part is better represented with 7.5 m. However, the high frequency domain is not the major contribution for the swell wave evolution. The 15 m cell size is used since it represents the low and peak frequency sufficiently and the computational demand is dramatically less. As a result, 17.8 million cells are used in the following 3D simulations. Both uni-directional irregular wave and a narrow spreading short-crested sea states that follow the Mitsuyasu directional spreading function (Mitsuyasu et al. 1975) with a spreading parameter of 20 are simulated. All simulations are performed for 12,800 s, a duration slightly longer than three hours. The three-hour time series between 2000 s and 12,800 s is used for the reconstruction of the statistical wave properties. The first 2000 s allow more than 200 wave components of the highest frequency to propagate through the domain. The simulations with long-crested and short-crested waves are completed in 15.1 and 15.7 h with 256 Intel Sandy Bridge cores (2.6 GHz) on the supercomputer Vilje.

The free surface elevations in the REEF3D::FNPF simulation with \(\textrm{d}x=15\) m at \(t=12800\)s are shown in Fig. 15. It is seen that wave shoaling starts right after the waves propagate outside the wave generation zone in the shallower regions, but the wave train continues in the principal direction of the incident waves following the deep water channel until they reach measurement point D and the island Harbeid. Along the shoreline of Harbeid (marked with a red curve), strong wave shoaling and refraction take place and wave fronts change direction and become parallel to the shoreline in this region. Then, waves start to diffract at the tip of Harbeid (end of the red curve) and spread inside the fjord. The incident waves and the diffracted waves meet near wave gauge A before continuing the propagation along the shoreline of Sula. The wave energy roughly follows the direction of the red arrows in Fig. 15a. In a qualitative manner, the visualisation shows a higher wave close to the shoreline of Sula inside the fjord, which confirms a similar finding in Wang et al. (2019). In addition, a square wave pattern is found at the offshore side of Harbei, which is marked as a red box in Fig. 15a. Here, the diffracted wave around the small island outside Harbeid meet with the refracted waves towards the shoreline of Harbeid in a near perpendicular direction. This square wave field persists during the entire simulation, indicating an extremely dangerous area for shipping and navigation under the input wave condition. A similar wave propagation pattern is also observed with the narrow spreading short-crested wave propagation except that a stronger reflection from Sula island is observed near the wave gauge A.

Fig. 11
figure 11

Surface elevation at 12,800 s in the simulations of wave propagation into Sulafjord. a long-crested irregular wave input; b narrow spreading short-crested irregular wave input

Full size image

Spectral wave models are also often used in the preliminary design in marine and coastal engineering. Here, the third-generation spectral wave model SWAN (Booij et al. 1999) is also used to verify the variation of the significant wave height \(H_s\) at given locations. SWAN is a phase-averaged wave model, the wave energy distribution in terms of \(H_s\) is calculated instead of wave kinematics, dynamics and free surface elevation. The same computational domain, topography and input wave conditions are used in the SWAN simulations. A narrow spreading wave condition is specified with a spreading parameter of 20. Four different cell sizes are investigated and the grid convergence study is shown in Fig. 12 at all three measurement points. It is seen that the \(H_s\) does not show significant variations when refining from a 80 m cell to a 40 m cell arrangement at all wave gauges, especially at D and A. Therefore, the results produced with \(\textrm{d}x=\)40 m are used for the comparison.

Fig. 12
figure 12

\(H_s\) at all wave gauges with four different cell sizes in the SWAN simulations of wave propagation into Sulafjord

Full size image

In Fig. 13, the distribution \(H_s\) is plotted over the entire numerical domain. At the entry of the fjord, wave heights increase and become higher than the input wave in the shallower area which present a similar observation as in REEF3D::FNPF. The incident waves following the deep water trend continue with a near constant wave height into the fjords. After the wave refraction and diffraction at the offshore side of the shoreline of Harbeid, the remaining waves decrease in amplitude and relatively higher waves propagate along the shoreline of Sula island. These findings also align with the observations of REEFD3::FNPF. However, the \(H_s\) distribution becomes unrealistic after the diffraction. Several ’rays’ of \(H_s\) are seen in the fjord in stead of a more continuous distribution. This exposes the spectral model’s limit in handling cases with strong diffractions.

Fig. 13
figure 13

Distribution of \(H_s\) in the simulation of wave field in Sulafjord using SWAN

Full size image

A quantitative comparison of \(H_s\) at given wave gauges between the models is shown in Fig. 14. Here, all \(H_s\) are normalised and the correlation among the wave gauges are demonstrated. The predicted wave height variations at the wave gauges are very similar between the models in general. The wave height decreases less from point D to point A under the short-crested wave conditions, possibly because the directionality in the wave field facilitates the diffraction and allow more energy to propagate around Harbeid. However, the SWAN simulation shows slightly higher waves at wave gauge B. In spite of the similarities in the results, the phase-resolved model provides more detailed information, including the square wave pattern beside the entry to the fjord. The spectral model also shows a limit for strong diffraction. For the wave propagation in Bjørnafjord, where diffraction is much stronger, the differences are expected to be more significant, as will be discussed in the next section.

Fig. 14
figure 14

Variation of significant wave heights at different gauges in Sulafjord (normalised by \(H_s\) at wave gauge D). L and S in the legend represents long-crested and short-crested waves situations

Full size image

In addition to \(H_s\) variations, the dominating frequency components inside the fjord are also among the major concerns for the design of floating structures. Even though there are few obstacles between the fjord and the open sea, the diffractions and reflections may lead to significant variation of dominating frequencies in the wave field. Here, the numerically simulated wave spectra are shown at wave gauge A and B inside the fjord in Fig. 15. At wave gauge A, the short-crested wave field has two dominating frequencies, one is at the peak frequency 0.056 Hz of the input wave, the other at 0.1 Hz in the high frequency domain. The long crested wave field has also have two main frequencies at 0.05 Hz and 0.074 Hz while very few energy is concentrated near the original peak frequency. The wave spectrum in the long-crested wave field is also significantly lower than that from the short-crested wave field, which confirms the lower \(H_s\) in Fig. 14. It indicates that the short-crested waves are more likely to propagate around the obstacles while maintaining the input wave spectrum properties. The secondary peaks are most possibly due to the wave trains passing the tip of Harbeid after the refractions and diffraction process. At wave gauge B, the short-crested wave shows a main peak near 0.06 Hz while a significant percentage of wave energy is concentrated near 0.08 Hz. For the long-crested wave, the majority of wave energy is concentrated near the new peak of the spectrum at 0.08 Hz. The shift of wave energy towards 0.08 Hz in both wave conditions shows that 0.08 Hz is the critical frequency when considering structure egen frequency, given the input wave properties.

Fig. 15
figure 15

Wave spectra at wave gauge A and B inside Sulafjord

Full size image
Fig. 16
figure 16

Bjørnafjord and its adjacent areas: a satellite image, b topographic map (Statens kartverk 2020)

Full size image

4.2 Bjørnafjord

Bjørnafjord is located to the south of the second largest city in Norway, Bergen. Many cruise ships and ferries are operating inside the fjord. The fjord and its surrounding area are shown in Fig. 16. The two dashed red lines in Fig. 16a are the proposed fjord crossing locations. As seen in Fig. 16a, Bjørnafjord is located to the east of an archipelago, which prevents most ocean swell from entering the fjord. Only the smaller fjords, Krossfjord to the north and Selbjørnsfjord to the south, provide the deep water channels for ocean swell to propagate into Bjørnafjord, as shown in Fig. 16b. Therefore, most significant waves inside the fjord are locally wind generated waves. However, it is of great significance to investigate how the ocean swell propagates, especially what are the main frequencies inside the fjord after the complicated wave transformations.

The chosen computational domain is 45 km in the x-direction and 35 km in the y-direction with the maximum water depth of 675 m. The topography included in the numerical wave tank is shown in Fig. 17. As can be seen, Krossfjord is the deepest fjord in this fjord system, and therefore it is suspected that more wave energy will propagate from the northern Krossfjord into Bjørnafjord.

Fig. 17
figure 17

Topography of Bjørnafjord in the numerical wave tank

Full size image
Fig. 18
figure 18

Wave spectra reproduced with different cell sizes in the 2D convergence tests for the wave condition in Bjørnafjord

Full size image

The input wave is chosen from the NORA 10 data set. The significant wave height \(H_s=14.2\) m, peak period \(T_p=21.8\) s and the principal direction for both the long-crested and short-crested waves is 270\(^{\circ }\) in nautical system. The JONSWAP spectrum (DNV-GL 2011) with a shape parameter of 3.3 is used for the long-crested wave simulation. In addition, Mitsuyasu’s spreading function (Mitsuyasu et al. 1975) with a spreading parameter of 20 is used for the narrow spreading short-crested wave simulation. A narrow frequency band [0.5\(f_p\), 2\(f_p\)] is used for the input swell wave with 1024 discrete frequency components based on an FFT analysis. Similar to the previous section, a 2D simulation is performed with a constant water depth of 675 m and the same input wave condition as for the 3D simulations. As can be seen in Fig. 18, the reproduced wave spectra are becoming near identical with the theoretical spectra when refining from 40 m cells to 20 m cells near the peak period. A further refinement improves the representation of the high frequency range slightly with 10 m cells. However, high-frequency short waves are less capable of propagating over large obstacles, 20 m is considered sufficient for investigating the evolution of the main wave energy near the wave peak period during the strong diffraction process around the archipelago outside Bjørnafjord. All simulations are performed with 10 vertical cells with a stretching factor of 2.5 for the deep water condition. With the chosen grid arrangement, the final number of cells for the simulations is 39.4 million.

The numerical wave tank arrangement and the wave gauges are shown in Fig. 19. The red box is the wave generation zone of one peak wavelength of 750 m at the offshore side with relatively constant water depth. Relaxation zones of the same widths are arranged along the three other boundaries to reduce reflections from these boundaries. Wave gauges G1 to G6 are designed to measure the variation of \(H_s\) in Krossfjord, while wave gauges G7 to G12 are used to represent the wave property evolution in Selbjørnsfjord. These analyses show the overall correlation between the offshore wave condition and the wave condition at the entry of Bjørnafjord. Wave gauges G13 to G15 are used to represent the spatial variation of the wave properties at the first possible fjord crossing site in the cross section of the fjord while G16 to G18 are for the second possible fjord crossing location. All simulations are performed with 256 Intel Sandy Bridge cores (2.6 GHz) on the supercomputer Vilje for 12,800 s. The long-crested wave and short-crested wave simulations take 32.0 and 32.1 h respectively.

Fig. 19
figure 19

Numerical configuration for the simulations of wave propagation into Bjørnafjord. The red box is the wave generation zone, the yellow boxes along the other three boundaries are numerical damping zone. The red lines show the coastlines and the yellow lines show the outer boundary of the coastal damping zone. The yellow dots are the wave gauges (colour figure online)

Full size image

The free surface elevation at the end of the simulations are shown in Fig. 20 for both wave conditions. Strong wave shoaling and refraction take place along the shoreline of the archipelago, seen as increased wave eight, shortened wave length and intersected wave patterns of wave trains traveling in different directions. The deep water channels Krossfjord and Selbjørnsfjord are seen to guide the incoming waves around the archipelago into the entry of Bjørnafjord as expected. However, there are almost no visible waves entering Bjørnafjord in the current scale. A close-in view with a narrower data range will be discussed later to reveal more details inside the fjord.

Fig. 20
figure 20

Surface elevation at 12,800 s in the simulations of wave propagation into Bjørnafjord. a long-crested irregular wave; b narrow spreading short-crested irregular wave

Full size image

The spectral wave model SWAN is also deployed here for verification. With the same domain, topography and input wave condition with a spreading parameter of 20, the grid convergence study for SWAN is shown in Fig. 21. It is seen that all different cell sizes provide similar \(H_s\) in the offshore area at gauges G1, G2, G11 and G12. When the waves propagate further into Krossfjord and Selbjørnsfjord, the results start to stabilise when refining from 80 m cells to 40 m cells, as seen at G3, G4, G9 and G10. Therefore, SWAN results obtained with 40 m cells are used for the comparison with the potential flow model.

Fig. 21
figure 21

\(H_s\) at all wave gauges with four different cell sizes in the SWAN simulations of wave propagation into Bjørnafjord at long-crested wave condition

Full size image

The distribution of \(H_s\) in the SWAN simulation is shown in Fig. 22. A similar wave shoaling process is observed as the wave heights increase along the coast of the archipelago. Some waves continue the propagation along Krossfjord and Selbjørnsfjord and nearly no waves are observed at the end of the two fjords.

Fig. 22
figure 22

Distribution of \(H_s\) at Bjørnafjord in the SWAN simulation

Full size image

In order to investigate the details of wave propagation inside Bjørnafjord, close-in views with a different scale of wave height are shown in Fig. 23. Here, it is seen that the diffracted waves from Krossfjord and Selbjønsfjord meet in the opposite directions at the entry of Bjørnafjord, creating a crossing sea. Then, the combined effects of refraction and diffraction lead this cross wave field further into Bjørnafjord. It is seen that higher waves propagate from the deeper Krossfjord as assumed. Similarly, a close-in view of the wave field simulated by SWAN in the same region is shown in Fig. 24. However, rays of wave energy are seen, the diffraction pattern is not well represented.

Fig. 23
figure 23

Close view of the surface elevation inside the fjord at 12,800 s in the simulations of wave propagation into Bjørnafjord with narrow spreading short-crested irregular waves

Full size image
Fig. 24
figure 24

Close view of the \(H_s\) distribution inside Bjørnafjord in the SWAN simulation with the same short-crested wave input as in Fig. 23

Full size image

The evolution of \(H_s\) normalised by the input wave height from offshore to the inner region of the fjord in both models are compared in Fig. 25. Both models represent the evolution of waves in Krossfjord and Selbjøqsfjord in a similar manner in terms of both the general trend and the absolute values. However, significant differences are observed inside the Bjørnafjord. At the first possible fjord crossing location (wave gauges G13–G15), the potential flow model shows higher wave heights as much as 2—3 times that of SWAN at all three wave gauges. In spite of the strong differences in the absolute values, both model predict higher waves closer to the northern coast. This finding agrees with the research reported by Eidnes et al. (2014) and Fergstad et al. (2018). Significant differences are also seen at the second possible crossing location (wave gauges G16–G18). The calculated \(H_s\) in the potential flow model are 1.5–4 times that of the SWAN and opposite trends of wave height variation are also observed. The insufficient representation of wave diffraction in the spectral wave model is most likely to be the reason for such discrepancies.

Fig. 25
figure 25

Variation of significant wave heights during narrow spreading wave propagation into Bjørnafjord, a gauges G1–G5 in the northern channel, b gauges G12–G7 int he southern channel, c gauges G13–G15 at the first possible crossing location, d gauges G16–G18 at the second possible crossing location. L indicates long-crested wave, (S) indicates short-crested wave

Full size image
Fig. 26
figure 26

Variation of wave spectra during long-crested irregular wave propagation into Bjørnafjord, a gauges G1–G5 in Krossfjord, b gauges G12–G7 in Selbjørnsfjord, c gauges G13– G15 at the first possible crossing location, d gauges G16–G18 at the second possible crossing location

Full size image
Fig. 27
figure 27

Variation of wave spectra during narrow spreading short-crested irregular wave propagation into Bjørnafjord, a gauges G1–G5 in Krossfjord, b gauges G12–G7 in Selbjørnsfjord, c gauges G13–G15 at the first possible crossing location, d gauges G16–G18 at the second possible crossing location

Full size image

\(H_s\) is not the only concern for floating structures in the fjord, the wave frequency composition in the fjord is another critical consideration for the design of floating structures. The time series provided by the potential flow model at all wave gauges are used to reconstruct the wave spectra in order to investigate the evolution of the wave energy distribution over frequencies. These reproduced wave spectra for both long-crested and short-crested sea states are shown in Fig. 26 and Fig. 27.

It is seen that the majority of wave energy is concentrated near the peak frequency \(f_p=0.0459\) Hz during the wave propagation in Krossfjord with both sea states. However, wave energy concentration is shifted to two new frequencies at the lower and higher side of the peak frequency. In the scenario with long-crested waves, two near equal peaks at \(f=0.0412\) Hz and \(f=0.0576\) Hz appear at G10. For short-crested incoming waves, the most wave energy is still around \(f_p\), but a secondary peak at \(f=0.0576\) Hz appear at G10. Inside the fjord, the wave energy distribution deviates from the input entirely. In both scenarios, two peaks of the spectrum emerge at wave gauges from G13 to G18. A significant amount of wave energy is now shifted to the low frequency range around \(f=0.0095\) Hz. At this frequency, the equivalent wavelength is near 10,000 m, resembling a constant current. This will cause a significant low frequency drift to the structure and its mooring system. Meanwhile, more than half of the wave energy is shifted to the high-frequency range around \(f=0.05\) Hz. A third peak at \(f=0.06\) Hz is also observed at G17 in the middle of the fjord, most likely as a result of the intersecting wave pattern created by the two wave trains coming from the two fjords outside Bjørnafjord. In general, the peak frequency does not represent the main wave energy anymore, the new energy distribution inside the fjord is divided into a low frequency part and a high frequency part. Despite that, \(H_s\) is greatly reduced inside Bjørnafjord in comparison to the offshore input waves, the emerging new wave frequencies create significant challenges for the floating structures. The low frequency waves contribute to the low frequency drift (Faltinsen 1990) for the mooring system and the high frequency waves might cause resonant excitations such as ringing (Faltinsen et al. 1995; Faltinsen 1999).

Along the potential fjord-crossings, the wave phase differences at different locations are of great considerations for the long-span structures. As the waves show spatial incoherence, different segments along the bridge might move out of phase or in phase, which create different structural behaviours. Therefore, the coherence factors among the three wave gauges at each of the two potential fjord-crossings are calculated. This is shown in Fig. 28 for the short-crested wave condition and in Fig. 29 for the long-crested wave conditions.

Fig. 28
figure 28

Coherence between the wave gauges at the two possible fjord-crossing locations at Bjørnafjord with short-crested waves

Full size image
Fig. 29
figure 29

Coherence between the wave gauges at the two possible fjord-crossing locations at Bjørnafjord with long-crested waves

Full size image

As can be seen from Fig. 28, the coherences among the wave gauges along the fjord-crossings are very low across the frequency band in spite of relatively higher coherences at the lower frequency range. This incoherence indicates very different structural dynamics along the bridge span. In comparison, relatively higher coherence factors are observed under the uni-directional wave conditions, as seen in Fig. 29. Here, high coherence factors between 0.4 and 0.5 are seen for both the low-frequency range and the high-frequency range. However, incoherence still predominates around the peak frequency. Though unidirectionality seems to lead to a higher coherence, it is still concluded that incoherence is the main characteristic of the wave field at Bjørnafjord, which can be attributed to the complex wave transformation along the two outer fjords and the local water depth effects at the different locations along the bridge.

5 Conclusions

The novel design of floating structures along the E39 coastal highway demands a comprehensive understanding of the wave field. The unique coastal conditions in the Norwegian fjords present several challenges for phase-resolved wave modelling: deepwater condition, fast-varying bathymetry, complicated coastal topography and large-domain of interest. This manuscript proposes the usage of a fully non-linear potential flow model REEF3D::FNPF with its novel coastline algorithm to address all the challenges imposed by such conditions.

The potential flow model is not restricted to water depth conditions, making it flexible with both the deepwater condition in the Norwegian fjords and the fast transitions between deep and shallow waters near the shorelines. The coastline algorithm detects the complicated coastlines and arrays of irregular islands accurately throughout the entire domain without extra efforts and costs on the grid generation. The fast potential flow solver together with the parallel high performance computation capacity enables the model to calculate large-scale wave propagation efficiently with available computational resources. The phase-resolved computational results show extensive details of the wave field, including wave shoaling, refraction, reflection, diffraction, wave breaking and special wave patterns such as square waves. The time series from the simulation provide information on statistical wave properties, wave spectra, inhomogeniety and incoherence.

Two of the major fjords along the planned E39 highway route are investigated. Sulafjord represents a scenario that is exposed to ocean swell. Bjørnafjord represents a condition that is mostly sheltered from offshore waves due to the archipelago outside the fjord entry. Both fjords present deep water conditions and the area of interest for the investigation of wave propagation are of tens of kilometres in each horizontal directions. Both long-crested and narrow spreading short-crested wave inputs are simulated for a duration of slightly more than threes hours. Using the supercomputers, these simulations show a calculation time to real time ratio of 5–10. The correlations between the offshore significant wave heights and the local significant wave heights inside the fjord are established.

For Sulafjord, the evolution of wave frequencies shows very different patterns with long- and short-crested waves but a critical low frequency at 0.08 Hz is found at wave gauge B in both scenarios. The spectral wave model SWAN is also used and compared with the potential flow model. The two models share a similar trend of wave height variations in Sulafjord as there are less obstacles in the path of wave propagation to create strong diffraction.

In contrast, the significant wave heights are underestimated by a factor of 2–6 in the SWAN simulation in comparison to those in the potential flow simulation for Bjørnafjord due to the incapacity of representing strong diffraction in the spectral model. The potential flow simulation also provides insight into the wave spectra evolution at all wave gauges in Bjørnafjord, and a redistribution of wave energy towards the lower and higher frequency range is observed, expressing critical design concerns for low-frequency drifting and high frequency excitation such as ringing. The varying significant wave heights inside the fjords shows strong spatial inhomogeneity bot along the wave propagation and across the fjord. In addition, the wave incoherences along the bridge span at the two potential fjord-crossing locations are identified, indicating out-of-phase structural responses at different locations of the bridge, a information that can only be analysed from the time-domain results in a phase-resolved simulation.

The utilisation of REEF3D::FNPF proves to be a unique and tailor-made solution for a credible calculation of large-scale wave propagation in the Norwegian coastal condition. Such a modelling approach can be utilised for a broader application and more in-depth met-ocean analyses. In the current study, the swell waves are the main focus. In the future, more flexible wave generation boundaries to allow different wave systems from both swell and wind-generated waves shall be included. In addition, surface current will be included and its impact on wave propagation shall be examined. The future development will take into consideration more physics for an even more realistic representation of the complex marine environment. Moreover, two important numerical aspects will be investigated in a dedicated future study to improve the model’s accuracy and efficiency for 3D waves at transitional water depths: 1) the vertical grid clustering optimisation, especially for irregular wave transformation; and 2) the higher-order finite difference operator’s influence on wave breaking, coastline arrangement and vertical grid arrangement.