High-fidelity modelling of moored marine structures: multi-component simulations and fluid-mooring coupling

Abstract

High-fidelity viscous computational fluid dynamics (CFD) models coupled to dynamic mooring models is becoming an established tool for marine wave-body-mooring (WBM) interaction problems. The CFD and the mooring solvers most often communicate by exchanging positions and mooring forces at the mooring fairleads. Mooring components such as submerged buoys and clump weights are usually not resolved in the CFD model, but are treated as Morison-type bodies. This paper presents two recent developments in high-fidelity WBM modelling: (i)  a one-way fluid-mooring coupling that samples the CFD fluid kinematics to approximate drag and inertia forces in the mooring model; and (ii) support for inter-moored multibody simulations that can resolve fluid dynamics on a mooring component level. The developments are made in the high-order discontinuous Galerkin mooring solver MoodyCore, and in the two-phase incompressible Navier–Stokes finite volume solver OpenFOAM. The fluid-mooring coupling is verified with experimental tests of a mooring cable in steady current. It is also used to model the response of the slack-moored DeepCwind FOWT exposed to regular waves. Minor effects of fluid-mooring coupling were noted, as expected since this a mild wave case. The inter-mooring development is demonstrated on a point-absorbing WEC moored with a hybrid mooring system, fully resolved in CFD-MoodyCore. The WEC (including a quasi-linear PTO) and the submerged buoys are resolved in CFD, while the mooring dynamics include inter-mooring effects and the one-way sampling of the flow. The combined wave-body-mooring model is judged to be very complete and to cover most of the relevant effects for marine WBM problems.

1 Introduction

Simulation of moored marine structures, including floating offshore renewable devices, are traditionally carried out using tools based on linear potential flow theories. Linear potential flow is based on the underlying assumptions of inviscid flow and small amplitude waves and motions. Weak nonlinearities can be approximated through the use of Wheeler stretching for wave kinematics and a nonlinear Froude–Krylov approach for wave-body interaction. Additional nonlinearities that are typically imposed are: (i) viscous drag, incorporated through Morison type approximations relying on empirical drag coefficients; (ii) mooring restraint forces, included as nonlinear external forces; and (iii) power take off (PTO) forces, also modelled as nonlinear external forces. Nevertheless, numerical models based on linear potential flow performs badly for simulations of survival conditions with large amplitude waves, and structures operating in the resonance region. For such cases, it can be beneficial to use high-fidelity tools, e.g. viscous computational fluid dynamics (CFD) models.

It is well-known that the dynamic contribution to the mooring force may be substantial (Brown and Mavrakos 1999). Therefore, a dynamic mooring model is strongly advised. The most common dynamic cable formulations use lumped-masses (Orcina Inc 2015; Hall and Goupee 2015) or linear finite elements (ANSYS Inc 2018; Aamo and Fossen 2000). Many other methods are also frequently used e.g. finite differences (Tjavaras 1996), third-order finite elements (Buckham et al. 2004) and hp-adaptive high-order discontinuous Galerkin methods (Palm et al. 2017).

When the moored structure is simulated using CFD models, the fidelity of the wave-body-mooring (WBM) interaction increases significantly, but the mooring forces have then often been reduced to representations such as a linear restoring matrix (Elhanafi et al. 2017), linear springs (Ransley et al. 2020) or quasi-static moorings (Liu et al. 2017; Burmester et al. 2020b). Nevertheless, coupled dynamic mooring analysis with viscous Reynolds-Averaged Navier-Stokes simulations (RANS) are becoming established (Palm et al. 2013, 2016; de Lataillade 2019; Burmester et al. 2020a; Jiang et al. 2020; Martin and Bihs 2021). This is an important step for better predictions of responses in extreme sea states and also for capturing low-frequency response correctly (Robertson et al. 2020). So far, the coupling has mostly been implemented by a straightforward exchange of positions and forces at the fairlead of each mooring line. The fluid velocity and acceleration used to compute the drag and inertia forces acting on the moorings are either given by linear potential flow (computed inside the mooring solver) or the cable is assumed to move in quiescent water. A few studies have proceeded to more advanced coupling strategies. de Lataillade (2019) implemented a one-way coupling in ProteusCFD by sampling the fluid in the RANS simulation at the mooring nodes to be used for drag and inertia in the mooring solver. A one-way coupling in the REEF3D CFD solver was also implemented by Martin and Bihs (2021).

In addition to the actual mooring cables, a mooring system is often made up of supplementary mooring components, such as submerged buoys and clump weights. Such components are generally assumed to be accurately modelled using the Morison approach (Mavrakos et al. 1996), also when CFD is used for the moored structure wave-body interaction. Less common in coupled CFD-mooring simulations is to resolve mooring components in the CFD domain. To resolve the mooring components in CFD clearly carries an extra computational burden, but if the main floater is to be resolved in CFD the extra cost can be justified. In addition, for larger submerged buoys relatively near the surface or even surface piercing, the flow may be complicated enough to justify the extra effort. Preliminary work on resolving mooring components with CFD was presented by Palm and Eskilsson (2020b) for a truncated WEC mooring system. Compared to resolving submerged buoys by Morison approaches, the CFD-resolved buoys showed smaller motion amplitudes and similar peak mooring loads. Multi-body simulations are available in the OpenFOAM CFD framework (Weller et al. 1998; OpenCFD Ltd 2022), within the rigidBodyDynamics library. It was used in a recent study to model a hinged wave energy device with four catenary moorings modelled in MoorDyn (Jiang and el Moctar 2022). However, to fully resolve a hybrid mooring system in CFD means that the CFD-mooring coupling must support multi-body simulations with inter-mooring capabilities, i.e. the same cable must feed forces into different objects in the CFD domain.

In this paper, we present recent developments in the mooring dynamics software MoodyCore (Palm and Eskilsson 2018), and how it can be used for complete system analysis together with OpenFOAM. MoodyCore is based on an hp-adaptive discontinuous Galerkin (DG) method and comes with an application programming interface (API) for coupling to different fluid solvers. In this paper, we use the two-phase RANS solver in OpenFOAM-v2012. We will look at the next steps in coupled mooring analysis using CFD such as:

• the fluid-structure coupling between the viscous fluid solver and the mooring system. We extend the OpenFOAM-MoodyCore coupling to include a one-way sampling of the fluid kinematics for all mooring lines in the CFD domain, similar to the work of de Lataillade (2019) and Martin and Bihs (2021). The sampled velocities and accelerations are used in a Morison formulation to provide high-fidelity drag and inertia forces on the moorings.

• to resolve mooring components directly in the viscous fluid simulations, e.g. submerged buoys and clump weights used in hybrid mooring systems. The sixDoFRigidBodyMotion library in OpenFOAM is extended to handle multi-body analysis with inter-mooring restraints realised as dynamic cables. This is, to the authors best knowledge, the first time mooring components have been resolved directly in CFD through inter-moored multi-body simulations.

2 Mooring solver

2.1 Equations for an elastic cable

A cable of length L is parametrised by a position vector $\vec {r}^c=\big [ r_x^c(s), r_y^c(s), r_z^c(s) \big ]^\mathrm {T}$ in a right-handed inertial coordinate system with z up. Here $s\in [0,L]$ is the unstretched cable coordinate. The equation of motion for an elastic cable including the effect of bending stiffness can be written

$$\begin{aligned} \gamma _0 \dfrac{\partial ^2 \vec {r}^c}{\partial t^2}&= \dfrac{{\mathrm {d}} \vec {T}}{{\mathrm {d}} s} + \vec {f}^c \, , \end{aligned}$$

(1)

$$\begin{aligned} \vec {T}&= T(\epsilon ,\, \dot{\epsilon }) \hat{t} + \vec {T}_\perp \, , \end{aligned}$$

(2)

$$\begin{aligned} \hat{t}&= \dfrac{\partial \vec {r}^c}{\partial s}\left( 1+\epsilon \right) ^{-1} \, , \end{aligned}$$

(3)

$$\begin{aligned} \epsilon&= {\left| \dfrac{\partial \vec {r}^c}{\partial s} \right| } -1 \, , \end{aligned}$$

(4)

where $\gamma _0$ is the cable mass per unit length, $\epsilon$ is the cable strain, $\dot{\epsilon }$ is the strain-rate and $\hat{t}$ is the tangential unit vector. The axial tension, $T(\epsilon ,\, \dot{\epsilon })$, is a function of the strain and constitutes the cable material properties. A linear visco-elastic cable is e.g. described by $T=EA_0\epsilon +\xi \dot{\epsilon }$ in which $EA_0$ is the axial stiffness and $\xi$ is the internal damping coefficient. Finally, $\vec {f}^c$ is the sum of the external forces on the cable, and $\vec {T}_\perp$ is the shear force of the cable. These two will be explained in further detail below.

2.1.1 External forces

The external forces are grouped in the variable $\vec {f}^c$, and contains the hydrodynamic forces of added mass $\vec {f}^a$, buoyancy $\vec {f}^b$ and drag from the Morison equation (Morison et al. 1950) $\vec {f}^d$ and contact forces from the ground $\vec {f}^g$ – see Equations (5) to (8). The sea-floor model is bi-linear spring-damper with dynamic friction, see details in Palm et al. (2017). In this paper, we will primarily discuss the hydrodynamic forces.

$$\begin{aligned} \vec {f}^c&= \vec {f}^a + \vec {f}^b + \vec {f}^d + \vec {f}^g \, , \end{aligned}$$

(5)

$$\begin{aligned} \vec {f}^a&= \rho A_0 \left( \vec {a}_{\mathrm {f\perp }} + C_{\mathrm {m\imath }} \vec {a}^*_\imath + C_{\mathrm {m\perp }} \vec {a}^*_\perp \right) \, , \end{aligned}$$

(6)

$$\begin{aligned} \vec {f}^b&= (A_0 \rho - \gamma _0) g\hat{z} \, , \end{aligned}$$

(7)

$$\begin{aligned} \vec {f}^d&= 0.5 d \rho \sqrt{1+\epsilon } \left( C_{\mathrm {d\imath }} \left| \vec {v}^*_\imath \right| \vec {v}^*_\imath + C_{\mathrm {d\perp }} \left| \vec {v}^*_\perp \right| \vec {v}^*_\perp \right) \, , \end{aligned}$$

(8)

Here, index $\imath$ denotes the tangential projection of a vector onto the cable direction, and $\perp$ the remaining normal components. $\vec {v}^*$ and $\vec {a}^*$ denote the relative velocity and acceleration between the water and the cable respectively. The hydrodynamic coefficients $C_{\mathrm {m}}$ refer to added mass, and $C_{\mathrm {d}}$ refer to drag.

2.1.2 Bending stiffness

The bending stiffness of the cable is introduced through the shear force $\vec {T}_\perp$, calculated from Euler-Bernoulli beam theory adapted for highly extensible members. Following the local Lagrangian derivation in Tjavaras (1996), the formulation was adapted to an inertial reference frame in Palm and Eskilsson (2020a). The governing equations introduce two new spatial derivatives, and can thus be written as

$$\begin{aligned} \vec {M}&= \hat{t} \times \left( EI \vec {\kappa } + \xi _b \dot{\vec {\kappa }} \right) \, , \end{aligned}$$

(9)

$$\begin{aligned} \vec {T}_\perp&= \dfrac{1}{l_\epsilon } \hat{t} \times \dfrac{\partial }{\partial s}\left( \dfrac{\vec {M}}{l_\epsilon ^2} \right) = \dfrac{1}{l_\epsilon } \hat{t} \times \dfrac{\partial \vec {M}_*}{\partial s}\, , \end{aligned}$$

(10)

in which EI is the bending stiffness, $\xi _b$ represents bending material damping in a visco-elastic material, and $l_\epsilon =(1+\epsilon )$. The moment in the stretched domain is $\vec {M}_*=\dfrac{\vec {M}}{l_\epsilon ^2}$. We further define the curvature $\vec {\kappa }=\dfrac{\partial \hat{t}}{\partial s}$, and its time derivative $\dot{\vec {\kappa }}=\bigg (\dfrac{\dot{\vec {q}} - \vec {q} \dot{\epsilon }}{l_\epsilon }\bigg )$. Here $\vec {q}$ is the spatial derivative of r and $\dot{\vec {q}}$ its time derivative. For simplicity, the equations of motion are formulated without torsional stiffness. See Tjavaras (1996) and Palm and Eskilsson (2020a) for a complete description.

2.2 High-order discontinuous Galerkin method

Equations (1) and (4) are solved with the MoodyCore mooring solver using an hp-adaptive DG method (Cockburn and Shu 2001). To use the locally conservative DG method, Eq. (1) is rewritten as a system of first order equations as

$$\begin{aligned} \dfrac{{\mathrm {d}} \vec {u}}{{\mathrm {d}} t}&= \dfrac{{\mathrm {d}} \vec {F}\left( \vec {u}\right) }{{\mathrm {d}} s} + \vec {G}\left( \vec {u}\right) \, , \end{aligned}$$

(11)

in terms of state vector $\vec {u}=\big [\vec {q}, \, \vec {\nu }\big ]^{\mathrm {T}}$, with $F=\big [\vec {v}/\gamma _0,\, \vec {T} \big ]$ and $G = \left[ 0,f^c\right]$. Here $\vec {\nu } = \gamma _0 \vec {v}$ is the cable momentum per meter (mass per meter $\gamma _0$ times velocity $\vec {v}$).

The computational domain $\Omega \in [0,L^c]$ is partitioned into $N_{el}$ elements $\Omega _e \in [s^e_L, s^e_R]$ of element size $h^e$. A function g(s, t) is approximated to an arbitrary order P within $\Omega ^e$ as:

$$\begin{aligned} g(s,t)&\approx g^e(s,t) = \sum _{k=0}^{k=P} \phi _k(s) \tilde{g}^e_k(t) \, , \end{aligned}$$

(12)

where $\tilde{g}^e_k$ is the k:th order expansion coefficient to trial function $\phi _k(s)$. Legendre polynomials are used as test and trial functions to obtain a diagonal local mass matrix. Also, let us define

$$\begin{aligned} \left( a(s,t) , b(s,t) \right) _{\Omega ^e}&= \int _{\Omega ^e} a(s,t) b(s,t) {\mathrm {d}}s \, , \end{aligned}$$

(13)

as the inner product operator $(\quad )_{\Omega ^e}$. Expressed in strong form within $\Omega ^e$, the DG formulation reads:

$$\begin{aligned} \left( \phi _l,\,\phi _m\right) _{\Omega ^e}\tilde{\dot{u}}^e&= \left( \phi _l,\,\dfrac{\partial \phi _m}{\partial \xi }\right) _{\Omega ^e} \tilde{F}^e + \left[ \widehat{\vec {F}} - \vec {F}^+ \right] ^{s^e_R}_{s^e_L} + \left( \phi _l,\,G\right) _{\Omega ^e} \, . \end{aligned}$$

(14)

A numerical flux (denoted with $\widehat{\cdot }$ in Eq. (14)) is in the DG method used to express the boundary value of a quantity. MoodyCore uses fluxes according to:

$$\begin{aligned} \widehat{\vec {F}}&= \dfrac{1}{2} \left( \vec {F}^+ + \vec {F}^- + \lambda \left( n^-\vec {u}^+ + n^+\vec {u}^- \right) \right) \, , \end{aligned}$$

(15)

$$\begin{aligned} \lambda&= \sqrt{\dfrac{1}{\gamma _0} \dfrac{\partial T}{\partial \epsilon }} \, , \end{aligned}$$

(16)

where n is the outward pointing unit normal, $\lambda$ is the speed of sound in the cable and $\widehat{\vec {F}}$ is the Lax–Friedrichs flux of $\vec {F}$. Superscripts $^+$ and $^-$ tell if values are taken from the interior domain (from $\Omega ^e$) or from the neighbouring element ($\Omega ^{e+1}$ or $\Omega ^{e-1}$ respectively). See Palm et al. (2017) for further details of the numerical flux used.

Please note that the bending stiffness is treated with auxiliary variables as a nested local discontinuous Galerkin (LDG) method (Cockburn and Shu 2001). Three auxiliary variables are used: (i) $\vec {\kappa }$, (ii) $\dot{\vec {\kappa }}$ and (iii) $\vec {\tau }$, which relates to shear force as $\vec {T}_\perp = \hat{t} \times \vec {\tau } l_\epsilon ^{-1}$. An LDG flux is used as numerical flux on the moment and the cable tangent, according to:

$$\begin{aligned} \widehat{\hat{t}}&= \dfrac{1}{2} \left( \hat{t}^+ + \hat{t}^- \right) + \beta \left( \hat{t}^+ n^- + \hat{t}^- n^+ \right) \, , \end{aligned}$$

(17)

$$\begin{aligned} \widehat{\vec {M}_* }&= \dfrac{1}{2}\left( \vec {M}^+_* + \vec {M}^-_*\right) - \beta \left( \vec {M}^+_* n^- + \vec {M}^-_* n^+ \right) \, , \end{aligned}$$

(18)

with $\beta =[-0.5,\, 0.5]$. Please see Palm and Eskilsson (2020b) for further details on the formulation including bending stiffness.

2.3 Coupled CFD solver for moored objects

The force and moment from the fluid acting on each computational face of the body surface is computed from the fluid pressure $p_i$ and the shear stress $\tau _i$ of the surrounding flow. The rigid-body motion is governed by Newton’s II law

$$\begin{aligned} \frac{{\mathrm {d}}}{{\mathrm {d}}t} \left( {\mathbf {M}}^f\vec {u}\right)&= \sum _{i=1}^{N_{\mathrm {cell}}} A_i {\left[ \begin{array}{c}{p_i \hat{{\mathrm {n}}}_i + \vec {\tau }_i} \\ r_i \times \left( p_i \hat{{\mathrm {n}}} + \vec {\tau }_i \right) \end{array}\right] } + \sum _{i=1}^ {N} r_i \times \vec {F}_i \, , \end{aligned}$$

(19)

where $r_i$ is the position vector from the centre of gravity to the cell face-centre or the mooring attachment point respectively, $\hat{{\mathrm {n}}}_i$ is the unit outward-pointing normal of face i and $A_i$ is the face area. The total number of cells on the body surface is $N_{\mathrm {cell}}$. Here the fundamental coupling between the mooring and the CFD domains is evident. The sum of N mooring line forces $\vec {F}_i$ is added to the rigid-body motion equation.

The mooring force computed by MoodyCore acts as a restraint to the rigid body solver in the CFD domain. For details and validation of the coupling see Palm et al. (2016) and Palm and Eskilsson (2018). The connection with MoodyCore was made using the quadratic interpolation scheme in the MoodyCore API, i.e., the attachment point positions attained from the CFD solution are interpolated and used to sub-step the position boundary condition in the mooring solver. The typical time step size for the mooring cables in these simulations is at least an order of magnitude smaller than the time step used in the fluid part.

2.4 CFD to resolve mooring components

To resolve mooring components in CFD means solving a multi-body problem. The forces and moments acting on the mooring component then follow directly as for any other body, see Eq. (19). OpenFOAM supports multi-body simulations through the so-called rigidBodyMotion class in which bodies are coupled through joints and the motion is computed by solving the forward-dynamics problem (Featherstone 2014). However, in this paper we prefer to use the classical sixDoFRigidBodyMotion class in which the motion of each body is simply solved by time-stepping Eq. (19). Both these classes use the spherical linear interpolation (SLERP) based mesh morphing algorithm (Shoemake 1985) to handle the mesh motion. The sixDoFRigidBodyMotion class has in this work been extended to handle multiple bodies, as well as inter-body mooring forces through a modified mooring restraint which distributes the mooring forces to act on each body. Please note that the extended multi-body solver could just as well be used with overset-meshes, albeit at a higher computational expense.

Fig. 1

Flow-chart of one-sided sampling implementation

2.5 Fluid sampling

So far MoodyCore has supported still water, uniform current and fluid motion from linear waves to compute the drag and added mass forces acting on the moving mooring lines. Clearly, this is a simplification in cases of nonlinear waves, as well as in the vicinity of any larger structure where near-field diffraction effects are significant. Introducing a one-sided coupling should in these cases serve to increase the fidelity of the resulting mooring loads. The fluid motion in the CFD domain is allowed to influence the mooring simulation via the parameterised Morison approximation, but the effect of the cable motion on the fluid flow is not simulated. Hence this is a one-way coupling. This simplification allows for the moorings to move also in regions of coarser mesh. The loads on the system are from Morison et al. (1950), according to Eqs. (6)–(8). As long as regions where there is a risk of large vortex-induced-motion (VIM) are avoided, a one-sided coupling is judged to be a sufficiently good approximation of the fluid-mooring interaction.

The flow-chart in Fig. 1 explains the working principle of the fluid velocity sampling. At each time step, the CFD solver collects important sampling points from the mooring solver. In the current implementation, we use the quadrature points of the Legendre polynomials, however a coarser sampling may very well be justified. The mooring points are converted to fluid probes, which sample the fluid density ($\rho$), the velocity (U), and the acceleration $\left( \frac{\partial U}{\partial t}\right)$. The sampled fluid state data is used by MoodyCore to determine the flow-dependent Morison loads from added mass and drag effects, including free-surface emergence effects. The domain sizes of the two solvers are allowed to be different, so for any point where the mooring lines are extending beyond the CFD domain, the fluid is assigned to be quiescent, and the density is selected based on the still water level.

3 Test cases

3.1 Catenary chain in current

Fig. 2

Time history of the tension in the fairlead for the case of no current, uniform current inside the MoodyCore mooring solver and uniform current sampled from the OpenFOAM CFD solver. Sinusoidal surge motion of the fairlead with 0.075 m amplitude and periods of a $T_f=0.79$ s, b $T_f=1.58$ s, c $T_f=3.16$ s and d $T_f=4.74$ s

A comprehensive experimental parameter study of catenary chain moorings was performed by Barrera et al. (2019), investigating the influence of chain properties, current velocity, wave action and bottom conditions. The experiments were carried out in the wave and current flume at IH Cantabria, Spain. Single catenary mooring chains at 1:40 Froude scale were tested in the 56 m long and 1.35 m deep experimental flume basin. The tests using still water and a steady current are compared with numerical simulations in this section.

The catenary chain was 7.305 m long, with a mass of 0.115 kg/m and an equivalent diameter of 0.0045 m. Standard chain coefficients for drag and added mass coefficients were used (DNV 2010). The choice of axial stiffness requires some explanation. The experimentally tested axial stiffness was too high compared to the full-scale equivalent, as it most commonly is except in a few cases (Bergdahl et al. 2016). The overall elasticity of the perfectly scaled mooring line was therefore experimentally mimicked by introducing horizontal springs at the anchor to lower the mean stiffness. To reduce model complexity and avoid uncertainties in the physical properties of the springs, the numerical results presented in this paper were instead made with a model scale axial stiffness (EA) of 20.7 kN, representing a perfect 1:40 model of the R3 grade $D=100$ mm link prototype chain reported as a prototype target in Barrera et al. (2019). The anchor was located at $\mathbf {x}_a = (0,0,0)$ m and the fairlead at rest at $\mathbf {x}_f = (6.97,0,1.2)$ m. A steady current velocity $\mathbf {U}_c=(0.08,0,0)$ m/s was used, assumed to be uniform for simplicity. A sinusoidal surge motion with amplitude 0.075 m was imposed at the fairlead for periods $T_f \in [0.79, 1.58, 2.37, 3.16, 4.74]$ s.

Fig. 3

Maximum (a) and minimum (b) fairlead tension for the case of no current, uniform current inside the Moody mooring solver and uniform current sampled from the OpenFOAM CFD solver. Sinusoidal surge motion of the fairlead with 0.075 m amplitude and period $T_f$ s. Experimental data from Barrera et al. (2019)

The chain was divided into $N_{el}=10$ elements of order $P=4$, employing a 3rd order explicit Runge–Kutta scheme for time integration. The CFD fluid domain was modelled as a quasi 2D domain, $x \in [-12,\, 12],\, y \in [-0.1,\, 0.1],\, z \in [0,\, 1.35]$ m, discretized into 430 000 rather uniform hexahedrals. As the cable is submerged and the flow assumed to be uniform, there is no free surface included in the CFD simulations. Thus, the initial condition and inflow/outflow boundaries are set to $u_x = 0.08$ m/s while the upper and lower boundaries are treated with slip conditions. The divergence terms are solved using the second-order van Leer scheme, and the gradient and diffusion operators are solved using a second-order central difference scheme. The time stepping in the CFD solver is done using the implicit Euler scheme with a CFL condition of 0.9.

Figure 2 shows the time history of the tension at the fairlead using (i) no current, (ii) a uniform current inside MoodyCore, and (iii) sampling the current from the CFD domain. We see that we get a slight difference in the peak load between the no current and current cases, where the current gives a larger peak load. This effect diminishes with increasing $T_f$. The CFD sampling and the internal uniform current cases yield virtually the same results, which verifies the fluid sampling procedure inside the OpenFOAM solver. The very minor differences are caused by the fact that the fluid velocity close to the bottom differs. In addition, some mooring nodes exit the CFD domain (very small value below the bottom) and thus experience zero fluid velocity in the sampled simulation.

Figure 3 compares the numerical simulations to the experimental data from Barrera et al. (2019). There is overall a very good fit between experimental and numerical results, however, the difference between current and still water is smaller in the numerical simulations than in the experiments. This is believed to be due to simplifications made in the numerical set up, such as neglecting the spring at the anchor and the approximation of uniform flow. In addition, the choice of hydrodynamic coefficients may affect the results. Nevertheless, the general behaviour of the maximum and minimum tension and the effect of current is very well captured in the numerical model.

3.2 DeepCwind floating offshore wind turbine

A much studied floating offshore wind turbine (FOWT) case is the DeepCwind semi-submersible that has been used in the OC5-OC6 projects in the International Energy Agency (IEA) Wind Task 30 (Robertson et al. 2017, 2020). DeepCwind is slack moored with three catenary mooring legs 120 degrees apart, with one leg facing the wave direction (see Fig. 4). In this section we present numerical results based on the parameters in the 1:50 scale model of the device that was tested in the wave basin at Marin, the Netherlands (Robertson et al. 2020).

The OC5 case has been modelled using the CFD solver ReFRESCO in a series of papers (Burmester et al. 2020a; Wang et al. 2020), as well as in the STAR-CCM+ model using bi-chromatic waves (Wang et al. 2021). Most of these studies focused on verification and validation (V &V) of the CFD method with the mooring only represented as simple restoring forces, but in Burmester et al. (2020a) the CFD model ReFRESCO was coupled to the dynamic mooring solver aNySIM to model the OC5 case. Recently Martin and Bihs (2021) simulated this case using a mooring model based on finite difference discretization of a geometrically exact beam model coupled to the REEF3D CFD model.

Fig. 4

Snapshot of slack-moored OC5 FOWT in regular waves ($H=0.147$ m and $T=1.71.$ s) propagating in the positive x-direction

The FOWT is set-up in OpenFOAM in a hexahedral-dominated mesh, see Fig. 5. The computational domain is $x \in [-11.4,\,11.4], \,y \in [-5,\,5],\, z \in [-3.6,\, 2.4]$ m, with the still water level at $z=0.4$ m. The mesh is deliberately rather coarse, consisting of 2M cells and only two cells in the boundary layer, as the main objective is to investigate the influence of the one-way fluid-mooring coupling. The mesh has refinement zones around the FOWT and at the free surface, but not around the positions of the mooring lines. Please note that the mooring lines extend beyond the computational domain. Mooring sampling points outside the CFD domain are assumed to be submerged in still water. The divergence terms are solved using the second-order van Leer scheme, and the gradient and diffusion operators are solved using a second-order central difference scheme. The inflow/outflow boundary conditions are set using the native wave generation/absorption in OpenFOAM-v2012. The upper boundary is set to zero total pressure and the bottom and side boundaries use slip conditions. The semi-sub has a no-slip condition with automatic wall functions. Turbulence is modelled using the standard $k-\omega$-SST model. The time-stepping uses first-order implicit Euler scheme with a CFL condition of 0.5, starting from still water. In MoodyCore the mooring lines are discretized into 10 elements of order 4 and the time-stepping is carried out using an explicit third-order Runge–Kutta scheme with a CFL of 0.9. See Table 1 for information about the data parameters of the semi-submersible and the mooring chains used in the simulation.

Fig. 5

Computational domain and mesh for the slack-moored OC5 FOWT case

Table 1 Properties of the FOWT the catenary mooring

Regular waves of height 0.147 m and period 1.71 s were used, without any wind present. There are only very minor differences in resulting FOWT motions and mooring tension when sampled moorings and still-water modelled moorings are compared, see Fig. 6. The heave and surge motions are virtually unaffected by the one-way coupling. The only visible difference is in the pitch motion which is slightly larger for the one-way coupling simulation. Focusing on the tension time history of the front mooring line (Fig. 6d), we again note that the tensions are generally similar between the simulations, although some very minor differences can be seen. In contrast to the simulations in steady current from Sect. 3.1, the trend is here that the one-way coupling gives slightly smaller tension forces. However, for all practical purposes the motion and tension results are the same, and there is little gain in using the one-way coupling. It should be noted that this conclusion is subject to the single wave case studied in this work. A more wide-banded and comprehensive test matrix is needed to pinpoint regions of validity for the still-water assumption of coupled dynamic mooring simulations with CFD.

Fig. 6

Comparison of using still water assumption (solid red line) and fluid-sampling (dashed black line) for estimating drag and added mass to the mooring solution. a surge, b heave, c pitch motion of the FOWT, and d tension in the front mooring cable

3.3 CFD modelling of a self-reacting WEC with hybrid mooring

Mooring component simulation can be done in several different ways. Here we refer to a mooring component as a submerged buoy or clump-weight which is of substantial size. A numerical model of the Waves4Power WEC buoy (self-reacting point-absorber) (Waves4Power AB 2022) is presented in this section. It was moored with a hybrid three-leg mooring system with submerged buoys and synthetic mooring ropes. Waves4Power used a very similar hybrid mooring set-up in their full-scale sea-trial deployed at Runde, Norway, which inspired the current model setup. The Waves4Power system consists of an axi-symmetric WEC, in which the PTO reacts against a heave plate inside a tube. The device is moored with three hybrid mooring legs 120 degrees apart with the front leg facing the incoming wave direction (see Fig. 7). Each mooring leg consists of a lower and an upper polyester rope, both attached to an intermediate submerged cylindrical buoy.

Fig. 7

Lay-out of self-reacting WEC with hybrid mooring

This device was investigated in detail by Yang (2018) using standard coupled mooring simulations based on linear potential flow theory. Table 2 outlines the parameters used in this section, obtained from Yang (2018).

Table 2 Properties of the Waves4Power system

Fig. 8

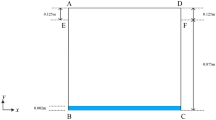
a Layout of the mooring system at equilibrium, showing the location of points A, B, C and F in the mooring leg. b Two-dimensional view of the buoy dimensions in the CFD domain. From Palm and Eskilsson (2020b)

A sub-problem of this case was studied by Palm and Eskilsson (2020b). They considered a single mooring-leg with prescribed fairlead motion, see Fig. 8. A detailed analysis focusing on the response of the submerged buoy and the mooring forces was performed using four different numerical methods:

• 1. xyz - Only translation implemented in the submerged buoy motion. Rotation is neglected, and ignored;

• 2. ind - The Morison drag loads due to rotating the submerged buoy are computed independently from the loads originating from the translating motion;

• 3. quad - In the quad method, the coupling between translation and rotation of the submerged buoy is solved using numerical quadrature along the symmetry axis;

• 4. cfd - A RANS simulation is used for loads influencing the buoy motion. The cylinder was simulated moving in still water with the entire computational domain. No free surface was accounted for.

Here we will add a fifth level of fidelity by fully resolving the entire problem in CFD:

• 5. cfd full - A full RANS simulation was used for the loads and motion of the full WEC system. Thus we modelled 4 bodies connected with 6 mooring lines, in which the mooring lines used the one-way mooring-fluid coupling, as well as bending stiffness. Here the submerged buoys were affected by, and affects, the surge, heave and pitch response of the WEC. They are also subject to wave action and free-surface variations.

The full CFD case used a hexahedral-dominated mesh made up of 37M cells, see Fig. 9. The computational domain was $x \in [-200,\,300], \,y \in [-150,\,150],\, z \in [-90,\, 30]$ m, with the still water level at $z=0$ m. The mesh was heavily refined around the free surface, and refinement zones were placed at the WEC and at the three submerged buoys. The PTO was modelled as a linear damper in the WEC local heave direction. The numerical settings of the CFD model were the same as in Sect. 3.2. The mooring lines were discretized into 5 and 10 elements of order 4 for the upper and lower line (1 and 2) respectively.

Fig. 9

Mesh used for WEC with hybrid mooring

Fig. 10

Envelope results for the submerged cylinder fo the front mooring leg. a–c Show normalised submerged buoy motion amplitudes for surge, heave and pitch respectively. d and e Compare the dynamic tension range (${\mathrm {max}}(T)-{\mathrm {min}}(T)$) at point B of cable 1 and at point C of cable 2 respectively

Fig. 11

Top view of the CFD simulations of the submerged buoy at $z=h^b/2$ with the $Q=200$ iso-surface. Colors are by velocity magnitude $U\in [0,4.3]$ m/s (blue to red). The snapshots were taken 0.2 time periods apart over one cycle: a $t/T_p=0.0$; b $t/T_p=0.2$; c $t/T_p=0.4$; d $t/T_p=0.6$ and e $t/T_p=0.8$. From Palm and Eskilsson (2020b) (color figure online)

Figure 10 shows the difference in result between different levels of fidelity used for estimating the buoy and mooring response. Please note that the used drag and added mass coefficients used in the parameterized models were selected from DNV tables, see (Palm and Eskilsson 2020b) for a detailed analysis. The xyz method is deviating considerably from the other three methods. Clearly, the rotational mode of motion has a large impact on the motion response of both the buoy and the mooring load. The cfd simulation matches relatively well with the quad and ind methods in terms of mooring force range, however, the predicted motion amplitudes of the buoy are overall smaller in the cfd model than in the Morison approaches. The cfd full method differs from the other four methods. This is only to be expected as the WEC gets a surge offset and generally there is much more interaction taking place. The surge and heave amplitudes are, generally similar to the other four results. The main difference is the pitch motion which is greatly exaggerated. This is due to the larger tension ranges, which probably were caused by the surge offset. A more detailed investigation of full CFD to resolve complete hybrid moored marine structures is ongoing but is left to future work.

To further illustrate the importance of high-fidelity simulations we consider the vorticity around the cylinder. Figure 11 shows that even around a simple geometric form in moderate motion amplitude (fairlead amplitude is $a=0.5$ m), the vortical influence can clearly be seen. For cases where the mooring system is fitted with large buoys or clump-weights, the importance of mooring component fidelity on the device motion and overall responses is clearly illustrated.

4 Conclusions

Two major improvements towards fully resolved wave-body-mooring (WBM) interaction were presented and analysed: (i) a one-way coupling to the dynamic mooring simulation that enables Morison drag and Froude–Krylov forces on the mooring lines based on sample high-fidelity fluid model kinematics; and (ii) a multi-body framework developed for the OpenFOAM-MoodyCore software that supports inter-mooring forces between floating bodies in the CFD domain.

Improvement (i) was verified against analytic fluid motion for a catenary chain in steady current, and against still-water coupled simulations for the moored DeepCwind FOWT. Although minor effects of the one-way coupling were recorded here, the uncertainties of the simulation decreased significantly. Mooring lines are slender structures and the one-way coupling has a high degree of accuracy for most mooring applications. For cases where the current has a strong spatial variation, the one-way sampling effectively transmits the CFD domain flow resolution to the dynamic mooring response. The sampling also takes care of the problem of near-field disturbance of the wave-field close to larger structures or complex geometries. In such cases, an analytic approximation based on assuming still water or an undisturbed incoming wave-field are both uncertain, and the one-way implementation guarantees a much more representative flow to estimate the fluid loads on the moorings. Of course, this benefit is highest close to the body and is less important for the lower parts of the mooring lines. However, as illustrated in the DeepCwind test case, for mild regular waves the influence can be negligible. Although most relevant dynamic effects on the mooring lines are judged to be captured by the one-way coupling, simulations with e.g. vortex-induced motion (VIM) would require a two-way coupling, where also the mooring line presence affects the flow field. Work on implementing a two-way coupling is ongoing work.

With regard to improvement (ii): for hybrid mooring with submerged buoys and/or clump weight of substantial size, there are clear benefits of resolving the mooring components directly in the CFD domain instead of relying on Morison approximations. This approach removes the need of calibrating drag and added mass coefficients. As illustrated in self-reacting WEC test case, the entire WBM system should be modelled as an inter-moored coupled system as the global motion response of the main structure heavily influences the mooring components.

Finally, it should be mentioned that even though the sampling has been developed for coupling OpenFOAM with MoodyCore, the sampling functionalities inside OpenFOAM are straightforward to use for any other mooring solver, by just adding a few routines to the mooring solver API (to send the mooring nodes to the CFD solver and to set the sampled fluid velocities in the mooring). These updates are included in the next release of MoodyCore. MoodyCore and the OpenFOAM API including the sampling routines will as usual be available from github (https://github.com/johannep/moodyAPI) and from the CCP-WSI repository (https://www.ccp-wsi.ac.uk).