Minimising turbine thrust variation in multi-rotor tidal fences

Abstract

Recent analysis of tidal stream energy devices has focussed on maximising power output. Studies have shown that significant performance enhancement can be achieved through the constructive interference effects that develop between tidal stream turbines by deploying them close together. However, this results in variation in the flow incident on the turbines and hence leads to thrust variation across the turbine fence. This may lead to varying damage rates across the fence with adverse impacts on operation and maintenance costs over the turbine lifetime. This study investigates strategies to reduce thrust variation across fences of tidal turbines using three-dimensional Reynolds-Averaged Navier–Stokes simulations. It is shown that the variation in turbine thrust across a fence of eight turbines can be reduced to within 1% with minimal impact on the fence power. Furthermore, by reducing the rotational speed of inboard turbines, or varying the blade pitch angle of the turbines across the fence, it is possible to reduce overall turbine loads and increase the power to thrust ratio of the turbines.

1 Introduction

Idealised representations of wind and tidal turbines as actuator disks that reduce the streamwise momentum of a flow have been used to establish theoretical upper bounds on performance. Betz and Prandtl (1919) demonstrated that the maximum power coefficient $C_\mathrm{P}$ of a turbine in an unbounded flow normalised on the undisturbed kinetic flux through the rotor plane was $C_\mathrm{P,max}=16/27$, achieved when the flow through the actuator disk was reduced to 2/3 of the freestream speed. Garrett and Cummins (2007) showed that the maximum power coefficient increased when flow expansion was constrained by the presence of lateral or vertical boundaries such as the sea bed, sea surface or channel walls. Garrett and Cummins proposed a new limit of $C_\mathrm{P,max}=16/27\left( 1-B\right) ^{-2}$ where the blockage ratio B is the ratio of the swept area of the turbine to the cross-sectional area of the flow passage surrounding the turbine.

The flow around a turbine can also be affected by adjacent turbines which also act to constrain flow expansion. The theoretical maxima described by Garrett and Cummins corresponds to a case in which a fence of turbines uniformly spans a channel (Garrett and Cummins 2007). However, turbine deployment constraints due to variations in bathymetry and restrictions due for environmental and other marine users will mean that turbine fences do not uniformly span the width of a channel. Nishino and Willden (2012) and Vogel et al. (2016) developed analytical models of fences of tidal turbines partially spanning a channel with non-deforming and deforming free-surfaces respectively, and showed that reducing inter-turbine spacing resulted in increased the fence power coefficient. These two scale models distinguish between the global blockage $B_\mathrm{G}$, the ratio of the swept area of all turbines to the channel cross-sectional area, and the local blockage $B_\mathrm{L}$, the ratio of the swept area of a single turbine to the surrounding flow passage bounded by neighbouring turbines.

To date, much of the multi-rotor turbine fence analysis has focussed on the maximum power condition. Hunter et al. (2015) showed that the power coefficient of a non-staggered fence of actuator disks is maximised when the turbine emulators are operated with a uniform resistance coefficient. In this idealised case there is a significant variation in the thrust and power coefficients across the fence which would be achieved through different turbine operating conditions or designs across the fence, as shown by experimentally by Cooke et al. (2015) and numerically by Vogel and Willden (2017, (2019). This variation, particularly in thrust coefficient, may cause significant differences in wear between turbines over the fence lifetime.

In addition to the improved performance potentially available through closely spacing turbines, additional benefits from shared infrastructure and reduction in deployment footprint may also be realised. A number of floating tidal turbine platforms have been developed. Minimising the cross-fence variation in thrust will help to minimise differences in turbine loading with corresponding benefits for required maintenance intervals and costs. This paper investigates operation strategies that minimise the cross-fence variation in turbine thrust at conditions close to the maximum fence performance. Reductions in fence thrust have the additional benefit of reducing turbines loads and may increase the turbine power to thrust ratio.

2 Numerical model

The commercial Computational Fluid Dynamics (CFD) software ANSYS Fluent v.18.1 was used to perform steady, incompressible Reynolds-Averaged Navier–Stokes (RANS) simulations of fences of four and eight actuator disks. Turbulence closure was provided using the $k{-}\omega$ Shear Stress Transport (SST) turbulence model introduced by Menter (1994). This model combines the advantages of the $k{-}\omega$ model near no slip boundaries with the $k{-}\epsilon$ model in the remainder of the domain. The eddy-viscosity limiter in the $k{-}\omega$ SST model has been shown to work well for applications with adverse pressure gradients such as turbine wakes (Abolghasemi et al. 2016; Shives and Crawford 2016).

Two turbine representations using actuator disks were implemented: porous disks which impose a streamwise momentum discontinuity on the flow, and blade element disks which impose both a streamwise and rotational momentum discontinuity on the flow, determined using blade element theory based on the computed local flow velocities. The former representation reflects the idealised turbine representations employed in theoretical such as Garrett and Cummins (2007), whereas the latter representation incorporates phenomena associated with real turbines such as rotation in the wake. The implementations are described below. A more detailed discussion of the state-of-the-art of different types of turbine representation can be found in Sanderse et al. (2011).

2.1 Computational setup

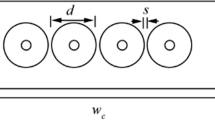
Fences of $d=20\,$m diameter turbines are simulated in a domain as shown in Fig. 1. Symmetry is exploited in the xy plane at the centre of the domain for computational efficiency. The depth of the channel is $h=2d$, and the computational domain extends 10d upstream and 40d downstream of the fence. The width of the domain w is scaled in order to achieve a low global blockage ratio $B_\mathrm{G}= n\pi d^2/4wh=0.02$ where n is the number of turbines. Inter-turbine spacing s is varied to control the local blockage ratio $B_\mathrm{L}=\pi d^2/4(s+d)h$ which describes the ratio of turbine swept area to the cross-sectional area of the surrounding flow passage.

Fig. 1

Schematic of the simulated channel cross-section at the turbine plane. A symmetry plane is employed for computational efficiency. The domain height h and width w are chosen to maintain a low global blockage coefficient $B_\mathrm{G}=0.02$

The top and bottom surfaces of the channel geometry are slip walls, and symmetry boundary conditions were applied to the lateral walls. A uniform velocity of 2 ms${}^{-1}$ was applied at the inlet, and a pressure-outlet condition was applied to the downstream boundary. A uniform turbulence profile with a turbulence intensity of approximately 20% was applied at the inlet, which decayed to a turbulence intensity of approximately 5% at the rotor plane as no shear stresses were applied to sustain the turbulence profile. The working fluid is water with density $\rho =$1000 kgm${}^{-3}$ and dynamic viscosity $\mu =8.9\times 10^{-4}$ Pa s.

A block-structured hexahedral mesh was created in the domain, with concentric O-Grids used around the turbine disks. The mesh resolution at the edge of the disks follows that used in previous studies (Nishino and Willden 2013; Hunter et al. 2015; Vogel et al. 2018). The initial cell height at the edge of the disks was fixed at d/200 with a geometric growth rate $\le 1.2$ in order to resolve the shear layer that develops at the edge of the disks. Figure 2 shows the variation in spatially-averaged $U_\mathrm{d}$, $U_\mathrm{d}^2$ and $U_\mathrm{d}^3$ at the rotor plane as the rotor disk mesh is refined. The computed mass, momentum and energy flux metrics did not change for meshes with greater than 5273 elements on the rotor plane, which was used for all simulations presented below.

Fig. 2

Evaluation of spatially averaged rotor plane velocity $U_\mathrm{d}$ (a) and higher order components $U_\mathrm{d}^2$ (b) and $U_\mathrm{d}^3$ (c), normalised relative to the respective free-stream averages as the number of elements on the rotor disk varies

2.2 Porous actuator disks

The porous-jump boundary condition in Fluent was used to model the porous disks. The thin porous medium has a finite thickness over which a static pressure discontinuity is imposed on the flow. By neglecting Darcy’s effects, the static pressure drop across the disk $\varDelta p$ is determined as

$$\begin{aligned} \varDelta p = K \left( \frac{1}{2}\rho {U_\mathrm{d}}^2 \right) , \end{aligned}$$

(1)

where K is the resistance coefficient that controls the thrust of the disk, $\rho =1000$ kgm${}^{-3}$ is the density of water, and $U_\mathrm{d}$ is the streamwise flow speed through the disk. Disk thrust T and power P are normalised on the upstream momentum and kinetic fluxes to give the thrust $C_\mathrm{T}$ and power $C_\mathrm{P}$ coefficients defined as follows:

$$\begin{aligned} C_\mathrm{T}= & {} \frac{T}{\frac{1}{2} \rho {U_\infty }^2 A} = K\frac{\langle U_\mathrm{d}^2\rangle }{{U_\infty }^2} \end{aligned}$$

(2)

$$\begin{aligned} C_\mathrm{p}= & {} \frac{P}{\frac{1}{2} \rho {U_\infty }^3 A} = K\frac{\langle {U_\mathrm{d}}^3\rangle }{U_\infty ^3}, \end{aligned}$$

(3)

where $\langle \cdot \rangle$ is spatially averaged over the frontal area of the disk, $U_\infty$ is the freestream flow speed and A is the frontal area of the disk.

The porous disk is a simplified model of a real turbine, parameterising the resistance of the turbines with the resistance coefficient K. The variation in resistance for a real turbine can be achieved by changing rotational speed, or through changing the pitch angle and/or solidity of the blades (Schluntz and Willden 2015). The porous disks represent idealised turbines which neglect losses due to the swirl imparted by turbine rotation and those due to factors such as turbine drag, tip and hub losses and, therefore, provide an upper bound to turbine performance.

Fig. 3

Contour plots of fence average power coefficient ($C_\mathrm{P}$), thrust coefficient ($C_\mathrm{T}$), and basin efficiency ($\eta = C_\mathrm{P}/C_\mathrm{T}$) as a function of changes in resistance coefficient K for a four turbine fence. $K_1$ is the resistance coefficient value for the inner turbines and $K_2$ the resistance coefficient of the outer turbines. The turbine spacing is $s/d=1$

2.3 Blade element actuator disks

Blade element methods enable a more detailed model of turbine performance to be described by characterising the influence of turbine geometry and operation on the flow. The Blade Element Actuator Disk (BE-AD) couples two-dimensional blade element equations with the simulated flow incident upon the actuator disk in order to determine the axial and tangential forces on the turbine. The forces are determined using two-dimensional hydrofoil lift and drag characteristics and imposed on the flow as a static pressure discontinuity $\varDelta p$ and increase in swirl velocity $U_\theta$ across the actuator disk. The BE-AD method was implemented as an ANSYS Fluent user-defined function as described by McIntosh et al. (2011). The static pressure discontinuity is calculated as follows:

$$\begin{aligned} \varDelta p = \frac{1}{2}\rho U(r)^2\sigma (r)\left( C_\mathrm {l}\cos \phi + C_\mathrm {d}\sin \phi \right) , \end{aligned}$$

(4)

where U(r) is the chordwise velocity component defined as the resultant between the axial and swirl velocities

$$\begin{aligned} U(r) = \sqrt{U_\mathrm{d}^2+U_\theta ^2}, \end{aligned}$$

(5)

which has a flow incidence angle $\phi$ relative to the plane of rotation

$$\begin{aligned} \phi = \tan ^{-1}\frac{U_\mathrm{d}}{U_\theta } \end{aligned}$$

(6)

The angle $\phi = \alpha +\beta$ where $\alpha$ is the local angle of attack and $\beta$ is the local blade twist angle, which is specified as part of the blade geometry, as is the solidity ratio $\sigma (r)$. Aerofoil data for the rotor blade must also be specified in order to define the lift and drag coefficients $C_\mathrm{l}$ and $C_\mathrm{d}$ respectively.

While $U_\mathrm{d}$ is directly computed as part of the flow simulation, an iterative approach is used to calculate the swirl velocity

$$\begin{aligned} U_\theta = -\frac{U(r)^2\sigma (r)\left( C_\mathrm{l}\sin \phi - C_\mathrm{d}\cos \phi \right) }{4U_\mathrm{d}} \end{aligned}$$

(7)

A swirl velocity $2U_\theta$ is imposed downstream of the turbine in order to conserve angular momentum in the flow. For further details on blade element theory the reader is referred to, for example, Burton et al. (2011).

The mesh described in Sect. 2.1 was modified to include nacelles with diameter $d_\mathrm{h}=0.15d$ and length 0.35d centred on the rotor plane. A no-slip wall boundary condition was applied on the nacelle. The blade twist and solidity profiles for the three-bladed horizontal axis turbine rotors simulated in this study were presented by Schluntz and Willden (2015), which feature the Risø-A1-24 hydrofoil section (Fuglsang and Bak 2004). The BE-AD model requires the rotational speed of the rotor to be specified as an input, which is varied to change the resistance presented by the rotor.

3 Results

Multi-rotor fences, consisting of 4 and 8 turbines, are modelled within this study. The porous actuator disks described in Sect. 2.2 are used to analyse the complex interdependencies between individual turbine resistance and overall fence performance characteristics. Blade-element actuator disks are then introduced to investigate the potential for cross-fence turbine control strategies by varying blade pitch angle and rotational speed to improve the turbine power-to-thrust ratio.

3.1 Porous actuator disk

Figure 3 shows the effect of varying individual turbine resistances on fence thrust and power characteristics within the 4 turbine porous actuator disk setup. It is clear that, as highlighted by Hunter et al. (2015), the fence power coefficient is maximised ($C_\mathrm{P}=0.728$) when the turbines are operated with a uniform resistance coefficient (K = 3 when $s/d=1$). The variation in fence power coefficient over a significant range of K is relatively small. Although the variations in $C_\mathrm{P}$ are relatively small, Fig. 3 shows that there is a much more significant variation in fence thrust coefficient $C_\mathrm{T}$ with K, and consequently the basin efficiency $\eta =C_\mathrm{P}/C_\mathrm{T}$, which is a metric of the power to thrust ratio, is higher for smaller values of K.

Increasing fence length, as shown in Fig. 4, to an eight turbine fence while maintaining the same turbine spacing $s/d=1$ leads to an increased fence power coefficient of $C_\mathrm{P}=0.783$, 7.5% greater than achieved by the four turbine fence with the same spacing. This is achieved by increasing the resistance coefficient uniformly to $K=3.5$, resulting in the higher fence thrust coefficient of $C_\mathrm{T}=1.28$, an uplift of 9.7% from the $C_\mathrm{T}$ at the peak power condition for the four turbine fence.

Fig. 4

Plots of power coefficient ($C_\mathrm{P}$) and Thrust coefficient ($C_\mathrm{T}$) versus resistance coefficient (K), for each rotor within an 8 turbine fence with turbine spacing $s/d=1$, with local and global blockage coefficients of $B_\mathrm{L}=0.196$ and $B_\mathrm{G}=0.02$ respectively. The resistance coefficients of all turbines are equal (i.e. $K_i = K, \, i=1,\ldots ,4$)

Figure 4 also shows the variation in turbine power and thrust coefficients as a function of K for an eight rotor fence. Utilising symmetry, turbines are numbered from 1 in the centre of the fence to 4 in the most outboard position. Turbine thrust coefficient increases with increasing K, although there is a general trend of higher turbine $C_\mathrm{T}$ being achieved by turbines closer to the centre of the fence. Cross-fence variation of turbine power coefficient also increases with K, with turbines further outboard reaching lower $C_\mathrm{P}$ than those inboard. Figure 4 shows that the inboard turbines of the eight turbine fence operate at almost identical thrust and power coefficients across the range of K considered in this study, whereas the performance of the outboard turbines is significantly different. At the peak power condition, the difference in thrust and power of the two innermost turbines is less than 1%, whereas the furthest outboard turbine, Rotor 4, operates at a thrust coefficient 5% lower than the fence mean and about 8% lower than the most inboard turbine.

Increasing fence length allows a greater difference to be established in the flow passing inboard and outboard turbines. The flow approaching the fence is decelerated due to the resistance presented by the turbines, resulting in a flow speed less than the freestream passing through the turbines at the rotor plane. Consequently, flow is accelerated around the edges of the array. At small values of K there is relatively little cross-fence variation in performance as the resistance presented by the turbines has little impact on the flow. However, as the fence thrust increases there becomes a greater difference in the performance of inboard and outboard turbines. Resistance to flow diversion around inboard turbines is provided by neighbouring turbines, whereas resistance to flow diversion is only supported on the inboard side for the outboard turbines. Consequently, the flow can be easily diverted into the array bypass around the outboard turbines, whereas the flow profile approaching the inboard turbines is more uniform. This in turn means that the inboard turbines can sustain the higher levels of thrust required to achieve higher power than the outboard turbines. The difference in the flow approaching inboard and outboard turbines is relatively small for short fences such as the four turbine fence, whereas greater differences are observed for longer fences, such as the eight turbine fence.

3.1.1 Minimising thrust coefficient variation

As noted above, there is an 8% variation in thrust coefficient $C_\mathrm{T}$ between the most inboard and furthest outboard turbines at the maximum power condition. The variations in performance result from the variations in local flow regimes that develop across finite-length fences. Variation in turbine loading may result in differences in turbine lifetime across the fence, which is undesirable for efficient operations and maintenance. Cross-fence variation in thrust can be minimised by increasing the resistance coefficient of the outboard turbines (‘Strategy A’), or reducing the resistance coefficient of the inboard turbines (‘Strategy B’). The $C_\mathrm{P}$ contour plot in Fig. 3 indicates that variations in K of almost 50% around the maximum $C_\mathrm{P}$ may cause a less than 1% reduction in mean fence $C_\mathrm{P}$.

Fig. 5

Variation in a actuator disk resistance coefficient K required to achieve constant thrust and b the effect on peak fence power coefficient for inter-turbine spacings of $s/d = 0.5, 1, 2, 4$. The global blockage ratio $B_\mathrm{G}=0.02$ remains constant

Figure 5 shows the necessary increase in the resistance coefficient of the outer turbines (Strategy A) to reduce the cross-fence variation in thrust coefficient to $\le 1\%$, where the two inner-most turbines operate at the K for peak performance. Four different inter-turbine spacing ratios are illustrated, where the global blockage ratio $B_\mathrm{G}=0.02$ is constant. The required resistance coefficient K for the inner turbines and the variation between inner and outer turbines increases as the inter-turbine spacing reduces ($B_\mathrm{L}$ increases). There is an increase in the associated fence losses due to the increased shear developed between the fence core and bypass flows. Figure 5 also demonstrates that the peak power coefficient increases with reducing inter-turbine spacing, and that the effect of minimising thrust variation across the fence has little impact on the peak power. Similar results are observed when K for the inboard turbines is reduced (Strategy B), and hence are not shown separately here. However, the fence thrust is reduced from the maximum power case using Strategy B, whereas it increases using Strategy A.

The blade element actuator disk model is used to more closely relate turbine resistance to the operation of tidal turbines. Two operational factors contribute to the turbine resistance: rotational speed $\varOmega$ (non-dimensionalised as the tip speed ratio $\lambda =\varOmega R/U_\infty$ where R is the turbine radius), and blade pitch angle $\beta _\mathrm{P}$. Turbine resistance also depends on the blade solidity and twist profiles, but these are considered to be fixed in this study as it is likely to be uneconomical to deploy multiple turbine designs within the same turbine fence, and thus the same rotor is used in all cases. The BE-AD study focusses on the eight turbine $s/d=0.5$ spacing case as this produced the largest cross-fence variation in the performance coefficients at the maximum power condition in the porous actuator disk study.

3.2 Blade-element actuator-disk

The maximum fence power achieved with a uniform tip speed ratio was found to be $C_\mathrm{P}=0.652$ at $\lambda =5.6$, a 20% reduction from the equivalent porous actuator disk case due to the additional losses introduced for example by blade drag and tip and hub losses. The hub-height flow contours shown in Fig. 6 illustrate the flow field through the turbine fence. Regions of high flow speed are observed close to the nacelles, arising from the jetting of flow around the hub due to insufficient blade solidity, and therefore flow resistance, near the root. The jetting of flow in this region limits the torque developed by the rotor compared to the porous actuator disk case.

Figure 6 clearly demonstrates the differences in wake development between the inner and outer turbines. As discussed in Sect. 3.1, the wakes downstream of the innermost turbines are more constrained due to the presence of adjacent wakes, and thus propagate uniformly in the streamwise direction. This phenomenon is primarily driven by variation in streamwise momentum in the flow; the change in rotational momentum that is modelled with the BE-AD approach makes little qualitative difference to cross-fence variations that are observed. Figure 6 also shows the significant lateral diversion of the wake that occurs for the outermost turbines and the accelerated bypass flow around the fence. This leads to a lateral velocity component incident on the outer turbines that both gives rise to azimuthally varying loads on the turbines and also results in reduced performance. This will be discussed further in Sect. 3.3. The lateral variation in static pressure is shown in Fig. 6, illustrating the variation in performance that occurs across the fence. The reduction in the static pressure drop for the outboard turbines limits the performance of the fence, and the consequent non-uniform turbine loading may result in varying turbine lifetime and maintenance requirements across the fence.

Fig. 6

Hub-height flow contours of a normalised x-velocity and b normalised static pressure for the 8-turbine fence, displayed in the xz plane. The fence is symmetric around the bottom of the figure. Flow is from left to right

3.2.1 Tip speed ratio control

The resistance of a horizontal axis turbine can be controlled by varying the tip speed ratio $\lambda$, with higher tip speed ratios producing higher thrusts. Thus, the control strategies defined in Sect. 3.1.1 now become increasing $\lambda$ for the outer turbines in Strategy A while holding the inner two constant at $\lambda =5.6$, and Strategy B reduces $\lambda$ for the inboard turbines whilst holding the outermost turbine (Rotor 4) at $\lambda =5.6$. As previously, the inner two turbines are controlled together, and it is sought to minimise the difference in turbine thrust coefficient whilst maintaining the reduction in fence power to within 1% of the maximum when all turbines operate at $\lambda =5.6$. Figure 7 shows that a greater cross-fence variation in $\lambda$ is required for Strategy A ($\varDelta \lambda =0.45$) than for Strategy B ($\varDelta \lambda =0.28$).

Fig. 7

Comparison of tip speed ratios $\lambda$ for each rotor required under Strategies A (red) and B (blue)

Fig. 8

Comparison of increasing outer turbine $\lambda$ (Strategy A), decreasing inner turbine $\lambda$ (Strategy B) and increasing blade pitch angle (Strategy C) on rotor performance. The solid lines indicate turbine power (a) and thrust (b) coefficient, and the dashed lines indicate the fence thrust and power coefficients. Rotor 1 is the furthest inboard turbine, and Rotor 4 is the furthest outboard

3.2.2 Pitch angle control

Some tidal turbines are designed with collective or individual blade pitch control as an additional control mechanism, following experience in the wind industry. Changing the pitch of the turbine blades results in a change in the angle of attack variation along the blade which in turn leads to a change in the blade forces and rotor torque. Adjusting the blade pitch angle of the turbines within a closely-spaced fence can be used to account for some of the flow variation across the fence to operate the turbines closer to their hydrodynamic optimum conditions. The precise relationship between blade pitch angle and the resulting change in flow around the turbine is a function of the hydrofoil characteristics of the blade and the blade geometry. For the turbine considered in this study, increasing the blade pitch angle to reduce angle of attack results in reduced thrust, denoted ‘Strategy C’. The alternative of decreasing pitch angle on the outer turbines to affect an increased angle of attack is not considered as this would result in increased thrust and operation closer to stall, which is considered undesirable. The thrust coefficients of the turbines in the fence were matched using Strategy C by increasing the blade pitch angles of Rotors 1, 2, 3, and 4 by $0.70^\circ$, $0.70^\circ$, $0.34^\circ$ and $0^\circ$, respectively.

3.3 Control strategy comparison

The variation in turbine power and thrust coefficients resulting from control strategies A, B, and C is shown in Fig. 8, and the key metrics are summarised in Table 1. There is an approximately 4% variation in turbine thrust coefficient across the fence at the maximum power condition, which is reduced to less than 1% with each control strategy. Strategies B and C both reduce the fence thrust coefficient by about 2.5% compared to the maximum power condition, whereas Strategy A results in a 1.5% uplift in the thrust coefficient relative to the maximum power condition. All strategies result in an increased cross-fence variation in turbine $C_\mathrm{P}$ relative to the maximum power condition (7%), with Strategy A resulting in the largest turbine $C_\mathrm{P}$ variation (11.5%). Strategies A and B achieve almost identical fence power coefficients, less than 1% lower than the maximum power condition, whereas the fence power coefficient achieved with Strategy C is unchanged from the maximum power condition. In all cases it is the reduced power achieved by the outermost turbine that limits the overall fence $C_\mathrm{P}$.

The impact that the different control strategies have on the hub-height streamwise and lateral flows upstream of the fence is shown in Fig. 9. An upstream distance of 2d is selected as a region that is affected by fence-scale flow dynamics, but is sufficiently far upstream for turbine-scale flow phenomena to be negligible. All control strategies result in less deceleration of the streamwise flow 2d upstream of the centre of the fence, although Strategy A results in greater deceleration of the flow near the fence edge between $4\le z/d\le 6$ due to the elevated level of thrust applied in that region. Consequently, the acceleration of the bypass flow ($z/d \ge 6$) is almost identical between Strategy A and the power maximisation case, whereas there is slightly reduced acceleration of the bypass flow with the lower thrust Strategies B and C. These dynamics are reflected in the lateral velocity profiles where Strategies B and C causing less lateral diversion of the flow, with the peak lateral velocity being approximately 7% less than that for the maximum power and Strategy A cases.

Table 1 Summary of tip-speed ratio range, average fence power coefficient $\overline{C_\mathrm{P}}$, average fence thrust coefficient $\overline{C_\mathrm{T}}$ and fence basin efficiency $\eta$ for the four cross-fence control strategies. The relative change in the metrics from the maximum power strategy case are also indicated

Fig. 9

Normalised streamwise (d) and spanwise (d) flow velocity evaluated at hub-height 2d upstream of the fence for the three different control strategies and power maximisation case

Reduced diversion of the flow around the fence helps to minimise the loss of streamwise momentum that ultimately limits the efficiency of energy extraction, as shown in Fig. 10. The basin efficiency achieved by the lowest thrust strategies is approximately 2.8% higher than that achieved in the maximum power case, and approximately 4.5% higher than Strategy A. The uplift in basin efficiency under Strategies B and C arises primarily as a result of the reduction in thrust that can be achieved with these approaches, as seen in the reduced disturbance to the flow in Fig. 9. Strategies that achieve lower basin efficiency require a bigger disturbance to the flow and hence are less efficient in their utilisation of the tidal resource.

Fig. 10

Basin efficiency $\eta$ of the fence under each control strategy

4 Conclusions

The performance of tidal turbine fences partially spanning idealised channels has been carried out using 3D incompressible RANS simulations. The turbines were modelled both as idealised porous disks to establish bounds on turbine performance, as well as blade element actuator disks to better represent the operational behaviour of tidal turbines. It was demonstrated using porous actuator disks that fence power is maximised when a uniform resistance coefficient is applied to each disk, although this results in thrust variation across the fence of up to 8% in the eight rotor fence case. As turbine loading drives the maintenance requirements for turbines, minimising thrust variation across a turbine fence is beneficial for reducing maintenance costs. Reducing cross-fence thrust coefficient variation to $\le 1\%$ by increasing the resistance of the outer turbines or reducing the resistance of the inner turbines was shown to cause only minimal reduction in overall fence power output. The required variation in resistance is a function of the inter-turbine spacing (local blockage ratio), with greater cross-fence variations required as the turbines were deployed more closely together.

The resistance of tidal turbines can be varied as a function of rotational speed or blade pitch angle. Three control strategies were investigated: increasing the rotational speed of the outer turbines (Strategy A), reducing the rotational speed of the inner turbines (Strategy B), and varying the blade pitch angle of the inner turbines (Strategy C). Strategies A and B resulted in a reduction in the fence power coefficient of less than 1% from the power maximisation case, whereas Strategy C resulted in negligible changes in fence $C_\mathrm{P}$. The fence thrust increased by 1.5% under Strategy A, whereas it reduced by 2.5% under Strategies B and C compared to the power maximisation case. Consequently, the basin efficiency, a metric of how efficiently the tidal resource is utilised increased with Strategies B and C, whereas it reduced under Strategy A.

Not all turbines currently under development include variable pitch control of the blades. However, similar levels of thrust reduction and basin efficiency can be achieved using variable speed or variable pitch cross-fence control to minimise turbine thrust variation. Thus, it is possible to employ strategies to minimise the variation in turbine loading and associated maintenance requirements across a fence of turbines that additionally reduce turbine loads and more efficiently utilise the available resource. The lifetime benefits of cross-fence control will vary from site-to-site according to the local tidal resource and is the subject of ongoing investigation.