Abstract
Quantitative reliability, availability, and maintainability (RAM) assessments are of fundamental importance at the early design stages, as well as planning and operation of marine renewable energy systems. This paper presents an RAM framework adaptable to different offshore renewable technologies, conceived to provide support in the choice of the device components and subsequent planning of the O&M strategies. A case study, characterizing a pilot farm of oscillating water column (OWC) wave energy converters (WECs), is illustrated together with the method used to obtain reliable estimate of its key performance indicators (KPIs). Based on a fixed feed-in-tariff for the project, economic figures are estimated, showing a direct relationship with the availability of the farm and the cost of maintenance interventions. Consequently, the probability distributions of the most relevant output variables are presented, and the mutual correlations between them investigated using principal components analysis (PCA) with the aim of discovering the relationships influencing the performance of the offshore farm. In this way, the contributions of the individual factors on the profitability of the project are quantified, and generic guidelines to support the decision-making process are derived. It is shown how this type of analysis provides important insights not only to ocean energy farm operators after the deployment of the devices, but also to device developers at the early design stage of wave energy concepts.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Ocean energy resources include wave, tidal (current and range), ocean currents, temperature gradient, and salinity gradients (European Ocean Energy Association 2010). Numerous wave power extraction concepts and technologies have been explored and developed (Cruz 2008; Falcão 2010; Falnes 2002a) in the last decades, making wave energy an active field of research and development with a number of demonstration projects aiming at reaching the commercialization stage. Several classifications exist according to the location where the device is deployed, its working principle, and its size. In this work, an oscillating water column (OWC) is considered. OWCs, which can be floating or fixed, have generally a partly submerged structure, open below the sea surface. The reciprocating motion of the water column is then used to produce an oscillation of the pressure in the air chamber and, as a consequence, an air flux through a turbine coupled to an electrical generator that constitutes the power take-off system (PTO) of the device (Falnes 2002b). Unlike other renewable energy systems, Wave Energy Converters (WECs) operate in an environment which is harsh and implies costly marine operations. Therefore, the design of offshore renewable energy systems presents additional challenges, and there is a need to develop flexible tools that allow for the assessment of the different technologies under various aspects. Among these, reliability, availability, and maintainability (RAM) assessments are of fundamental importance, because these help to reduce the significant costs associated with the deployment of marine renewable energy systems, not only at the early design stages but also during their maintenance planning and operation (Li et al. 2015).
To this end, this paper presents an RAM framework that can be used to evaluate marine renewable energy systems to identify limitations and possible areas of improvement for specific devices or sites. Computational simulation based on Monte Carlo discrete event modeling is used to provide reliable estimates of the key performance indicators (KPIs) of an offshore renewable project. These, and their mutual correlation, are then analyzed by means of multivariate analysis based on the principal component analysis (PCA) technique to extract valuable information for the project assessment. In this way, beneficial indications for assets owners and operators committed to the selection of the optimal maintenance strategies, as well as device designers and developers at the preliminary stages of development of an ocean energy technology, are derived. The remaining paper is structured in four sections: Sect. 2 describes the methodology adopted in this work, including the modeling tool used within the RAM framework (Sect. 2.1), the reliability data assessment methodology (Sect. 2.2), and the multivariate statistics analysis using PCA (Sect. 2.3). The OWC case study is detailed and the results are reported in Sect. 3. The wave energy farm model, consisting of an array of floating OWC WECs, is introduced with the detailed reliability data in Sect. 3.1, while the other input data are described in Sect. 3.2. The model outputs are presented and described in Sect. 3.3. The paper closes with the discussion of the results in Sect. 4 and general conclusions in Sect. 5.
2 Methodology
2.1 Reliability, availability, and maintainability characterization of marine renewable farms
Early determination of feasibility and risks related to the deployment of marine renewables is pivotal to attract investments and establish trust in this sector. For this reason, a number of combined economic and reliability methodologies and tools have been developed in the last few years to characterize the lifecycle logistics of ocean energy devices, and optimize their maintenance and inspection strategies. Most of these are specific for offshore wind farms, due to the technology’s higher stage of maturity and the wider diffusion of the existing projects. A thorough review of these is presented in Hofmann (2011), while a complete framework for the classification of available research studies and industrial works on this subject is introduced in Shafieea and Sørensen (2017). Due to the lack of operational experience, specific reliability measures have not been established for the wave energy sector. Numerous methodologies have been proposed to update generic failure rate data for use in reliability calculations including the part-stress method by the Military Handbook (United States Department of Defence 1991) (as explained in Sect. 3.1), quantification of specific failure modes (Ambühl et al. 2014), and the Bayesian statistical framework (Thies 2012). However, a limited number of computational models and research tools aimed at supporting the decision-making process for WECs or combined wind/wave technologies exist in literature (Gray et al. 2017; Mcauliffe et al. 2015; Rinaldi et al. 2016).
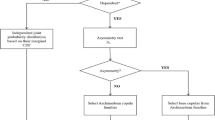
An RAM assessment is employed in this work to consider all the operational aspects of a wave energy array, evaluate the system effectiveness, estimate production values, and identify possible areas of improvements. A computational tool is used to simulate the lifecycle logistics of an offshore farm and to assess the performance of the WECs farm. This tool has been developed for the marine renewable sector, allowing for flexibility among a range of technologies, namely WECs, offshore wind, and tidal energy converters. It can be used for the characterization and optimization of all the operational aspects of the energy farm, aiming to reduce the assumptions frequently needed in the assessment of the optimal management and O&M procedures for offshore renewables. The aim of this characterization is the identification and mitigation of possible issues in the lifecycle of the devices, finding a trade-off between operation costs and generated revenue, with the final goal of measuring and improving the effectiveness of the offshore energy farm. A simple representation of the model is presented in Fig. 1. The model is constituted by four main submodules. The first is the energy module, which uses the MetOcean data of the selected location and the offshore renewable energy (ORE) farm information to provide estimations on the productivity of the farm. The second is the O&M model, which considers the corrective and preventive maintenance strategies for the farm. The third is the access module, which relies on the access system information and the analysis of the offshore planning software Mermaid (Mojo Maritime Ltd. 2017) to provide the information related to the accessibility of the farm. Finally, the last submodule considers the reliability data of the device to provide the failure distributions of the farm. The four submodules interact in an individual probabilistic model based on Monte Carlo simulation (Korver 1994; Raychaudhuri 2008; Takeshi 2013), a computational technique that relies on repeated random sampling and consequent statistical analysis to support a decision-making process subject to one or more uncertain parameters. In this case, the random sampling regards the failures of the devices in the farm, and outcome is a series of outputs that permit to obtain an integrated view of the farm performance along its lifetime.
To perform the RAM assessment, different sets of inputs are required for the evaluation of the ORE farm. The first set considers the reliability data of the device, especially the failure rates of all the individual components (a component denotes any element of the device’s infrastructure, e.g., subassembly, subsystem, or individual item). These are based on the previous experiences with the same components, provided by the individual suppliers, or extracted from the existing databases and then adjusted with correction factors (Thies et al. 2009). For the modeling tool used in this work, failure rates either based on a Poisson or Weibull distribution can be used. Procurement and repair times have to be included to consider the logistic delays and downtimes caused by each failure. The number of spare parts in stock, eventual redundancies, and dependencies on other components and subsystems, including common cause and or cascading failures, are the other properties that can be considered for a more complete assessment of the device. Finally, the maintenance and fault category of each component permit to obtain consistency between the device requirements and the capabilities of the access systems considered for their maintenance.
In fact, the second set of inputs regards the vessels, workboats, helicopters, or any other access system to be contracted for all the maintenance operation of the device. Here, all the cost entries of the access system are specified (daily rate, standby rate, mobilization rate, crew, fuel, etc.) together with the specific capabilities of the same, to verify the match with each component included in the reliability analysis.
The third set of inputs, used in the energy model is the MetOcean data of the selected site location. These are provided in terms of regularly spaced time-series (forecast, hindcast, or synthetic data) of wave height, wave period, wind speed, and current speed. Together with the information regarding the access systems, these data are used to establish the accessibility of the farm and the length of weather windows and maintenance operations. The exact transit time from the maintenance port to the farm is then calculated using the Mermaid project planning tool (Mojo Maritime Ltd. 2017), in which probabilistic response times are calculated for the selected vessels or helicopters and for each day of the simulation period. These calculations take into account distance from ports, changing MetOcean conditions, capabilities, and limits of the different vessels, and weather window availability. This allows marine operations to precisely drive and condition the lifecycle model, reducing the uncertainties of otherwise common assumptions in this area. An additional set of inputs specifying all the pre-scheduled operations can be included to account for the planned maintenance of the devices. The lifecycle is then simulated for a pre-established number of times according to discrete event modeling based on Monte Carlo simulation. In this way, all the results obtained are averaged over the total number of iterations, permitting to obtain and quantify the outcomes distributions, probability exceedances, and levels of confidence on the outcomes. An iteration is intended here as a single run of the overall Monte Carlo simulation. The results form a series of key performance metrics to give a complete overview of the effectiveness of the farm. These include, but are not limited to: energy yield and losses, economic production, and losses, reliability of the devices, availability of the farm, and associated statistics. For a full description of the model used in this work, the readers can refer to Rinaldi et al. (2017).
a Geometric variables of the Spar–Buoy OWC, from (Gomes et al. 2012). b Three-dimensional view of the optimized Spar–Buoy OWC
2.2 Reliability data assessment methodology
Reliability assessment is an established stochastic tool widely used for prediction of product performance with a focus on optimization of the device. ISO 8402 (1986) defines reliability as “the ability of an item to perform a required function, under given environmental and operational conditions and for a stated period of time”. Therefore, system reliability of a WEC may be defined as the probability that the device will perform its active function (i.e., generate electricity) for a specified period of time. This has not to be confused with the availability of the WEC, which refers instead to the probability that the system is not failed, or undergoing a repair, when it is needed to generate electricity. Despite reliability and availability are generally linked, while a reliable device will have high availability that an available device may or may not be very reliable. A failure is the inability of a system/subsystem to operate under the defined conditions (Spinato et al. 2009) which may be quantified by statistical reliability metrics like failure rate with an associated probability distribution.
Ideally, the reliability assessment for a WEC is based on statistical estimates of subassembly failure rates based on a large sample of failure events of identical devices deployed at locations with similar operational conditions. However, due to the broad range of equipment and operating conditions for WECs, compilation of such a detailed database is challenging. Currently, due to the embryonic stage of the wave energy industry, no industry-specific failure data are publically available; therefore, reliability data from more mature industries using similar subassemblies are commonly used (Ambühl et al. 2015; Mcauliffe et al. 2015; Thies 2012; Wolfram 2006) to populate energy reliability models. Several extensive failure databases have been compiled in other industries like aviation, offshore oil and gas, and electronics. For the scope of this research, the Offshore Reliability Data (OREDA) (SINTEF 2002) Handbook and its derivatives have primarily been the reference of choice, since data for the handbook are collected from a marine environment. In addition, the OREDA project provides high-quality reliability data collated over extended period of time, covering a broad spectrum of structural and mechanical equipments. However, failure rates extracted from databases are subject to interpretation by the analyst, and, consequently, must be adjusted for any change in the equipment use, operating environment, failure modes, and applicability of data source (Thies 2012). Therefore, despite the similarity in WEC subsystems and offshore Oil & Gas equipment, the failure rate data used in this work have been adjusted for the altered size, design, and novel use in WECs.
2.3 Multivariate analysis
When the computational simulation is completed, a set of output variables is obtained. However, due to their relatively high number, it may prove challenging reading through the outcomes and their probability distributions to assess the contributions of the different factors. Besides, it is useful to analyze the high quantity of data obtained to acquire a clearer overview of the farm’s dynamics and, as a consequence, discover possible patterns that can help in achieving the objectives of the decision-maker and the requirements of the offshore energy farm in terms of availability, reliability, and profitability. Multivariate analysis (Dempster 1971) is generally used to gain a deeper understanding of complex data sets, by simultaneously examining the mutual correlations between several variables at a time, and permitting the identification of underlying patterns and the understanding of their relevance to the problem. Despite a number of techniques exist to conduct multivariate statistical analysis, as well as easier way of visualizing high-dimensional data (e.g., displaying the relationship only between two or three variables at a time), the principal components analysis (PCA) (Haipeng Shen 2008) is chosen in this work. This technique is selected for its suitability in analyzing the set of data produced during the simulation, with the aim of finding attributes and trends that might have been hidden at a first analysis of the output variables.
The main advantage of a PCA consists in preserving as much information as possible in a data set composed by a large number of interdependent variables, while reducing its dimensionality for an easier investigation. This is achieved by generating a new set of variables, called principal components, which are a linear combination of the original variables. The principal components are not directly correlated, but are generated to retain most of the variation existing in the original variables. Thus, although the complete set of principal components can be as large as the original set of examined variables, usually, the first two principal components contain the great majority (more than 80%) of the total variance of the original data set, therefore, accounting for most of its variability and mutual correlations. Hence, this technique allows for the reduction of the dimensionality of the problem while retaining the information related to trends and variations of the inter-related variables. In this way, it is possible to examine the results obtained in a simpler way, in terms of fewer variables, obtaining more insights in the causes that they generated the original data set and discovering tendencies that were harder to find before of the transformation. More information on multivariate analysis using PCA can be found in Rencher (2003) and Jolliffe (1986).
3 Case study: WECs farm
The case study presented in this work considers a pilot wave energy converter farm of 10 Spar–Buoy OWCs to be deployed at the Portuguese Pilot Zone (Fig. 7), which is located between Figueira da Foz and Nazar, with an area of \(320\hbox { km}^{2}\) (REN 2012). The selected area is between 20.8 km and 8 km away from the coast, with depths varying between 40 and 80 m. The farm is located around 8 km far from the coast, equipped with pre-installed electrical cables to bring the energy produced ashore, and the nearest port for O&M is Figueira de Foz’ Port.
a Dimensionless flow rate, \(\Phi \), dimensionless power coefficient, \(\Pi \), and efficiency, \(\eta \), as functions of the dimensionless pressure head, \(\Psi \), for the biradial turbine used in the numerical simulations, based on (Falcão et al. 2013b). b Generator efficiency curve taken from (Tedeschi et al. 2011)
The technical drawing in Fig. 2 depicts a Spar–Buoy OWC, with a real prototype shown in Fig. 3 and the power matrix used for this work in Fig. 4. The system is a spar offshore structure, open at the bottom to allow the water to flow inside. The relative movement between the water and the structure of the device drives an oscillatory air flow in the air chamber. The selected geometry, designed following the wave energy development methodology presented in Henriques et al. (2016) and Gomes et al. (2012), has a floater diameter of 12 m and a generator rated power of 150 kW. The power take-off system consists of a biradial self-rectifying impulse turbine coupled to a generator, as shown in Fig. 5 and described in Falcão et al. (2013a), that allows to extract power for air flowing in both the inward and outward directions.
The characteristic curves for the turbine and the generator are shown in Fig. 6. While an isolated device is conceived to have three mooring lines connecting the buoy to the seabed, the farm mooring system comprises eight mooring lines to secure the array to the seabed and a set of lines for the inter-body connections (Fig. 7). This configuration is depicted in Fig. 8. The hybrid mooring system includes small floaters, synthetic ropes, and a chain to guarantee survivability of the array while allowing the devices to move freely in heave. In operation, the system is subject to rotational speed control (Falcão et al. 2017; Henriques et al. 2015). All the electrical cables are collected into a connector hub, which is then connected to shore station through a single export cable (see Fig. 9).
3.1 WEC reliability data characterization
The Spar–Buoy can be divided into four main subassemblies, namely, moorings, structure, power take-off, and power transmission. A control system is introduced as an additional subassembly. These subassemblies may be further divided into smaller subsystems. A total of 15 subsystems are identified for use in the reliability assessment. Table 1 states the various subassemblies, constituent subsystems, and the associated annual failure rates collected from various sources. Although it is possible to further split the subsystems in individual components, inputs at subsystem level are considered feasible for the early stage wave energy reliability assessments. Caution should be used when considering the adjusted failure rates, as the derived values may still differ from those observed in real life for the same application (a floating WEC). Thus, these are considered for the exclusive purposes of this work and are not to be taken as a reference for future studies.
Numerous approaches exist for reliability assessment, which can be distinguished between top–down and bottom–up methods (Thies et al. 2009). Here, we utilize a bottom–up method based on the part stress analysis of the Military Handbook to translate database failure rates from the environment of data collection to that of application (United States Department of Defence 1991). Environmental adjustment factors (\(\pi _\mathrm{{E}}\)) based on comparative environmental loading conditions (Thies 2012) are used in conjunction with the base failure rate from Table 1 to calculate the adjusted failure rate for individual subassemblies according to Eq. (1):
whereby
- \(\lambda _\mathrm{{C}}\) :
-
Adjusted failure rate of the component
- \(\lambda _\mathrm{{B}}\) :
-
Base failure rate
- \(\pi _\mathrm{{E}}\) :
-
Environmental adjustment factor
- \(\pi _\mathrm{FM}\) :
-
Failure mode adjustment factor
- \(\pi _\mathrm{DS}\) :
-
Data source adjustment factor.
Table 1 provides the details regarding the environmental adjustment factors used for each subassembly based on the contrast between database collection environment and degree of exposure at the WEC. It must be noted that the use of generic environmental adjustment factors introduces a higher degree of uncertainty in the reliability assessment, since loading conditions, and consequently failure frequency, may vary between benign and dynamic deployment sites (Khalid et al. 2016). This limitation can be eliminated by the acquisition of detailed site-specific reliability data for individual failure modes.
Table 1 also provides the resultant component failure rates \(\lambda _\mathrm{{C}}\) used in the modeling tool. For most subsystems, industry-specific data are readily available. As it can be seen, some industry-specific data (umbilical, mooring) did not require any adjustment, since the data are collected and are applied to unsheltered offshore conditions. For other subassemblies, like power electronics and circuit breaker, an adjustment factor is introduced. This is done to account for the increased motion of the floating WEC relative to a stable offshore platform. Adjusted failure rates for all subsystems can be observed to be in excess of the database failure rate except that for the transformer, since it is land-based.
3.2 Other inputs
The reliability data described in Sect. 3.1 and the inputs on components referred in Sect. 2.1 comply with the guidelines described in Rinaldi et al. (2016), and were used as part of the inputs in the RAM tool. Moreover, additional information such as the procurement time and repair time, criticality factors, and number of spare parts in stock is also considered for the RAM tool.
The procurement time and repair time are the amount of time to secure a spare part if it is not in stock, and the time to complete the repair or replacement in case of failure, respectively. A criticality property is assigned to consider if each subsystem and component is essential for the functioning of the device, i.e., causes loss of production, in case of a failure. Another factor considered is the overnight repairability, which indicates whether it is possible to operate on a particular component during the night or not, with related impacts on weather windows availability and total downtime in case of failure. In the model, the number of elements or spare parts of the same kind for each considered component is also defined; it is also possible to specify how many of these elements are actually needed in a working condition for the functioning of the device. If needed, common cause events or cascading failures can be introduced to take into account the mutual relationships between components. The cost of replacing each component is also required, to allow the calculation of the O&M intervention cost. All the values of these parameters, estimated after discussion among the authors and following the work in Galvao (2015), are hereinafter reported in Table 2, and are solely for the purpose of demonstrating how the model is used. In case, more failure modes existed for the same components, only the most catastrophic event (and related replacement cost) is considered to remain in a conservative hypothesis.
Further inputs are used to account for expenses and capabilities of the access systems. For this work, two maintenance vessels were considered. The first one is a generic Crew Transfer Vessel (CTV), generally used to transport personnel, and supplies to and from offshore sites and to perform minor maintenance interventions. The second is a generic Multicat Workboat, a bigger and more versatile multipurpose vessel, ideal for various tasks and generally used for more relevant maintenance interventions. An illustration of these two vessel categories is shown in Fig. 10, and their MetOcean limits are reported in Table 3.
Regarding the wave resource, hindcast data for the selected location are assessed using the numerical model WAVEWATCH III (Tolman et al. 2002), and are used for all the productivity and accessibility calculations over a simulated lifetime of 10 years (from 2000 to 2009).
3.3 Outputs
Taking advantage of the complimentary capabilities and maintenance possibilities of the vessels, the simulation is run considering their combined use in a mixed fleet. Hence, in case of failure, the simulation tool will check if the vessels are able to perform the maintenance task on the failed component, and in case of multiple suitability, the vessel that is cheaper to mobilize is used. As a consequence, the Multicat Workboat is used only for major maintenance interventions where the CTV does not possess the capabilities to operate. For the figures, for the economic indicators for the energy production, these are obtained assuming a strike price of 260 €/MWh. This value corresponds to the feed-in-tariff mechanism to support wave energy projects in their demonstration phase in Portugal. Under these premises, the values for the different output variable obtained by averaging the results over the total number of simulations (100) are reported in Table 4. This value for the number of simulation has been chosen by looking at the trends indicating the convergence of the estimated performance indicators, to obtain meaningful results without exceeding with the computational time required. This is strongly dependent, apart from the machine used, on the number of elements considered (i.e., number of devices, length of the time-series, timestep, number of access systems, and number of components). To give an idea, for the case study considered in this work, approximately 2 days were required to complete the 100 runs of the simulation.
However, to add statistical relevance to the research, check the properties of the output variables, and establish a correlation between their mutual influences with the aim of gaining insights on the properties of the farm, the results generated during each run of the simulation are analyzed. First, the cumulative probabilities of the most relevant performance indicators, together with their exceedance probabilities P10, P50, and P90, are plotted together (Fig. 11). The selected indicators are: energy delivered over the lifetime, total gross revenue, availability, income after O&M costs, cost of repairs and replacements, and total number of simulated failures for the whole offshore farm.
These variations can be visualized also by means of box plots, as illustrated in Fig. 12. On each box, the central red line indicates the median, while the bottom and top edges of the box indicate the 25th and 75th percentiles, respectively, and the red ’+’ symbol indicates the outliers.
Therefore, the selected KPIs are plotted against each other two at a time, with the respective histograms along the diagonal in Fig. 13.
At this point, the PCA is used on these sets of data to plot all the results of the iterations simultaneously, as illustrated in Fig. 14. Here, all the selected variables (energy, revenue, income, availability, cost of repairs, and number of failures) are represented by a vector, whose length and direction indicate the contribution of each variable to the two principal components in the plot. Thus, the first principal component (i.e., the horizontal axis) mainly distinguishes between solutions having high (on the right) or low (on the left) repair cost and number of failures, as well as low (on the right) and high (on the left) availability, energy production, and gross revenue. Instead, the second principal component (i.e., the vertical axis) can be used to distinguish solutions having high (below x-axis) and low (above x-axis) incomes, as well as high (above x-axis) and low (below x-axis) availability, energy production, and gross revenue. Only the first two principal components are selected, because, after analyzing the percent variability explained by each principal component, these contain 93% of the total variance (68% for the first component and 25% for the second, respectively). In this figure, each of the 100 observations produced during the simulation is represented by a red dot, whose coordinates indicate the score of each observation with respect to the two principal components. The utmost points of the plot represent the most significant variations in terms of one or more of the original output variables, and, hence, are selected for their relevance and labelled by their number. Therefore, these observations are investigated in terms of the original KPIs, and the values shown in Table 5 are obtained. These and the other results of the analysis will be discussed in the following section.
4 Discussion of the results
When looking at the KPIs averaged over all the iterations of the Monte Carlo simulation, the following considerations can be made. First, the value of energy produced is very close to that obtainable in the ideal case of absence of corrective maintenance interventions; analogously, the average availability is close to 100%. This can be explained due to two main reasons. The first one, as already mentioned, is the exploitation of the great difference in the capabilities of the access systems. This permits to use the cheaper and faster CTV for most of the maintenance (around 97% of the interventions) switching to the Multicat only when major maintenance actions are needed. This, in turn, allows for quicker repairs and replacements that reduce the inactivity of the devices and avoid the risk of persistent downtimes due to the lack of proper maintenance systems available. The second reason is the choice of the offshore farm site. This is not only close to the coast, but also to the harbour for the maintenance operations (Figueira da Foz’ Port), making all procedures shorter and more efficient. In addition, the wave climate is relatively mild, allowing for high weather windows availability (therefore, accessibility of the offshore farm); for most of the times, a maintenance operation is needed. Nonetheless, even under these favourable conditions, the values of availability seem still too high for these kinds of devices, especially if compared with typical values for more mature technologies such as offshore wind turbines. Therefore, it is likely that the assumed failure rates are not fully representative of the devices and somehow overestimate their reliability.
The capacity factor, despite its low value, is a relative measure and it is strongly sensitive to the rated power selection, which, in turn, has important implications on the annual energy produced (Falcão et al. 2017). Analogous considerations can be made for the equivalent hours. Regarding the economic indicators, as mentioned in the previous section, these have been estimated according to the feed-in-tariff for demonstration projects. Although, for this case, they are positive reaching 2.28 m€ of generated income over the simulated lifetime (10 years), it is noted that current electricity market prices might be lower than those offered in the feed-in-tariff mechanisms, and care should be taken when assessing economically the O&M costs versus the revenues and profits.
When the statistical distributions are analyzed, different ranges of variations are observed for the selected KPIs. Looking at the chart for the observed variables plot two at a time in Fig. 13, it is possible to notice a certain linearity between two sets of variables: energy production with revenue (but this is intuitive, because the revenue is calculated proportionally to the energy produced and the electricity strike price) and the cost of repairs with the incomes. Less marked linearities can be seen between revenue and income, and failures and income. This can be better observed when only the economic quantities are selected and visualized in the same boxplot using the same scale on the y-axis, as shown in Fig. 15. Income and cost of repairs distributions are wider than the revenue distribution; therefore, there is not much variability along the simulation for the energy production (then the revenue), while there is more variation for the cost of repairs/replacements (then income). This gives further proof of a significant relationship between repairs cost and generated income. However, from the results shown in Fig. 13, while the linear dependence between cost of repairs and generated income is evident, it is not possible to clearly identify a similar dependency for energy, revenue, and availability. This is because the non-linearity of some correlations could make the interdependencies harder to be noticed in a simple 2D scatter plot. Hence, this supports the hypothesis that alternative techniques, such as the multivariate analysis using PCA, are needed to gain a deeper level of understanding on the mutual dependencies among variables.
Finally, thanks to the indications of the PCA from Fig. 14, the values in Table 5 for the utmost selected solutions are obtained. In this table, the first column simply indicates the order in which the results of each iteration of the simulation are considered, the second column indicates the corresponding iteration over the total 100 produced during the Monte Carlo simulation (these correspond to the utmost solution labelled by a number in Fig. 14), and all the successive columns represent the values of the original output variables for the related case. Thus, by examining the values in Table 5, the following observations can be made:
-
The best income (case 15) is obtained not in correspondence of the maximum energetic production or availability (case 17), but for the minimum repair cost (case 15);
-
Cases 15 and 17 have the same number of failures (15), but the repair costs of case 17 are twice those of case 15;
-
Although case 7 has the highest number of failures (40) and case 3 many less (24), the repair cost for case 3 (2.6 m€) are much higher than for case 7 (1.8 m€);
-
Energy production and gross revenue are proportional to one another for all the cases (due to the way the gross revenue is calculated); however, the availability is not necessarily proportional to these because of the differences in wave resource distribution over time (if a device enters in downtime when the wave resource is scarce or null, the energy production will not be affected).
As a consequence, the cases that provide the most significant singularities (cases 3, 7, 15, 17) are further analyzed and the following outcomes emerged:
-
Case 3 is the only one in which a failure of the buoy structure is simulated (this is by far the most expensive failure, 1.3 m€);
-
The high number of failures in case 7 are due mostly to moorings (17) and the electric generator (10). In this regard, the failure rate of the electric generator is much higher than that of the buoy structure. However, ten failures of the electric generator are still cheaper to repair than one of the buoy structures, which explains the difference in replacement cost with case 3;
-
Repair costs of case 15 are lower than those of other cases, because most of the failures are due to the moorings, which are cheap to repair compared to other components;
-
In case 17, there are failures of components having relatively low failure rate (like turbine, sensors, and PTO control system). Even if these are a limited number (1–3), this significantly increases the cost of repairs.
5 Conclusions
This paper presents a multivariate analysis following the quantitative RAM assessment of a wave energy farm of Spar–Buoy OWCs. Key performance metrics of a Spar–Buoy WECs farm over a period of 10 years are defined and analyzed. The results show how different factors contribute in affecting the projected energy production and consequent profitability of the project. Different maintenance assets are considered for the optimization of the logistics of the farm to quantitatively assess the effectiveness of a combined maintenance fleet with reference to the specific location and technology selected. Although only the effect of corrective interventions on the availability of the farm has been quantified in this work, the impact of planned maintenance actions could be assessed by taking advantage of the dedicated feature in the modeling tool used (provided that variable failure rates, obtained from accurate sources, are considered). The range of indicators selected to characterize reliability, availability, and maintainability of the offshore farm have been estimated by picking the average of the results produced over 100 iterations of a Monte Carlo simulation, and their probability distributions analyzed. Visualizing these using multivariate analysis according to the PCA technique, several attributes of individual iterations have been noticed and further insights on mutual correlations between output variables obtained. From these, generic conclusions that could have not been drawn by only looking at the results averaged over all the simulations are:
-
The cost of repairs is a major driver of the O&M costs;
-
The reliability of the components, especially due to the cost of eventual repair actions, is pivotal for the profitability of a project;
-
Solutions that maximize the energy production or the availability of the farm may not be the most cost-effective if the other cost drivers are neglected or secondary importance is given to these;
-
The failures of a few components might make the difference between a successful and an unsuccessful project;
-
The effects of a failure (caused downtime and, especially, repair cost) are more relevant than the frequency of a failure (failure rate) for the purpose of profitability. Thus, if a choice is available, it may be better to use components with higher failure rate, but that are cheaper to repair or replace than components that are more reliable but more expensive to repair;
-
The choice of using less reliable components may be mitigated by more frequent maintenance interventions when the resource is smaller and the production is not affected, especially if eventual maintenance interventions are facilitated by proximity to the O&M port.
Despite these conclusions are specific for the case studied in this work, similar considerations can apply to other offshore renewable projects. Therefore, it can be seen how computational simulation is extremely useful to quantify the risks associated with an offshore farm project before the actual installation of the devices. The early incorporation of this type of analysis in offshore renewable energy projects contributes to achieving an effective and efficient resource allocation, both in terms of capital and operational expenses, to achieve the lowest overall cost of electricity. For this purpose, the modeling tool supports the decision-maker in the pursuit of the most reliable and easy to maintain device design but also reports the trade-off between energetic yield and O&M efforts.
Validation, intended as a comparison with a real-case scenario, would ensure that the conclusion is correct also in reality and permit to improve the overall approach. However, due to the fact that the case study considers a fictitious WECs farm and other limitations, this process is currently impractical. On the other hand, the outputs of the model have been systematically investigated in the past for very different cases and technologies, and the results compared against those provided by similar tools in this area to verify the Monte Carlo simulation framework (Rinaldi et al. 2018). This permits to increase the confidence in the outputs and acquire reliance for the figures obtained.
To summarise, the use of a verified computational tool allows for the accurate estimation of the key performance indicators of an offshore energy farm, while the multivariate analysis permits the identification of previously unidentified interdependencies and correlations. In this way, more effective improvements on the viability of the project, calibrated to the specific offshore farm considered, can be obtained in an efficient way and with reduced cost and effort.
Further work shall use the same methodology to evaluate different options for this technology, in terms of improvements both in device availability and maintenance procedures, and compare them against the additional cost introduced by these variations. In this respect, due to the lack of operational experience, the influence of several input parameters (e.g., adjustment factors for failure rates, or procurement and repair time for the different components) could be assessed in a sensitivity analysis to estimate how much their variation will eventually affect the output results. Comprehensive input data for the maintenance workboats and their charter strategy can be used to refine the simulations. Another aspect to consider is that although the MetOcean data derived from ocean-wave numerical models provide inexpensive pre-analysis of most productive sites, real measurements of longer time-series with reduced time-steps and including seasonality effects would reduce the uncertainty on the results obtained. Finally, the consideration of more sophisticated repair actions and operational arrangements in the developed model, like the distinction between in-situ procedures and tow-to-port strategy for the different components, will allow for a detailed representation of the O&M management.
Future work will also consider the use of surrogate models and other techniques (e.g., neural networks) to further investigate the nature of the mutual correlations among input and output variables for the considered problem. The objective will be the characterization of non-linear relationships and the identification of hidden attributes.
References
Ambühl S, Kramer M, Sørensen JD (2014) Reliability-based structural optimization of wave energy converters. Energies 7(12):8178–8200. http://www.mdpi.com/1996-1073/7/12/8178
Ambühl S, Kramer M, Sørensen JD (2015) Different reliability assessment approaches for wave energy converters. In: Proceedings of the 11th European Wave and Tidal Energy Conference, Nantes, France
AME (1992) Advanced Mechanics and Engineering Ltd., Reliability and availability assessments of wave energy devices: main report. Energy Technology Support Unit (ETSU), Harwell
Cruz JL (2008) Ocean wave energy: current status and future perspectives. Springer, Berlin Heidelberg, Germany
Dempster A (1971) An overview of multivariate data analysis. J Multivar Anal 1:316–346
European Ocean Energy Association (2010) Oceans of Energy: European Ocean Energy Roadmap 2010 2050. Belgium, Brussels
Falcão AFO (2010) Wave energy utilization: a review of the technologies. Renew Sustain Energy Rev 14(3):899–918
Falcão AFO, Gato LMC, Nunes EPAS (2013a) A novel radial self-rectifying air turbine for use in wave energy converters. Renew Energy 50:289–298
Falcão AFO, Gato LMC, Nunes EPAS (2013b) A novel radial self-rectifying air turbine for use in wave energy converters. Part 2. Results from model testing. Renew Energy 53:159–164
Falcão AFO, Henriques J, Gato L (2017) Rotational speed control and electrical rated power of an oscillating-water-column wave energy converter. Energy 120:253–261
Falnes J (2002a) Ocean Waves and Oscillating Systems. Cambridge University Press, Cambridge, UK
Falnes J (2002b) Optimum control of oscillation of wave-energy converters. Int J Offshore Polar Eng 12:147–155
Galvao R (2015) Technical and economical viability of a floating coaxial ducted OWC. Tech. rep, Instituto Superior Tecnico
Gomes R, Henriques J, Gato L, Falcão AFO (2012) Hydrodynamic optimization of an axisymmetric floating oscillating water column for wave energy conversion. Renew Energy 44:328–339
Gray A, Dickens B, Bruce T, Ashton I, Johanning L (2017) Reliability and O&M sensitivity analysis as a consequence of site specific characteristics for wave energy converters. Ocean Eng 141:493–511
Haipeng Shen JZH (2008) Sparse principal component analysis via regularized low rank matrix approximation. J Multivar Anal 99:1015–1034
Henriques J, Portillo J, Fay F, Robles E, Gato L, Touzon I (2015) On latching control for wave energy converters: the case of an oscillating water column. In: Proceedings of the 11th European Wave and Tidal Energy Conference, Nantes, France
Henriques J, Portillo J, Gato L, Gomes R, Ferreira D, Falcão AFO (2016) Design of oscillating-water-column wave energy converters with an application to self-powered sensor buoys. Energy 112:852–867
Hofmann M (2011) A review of decision support models for offshore wind farms with an emphasis on operation and maintenance strategies. Wind Eng 35:1–16
ISO 8402 (1986) Quality Vocabulary. International Standards Organization, Geneva
Jolliffe IT (1986) Principal component analysis and factor analysis. Springer, New York, pp 115–128
Khalid F, Thies PR, Johanning L (2016) Reliability assessment of tidal stream energy : significance for large-scale deployment in the UK. In: 2nd International Conference on Renewable Energies Offshore, Lisbon, Portugal, pp 751–758
Korver B (1994) The Monte Carlo method and software reliability theory. Tech. rep. http://www-cs-students.stanford.edu/~briank/BrianKorverMonteCarlo.pdf
Li Y, Valla S, Zio E (2015) Reliability assessment of generic geared wind turbines by gtst-mld model and Monte Carlo simulation. Renew Energy 83:222–233
Mcauliffe FD, Macadré Lm, Donovan MH, Murphy J, Lynch K (2015) Economic and Reliability Assessment of a Combined Marine Renewable Energy Platform. Proceedings of the 11th European Wave and Tidal Energy Conference, Nantes, France
Mojo Maritime Ltd. (2017) Mermaid. In: http://mojomermaid.com/
Raychaudhuri S (2008) Introduction to Monte Carlo Simulation. In: Proceedings of the 2008 Winter Simulation Conference, pp 91–100
REN (2012) Enondas—a zona piloto portuguesa http://www.ren.pt/pt-PT/o_que_fazemos/outros_negocios/enondas/
Rencher AC (2003) Principal component analysis. Wiley-Blackwell, Ch. 12, pp 380–407. https://onlinelibrary.wiley.com/doi/abs/10.1002/0471271357.ch12
Rinaldi G, Pillai AC, Thies PR, Johanning L (2018) Verification and benchmarking methodology for O&M planning and optimization tools in the offshore renewable energy sector. In: International Conference on Ocean, Offshore and Arctic Engineering (OMAE). Madrid, 2018
Rinaldi G, Thies PR, Walker R, Johanning L (2016) On the analysis of a wave energy farm with focus on maintenance operations. J Mar Scie Eng 4(51):1–11
Rinaldi G, Thies PR, Walker R, Johanning L (2017) A decision support model to optimise the operation and maintenance strategies of an offshore renewable energy farm. Ocean Eng 145:250–262
Shafieea M, Sørensen JD (2017) Maintenance optimization and inspection planning of wind energy assets: Models, methods and strategies. Reliab Eng Syst Saf
SINTEF (2002) OREDA—offshore reliability data handbook. No. 4 in Det Norske Veritas handbooks
Smith D (2005) Reliability, maintainability and risk: Practical methods for engineers including RCM and safety-related systems. Butterworth Heinemann
Spinato F, Tavner P, van Bussel G, Koutoulakos E (2009) Reliability of wind turbine subassemblies
Takeshi M (2013) A Monte Carlo simulation method for system reliability analysis. Nucl Saf Simul 4:44–52
Tedeschi E, Carraro M, Molinas M, Mattavelli P (2011) Effect of control strategies and power take-off efficiency on the power capture from sea waves. IEEE Trans Energy Convers 26(4):1088–1098
Thies P, Flinn J, Smith G (2009) Is it a showstopper? reliability assessment and criticality analysis for wave energy converters. In: 8th Eur. Wave Tidal Energy Conf., Uppsala, Sweeden
Thies PR (2012) Advancing reliability information for Wave Energy Converters
Tolman HL, Balasubramaniyan B, Burroughs LD, Chalikov DV, Chao YY, Chen HS, Gerald VM (2002) Development and implementation of wind-generated ocean surface wave modelsat ncep. Weather Forecast 17(2):311–333
United States Department of Defence (1991) Reliability Prediction of Electronic Equipment, Military Handbook 217
Wolfram J (2006) On assessing the reliability and availability of marine energy converters: the problems of a new technology. In: Proceedings of the Institution of Mechanical Engineers, Part O: Journal of Risk and Reliability 220
YARD Ltd. (1980) Reliability of six wave power devices. Report ETSU WV 1581, AEA Technology, Harwell
Acknowledgements
The first and second authors were partially funded by the Marie Curie Actions of the European Union’s Seventh Framework Programme FP7/2007-2013/ under REA grant agreement number 607656 (OceaNet project). The fourth author was funded by FCT researcher grant No. IF/01457/2014. This work has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No. 654444 (OPERA Project) and from the FCT project PTDC/MAR-TEC/0914/2014.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Rinaldi, G., Portillo, J.C.C., Khalid, F. et al. Multivariate analysis of the reliability, availability, and maintainability characterizations of a Spar–Buoy wave energy converter farm. J. Ocean Eng. Mar. Energy 4, 199–215 (2018). https://doi.org/10.1007/s40722-018-0116-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40722-018-0116-z