Numerical modeling of oscillatory turbulent boundary layer flows and sediment suspension

Abstract

In this study, an integrated numerical model is developed and applied to simulate oscillatory boundary layer flows and the corresponding sediment suspension. The model solves the Reynolds-averaged Navier–Stokes (RANS) equations for flows and the transient transport equation for sediment. The turbulence closure is accomplished by the baseline (BSL) $k$–$\omega$ two-equation model. The model is capable of simulating oscillatory boundary flows at different Reynolds number regimes, namely, laminar, transitional and turbulent. The model can provide detailed mean (ensemble average) flow velocity, turbulence characteristics and sediment suspension within the boundary layer. The numerical results of mean flow velocity and turbulence kinetic energy are in agreement with the available experimental data and analytical solutions. In addition, the calculated results of period-averaged sediment concentration are also validated against the measurement data, yet the instantaneous results exhibit small phase differences. The proposed model improves the predictive capability for sediment suspension within boundary layers, which is helpful in defining a suitable model for relevant practical applications in coastal engineering.

1 Introduction

The oscillatory boundary layer flow plays an important role in coastal zones, which has significant influences on near-shore sediment transport and the resulting morphological changes. This topic has been studied for many years through theoretical analysis, experimental studies and numerical modeling. Lamb (1932) presented the well-known ‘Lamb’s solution’ for linear wave-induced laminar boundary layer. Jonsson (1963), followed by Jonsson and Carlsen (1976), are among the first to perform experimental studies of oscillatory turbulent boundary layers. They measured the velocity distribution over a rough boundary and inferred the bottom shear stress from the measured velocity profiles. Sleath (1987) studied the characteristics of oscillatory boundary layers experimentally which included a large range of Reynolds number, $R_{e}$ ($2\times 10^{3}$ to $3\times 10^{5})$. Jensen et al. (1989) carried out a similar experimental study to Sleath (1987) in a higher range of $R_{e}$ ($7.5\times 10^{4 }$ to $6\times 10^{6})$ and obtained results for both smooth and rough sinusoidal turbulent oscillatory boundary layers.

Lin and Zhang (2008) simulated the laminar boundary layer under various waves using a three-dimensional hydrodynamic numerical model and provided accurate results for all types of wave-induced laminar boundary layer flows. The two-equation eddy-viscosity closure models have been used since 1970s to simulate turbulent oscillatory boundary layer flows. These models solve two coupled equations for the production and the dissipation rate of the turbulent kinetic energy. Among all the two-equation models, the $k$–$\varepsilon$ model is the most widely used. The first low Reynolds number $k$–$\varepsilon$ model was developed by Jones and Launder (1972), (hereafter referred to as JL $k$–$\varepsilon$ model) and has subsequently been improved and applied to oscillatory turbulent boundary layer flows by many researchers (e.g., Hagatun and Eidsvik 1986; Justesen 1991; Sana and Shuy 2002; Foti and Scandura 2004). Sana and Tanaka (2000) tested the predictive capability of five low Reynolds number $k$–$\varepsilon$ models for oscillatory boundary layer flows, and the comparison results with the direct numerical simulation (DNS) by Spalart and Baldwin (1989) revealed that the JL $k$–$\varepsilon$ model (1972) provided superior numerical results to the other models. However, the JL $k$–$\varepsilon$ model also shows drawbacks of underestimating the peak value of the turbulent kinetic energy (Sana and Tanaka 2000) and overpredicting the turbulence length scale and the shear stress levels in the near-bed region under adverse pressure gradient conditions due to its poor sensitivity to the pressure gradient (Wilcox 1988; Menter 1994). Many models have been designed to overcome the shortcomings of the $k$–$\varepsilon$ model; one of the alternative models is the $k$–$\omega$ model developed by Wilcox (1988), (hereafter referred to as Wilcox $k$–$\omega$ model). It does not require damping functions, but employs straightforward Dirichlet boundary conditions in the viscous sublayer and allows a more suitable choice of dependent variables by introducing an additional term to suppress the increase rate of turbulence length scale; therefore, the Wilcox $k$–$\omega$ model can provide more accurate results for boundary layers in an adverse pressure gradient than the $k$–$\varepsilon$ model. Many researchers (e.g., Suntoyo 2006; Fuhrman et al. 2013) have applied Wilcox $k$–$\omega$ model to simulate oscillatory turbulent boundary layer flows. However, the Wilcox $k$–$\omega$ model produces results that strongly depend on the free stream value of the turbulence variables, in particular $\omega$, even at fairly low free stream eddy viscosity levels (Menter 1992).

Because free stream dependency has not been found in the $k$–$\varepsilon$ model generally, Menter (1994) proposed a new turbulence model called baseline $k$–$\omega$ model (BSL $k$–$\omega$ model hereafter) to resolve the free stream dependency of Wilcox $k$–$\omega$ model by a blending function between the Wilcox $k$–$\omega$ model and the JL $k$–$\varepsilon$ model (in a $k$–$\omega$ formulation). The basic idea of the BSL $k$–$\omega$ model is to keep the sound and accurate formulation of the Wilcox $k$–$\omega$ model in the near-wall region, while taking advantage of the free stream independence of the $k$–$\varepsilon$ model in the outer part of the boundary layer. In other words, the BSL $k$–$\omega$ model’s results are expected to be similar to the $k$–$\omega$ model in the inner boundary layer, and switch gradually to the JL $k$–$\varepsilon$ model toward the outer boundary layer and in free shear flows. Suntoyo (2006) applied the JL $k$–$\varepsilon$ model, Wilcox $k$–$\omega$ model and the BSL $k$–$\omega$ model in simulating the oscillatory turbulent boundary layer flows and showed that the BSL $k$–$\omega$ model provides the best results among the three models.

In the oscillatory boundary layer flows, sediment suspension is another important research topic. Besides substantial experiments investigating the suspended sediment concentration in oscillatory flow over the bed of sediment (e.g., Horikawa et al. 1982; Dick and Sleath 1991; Ribberink and Al-Salem 1992), numerical studies have also been conducted by many researchers. Both the $k$–$\varepsilon$ turbulence closure (Savioli and Justesen 1997; Ruessink et al. 2009; Hassan and Ribberink 2010; Zhang et al. 2011b, 2014), and the $k$–$\omega$ turbulence closure (Guizien et al. 2003; Fuhrman et al. 2013) have been successfully applied to sediment transport modeling. The second suspended sediment concentration peak over the decelerating and flow reversal has been well predicted by Savioli and Justesen (1997) who applied a standard (without low-Reynolds-number effects) $k$–$\varepsilon$ model (Rodi 1980) in a fully rough turbulent oscillating boundary layer model and proposed a modified reference concentration condition. Zhang et al. (2011a, b) developed a new model for sediment transport and applied the $k$–$\varepsilon$ model for turbulence closure. The model showed overall good results compared with experimental data, but it underestimated the near-bed concentration during flow reversals (at phase 0$^{\circ }$ and 150$^{\circ })$. Guizien et al. (2003) indicate that these are because the $k$–$\varepsilon$ model lacks sensitivity to strong adverse pressure gradient that occurs during the decelerating cycle and causes shear instability and turbulent separation. Therefore, a better turbulence model is needed to pursue further improvement of the modeling approach for sediment suspension in oscillatory boundary layers.

As mentioned above, the BSL $k$–$\omega$ model combines the advantages of both Wilcox $k$–$\omega$ model and JL $k$–$\varepsilon$ model as an integrated turbulence closure of them. It has been widely applied to investigate the characteristics of oscillatory turbulent boundary layer flows and the resulting sediment transport, including velocity and turbulent intensity profiles (Suntoyo 2006; Rachman et al. 2013), eddy viscosity profiles (Absi et al. 2012), shear stress distributions (Suntoyo 2006) and net sediment transport (Suntoyo et al. 2008). However, all of their work are focused on net sediment transport rate rather than the instantaneous sediment concentration distribution, the latter of which will be achieved in this study, which combines the Reynolds-averaged Navier–Stokes equations for mean flow motion, the BSL $k$–$\omega$ model for turbulence closure and the transient equation for sediment suspension. The characteristics of oscillatory boundary layer flows which change from laminar through transitional to turbulent and the related sediment suspension are systematically investigated. The comparison results (theoretical, experimental and numerical) show that the model has the capability of simulating oscillatory boundary layers and suspended sediment in different flows and bed conditions without tuning the coefficients.

2 Model description

2.1 Governing equation

The oscillatory boundary layer and the associated sediment suspension are studied by an integrated numerical model. The model is built upon a Cartesian coordinate, in which the horizontal coordinate is given as $x$, and the vertical coordinate is given as $z$. Figure 1 shows the definition sketch of the laminar and turbulent boundary layer flows, and $\delta _\mathrm{L}$ and $\delta _\mathrm{T}$ represent the laminar and the turbulent boundary layer thickness, respectively.

Fig. 1

Definition sketch of the laminar and turbulent boundary layer

The Reynolds equation for the stream-wise component of flow in the $x-z$ plane with a coordinate system shown in Fig. 1 can be expressed as

$$\begin{aligned} \frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+w\frac{\partial u}{\partial z}=-\frac{1}{\rho }\frac{\partial p}{\partial x}+\frac{1}{\rho }\left( {\frac{\partial \tau _{xx} }{\partial x}+\frac{\partial \tau _{xz} }{\partial z}}\right) , \end{aligned}$$

(1)

where $u$ and $w$ are the velocities in the $x$ and $z$ directions, respectively, $t$ is time, $\rho$ is the fluid density, $p$ is the pressure,and $\tau _{xx}$ and $\tau _{xz}$ are the shear stresses. Since the velocity component $w$ in the boundary layer is very small, the gradients of velocity and shear stress in the $x$-direction are small compared with that in the $z$-direction. Therefore, for 1-D incompressible unsteady flow, the motion equation within the boundary layer can be simplified as follows:

$$\begin{aligned} \frac{\partial u}{\partial t}=-\frac{1}{\rho }\frac{\partial p}{\partial x}+\frac{1}{\rho }\frac{\partial \tau }{\partial z}. \end{aligned}$$

(2)

Recent studies have shown that under progressive waves, those moved terms may influence the streaming and net sediment transport (Fuhrman et al. 2013). However, for oscillatory flows in this paper, the simplifying process is justified (Suntoyo 2006; Zhang et al. 2011b). In this paper, $\tau$ is used to replace the notation $\tau _{xz}$ from here on for simplicity. Outside the boundary layer, the shear stress vanishes where $\tau$ = 0 and $u=U$; $U$ is the free stream velocity. Thus, in the free stream domain, Eq. (2) reduces to

$$\begin{aligned} \frac{\partial U}{\partial t}=-\frac{1}{\rho }\frac{\partial P}{\partial x}, \end{aligned}$$

(3)

where $P$ is the pressure at the upper edge of the boundary layer. Assume the pressure gradient remains constant inside the thin boundary layer, e.g., $\frac{\partial P}{\partial x}=\frac{\partial p}{\partial x}$.

Substituting Eq. (3) into Eq. (2) and introducing the Boussinesq hypothesis ($\tau =\rho ( {\nu +\nu _t }){\partial u} / {\partial z}$, where $\nu$ is the kinematic molecular viscosity and $\nu _{t}$ is the eddy viscosity), the governing equation can be expressed as:

$$\begin{aligned} \frac{\partial u}{\partial t}=\frac{\partial U}{\partial t}+\frac{\partial }{\partial z}\left( {( {\nu +\nu _t })\frac{\partial u}{\partial z}}\right) . \end{aligned}$$

(4)

Within the oscillatory boundary layer, the sediment concentration $c$ is described as

$$\begin{aligned} \frac{\partial c}{\partial t}=w_s \frac{\partial c}{\partial z}+\frac{\partial }{\partial z}\left( {\varepsilon _s \frac{\partial c}{\partial z}}\right) , \end{aligned}$$

(5)

where $\varepsilon _{s}$ is the sediment diffusivity which is assumed to be the sum of turbulent eddy viscosity $\nu _{t}$ and kinematic molecular viscosity $\nu$ , i.e., $\varepsilon _s =\nu _t +\nu$, $w_{s}$ is the settling velocity of suspended sediment, and sediment concentration effect known as hindered setting will also be considered. In this paper, van Rijn (1993) formula is adopted:

$$\begin{aligned} w_s =( {1-c})^4\left\{ {\begin{array}{ll} \frac{( {s-1})gd^2}{18\nu } &{} 1<d\le 100\,\upmu {\text {m}} \\ \frac{10\nu }{d}\left[ {( {1+\frac{0.01( {s-1})gd^3}{\nu ^2}})^{0.5}-1} \right] &{} 100~\upmu {\text {m}}<d<1{,}000\,\upmu {\text {m}} \\ 1.1\left[ {( {s-1})gd} \right] ^{0.5} &{} d\ge 1{,}000\,\upmu {\text {m}} \\ \end{array}} \right. \end{aligned}$$

(6)

where $s$ = 2.65 is the specific gravity of sediments, $d$ the median particle size and $g$ the gravity acceleration.

In this paper, the BSL $k$–$\omega$ turbulence model proposed by Menter (1994) is used to obtained $\nu _{t}$. As described above, the BSL $k$–$\omega$ model is a combination turbulence closure model that gives results similar to the $k$–$\omega$ model of Wilcox (1988) in the inner regime of the boundary layer, but changes gradually to the $k$–$\varepsilon$ model of Jones and Launder (1972) in the outer region of the boundary layer. The blending between the two models is realized by a blending function $F_{1}$, which changes gradually from 1 to 0 from the bottom to the free stream. The Wilcox model and the transformed $k$–$\varepsilon$ model are first multiplied by the functions $F_{1}$ and (1–$F_{1}),$ respectively, and then summed up. Refer to Menter (1994) for the details of the transformation and the blending process .

The BSL $k$–$\omega$ model equations are given as

$$\begin{aligned} \frac{\partial k}{\partial t}&= \frac{\partial }{\partial z}\left\{ {(\nu +\nu _t \sigma _{k\omega } )\frac{\partial k}{\partial z}} \right\} +\nu _t \left( {\frac{\partial u}{\partial z}}\right) ^2-\beta ^*\omega k\end{aligned}$$

(7)

$$\begin{aligned} \frac{\partial \omega }{\partial t}&= \frac{\partial }{\partial z}\left\{ {(\nu +\nu _t \sigma _\omega )\frac{\partial \omega }{\partial z}} \right\} +\gamma \left( {\frac{\partial u}{\partial z}}\right) ^2-\beta \omega ^2\nonumber \\&\quad +2(1-F_1 )\sigma _{\omega _2} \frac{1}{\omega }\frac{\partial k}{\partial z}\frac{\partial \omega }{\partial z}\end{aligned}$$

(8)

$$\begin{aligned} v_t&= \frac{k}{\omega }, \end{aligned}$$

(9)

where $k$ is turbulent kinetic energy and $\omega$ is the specific dissipation rate, which is defined as $\omega =\varepsilon / {(\beta ^*k)}$, and $\varepsilon$ is the turbulence dissipation rate. The $k$–$\omega$ model is able to provide more suitable dependent variables by introducing an additional term, see the last term on the right-hand side of Eq. (8), whose net effect is to suppress the increase rate of turbulence length scale. In the presence of adverse pressure gradient, the Jones–Launder turbulence length scale tends to be much larger than that of the $k$–$\omega$ model in the near-wall region.

$\sigma _{k\omega } , \beta ^*, \sigma _\omega , \gamma , \beta$ and $\sigma _{\omega _2}$ are model constants and some can be obtained by simple linear superposition. Let $\psi$ represent any constant in the Wilcox $k$–$\omega$ model, $\psi _{2}$ for any constant in the transformed $k$–$\varepsilon$ and $\psi$ the corresponding constant of the BSL $k$–$\omega$ model. The relationship between them is:

$$\begin{aligned} \psi =F_1 \psi _1 +(1-F_1 )\psi _2. \end{aligned}$$

(10)

The model parameters given by Menter (1994) are listed in Table 1:

Table 1 Parameters set up for BSL $k$–$\omega$ model

The blending function $F_{1 }$ is defined as

$$\begin{aligned} F_1&= \tanh (\text{ A }_1^4 )\end{aligned}$$

(11)

$$\begin{aligned} \text{ A }_1&= \min \left[ {\max \left( \frac{\sqrt{k} }{0.09\omega z};\frac{500\nu }{z^2\omega }\right) ;\frac{4\rho \sigma _{\omega ^2} k}{C_{k\omega } z^2}} \right] , \end{aligned}$$

(12)

where $z$ is the distance to the surface and $C_{k\omega }$ is the positive portion of the cross-diffusion which is defined as

$$\begin{aligned} C_{k\omega } =\max \left( 2\rho \sigma _{\omega 2} \frac{1}{\omega }\frac{\partial k}{\partial z}\frac{\partial \omega }{\partial z};10^{-20}\right) . \end{aligned}$$

(13)

2.2 Boundary conditions

2.2.1 The bottom

At the bottom $z=0$, the no-slip condition is applied for flow velocity

$$\begin{aligned} u=0. \end{aligned}$$

(14)

The bottom condition for turbulence quantities $k$ and $\omega$ are given as follows,

$$\begin{aligned} k=0,\omega =\left\{ \begin{array}{ll} \mathop {\lim }\limits _{z\rightarrow 0} \frac{6\nu }{\beta _1 z^2}, &{} \text{ when } \quad \,k_s^+ <3.3 \\ {u_*^2 S_R } / \nu , &{} \text{ when } \quad k_s^+ \ge 3.3 \\ \end{array} \right. \end{aligned}$$

(15)

where $\beta _{1}=0.075$, $k_s^+ ={k_s u_*} / \nu$, $k_{s}$ is the grain roughness, and $k_{s}= 2.5\,d$ is adopted for a flat bed of sand with median size $d$ (Nielsen 1979). $u_{*}$ is the friction velocity and $u_*=\sqrt{{\tau _b } / \rho }$, where $\tau _b$ is the bottom shear stress. The parameter $S_{R}$ is defined as

$$\begin{aligned} S_R =\left\{ \begin{array}{ll} ( {{50} / {k_s^+ }})^2,&{} \text{ when }\quad \,k_s^+ <25 \\ {100} / {k_s^+ ,} &{} \text{ when }\quad \,k_s^+ \ge 25 \\ \end{array} \right. \end{aligned}$$

(16)

For sediment, a pickup function is employed to describe the time-dependent vertical gradient of the near-bed sediment concentration at a reference level $z~=~z_{a}$ = 2$d$ (Nielsen 1992):

$$\begin{aligned} \frac{\partial c}{\partial z}=-\frac{w_s }{\varepsilon _s }C_a, \end{aligned}$$

(17)

where $z_{a }$ is a near-bed reference height and $C_{a }$ is the reference sediment concentration at $z_{a,}$ and can be obtained from the instantaneous Shields parameter by the formula of Zyserman and Fredsøe (1994):

$$\begin{aligned} C_a&= \frac{0.331(\theta -\theta _c )^{1.75}}{1+0.72(\theta -\theta _c )^{1.75}}\end{aligned}$$

(18)

$$\begin{aligned} \theta&= \frac{u_*^2 }{( {S-1})gd}, \end{aligned}$$

(19)

where $\theta _{c}$ is the critical value of the Shields parameter for initial motion and can be obtained by the van Rijn (1993) formula:

$$\begin{aligned} \theta _c =\left\{ \begin{array}{ll} 0.24D_*^{-1}&{}\quad 1<D_*\le 4 \\ 0.14D_*^{-0.64} &{}\quad 4<D_*\le 10 \\ 0.04D_*^{-0.1} &{}\quad 10<D_*\le 20 \\ 0.013D_*^{0.29} &{}\quad 20<D_*\le 150 \\ 0.055D_*&{}\quad D_*>150 \end{array} \right. \end{aligned}$$

(20)

where $D_{*}$ is the non-dimensional grain size given by $D_*=\left[ {( {s-1})g/\nu ^2} \right] ^{1 / 3}d$.

2.2.2 Upper edge of the boundary layer

The condition of no shear is applied at the upper edge of the boundary layer $z=z_{h}$. The gradient of velocity is equal to zero, i.e.,

$$\begin{aligned} \frac{\partial u}{\partial z}=0. \end{aligned}$$

(21)

At the top boundary, zero flux conditions for both turbulence and sediment concentration are imposed:

$$\begin{aligned}&\frac{\partial k}{\partial z} = 0\end{aligned}$$

(22)

$$\begin{aligned}&\frac{\partial \omega }{\partial z}= 0 \end{aligned}$$

(23)

$$\begin{aligned}&w_s c+\varepsilon _s \frac{\partial c}{\partial z}= 0. \end{aligned}$$

(24)

Following Fredsøe et al. (1985), this vertical flux condition can be simplified because of the limited vertical extent of the oscillatory boundary layer. Equation (24) will always degenerate to:

$$\begin{aligned} c\rightarrow 0,\, \text{ when }\,z\rightarrow \infty . \end{aligned}$$

(25)

Hence, Eq. (25) is implemented at $z=z_{h}$ in the present work.

2.3 Numerical methods

In the present model, semi-implicit finite difference method is used to solve Eqs. (4), (5), (7) and (8) using central differences in space, while forward difference is employed in the edge boundary conditions. To achieve better solutions for the thin oscillatory boundary layer, a stretched grid is applied by allowing grid spaces to increase exponentially from the bed, which are given as:

$$\begin{aligned} \Delta z_1 =(q-1)z_h /(q^n-1) \end{aligned}$$

(26)

where $q$ is the ratio between two consecutive grid spaces and $n$ is the total number of grid points (Suntoyo et al. 2008). To establish a fully developed flow and a complete vertical structure of sediment suspension, a computational domain $z_{h}$ which is much larger than $\delta _{T}$ is applied. The initial conditions of velocity and concentration are set to zero, and very small values are given to $k$, $\omega$ and $\nu _{t}$ for the initial start. $k=\frac{1}{2}\zeta U_0^2$, $\omega =k/\nu _{t}$ with $\nu _{t}=\xi \nu$, the value of $\zeta$ is chosen to be $2.5 \times 10^{-4}$ and $\xi$ is chosen to be 0.1 in the present computations. For the flow with low Reynolds number, the calculated value of $k$ based on the present model will remain low, representing that the flow is laminar. However, for the flow with high Reynolds number, the calculated $k$ will grow and stabilize on the level corresponding to the turbulent flow. The computation will carry on without additional parameter adjustment and which flow regime it belongs to will be determined by the end results.

The entire computational procedure includes three steps. The first step is to update the velocity $u$ by solving Eq. (4). The second step is to update the turbulence kinetic energy $k$, the specific turbulence dissipation rate $\omega$ and the eddy viscosity $\nu _{t}$ by solving the BSL $k$–$\omega$ Eqs. (7), (8). The third step is to update the suspended sediment concentration by solving Eq. (5).

3 Results and discussions

3.1 Bottom friction factor

The numerical model described above is applied to a series of validations. A simple but useful means for validating the present model (especially in the laminar to turbulent transition region) is to compare the bottom friction coefficient $f_w$ (equivalently to the bed shear stress) as a function of Reynolds number $R_{e}$ for hydraulically smooth flow, and relative bottom roughness $A/k_{s }$ for hydraulically rough flow, between the model results and the existing results (numerical, experimental and theoretical). $R_{e }$ is the Reynolds number and equals to ${U_0^2 } / {\sigma \nu }$, $U_{0}$ is the maximum free stream velocity, $A$ is the amplitude of the free stream motion and equals to $U_{0}/\sigma ,\sigma$ is the angular frequency and $\sigma ={2\pi } / T$, where $T$ is the period of oscillation. The free stream has oscillating flow with sinusoidal velocity variation in this study.

The bottom friction factor $f_w$ is defined as

$$\begin{aligned} f_w =\frac{2\tau _{0} }{\rho U_0^2 }, \end{aligned}$$

(27)

where $\tau _{0}$ is the maximum bed shear stress. In the following computations, the values of $\rho =998.2$ kg/m$^{3 }$ and $\nu =1.004\times 10^{-6}$ m$^{2}$/s for water at 20 $^\circ$C and under one atmospheric pressure are adopted.

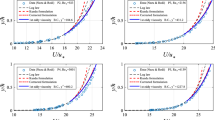
For hydraulically smooth bed, numerical results of bottom friction coefficient $f_w$ with variation of $R_{e}$ in the present model are compared with the experimental results of Kamphuis (1975), Sleath (1987) and Jensen et al. (1989), as well as DNS simulation results of Spalart and Baldwin (1989) in Fig. 2.

Fig. 2

Comparisons of bottom friction factor for hydraulically smooth bed as function of $R_{e}$

Computed results are shown for Reynolds number from $10^{3 }$ to $10^{7}$, including the laminar, transitional and turbulent flows. Jensen et al. (1989) discovered that the transition from laminar to turbulent flow takes place for the $R_{e }$ number in the interval between $2.0\times 10^{5}$ and $6.0\times 10^{5}$. In Fig. 2, when $R_e \le 2.0\times 10^5$, the model results agree well with the classical theoretical solution for laminar flows

$$\begin{aligned} f_w =2R_e ^{-0.5}. \end{aligned}$$

(28)

Under transitional condition where $2.0\times 10^5<R_e <6.0\times 10^5$, though slight difference exists between model results and DNS results of Spalart and Baldwin (1989), the model results overall agree well with the experimental data.

Under turbulent condition where $R_e \ge 6.0\times 10^5$, the model results are in good agreement with the empirical relation of Fredsøe and Deigaard (1992)

$$\begin{aligned} f_w =0.035R_e ^{-0.16}. \end{aligned}$$

(29)

For hydraulically rough bed, $f_w$ depends on the relative bottom roughness $A/k_{s}$. Same as before, numerical results with variation of $A/k_{s}$ of the present model are compared with experimental data of Kamphuis (1975), Jonsson and Carlsen (1976), Sleath (1987) and Jensen et al. (1989) in Fig. 3.

Fig. 3

Comparisons of bottom friction factor for hydraulically rough bed as function of $A/k_{s}$

As shown in Fig. 3, the model provides a good series of results that agree well with the empirical expression which has been modified from the equation of Nielsen (1992) $f_w =\exp [ {5.213( {A / {k_s }})^{-0.194}-5.977}]$ to provide a better match to the existing experimental data, given as

$$\begin{aligned} f_w =\exp \left[ {6.0( {A/k_s })^{-0.175}-6.8} \right] \end{aligned}$$

(30)

The agreement among model results, experimental data and theoretical solutions over a wide range of $R_{e}$ and $A$/$k_{s}$ indicates that the model is able to provide good predictions of the bottom friction factor (bed shear stresses) for different oscillatory boundary flows (from laminar to transitional to turbulent) under both hydraulically smooth and rough bed conditions.

3.2 Boundary layer flows in different $R_{e}$ regimes

In this section, the present model is applied to study the characteristics of oscillatory boundary layer flows at different $R_{e}$. The reference case of the turbulent boundary layer flow is based on the 13$^{th}$ test of Jensen et al. (1989), which has $R_{e} =6\times 10^{6 }$ (see Case 1 in Table 2, hereafter referred to as J13). In the following cases, the Reynolds numbers are set to increase from $7.5\times 10^{3}$ to $6\times 10^{6}$, simulating the flows under conditions from laminar to turbulent through transitional process (as shown in Table 2).

Table 2 Problem setup for oscillatory boundary layers at different $R_{e}$

In the simulation, a computational domain with a height of 0.69 m is discretized into 80 grids with a minimum grid size of 0.0001 m near the bottom and $q=1.12$. A constant time step $\Delta t=1.0\times 10^{-5} \text{ s }$ is used to run the model for up to 15 wave periods to present a fully developed flow. The numerical results of the last wave period are used in the comparison with the theoretical solution and experimental data for all cases in this paper.

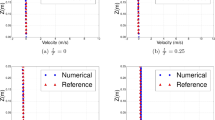
Figure 4 shows the comparisons of mean velocity distributions at different phases between numerical results, analytical solutions and available experimental data. It is found that the numerical results are in satisfactory agreement with the experimental data for oscillatory turbulent boundary layer flow. Besides, the model results for laminar boundary layer flow agree well with the analytical solution of Lamb (1932)

$$\begin{aligned} u=U_0 \left[ {\cos ( {\sigma t})-\exp ( {-\alpha z})\cos ( {-\sigma t+\alpha z})} \right] , \end{aligned}$$

(31)

where $\alpha =\sqrt{\sigma / {2\nu }}$. In terms of the boundary layer thickness, many formulae for both smooth and rough laminar and turbulence boundary thickness have been proposed by researchers (e.g., Sleath 1987; Jensen et al. 1989; Fredsøe and Deigaard 1992). The essentials of defining boundary thickness is how to define the top boundary layer. Sleath (1987) defined the top as the distance from the bottom to the point where defect velocity amplitude is 5 % of the free stream velocity amplitude, and Jensen et al. (1989) defined it as the distance from the bottom to the point where the maximum velocity occurs. As we know, the boundary layer is very thin, so the thickness difference between these definitions is very small. It is shown that in Fig. 4, both the simulated laminar boundary layer thickness $\delta _\mathrm{L3}$ for Case 3 and turbulence boundary layer thickness $\delta _\mathrm{T1}$ for Case 1 agree well with the empirical relation of Sleath (1987):

$$\begin{aligned} \delta _\mathrm{L}&= 3\sqrt{\frac{2\nu }{\sigma }}\end{aligned}$$

(32)

$$\begin{aligned} \delta _\mathrm{T}&= k_s 0.26\left( {\frac{A}{k_s }}\right) ^{0.7}. \end{aligned}$$

(33)

Fig. 4

Comparisons of mean velocity profiles for oscillatory boundary flows at $\sigma t=n\pi /6 \, (n=0,1,2\ldots 5)$. (Dashed line numerical results for laminar flow, dashed dotted line numerical results for transitional flow, solid line numerical results for turbulent flow, circle theoretical solution for laminar flow, dot experimental data for turbulent flow of J13, 1989)

Figure 5 shows the comparisons of turbulence kinetic energy at different phases between numerical results and the experimental data. The turbulence kinetic energy are all reproduced well by the model, though there are slight underpredictions at phase $\sigma$t = 30$^{\circ }$ and 150$^{\circ }$. Figure 6 shows the eddy viscosity profiles at different phases. As expected, the kinetic energy and eddy viscosity are very small for laminar flow and increase rapidly from transitional flow to turbulent flow. Figure 7 shows the comparisons of friction velocity between the numerical results and the measured data. The results by the present BSL $k$–$\omega$ model and the $k$–$\varepsilon$ model of Zhang et al. (2011a) are in generally good agreement with the experimental data, whereas the $k$–$\varepsilon$ model produced a slight overprediction of friction velocity, which is in agreement with the findings of Sana and Tanaka (2000) and Menter (1994).

Fig. 5

Comparisons of turbulence kinetic energy profiles for oscillatory boundary flows at $\sigma t=n \pi /6 \, (n=0,1,2\ldots 5)$. (Dashed line numerical results for laminar flow, dashed dotted line numerical results for transitional flow, solid line numerical results for turbulent flow, dot experimental data for turbulent flow of J13, 1989)

Fig. 6

The eddy viscosity profiles for oscillatory boundary flows at $\sigma t=n \pi /6 \, (n=0,1,2\ldots 5)$. (Dashed line numerical results for laminar flow, dashed dotted line numerical results for transitional flow, solid line numerical results for turbulent flow)

Fig. 7

Comparison of friction velocity among the present model’s results (solid line), numerical results (dashed line) of Zhang et al. (2011a) and experimental data (dot) of J13 (1989)

3.3 The suspended sediment concentration in oscillatory flows

The capability of the integrated BSL $k$–$\omega$ model for predicting oscillatory boundary flows at different $R_{e}$ regimes has been tested and verified. In the following, the model is applied to simulate the sediment suspension under oscillatory boundary flows. Comparisons are performed with the tests of Horikawa et al. (1982) for $R_{e}=9.22\times 10^{5 }$ (see Case 4 in Table 3), Case 5 is a laminar flow, which is used as a reference case for Case 4. Because the friction velocity and the sediment diffusivity are very small for laminar flow, the sediments with relative large grain size are not able to be suspended easily. Therefore, to observe the sediment suspension clearly in laminar flow, fairly fine sediment particles are used for Case 5 (referred to Table 3).

Table 3 Problem setup for oscillatory boundary layers and sediment suspension

In the simulations of Case 4 and 5, a computational domain with a height of 0.335 m is discretized into 80 grids with a minimum grid size of 0.000018 m near the bottom and a constant stretching factor $q=1.1$ is applied. A constant time step of $\Delta t=2.0\times 10^{-6} \text{ s }$ is used to run the model for up to 15 wave periods to ensure that the sediment particles are perfectly suspended and diffused.

Figure 8 shows the comparisons of mean velocity profiles among numerical results of both the present model and Zhang et al. (2011b), experimental data (Horikawa et al. 1982) and the theoretical solutions (Sleath 1987) for Case 4 and Case 5. The present model provides good agreements of the velocity profiles for both laminar and turbulent flows. Besides, the theoretical turbulent boundary layer thickness $\delta _\mathrm{T4}$ and the theoretical laminar boundary layer thickness $\delta _\mathrm{L5}$ also match well with the empirical solutions of Sleath (1987). For turbulent flow, Zhang’s model provides more or less the same velocity results as the present model.

Fig. 8

Comparisons of mean velocity profiles for oscillatory boundary flows at $\sigma t=n \pi /6 \, (n=0,1,2\ldots 5)$. (Dashed line numerical results for laminar flow Case 5, solid line numerical results for turbulent flow Case 4, cross numerical results of Zhang et al. (2011b) for Case 4, circle theoretical solution for laminar flow, dot experimental data for turbulent flow of Horikawa et al. 1982)

Figure 9 shows the comparisons between the numerical results and the experimental data for time-dependent profiles of suspended sediment concentration at different phases in a half period. Though there is a slight underprediction at phase $\sigma t=150^{\circ }$, the simulated sediment suspension profiles generally agree well with the measured data. Especially near the bottom and at phase $\sigma t=0^{\circ }$ and 150$^{\circ }$ where the adverse pressure gradient is strong, the BSL $k$–$\omega$ model shows much better prediction than the $k$–$\varepsilon$ model of Zhang et al. (2011b). Figure 10 shows the comparison between the numerical results and the experimental data for sand flux profiles at different phases. The BSL $k$–$\omega$ model shows better agreement once again. Though the $k$–$\varepsilon$ model of Zhang provided more or less the same velocity profiles as the BSL $k$–$\omega$ model, the BSL $k$–$\omega$ model shows better ability of predicting the instantaneous suspended sediment characteristics. As shown in Fig. 11, the time-averaged sediment concentration in the turbulent oscillatory flow is well reproduced by both BSL $k$–$\omega$ model and the $k$–$\varepsilon$ model of Zhang et al. (2011b). Figure 11 also shows that the sediment concentration in laminar is very low (almost zero) due to the near-zero eddy viscosity in laminar flow, even though the sediment size is very small. Figure 12 shows the time-dependent sediment concentration at different levels $z=5$ mm, $z=10$ mm, $z=15$ mm and $z=20$ mm for Case 4. The time $t/T=0$ corresponds to the phase $0^{\circ }$ when the velocity changes the direction, and $t/T=0.25$ corresponds to the phase $90^{\circ }$ when the velocity reaches a maximum value. As can be seen, the simulated sediment concentrations generally agree with the experimental data of Horikawa et al. (1982). A phase lag exists between the simulated and experimental results, and the phase lag exists and increases with increase in elevation.

Fig. 9

Comparisons of vertical distributions of suspended sediment concentration at $\sigma t=n \pi /6 \, (n=0,1,2\ldots 5)$ among the present model’s results (solid line), numerical results (dashed line) of Zhang et al. (2011b) and experimental data (dot) of Horikawa et al. (1982)

Fig. 10

Comparisons of vertical distributions of sand flux at $\sigma t=n\pi /6 \, (n=0,1,2\ldots 5)$ among the present model’s results (solid line), numerical results (dashed line) of Zhang et al. (2011b) and experimental data (dot) of Horikawa et al. (1982)

Fig. 11

Comparisons of period-averaged suspended sediment concentration between the numerical results (solid line) and the experimental data (dot) of Horikawa et al. (1982) for Case 4. Numerical results (dashed line) of period-averaged suspended sediment concentration for Case 5

Fig. 12

Comparison of time-dependent suspended sediment concentration at different levels for Case 4 between the present model’s results (solid line) and the experimental data (dot) of Horikawa et al. (1982)

To further study the capability of BSL $k$–$\omega$ model in predicting sediment suspension, one more case is conducted. In Case 6, a computational domain with a height of 0.465 m is discretized by 80 grids with a minimum grid size of 0.000025 m near the bottom and a constant stretching factor $q=1.1$ is applied. A constant time step is $\Delta t=2.0\times 10^{-6} \text{ s }$, and the total simulation time is up to 15 wave periods to ensure that the sediment particles are perfectly diffused. Comparisons are made between the simulated results of the present BSL $k$–$\omega$ model and the $k$–$\varepsilon$ model of Savioli and Justesen (hereafter referred to as SJ), (1997), and the experimental data of Ribberink and Al-Salem (1992).

Figure 13 shows the comparison of time-dependent suspended sediment concentration for Case 6 at $z=5$ mm, $z=11$ mm, $z=16$ mm and $z=31$ mm between the numerical results and experimental data (Ribberink and Al-Salem 1992) during one period. It can be observed that the SJ $k$–$\varepsilon$ model well predicted the presence of a second peak at $z=5$ mm and $z=11$ mm due to the inclusion of a modified bed reference concentration. However, the model on the whole underestimated the suspended sediment concentration. Better than the SJ $k$–$\varepsilon$ model, the simulating results provided by the BSL $k$–$\omega$ model show good agreements with experimental data, especially in the accurate prediction of the peak value of sediment concentration over the flow reversal. Similar to the behaviors in Case 4, Case 6 shows a phase lag between the numerical results and the measured data, which increases with the increase in elevation. However, the period-averaged concentration for a stable period in Fig. 14 shows good agreement with the experimental data.

Fig. 13

Comparison of time-dependent suspended sediment concentration at different levels between the results of present BSL $k$–$\omega$ model (solid line), $k$–$\varepsilon$ model (dashed line) of Savioli and Justesen (1997) and the experimental data (dot) of Ribberink and Al-Salem (1992)

Fig. 14

Comparison of period-averaged suspended sediment concentration for Case 6 among the present model’s results (solid line), numerical results (dashed line) of Zhang et al. (2011a) and the experimental data (dot) of Ribberink and Al-Salem (1992)

4 Conclusion

In this study, the oscillatory boundary layer flows and sediment suspension have been investigated by an integrated model which solves Reynolds-averaged Navier–Stokes equations for flows and convection–dispersion equation for sediments. The BSL $k$–$\omega$ model which retains the robust and accurate formulation of the Wilcox $k$–$\omega$ model in the near-wall region, and takes advantage of the free stream independence of the JL $k$–$\varepsilon$ model in the outer parts of the boundary layer is adopted for turbulence closure. The model considers the flow Reynolds number $R_{e }$ and bottom roughness $k_{s}$ automatically and thus is capable of simulating laminar, transitional and turbulent boundary layer flows accordingly based on the flow and bed conditions provided.

The reliability and robustness of the proposed model are validated by a series of numerical tests that include oscillatory laminar, transitional and turbulent boundary layer flows and the resulting sediment suspension. The prediction results of the bottom friction factor, boundary layer thickness, velocity, kinetic energy and eddy viscosity under different types of oscillatory boundary layer flows show good agreements with the available experimental data, numerical results and analytical solutions. Besides, the model provides good results of the friction velocity, the time-dependent suspended sediment concentration and the period-averaged suspended sediment concentration, though there are small phase differences. Moreover, the model shows better instantaneous sediment concentration distribution prediction ability than the $k$–$\varepsilon$ model and improves the predictive capability of a Reynolds-averaged Navier–Stokes (RANS) approach for turbulence and sediment suspension in boundary layer flows, which is helpful in defining a suitable model for relevant practical applications in coastal engineering.

However, considering the complex natures of oscillatory boundary flows and sediment transport, in this study we focus ourselves on the 1D modeling only. In future studies, the methodology validated in this study will be extended to a 3D model for practical problems, which solves the full Navier–Stokes equations in the entire domain and can be used to model large-scale hydrodynamics and beach morphology in coastal waters.