1 Introduction

According to recent statistics, water lost through leaks and bursts constitutes one-third of the total water supplied through distribution systems (Vrachimis et al. 2021). This non-revenue water (NRW) causes enormous financial losses (Puust et al. 2010). In Hong Kong alone, leaks and bursts cost US$173 million worth of damages annually (Gupta 2017). False alarms and localization errors cost time, money, and considerable effort. Unnecessary interference with the soil-pipeline environment can also cause damage to infrastructure. Therefore, accurate and timely leak localization is one of the pressing challenges in the world of water infrastructure expertise. Early localization of leaks can save repair costs by helping practitioners actively plan pipe repair/replacements (Hu et al. 2021).

Traditionally, leak localization methods can be divided into observation-based methods and data-driven methods (Covas et al. 2005). The observation-based methods require skilled workers to manually survey the pipes using listening sticks and ground microphones for condition assessment and to find the leak location. However, manual observation methods are time-consuming and labor-intensive. Besides, the accuracy largely depends on the experience of workers (Muggleton and Brennan 2004; Fahimipirehgalin et al. 2021). Data-driven methods, on the other hand, are mainly based on data modeling. Such data include water flow, pressure changes, in-pipe acoustics, or pipe wall vibrations. They are collected via sensing technologies either on-site or wirelessly. For example, Candelieri et al. (2014a) proposed a spectral clustering-based approach to analyze the water flow and localize leak points. The dataset was derived from a hydraulic simulation model and transformed into a similarity graph applying spectral clustering. Similarly, Wang et al. (2019b) adopted the spectral-based method to localize pipeline leaks. Alternatively, acoustics sensors have increasingly been used for leak localization (Gao et al. 2022; Cui et al. 2023).

However, the research mentioned above is mainly based on laboratory experiments and has low practicality. The proposed method can find leaks in a single leak scenario and provide a potential alternative for localizing multiple leaks. Lin et al. (2008) recently proposed a feature engineering-based localization method using multiple sensors. Leaks were identified and localized by modeling extracted features. Hu et al. (2021) conducted a critical literature survey to compare the performance of localization methods. They concluded that acoustic methods provide a balanced localization ability, simultaneously considering sensitivity, accuracy, error rate, time, investment cost, and service time.

Acoustic methods localize leaks using signals collected from pipelines non-invasively through acoustic sensors like accelerometers, hydrophones, or noise loggers. Micro-electromechanical system (MEMS) accelerometers are low-cost (Guru Manikandan et al. 2021), require less initial deployment cost compared to hydrophones and noise loggers, and are more effective in plastic pipes (Tariq et al. 2021b, a). The application of MEMS-based accelerometers for leak detection was recently investigated by Tariq et al. (Tariq et al. 2021a). Their use for leak detection in the Hong Kong pipeline systems was successfully reported (Tariq et al. 2021a). As a follow-up, this study further investigates using MEMS accelerometers to locate leaks in real urban water systems such as Hong Kong.

The length of the water distribution network (WDN) of Hong Kong is more than 8605 km. Hong Kong Water Supplies Department (WSD) has made great efforts in the last two decades and reduced the leakage rate from exceeding 25% in 2000 to about 15% in 2019 (Water Supplies Department 2020). These efforts include replacing deteriorated pipelines and establishing new monitoring systems (Yue and Tang 2011). Data-driven models based on machine learning assist in increasing efficiency and reducing losses. The current study, therefore, adopts a machine learning-driven methodology for facilitating water leak localization, increasing model accuracy and efficiency. The objectives of this study are three-fold: 1) to investigate the capability of MEMS-based accelerometers for localizing water pipe leaks in real WDNs; 2) to evaluate the performance of support vector machine (SVM) and artificial neural network (ANN) for localizing leaks in WDNs; and 3) to develop a model to localize the pipe leakages in real networks.

This study presents a novel approach utilizing accelerometers for leak localization in water distribution networks. The model result demonstrates the applicability of MEMS accelerometers and machine learning models for leak localization and points out the current limitation. By introducing these innovative methods, this study provides potential solutions for efficient water resource management in other megacities.

2 Literature Review

The vibration signal-based localization methodology can be categorized into traditional signal processing, beamforming, and statistical methods (Hu et al. 2021). Traditional signal processing mainly involves denoising the leak signal and extracting informative signal components for localizing leaks. For example, Mahmutoglu and Turk (2018) proposed an innovative passive acoustic system for leak localization. Based on background noise, detection method, receiver number, signal strength, and measurement number, leaks can be found with low average position errors from several kilometers away. On the other hand, Mahmutoglu and Turk (2019) used signal strength differences to locate pipeline leaks without any information on leak signal strength in absolute terms. Ting et al. (2021) recently introduced a dual-tree complex wavelet transform for water pipe signal processing. The proposed denoising algorithm highlights the peak of the cross-correlation function and improves the localization accuracy manifold. These signal-processing methods have greater robustness and ease of practical implementation. However, the results are sensitive to environmental uncertainties, such as different pipe materials, ambient noise, and soil characteristics.

Beamforming is also an alternative signal processing technique for obtaining directional signals from the sensor array. For example, (Wang and Ghidaoui 2018, 2019; Wang et al. 2019a) adopted an iterative beamform method for locating multiple leaks. Moreover, beamforming has been widely applied to detect the acoustic signal under a noisy background. For example, Maxit et al. (2022) also adopted the beamform technique to improve the signal-to-noise ratio (SNR) of collected vibration data. The array gains are calculated using both the traditional and beamforming techniques. The result shows that the beamforming has improved performance, resulting in a much larger array gain. Overall, the beamforming method benefits from higher accuracy and reliability, requires more sensors and experiment points, and suffers from the high economic cost. Zhi et al. (2023) utilized cross-correlation for leak localization. Agrawal et al. (Agrawal et al. 2023) and Kousiopoulos et al. (2022) utilized the technique of multiple time difference arrival, relying on cross-correlation calculations using signals acquired from pairs of sensors. However, the validation majorily took place through laboratory testing on bare pipes (not buried).

Lastly, statistical methods use extensive data to pinpoint the locations of pipe leaks. By analyzing the collected data, the characteristics of the signal can be summarized and proposed, thereby aiding in the localization of leaks. Advanced statistical techniques like machine learning-based regression and classification algorithms are considered effective for leak localization. Applied algorithms include ANN, SVM, Bayesian, and convolutional neural networks (Poulakis et al. 2003; Jin et al. 2014; El-Abbasy et al. 2016; Tijani and Zayed 2022). For instance, El-Abbasy et al. (2016) developed regression and ANN models based on the acoustic data from noise loggers. The developed models have been validated and proven to have around 90% localization accuracy in the established laboratory testbed. Zhou et al. (2019) innovatively proposed a deep-learning framework to localize pipe bursts further. The validation results show that the model has better robustness and applicability than the linear neural network. Recently, Quiñones-Grueiro et al. (2021) attempted to solve the leak location problem from an inverse perspective and developed a deep learning model considering the topology of the WDN, modifying the location space and combining time series. The result reveals that the proposed model performs well on the extensive pipe network of 268 nodes and 9 sensors. El-Zahab et al. (2022) developed a wireless leak detection and localization system for a building. In the study, vibration sensors were used to test the effectiveness of a wireless system to find leaks in PVC and iron pipes. More details about data-driven approaches and the use of machine learning can be found in recent literature review articles (Yussif et al. 2023; Nimri et al. 2023). Overall, data-driven methods have better performance as compared to other methods.

Previous research has made significant contributions to understanding the pipe leak localization problem. However, most studies are based on lab/testbed experiments (Martini et al. 2015; El-Zahab et al. 2018; Li et al. 2021). Due to the complicated influencing factors on-site, the leak models developed by lab experiments cannot be directly applied to a real WDN (El-Abbasy et al. 2016). First, the actual water distribution has high background noise, which does not conform to assumptions made while conducting experiments in the lab/testbed. Additionally, tests are performed on simplified pipe networks (e.g., a straight pipe) (Mostafapour and Davoudi 2013; El-Abbasy et al. 2016), which cannot reveal the complexity of the in-service pipe network (Tariq et al. 2021a). Thus, there is a need to test methods on real sites with reported leaks. In line with the argumentation and data availability, machine learning has been adopted in the current study as the optimum choice for leak localization in real water networks. In particular, SVM and ANN were adopted and compared to identify their robustness to address the leak localization problem.

3 Research Method

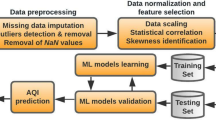
Figure 1 depicts the outline procedures to develop a localization model for water pipe leaks. The adopted research methodology can be divided into data collection, analysis, and machine learning modeling. First, field experiments were conducted on the WDN of Hong Kong in collaboration with the water supplies department (WSD). As the current study has been conducted with the assistance of the WSD, rich field data has been collected. MEMS accelerometers were deployed to collect signals from leak points. The collected information was further analyzed and processed in the data analysis step. In this step, we filtered the collected data to reduce the bias imposed by outliers. In the modeling phase, the feature optimization algorithm was applied to extract the acoustic characteristics of the dataset. Then, the parameters of the machine learning models were optimized. The proposed model can output the leak distances, which are defined as the distance between the deploy site and the leak point. Finally, models with the optimized parameters were validated using samples from other WSD sites.

Fig. 1
figure 1

Research framework for developing leak localization models

Full size image

3.1 Data Collection

The experiment sites included the municipal water distribution network and the underground pipe leak detection center established by WSD. The experimental duration ranged from Oct 1st, 2020 to Oct 19th, 2021. First, WSD reported leak points and provided the water pipe network map and corresponding pipe information (including pipe diameter, pipe material, and connection), as shown in Fig. 2. The research team subsequently designed the experimental plan and deployed sensors on proposed sites. For each site, 1 to 3 accelerometers were deployed depending on the availability of surrounding chambers. Data collection at each site lasted for one to three days, collecting data at different time points for one minute duration. Leak distance was defined as the distance between the leak point and the location where the sensor was deployed. The field experiments were always conducted at midnight, avoiding the impact of noise caused by surrounding traffic vehicles and passengers. Furthermore, the pipe flow is relatively stable at night.

Fig. 2
figure 2

A typical location in real water supply network where the MEMS accelerometers were deployed

Full size image

The experiment equipment was MEMS accelerometer brand Beanair, enabling wireless data transmission and collecting time-synchronized data. Figure 3 depicts how the accelerometers were used to collect signals on-site. The sampling frequency was 3000 Hz and the sample duration was 60 s. Therefore, each sample had 180000 data points. The data was collected from the Z-axis (Tariq et al. 2021b). The accelerometer sensors were deployed on the valve within the chamber. The gateway (the central controller) was connected to the laptop, sending commands to sensors through Beanscape software. Overall, 1347 samples were collected and saved in the format of text (g values at every 1/3000 s) for further analysis.

Fig. 3
figure 3

Data collection system

Full size image

3.2 Data Preprocessing

The quality of training data heavily impacts the performance of machine learning models (Budach et al. 2022). In this study, the collected acoustic dataset suffered from missing data (caused by inconsistent signal transmission) and background noises (emitted by vehicles and pedestrians). Therefore, it is necessary to adopt data preprocess, laying the foundation for the modeling phase.

We adoptrd the outlier removal process to eliminate the errors brought by noise signals. The interquartile rule (IQR) method was applied to find outliers. Specifically, quartiles and maximum and minimum values of signal data were computed. IQR and upper and lower bound values were calculated using Eq. (1), where Q1 represents the 25th percentile of the data; Q3 represents the 75th percentile of the data. Any data values above the upper and below the lower bounds were removed.

$$\begin{array}{c}IQR={Q}_{3}-{Q}_{1}\\ \mathrm{Upper\ bound }={Q}_{1}-1.5 IQR\\ \mathrm{Lower\ bound}={Q}_{3}+1.5 IQR\end{array}$$
(1)

Ultimately, a total of 1347 samples remained. Table 1 depicts the details of the data distribution. Most samples (84%) were collected within a 15 m of leak distance from metal pipelines. Distance is the label of the dataset, and its unit is meter (m). Considering that this study did not use a deep learning model and the complexity of the model was relatively low, a more significant proportion of data was assigned to the test set and validation set to evaluate the model. A hold-out method was adopted, and 1347 samples were randomly split into the training dataset (808 samples), testing dataset (269 samples), and validation dataset (270 samples), taking up 60%, 20%, and 20%, respectively.

Table 1 Details of the finalized dataset
Full size table

3.3 Feature Extraction and Selection

Adopted features constitute the most critical building block for machine learning modeling, assisting to summarize the characteristics of signals and promote model learning (Li et al. 2017). The quality of modeling training data and feature extraction determines the performance optimality of machine learning models. Parameter optimization and experiment testing facilitate achieving more optimum performance. Feature extraction consists of two steps: feature collection and feature selection.

A literature review was conducted to select water pipe leak localization features in the feature collection step. Various studies adopted different combinations of acoustic-based features. These features consist of time, frequency, and power dimensions. A total of 17 features were initially introduced from the literature.

Table 2 depicts the corresponding expression of these features, where \({x}_{i}\) and \({x}_{f}\) refers to the signal in the time specturm and frequency spectrum. f represents the frequency band. df is the resolution of the spectrum. N denotes the number of data samples. F is the maximum frequency in a spectrum. T is the time length of the signal. j is the index when \({x}_{i}-{x}_{j}\) is the smallest over the signal. \({R}_{xx}\) is the autocorrelation function of x. \({\mu }_{xx}\) and \({\sigma }_{xx}\) are the mean and standard deviation of \({R}_{xx}\). n is the number of data where \({x}_{f}\) is larger than 33 percent of max \({x}_{f}\). \({\mu }_{f}\) and \({\sigma }_{f}\) are mean and the standard deviation of \({x}_{f}\).

Table 2 Result and expression of feature collection
Full size table

Table 3 depicts the value distribution of extracted features. The distribution is categorized by leak distances, including lower than 3.5 m, between 3.5 m to 15 m, and larger than 15 m. The comparison of the values of each feature was visualized through box plots appended in Supplementary Material (SM) Figures SM.1 to SM.17. The result shows that there is generally a distinction in values for different leak distances. Though values of features under different leak distances overlap, machine learning models can utilize various features and fit the multiple dimensions dataset. In the next stage, the initially collected 17 features would be analyzed and finalized.

Table 3 Range of the values of the extracted features
Full size table

Though features help to develop the relationship between the input dataset and target output (Mitra et al. 2002; Naghibi et al. 2015), inappropriate feature selection would decrease model accuracy and performance (Li et al. 2017). Thus, feature selection and optimization is urgently needed for establishing the water pipe leak localization models. Current feature optimization methodologies can be divided into three types, Filter (Peng et al. 2005; Wang et al. 2008), Wrapper (Yang and Ong 2011; Mafarja and Mirjalili 2018), Embedded method (Guyon et al. 2002).

Considering that the acoustic features are generally co-correlated and data volume is limited, this study has adopted the Wrapper method to optimize the features. Regarding Wrapper, this method would packaged all features as a feature set. Each sub-feature set would be used to establish a model to learn or fit the target dataset. The performances of these models were compared to find the optimum feature set (Liu and Wang 2021). Though Wrapper considers the combination of features, it requires a significant additional time when there are numerous features. In addition, Wrapper might suffer from overfitting when there are limited data samples (Maldonado and Weber 2009).

Specifically, the backward selection, as a category of Wrapper method, was selected. First all features were used for modeling. Then, it temporarily discards one feature to check whether the model performance has decreased. If such a decrease is observed, the feature is retained; otherwise, it is dropped. This process is repeatedly conducted for each feature. Because the feature optimization results are varied for different models, the backward selections are respectively conducted on ANN and SVM. The 17 features that are presented in Table 2 were used as the initial feature set for the backward selection algorithm.

Feature selection for the SVM yielded 15 critical features, including Level, Spread, RMS, TD Avg. Amp, Peak Amp., Energy, MLE, Autocorr. MLE, FD Avg. Amp., Peak Freq., Max. Amp., Freq. Centroid, Skewness, Kurtosis, Autocorr. MLE, Freq. Spread. Only four features were selected for the ANN model, which included Skewness, RMS, Level, and Freq. Centroid. The optimized features were adopted to train the models.

3.4 Modeling and Optimization

Leak distance estimation in water distribution networks presents a complex challenge due to the various distinct characteristics of this task (Tyagi et al. 2023). The multi-dimensional nature of sensor data, including parameters like pressure, flow rate, and acoustic signals, increases the complexity (Cody and Narasimhan 2020). Additionally, the relationships between these sensor parameters and leak distances are often non-linear, making traditional linear methods less effective. Real-world data introduces noise and variability into the equation, further complicating accurate predictions.

In this context, SVM and ANN offer unique strengths compared to other machine learning models. SVM excels at recognizing complex patterns within multi-dimensional data, making it suitable for capturing intricate relationships between sensor readings and leak distances. ANN, especially deep neural networks, is highly adept at modeling non-linear relationships, which is essential for accurate leak distance prediction (Fan et al. 2021).

In summary, SVM and ANN are well-suited for leak distance estimation due to their capacity to address the multi-dimensional, non-linear, and noisy aspects of this task. Thus, this study adopted SVM and ANN for subsequent modeling.

3.4.1 Basic Theory

  1. (i)

    Artificial Neural Network (ANN): The artificial neural network is inspired by the structure of bio-neuron (Abiodun et al. 2018). It is designated to solve multi-dimensional and complicated problems (Nagajothi and Elavenil 2020). An ANN model mainly consists of three layers: input, hidden, and output, as shown in Fig. 4. The input layer represents dataset features, and the hidden layer, which can vary in complexity, is the core of the ANN, and the output layer produces model results. In literature, ANN has been widely applied to solve the leak problems in gas (Wang et al. 2021) and water (Sattar et al. 2019; Almheiri et al. 2020) pipelines. Thus, it is introduced as an effective method for pinpointing water leaks in the actual water distribution network case of Hong Kong.

  2. (ii)

    Support vector machine (SVM): Support vector machine is a supervised learning approach based on the linear classifier (Cortes and Vapnik 1995). As shown in Fig. 5, the SVM model tries to establish a hyperplane to classify different samples. The samples closest to the hyperplane are defined as the support vector. Margin is the distance between the support vector and hyperplane. SVM model is trained by maximizing the margin. Meanwhile, introducing the kernel helps the model to establish a more complicated hypersurface (decision boundary), solving the linear inseparable problem (Jain et al. 2018). In the literature, SVM reaches promising performance in solving water pipe leak problems (Mounce et al. 2011; Mashford et al. 2012).

  3. (iii)

    Performance Evaluation of Machine Learning Models: The performance of the classification models can be directly evaluated using explicit indicators such as prediction accuracy, recall rate, and precision. However, the regression model output is continuous and requires different types of performance indicators, including the mean square error (MSE), root mean squared error (RMSE), and mean absolute error (MAE). These indicators have been widely used in significant regression models (Chicco et al. 2021) and are presented in Eqs. (2) to (4).

Fig. 4
figure 4

Basic Structure for artificial neural network (ANN) model

Full size image
Fig. 5
figure 5

The basic concept of SVM

Full size image

The values of MAE, MSE and RMSE denote the model error. Thus, the model with the lower MAE, MSE, and RMSE has a better model prediction. In Eqs. (2) to (4), \({\widehat{y}}_{t}\) denotes the value deduced by the model. \({y}_{t}\) denotes the real value of samples. and T denotes the total number of samples.

$$RMSE=\sqrt{\frac{{\sum }_{t=1}^{T}{\left({\widehat{y}}_{t}-{y}_{t}\right)}^{2}}{T}}$$
(2)
$$MSE=\frac{{\sum }_{t=1}^{T}{\left({\widehat{y}}_{t}-{y}_{t}\right)}^{2}}{T}$$
(3)
$$MAE=\frac{{\sum }_{i=1}^{T}\left|{\widehat{y}}_{t}-{y}_{t}\right|}{T}$$
(4)

MAE directly reveals the real bias or error between real and fake values. Its robustness to outliers and interpretability make it suitable for practical understanding. RMSE emphasizes large errors and retains the same unit of measurement compared to MSE (Chai and Draxler 2014; Hodson 2022).

This study also introduces the model accuracy as the indicator. If the leakage distance output by the model deviates from the actual leakage distance by less than 1 m, it will be considered as correctly identified. Therefore, the model accuracy reflects the proportion of cases where the leakage prediction error is less than 1 m. Thus, the current study adopts RMSE, MAE, and Accuracy as the model performance indicators.

3.4.2 Model Optimization

  1. (i)

    ANN model optimization: In the current study, ANN was developed using RapidMiner. The proposed model adopts Sigmoid as the activation function between the input and hidden layers. In the structure of ANN, the number of neurons in the input layer is 4, corresponding to the features mentioned in the last section. However, there is no specific methodology to determine the structure of ANN (Jin et al. 2021). In addition, the learning rate and the training recycling also significantly affect the model performance. Thus, experiments and tests were conducted to regulate the model structure to reach the optimum result.

Considering ANN only uses four features, this study adopted one hidden layer to simplify and avoid overfitting. Figure 6 depicts the performance of ANN models with different neurons. The architectures featuring 6 and 9 hidden neurons demonstrate superior performance, reaching closely comparable RMSE and MAE. Considering that complex structures demand higher computational resources and may potentially give rise to overfitting issues (Sun et al. 2017), this study adopts hidden layer comprising 6 neurons for the subsequent modeling phase. The overall structure of ANN is shown in Fig. 7. Based on parametric experiments and empirical rules, the learning rate is 0.03, and the training epochs are 300.

Fig. 6
figure 6

Impacts of the number of neurons on ANN performance

Full size image
Fig. 7
figure 7

Selected optimum ANN structure

Full size image

The established ANN models were transformed into a mathematical expression to describe the relationship among input attributes, variables, and the final output. Hence, the weights and biases of the selected optimum architectures are presented in Table 4, which were used accordingly to develop the prediction expression.

Table 4 Weights and biases of the selected optimum ANN structure
Full size table

Subsequently, the resulting mathematical expression based on the weights and biases of the model for WDNs is presented in Eq. (5). LD denotes the leak location formulation. xi can be obtained based on the weights and bias in Table 4. \(f(x)\) denotes the activation function:

$$\begin{array}{c}x_1=w_{1-1}\times f\begin{bmatrix}6.643\;level+0.23\;RMS-1.638\;Freq.Centroid\\+4.248\;Skewness+1.514\end{bmatrix}\\x_2=w_{1-2}\times f\begin{bmatrix}1.267\;level+2.248\;RMS+9.14\;Freq.Centroid\\+1.251\;Skewness-3.09\end{bmatrix}\\\begin{array}{c}x_3=w_{1-3}\times f\begin{bmatrix}-24.439\;level+13.47\;RMS+16.253\;Freq.Centroid\\-8.222\;Skewness-18.919\end{bmatrix}\\x_4=w_{1-4}\times f\begin{bmatrix}0.996\;level-1.075\;RMS+0.433\;Freq.Centroid\\+1.46Skewness-3.186\end{bmatrix}\\\begin{array}{c}x_5=w_{1-5}\times f\begin{bmatrix}1.334\;level-0.7\;RMS+0.64\;Freq.Centroid\\+0.889Skewness-3.174\end{bmatrix}\\\begin{array}{c}x_6=w_{1-6}\times f\begin{bmatrix}1.017\;level-0.795\;RMS-2.721\;Freq.Centroid\\-0.005\;Skewness-2.136\end{bmatrix}\\LD=\sum_{i=1}^6x_i-B_2\end{array}\end{array}\end{array}\end{array}$$
(5)

  • (ii) SVM model optimization: The performance of SVM is greatly dependent on the type of kernel function k and the corresponding parameters (Liu et al. 2016). This study adopted the radial kernel, the Gaussian kernel function (Liu et al. 2011). The main parameter of the radial kernel is the penalty coefficient C and kernel gamma, \(\gamma\).

The above two parameters mainly balance the relationship between the model complexity and the error rate. When C is large, the loss function will be more significant, and the model gives up distant outliers. SVM establishes a more complex hyperplane to fit the distant sample and reach higher accuracy. However, it is also easier to cause the overfitting problem.

On the other hand, \(\gamma\) is the other parameter of the kernel function. It mainly defines the influence of a single sample on the whole classification hyperplane. When \(\gamma\) is small, a single sample imposes a greater impact on the hyperplane, and the sample is easier to be selected as a support vector.

Overall, SVM is more complicated and have more support vector when C and \(\gamma\) are large. Conversely, the model would be simpler when C and \(\gamma\) are minor. Thus, the setting of C and \(\gamma\) should be optimized by comparing the RMSE and MAE of models.

Figure 8 depicts the optimization result of SVM. The analysis reveals that RMSE falls within the range of 2 to 4 for most SVM models. As observed in Fig. 8, models exhibited lower RMSE when γ and C values are high. However, it is crucial to exercise caution with elevated γ and C values, as they may induce overfitting. To balance the model performance and structure complexity, SVM parameters were configured as follows: γ is 0.42, and C is 10. Table 5 shows the weights of 15 adopted features and biases for better describing the established signal. The total number of support vectors is 809.

Fig. 8
figure 8

Optimization results of the SVM model for different parameters: a RMSE; b MAE

Full size image
Table 5 Weights of SVM model
Full size table

4 Results

4.1 Model Testing Results

Table 6 presents the test results of ANN and SVM. Regarding RMSE, the value of ANN (1.9960) is about 20% less than SVM (2.5410). The mean average error of ANN is \(\pm 0.8580\mathrm{ m}\), which is more than 0.1 m lower than the respective value of SVM (\(\pm 0.9500 m\)). The accuracy of ANN (86.25%) is more than 6% better than SVM (80.67%). Regarding the training results, ANN might have a more accurate prediction ability than SVM. On the other hand, both the MAE of ANN and SVM are lower than 1 m. The prediction accuracies of the two models are over 80%. The testing result reveals that the proposed ANN and SVM models have been well-trained and achieved promising localization ability. However, it still needs further validation.

Table 6 Testing results of ANN and SVM model
Full size table

4.2 Model Validation Results

For model validation, this study randomly extracted 20% of the dataset before model training, including 270 samples (167 samples were collected within 3.5 m, and 57 samples were collected from leak distances between 3.5 m to 5 m; 46 samples were collected from leak distance larger than 15 m). The trained ANN and SVM models have been respectively applied to the validation set. When models fail to meet the validation requirements, it necessitates revisiting the data preprocessing stage to identify and address issues in order to enhance model performance.

Table 7 shows the validation result of ANN and SVM. Regarding RMSE, MAE, and accuracy, the performance of ANN was slightly better than SVM. The accuracy gap between ANN and SVM is lower than 2%, with 80.37% and 78.89%, respectively. Overall, the MAE of ANN and SVM are close to 1 m, and the accuracy rates are close to 80%. The model validation performance is generally lower than the performance in the testing set. However, the performance of ANN and SVM is still acceptable, with MAE 1.074 and 1.088, denoting that the performance of SVM and ANN initially meets the standard requirement.

Table 7 Validation results of ANN and SVM models
Full size table

Figure 9 depicts the distribution of absolute bias from the SVM and ANN models. The absolute bias denotes the absolute value of the difference between the model distance and the real distance. From the perspective of the SVM model, nearly 21% of the bias was larger than 1 m. Only 7% of bias was between 1 and 2 m. The bias among 2 m to 3 m and 3 m to 4 m only took up 4% and 2% of the total sample, respectively. Nearly half of the samples were from 1 to 2 m. The bias distribution of ANN was similar to SVM, but the overall bias of ANN was slightly lower than SVM. In this regard, most biases were below or close to 1 m, and only nearly 7% to 8% of the samples had more than 4 m bias.

Fig. 9
figure 9

The absolute bias distribution of ANN and SVM model

Full size image

In the validation set, the location of the water leak mainly consisted of three ranges, including lower than 3 m, between 3.5 and 15 m, and larger than 15 m. The validation results categorized into different leak distances are shown in Table 8. Regarding ANN, the model reached 88.02% accuracy for leaks within the range below 3.5 m and 82.76% accuracy for leaks within the range of 3.5 m to 15 m. However, the localization accuracy was decreased to 48.89% in the leak distance larger than 15 m. When the leak distance was lower than 15 m, MAE in other points was all under or close to 1 m. Regarding SVM, most leaks between 3.5 and 15 m have been correctly predicted, with 94.83% accuracy. Regarding leaks lower than 3.5 m, SVM achieved over 86.83% accuracy. However, the model was invalid in finding leaks larger than 15 m, with only 28.89% accuracy. When the distances of leaks were lower than 15 m, MAE values were all below 0.51. When the distances of leaks were larger than 15 m, the MAE value was larger than the value in other points, with 4.43.

Table 8 The validation result from the perspective of leak distance
Full size table

5 Discussion

The validation results show that ANN and SVM reach nearly 80% accuracy and the MAE close to 1 m. However, it is worth noting that other studies have achieved a higher localization performance. For instance, Candelieri et al. (2014b) have developed SVM and achieved nearly 98% accuracy. Besides, Fan and Yu (2021) also developed a WDN machine learning model with over 83% localization accuracy. Though previous models reached high-level prediction accuracy, most were conducted based on hypothetical conditions or simulated experiments. The modeling and validation data are characterized by clarity and less noise. This controlled setting may explain the higher prediction accuracy they achieved.

In contrast, when the laboratory-based model is applied to real-world scenarios, its performance may significantly deteriorate. Real-world conditions introduce various complexities and uncertainties that are not present in controlled laboratory settings, leading to decreased model performance. The performance of the laboratory-based model was significantly deteriorate when applied to other scenarios (Terao and Mita 2008; Tariq et al. 2021a). It is crucial to consider the limitations and potential performance degradation when comparing laboratory-based models to field-experiment-based models. Thus, the proposed models still demonstrate their applicability in accurately localizing leaks in real-world scenarios.

Regarding leak distance, both models demonstrate limited performance in finding leaks at long distances (larger than 15 m). This is caused by the attenuation of the acoustic signal during propagation. As the acoustic signal travels longer distances, it gradually weakens and loses its strength, making it more challenging for the models to identify and accurately locate leaks (Muggleton and Brennan 2004; Almeida et al. 2015). Similarly, Bui Quy and Kim (2020) also find difficulty locating pipeline leaks influenced by attenuation. Regarding accuracy using the mean absolute error (MAE) and the root mean square error (RMSE), the ANN and SVM models demonstrated comparable levels of accuracy.

6 Conclusions

This study adopted an acoustic methodology, using the Micro-electromechanical System (MEMS) accelerometer to localize pipe leaks in the Hong Kong water distribution network. First, field experiments were conducted to collect accelerometer signals. Subsequently, backward selection was respectively applied to ANN and SVM models for feature selection. As a result, four features were selected for the ANN model, while the SVM model utilized fifteen features. Through model optimizing experiments, parameters of ANN and SVM were finalized, reaching the optimum performance. Finally, models have been tested and validated through various perspectives.

According to modeling results, ANN and SVM reach promising performance on the testing set, with over 80% accuracy (86.25% for ANN; 80.67% for SVM), and MAE lower than 1 m (0.858 for ANN; 0.95 for SVM). However, the model performance decreased in the validation cases, indicating that models have an encouraging result when finding long-distance leaks. Overall, the above results have proved that the applicability of implementing MEMS accelerometer signals in localizing water pipe leaks, which reveals the potential of applying machine learning models, ANN and SVM, to pinpoint water pipe leaks.

However, certain limitations still hinder the validity of current models. First, the experiments were conducted in the city center, and the maximum detection range of the method in real situations has not been thoroughly tested. Second, because of the limitation of the collected dataset, the model cannot correctly handle the long-distance leaks. Third, the localization accuracy can be further improved by utilizing larger databases and enhancing data. Thus, future research should investigate using MEMS accelerometers that can be permanently installed and enable wireless remote distance signal transmission. Transfer learning algorithms can be used in water leak localization, which might help to combine and best use the previous models and water pipe leak datasets.