Abstract
Anthropogenically influenced transboundary catchment areas require an appropriately adapted exposure modelling. In such catchments, water management decisions strongly influence and override natural river hydrology. We adapted the existing exposure assessment model GREAT-ER to better represent artificially overprinted hydrological conditions in the simulations. Changes in flow directions and emission routes depending on boundary conditions can be taken into account by the adopted approach. The approach was applied in a case study for the drug metformin in the cross-border catchment of Vecht (Germany/Netherlands). In the Dutch part, pumps to maintain necessary water levels and minimum flow rates during dry periods lead to a reversal of the (natural) flow directions and as a consequence to additional pollutant input from the Lower Rhine/Ijssel along with a spatial redistribution of emissions in the catchment area. The model results for the pharmaceutical product metformin show plausible concentration patterns that are consistent with both monitoring results and literature findings at mean discharges and the effects of the changed hydrology in times of low natural discharges, namely an increase in polluted river sections under dry conditions due to the pumping activities. The adapted methodology allows for realistic application of the GREAT-ER model in anthropogenically modified catchments. The approach can be used in similar catchments worldwide for more realistic aquatic exposure assessment.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
River basin management in densely populated regions is a difficult and challenging task. Surface waters fulfil numerous, often competing functions. Wiering et al. (2010) state that integrative goals of river basin management are characterised by the connection and combination of different aspects of water systems, such as water quality and water quantity. Integrative river basin management also puts forth the need for communication and cooperation between water management and other policy domains such as spatial planning, agriculture, housing or nature conservation. Since river basins not only stretch out over geographical but also administrative borders, they can be taken as unit for cooperation among different regulators and stakeholders. For large rivers in Europe, cross-border work has been common practice for years. For example, the International Commission for the Protection of the Rhine (ICPR) was already founded in 1950. Since the beginning of the new millennium, the Water Framework Directive (WFD, Directive 2000/60/EC 2000) and the European Flood Risk Directive (EFD, Directive on the assessment and management of flood risks; 2007/60/EC) are additionally calling for this cross-border practice. Especially the WFD strongly influences both national and regional water policy practices. In the WFD, river basin means “the area of land from which all surface run-off flows through a sequence of streams, rivers and, possibly, lakes into the sea at a single river mouth, estuary or delta” (art 2(13)). In terms of the WFD, it is therefore necessary to move towards transboundary, catchment-related risk assessment replacing old-fashioned national approaches within country borders (Coppens et al. 2015; Vissers et al. 2017).
The main subjective of the WFD is the good status of European water bodies including the good chemical status of European surface waters (EU 2000). The directive constitutes a legal framework that imposes the protection of common water resources on European states (Tsakiris 2015; Zacharias et al. 2020). In this context, the first version of the WFD listed 45 priority substances in annex X of the directive. Exposure and risk assessment of micro-pollutants such as pharmaceuticals and antibiotics followed by development and implementation of reduction measures for critical compounds are necessary to achieve the goals of the WFD (Kallis and Butler 2001; Allan et al. 2006). A prerequisite for the definition and implementation of mitigation measures is knowledge of the exposure concentrations of these substances in the environment. This has led to large monitoring efforts for so-called emerging contaminants (Richardson 2009; Gogoi et al. 2018). Obviously, a permanent, basin-wide and comprehensive monitoring of the 45 priority substances and of thousands of potentially relevant micro-contaminants is impossible for European surface waters. At this point, models can be a valuable aid for exposure and risk assessment, filling knowledge gaps and supporting existing monitoring efforts (Boxhall et al. 2014). The GREAT-ER model (Geo-referenced Exposure Assessment Tool for European Rivers; program and more details available at: https://tinyurl.com/y8h9y8rq), for example, is a spatially resolved fate model that predicts chemical exposure at river basin level (Kehrein et al. 2015; Lämmchen et al. 2021). It was developed within the framework of the European ecotoxicological risk assessment system (Feijtel et al. 1998) and has been successfully applied to simulate a wide range of pollutants in several river basins all over the world (Hüffmeyer et al. 2009; Alder et al. 2010; Aldekoa et al. 2013; Archundia et al. 2018; Duarte et al. 2021). In this context, modelling of transboundary catchments imposes particular challenges to overcome such as country-specific administrative structures and water management systems (e.g., Watson 2004; Podimata and Yannopoulos 2013) or availability of required input data. For modelling of pharmaceuticals, other aspects like differences in consumption patterns and drug regulations have to be taken into account, where a main obstacle to modelling studies of micropollutants in transboundary catchments is the restricted access to detailed national and regional consumption data (Tiedeken et al. 2017).
Exposure models for surface waters always require a realistic representation of the hydrological conditions on the selected spatial and temporal scale. This is especially difficult in anthropogenic regulated river systems, in which numerous canals, sluices, weirs and pumping stations override natural river flow conditions (Gregory 2006; Lespez et al. 2015). Here, river flow extremes are attenuated and flow dynamics are reduced to prevent from negative consequences such as flooding or drought. Existing hydrological models were mostly developed to represent natural water flow (Schowanek and Webb 2002), and were thus not designed for consideration of flow regime regulations driven by requirements for shipping, flood control, drainage or irrigation. This is also the case with the standard hydrological representation in the GREAT-ER model (Kehrein et al. 2015).
Chemical exposure in strongly canalized river systems cannot sufficiently be simulated when only natural flow is considered. For example, in large parts of the Dutch canal system, distribution of emissions is known to be quite different during summer time compared to the rest of the year (Fiselier et al. 1992; Prinsen and Becker 2011; Coppens et al. 2015). Many of the challenges faced here also apply for similar catchments, for example in Belgium (Verhelst et al. 2018) or in numerous potentially similarly influenced catchments worldwide (Gregory 2006). To improve the prediction accuracy of aqueous exposure models in general, and GREAT-ER in particular, coverage of these aspects must be enabled.
Therefore, the aim of this study was the adaptation of the GREAT-ER 4.1 model environment (Lämmchen et al. 2021) to allow for realistic representation of the hydrological situation in highly anthropogenic regulated cross-border basins. The adapted methodology for the first time opens up the possibility of applying GREAT-ER in strongly anthropogenic modified catchments which are expected to increase worldwide (Vitousek et al. 1997; Petts 2007; Scorpio et al. 2018). The applicability of the adapted exposure model is demonstrated by a case study for the heavily used pharmaceutical ingredient metformin in the German-Dutch cross-border catchment of Vecht. By combining more realistic water quantity information with regionalized human consumption data, model simulation results can effectively contribute to integrated cross-border river basin management.
2 GREAT-ER Model
In principle, the GREAT-ER model consists of three components. The hydrological network, the emission model and the fate model. Here, the focus is on the hydrological parameterization of the river network. A detailed description of the other functions of the model and its application can be found in Kehrein et al. (2015) and Lämmchen et al. (2021).
2.1 General Hydrological Representation
The model’s backbone is formed by a GIS-based hydrological network, which is created during a number of preprocessing steps. Hereby, the surface water network is discretized into river segments with a length of less than 2 km. Each segment holds attributes about flow direction, flow velocity, discharge and others, which are used to calculate the chemical fate and concentration. To do so, a consistent water balance across the whole river network for three defined flow conditions, namely the long-term annual average stream flow (MQ), the long-term annual low flow (MNQ) and the 50-percent-flow-percentile (Q50) is created. The GREAT-ER preprocessing provides a semi-automatic procedure for estimating runoff in each segment. We use grid data for effective precipitation in the entire catchment from available data sources or established rainfall-runoff models. Sub-catchments for all river segments are derived from the digital elevation model (DEM) by Lehner et al. (2008) known as HydroSHEDS.
For each sub-catchment, the total runoff under MQ, MNQ and Q50 conditions is estimated by weighted averaging of the grid data on effective precipitation. The slope extracted from the DEM is then used to allocate runoff to the next downstream segment. These values are added up along the flow path to give cumulated runoff for each hydrological condition in each segment. Local discharge from WWTPs (Wastewater treatment plants) as well as water abstraction (e.g., for drinking water or irrigation) are also explicitly considered in this water balance if quantitative information was available from local water authorities. Actual average daily river flow is usually available from data series of gauging stations covering differently large sub-catchments. Estimated river flow values are compared and calibrated against the available long-term gauging data. The more gauges are available for this purpose, the more accurate the final water balance will be.
This procedure leads to a consistent water balance in the whole catchment for the respective hydrologic situation. Although situations with the same flow condition in the whole catchment at the same time will hardly occur in reality (see also Supplementary Material (SM) Fig. SM1), this approach forms a standardized, solid basis for spatially distributed exposure assessment.
2.2 Emission Model
In general, the model distinguishes between domestic and hospital consumption of pharmaceuticals. The load of domestic usage is calculated based on the number of inhabitants connected to a WWTP and a specific compound per-capita consumption rate. This is based on the assumption that the inhabitants connected to a certain WWTP constitute a representative sub-group of the general population with respect to the prescription frequency of the pharmaceutical. Similarly, the hospital consumption is calculated by considering the number of beds in hospitals that are connected to the WWTP and a specific compound per-bed consumption rate. Since most pharmaceuticals are metabolized after uptake, only a certain percentage is included in the calculations. The final load emitted into the receiving water is reduced based on the removal efficiency of the compound during the treatment process at the WWTP and is then implemented as a point source in the river network. Other loss processes, for example, in-sewer transformation processes are not considered.
In addition, GREAT-ER 4.1 allows for introducing artificial emission points at inlets where substance loads cannot be individually simulated by the model, but must be provided as constant external input. The loads (L) at such inlet points are estimated from monitoring data at the nearest upstream sampling site in the inflowing waterbody, an approach that has already been used elsewhere (Coppens et al. 2015).
The general equation for estimation of the average load at the monitoring site Lmoni is as follows:
where n is the number of total measurements, Qi is the river flow at the time of each measurement, and Ci is the concentration of the substance at measurement i.
In case the monitoring site is located distant from the catchment inlet, it can be necessary to consider the effect of loss processes along the travel distance. For this purpose, loss processes of the individual chemical need to be described by a cumulative pseudo first-order loss rate constant k. The load is then reduced according to the following equation:
with t being the travel time from the monitoring site to the catchment inlet.
The situation is even more complicated when additional emissions occur between the monitoring site and the catchment inlet. In this case, the contributions of the respective WWTPs are estimated with the usual per-capita approach (Lämmchen et al. 2021). Reduction through loss processes is considered as described above, whereby the individual travel times of the different WWTP load contributions (ti) are applied.
where capi is the number of inhabitants treated by WWTPi, PCC is the average per capita emission rate, R is the (constant) percent removal of the substance in WWTPs, k is the lumped first-order instream loss rate and ti is the individual travel time from WWTPi to the inlet. The total emission at the respective inlet is then calculated from the sum of all relevant terms.
2.3 Fate Model
After entering the water system, concentrations are calculated by dividing the total load at the beginning of a segment by the river flow defined by the hydrological model. Mass flows are propagated through the network based on flow directions, flow velocities and discharges. Loss processes such as sedimentation, photolysis and biodegradation are taken into account as first-order reduction along the travel distance analogously to Eq. (2).
In principle, natural variability of environmental parameters, uncertainty of substance parameters and temporal fluctuation of consumption patterns could be considered by the probabilistic Monte Carlo routine implemented in GREAT-ER (Lämmchen et al. 2021). However, this routine is not yet applicable to other than natural river flow situations, and thus, not used in the case study.
2.4 Model Output
Simulation results provide an overview of the spatial variability of surface water contaminations and can be used to easily identify river sites with increased concentrations above a defined target value (e.g., a given environmental quality standard). GREAT-ER additionally allows the simulation of management scenarios for selected reduction measures and a priori evaluation of their effectiveness. Results are primarily presented as color-coded maps or concentration profiles along a selected river course.
GREAT-ER finally allows for performing numerous statistical analyses. This includes, for example, sorting all river segments by their concentration in ascending order along with the cumulated flow length resulting in a cumulative distribution function (CDFs) of the concentrations.
3 Adaptation of the GREAT-ER Structure
GREAT-ER usually represents annual average situations in terms of substance loads and uses a closed water balance for a specific hydrological situation such as MNQ or MQ. The GREAT-ER standard representation is based on the directed river network graph given by the underlying river network. To propagate loads and emissions through the river network system, directional data in form of ‘from-to-relationships’ must be stored at the nodes in the river system.
In anthropogenically influenced catchments, however, this standard approach cannot always be applied. For example, it may happen that due to water management-based pumping activities (e.g., for irrigation purposes) in some parts of the river system the flow directions occasionally change. However, the directed river network is currently represented by a static database structure, and thus, such changes cannot be simply managed by flipping the flow directions on a case-by-case procedure. Consequently, two representations of the catchment have been set up representing the different situations of flow directions during days with and without pumping activities in separate databases. One database reflects regular average flow conditions without artificial pumping and the second one represents the periods, where water management instruments partly override natural flow conditions. Each database contains a copy of the basic hydrological network considering respective flow direction changes. Flow rate calibration against data from gauging stations were carried out individually for the two databases. Reference values were calculated individually for both situations, meaning that values representative for the respective scenario were selectively aggregated.
4 Case Study
To demonstrate the capability of the advanced GREAT-ER approach for realistic resemblance of complex hydrological conditions an exemplary case study for the diabetic drug Metformin in the Vecht catchment has been performed.
4.1 Substance Information Metformin
Metformin (CAS number: 657-24-9) is a highly consumed anti-diabetic, with over 600 million DDD (2 g; WHO 2020) prescriptions per year in Germany (Schwabe et al. 2019) and over 100 million DDD in the Netherlands (RIVM 2014). For the simulations, regionalized prescription data (based on sales data on postcode level) from IQVIA (https://www.iqvia.com/) and the Dutch Foundation for Pharmaceutical Statistics (SFK; https://www.sfk.nl/) for the years 2016 to 2018 were used as input. This results in an average per-capita consumption of 13.6 g/a in Germany and 19.8 g/a in the Netherlands, of which approximately 70 % of this administered dose is excreted from the human body as parent drug, mainly via urine, entering the wastewater pathway (Moffart et al. 2011). The hospital consumption figures were obtained from several cooperating hospitals in the study area. From these figures, a national or regional per patient consumption was calculated and assigned to the German (0.26 kg/a/bed) and the Dutch hospitals (0.18 kg/a/bed), respectively. Even though the individual administration rate in hospitals is significantly higher than in the general population, the overall contribution of hospitals to total emission is almost negligible (3.3 %). The detailed simulation parameters can be found in Table 1.
The combination of large prescription numbers with a high excretion rate leads to high concentrations in raw wastewater of up to 129 mg/L (Scheurer et al. 2009; Van Nuijs et al. 2010). Fortunately, Metformin is efficiently removed in treatment plants by 90 % for lagoon and wetland treatment plants (Auvinen et al. 2017), and 97.5 and 98 % for biofilm (Oosterhuis et al. 2013) and activated sludge plants (Oosterhuis et al. 2013; Gaffney et al. 2017), respectively. The Kd value was found to be 19 L/kg (Scheurer et al. 2012). Metformin is also not fully persistent in surface water according to the PBT assessment under REACh (t1/2 < 40 days). For example, oxidation by OH radicals is reported to occur with an estimated half-life of 24 days (Neamtu et al. 2014) to 28.3 days (Straub et al. 2019) under simulated sunlight conditions. Nevertheless, Metformin is almost ubiquitously detected in surface waters (Scheurer et al. 2009; Vulliet and Cren-Olive 2011) in concentrations of up to 1700 ng/L.
To date, no legally binding environmental quality standard (EQS) has been set. Proposed values range from 88 µg/L (Godoy et al. 2018) up to 780 µg/L (RIVM 2014). An environmental risk assessment document of one of the major producers reports a PNEC (predicted no-effect concentration) value as low as 10 µg/L (AstraZeneca 2017). This is still at least factor six higher than the above reported surface water concentrations.
For model evaluation, we used monitoring data from a 2018/2019 sampling campaign (van Heijnsbergen, in preparation), where 116 samples from 32 sites within the Vecht catchment were analysed for metformin with a standard combination of high-performance liquid chromatography and mass spectrometry (LC/MS) (Trautwein and Kümmerer 2011; Scheurer et al. 2012).
4.2 Catchment Area
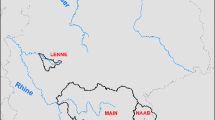
The study area comprises the catchment area of the German-Dutch border river Vecht (Fig. 1), a tributary of the Dutch river Ijssel.
The cross-border Vecht catchment in Germany and the Netherlands. Rivers are indicated as blue lines, while canals are given as framed cyan lines. Blue arrows symbolize the natural flow direction in the Vecht River. Cyan arrows with red frame symbolize artificially changed flow directions due to pumping activities in summer (at Zutphen) and year-round (at Enschede)
The cumulated length of surface waters in the catchment sums up to 2,760 km with approximately 2,000 km of rivers and around 760 km of canal-like structures. The longest possible flow path through this network is about 187 km considering the way from the spring of the Vecht to its outlet point north of Zwolle. A summary of important catchment characteristics can be found in Table 2.
The only relevant lake in the catchment area is Lake Vecht with an average depth of 1.67 m and a surface area of 160,000 m² (Messager et al. 2016). The lake serves as an artificial sediment trap (NLWKN 2012), which also makes it a sink for substances adsorbed to suspended matter. The residence time of water in the lake is between 11 h and 4 days, depending on the actual discharge conditions in Vecht.
In the past, Vecht used to have natural flow conditions with relatively high peaks in wet periods and sometimes extremely low water levels in summer (Lulofs and Coenen 2007), mostly in the period between May and September. Today, this is still the case in the German part, while on the Dutch side, Vecht has been canalized from 1896 on, when it was declared a state waterway. Because of the intensive straightening, water levels in summer were lowered while flow rate and velocity increased during wet seasons (Lulofs and Coenen 2007). In order to maintain ecosystem services for tourism, shipping and irrigation provided by Vecht, a minimum water level is necessary. Therefore, in summer water from the Ijssel is pumped into the Vecht basin via the Twente Canal (RWS 2017). Pumping stations are located at Delden (near Enschede) and Eefde near Zutphen (Fig. 1). The former is working almost all year round to prevent the city of Enschede from being flooded, while Eefde is running only during the dry periods that can occur between March and November. The main canal waterways in the Dutch part of the catchment are designed to handle up to 8 m³/s of additional water from pumping activities. Surplus water is either distributed via the canal system to the numerous withdrawal points installed for irrigation purposes or routed into Vecht main river. Flow direction in large parts of the catchment is reversed and river flow is strongly affected when the pumps are in action.
4.3 Hydrological Parameterisation
The hydrological representation in the model has two prerequisites. First, the river network must be topologically sound with defined outlet points, so that it is possible to traverse through the river system (along defined flow directions) from any point in the river network to the designated outlets. Secondly, stream flow information must be available for each river segment. Due to the transboundary nature of the Vecht catchment river network, data from two German authorities (NLWKN, LANUV) and three Dutch water boards (WVS, WRIJ, WDOD) had to be collected. As there are no international or even national standards, available data substantially differ in the level of detail leading to barely compatible datasets. More details on how the river network was created under these boundary conditions can be found in Fig. SM 2.
Average effective precipitation data for Germany was taken from the Hydrological Atlas (HAD; Leibundgut and Kern 2003) for the period from 1960 to 1990. The HAD offers one grid (1 × 1 km) each for low flow and average conditions. For the Dutch part of the catchment, however, comparable data in a ready-to-use format are not publicly available. Therefore, based on the assumption that long-term effective precipitation patterns do not differ greatly over short distances in this relatively flat landscape, the HAD runoff grid was extrapolated across the German border to the Dutch area. Resulting uncertainties in the river flow estimation from not taking into account different soil properties are compensated for in the calibration procedure.
The resulting MQ and MNQ estimations were calibrated against long-term data from 43 gauging stations, which are evenly distributed across the Netherlands and Germany, considering daily discharges from 2000 to 2017. However, at some of the Dutch gauges (e.g., Almen gauge) negative daily flow rates are reported when the flow direction is reversed during the dry season making calibration of the dry summer scenario with the original data impossible. Therefore, daily flow data from the gauging stations were separated and assigned to one of the two hydrological scenarios.
4.4 Regional-specific Pumping Activities
For this case study, two different hydrological conditions during dry summer days (equivalent to MNQ conditions) and average humid days (equivalent to MQ conditions) are considered and represented in separate databases. The latter database reflects regular average flow conditions (Qavg) without artificial pumping and the former represents the dry-summer-period (Qlow), where under low flow conditions water is pumped from the Ijssel into the Vecht catchment. Pumping data during periods of water compensation are specified in the ‘Waterakkoord Twenthekanalen / Overijsselsche Vecht’ (RWS 2017). The gauging station ‘Almen’ in the Twente Canal is located next to the Eefde pumping system (Fig. 1) and is used to monitor the effect of the pumping action on the calibration of the two different hydrological scenarios. First, pumping days were defined as to when the pump was active for at least 12 h supplying 1 m3/s of Ijssel water or more. Secondly, hourly flow data were separated into the two scenarios and re-aggregated to give estimates for MQ, Q50 and MNQ representing the respective situation. Negative values were interpreted as flow rates in opposite direction to natural flow. The resulting dataset was used for calibration of MQ, Q50 and MNQ in the two scenario databases Qavg and Qlow. The specific simulation parameters for Qlow can be found in the following Table 3.
In a similar approach, Coppens et al. (2015) chose the driest and wettest periods of the year, i.e., from July to September and October to December, and selected data from extreme years for both conditions (2003 and 1998, respectively) to predict the maximum and minimum concentrations that can be expected. The Qavg and Qlow set-up is similar, but we think closer to reality, since the year is divided into the period from November to March and from March to November with regard to pumping activities and not to seasons.
4.5 Inflow from the Ijssel
GREAT-ER usually propagates emissions from all known contaminant sources through the whole river basin network starting with the segments at the individual springs down to the outlet point(s). In contrast to country-based approaches (Coppens et al. 2015; Vissers et al. 2017), this catchment approach normally avoids uncertainties attributed to the inflow from upstream areas originating from other countries. Without inclusion of these areas into the model, such upstream emissions can hardly be estimated a priori, but have to be estimated from monitoring data. The Vecht catchment in our study is represented by the complete hydrological network including all source regions and three outlets (Zwaarte Water, Ems-Vecht Canal, Twente Canal). However, due to pumping action under Qlow, Ijssel water enters the catchment turning the former outlet point Twente-Canal into a potential inflow point for chemicals from the Ijssel. Realistic parameterization of this situation constitutes a major challenge in the simulations.
The LANUV operates a gauging and monitoring station in the Rhine near Lobith directly at the Dutch-German border, from which concentration data of several hundred substances including metformin are available (ELWAS 2020). The average metformin load at the monitoring site was estimated from these data using Eq. (1). Since input occurs only under active pumping, we considered only concentration data from sampling days when the dry summer scenario applied in the study area resulted in 35 samples in the period from 2013 to 2019.
Via the Nederrijn and Ijssel, Rhine water reaches the Twente Canal after about 50 km flow length corresponding to a travel time (t) of 10–15 h (RWS 2020). Before entering the Twente Canal near Zutphen, wastewater from WWTP Etten (136,000 connected inhabitants), Nieuwgraaf (177,000) and 8 smaller treatment plants (145,000 connected inhabitants) is introducing additional wastewater from 458,000 inhabitants. Loss processes along the flow path are taken into account with the same first-order loss rate k that is used as simulation parameter in the GREAT-ER model. To estimate the substance loads from these point sources at the Twente Canal inlet, Eqs. (2) and (3) were applied.
In the Qlow database, a virtual emission source was then placed at the inlet near Zutphen, which provided the estimated load via the Ijssel inflow in the simulations according to the formula already introduced.
5 Results and Discussion
5.1 Average Flow Scenario
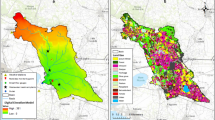
Figure 2A shows simulated mean predicted environmental concentrations (PEC) in the whole river basin in the standard Qavg scenario assuming MQ discharge conditions. Predicted mean concentrations are almost completely within the range of 100 ng/L – 1,700 ng/L, which is in agreement with observations from other studies (Scheurer et al. 2012). Higher concentrations are found at the outlets of WWTPs with unfavorable dilution ratios. For example, predicted concentrations downstream of WWTPs Enschede-West, Hengelo or Oldenzaal reach values of more than 2,000 ng/L. Overall, 961 km of river segments (making up 35 % of the total river network) are predicted to exhibit metformin concentrations larger than zero. In contrast to large-scale, national simulations (e.g., Coppens et al. 2015), the model can identify river reaches with potential high concentrations also in small brooks serving as receiving waters. Such information is important when nature protection is not restricted to the main rivers in the basin. It supports planning of monitoring campaigns and development of targeted local reduction measures or regional mitigation strategies.
In general, simulated concentrations are higher in the Netherlands due to the higher population density. This effect is intensified by the fact that the per capita consumption of metformin in the Dutch part of the catchment is 45 % higher than in the German part (based on IQVIA and SFK numbers). Nevertheless, mean PEC values do not exceed the proposed EQS values in none of the countries in the average scenario, indicating that the substance does currently not carry a substantial aquatic risk potential. At this point, it has to be emphasized that risk assessment should not only be based on single values from grab samples or mean values from model simulations. Natural flow variability can cause significant concentration differences over time even when the assumption of more or less constant mass flow of a pharmaceutical compound was true.
5.2 Dry Summer Scenario
In the dry summer scenario, simulated metformin concentrations show significant differences compared to the average scenario due to the pumping activities along with generally lower flow values in summer. The respective color-coded concentration map can be found in SM (Fig. SM3). For example, the metformin concentration at the outlet Zwarte Water increases from 450 ng/L to 1300 ng/L. The effect of the pumping action can best be seen by the difference in estimated loads between the two scenarios (Fig. 2B).
A major difference occurs at the Twente Canal, which in the dry summer scenario serves as additional metformin source. Applying Eq. (1) to (3), an additional input of 0.28 kg metformin per pumping day was estimated with metformin concentrations at the confluence of around 700 ng/L. This inflowing water is either distributed for irrigation purposes or remains in the river system to secure water levels necessary for shipping. As a consequence, some parts of the catchment that are pristine under average conditions experience substance loads in the Qlow scenario through the re-routing of Ijssel water into the Vecht catchment. Respective segments appear blue in Fig. 2A (zero concentration), but colored in Fig. 2B due to the corresponding daily loads. Metformin concentrations in these segments are estimated to be partly above 2 µg/L, which is graphically highlighted in Fig. SM 4.
No load differences (grey segments in Fig. 2B) occur at Enschede, since here pumping is consistently maintained all-year long. The same applies to all other segments that are pristine or equally contaminated in both scenarios, e.g., the more natural part of the catchment in Germany.
Surprisingly, metformin loads at the outlet are lower in the Qlow scenario than in Qavg (Fig. 2B) despite the additional input from the Ijssel. First, more than 70 % of the additional metformin load from the Ijssel inflow in the dry period do not remain in the water body (RWS 2017), since the water is used for irrigation. This mass transfer into ditches or directly onto agricultural fields is explicitly considered in the model as localized system outflow. The remaining Ijssel water fraction is used to maintain sufficiently high water levels for navigation in the Dutch part of the catchment. Due to the changing flow directions, this results in large-scale metformin load redistributions (Fig. 2B). Loads that enter the Vecht River under Qavg conditions ending up in canals under Qlow result in higher concentrations in some of the channels connected to the Vecht, e.g., the Meppeldiep or the Overijssels Canal (marked in orange). These concentration shifts had also been observed by Coppens et al. (2015), but could not be investigated in detail due to the lower spatial resolution of their model approach. In addition, slower flow velocity in summer results in higher residence times of metformin and associated slightly increased degradation.
It must be pointed out that lower emissions do not automatically translate into lower concentrations. Due to the much higher flow rates under average conditions (approximately factor 10, see Table 1), concentrations are expected to be significantly lower only by the dilution effect. However, the decrease in metformin PEC values from 1300 ng/L to 450 ng/L is much smaller (factor three). This is a good example of how the model can explain respective monitoring results by considering the effects of overlying processes in a geo-referenced approach.
A: Predicted environmental concentrations (PEC) of metformin in the Vecht catchment for average flow conditions (MQ) within the Qavg scenario. WWTPs in the catchment varying in size with regard to the connected inhabitants. Marked as red crosses are the hospitals in the catchment area. B: Difference of simulated metformin loads between dry-summer-scenario Qlow and average-flow-scenario (2 A). Negative values indicate higher loads in the average scenario. Arrows mark the specific flow directions in Qlow
To compare the spatial concentration distribution between the two scenarios, Fig. 3 shows the cumulative distribution function (CDF) of the spatially resolved predicted concentrations. Data points indicate the fraction of total river length in the catchment below the respective concentration. Therefore, the outmost left data point specifies the fraction of total river length with zero concentrations. This means that in the Vecht catchment approx. 62 % of the river length is not polluted with metformin under average conditions, while in Qlow this fraction reduces to 49 %. This difference is a result from water redistribution due to the pumping activities and irrigation (as highlighted in Fig. SM 4).
In general, PEC values are shifted towards higher concentrations in the dry summer scenario. For example, in the average scenario, 70 % of total river length exhibits metformin concentrations below 500 ng/L, while in the dry summer scenario, this fraction is only 52.5 %. This result is a combination of the effect of lower flow values and additional metformin input from the Ijssel.
Highest concentrations of up to 8 µg/L (Fig. 3) are predicted in small creeks serving as receiving river for WWTP effluents (see also red marked stretches in Fig. SM 3), since they offer a very unfavorable dilution ratio with effluent fractions of more than 80 % during dry periods. These values are close to the proposed PNEC value of 10 µg/L (AstraZeneca 2017) indicating the potential for temporary risk.
5.3 Model Evaluation
Results of the two scenarios were compared with available monitoring data. Measurements were carried out over a period of 12 months so that data under conditions representative for both of the two hydrological scenarios could be obtained. According to the available pumping information at the sampling day, monitoring data were assigned to one of the scenarios. Figure 4 shows the longitudinal PEC profile along a 187 km flow path starting at the spring of the Steinfurter Aa to the Vecht entering the Ijssel at Zwarte Water along with multiple monitoring data from 11 sampling sites.
First, it can be seen, that measured concentrations at the individual sites vary considerably for both conditions due to natural flow variability. For this reason, a maximum deviation of factor three is generally accepted as quality criterion for good agreement between monitoring and modelling results (Ort et al. 2009; Verlicchi et al. 2014; Gimeno et al. 2017). This region is displayed as shaded area around the mean PEC in Fig. 4. Most of the data points are covered by this region in both scenarios indicating that the model parameterization allows for realistic predictions of metformin concentrations in the Vecht catchment.
Both scenarios show a concentration drop at km 75, which is caused by Lake Vecht. The calculated residence time of up to 4 days along with the partitioning coefficient between water and suspended particles (Kd) of 19 L/Kg (Scheurer et al. 2012) is sufficient to reduce metformin by sedimentation. Directly after the lake, a WWTP is causing concentrations to rise again.
At km 118, the additional load from the Twente Canal results in a concentration increase in the Qlow scenario. Another WWTP at km 119 introduces metformin in both scenarios causing the concentration to rise. This is covered in Qlow by the input from the Twente Canal, because the treatment plant is too close to this point and can be mistaken otherwise.
The accuracy of the model predictions can be assessed by comparing PEC values with measured environmental concentrations (MEC). According to the environmental conditions during sampling, data were assigned to one of the two scenarios resulting in 53 measured values for Qlow and 51 measured values for Qavg. However, statistical evaluation is difficult, since MEC values from grab samples at the very same monitoring site are affected by the natural variability of the flow rate (Factor 3, see Fig. 4). Model simulations represent the hypothetical situation of average flow conditions in the whole catchment and are, thus, hardly comparable to single measurements. Instead, the median of all metformin data at each of the 21 sites was used to calculate the correlation coefficient R² for the two simulation runs. The R² values are 0.57 for Qavg and 0.47 for Qlow with a significance of p < 0.005. The corresponding graphs are shown in the SM (Fig. SM5).
Secondly, in order to evaluate the degree of realism of the summer scenario, we compared this scenario with the standard simulation setup (Qavg), but under MNQ conditions, i.e., a simulation in which pumping activities and reversed flow directions are not included (QMNQ). The comparison of these two simulation runs demonstrates the necessity of model adaptations. From Fig. 5, it can be seen that the standard GREAT-ER run QMNQ clearly underestimates measured environmental concentrations whereas the adapted model in the dry summer scenario Qlow is in much better accordance with the monitoring data.
This result again confirms the assumption that during Qlow a redistribution of loads into canals and onto agricultural land takes place, so that the major part of the additional Ijssel emissions does not end up in the Vecht (Fig. 2B). Since these processes are not taken into account in QMNQ, a much higher concentration is incorrectly predicted in Vecht, despite the lack of input from the Ijssel.
The adequacy of the assumptions made can be checked by calculating the mean squared error MSE of the PEC from the MEC using the following formula:
where CMECi is the measured concentration at monitoring site i and CPECi is the corresponding predicted concentration.
The result is a calculated MSE of 0.176 µg/L for Qlow and 0.982 µg/L QMNQ, supporting the improvements achieved with the adaptions made within Qlow.
6 Conclusions
Existing models for exposure assessment of chemicals in surface waters are usually not prepared to represent hydrological conditions that are strongly affected by anthropogenic interventions in a realistic way. We adapted the existing model GREAT-ER to reflect such a complex hydrology by implementing different databases for distinct hydrological scenarios. The usefulness of the approach was demonstrated in a case study for metformin in the German-Dutch cross-border catchment of the River Vecht. It was shown that metformin concentration data from samples taken in the dry summer season are much better represented by model simulations adapted to the specific situation of changing flow directions caused by pumping actions in the Dutch part of the catchment during summer. As a result, a significant part of previously pristine river segments of the catchment area is affected during these periods. The observed redistribution of pollution patterns in the Vecht catchment by the anthropogenic interventions is also relevant for other, possibly more hazardous substances.
The use of the GREAT-ER model in the modified application allows for more insight into these issues as compared to standard model approaches. The adapted methodology opens up the possibility for application of the GREAT-ER exposure model in anthropogenically modified catchments in a more realistic way. It can be used in other catchments worldwide, for which the challenges faced in the Vecht basin also apply. Additionally, anthropogenic overprinting of river systems may increase further, which makes inclusion of such influences into modeling approaches even more important.
Data Availability
The datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.
Code Availability
Current GREAT-ER model version can be downloaded under: https://www.usf.uni-osnabrueck.de/en/research/applied_systems_science/great_er_project.html.
References
Aldekoa J, Medici C, Osorio V, Pérez S, Marcé R, Barceló D, Francés F (2013) Modelling the emerging pollutant diclofenac with the GREAT-ER model: Application to the Llobregat River Basin. J Hazard Mater 263:207–213. https://doi.org/10.1016/j.jhazmat.2013.08.057
Alder AC, Schaffner C, Majewsky M, Klasmeier J, Fenner K (2010) Fate of β-blocker human pharmaceuticals in surface water: Comparison of measured and simulated concentrations in the Glatt Valley Watershed, Switzerland. Water Res 44:936–948. https://doi.org/10.1016/j.watres.2009.10.002
Allan IJ, Vrana B, Greenwood R, Mills GA, Knutsson J, Holmberg A, Guigues N, Fouillac AM, Laschi S (2006) Strategic monitoring for the European Water Framework Directive. TrAC - Trends Anal Chem 25:704–715. https://doi.org/10.1016/j.trac.2006.05.009
Archundia D, Boithias L, Duwig C, Morel MC, Flores Aviles G, Martins JMF (2018) Environmental fate and ecotoxicological risk of the antibiotic sulfamethoxazole across the Katari catchment (Bolivian Altiplano): Application of the GREAT-ER model. Sci Total Environ 622–623:1046–1055. https://doi.org/10.1016/j.scitotenv.2017.12.026
AstraZeneca (2017) Environmental risk assessment data metformin hydrochloride. https://www.astrazeneca.com/content/dam/az/our-company/Sustainability/2017/Metformin.pdf. Accessed 7 Dec 2020
Auvinen H, Havarn I, Hubau L, Vanserveren L, Gebhardt W, Linnemann V, Van Oirschot D, Du Laing G, Rosseau DPL (2017) Removal of pharmaceuticals by a pilot aerated sub-surface flow constructed wetland treating municipal and hospital wastewater. Ecol Eng 100:157–164. https://doi.org/10.1016/j.ecoleng.2016.12.031
Boxall ABA, Keller VDJ, Straub JO, Monteiro SC, Fussell R, Williams RJ (2014) Exploiting monitoring data in environmental exposure modelling and risk assessment of pharmaceuticals. Environ Int 73:176–185. https://doi.org/10.1016/j.envint.2014.07.018
Ching-Ling C, Lawrence XY, Hwei-Ling L, Chyun-Yu Y, Chang-Sha L, Chen-His C (2004) Biowaiver extension potential to BCS Class III high solubility-low permeability drugs: bridging evidence for metformin immediate-release tablet. Eur J Pharm Sci 22:297–304. https://doi.org/10.1016/j.ejps.2004.03.016
Coppens LJC, van Gils JAG, ter Laak TL, Raterman BW, van Wezel AP (2015) Towards spatially smart abatement of human pharmaceuticals in surface waters: Defining impact of sewage treatment plants on susceptible functions. Water Res 81:356–365. https://doi.org/10.1016/j.watres.2015.05.061
de Jesus Gaffney V, Cardoso VV, Cardoso E, Teixeira AP, Martins J, Benoliel MJ, Almeida CMM (2017) Occurrence and behaviour of pharmaceutical compounds in a Portuguese wastewater treatment plant: Removal efficiency through conventional treatment processes. Environ Sci Pollut Res 24:14717–14734. https://doi.org/10.1007/s11356-017-9012-7
Duarte DJ, Niebaum G, Lämmchen V, van Heijnsbergen E, Oldenkamp R, Hernandez-Leal L, Schmitt H, Ragas AMJ, Klasmeier J (2021) Ecological Risk Assessment of Pharmaceuticals in the Transboundary Vecht River (Germany/Netherlands). Environ Toxicol Chem. https://doi.org/10.1002/etc.5062
ELWAS (Elektronisches wasserwirtschaftliches Verbundsystem) (2020) www.elwasweb.nrw.de. Accessed 7 Dec 2020
EU (2000) EU Directive 2000/60/EC of the European Parliament and of the Council (Water Framework Directive) Establishing a Framework for Community Action in the Field of Water Policy. Off J Eur Communities OJ L327/1
Feijtel T, Boeije G, Matthies M, Young A, Morris G, Gandolfi C, Hansen B, Fox K, Matthijs E, Koch V, Schroder R, Cassani G, Schowanek D, Rosenblom J, Holt M (1998) Development of a geography-referenced regional exposure assessment tool for European rivers GREAT-ER. J Hazard Mater 61:59–65. https://doi.org/10.1016/S0304-3894(98)00108-3
Fiselier J, Klijn F, Duel H, Kwakernaak C (1992) The choice between desiccation of wetlands or the spread of Rhine water over The Netherlands. Wetl Ecol Manag 2(I/2):85–93. https://doi.org/10.1007/BF00178138
Gimeno P, Marcé L, Bosch l, Comas J, Corominas L (2017) Incorporating model uncertainty into the evaluation of interventions to reduce microcontaminant loads in rivers. Water Res 124:415–424. https://doi.org/10.1016/j.watres.2017.07.036
Godoy AA, Domingues I, Arsénia Nogueira AJ, Kummrow F (2018) Ecotoxicological effects, water quality standards and risk assessment for the anti-diabetic metformin. Environ Pollut 243:534–542. https://doi.org/10.1016/j.envpol.2018.09.031
Gogoi A, Mazumder P, Tyagi VK, Tushara Chaminda GG, An AK, Kumar M (2018) Occurrence and fate of emerging contaminants in water environment: A review. Groundw Sustain Dev 6:169–180. https://doi.org/10.1016/j.gsd.2017.12.009
Gregory KJ (2006) The human role in changing river channels. Geomorphology 79:172–191. https://doi.org/10.1016/j.geomorph.2006.06.018
Hüffmeyer N, Klasmeier J, Matthies M (2009) Geo-referenced modeling of zinc concentrations in the Ruhr River basin (Germany) using the model GREAT-ER. Sci Total Environ 407:2296–2305. https://doi.org/10.1016/j.scitotenv.2008.11.055
Kallis G, Butler D (2001) The EU water framework directive: Measures and implications. Water Policy 3:125–142. https://doi.org/10.1016/S1366-7017(01)00007-1
Kehrein N, Berlekamp J, Klasmeier J (2015) Modeling the fate of down-the-drain chemicals in whole watersheds: new version of the GREAT-ER software. Environ Model Softw 64:1–8. https://doi.org/10.1016/j.envsoft.2014.10.018
Lämmchen V, Niebaum G, Berlekamp J, Klasmeier J (2021) Geo-referenced simulation of pharmaceuticals in whole watersheds - Application of GREAT-ER 4.1 in Germany. Environ Sci Pollut Res 28:21926–21935. https://doi.org/10.1007/s11356-020-12189-7
Lehner B, Verdin K, Jarvis A (2008) New global hydrography derived from spaceborne elevation data. Eos Trans AGU 89(10):93–94. https://doi.org/10.1029/2008EO100001
Leibundgut C, Kern FJ (2003) Die Wasserbilanz der Bundesrepublik Deutschland - Neue Ergebnisse aus dem Hydrologischen Atlas. Petermanns Geogr Mitt 147(6):6–11
Lespez L, Viel V, Rollet AJ, Delahaye D (2015) The anthropogenic nature of present-day low energy rivers in western France and implications for current restoration projects. Geomorphology 251:64–76. https://doi.org/10.1016/j.geomorph.2015.05.015
Lulofs K, Coenen F (2007) Cross border co-operation on water quality in the Vecht river basin. In: Verwijmeren J, Wiering M (eds) Many rivers to cross - cross border cooperation in river management. Eburon, Delft, pp 71–91
Messager M, Lehner B, Grill G, Nedeva I, Schmitt O (2016) Estimating the volume and age of water stored in global lakes using a geo-statistical approach. Nat Commun 7:13603. https://doi.org/10.1038/ncomms13603
Moffat AC, Osselton MD, Widdop B, Watts J (2011) Clarke’s analysis of drugs and poisons, 4th edn. Pharmaceutical Press, London
Neamtu M, Grandjean D, Sienkiewicz A, Le Faucheur S, Slaveykova V, Colmenares JJV, Pulgarín C, De Alencastro LF (2014) Degradation of eight relevant micropollutants in different water matrices by neutral photo-Fenton process under UV254 and simulated solar light irradiation - A comparative study. Appl Catal B Environ 158–159:30–37. https://doi.org/10.1016/j.apcatb.2014.04.001
NLWKN (Lower Saxony Water Management, Coastal Defence and Nature Conservation Agency) (2012) Wasserkörperdatenblatt - Stand November 2012–32001 Vechte Ohne-Nordhorn. https://www.nlwkn.niedersachsen.de/download/75090/WK32001_Vechte_Ohne-Nordhorn_.pdf Accessed 7 Dec 2020
Oosterhuis M, Sacher F, ter Laak TL (2013) Prediction of concentration levels of metformin and other high consumption pharmaceuticals in wastewater and regional surface water based on sales data. Sci Total Environ 442:380–388. https://doi.org/10.1016/j.scitotenv.2012.10.046
Ort C, Hollender J, Schaerer M, Siegrist H (2009) Model-based evaluation of reduction strategies for micropollutants from wastewater treatment plants in complex river networks. Environ Sci Technol 43:3214–3220. https://doi.org/10.1021/es802286v
Petts GE (2007) Hydroecology and water resources management. In: Wood PJ, Hannah D, Sadler JP (eds) Hydroecology and ecohydrology: past, present and future. Wiley, Chichester, pp 205–252
Podimata MV, Yannopoulos PC (2013) Evaluating challenges and priorities of a trans-regional river basin in Greece by using a hybrid SWOT scheme and a stakeholders’ competency overview. Int J River Basin Manag 11:93–110. https://doi.org/10.1080/15715124.2013.768624
Prinsen GF, Becker BPJ (2011) Application of SOBEK hydraulic surface water models in the Netherlands hydolgocial modelling instrument. Irrig and Drain 60:35–41. https://doi.org/10.1002/ird.665
Richardson SD (2009) Water analysis: emerging contaminants and current issues. Anal Chem 81:4645–4677. https://doi.org/10.1021/acs.analchem.9b05269
RIVM (National Institute for Public Health and the Environment) (2014) Environmental Risk Limits for Pharmaceuticals. Derivation of WFD Water Quality Standards for Carbamazepine, Metoprolol, Metformin and Amidotrizoic Acid. RIVM Letter report 270006002/2014. https://www.rivm.nl/bibliotheek/rapporten/270006002.pdf. Accessed 7 Dec 2020
RWS (Rijkswaterstraat) (2017) Waterakkoord Twenthekanalen en Overijsselsche Vecht - versie 21 maart 2017. https://api1.ibabs.eu/publicdownload.aspx?site=wdodelta&id=100025303. Accessed 7 Dec 2020
RWS (Rijkswaterstraat) (2020) Rijkswaterstraat Waterinfo - https://waterinfo.rws.nl/#!/kaart/. Accessed 7 Dec 2020
Scheurer M, Brauch HJ, Lange FT (2009) Analysis and occurrence of seven artificial sweeteners in German waste water and surface water and in soil aquifer treatment (SAT). Anal Bioanal Chem 394:1585–1594. https://doi.org/10.1007/s00216-009-2881-y
Scheurer M, Michel A, Brauch HJ, Ruck W, Sacher F (2012) Occurrence and fate of the antidiabetic drug metformin and its metabolite guanylurea in the environment and during drinking water treatment. Water Res 46:4790–4802. https://doi.org/10.1016/j.watres.2012.06.019
Schowanek D, Webb S (2002) Exposure simulation for pharmaceuticals in European surface waters with GREAT-ER. Toxicol Lett 131:39–50. https://doi.org/10.1016/S0378-4274(02)00064-4
Schwabe U, Paffrath D, Ludwig WD, Klauber J (2019) Arzneiverordnungs-Report 2019. Springer-Verlag Berlin-Heidelberg. https://doi.org/10.1007/978-3-662-59046-1$4
Scorpio V, Zen S, Bertoldi W, Surian N, Mastronunzio M, Prá ED, Comiti F (2018) Channelization of a large Alpine river: what is left of its original morphodynamics? Earth Surf Process Landforms 43:1044–1062. https://doi.org/10.1002/esp.4303
Straub JO, Caldwell DJ, Davidson T, D’Aco V, Kappler K, Robinson PF, Simon-Hettich B, Tell J (2019) Environmental risk assessment of metformin and its transformation product guanylurea. I. Environmental fate. Chemosphere 216:844–854. https://doi.org/10.1016/j.chemosphere.2018.10.036
Tiedeken EJ, Tahar A, McHugh B, Rowan NJ (2017) Monitoring, sources, receptors, and control measures for three European Union watch list substances of emerging concern in receiving waters – A 20-year systematic review. Sci Total Environ 574:1140–1163. https://doi.org/10.1016/j.scitotenv.2016.09.084
Trautwein C, Kümmerer K (2011) Incomplete aerobic degradation of the antidiabetic drug Metformin and identification of the bacterial dead-end transformation product Guanylurea. Chemosphere 85:765–773. https://doi.org/10.1016/j.chemosphere.2011.06.057
Tsakiris G (2015) The status of the European waters in 2015: a review. Environ Process 2:543–557. https://doi.org/10.1007/s40710-015-0079-1
Van Nuijs ALN, Tarcomnicu I, Simons W, Bervoets L, Blust R, Jorens PG, Neels H, Covaci A (2010) Optimization and validation of a hydrophilic interaction liquid chromatography-tandem mass spectrometry method for the determination of 13 top-prescribed pharmaceuticals in influent wastewater. Anal Bioanal Chem 398:2211–2222. https://doi.org/10.1007/s00216010-4101-1
Verhelst P, Baeyens R, Reubens J, Benitez JP, Coeck J, Goethals P, Ovidio M, Vergeynst J, Moens T, Mouton A (2018) European silver eel (Anguilla anguilla L.) migration behaviour in a highly regulated shipping canal. Fish Res 206:176–184. https://doi.org/10.1016/j.fishres.2018.05.013
Verlicchi P, Al Aukidy M, Jelic A, Petrovic M, Barcelo D (2014) Comparison of measured and predicted concentrations of selected pharmaceuticals in wastewater and surface water: A case-study of a catchment area in the Po Valley (Italy). Sci Total Environ 470–471:844–854. https://doi.org/10.1016/j.scitotenv.2013.10.026
Vissers M, Vergrouwen L, Witteveen S (2017) Landelijke hotspotanalyse geneesmiddelen RWZI’s. Rapport 2017-42. https://www.stowa.nl/publicaties/landelijke-hotspotanalyse-geneesmiddelen-rwzis. Accessed 7 Dec 2020
Vitousek PM, Mooney HA, Lubchenco J, Melillo JM (1997) Human domination of Earth’s ecosystems. Science 277:494–499. https://doi.org/10.1126/science.277.5325.494
Vulliet E, Cren-Olivé C (2011) Screening of pharmaceuticals and hormones at the regional scale, in surface and groundwaters intended to human consumption. Environ Pollut 159:2929–2934. https://doi.org/10.1016/j.envpol.2011.04.033
Watson N (2004) Integrated river basin management: A case for collaboration. Int J River Basin Manag 2:243–257. https://doi.org/10.1080/15715124.2004.9635235
Wiering M, Verwijmeren J, Lulofs K, Feld C (2010) Experiences in regional cross border co-operation in river management. Comparing three cases at the Dutch-German border. Water Resour Manag 24:2647–2672. https://doi.org/10.1007/s11269-009-9572-5
WHO (2020) Collaborating Centre for Drug Statistics Methodology, ATC classification index with DDDs - Metformin. Oslo, Norway
Zacharias I, Liakou P, Biliani I (2020) A review of the status of surface European waters twenty years after WFD introduction. Environ Process 7:1023–1039. https://doi.org/10.1007/s40710-020-00458-z
Acknowledgements
The authors would also like to thank the water authorities Agency for Nature, Environment and Consumer Protection NRW (LANUV), Lower Saxony Water Management, Coastal Defence and Nature Conservation Agency (NLWKN) and the water boards of Waterschap Vechtstromen (WVS) and Waterschap Drents Overijsselse Delta (WDOD) for providing data.
Funding
Open Access funding enabled and organized by Projekt DEAL. The authors acknowledge funding by the European Regional Development fund of the European Union under the project MEDUWA-Vecht(e) (project number 142118).
Author information
Authors and Affiliations
Contributions
All authors contributed to the study conception and design. All authors performed material preparation, data collection and analysis. The first draft of the manuscript was written by Volker Lämmchen and Jürgen Berlekamp. All authors commented on previous versions of the manuscript. All authors read and approved the final manuscript.
Conceptualization: Volker Lämmchen, Jörg Klasmeier, Jürgen Berlekamp; Methodology: Volker Lämmchen, Jörg Klasmeier, Lucia Hernandez-Leal, Jürgen Berlekamp; Formal analysis and investigation: Volker Lämmchen, Jörg Klasmeier, Jürgen Berlekamp; Writing - original draft preparation: Volker Lämmchen, Jürgen Berlekamp; Writing - review and editing: Volker Lämmchen, Jörg Klasmeier, Lucia Hernandez, Jürgen Berlekamp; Funding acquisition: Jörg Klasmeier; Supervision: Jürgen Berlekamp, Jörg Klasmeier.
Corresponding author
Ethics declarations
Conflicts of Interests
The authors have no conflicts of interest to declare that are relevant to the content of this article.
Ethics Approval
Not applicable.
Consent to Participate
Not applicable.
Consent for Publication
Not applicable.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Highlights
• Spatially explicit exposure assessment in strongly regulated catchments is enabled.
• Representation of hydrological conditions in the GREAT-ER model was improved.
• Model simulation results reproduce measured concentration patterns of metformin.
Supplementary Information
ESM 1
(DOCX) 1.33 MB
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lämmchen, V., Klasmeier, J., Hernandez-Leal, L. et al. Spatial Modelling of Micro-pollutants in a Strongly Regulated Cross-border Lowland Catchment. Environ. Process. 8, 973–992 (2021). https://doi.org/10.1007/s40710-021-00530-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40710-021-00530-2