High-dimensional density estimation with tensorizing flow

Abstract

We propose the tensorizing flow method for estimating high-dimensional probability density functions from observed data. Our method combines the optimization-less feature of the tensor-train with the flexibility of flow-based generative models, providing an accurate and efficient approach for density estimation. Specifically, our method first constructs an approximate density in the tensor-train form by efficiently solving the tensor cores from a linear system based on kernel density estimators of low-dimensional marginals. Subsequently, a continuous-time flow model is trained from this tensor-train density to the observed empirical distribution using maximum likelihood estimation. Numerical results are presented to demonstrate the performance of our method.

Appendices

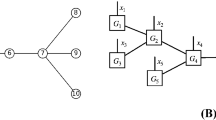
Appendix A. Proof of Proposition 3.3

In this appendix, we prove Proposition 3.3 from Sect. 3.1:

Proof of Proposition 3.3

For $2\le k\le d$, it suffices for us to consider the k-th equation in (3.1):

$$\begin{aligned} \sum _{\alpha _{k-1}=1}^{r_{k-1}}\Phi _{k-1}(x_{1:k-1}; \alpha _{k-1})G_k(\alpha _{k-1};x_k,\alpha _k)=\Phi _k(x_{1:k-1};x_k,\alpha _k). \end{aligned}$$

(A.1)

By Definition 3.1, there exist orthonormal right singular vectors

$$\begin{aligned} \{\Psi _{k-1}(\alpha _{k-1};x_{k:d})\}_{1\le \alpha _{k-1} \le r_{k-1}} \subset L^2(I^{d-k+1}) \end{aligned}$$

of $p(x_{1:k-1};x_{k:d})$ and

$$\begin{aligned} \{\Psi _k(\alpha _{k};x_{k+1:d})\}_{1\le \alpha _k\le r_{k}} \subset L^2(I^{d-k}) \end{aligned}$$

of $p(x_{1:k};x_{k+1:d})$, and corresponding singular values $\sigma _{k-1}(1)\ge \cdots \ge \sigma _{k-1}(r_{k-1})$ and $\sigma _{k}(1)\ge \cdots \ge \sigma _{k}(r_{k})$, satisfying

$$\begin{aligned} p(x_{1:k-1};x_{k:d})= \sum _{\alpha _{k-1}=1}^{r_{k-1}}\sigma _{k-1}(\alpha _{k-1})\Phi _{k-1}(x_{1:k-1};\alpha _{k-1})\Psi _{k-1}(\alpha _{k-1};x_{k:d}), \end{aligned}$$

(A.2)

and

$$\begin{aligned} p(x_{1:k};x_{k+1:d})= \sum _{\alpha _{k}=1}^{r_{k}}\sigma _{k}(\alpha _{k})\Phi _{k}(x_{1:k};\alpha _{k})\Psi _k(\alpha _{k};x_{k+1:d}). \end{aligned}$$

Define $\Xi _k(x_{k+1:d};\alpha _k)=\sigma _k(\alpha _k)^{-1}\Psi _k(\alpha _k;x_{k+1:d})$. It is easy to check that

$$\begin{aligned} \begin{aligned}&\int _{I^{d-k}} p(x_{1:k};x_{k+1:d})\Xi _k(x_{k+1:d};\alpha _k) \textrm{d}x_{k+1:d} \\ =&\int _{I^{d-k}} \sum _{\alpha '_k=1}^{r_{k}}\sigma _{k}(\alpha '_{k})\sigma _{k}(\alpha _{k})^{-1}\Phi _{k}(x_{1:k}; \alpha '_{k})\Psi _k(\alpha '_{k};x_{k+1:d})\Psi _k(\alpha _{k};x_{k+1:d})\textrm{d}x_{k+1:d} \\ =&\Phi _{k}(x_{1:k};\alpha _{k}). \end{aligned} \end{aligned}$$

Therefore, by contracting $\Xi _k(x_{k+1:d};\alpha _k)$ to both sides of (A.2), we have

$$\begin{aligned} \begin{aligned} \Phi _{k}(x_{1:k};\alpha _{k})&= \int _{I^{d-k}} p(x_{1:k-1};x_{k:d}) \Xi _k(x_{k+1:d};\alpha _k) \textrm{d}x_{k+1:d} \\&= \sum _{\alpha _{k-1}=1}^{r_{k-1}}\sigma _{k-1}(\alpha _{k-1})\Phi _{k-1}(x_{1:k-1};\alpha _{k-1})\int _{I^{d-k}} \Psi _{k-1}(\alpha _{k-1};x_{k:d})\Xi _k(x_{k+1:d};\alpha _k)\textrm{d}x_{k+1:d}, \end{aligned} \end{aligned}$$

and consequently,

$$\begin{aligned} G_k(\alpha _{k-1};x_k,\alpha _k)=\sigma _{k-1}(\alpha _{k-1})\int _{I^{d-k}} \Psi _{k-1}(\alpha _{k-1};x_{k:d})\Xi _k(x_{k+1:d};\alpha _k)\textrm{d}x_{k+1:d} \end{aligned}$$

solves equation (A.1).

The uniqueness of the solution is guaranteed by the orthogonality of the functions $\{\Psi _{k-1}(\alpha _{k-1};x_{k:d})\}_{1\le \alpha _{k-1} \le r_{k-1}}$ by definition. Once $G_k$ is ready, it is easy to check the validity of (3.2) by plugging the CDE in (3.1) one into the next successively.

Appendix B. Hyperparameters

This section presents the hyperparameters of our tensorizing flow algorithm used for each example in Sect. 4. For simplicity, we choose the internal ranks $r_k=2$ for $1\le k\le d-1$, and the number of quadrature points $l=20$ for all numerical integrations involved. We set the time horizon $T=0.2$ with step-size $\tau =0.01$ in the flow model. We choose the bandwidth parameter h in (3.6) to be 5% of the range of the data. We generate N/2 samples separately from the training samples as the test samples. The rest of the hyperparameters are organized in Table 1.

Table 1 Hyperparameters used in the examples