Abstract
Beben and Wu showed that if M is a \((2n-2)\)-connected \((4n-1)\)-dimensional Poincaré Duality complex such that \(n\ge 3\) and \(H^{2n}(M;{{\mathbb {Z}}})\) consists only of odd torsion, then \(\Omega M\) can be decomposed up to homotopy as a product of simpler, well-studied spaces. We use a result from Beben and Theriault (Doc Math 27:183-211, 2022) to greatly simplify and enhance Beben and Wu’s work and to extend it in various directions.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
An orientable Poincaré Duality complex is a connected CW-complex whose cohomology satisfies Poincaré Duality. An orientable manifold is an example. In [6], Beben and Wu gave a homotopy decomposition of \(\Omega M\) where M is any \((2n-2)\)-connected \((4n-1)\)-dimensional orientable Poincaré Duality complex, provided \(n\ge 3\) and \(H^{2n}(M;{\mathbb {Z}})\) has no 2-torsion. They used this to show that the homotopy type of \(\Omega M\) depended only on homological properties of M. This is in contrast to the homotopy type of M, which is known to depend on other properties as well. In particular, their result implies that the homotopy groups of M depend only on its homological properties.
In this paper, we revisit Beben and Wu’s result. We give a simpler approach involving much less spectral sequence calculation, instead relying on a result proved in [5]. This allows for the results to be significantly extended and advanced in various directions, complementing work in [3, 4].
It should also be noted that earlier work of Selick [14] using different methods can be used to give a p-local homotopy decomposition of \(\Omega M\) when p is an odd prime and \(H^{2n}(M;{\mathbb {Z}})\cong {\mathbb {Z}}/p^{r}{\mathbb {Z}}\). This has the advantage that it avoids calculating the mod-p homology of \(\Omega M\) entirely but it also cedes a level of precision that we will later require; this is explained more fully in Sect. 3.
For any \((2n-2)\)-connected \((4n-1)\)-dimensional Poincaré Duality complex M, we have
where \(d\ge 0\), each \(p_{k}\) is prime and each \(r_{k}\ge 1\). The case when \(d\ge 1\) has been dealt with in [5, Examples 4.4 and 5.3] (see [2] for a different approach to the homotopy type) so we restrict to the case when \(d=0\). In this case, the description of \(H^{2n}(M;{\mathbb {Z}})\) implies that the 2n-skeleton \(M_{2n}\) of M is homotopy equivalent to a wedge of Moore spaces, \(M_{2n}\simeq \bigvee _{k=1}^{\ell } P^{2n}(p_{k}^{r_{k}})\). If each \(p_{k}\) is an odd prime, we show the following. Let m be the least common multiple of \(\{p_{1}^{r_{1}},\ldots ,p_{\ell }^{r_{\ell }}\}\) and let \(m={\bar{p}}_{1}^{{\bar{r}}_{1}}\cdots {\bar{p}}_{s}^{{\bar{r}}_{s}}\) be its prime decomposition. Notice that \(\{{\bar{p}}_{1},\ldots ,{\bar{p}}_{s}\}\) is the set of distinct primes in \(\{p_{1},\ldots ,p_{\ell }\}\) and each \({\bar{r}}_{j}\) is the maximum power of \({\bar{p}}_{j}\) appearing in the list \(\{p_{1}^{r_{1}},\ldots ,p_{\ell }^{r_{\ell }}\}\). By [12], the wedge of Moore spaces \(\bigvee _{j=1}^{s} P^{2n}({\bar{p}}_{j}^{{\bar{r}}_{j}})\) is homotopy equivalent to \(P^{2n}(m)\). Write \(M_{2n}\simeq P^{2n}(m)\vee \Sigma A\) where \(\Sigma A\) is the wedge of the remaining Moore spaces in \(M_{2n}\). Let f be the composite of inclusions \(f:\Sigma A \xrightarrow {}M_{2n}\xrightarrow {}M\) and define the space V and the map \(\mathfrak {h}\) by the homotopy cofibration \(\Sigma A \xrightarrow {f}M\xrightarrow {\mathfrak {h}}V\). We show that V is a Poincaré Duality complex with \(H^{2n}(V;{\mathbb {Z}})\cong {\mathbb {Z}}/m{\mathbb {Z}}\), and \(\Omega \mathfrak {h}\) has a right homotopy inverse \(s:\Omega V\xrightarrow {}\Omega M\) and prove the following.
In general, for a space X let \(ev:\Sigma \Omega X\xrightarrow {}X\) be the canonical evaluation map. Given two maps \(a:\Sigma X\xrightarrow {}Z\) and \(b:\Sigma Y\xrightarrow {}Z\), let \([a,b]:\Sigma X\wedge Y\xrightarrow {}Z\) be the Whitehead product of a and b. Let \(S^{2n+1}\{p^{r}\}\) be the homotopy fibre of the degree \(p^{r}\) map on \(S^{2n+1}\).
Theorem 1.1
Let M be a \((2n-2)\)-connected, \((4n-1)\)-dimensional Poincaré Duality complex such that \(n\ge 2\). Suppose that
where each \(p_{k}\) is an odd prime. Then with V and A chosen as above:
-
(a.)
there is a homotopy fibration
$$\begin{aligned} (\Sigma \Omega V\wedge A)\vee \Sigma A\xrightarrow {[\gamma ,f]+f} M\xrightarrow {\mathfrak {h}}V, \end{aligned}$$where \(\gamma \) is the composite \(\gamma :\Sigma \Omega V \xrightarrow {\Sigma s}\Sigma \Omega M\xrightarrow {ev}M\);
-
(b.)
the homotopy fibration in (a) splits after looping to give a homotopy equivalence
$$\begin{aligned} \Omega M\simeq \Omega V\times \Omega ((\Sigma \Omega V\wedge A)\vee \Sigma A); \end{aligned}$$ -
(c.)
there is a homotopy equivalence
$$\begin{aligned} \Omega V\simeq \prod _{j=1}^{s} S^{2n-1}\{{\bar{p}}_{j}^{{\bar{r}}_{j}}\}\times \Omega S^{4n-1}. \end{aligned}$$
As a notable special case, if the primes \(p_{k}\) for \(1\le k\le \ell \) all equal a common prime p, and r is the maximum of \(\{r_{1},\ldots ,r_{k}\}\) then \(\Omega V\simeq S^{2n-1}\{p^{r}\}\times \Omega S^{4n-1}\).
In [6], the decompositions in parts (b) and (c) of Theorem 1.1 were proved for \(n\ge 3\). Part (a) is new as is the \(n=2\) case for 2-connected 7-dimensional Poincaré Duality complexes. Further, while [6] gives no information in 2-torsion cases, in Theorem 5.7 we prove analogues of parts (a) and (b) when \(H^{2n}(M;{\mathbb {Z}})\cong \bigoplus _{k=1}^{\ell }{\mathbb {Z}}/p_{k}^{r_{k}} {\mathbb {Z}}\oplus \bigoplus _{s=1}^{t}{\mathbb {Z}}/2^{r_s}{\mathbb {Z}}\), where each \(p_{k}\) is an odd prime, each \(r_s\ge 2\), and \(\ell \ge 1\), and in Proposition 6.1 we consider special cases when 2-primary analogues of part (c) of Theorem 1.1 hold.
An interesting consequence is a rigidity result. In Remark 4.6, we show that the space \((\Sigma \Omega V\wedge A)\vee \Sigma A\) is homotopy equivalent to a wedge W of Moore spaces, so part (b) may be written more succinctly as \(\Omega M\simeq \Omega V\times \Omega W\). As observed in [6], the homotopy types of \(\Omega V\) and \(\Omega M\) depend only on information from \(H^{2n}(M;{\mathbb {Z}})\). Thus, if M and \(M'\) are both \((2n-2)\)-connected \((4n-1)\) dimensional Poincaré Duality complexes satisfying the hypotheses of Theorem 1.1, and \(H^{2n}(M;{\mathbb {Z}})\cong H^{2n}(M';{\mathbb {Z}})\), then \(\Omega M\simeq \Omega M'\).
We also prove an additional statement that was unaddressed in [6]. Let \(I:M_{2n}\xrightarrow {}M\) be the inclusion of the 2n-skeleton. We show that there is a homotopy cofibration \(P^{4n-1}(m) \xrightarrow {\mathfrak {G}}M_{2n}\vee S^{4n-1}\xrightarrow {I+H}M\) where \(\Omega (I+H)\) has a right homotopy inverse \(S:\Omega M\xrightarrow {}\Omega (M_{2n}\vee S^{4n-1})\), and prove the following.
Theorem 1.2
With the same hypotheses as in Theorem 1.1, there is a homotopy fibration
where \(\Gamma \) is the composite \(\Sigma \Omega M \xrightarrow {\Sigma S}\Sigma \Omega (M_{2n}\vee S^{4n-1})\xrightarrow {ev}M_{2n}\vee S^{4n-1}\), and this homotopy fibration splits after looping to give a homotopy equivalence
Theorem 1.2 is interesting. Since \(M_{2n}\) is homotopy equivalent to a wedge of simply connected Moore spaces, it is a suspension. The theorem therefore shows that \(\Omega M\) retracts off a loop suspension, it identifies the complementary factor, and it explicitly describes how the complementary factor maps into the loop suspension.
The authors would like to thank the referee for several comments that have improved the paper.
2 Preliminary results
This section contains preliminary results that will be referred to frequently in the subsequent sections. We start with a general result from [5, Proposition 3.5].
Theorem 2.1
Let \(\Sigma A \xrightarrow {f}Y\xrightarrow {h}Z\) be a homotopy cofibration. Suppose that \(\Omega h\) has a right homotopy inverse \(s:\Omega Z\xrightarrow {}\Omega Y\). Let \(\gamma \) be the composite \(\gamma :\Sigma \Omega Z \xrightarrow {\Sigma s}\Sigma \Omega Y\xrightarrow {ev}Y\). Then there there is a homotopy fibration
which splits after looping to give a homotopy equivalence
\(\Box \)
Remark 2.2
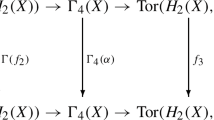
As pointed out in [15, Remark 2.2], Theorem 2.1 has a naturality property. If there is a homotopy cofibration diagram

and both \(\Omega h\) and \(\Omega h'\) have right homotopy inverses s and \(s'\), respectively, such that there is a homotopy commutative diagram

then the homotopy fibration in Theorem 2.1 is also natural.
Next, we prove two general lemmas about the existence of certain right homotopy inverses.
Lemma 2.3
Suppose that there is a homotopy equivalence
for some maps f and g, where \(\mu \) is the loop multiplication, and suppose that there is a map \(\Omega W\xrightarrow {\Omega h}\Omega Z\). If both f and g lift through \(\Omega h\), then \(\Omega h\) has a right homotopy inverse.
Proof
Let \(s:X\xrightarrow {}\Omega W\) and \(t:Y\xrightarrow {}\Omega W\) be lifts of f and g, respectively, through \(\Omega h\). Consider the diagram

The left triangle homotopy commutes by definition of s and t and the right square homotopy commutes since \(\Omega h\) is an H-map. The lower direction around the diagram is the definition of the homotopy equivalence e, so the upper row is a lift of e through \(\Omega W\). Therefore, \(\Omega h\) has a right homotopy inverse. \(\square \)
Lemma 2.4
Suppose that there is a homotopy fibration diagram

of path-connected CW-complexes, where \(\Omega b\), \(\Omega f\) and \(\Omega p\) have right homotopy inverses. Then, \(\Omega e\) has a right homotopy inverse.
Proof
Let \(r:\Omega B'\xrightarrow {}\Omega B\), \(s:\Omega F'\xrightarrow {}\Omega F\) and \(t:\Omega B\xrightarrow {}\Omega E\) be right homotopy inverses for \(\Omega b\), \(\Omega f\) and \(\Omega p\), respectively. Let \(\theta \) be the composite
Consider the diagram

where \(i_{2}\) is the inclusion of the second factor and \(\pi _{1}\) is the projection onto the first factor. The lower left square homotopy commutes by definition of \(\theta \) and \(\Omega p\) being an H-map. The left column is a fibration, so the homotopy commutativity of the lower left square implies there is an induced map of fibres \(\Omega F'\xrightarrow {}\Omega F\). Since \(\theta \circ i_{2}=\Omega q\circ s\), a choice of map of fibres is s. Thus, the left side of the diagram is a map of homotopy fibrations, as is the right by hypothesis. Therefore, the composite from the left to the right column is a self-map of a homotopy fibration in which the top and bottom maps are homotopic to the identity. Therefore, by the Five Lemma, \(\Omega e\circ \theta \) induces an isomorphism on homotopy groups and so is a homotopy equivalence by Whitehead’s Theorem. \(\square \)
3 The case when \(H^{2n}(M;{\mathbb {Z}})\cong {\mathbb {Z}}/p^{r}{\mathbb {Z}}\)
Let V be a \((2n-2)\)-connected \((4n-1)\)-dimensional Poincaré Duality complex with \(H^{2n}(V;{\mathbb {Z}})\cong {\mathbb {Z}}/p^{r}{\mathbb {Z}}\) where p is a prime. As a CW-complex, \(V=P^{2n}(p^{r})\cup e^{4n-1}\), and there is a homotopy cofibration
where f is the attaching map for the top cell and i is the inclusion of the \((4n-2)\)-skeleton. In this section, we prove Theorems 1.1 and 1.2 in the special case when \(M=V\), assuming that \(n\ge 2\) and p is odd. Some 2-primary cases of Theorem 1.1 (c) will be deferred to Sect. 6.
A decomposition of \(\Omega V\) was proved by Beben and Wu [6] for \(n\ge 3\) and p odd. Their method was more elaborate as it kept track of homology information in the general case of \(\Omega M\) where M is any \((2n-2)\)-connected \((4n-1)\)-dimensional Poincaré Duality complex with degree 2n cohomology consisting only of odd torsion. We give a much simpler approach to the general case in Sect. 4, and so only need to keep track of homology information for the special case of V.
Different methods were used by Selick [14] to give a p-local decomposition of \(\Omega V\) for \(n\ge 2\) and p odd. He used a generalization of methods developed by Dyer-Lashof and Ganea to produce a p-local homotopy fibration
where \(\partial \) is null homotopic, implying that there is a p-local homotopy equivalence \(\Omega V\simeq S^{2n-1}\{p^{r}\}\times \Omega S^{4n-1}\), analogous to our Proposition 3.7. The advantage of Selick’s method is that it avoids homology calculations entirely. Ideally, we would like this to be an integral result rather than a p-local one; the method itself cannot be upgraded to do this as it depends on \(S^{2n-1}\) being an H-space which rarely happens integrally; however, a Sullivan square type argument could potentially be used to rectify this given that V localized at primes not equal to p or rationally is homotopy equivalent to \(S^{4n-1}\). The real disadvantage of Selick’s method for our purposes is that it does not describe the homotopy class of the map \(h'\) with enough precision for later use in Lemma 3.8 and Proposition 3.9. It would be interesting to see if his techniques could be enhanced to do this, but in the meantime, we fall back to homology calculations to deal with \(\Omega V\).
Lemma 3.1
In degrees \(\le 4n\), there is an algebra isomorphism \(H_{*}(\Omega V;{\mathbb {Z}}/p{\mathbb {Z}})\cong {\mathbb {Z}}/p{\mathbb {Z}}[x,y]\) where \(\vert x\vert =2n-2\) and \(\vert y\vert =2n-1\).
Proof
Throughout, take cohomology and homology with mod-p coefficients. By Poincaré Duality, there is an algebra isomorphism \(H^{*}(V)\cong \Lambda (a,b)\) where \(\vert a\vert =2n-1\), \(\vert b\vert =2n\). Dualizing, there is a coalgebra isomorphism \(H_{*}(V)\cong \Lambda (u,v)\) where u, v are the duals of a, b, respectively. In particular, if \({\overline{\Delta }}\) is the reduced diagonal, then u and v are primitive and \({\overline{\Delta }}(uv)=u\otimes v+v\otimes u\).
Consider the mod-p homology Serre spectral sequence for the principal homotopy fibration \(\Omega V \xrightarrow {}*\xrightarrow {}V\). We have \(E^{2}\cong H_{*}(\Omega V)\otimes H_{*}(V)\) and the spectral sequence converges to \(H_{*}(*)\). For degree reasons, the first possible nontrivial differential is \(d^{2n-1}\), and for convergence reasons, we must have \(d^{2n-1}(u)=x\) for some \(x\in H_{2n-2}(\Omega V)\). Also, for convergence reasons, we must have \(d^{2n}(v)=y\) for some \(y\in H_{2n-1}(\Omega V)\). Thus, in the \(E^{2}\)-term, we also have the elements \(x\otimes u, x\otimes v, y\otimes u,y\otimes v\). Since the spectral sequence is principal, \(d^{2n-1}\) and \(d^{2n}\) are differentials, so \(d^{2n-1}(x\otimes u)=x^{2}\), \(d^{2n-1}(y\otimes u)=xy\) and \(d^{2n}(y\otimes v)=y^{2}\). We claim that \(d^{2n-1}(uv)=t\cdot (x\otimes v)\) for some unit \(t\in {\mathbb {Z}}/p{\mathbb {Z}}\). The diagonal map gives a morphism of fibrations from \(\Omega V \xrightarrow {}*\xrightarrow {}V\) to \(\Omega V\times \Omega V \xrightarrow {}*\xrightarrow {}V\times V\) that induces a morphism of mod-p homology Serre spectral sequences. Note that in the product fibration there is a Künneth isomorphism that lets us regard the homology of the product as the tensor product of the homologies of the factors. Since the diagonal map induces the coalgebra structure in homology, this morphism of Serre spectral sequences implies that the differentials commute with the reduced diagonal. Therefore \({\overline{\Delta }}(d^{2n-1}(uv))=(d^{2n-1}\otimes d^{2n-1})(u\otimes v+v\otimes u)=x\otimes v+v\otimes x\) (noting that \(d^{2n-1}(v)=0\)). In particular, \({\overline{\Delta }}(d^{2n-1}(uv))\ne 0\), so \(d^{2n-1}(uv)\ne 0\). For degree reasons, this implies that \(d^{2n-1}(uv)=t\cdot (x\otimes v)\) for some unit \(t\in {\mathbb {Z}}/p{\mathbb {Z}}\). Thus at the \(E^{2n+1}\)-page, all elements of degree \(\le 4n\) have vanished. Consequently, in degrees \(\le 4n\), there is an algebra isomorphism \(H_{*}(\Omega V)\cong {\mathbb {Z}}/p{\mathbb {Z}}[x,y]\). \(\square \)
Next consider the effect of the map \(\Omega P^{2n}(p^{r})\xrightarrow {\Omega i}\Omega V\) in mod-p homology. Since \(n\ge 2\), \(P^{2n}(p^{r})\) is a suspension, so by the Bott–Samelson Theorem there is an algebra isomorphism
where \(T(\ \ )\) is the free tensor algebra functor, \(\vert x\vert =2n-2\), \(\vert y\vert =2n-1\) and \(\beta ^{r}y=x\). Since i is the inclusion of the \((4n-2)\)-skeleton, it induces a homotopy equivalence in dimensions \(\le 4n-3\), so \(\Omega i\) induces a homotopy equivalence in dimensions \(\le 4n-4\). In particular, \((\Omega i)_{*}\) induces an isomorphism in degrees \(2n-2\) and \(2n-1\) in mod-p homology. As \((\Omega i)_{*}\) is an algebra map, from Lemma 3.1 we obtain the following.
Lemma 3.2
In mod-p homology, the generator of least degree in the kernel of \((\Omega i)_{*}\) is [x, y]. \(\square \)
Let \(\widetilde{f}:S^{4n-3}\xrightarrow {}\Omega P^{2n}(p^{r})\) be the adjoint of f. Let \(\iota _{m}\in H_{m}(S^{m};{\mathbb {Z}}/p{\mathbb {Z}})\) be a choice of a generator.
Lemma 3.3
In mod-p homology, there is a choice of \(\iota _{4n-3}\) such that \(\widetilde{f}_{*}(\iota _{4n-3})=[x,y]\).
Proof
Recall the cofibration \(S^{4n-2} \xrightarrow {f}P^{2n}(p^{r})\xrightarrow {i}V\). Define the space F by the homotopy fibration \(F \xrightarrow {}P^{2n}(p^{r})\xrightarrow {i}V\) and consider the mod-p homology Serre spectral sequence for the principal fibration \(\Omega V \xrightarrow {}F\xrightarrow {}P^{2n}(p^{r})\). The \(E^{2}\)-page of the spectral sequence is given by \(H_{*}(P^{2n}(p^{r}))\otimes H_{*}(\Omega V)\). Let u, v be the generators of \(H_{*}(P^{2n}(p^{r}))\) in degrees \(2n-1,2n\), respectively. By Lemma 3.1, \(H_{*}(\Omega V)\cong {\mathbb {Z}}/p{\mathbb {Z}}[x,y]\) in degrees \(\le 4n\), where \(\vert x\vert =2n-2\) and \(\vert y\vert =2n-1\). Since i is the inclusion of the 2n-skeleton, we have \(d^{2n-1}(u)=x\) and \(d^{2n}(v)=y\). As the fibration is principal, the differentials in the spectral sequence are derivations so we obtain \(d^{2n-1}(u\otimes x)=x^{2}\), \(d^{2n-1}(u\otimes y)=xy\) and \(d^{2n}(v\otimes y)=v^{2}\). Thus by the \(E^{2n+1}\)-page of the spectral sequence, there is only one element left in degrees \(\le 4n-2\), and that is the image of the \(E^{2}\)-page element \(v\otimes x\). For degree reasons, this element is in the kernel of all higher differentials and therefore survives the spectral sequence. Thus, the \((4n-2)\)-skeleton of F is \(S^{4n-2}\).
Returning again to the cofibration \(S^{4n-2} \xrightarrow {f}P^{2n}(p^{r})\xrightarrow {i}V\), there is clearly a lift

for some map \(\lambda \). By the Blakers–Massey Theorem, \(\lambda \) is a homotopy equivalence in dimensions less than \(4n-2\), so up to multiplication by a unit, \(\lambda \) may be regarded as the inclusion of the bottom cell of F. Taking adjoints, \(\widetilde{f}\) factors as the composite \(S^{4n-3} \xrightarrow {\widetilde{\lambda }}\Omega F\xrightarrow {}\Omega P^{2n}(p^{r})\), where \(\widetilde{\lambda }\) is the adjoint of \(\lambda \). Now \(\widetilde{\lambda }\) is the inclusion of the bottom cell in \(\Omega F\), and Lemma 3.2 implies that the inclusion of this bottom cell has image equal to the generator of least degree in the kernel of \((\Omega i)_{*}\), which is [x, y]. Thus, there is a choice of generator \(\iota _{4n-3}\) in \(H_{4n-3}(S^{4n-3};{\mathbb {Z}}/p{\mathbb {Z}})\) such that \(\widetilde{f}_{*}(\iota _{4n-3})=[x,y]\). \(\square \)
The low degree calculations made so far now let us calculate \(H_{*}(\Omega V;{\mathbb {Z}}/p{\mathbb {Z}})\) and \((\Omega i)_{*}\) in full.
Proposition 3.4
Let V be a \((2n-2)\)-connected, \((4n-1)\)-dimensional Poincaré Duality complex with \(H_{2n-1}(V;{\mathbb {Z}})\cong {\mathbb {Z}}/p^{r}{\mathbb {Z}}\) for p a prime and \(r\ge 1\). Then, there is an algebra isomorphism
where \(\vert x\vert =2n-2\), \(\vert y\vert =2n-1\) and \(\beta ^{r}y=x\), where \(\beta ^{r}\) is the \(r^{th}\)-Bockstein. Further, in mod-p homology, the map \(\Omega P^{2n}(p^{r})\xrightarrow {\Omega i}\Omega V\) induces the algebra epimorphism \(T(x,y)\xrightarrow {}{\mathbb {Z}}/p{\mathbb {Z}}[x,y]\).
Proof
In general, if X is a simply connected CW-complex and R is a ring, then there is an Adams–Hilton model AH(X) for calculating \(H_{*}(\Omega X;R)\) as an algebra. The model is a differential graded algebra of the form \(T(a_{1},\ldots ,a_{k};d)\) where \(T(\ \ )\) is the free tensor algebra functor, there is a generator \(a_{i}\) for each cell of X, the degree of \(a_{i}\) is one less than the dimension of the corresponding cell, and d is a differential. There is an algebra isomorphism \(H(AH(X))\cong H_{*}(\Omega X; R)\).
To describe d, let \(X_{t}\) be the t-skeleton of X and let \(S^{t}\xrightarrow {f_{i}}X_{t}\) attach a \((t+1)\)-cell corresponding to \(a_{i}\). Let \(AH(X_{t})\) be the Adams–Hilton model obtained from AH(X) by restriction to the generators corresponding to cells in \(X_{t}\). Then, \(d(a_{i})\) is determined by the image of the adjoint \(S^{t-1}\xrightarrow {\widetilde{f}_{i}}\Omega X_{t}\) in the Adams–Hilton model \(AH(X_{t})\).
In our case, as V has three cells there is an Adams–Hilton model \(AH(V)=T(x,y,z;d)\) with \(\vert x\vert =2n-2\), \(\vert y\vert =2n-1\) and \(\vert z\vert =4n-2\), and an algebra isomorphism \(H(AH(V))\cong H_{*}(\Omega V;{\mathbb {Z}}/p{\mathbb {Z}})\). The inclusion of the \((4n-2)\)-skeleton of V is the map \(P^{2n}(p^{r})\xrightarrow {i}V\), so \(AH(P^{2n}(p^{r}))=T(x,y;d')\) is an Adams–Hilton model whose homology is isomorphic as an algebra to \(H_{*}(\Omega P^{2n}(p^{r});{\mathbb {Z}}/p{\mathbb {Z}})\). By the Bott–Samelson theorem, the latter is known to be T(x, y), so \(d'\) must be identically zero. Thus, in this case, \(AH(P^{2n}(p^{r}))\cong H_{*}(\Omega P^{2n}(p^{r});{\mathbb {Z}}/p{\mathbb {Z}})\), so to determine the differential dz, which corresponds to the attaching map \(S^{4n-2}\xrightarrow {f}P^{2n}(p^{r})\) for the top cell of V, we need to determine the image in mod-p homology of the adjoint \(S^{4n-3}\xrightarrow {\tilde{f}}\Omega P^{2n}(p^{r})\). By Lemma 3.3, this image is [x, y]. Thus, \(dz=[x,y]\), so we obtain algebra isomorphisms
Further, the skeletal inclusion \(P^{2n}(p^{r})\xrightarrow {i}V\) induces the map of Adams–Hilton models \(T(x,y;d')\xrightarrow {}T(x,y,z;d)\), which upon taking homology gives the projection \(T(x,y)\xrightarrow {(\Omega i)_{*}}{\mathbb {Z}}/p{\mathbb {Z}}[x,y]\). \(\square \)
Now specialize to p being an odd prime; we will return to \(p=2\) in Sect. 6. By [1], for \(m\le (2n-2)p\), the homotopy groups \(\pi _{m}(P^{2n}(p^{r}))\) have the property that \(p^{r}\cdot \pi _{m}(P^{2n}(p^{r}))\cong 0\). Notice that \(4n-2\le (2n-2)p\) for all \(n\ge 2\) and \(p\ge 3\). Thus, \(S^{4n-2}\xrightarrow {f}P^{2n}(p^{r})\) extends to a map \(g:P^{4n-1}(p^{r})\xrightarrow {}P^{2n}(p^{r})\), and there is a homotopy cofibration diagram

where q is the pinch map to the top cell and h is an induced map of cofibres. Let \(\widetilde{h}:S^{4n-2}\xrightarrow {}\Omega V\) be the adjoint of h.
Lemma 3.5
Let p be an odd prime and take mod-p homology. If \(n\ge 3\), then \(\widetilde{h}_{*}(\iota _{4n-2})=y^{2}\). If \(n=2\), then \(\widetilde{h}_{*}(\iota _{4n-2})=y^{2}+t\cdot x^{3}\) for some \(t\in {\mathbb {Z}}/p{\mathbb {Z}}\).
Proof
Let \(\widetilde{g}:P^{4n-2}(p^{r})\xrightarrow {}\Omega P^{2n}(p^{r})\) be the adjoint of g and first consider \(\widetilde{g}_{*}\). By Lemma 3.3, in mod-p homology, we have \(\widetilde{f}_{*}(\iota _{4n-3})=[x,y]\). So if u and v are the generators in dimensions \(4n-3\) and \(4n-2\) of \(H_{*}(P^{4n-2}(p^{r});{\mathbb {Z}}/p{\mathbb {Z}})\), respectively, then the left square in (1) implies that \(\widetilde{g}_{*}(u)=[x,y]\). The naturality of the Bockstein therefore implies that \([x,y]=\widetilde{g}_{*}(u)=\widetilde{g}_{*}(\beta ^{r}(v))=\beta ^{r}(\widetilde{g}_{*}(v))\). The only generator of \(H_{4n-2}(\Omega P^{2n}(p^{r});{\mathbb {Z}}/p{\mathbb {Z}})\) with a nonzero \(r^{th}\)-Bockstein is \(\beta ^{r}(y^{2})=xy-yx= [x,y]\). Thus, \(\widetilde{g}_{*}(v)=y^{2}+z\) where \(\beta ^{r}(z)=0\). If \(n\ge 3\) then, for degree reasons, the only generator of \(H_{4n-2}(\Omega P^{2n}(p^{r});{\mathbb {Z}}/p{\mathbb {Z}})\) is \(y^{2}\). Thus, \(\widetilde{g}_{*}(v)=y^{2}\). If \(n=2\), then \(H_{4n-2}(\Omega P^{2n}(p^{r});{\mathbb {Z}}/p{\mathbb {Z}})\) has one other generator, that being \(x^{3}\), so  for some
for some  .
.
Next, consider \(\widetilde{h}_{*}\). Note that q is the suspension of the pinch map \(P^{4n-2}(p^{r})\xrightarrow {{\bar{q}}}S^{4n-2}\). Taking adjoints for the right square in (1) then implies that \(\Omega i\circ \widetilde{g}\simeq \widetilde{h}\circ {\bar{q}}\). Since \({\bar{q}}_{*}(v)\) is a choice of \(\iota _{4n-2}\) and \((\Omega i)_{*}\) is an epimorphism by Proposition 3.4, from the description of \(\widetilde{g}_{*}(v)\) we obtain \(\widetilde{h}_{*}(\iota _{4n-2})=y^{2}\) if \(n\ge 3\) and \(\widetilde{h}_{*}(\iota _{4n-2})=y^{2}+t\cdot x^{3}\) for some \(t\in {\mathbb {Z}}/p{\mathbb {Z}}\) if \(n=2\). \(\square \)
Remark 3.6
Observe that (1) implies that in mod-q homology for q a prime different from p, or in rational homology, the map h induces an isomorphism.
For any prime p, let \(S^{2n-1}\{p^{r}\}\) be the homotopy fibre of the degree \(p^{r}\) map on \(S^{2n-1}\). The principal fibration \(\Omega S^{2n-1} \xrightarrow {}S^{2n-1}\{p^{r}\}\xrightarrow {}S^{2n-1}\) is induced by the degree \(p^{r}\) map so the mod-p homology Serre spectral sequence collapses at the \(E^{2}\)-term, giving an isomorphism of \({\mathbb {Z}}/p{\mathbb {Z}}\)-modules
where \(\vert a\vert =2n-1\), \(\vert b\vert =2n-2\) and \(\beta ^{r}(a)=b\). Since \(P^{2n}(p^{r})\) is the homotopy cofibre of the degree \(p^{r}\) map on \(S^{2n-1}\), there is a homotopy fibration diagram

where j is the inclusion of the bottom cell and s is an induced map of fibres. Observe that j is the suspension of the map \({\bar{j}}:S^{2n-2}\xrightarrow {}P^{2n-1}(p^{r})\) that includes the bottom cell, and this inclusion induces an isomorphism in degree \(2n-2\) in mod-p homology. The naturality of the Bott–Samelson Theorem therefore implies that \((\Omega j)_{*}=(\Omega \Sigma {\bar{j}})_{*}\) is an algebra map sending \({\mathbb {Z}}/p{\mathbb {Z}}[b]\) isomorphically onto the subalgebra \({\mathbb {Z}}/p{\mathbb {Z}}[x]\subseteq T(x,y)\). The left square in (2) then implies that \(s_{*}\) sends \({\mathbb {Z}}/p{\mathbb {Z}}[b]\subseteq H_{*}(S^{2n-1}\{p^{r}\};{\mathbb {Z}}/p{\mathbb {Z}})\) isomorphically onto the subalgebra \({\mathbb {Z}}/p{\mathbb {Z}}[x]\subseteq T(x,y)\). The \(r^{th}\)-Bockstein is a differential, implying that \(s_{*}\) sends \(\Lambda (a)\otimes {\mathbb {Z}}/p{\mathbb {Z}}[b]\) isomorphically onto the sub-module \(\Lambda (y)\otimes {\mathbb {Z}}/p{\mathbb {Z}}[x]\subseteq T(x,y)\).
Let t be the composite
Then, the description of \(s_{*}\) implies that \(t_{*}\) injects onto the submodule \(\Lambda (y)\otimes {\mathbb {Z}}/p{\mathbb {Z}}[x]\subseteq {\mathbb {Z}}/p{\mathbb {Z}}[x,y]\). Let e be the composite
where \(\mu \) is the loop space multiplication. Again, we focus on odd primes, leaving \(p=2\) to Sect. 6.
Proposition 3.7
Let p be an odd prime. If \(n\ge 2\), then the map \(S^{2n-1}\{p^{r}\}\times \Omega S^{4n-1}\xrightarrow {e}\Omega V\) is a homotopy equivalence.
Proof
We will show that after localizing at each prime and rationally, e is a homotopy equivalence. This would imply that e is an integral homotopy equivalence.
First consider the case when \(n\ge 3\). Localizing at p, \(H_{*}(\Omega S^{4n-1};{\mathbb {Z}}/p{\mathbb {Z}})\cong {\mathbb {Z}}/p{\mathbb {Z}}[c]\) for \(\vert c\vert =4n-2\). The restriction of \(\Omega h\) to the bottom cell of \(\Omega S^{4n-1}\) is \(\widetilde{h}\), so by Lemma 3.5, \((\Omega h)_{*}(c)=y^{2}\). As \((\Omega h)_{*}\) is an algebra map, it sends \({\mathbb {Z}}/p{\mathbb {Z}}[c]\) isomorphically onto the subalgebra \({\mathbb {Z}}/p{\mathbb {Z}}[y^{2}]\subseteq {\mathbb {Z}}/p{\mathbb {Z}}[x,y]\). The description of \(t_{*}\) then implies that \(e_{*}\) induces an isomorphism in mod-p homology, implying that e is a p-local homotopy equivalence by Whitehead’s Theorem. Localized at a prime \(q\ne p\) or rationally, \(S^{2n-1}\{p^{r}\}\) is contractible, V is equivalent to \(S^{4n-1}\), and Remark 3.6 implies that h is a q-local or rational homotopy equivalence. Thus, in these cases, e is also a q-local or rational homotopy equivalence.
Next, consider the case when \(n=2\). Localize at p. Going back to the description of V as a CW-complex, observe that the composite \(S^{6} \xrightarrow {f}P^{4}(p^{r})\xrightarrow {q}S^{4}\) is null homotopic, where q is the pinch map to the top cell. This is because the generator of \(\pi _{6}(S^{4})\cong {\mathbb {Z}}/2{\mathbb {Z}}\) cannot factor through an odd primary Moore space. Thus, q extends to a map \({\overline{q}}:V\xrightarrow {}S^{4}\). Since \({\overline{q}}\) extends q, in mod-p homology we have \(\Omega {\overline{q}}\) inducing the projection \({\mathbb {Z}}/p{\mathbb {Z}}[x,y]\xrightarrow {}{\mathbb {Z}}/p{\mathbb {Z}}[y]\). Now consider the composite \(\Omega S^{7} \xrightarrow {\Omega h}\Omega V\xrightarrow {\Omega {\overline{q}}}\Omega S^{4}\). The restriction of \(\Omega h\) to the bottom cell is \(\widetilde{h}\), so Lemma 3.5 implies that \((\Omega {\overline{q}}\circ \Omega h)_{*}\) is an injection onto the subalgebra \({\mathbb {Z}}/p{\mathbb {Z}}[y^{2}]\subseteq {\mathbb {Z}}/p{\mathbb {Z}}[y]\). Since \(\Omega S^{4}\simeq S^{3}\times \Omega S^{7}\) because of the existence of an element of Hopf invariant one, there is a projection \(\pi :\Omega S^{4}\xrightarrow {}\Omega S^{7}\) which in mod-p homology projects \({\mathbb {Z}}/p{\mathbb {Z}}[y]\) onto \({\mathbb {Z}}/p{\mathbb {Z}}[y^{2}]\). Thus, the composition \(\Omega S^{7}\xrightarrow {\Omega h}\Omega V\xrightarrow {\Omega {\overline{q}}}\Omega S^{4}\xrightarrow {\pi }\Omega S^{7}\) induces an isomorphism in homology and so is a homotopy equivalence. Consequently, there is a homotopy equivalence \(\Omega V\simeq F\times \Omega S^{7}\) where F is the homotopy fibre of \(\pi \circ \Omega {\overline{q}}\). Notice that as \({\overline{q}}\) extends q, from the definition of s there is a homotopy commutative diagram

where E is the inclusion of the bottom cell. The top row is the definition of t. Consequently, \(\pi \circ \Omega {\overline{q}}\circ t\) is null homotopic, so t lifts to a map \({\overline{t}}:S^{3}\{p^{r}\}\xrightarrow {}F\). Since \(t_{*}\) is an injection in mod-p homology, so is \({\overline{t}}_{*}\). The decomposition \(\Omega V\simeq F\times \Omega S^{7}\) implies that F has the same Euler–Poincaré series as \(S^{3}\{p^{r}\}\); therefore, \({\overline{t}}_{*}\) is an isomorphism. Hence, the map e induces an isomorphism in mod-p homology and so is a p-local homotopy equivalence by Whitehead’s Theorem. Localizing at a prime \(q\ne p\) or rationally, arguing exactly as in the \(n\ge 3\) case shows that e is also a q-local or rational homotopy equivalence. \(\square \)
We can go further. In general, suppose that there is a homotopy pushout

of simply connected spaces where A is a suspension. The suspension hypothesis implies that the set of homotopy classes of maps [A, Z] is a group for any space Z. A Mayer–Vietoris style argument then shows that there is a homotopy cofibration
Since \(P^{4n-1}(p^{r})\) is the suspension of \(P^{4n-2}(p^{r})\), applying this to the right square in (1) we obtain a homotopy cofibration
Lemma 3.8
The map \(\Omega (P^{2n}(p^{r})\vee S^{4n-1})\xrightarrow {\Omega (i+h)} \Omega V\) has a right homotopy inverse.
Proof
By Proposition 3.7, there is a homotopy equivalence \(S^{2n-1}\{p^{r}\}\times \Omega S^{4n-1}\xrightarrow {t\times \Omega h}\Omega V\times \Omega V\xrightarrow {\mu }\Omega V\). By Lemma 2.3, to show that \(\Omega (i+h)\) has a right homotopy inverse, it suffices to show that both t and \(\Omega h\) lift through \(\Omega (i+h)\).
Let \(i_{1}:P^{2n}(p^{r})\xrightarrow {}P^{2n}(p^{r})\vee S^{4n-1}\) and \(i_{2}:S^{4n-1}\xrightarrow {}P^{2n}(p^{r})\vee S^{4n-1}\) be the inclusions of the left and right wedge summands, respectively. Then, \((i+h)\circ i_{1}=i\) and \((i+h)\circ i_{2}=h\). By definition, \(t=\Omega i\circ s\), so the composite
equals t, while \(\Omega S^{4n-1}\xrightarrow {\Omega i_{2}}\Omega (P^{2n}(p^{r})\vee S^{4n-1})\xrightarrow {\Omega (i+h)}\Omega V\) is \(\Omega h\). Thus, both t and \(\Omega h\) lift through \(\Omega (i+h)\), as required. \(\square \)
Next, the homotopy fibre of \(\Omega (i+h)\) is identified. Let \(s:\Omega V\xrightarrow {}\Omega (P^{2n}(p^{r})\vee S^{4n-1})\) be a right homotopy inverse for \(\Omega (i+h)\). Let \(\gamma \) be the composite
Let \(\mathfrak {g}=g-q\).
Proposition 3.9
There is a homotopy fibration
which splits after looping to give a homotopy equivalence
Proof
Since there is a homotopy cofibration \(P^{4n-1}(p^{r}) \xrightarrow {\mathfrak {g}}P^{2n}(p^{r})\vee S^{4n-1}\xrightarrow {i+h}V\) and, by Lemma 3.8, \(\Omega (i+h)\) has a right homotopy inverse, the assertions follow immediately from Theorem 2.1. \(\square \)
Note that Proposition 3.7 proves Theorem 1.1 in the special case when \(M=V\) while Proposition 3.9 proves Theorems 1.2.
4 The general case when \(H^{2n}(M;{\mathbb {Z}})\) is odd torsion
Let M be a \((2n-2)\)-connected \((4n-1)\)-dimensional Poincaré Duality complex such that \(n\ge 2\) and
where each \(p_{k}\) is an odd prime. Then, the 2n-skeleton \(M_{2n}\) of M is homotopy equivalent to a wedge of Moore spaces
For \(1\le k\le \ell \), let \(a_{k}\in H^{2n-1}(M;{\mathbb {Z}}/p_{k}{\mathbb {Z}})\) and \(b_{k}\in H^{2n}(M;{\mathbb {Z}}/p_{k}{\mathbb {Z}})\) be generators corresponding to the wedge summand \(P^{2n}(p_{k}^{r_{k}})\) of \(M_{2n}\). In [6, Section 6], Beben and Wu used a Poincaré Duality argument to prove the following.
Lemma 4.1
Let \(p\in \{p_{1},\ldots ,p_{\ell }\}\) be an odd prime. Let \(\{i_{1},\ldots ,i_{t}\}\subseteq \{1,\ldots ,\ell \}\) be the subset satisfying \(p_{i_{j}}=p\) and let \(r=\max \{r_{i_{1}},\ldots ,r_{i_{t}}\}\). If \(p_{i_{j}}^{r_{i_{j}}}=p^{r}\), then \(a_{i_{j}}\cup b_{i_{j}}\) is a generator of \(H^{4n-1}(M;{\mathbb {Z}}/p{\mathbb {Z}})\).
As in the Introduction, let m be the least common multiple of \(\{p_{1}^{r_{1}},\ldots ,p_{\ell }^{r_{\ell }}\}\) and let \(m={\bar{p}}_{1}^{{\bar{r}}_{1}}\cdots {\bar{p}}_{s}^{{\bar{r}}_{s}}\) be its prime decomposition. Notice that \(\{{\bar{p}}_{1},\ldots ,{\bar{p}}_{s}\}\) is the set of distinct primes in \(\{p_{1},\ldots ,p_{\ell }\}\) and each \({\bar{r}}_{j}\) is the maximum power of \({\bar{p}}_{j}\) appearing in the list \(\{p_{1}^{r_{1}},\ldots ,p_{\ell }^{r_{\ell }}\}\). In general, if a and b are coprime, then by [12, proof of Proposition 1.5] there is a homotopy equivalence \(P^{t}(ab)\simeq P^{t}(a)\vee P^{t}(b)\). In our case, since \(\{{\bar{p}}_{1},\ldots ,{\bar{p}}_{s}\}\) are distinct primes and \(m={\bar{p}}_{1}^{{\bar{r}}_{1}}\cdots {\bar{p}}_{s}^{{\bar{r}}_{s}}\), there is a homotopy equivalence
Therefore, \(M_{2n}\) can be rewritten as
where \(\Sigma A\) is the wedge of the remaining Moore spaces in \(M_{2n}\).
Define \(j'\) and j by the composites
Define the space V and the map \(\mathfrak {h}\) by the homotopy cofibration
Then, V is a three-cell complex, \(V=P^{2n}(m)\cup e^{4n-1}\), and the inclusion of the \((4n-2)\)-skeleton is given by the composite
Observe that Lemma 4.1 implies that V is a Poincaré Duality complex since the power of each \({\bar{p}}_{j}\) appearing as a factor of \(m={\bar{p}}_{1}^{{\bar{r}}_{1}}\cdots {\bar{p}}_{s}^{{\bar{r}}_{s}}\) is maximal.
Let \(F:S^{4n-2}\xrightarrow {}M_{2n}\) be the attaching map for the top cell of M. Define f by the composite \(f:S^{4n-2} \xrightarrow {F}M_{2n}\xrightarrow {\mathfrak {q}}P^{2n}(m)\) where \(\mathfrak {q}\) collapses \(\Sigma A\) in \(M_{2n}\simeq P^{2n}(m)\vee \Sigma A\) to a point. Observe that there is a homotopy pushout diagram pushout diagram

that defines the map \(i'\). By definition of \(\mathfrak {q}\) the composite \(P^{2n}(m)\hookrightarrow P^{2n}(m)\vee \Sigma A \xrightarrow {\simeq }M_{2n}\xrightarrow {\mathfrak {q}}P^{2n}(m)\) is the identity map. Therefore, \(i'\) is homotopic to the composite \(P^{2n}(m)\hookrightarrow P^{2n}(m)\vee \Sigma A\xrightarrow {\simeq }M_{2n}\xrightarrow {}M\xrightarrow {\mathfrak {h}}V\), which, by definition of \(j'\), is \(\mathfrak {h}\circ j'\). But \(\mathfrak {h}\circ j'\) is the definition of i, so we have \(i'=i\). Therefore, f is the attaching map for the top cell of V, and F is a lift of f through \(\mathfrak {q}\).
We wish to show that \(\Omega \mathfrak {h}\) has a right homotopy inverse. Doing so will involve decomposing \(\Omega V\) in a manner analogous to that for the special case when \(m=p^{r}\) in Sect. 3. We first aim for the analogue of (1).
Lemma 4.2
The map \(S^{4n-2}\xrightarrow {F}M_{2n}\) extends to a map \(G:P^{4n-1}(m)\xrightarrow {}M_{2n}\).
Proof
It is equivalent to show that the map F has order m, and showing this is equivalent to showing that the adjoint \(\widetilde{F}:S^{4n-3}\xrightarrow {}\Omega M_{2n}\) of F has order m.
Since \(M_{2n}\simeq \bigvee _{k=1}^{\ell } P^{2n}(p_{k}^{r_{k}})\), by the Hilton–Milnor Theorem
where \(1\le j_{1},j_{2}\le \ell \), \(j_{1}\ne j_{2}\), and N is \((4n-2)\)-connected. Thus, \(\widetilde{F}\) is a sum of maps of the form \(\widetilde{F}_{k}:S^{4n-3}\xrightarrow {}\Omega P^{2n}(p_{k}^{r_{k}})\) and \(\widetilde{F}_{j}:S^{4n-3}\xrightarrow {}\Omega (\Sigma P^{2n-1}(p_{j_{1}}^{r_{j_{1}}})\wedge P^{2n-1}(p_{j_{2}}^{r_{j_{2}}}))\). As before, by [1] each map \(\widetilde{F}_{k}\) has order at most \(p_{k}^{r_{k}}\). As \(p_{k}^{r_{k}}\) is a factor of m, we obtain a null homotopy for \(\widetilde{F}_{k}\circ m\), for \(1\le k\le \ell \). By [12, Corollary 6.6], if p and q are distinct primes then \(P^{a}(p^{r})\wedge P^{b}(q^{s})\) is contractible, and if \(r\le s\) and \(p^{r}\ne 2\), then there is a homotopy equivalence \(P^{a}(p^{r})\wedge P^{b}(p^{s})\simeq P^{a+b}(p^{r})\vee P^{a+b-1}(p^{r})\). Thus, if \(p_{j_{1}}\ne p_{j_{2}}\), then \(\widetilde{F}_{j}\) is null homotopic, while if \(p_{j_{1}}=p_{j_{2}}\) and we assume without loss of generality that \(r_{j_{1}}\le r_{j_{2}}\), then for dimensional reasons the Hilton-Milnor Theorem implies that \(\widetilde{F}_{j}\) factors through \(\widehat{F}_{j}:S^{4n-3}\xrightarrow {}\Omega P^{4n-1}(p_{j_{1}}^{r_{j_{1}}})\times \Omega P^{4n-2}(p_{j_{1}}^{r_{j_{1}}})\). For dimension and connectivity reasons, \(\widehat{F}_{j}\) is trivial on the \(\Omega P^{4n-1}(p_{j_{1}}^{r_{j_{1}}})\) factor and is a multiple of the inclusion of the bottom cell on the \(\Omega P^{4n-2}(p_{j_{1}}^{r_{j_{1}}})\) factor. This inclusion has order \(p_{j_{1}}^{r_{j_{1}}}\), so as \(p_{j_{1}}^{r_{j_{1}}}\) is a factor of m, we obtain a null homotopy for \(\widehat{F}_{j}\circ m\), and therefore one for \(\widetilde{F}\circ m\). Hence, \(F\circ m\) is null homotopic. \(\square \)
Lemma 4.2 implies that there is a homotopy cofibration diagram

where I is the skeletal inclusion, q is the pinch map to the top cell, and H is an induced map of cofibres. Combining this with (5) gives an iterated homotopy pushout diagram

We now give a homotopy decomposition of \(\Omega V\). By definition, \(P^{2n}(m)\simeq \bigvee _{j=1}^{s} P^{2n}({\bar{p}}_{j}^{{\bar{r}}_{j}})\). For \(1\le j\le s\), define \(S_{j}\) by the composite
where \(s_{j}\) is from (2) and \(i_{j}\) is the inclusion of the \(j^{th}\)-wedge summand. Define S by the composite
and define T by the composite
Finally, define e by the composite
Proposition 4.3
If \(n\ge 2\), then the map e is a homotopy equivalence.
Proof
We will show that after localizing at each prime p and rationally, e is a homotopy equivalence. This would imply that e is an integral homotopy equivalence.
Localize at a prime p where \(p={\bar{p}}_{j}\) for some \(1\le j\le s\). Let \(r={\bar{r}}_{j}\). If q is a prime distinct from p, then the Moore space \(P^{a}(q^{s})\) is contractible for \(a\ge 2\). Therefore, as \(P^{a}(m)\simeq \bigvee _{j=1}^{s} P^{a}({\bar{p}}_{j}^{{\bar{r}}_{j}})\) and the primes \({\bar{p}}_{1},\ldots ,{\bar{p}}_{s}\) are distinct, there is a p-local homotopy equivalence.
Applying this to (7), we obtain a p-local homotopy cofibration diagram

where \(g=\mathfrak {q}\circ G\) and \(h=\mathfrak {h}\circ H\). This is a p-local version of (1) so we may argue as in Lemma 3.5 and Proposition 3.7 to show that the composite
is a p-local homotopy equivalence. Notice that the spaces \(S^{2n-1}\{{\bar{p}}_{j}^{{\bar{r}}_{j}}\}\) are contractible if \({\bar{p}}_{j}\ne p\), so in fact we have shown that e is a p-local homotopy equivalence.
Next, localize at a prime \(p\notin \{{\bar{p}}_{1},\ldots ,{\bar{p}}_{s}\}\). Then, \(P^{a}(m)\) for \(a\ge 2\) and the Moore space wedge summands of \(M_{2n}\) are all contractible. Therefore, in (7), both M and V are homotopy equivalent to \(S^{4n-1}\) and the maps H and \(\mathfrak {h}\) are both homotopy equivalences. On the other hand, the spaces \(S^{2n-1}\{{\bar{p}}_{j}^{{\bar{r}}_{j}}\}\) are also contractible so e reduces to \(\Omega (\mathfrak {h}\circ H)\), which we have just seen is a homotopy equivalence. The same argument shows that e is also a rational homotopy equivalence. \(\square \)
Proposition 4.3 will be used to show that the map \(\Omega M\xrightarrow {\Omega \mathfrak {h}}\Omega V\) has a right homotopy inverse. Thinking ahead, this is drawn from a slightly stronger statement.
Lemma 4.4
The composite \(\Omega (P^{2n}(m)\vee S^{4n-1})\xrightarrow {\Omega (j'+H)} \Omega M\xrightarrow {\Omega \mathfrak {h}}\Omega V\) has a right homotopy inverse.
Proof
By Proposition 4.3, there is a homotopy equivalence
By Lemma 2.3, to show that \(\Omega \mathfrak {h}\circ \Omega (j'+H)\) has a right homotopy inverse, it suffices to show that both T and \(\Omega (\mathfrak {h}\circ H)\) lift through \(\Omega \mathfrak {h}\circ \Omega (j'+H)\).
By definition, T is the composite \(\prod _{j=1}^{s} S^{2n-1}\{{\bar{p}}_{j}^{{\bar{r}}_{j}}\} \xrightarrow {S}\Omega P^{2n}(m)\xrightarrow {\Omega i}\Omega V\) and, by definition, i is the composite \(P^{2n}(q) \xrightarrow {j'}M\xrightarrow {\mathfrak {h}}V\). Thus, \(T=\Omega \mathfrak {h}\circ \Omega j'\circ S\). This implies that T lifts through \(\Omega \mathfrak {h}\circ \Omega j'\) and hence through \(\Omega \mathfrak {h}\circ \Omega (j'+H)\). Clearly, \(\Omega (\mathfrak {h}\circ H)\simeq \Omega \mathfrak {h}\circ \Omega H\) lifts through \(\Omega \mathfrak {h}\circ \Omega (j'+H)\). \(\square \)
Corollary 4.5
The map \(\Omega M\xrightarrow {\Omega \mathfrak {h}}\Omega V\) has a right homotopy inverse.
We can now prove Theorem 1.1.
Proof of Theorem 1.1
From the homotopy cofibration \(\Sigma A \xrightarrow {j}M\xrightarrow {\mathfrak {h}}V\) and the right homotopy inverse of \(\Omega \mathfrak {h}\) in Corollary 4.5, parts (a) and (b) follow immediately from Theorem 2.1. Part (c) is Proposition 4.3.\(\square \)
Remark 4.6
By Theorem 1.1, \(\Omega M\simeq \Omega V\times \Omega ((\Sigma \Omega V\wedge A)\vee \Sigma A)\). We claim that the space \((\Sigma \Omega V\wedge A)\vee \Sigma A\) is homotopy equivalent to a wedge W of spheres and odd primary Moore spaces. If so, then we may more simply write \(\Omega M\simeq \Omega V\times \Omega W\). To prove the claim, fist consider
In general, if B and C are path-connected spaces, then \(\Sigma (B\times C)\simeq \Sigma B\vee \Sigma C\vee (\Sigma B\wedge C)\); by [10], the space \(\Sigma \Omega S^{t+1}\) is homotopy equivalent to a wedge of suspended spheres; by [9], the space \(\Sigma S^{2n-1}\{p^{r}\}\) is homotopy equivalent to a wedge of mod-\(p^{r}\) Moore spaces; and by [12, Corollary 6.6], there is a homotopy equivalence \(P^{a}(p^{r})\wedge P^{b}(p^{s})\simeq P^{a+b}(p^{s})\vee P^{a+b-1}(p^{s})\) if \(s\le r\) and p is odd while \(P^{a}(p^{r})\wedge P^{b}(q^{s})\) is contractible if p and q are distinct primes. Collectively, these statements imply that \(\Sigma \Omega V\) is homotopy equivalent to a wedge of spheres and odd primary Moore spaces. Since A is defined as a wedge of odd primary Moore spaces, we therefore also obtain that \((\Sigma \Omega V\wedge A)\vee \Sigma A\) is homotopy equivalent to a wedge of spheres and odd primary Moore spaces.
Next, we consider the analogue of Proposition 3.9. This will be done in two steps, first with respect to \(P^{2n}(m)\xrightarrow {i}V\) and then with respect to \(M_{2n}\xrightarrow {I}M\). First, the homotopy pushout

in (7) implies that there is a homotopy cofibration
Lemma 4.7
The map \(\Omega (P^{2n}(m)\vee S^{4n-1})\xrightarrow {\Omega (i+(\mathfrak {h}\circ H))} \Omega V\) has a right homotopy inverse.
Proof
This follows immediately from Lemma 4.4 since \(i=\mathfrak {h}\circ j'\). \(\square \)
Second, the homotopy pushout in (6) implies that there is a homotopy cofibration
Lemma 4.8
The map \(\Omega (M_{2n}\vee S^{4n-1})\xrightarrow {\Omega (I+H)} \Omega M\) has a right homotopy inverse.
Proof
The plan is to use the right homotopy inverse for \(\Omega (i+(\mathfrak {h}\circ H))\) in Lemma 4.7 and the naturality of Remark 2.2. This will be done in steps.
Step 1. By (4), \(M_{2n}\simeq \Sigma A\vee P^{2n}(m)\). Let \(\Sigma A\xrightarrow {a}M_{2n}\) be the inclusion of the wedge summand and recall that the composite \(\Sigma A \xrightarrow {a}M_{2n}\xrightarrow {I}M\) is the definition of the map j appearing in (5), whose cofibre is the map \(M\xrightarrow {\mathfrak {h}}V\). From this and the homotopy cofibration \(P^{4n-1}(m)\xrightarrow {G-q} M_{2n}\vee S^{4n-1}\xrightarrow {I+H}M\), we obtain a homotopy pushout diagram

where \(i_{2}\) is the inclusion of the second wedge summand, \(p_{1}\) is the pinch map onto the first wedge summand, and \(\overline{\mathfrak {h}}\) is defined as \(\mathfrak {h}\circ (I+H)\).
Step 2. By Lemma 4.4, \(\Omega \overline{\mathfrak {h}}\) has a right homotopy inverse \(s:\Omega V\xrightarrow {}\Omega (M_{2n}\vee S^{4n-1})\). Let \(s'\) be the composite \(s':\Omega V\xrightarrow {s} \Omega (M_{2n}\vee S^{4n-1})\xrightarrow {\Omega (I+H)}\Omega M\). Then, \(s'\) is a right homotopy inverse for \(\Omega \mathfrak {h}\) and there is a homotopy commutative diagram

Step 3. The homotopy cofibration \(\Sigma A \xrightarrow {j}M\xrightarrow {\mathfrak {h}}V\) and the existence of a right homotopy inverse \(s'\) for \(\Omega \mathfrak {h}\) led to the identification of the homotopy fibre of \(\mathfrak {h}\) as \((\Sigma \Omega V\wedge A)\vee \Sigma A\) via Theorem 2.1. Similarly, the homotopy cofibration
and the existence of a right homotopy inverse s for \(\Omega \overline{\mathfrak {h}}\) lets us use Theorem 2.1 to identify the homotopy fibre of \(\overline{\mathfrak {h}}\) as \((\Sigma \Omega V\wedge (A\vee P^{4n-2}(m)))\vee (\Sigma A\vee P^{4n-1}(m)).\) The compatibility of the s and \(s'\) in (8) lets us apply the naturality property in Remark 2.2 to obtain a homotopy fibration diagram

Step 4. Finally, observe that the map \((\Sigma 1\wedge p_{1})\vee \Sigma p_{1}\) has a right homotopy inverse, and clearly the identity map on V does as well. Since \(\Omega (i+(\mathfrak {h}\circ H))\) has a right homotopy inverse by Lemma 4.7 and it factors as
\(\Omega \overline{\mathfrak {h}}\) also has a right homotopy inverse. Therefore, Lemma 2.4 implies that \(\Omega (I+H)\) has a right homotopy inverse. \(\square \)
Now we can prove Theorem 1.2.
Proof of Theorem 1.2
From the homotopy cofibration \(P^{4n-1}(m) \xrightarrow {\mathfrak {G}}M_{2n}\vee S^{4n-1}\xrightarrow {I+H}M\), where \(\mathfrak {G}=G-q\), and the right homotopy inverse for \(\Omega (I+H)\) in Lemma 4.8, the assertions follow immediately from Theorem 2.1. \(\square \)
5 An extension to some 2-torsion cases I
In this section, we consider a partial extension for parts (a) and (b) of Theorem 1.1 to cases involving 2-torsion. A full extension may not be possible due to issues involving Poincaré Duality as indicated by the lack of a 2-primary analogue of Lemma 4.1. Let M be a \((2n-2)\)-connected \((4n-1)\)-dimensional Poincaré Duality complex such that \(n\ge 2\) and
where each \(p_{k}\) is an odd prime and \(\ell \ge 1\). Then, the 2n-skeleton \(M_{2n}\) of M is homotopy equivalent to a wedge of Moore spaces
Note the absence of mod-2 Moore spaces: this has to do with the smash product of two mod-2 Moore spaces as described in Remark 5.2.
As in the Introduction and Sect. 4, let m be the least common multiple of \(\{p_{1}^{r_{1}},\ldots ,p_{\ell }^{r_{\ell }}\}\) and let \(m={\bar{p}}_{1}^{{\bar{r}}_{1}}\cdots {\bar{p}}_{s}^{{\bar{r}}_{s}}\) be its prime decomposition. Notice that \(\{{\bar{p}}_{1},\ldots ,{\bar{p}}_{s}\}\) is the set of distinct primes in \(\{p_{1},\ldots ,p_{\ell }\}\) and each \({\bar{r}}_{j}\) is the maximum power of \({\bar{p}}_{j}\) appearing in the list \(\{p_{1}^{r_{1}},\ldots ,p_{\ell }^{r_{\ell }}\}\). Therefore, \(M_{2n}\) can be rewritten as
where \(\Sigma A\) is the wedge of the remaining Moore spaces in \(M_{2n}\).
Define j and \(j'\) by the composites
Define the spaces V and \(V'\), and the maps \(\mathfrak {h}\) and \(\mathfrak {h}'\), by the homotopy pushout diagram

Then, \(V=P^{2n}(m)\cup e^{4n-1}\) and \(V'=\big (P^{2n}(m)\vee \bigvee _{s=1}^{t} P^{2n}(2^{r_{s}})\big )\cup e^{4n-1}\). Observe that the bottom row implies that there is a p-local homotopy equivalence \(V\simeq V'\) for any odd prime p.
We wish to show that \(\Omega \mathfrak {h}'\) has a right homotopy inverse. That is, the analogue of Theorem 1.1 we aim to prove is based on a decomposition of \(\Omega M\) involving \(\Omega V'\) as a factor rather than \(\Omega V\). To do so we will take a local-to-global approach by applying the fracture theorem of [11, Theorem 8.1.3]. However, first we need a functional version of Lemma 4.2 and a modification of Proposition 4.3.
Let \(F:S^{4n-2}\xrightarrow {}M_{2n}\) be the attaching map for the top cell of M. Define f and \(f'\) by the composites
where \(\mathfrak {q}\) and \(\mathfrak {q}'\) collapse \(\Sigma A\vee \bigvee _{s=1}^{t} P^{2n}(2^{r_{s}})\) and \(\Sigma A\) in \(M_{2n}\) to a point, respectively. Then, f and \(f'\) are the attaching maps for the top cell of V and \(V'\), respectively. In particular, there is a homotopy pushout

where i is the inclusion of the 2n-skeleton.
Let \(\widehat{m}\) be the least common multiple of \(\{p_{1}^{r_{1}},\ldots ,p_{\ell }^{r_{\ell }}\}\cup \{2^{r_{1}},\ldots ,2^{r_t}\}\). In particular, \(\widehat{m}=2^v m\) with \(2^v=\mathrm{max}\{2^{r_{1}},\ldots ,2^{r_t}\}\). Anticipating that the upper bound on the exponent for \(\pi _{*}(P^{2n}(2^{r}))\) in [1] is higher than for odd primes, let \(\widetilde{v}=v+1\) and let \(\widetilde{m}=2^{\widetilde{v}}m\). By [12, proof of Proposition 1.5], there is a canonical morphism of homotopy cofibrations

where Q collapses \(P^{4n-1}(\widetilde{m})\simeq P^{4n-1}(2^{\widetilde{v}})\vee P^{4n-1}(m)\) to \(P^{4n-1}(m)\) and \(\widetilde{q}\) and q are the pinch maps to the top cell. The following lemma is the analogue of Lemma 4.2.
Lemma 5.1
The maps \(S^{4n-2}\xrightarrow {F}M_{2n}\) and \(S^{4n-2}\xrightarrow {f}P^{2n}(m)\) extend to maps \(G:P^{4n-1}(\widetilde{m})\xrightarrow {}M_{2n}\) and \(g:P^{4n-1}(m)\xrightarrow {}P^{2n}(m)\), respectively. Moreover, the extensions are compatible, that is, there is the homotopy commutative diagram

Proof
The existence of G follows exactly as in the proof of Lemma 4.2, using the fact that [1] implies that \(2^{r+1}\cdot \pi _{4n-2}(P^{2n}(2^{r}))\cong 0\) if \(r\ge 2\).
A choice of the map g is given by Lemma 4.2, but we need to make sure that a choice is made that also gives the asserted homotopy commutative diagram. Notice that there is a homotopy cofibration \(P^{4n-1}(2^{\widetilde{v}}) \xrightarrow {\omega }P^{4n-1}(\widetilde{m})\xrightarrow {Q}P^{4n-1}(m)\) where \(\omega \) is the inclusion into \(P^{4n-1}(\widetilde{m})\simeq P^{4n-1}(m)\vee P^{4n-1}(2^{\widetilde{v}})\). If the composite
is null homotopic, then \(\mathfrak {q}\circ G\) extends along Q to a map \(g:P^{4n-1}(m)\xrightarrow {}P^{2n}(m)\) and we are done. To see that \(\mathfrak {q}\circ G\circ \omega \) is null homotopic, observe that it represents an element of 2-torsion in \(\pi _{4n-2}(P^{2n}(m))\). But the space \(P^{2n}(m)\) is 2-locally contractible since m is a product of odd primes. \(\square \)
Remark 5.2
It is the use of Lemma 4.2 that prevents us from considering 2-torsion in the cohomology of M. Its proof uses the property that the smash product \(P^{a}(p^{r})\wedge P^{b}(p^{r})\) is homotopy equivalent to a wedge of two mod-\(p^{r}\) Moore spaces: this only holds if \(p^{r}\ne 2\).
From the extension of F to G in Lemma 5.1, we obtain a homotopy cofibration diagram

where I is the skeletal inclusion and H is an induced map of cofibres.
Lemma 5.3
There is a homotopy commutative diagram

for a map h satisfying \(h\circ q\simeq i\circ g\).
Proof
Consider the cube

where the map h will be defined momentarily. The top face is a homotopy pushout by (13), the rear face homotopy commutes by (12), the left face homotopy commutes by Lemma 5.1, and the bottom face homotopy commutes by (12). The homotopy commutativity of these four faces implies that \(i\circ g\circ Q\simeq \mathfrak {h}\circ H\circ \widetilde{q}\). Therefore, as the top face is a homotopy pushout, there is a pushout map \(h:S^{4n-1}\xrightarrow {}V\) such that \(h\circ q\simeq i\circ g\) and \(h\circ 2^{\widetilde{v}}\simeq \mathfrak {h}\circ H\). In particular, the homotopy \(h\circ 2^{\widetilde{v}}\simeq \mathfrak {h}\circ H\) gives the homotopy commutative diagram asserted by the lemma. \(\square \)
Next, we modify Proposition 4.3. Similarly to the map e in Sect. 4, define \(e'\) by the composite
Notice that \(e'\) replaces the map \(\mathfrak {h}\circ H\) in the definition of e appearing in Sect. 4 by h, but the property from Lemma 5.3 that \(h\circ q\simeq i\circ g\) ensures that the argument for Proposition 4.3 also applies to \(e'\).
Proposition 5.4
If \(n\ge 2\), then the map \(e'\) is a homotopy equivalence.
Finally, we show that \(\Omega \mathfrak {h}'\) has a right homotopy inverse using a local-to-global approach. Let \(T_o\) be the set of odd primes and \(T_e=\{2\}\).
Lemma 5.5
The map \(\Omega M\xrightarrow {\Omega \mathfrak {h}'}\Omega V'\) has:
-
(i)
a \(T_{o}\)-local right homotopy inverse \(\theta _{o}:\Omega V'\xrightarrow {}\Omega M\) and
-
(ii)
a \(T_{e}\)-local right homotopy inverse \(\theta _{e}:\Omega V'\xrightarrow {}\Omega M\),
both of whose rationalizations are the identity map on \(\Omega S^{4n-1}\).
Proof
For (i), by (11) the composite \(M \xrightarrow {\mathfrak {h}'}V'\xrightarrow {}V\) is homotopic to \(M\xrightarrow {\mathfrak {h}}V\). As \(V'\xrightarrow {}V\) is a \(T_{o}\)-local equivalence, to show that \(\Omega \mathfrak {h}'\) has a \(T_{o}\)-local right homotopy inverse it suffices to prove that \(\Omega \mathfrak {h}\) has a \(T_{o}\)-local right homotopy inverse \(\theta '_{o}:\Omega V\xrightarrow {}\Omega M\). We then take \(\theta _{o}\) to be the composite \(\Omega V' \xrightarrow {\simeq }\Omega V\xrightarrow {\theta '_{o}}\Omega M\).
Localize spaces and maps at \(T_{o}\). Arguing as for Lemma 4.4 and using Lemma 5.3 gives a homotopy commutative diagram

while Proposition 5.4 implies that the bottom row is the homotopy equivalence \(e'\). Therefore, \(\theta '_{o}=\Omega (j'+H)\circ \mu \circ (S\times \Omega (\frac{1}{2^{\widetilde{v}}}))\circ e'\) is a (\(T_{o}\)-local) right homotopy inverse for \(\Omega \mathfrak {h}\). Rationally, \(\mathfrak {h}\) is the identity map on \(S^{4n-1}\), as is h since \(e'\) is an integral homotopy equivalence (technically, h could have degree \(\pm 1\) but if it is degree \(-1\) we can replace h by its negative). Thus, the homotopy commutativity of (15) implies that, rationally, \(\theta '_{o}\) must be the identity map on \(\Omega S^{4n-1}\).
For (ii), the homotopy cofibration \(\Sigma A \xrightarrow {j'}M\xrightarrow {\mathfrak {h}'}V'\) from (11) implies that \(\mathfrak {h}'\) is a \(T_{e}\)-local homotopy equivalence since \(\Sigma A\) is a wedge of odd primary Moore spaces and so is contractible when localized at 2. Therefore, \(\mathfrak {h}'\) has a \(T_{e}\)-local right homotopy inverse \(\theta '_{e}\). Further, as the rationalization of \(\mathfrak {h}'\) is the identity map on \(S^{4n-1}\), so is the rationalization of \(\theta '_{e}\). Thus, \(\theta _{e}=\Omega \theta '_{e}\) is a \(T_{e}\)-local right homotopy inverse for \(\Omega \mathfrak {h}'\) whose rationalization is the identity map on \(\Omega S^{4n-1}\). \(\square \)
The local right homotopy inverses for \(\Omega \mathfrak {h}'\) in Lemma 5.5 are now assembled into an integral one.
Lemma 5.6
The map \(\Omega M\xrightarrow {\Omega \mathfrak {h}'}\Omega V'\) has a right homotopy inverse \(\theta \).
Proof
By the fracture theorem of [11, Theorem 8.1.3], for any simply connected space X, there is a homotopy pullback

where \(X_{T_{o}}\), \(X_{T_{e}}\) and \(X_{\mathbb {Q}}\) are the \(T_{o}\), \(T_{e}\) and \(\mathbb {Q}\)-localizations of X, respectively, r is rationalization and \(\Delta \) is the diagonal map. In our case, consider the diagram

where \(\theta _o\) and \(\theta _e\), respectively, are the \(T_{o}\) and \(T_{e}\)-local right homotopy inverses for \(\Omega \mathfrak {h}'\) in Lemma 5.5 and \(\theta _{Q}\) is the rationalization of the identity map on \(\Omega S^{4n-1}\). The left square homotopy commutes by Lemma 5.5 and the right square commutes by the naturality of the diagonal map. By the fracture theorem, the homotopy pullback of the maps in the top row is \(\Omega V'\) and the homotopy pullback of the maps in the bottom row is \(\Omega M\). The pullback property for \(\Omega M\) and the homotopy commutativity of the two squares implies that there is a pullback map \(\theta :\Omega V'\xrightarrow {}\Omega M\) with the property that its \(T_{e}\)-localization is \(\theta _{e}\), its \(T_{o}\)-localization is \(\theta _{o}\) and its rationalization is \(\theta _{\mathbb {Q}}\). Thus, \(\theta \) is a right homotopy inverse for \(\Omega \mathfrak {h}'\) because it is when localized at any prime or rationally. \(\square \)
From the homotopy cofibration \(\Sigma A \xrightarrow {j'}M\xrightarrow {\mathfrak {h}'}V'\) and the right homotopy inverse \(\theta \) of \(\Omega \mathfrak {h}'\) in Lemma 5.6, the following theorem follows immediately from Theorem 2.1.
Theorem 5.7
Let M be a \((2n-2)\)-connected \((4n-1)\)-dimensional Poincaré Duality complex such that \(n\ge 2\) and
where each \(p_{k}\) is an odd prime, each \(r_s\ge 2\), and \(\ell \ge 1\). Then with \(V'\) and A chosen as above:
-
(a)
there is a homotopy fibration
$$\begin{aligned}(\Sigma \Omega V'\wedge A)\vee \Sigma A\xrightarrow {[\gamma ,j']+j'} M\xrightarrow {\mathfrak {h}'}V'\end{aligned}$$where \(\gamma \) is the composite \(\gamma :\Sigma \Omega V' \xrightarrow {\Sigma \theta }\Sigma \Omega M\xrightarrow {ev}M\);
-
(b)
the homotopy fibration in (a) splits after looping to give a homotopy equivalence
$$\begin{aligned}\Omega M\simeq \Omega V'\times \Omega ((\Sigma \Omega V'\wedge A)\vee \Sigma A).\end{aligned}$$
Note that when \(t=0\), Theorem 5.7 reduces to part (a) and (b) of Theorem 1.1. Note also that, unlike Theorems 1.1, 5.7 does not decompose \(\Omega V'\) any further.
6 An extension to some 2-torsion cases II
Finally, we consider an extension for part (c) of Theorem 1.1 to certain special cases involving 2-torsion. In general, when \(V=P^{2n}(2^{r})\cup e^{4n-1}\), it is unreasonable to expect a decomposition \(\Omega V\simeq S^{2n-1}\{2^{r}\}\times \Omega S^{4n-1}\) since this implies that the space \(S^{2n-1}\{2^{r}\}\) is an H-space. Often this is not the case, for example, if \(n=3\) or \(n\ge 5\) then \(S^{2n-1}\{2\}\) is not an H-space [8]. A full classification of when \(S^{2n-1}\{2^{r}\}\) is an H-space seems not to appear in the literature. However, by [7, Corollary 21.6], it is known that \(S^{3}\{2^{r}\}\) is an H-space if \(r\ge 3\) and \(S^{7}\{2^{r}\}\) is an H-space if \(r\ge 4\). In these cases, we show that the arguments in Sect. 3 hold, giving a decomposition of \(\Omega V\).
Lemma 3.3 and Proposition 3.4 were proved for all primes p. The first point in Sect. 3 where the restriction \(p\ge 3\) occurred was in the the existence of the extension g for f in (1). In general, it may not be the case that \(2^{r}\cdot \pi _{4n-2}(P^{2n}(2^{r}))\cong 0\). However, Sasao [13] showed that \(2^{r}\cdot \pi _{6}(P^{4}(2^{r}))\cong 0\) if \(r\ge 3\) and \(2^{r}\cdot \pi _{14}(P^{8}(2^{r}))\cong 0\) if \(r\ge 4\). Thus, in these cases, we obtain a homotopy cofibration diagram as in (1). The argument for Lemma 3.5 now goes through in exactly the same manner. The maps s, t and e following Lemma 3.5 were defined for all primes p, and the restriction to odd primes in Proposition 3.7 was present only to: (i) invoke Lemma 3.5 and (ii) in the \(n=2\) case, ensure that the composite \(S^{6} \xrightarrow {f}P^{4}(2^{r})\xrightarrow {q}S^{4}\) is null homotopic so that there is an extension of q to a map \(V\xrightarrow {}S^{4}\). Therefore, Proposition 3.7 will hold: (i) for \(n=4\) and \(r\ge 4\), and (ii) for \(n=2\) and \(r\ge 3\) with the extra assumption that there is a map \(V\xrightarrow {}S^{4}\) inducing a surjection in mod-2 homology.
Proposition 6.1
Let \(V=P^{2n}(2^{r})\cup e^{4n-1}\) be a Poincaré Duality complex.
-
(a)
If \(n=2\), \(r\ge 3\) and there is a map \(V\xrightarrow {}S^{4}\) inducing a surjection in mod-2 homology, then there is a homotopy equivalence \(\Omega V\simeq S^{3}\{2^{r}\}\times \Omega S^{7}\);
-
(b)
if \(n=4\) and \(r\ge 4\), then there is a homotopy equivalence \(\Omega V\simeq S^{7}\{2^{r}\}\times \Omega S^{15}\).
For example, if \(\tau (S^{2n})\) is the unit tangent bundle of \(S^{2n}\) then, as a CW-complex, \(\tau (S^{2n})=P^{2n}(2)\cup e^{4n-1}\), and there is a fibration \(S^{2n-1} \xrightarrow {}\tau (S^{2n})\xrightarrow {}S^{2n}\). For \(r\ge 2\), define the “mod-\(2^{r}\) tangent bundle” by the homotopy pullback

where \({\underline{2}}^{r-1}\) is the map of degree \(2^{r-1}\). As a CW-complex, \(\tau _{r}(S^{2n})=P^{2n}(2^{r})\cup e^{4n-1}\) and \(H^{*}(\tau _{r}(S^{2n}))\) satisfies Poincaré Duality. Proposition 6.1 implies that there are homotopy equivalences \(\Omega \tau _{r}(S^{4})\simeq S^{3}\{2^{r}\}\times \Omega S^{7}\) if \(r\ge 3\) and \(\Omega \tau _{r}(S^{8})\simeq S^{7}\{2^{r}\}\times \Omega S^{15}\) if \(r\ge 4\).
Remark 6.2
The argument for Proposition 6.1 is independent of prior knowledge that \(S^{3}\{2^{r}\}\) for \(r\ge 3\) or \(S^{7}\{2^{r}\}\) for \(r\ge 4\) are H-spaces. So the loop space decompositions of the mod-\(2^{r}\) tangent bundles is a new proof of this property, since the retractions of \(S^{3}\{2^{r}\}\) for \(r\ge 3\) and \(S^{7}\{2^{r}\}\) for \(r\ge 4\) off loop spaces imply that they are H-spaces. The previous argument in [7] examined the H-deviation of the degree \(2^{r}\) map.
Generalizing to the case \(V=P^{2n}(2m)\cup e^{4n-1}\) where m is divisible by more than one prime seems to be much more difficult.
Our argument breaks down with the loss of Lemma 4.1. It would be interesting to know if a different argument can be used to make progress.
Data Availability Statement
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
References
Barratt, M.G.: Spaces of finite characteristic. Q. J. Math. 11, 124–136 (1960)
Basu, S.: The homotopy type of the loops on \((n-1)\)-connected \((2n+1)\)-dimensional manifolds. In: Singh, M., Song, Y., Wu, J. (eds.) Algebraic Topology and Related Topics. Trends in Mathematics, pp. 1–25. Birkhauser, Singapore (2019)
Basu, S., Basu, S.: Homotopy groups of highly connected manifolds. Adv. Math. 337, 363–416 (2018)
Beben, P., Theriault, S.: The loop space homotopy type of simply-connected four-manifolds and their generalizations. Adv. Math. 262, 213–238 (2014)
Beben, P., Theriault, S.: Homotopy groups of highly connected Poincaré duality complexes. Doc. Math. 27, 183–211 (2022)
Beben, P., Wu, J.: The homotopy type of a Poincaré duality complex after looping. Proc. Edinb. Math. Soc. 58, 581–616 (2015)
Cohen, F.R.: A short course in some aspects of classical homotopy theory. In: Lecture Notes in Mathematics, vol. 1286, pp. 1–92. Springer (1987)
Cohen, F.R.: Applications of loop spaces to some problems in topolog. In: London Mathematical Society Lecture Note Series, vol. 139, pp. 10–20 (1989)
Cohen, F.R., Moore, J.C., Neisendorfer, J.A.: Torsion in homotopy groups. Ann. Math. 109, 121–168 (1979)
James, I.M.: Reduced product spaces. Ann. Math. 62, 170–197 (1955)
May, J.P., Ponto, K.: More concise algebraic topology. In: Localization, completion, and model categories. Chicago Lectures in Mathematics, xxviii+514 pp. University of Chicago Press, Chicago (2012)
Neisendorfer, J.A.: Primary Homotopy Theory, vol. 232. Memoirs of the American Mathematical Society, Providence (1980)
Sasao, S.: On homotopy type of certain complexes. Topology 3, 97–102 (1965)
Selick, P.: Constructing product decompositions by means of a generalization of Ganea’s theorem. Trans. Am. Math. Soc. 348, 3573–3589 (1996)
Theriault, S.: Homotopy fibrations with a section after looping. Mem. Amer. Math. Soc. (to appear)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Research supported in part by the National Natural Science Foundation of China (Grant Nos. 11801544 and 11688101), the National Key R &D Program of China (No. 2021YFA1002300), the Youth Innovation Promotion Association of Chinese Academy Sciences, and the “Chen Jingrun” Future Star Program of AMSS.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Huang, R., Theriault, S. Loop space decompositions of \((2n-2)\)-connected \((4n-1)\)-dimensional Poincaré Duality complexes. Res Math Sci 9, 53 (2022). https://doi.org/10.1007/s40687-022-00338-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40687-022-00338-y