Abstract
We propose a method to estimate the cost of debt in a continuous-time framework with an infinite time horizon. The approach builds on the class of well-known earnings before interest and taxes (EBIT)-based models. It extends other approaches based on option-pricing theory with a finite one-period horizon. The model is capable of splitting the observed yield spread of a corporate bond into the risk premium, which adds to the expected return of bondholders, and the default premium, which accounts for expected losses. The model can easily be calibrated for non-public firms, since most of its input parameters are readily observable, while the output, the model-implied cost of debt, proves to be very insensitive with respect to the remaining non-observable parameters, the EBIT growth rate, and the bankruptcy costs of the firm. We demonstrate the applicability of the cost of debt to calculate an approximate weighted average cost of capital for the purpose of firm and project valuation, and its usage and limitations.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Cost of capital is one of the central issues in corporate finance. For a company’s management, the cost of capital is an important benchmark for capital budgeting and performance measurement. For external investors, the cost of capital is the appropriate discount rate for future cash flows to determine the value of a company. Estimating this key figure comes down to estimating its components, cost of equity, and cost of debt.
While there is a large amount of literature concentrating on the estimation of the cost of equity (for a recent overview, see, for example, Da et al. (2012)), a little attention has been focused on the cost of debt. It is common practice to simply use the yield to maturity of the company’s debt securities as an approximation.Footnote 1 However, using the yield to maturity neglects the risk of default, and is, therefore, only a reasonable approximation when default risk is small. Instead, cost of capital, defined as opportunity costs, is the required expected return to capital suppliers, as described, for example, in the textbook of Brealey et al. (2016). While the cost of equity is the expected return to stockholders, the cost of debt is the expected return to bondholders. When the debt is risky, meaning, when there is a non-zero probability of default, the expected return is not identical to the yield to maturity of corporate debt securities, because the risk of possible loss in the event of a default lowers the expected return.
In this paper, we take a closer look at how the cost of debt is estimated for a defaultable firm. We consider a situation in which the decision maker—either internally for capital budgeting, etc. or externally for firm valuation—has already carried out a reasonable estimation for the cost of equity. He or she additionally needs an estimation for the cost of debt. We take the yield to maturity of corporate debt as given and show how the actual cost of debt can be calculated as a value between the risk-free interest rate and this yield to maturity. As an input, the approach requires a current value of the fair corporate interest rate, either from a publicly traded debt instrument or, for example, from recent conditions of a fair bank loan.
In particular, during the past financial crisis, it became obvious that the yield to maturity is not a good choice when default risk is large. The very large yields observed for many companies reflect the increased probability of default, especially in cases where the yield exceeds the cost of equity. Basically, an expected return can be calculated based on a given yield to maturity when the probability of default and the expected recovery rate are given. In the general case, for multi-period or continuous-time settings, time-dependent (marginal) probabilities of default or hazard rates are required to calculate the actually expected return and thus the cost of capital.Footnote 2 However, estimations of default probabilities are difficult to obtain and suffer from a large estimation error.
As an alternative, the expected return on debt could be calculated analogously to the common approach of calculating the expected return on equity, using the capital asset pricing model (CAPM). According to the CAPM, the expected return on any security is determined by its systematic risk, measured by the beta coefficient. To reasonably estimate the beta of corporate debt, a reliable and stable time series of bond values is required. Unfortunately, many bonds are not exchange-traded at all, and for those that are, trading volume is often so low that observed bond quotes are not accurate. Thus, this approach is only feasible for a small number of companies with outstanding bonds that are frequently traded.
Hsia (1981) demonstrates the consistency of the CAPM with option-pricing theory. On this basis, Hsia (1991) suggests calculating the cost of capital in an option-pricing framework.Footnote 3 Cooper and Davydenko (2007) pick up this idea and propose a method of calculating the expected return on a debt security based on the Merton (1974) model.Footnote 4 They use the model to split the observed yield spread of a bond; specifically, the difference between the bond’s yield to maturity and the corresponding default-free rate, into two components: the default premium (expected default effect), which reflects the probability of default, and the risk premium (expected excess return), which reflects the bondholders’ surplus on the expected return for bearing additional risk compared to a risk-free bond. The actual cost of debt is the risk-free rate plus the second component, the risk premium.
The great advantage of this approach is that the Merton model is not needed to estimate the absolute yield spread, which is already known as an input parameter. Instead, the model is applied to calculate the relative proportion of the default premium and the risk premium. The approach proves to be very robust with respect to the debt-to-equity ratio and the equity premium, but it is less robust with respect to equity volatility. This is not a serious concern when the equity volatility can be estimated from stock-price time series. For the purpose of capital budgeting, goal-setting, performance measurement, etc. in an exchange-traded company, the approach is easily applicable. However, for the purpose of firm valuation, an equity value, as well as its volatility, is not available, as it is the very objective of the valuation process to calculate this value.
As a second drawback, the approach proves to be theoretically incompatible to the analysis of long-term valuation problems—either internally, such as for capital budgeting of long-term projects, or externally, for firm valuation. The Merton model is a single-period model by nature, so any conjunction of the Merton model and multi-period capital budgeting, or firm valuation techniques, suffers from a kind of incompatibility.
In this paper, we propose a method to calculate the cost of debt capital which is theoretically compatible with long-term applications, and which can be used for firm valuation, as well as in cases where the equity value and its volatility are not known a priori. Our approach is based on a structural asset-value model, like the Merton model. However, we do not follow Merton’s restrictive assumption of modeling debt as a single zero bond with finite maturity. Instead, debt is modeled as a perpetual bond which pays a continuous coupon. This approach is compatible with the common method of discounted cash flows for firm valuation, where an infinite time horizon is considered. Furthermore, our approach has the advantage of no debt maturity being necessary as a model parameter. The approach basically builds on the model of Leland (1994). In Goldstein et al. (2001), we do not model the asset value directly, but instead consider the flow of earnings as the source of firm value.
Within a structural model, the cost of debt can be deduced from the yield spread based on market risk aversion. When risk aversion is zero, the total yield spread refers to the default premium; the risk premium is zero, and the cost of debt equals the risk-free rate. When risk aversion is greater than zero, the model can be used to split the yield spread into the default premium and the risk premium: using risk-neutral valuation, the debt value is the sum of expected payments to bondholders under the risk-neutral measure, discounted by the risk-free rate. On the other hand, given the expectation of payments under the physical measure, the expected return to bondholders is defined by that discount rate which gives the current debt value when applied to expected payments. This expected return must be larger than the risk-free rate, but smaller than the yield to maturity. The relative proportion of default premium (yield to maturity minus expected return) and risk premium (expected return minus risk-free rate) depends on the difference between the physical and the risk-neutral measure, hence the market risk aversion.
Basically, the approach outlined in the present paper tries to give decision makers a tool for estimating the cost of debt (as the missing component when the cost of equity is given) based on parameters which are either observable or which do not have a large impact on the estimate. Instead of directly calculating the cost of capital for the total firm, it is very common in practice to estimate the cost of equity and the cost of debt separately. Such an approach allows us to place the actual cost of debt between the two polar values: the risk-free rate and the yield to maturity of corporate debt.
In Sect. 2 of this paper, we describe the approach in more detail. Based on the structural asset-value model, we show how to calculate the cost of capital (debt and equity) within this framework. Section 3 demonstrates how the model is calibrated to input data and provides a quantitative analysis of the model results for a typical investment grade and for a typical highly leveraged company. Furthermore, the aspects of the calibration and potential bond covenants are discussed. Section 5 gives attention to the application of the model for the valuation of a firm or projects within the firm. We show the applicability of the textbook formula of the weighted average cost of capital (WACC) for instantaneous returns, but demonstrate its inconsistencies for long-term returns. As a use case, we apply the model for a situation in which the WACC is valid (because of exogenous financing with constant leverage) and analyze the approximation error of the cost of debt calculated within the model for a situation which deviates in the financing assumption. Section 6 is the conclusion.
2 Firm valuation in continuous time and the cost of capital
2.1 Model setup
The basis of our model is earnings before interest and taxes (EBIT). In contrast to classical firm valuation methods based on free cash flows after taxes, such an approach allows us to treat all claimants to EBIT consistently, namely the government (taxes), bondholders (interest), and shareholders (dividends).Footnote 5 The model is very similar to Goldstein et al. (2001).Footnote 6 EBIT is assumed to follow a continuous stochastic process. To be more precise, the EBIT flow X grows on average at a growth rate g and is subject to random fluctuations, modeled by a geometric Brownian motion with variance rate \(\sigma\),Footnote 7
where dW is the differential of a Wiener process. In contrast to accounting practice, EBIT is not a discrete figure which is calculated periodically, but is rather modeled as a continuous flow. This means that the flow of an infinitesimal time interval \(\mathrm{d}t\) is given by \(X \, \mathrm{d}t\). In the case of an all-equity firm, this EBIT flow is distributed by a fraction \(\tau\), the corporate tax rate, to the government, and the rest to shareholders.Footnote 8
In the general case, the company has issued a certain amount of debt. To be compatible with the firm valuation approach, we need a debt structure that is not redeemed after one period, as it is in the Merton model. In line with Leland (1994) and Goldstein et al. (2001), we consider a perpetual coupon bond. The bond pays continuous interests i with respect to face value F; thus, the bondholders receive continuous payments at a rate \(i \, F\) as long as the firm is not bankrupt. The remainder of the EBIT flow is distributed among the government and shareholders, as above, i.e., the government receives taxes at a rate \(\tau (X - i \, F)\) and the rest goes to shareholders. The total claim to the EBIT flow will be called the asset value in the following. This asset value is the sum of the claims of shareholders (E), bondholders (D), and the government (G), along with the present value of bankruptcy costs (BC).Footnote 9
Using risk-neutral valuation, the asset value is given by (see Goldstein et al. 2001)Footnote 10
where \(\gamma\) is the risk-neutral drift of the EBIT flow. The relation between the actual drift, g, and the risk-neutral drift, \(\gamma\), depends on market risk aversion. In line with Goldstein et al. (2001), we model market risk using the continuous-time capital asset pricing model (Merton 1973), considering the dynamics of the asset value A. As r and \(\gamma\) are constant, A follows the same geometric Brownian motion as X:
On the other hand, we can write the asset dynamics using an expected (instantaneous) asset return, \({\mu }\), and the asset payout rate. As the total EBIT flow is immediately paid out to the claimants, the payout rate on asset value equals X / A. Thus
using (2). Based on the continuous-time CAPM, the expected instantaneous asset return is given by the instantaneous security market line:
where \(\theta\) is the market price of risk, defined as the market excess return per one unit of market risk:
and \(\rho\) is the (instantaneous) correlation between asset return, \(r_A\), and market return, \(r_M\).
From the identity of (3) and (4), using the security market line (5), it follows
The difference between actual and risk-neutral EBIT drift is given by the product of the market price of risk and the systematic part of EBIT volatility. As indicated in the introduction, and as we discussed in greater detail below, this difference is also crucial for splitting the yield spread into the default premium and the risk premium, and thus for estimating the cost of debt.
We now model default risk. When the EBIT flow falls below the claim of the bondholders, \(i \, F\), the company does not necessarily default, as shareholders can opt to infuse payments to avoid bankruptcy. Goldstein et al. (2001) show that it is optimal for shareholders to do so as long as the asset value does not fall below a threshold B, which is specified below. In this case, the remaining asset value (which is identical to the threshold B) goes to bondholders. However, bankruptcy costs occur, and the bondholders receive only a fraction \(1 - \alpha\) of the remaining asset value.Footnote 11
The bankruptcy threshold B is given by (see Goldstein et al. 2001)
with
In the following, we determine the value of the different claims, in particular, the value of debt, the value of equity, the present value of taxes (government’s claim), and the present value of bankruptcy costs. The debt value is the sum of discounted interest payments until a potential bankruptcy date \(t^*\) plus the present value of the recovery payment at default.Footnote 12 Using risk-neutral valuation techniques, the debt value is given by (see Leland 1994 and Goldstein et al. 2001)
where \(\eta\) is the present value of receiving 1 at bankruptcy:
The present value of bankruptcy costs is given by
The remaining asset value after bankruptcy costs and the claim of bondholders is distributed among the government and shareholders:
For the following derivation of the cost of capital, we note that, using the definitions in (2), (10), and (12):
2.2 The cost of capital
Once we know the current values of debt and equity, we can use the expected payments under the physical measure to calculate the cost of capital. The cost of debt \(c_\mathrm{D}\) is the expected internal rate of return to bondholders. Therefore, we can again use the expectation of payments as in (10), but, using the physical instead of the risk-neutral measure, and discounting payments by the expected return on debt—the cost of debt \(c_\mathrm{D}\)—to obtain the current debt value:
This equation implicitly defines the cost of debt \(c_\mathrm{D}\). It is worth noting that the cost of debt is considered for a time horizon either until bankruptcy or to infinity. Calculating the cost of debt over a finite time horizon could yield different results. Instead of considering time-varying cost of capital, we refer to cost of capital as an average value over an unlimited time horizon.
Basically, the right-hand side of Eq. (15) is nothing else than the debt value in Eq. (10), with expectation taken under the physical measure and the discount factor \(c_\mathrm{D}\) instead of r. Therefore, to solve the integral, we can simply use Eq. (10), with \(\gamma\) replaced by g and r by \(c_\mathrm{D}\):
This equation can easily be solved iteratively for \(c_\mathrm{D}\).Footnote 13
The cost of equity is determined analogously. The expected flow to shareholders at time t equals \({\mathbb {E}}[(1 - \tau ) (X_t - i \, F)]\), where expectations of the random EBIT flow \(X_t\) are taken under the physical measure. However, payments are only received until a potential bankruptcy at time \(t^*\). Accordingly, the cost of equity, \(c_E\), is implicitly given by
Again, we can use Eq. (13) together with (14), with \(\gamma\) replaced by g and r by \(c_E\):
Analogously to the cost of debt, this equation can be solved iteratively for \(c_E\).
3 Model application and analysis
3.1 Input parameters and sensitivity analysis
Having derived an expression for the cost of debt capital in the model framework, this section analyzes the applicability of the model in terms of input requirements, calibration, and outcome sensitivity. We have two general types of applications in mind: internal applications, for capital budgeting, performance measurement, etc., and external applications, for firm valuation.
According to (10), the model value of debt depends on the following input parameters:
-
current level of EBIT flow, \(X_0\),
-
EBIT growth rate, g,
-
face value of debt, F,
-
interest rate on corporate debt, i,
-
bankruptcy costs, \(\alpha\),
-
corporate tax rate, \(\tau\),
-
risk-free interest rate, r,
-
market price of risk, \(\theta\),
-
correlation between asset returns and market returns, \(\rho\), and
-
EBIT and asset volatility, \(\sigma\).
We can divide the parameters into two groups: some are readily observable, while the others have to be estimated. Belonging to the first group are the company-specific parameters \(X_0\), F, i, and \(\tau\), and the risk-free rate r. The current level of EBIT flow can be taken from the latest financial report.Footnote 14 The same is true for the face value of debt, while the interest rate is the nominal interest rate that the company pays for its long-term debt. The corporate tax rate can also be deduced from the financial report, by relating paid taxes to earnings before taxes. The risk-free rate is the yield of long-term government bonds.
Within the second group, the EBIT growth rate has to be estimated.Footnote 15 While this is a standard requirement in firm valuation (e.g., Damodaran 2012), an estimation suffers from considerable potential errors. In addition, it is not easy to estimate the bankruptcy costs. Approaches could be based on historical recovery rates of comparable companies. Furthermore, we have the market price of risk, based on the market risk premium, as a global parameter. While accepted as one of the most important figures in finance, there is considerable controversy about its value.Footnote 16 In addition, the correlation between asset returns and market returns has to be estimated. For listed companies, the stock-price time series can be used. Alternatively, average sector correlations can be applied. Within our calibration analysis in Sect. 3.2, we put a special emphasis on the model behavior with respect to the uncertain input parameters g, \(\alpha\), \(\theta\), and \(\rho\).
Finally, the EBIT and asset volatility is left as an input parameter. In contrast to Cooper and Davydenko (2007), we do not attempt to estimate this value directly. While estimates could be based on stock-price volatility for listed companies, this would be difficult for private companies. Instead, we imply a value for volatility based on other input data. As an identifying assumption, we suppose that the debt of the firm trades at par, in other words, that the paid corporate interest rate reflects current market conditions.Footnote 17 This means that the debt value D equals its face value F.Footnote 18 As we know the debt value according to this assumption, we can use the model equation for the debt value (10) to obtain an implied volatility which yields this value. In the appendix, we can derive an expression for the unknown asset volatility \(\sigma\):
This equation can be solved iteratively for \(\sigma\).
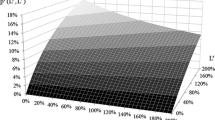
Figure 1 shows the cost of debt for a typical company dependent on the market price of risk \(\theta\). The parameters are: current EBIT flow \(X_0 = 5\), EBIT growth rate \(g = 1\%\), face value of debt \(F = 30\), bankruptcy costs \(\alpha = 50\%\), tax rate \(\tau = 30\%\), risk-free rate \(r = 3\%\), and correlation \(\rho = 0.6\). The corporate interest rate varies from 4 to \(7\%\). The graphs show the relative growth of the risk premium with respect to the total yield spread when the market price of risk increases. When the market price of risk is low, the major part of the yield spread refers to the default premium, which compensates for lower expected returns. The actual expected return is only a little above the risk-free rate, although the nominal interest rate might be considerably larger. This means that bondholders receive only a small premium as an add-on to the risk-free rate for bearing substantial default risk. For high values of the market price of risk on the other hand, the major part of the yield spread refers to the risk premium. Although the actual default risk might be low, bondholders receive large compensation for bearing that risk. For instance, at a market price of risk of \(\theta = 0.6\), the expected return for bondholders (and thus, the cost of debt) with an interest rate of 4% is 3.97%. This means that, for bearing the risk of an expected loss of only 0.03%, they receive a risk premium above the risk-free rate of 0.97%.
Cost of debt with respect to market price of risk. The basic parameters are initial EBIT flow \(X_0 = 5\), EBIT growth rate \(g = 1\%\), relative bankruptcy costs \(\alpha = 50\%\), corporate tax rate \(\tau = 30\%\), risk-free interest rate \(r = 3\%\), and correlation \(\rho = 0.6\). The model is calibrated (by means of volatility), so that the debt value equals its face value \(D = F = 30\). The four lines refer to four different levels of the corporate interest rate, ranging from \(i = 4\%\) to \(i = 7\%\)
Figure 2 shows the cost of debt with a fixed market price of risk \(\theta = 0.25\) dependent on the corporate interest rate. The model is re-calibrated for each value of the interest rate, so that the debt value equals par value. Accordingly, the volatility parameter changes along the x-axis. The figure thus displays the cost of debt for different levels of the interest rate under the assumption that \(D = F\).
The cost of debt increases concavely with the interest rate. While, for smaller interest rate values, the major part of the yield spread reflects the risk premium, for larger interest rates, the relative share of the expected default premium gains in importance. The concave shape of the graph is explained by the asymmetric distribution of bond returns. Within the (continuous) CAPM framework, the risk premium is driven by the covariance of bond returns and market returns. This covariance increases with the default risk, and thus, with the paid interest rate, but, because the asymmetry of the distribution becomes less pronounced with increasing default risk, the increase of covariance is concave.Footnote 19
Cost of debt with respect to the corporate interest rate. The basic parameters are initial EBIT flow \(X_0 = 5\), EBIT growth rate \(g = 1\%\), relative bankruptcy costs \(\alpha = 50\%\), corporate tax rate \(\tau = 30\%\), risk-free interest rate \(r = 3\%\), market price of risk \(\theta = 0.25\), and correlation \(\rho = 0.6\). The model is calibrated (by means of volatility), so that the debt value equals its face value \(D = F = 30\). The light straight line, as a benchmark, is the identity \(c_\mathrm{D} = i\). Accordingly, the dark line divides the yield spread \(i - r\) into the risk premium (below) and the default premium (above)
Table 1 provides a sensitivity analysis of the model with respect to the key input variables. Two different settings are considered: a typical investment-grade firm (debt-to-equity ratio 0.4) and a highly leveraged firm (debt-to-equity ratio 2.0). In both cases, the EBIT growth rate is 1%, the corporate tax rate is 30%, bankruptcy costs are 50%, the risk-free interest rate is 3%, the market price of risk is 0.25, and the correlation is 0.6. In the base case, the investment-grade firm pays an interest rate of 4%, and the highly leveraged firm pays an interest rate of 7%. These parameters are consistent with asset volatilities of 21.8 and 28.1%, respectively. For the investment-grade firm, about 70% of the yield spread represent the risk premium. The cost of debt capital thus equals 3.7%. For the highly leveraged firm, a smaller proportion of less than 50% of the overall yield spread refers to the risk premium. This observation is in line with Fig. 2, which shows a concave increase in the cost of debt with the corporate interest rate.
The table reports the fair corporate interest rate (for debt at par value) together with the cost of debt when the input parameters are changed. Parallel to variations in the corporate interest rate, the cost of debt varies with respect to changes in the parameters. For example, when the level of EBIT flow falls, the bankruptcy threshold comes closer and default risk increases, so the fair corporate interest rate must rise. However, the relative proportion a of the risk premium with respect to the yield spread stays within a quite narrow range, 63%–73% for the investment-grade firm and 37–52% for the highly leveraged firm.
These results are fairly in line with the figures reported by Cooper and Davydenko (2007) based on the Merton (1974) model. Their relative proportions of the risk premium are about 80% for the investment-grade firm and about 40% for the highly leveraged one.Footnote 20 However, as their model is calibrated differently, the results are not directly comparable.
3.2 Calibration analysis
In addition to a sensitivity analysis, for a practical application, the impact of parameter misestimations on the model calibration is of interest. For example, the EBIT growth rate is not directly observable. If we retain the assumption that the corporate interest is known and debt trades at par, a given parameter set transfers into an implied value of the asset volatility. Such a calibration acknowledges that the model does not perfectly reflect reality, but sets the input parameters consistent to observable data—in particular, the corporate interest rate.Footnote 21
The calibration analysis in Table 2 shows the impact of parameter misestimations on the calculated cost of debt, if the model is re-calibrated in the described way that it is still consistent with the given corporate interest rate. This re-calibration involves a new estimation of the asset volatility. It is implicitly assumed that there is no “true” volatility to be inferred, but the implied asset volatility is the best fit to the observable corporate interest rate. For example, lines 1 and 2 tell us that (for the investment-grade firm) both combinations of the unobservable parameters \(g = 1.0\%\), \(\sigma = 21.8\%\) and \(g = 0.5\%\), \(\sigma = 20.4\%\) lead to the same model output in terms of \(D = F\) when the corporate interest rate is \(i = 4\%\).
As shown in the table, the calculated cost of debt is very insensitive to such different model calibrations with respect to the unobservable parameters EBIT growth rate and bankruptcy costs.Footnote 22 Shifting these parameters by 0.5 or 10 percentage points, respectively, leads to a change of as little as 1–5 base points in the cost of debt. Naturally, the cost of debt, in particular the relative proportion of the risk premium, is most sensitive to the market price of risk (and also to the correlation), as demonstrated in Fig. 1.
Therefore, the market price of risk is a key input to the model, as it is prone to estimation errors, and the model output is relatively sensitive with respect to this parameter. As an alternative to a direct input of the market price of risk, we consider in the following an implied calculation based on an available estimate of the second component of the cost of capital, the cost of equity. The reasoning is that most applications focus on an accurate estimate of the cost of equity and give a little attention to the cost of debt. We, therefore, analyze how an existing estimate of the cost of equity can be used to calibrate the model and consistently obtain an estimate for the cost of debt without explicitly estimating the market price of risk.
The idea is simply to calibrate the model by choosing a value for the market price of risk, so that the cost of equity calculated according to (18) equals the externally given value. As the external estimate for the cost of equity also depends on the market price of risk, we cannot expect to eliminate the associated estimation error. However, we can use the model to obtain a consistent value for the cost of debt when the external value for the cost of equity is considered reliable.
According to (5), it is not the market price of risk \(\theta\) alone, but instead its product with the correlation \(\rho\) which determines the expected asset return. We can, therefore, also refrain from estimating \(\rho\) and iteratively calculate an implied value for the product \(\rho \theta\), as follows:
-
Given starting values \(\rho \theta ^0, \rho \theta ^1\).
-
For each iteration j
-
Calculate an implied asset volatility \(\sigma ^j\) according to (19).
-
Calculate model values for the bankruptcy threshold B, the asset value A, and the equity value E.
-
Calculate a value for the cost of equity \(c_E\) by iteratively solving (18).
-
Calculate a new estimate for the correlation-adjusted market price of risk using regula falsi:
$$\begin{aligned} \rho \theta ^{j+1} = \rho \theta ^j - \frac{ c_E^j - c_E }{ c_E^{j-1} - c_E^j } (\rho \theta ^{j-1} - \rho \theta ^j). \end{aligned}$$
-
Table 3 summarizes the results of an analysis when the model is calibrated based on a given value for the cost of equity. Again, we consider an investment-grade firm and a highly leveraged firm. The externally given cost of equity for the investment-grade firm is assumed to be 7%, that of the highly leveraged firm 9%, well in line with the basic settings of Table 2. The results are similar; however, the model output is now more sensitive. With respect to the unobservable parameters, EBIT growth rate, and bankruptcy costs, the sensitivity is now twice as large, although it is still quite small in absolute terms. A change in g of 0.5 percentage points or a change in \(\alpha\) of 10 percentage points leads to a change of 2–10 base points in the cost of debt.
3.3 The identifying assumption
The calibration of the model depends on the identifying assumption that debt trades at par, i.e., its value D equals the face value F. If this is not the case, the calibration is biased. For example, if the EBIT value X and in parallel the asset value A drops, default risk and thus the value of \(\eta\) in Eq. (11) becomes higher, so the debt value (10) shrinks. New potential debtholders will anticipate the actual default risk after a change in the EBIT flow, so they will adjust their required interest rates accordingly. The true cost of debt will, therefore, be higher if \(D < F\).
This pattern of a decreasing cost of debt with respect to its relative value is shown in Fig. 3 for the highly leveraged firm (solid line). For example, if the debt value drops to 80% of its original value (equivalent to a drop in the EBIT flow from 5 to 3.36), the cost of debt rises from 4.88% to 5.33%.
Relevance of the identifying assuming that debt trades at par. The solid line depicts the true cost of debt with dependence on relative debt value D / F. For lower debt value, meaning higher default probability, cost of debt becomes higher. The dashed line shows the model outcome if no volatility adjustment was made—the relationship is turned upside down. The dotted line represents the model outcome with volatility re-calibration as suggested. The outcome is almost insensitive with respect to the debt value. However, this means that the outcome becomes biased with respect to the true value if the debt value is considerably different from par. The figure is based on the highly leveraged firm (EBIT flow \(X_0 = 5\), EBIT growth rate \(g = 1\%\), face value of debt \(F = 40\), corporate interest rate \(i = 7\%\), volatility \(\sigma = 28.1\%\), relative bankruptcy costs \(\alpha = 50\%\), corporate tax rate \(\tau = 30\%\), risk-free interest rate \(r = 3\%\), market price of risk \(\theta = 0.25\), and correlation \(\rho = 0.6\))
The dashed line depicts the resulting cost-of-debt estimate if the model was erroneously applied with the original volatility value (here, 28.1%) under the false assumption that \(D = F\) holds. If actually \(D < F\), that is, the default probability is higher, then the cost-of-debt estimate needs to be low to produce a debt value equal to the face value. Thus, the estimation procedure underestimates the cost of debt in the case that \(D < F\); counter to economic intuition, the cost of debt decreases with increasing default probability.
However, this is not the way the model should actually be applied. Instead, a drop in the EBIT flow leads to a re-calibration of volatility. Therefore, to produce a debt value equal to the face value if actually \(D < F\) (higher default probability), not the cost-of-debt estimate, but the volatility estimate is adjusted (here, it drops to 21.2%). This re-calibration attenuates the bias in the estimated cost of debt. Therefore, the model output with the adjusted volatility estimate is rather insensitive with respect to the debt value. It is shown as the dotted line in Fig. 3. For \(D / F = 80\%\), the estimated cost of debt is 4.82%.
Therefore, it is important that the identifying assumption of \(D = F\) is not too far away from actual market conditions, although the re-calibration of volatility prevents the model from delivering strongly biased results. A decision maker using the model should, therefore, take care that the latest debt issue with the corresponding interest rate plugged into the model took place in the past, or that economic conditions have remained more or less stable since then.
3.4 Bond covenants
The preceding analysis was based on the assumption that shareholders can decide when the firm defaults. If the current level of the EBIT flow falls below the claim of bondholders, \(i \cdot F\), they may choose to infuse equity to prevent bankruptcy. In practice, covenants may be in place that give bondholders the right to enforce bankruptcy when certain conditions are met, for example, when the EBIT flow falls below \(i \cdot F\). In this case, the effective bankruptcy threshold would rise to
given the relation between EBIT flow and asset value according to Eq. (2).
In this section, we analyze the impact of such covenants on the cost of debt. A high bankruptcy threshold enforces an earlier redemption of debt. However, this is only beneficial for bondholders if bankruptcy costs are sufficiently low. Otherwise, they get an early redemption with high probability, but the redemption amount may be quite low. Whether a bond covenant, given by a bankruptcy threshold, provides an additional value to bondholders, therefore, crucially depends on the bankruptcy costs \(\alpha\).
Figure 4 shows the cost of debt in dependence on the bankruptcy costs, when a debt-service bond covenant is in place (dashed lines), together with the base case without covenant (solid lines). The two lines represent the exemplary firms (investment-grade firm with \(F = 20\) and \(i = 4\%\); highly leveraged firm with \(F = 40\) and \(i = 7\%\)). The figure reveals that a covenant reduces the cost of debt only for smaller levels of bankruptcy costs, while it increases it for larger levels. This observation is in line with the finding of Leland (1994) that debt being protected by a similar covenant in his model ceteris paribus exhibits a lower value than unprotected debt when bankruptcy costs are high.
Influence of a bond covenant based on debt-service coverage. The dashed lines show the cost of debt with dependence on relative bankruptcy costs when a bond covenant is in place; the solid lines show the respective values without a covenant. Two cases are considered: an investment-grade firm (\(F = 20\), \(i = 4\%\)) and a highly leveraged firm (\(F = 40\), \(i = 7\%\)). The remaining parameters are the initial EBIT flow \(X_0 = 5\), EBIT growth rate \(g = 1\%\), corporate tax rate \(\tau = 30\%\), risk-free interest rate \(r = 3\%\), market price of risk \(\theta = 0.25\), and correlation \(\rho = 0.6\). Only when bankruptcy costs are low, a bond covenant is actually beneficial for bondholders. Otherwise, an early default triggered by the covenant destroys value because of bankruptcy costs
Not surprisingly, the effect is least pronounced for the investment-grade firm. For this firm, the probability that a default event occurs or the covenant becomes effective is quite low, so the covenant has no great impact on the cost of debt. For the highly leveraged firm in contrast, the impact is large. When bankruptcy costs are high, the covenant triggers the early default with low redemption and destroys bondholder value, resulting in higher costs of debt. When bankruptcy costs are low, the redemption amount in the case of default is close to the face value of debt, so bondholders bear a little risk, moving the cost of debt closer to the risk-free rate.
4 Empirical application
In this section, we demonstrate the application of the model for real-world data. It is not intended to provide a full-blown empirical analysis. Rather, the purpose is to showcase the usability of the model and the reasonability of its outcome when applied to empirical data. The major strength of the model is its low requirement of input data and hence its applicability also for non-public firms. However, the model should yield reasonable results, also for public firms, that are in line with those of other techniques applicable in these cases.
For this purpose, we consider large public-traded companies, which also have issued corporate bonds. Bond data can be used to infer the corporate interest rate. In particular, we consider US corporate issuers of jumbo bonds with an outstanding amount of at least one billion dollars and a remaining time to maturity exceeding 15 years as of September 2017. Distant maturities are required to approximate the model assumption of perpetuate debt. After eliminating issuers with currently negative EBIT values, we are left with a total number of 38 companies. For those companies with several bonds that meet the criteria, we take that one with the larger time to maturity. All bond data are retrieved from Thomson Reuters Eikon.
The observable bond price theoretically allows for a deviation of the assumption that corporate debt trades at par, i.e., \(D = F\). However, the considered bond will not be the only layer of debt of the respective company, so a generalization of the bond price to the total debt is questionable. We, therefore, consider two alternative identifying assumptions:
-
1.
The observed bond is of negligible size compared to total debt, and all remaining debts consist of a single layer with a single interest rate and trades at par. This is the known assumption \(D = F\). In this case, the fair corporate interest rate i equals the yield to maturity of the bond, because it is the rate that a bond investor accepts under the current market conditions.Footnote 23
-
2.
The whole debt is identical to the bond. Under that assumption, the corporate interest rate equals the bond coupon rate and the debt value equals the face value times the bond price. It is straightforward to calibrate the model under this alternative identifying assumption.
The remaining model input data are calculated as follows:
-
The current level of EBIT flow, \(X_0\), and the face value of debt, F, are taken from the latest annual report.
-
The corporate tax rate, \(\tau\), is calculated as an average from the latest three financial reports.
-
The risk-free interest rate, r, is taken from the US treasury yield curve with a maturity matching that of the bond.
-
The correlation between asset returns and market returns, \(\rho\), is calculated from 2-year historical time series of the company stock price and the S&P 500 index.
For the unobservable parameters, we take the same values as in the previous section, that is, the EBIT growth rate \(g = 1\%\), bankruptcy costs \(\alpha = 50\%\), and the market price of risk \(\theta = 0.25\).
The results are shown in Table 4, where \(c_\mathrm{D}^{(1)}\) and \(c_\mathrm{D}^{(2)}\) refer to the two alternative identifying assumptions. As a benchmark, cost of debt estimates based on historical default rates for the respective rating class are also given.Footnote 24 Although there are some deviations, the results of the methods are fairly in line. On average, cost-of-debt estimates based on historical default rates are about 20 basis points larger than those calculated with the model under Assumption 1, whereas average values almost coincide under Assumption 2. This is, however, not a proof that Assumption 2 is actually correct. First, there are deviations both upwards and downwards. Second, there are further calibration issues—as discussed in Sect. 3.2, cost of debt increases when the unobservable market price of risk is increased, and the observed yield spreads might also be influenced by other factors such as liquidity risk, which are not captured by the model. All in all, the empirical results tend to be reasonable and can be seen as a justification for the applicability of the model.
5 WACC and firm valuation
5.1 Instantaneous returns
Cost of debt and cost of equity are the components of the overall cost of capital for the company. In theory and practice, the “weighted average cost of capital” (WACC) as a value-weighted average, incorporating the tax shield of debt financing, is in widespread use. In this section, we calculate this figure within our model framework.
In doing so, we distinguish between the long-term average cost of capital, as considered so far, and the instantaneous cost of capital. As discussed, for most applications, such as capital budgeting, long-term project analysis, or firm valuation, a long-term time horizon is required. The cost of debt and cost of equity derived and analyzed in the preceding sections fulfill this requirement. Equations (16), (18) are based on the discounting of all cash flows to capital suppliers until the time of bankruptcy, or until infinity if no bankruptcy occurs.
For shorter time horizons, expected returns can be different. In the following, we consider the expected instantaneous returns over an infinitesimally short-time horizon. As will become clear, in contrast to the long-term cost of debt and equity, we can derive the well-known WACC formula for the instantaneous costs.Footnote 25
The expected returns over an infinitesimally short-time horizon can be deduced based on the continuous-time CAPM. The security market line holds for any security, hence, in particular also for the expected (instantaneous) equity return and the expected (instantaneous) debt return:Footnote 26
and
For the variance rates,Footnote 27
holds, where Y is the value of an arbitrary claim on the asset value—in particular, debt D or equity E. The derivatives of E and D with respect to A are given by the following (see the appendix):
and
According to the foundations of the model, the EBIT flow, plus the change in asset value, are distributed among the bondholder, shareholder, and government claimants, and the bankruptcy costs:
In the following, we ignore bankruptcy costs to keep things in line with the standard approaches.Footnote 28 Taking expectations yields
where \({\mu }_D\) and \({\mu }_E\) denote the instantaneous returns on debt and equity, respectively. As the shareholders and government share claims on the identical remainder \(A - D\), their instantaneous returns are identical.Footnote 29 Inserting \(E + G = E / (1 - \tau )\) (according to (13)) and \(A = D + E / (1 - \tau )\) yields
The WACC is defined as the expected return on firm value, \(V = D + E\), after taxes, with taxes applied to the total EBIT without the tax shield of debt financing. The expected cash flow after taxes is \(A \, {\mu } \, (1 - \tau )\). Hence, the instantaneous WACC, \({\mu }_{\mathrm{WACC}}\), is given by
This yields the textbook formula for the instantaneous WACC:
5.2 Long-term returns
The reason why the textbook formula is valid for an infinitesimally small time horizon is related to the financing policy of the firm. Miles and Ezzell (1980) have shown that the textbook WACC is valid for all time horizons if the unleveraged cost of capital, the cost of debt, the tax rate, and the leverage of the firm are all constant. Brennan (2003) and Gamba et al. (2008) extend the analysis in several aspects, in particular with regard to personal taxes. They derive conditions that are necessary and sufficient for the discounted cash flow approach using the textbook WACC to be correct. The crucial point is the leverage ratio kept constant by the firm, as an exogenously given financing policy. For an infinitesimally small time horizon, the leverage ratio is constant by nature, so the consistency of the instantaneous WACC derived in the previous section is in line with these results. However, for longer time horizons, the leverage ratio may vary in the Goldstein et al. (2001) model. We cannot, therefore, expect the textbook formula to hold for the long-term cost of debt, \(c_\mathrm{D}\), and the long-term cost of equity, \(c_E\).
The actual weighted average cost of capital for the firm, \(c_V\), is defined as the expected long-term return on firm value after taxes—analogous to the instantaneous case:
The value of this actual WACC differs from the textbook WACC:
Figure 5 shows the actual WACC and the textbook WACC in dependence on the leverage for a typical model setup with initial EBIT flow \(X_0 = 5\), EBIT growth rate \(g = 1\%\), EBIT volatility \(\sigma = 20\%\), corporate tax rate \(\tau = 30\%\), market price of risk \(\theta = 0.25\), and correlation \(\rho = 0.6\). The interest rate is chosen, so that the value of debt equals its respective face value, which varies at the x-axis. In this setting, total asset value equals 100.
Actual and textbook WACC. The basic parameters are the initial EBIT flow \(X_0 = 5\), EBIT growth rate \(g = 1\%\), corporate tax rate \(\tau = 30\%\), market price of risk \(\theta = 0.25\), correlation \(\rho = 0.6\), and volatility \(\sigma = 20\%\). The model is calibrated (by means of nominal interest rate), so that the debt value equals its face value, which varies at the x-axis. Total asset value is 100. The dark black lines represent relative bankruptcy costs \(\alpha = 50\%\), while the light grey lines represent no bankruptcy costs (\(\alpha = 0\)). The solid lines refer to the actual WACC; the dashed lines refer to the “textbook WACC”. Note that the “textbook WACC with bankruptcy costs” actually ignores the existence of these costs and is, therefore, monotonically decreasing
The dotted lines show the textbook WACC, while the solid lines refer to the actual WACC. The grey pair of lines ignore bankruptcy costs (\(\alpha = 0\%\)), and the dark pair of lines incorporate bankruptcy costs with \(\alpha = 50\%\).
Without bankruptcy costs, the tax shield of debt financing leads to a monotonically negative relationship between leverage and the cost of capital, both for the actual WACC and the textbook formula. The textbook WACC when bankruptcy costs exist (solid grey line) also decreases monotonically—because it simply ignores bankruptcy costs.Footnote 30 The actual WACC in the presence of bankruptcy costs, however, reaches a minimum at a certain leverage and starts to increase again for high values of leverage. This shape is a representation of the well-known trade-off theory. For small levels of leverage, the tax shield of debt financing leads to a decrease in the cost of capital with increasing leverage. Increasing leverage, on the other hand, leads to increasing bankruptcy costs. At a certain level of leverage, the trade-off between the positive effect of the tax shield and the negative effect of bankruptcy costs is optimal. For yet higher levels of leverage, the negative effect of bankruptcy costs starts to dominate, and the cost of capital increases again.
Comparing the actual WACC with the textbook WACC, the textbook formula overestimates the actual WACC for small levels of leverage, and underestimates it for higher levels of leverage. As Miles and Ezzell (1980) point out, the textbook formula assumes a constant level of leverage over time. In our model, however, an initially high level of leverage decreases over time, on average (in terms of expectations), as a positive development of the EBIT flow strengthens the equity value more than it does the debt value. Hence, the textbook formula puts too much weight on the cost of debt, and as the cost of debt is smaller than the cost of equity, it underestimates the actual WACC. On the other hand, an initially low level of leverage increases over time (on average). The reason is that while a positive development of the EBIT flow can further decrease an initially very low leverage only marginally, a negative development of the EBIT flow can substantially increase the leverage. Hence, the textbook formula puts too much weight on the cost of equity, and, as it is larger than the cost of debt, overestimates the actual WACC.
5.3 Adjusted net present value and the tax shield
If the cost of debt calculated as in Sect. 3 is not well suited to estimate the weighted cost of capital within the model, one may ask what it is good for. As the leverage in the Goldstein et al. (2001) model is not constant, using the WACC method is not recommended at all within its scope. Instead, for the purpose of firm valuation, an adjusted net present value approach would be appropriate. With the value of the unlevered firm, \(V_0 = (1 - \tau ) A\), the value of the levered firm reads
where \(\tau \, D\) represents the tax shield.
As the tax shield is directly related to the cash flows to bondholders, the cost of debt might be useful to approximate its value. However, if the cost of debt is obtained based on the identifying assumption as above, its value would be given by its face value F. If we drop this assumption and take a value for the cost of debt as given, Eq. (10) gives us an indication for its usefulness to approximate the value of the tax shield: while the value of debt is composed of interest payments and the final payment in the event of a bankruptcy, only the former enters the value of the tax shield. Therefore, the approximation is good if either default risk is low or bankruptcy costs are high. It always underestimates the true value, because the cost of debt is too high as a discount rate. Nonetheless, the approximation might be useful in some cases.
However, by dropping the identifying assumption of debt trading at par, the EBIT volatility is needed as an additional input parameter. Furthermore, the value of the tax shield is not sufficient to apply the adjusted net present value approach, as the value of bankruptcy costs is also needed. One might argue that, if the model parameters are known, one could directly calculate the value of the tax shield and of bankruptcy costs without using the cost of debt within the model. Hence, the scope for an application lies outside the model. The following subsection demonstrates how the cost of debt—calculated within the model—can be useful as an approximation when the framework of the model is left.
5.4 Firm valuation outside the model
As mentioned in the introduction, a main application of calculating the cost of debt within the presented framework could be a situation in which the cost of equity is already given. In this subsection, we consider a firm that maintains an exogenous financing strategy, keeping the initial leverage ratio constant. We assume that the firm has already carried out a reasonable estimate for the cost of equity. According to the constant-leverage strategy, using the WACC to value the firm or a project of the firm is adequate. To calculate the WACC, the cost of debt must be estimated. For this, the firm uses the approach presented in this paper, although the model deviates from its actual policy, as the model assumes a financing policy with a time-varying leverage ratio. In the following, we analyze whether the cost of debt thus derived is a reasonable approximation in this situation.Footnote 31
The true cost of debt is calculated within a simulation study. The company has issued a perpetual bond which pays interest at a fixed rate i, as assumed in the model. The EBIT flow is modeled according to Eq. (1) on a yearly basis, which gives new values for debt and equity at the end of each period. If the EBIT and thus the asset value fall, the debt ratio increases. To retain the initial leverage ratio, the firm redeems part of the debt.Footnote 32 Conversely, if the asset value rises, the firm takes on new debt at a coupon rate according to fair market conditions. The firm defaults if the asset value breaches the initial bankruptcy threshold B.Footnote 33
By repeating the simulation many times (we run 50,000 paths, each until either bankruptcy or a final date \(T = 100\) is reached), we obtain a flow of expected payments to bondholders (including interests, redemptions, and new debt issues) for the successive periods. The actual cost of debt is the internal rate of return of this payment flow.
We analyze this “true” cost of debt compared to the approximate cost of debt obtained by the model. The base data for the firm are the same as in Sect. 3, where the corporate interest rate varies between 3 and 7%. Figure 6 shows the results. For corporate interest rates up to about 5.5%, the deviations are fairly small, remaining below 0.2%. For higher rates, deviations can become larger—at a corporate interest rate of 7%, the model gives a cost of debt of 4.9%, whereas the true value is 5.5%. The reason for this underestimation of the actual cost of debt lies in the financing policy: a high initial corporate interest rate goes hand in hand with a high initial leverage ratio and thus a high level of default risk. The constant-leverage policy reduces the effects of default risk for bondholders, as parts of the outstanding debt are redeemed in full when the bankruptcy threshold approaches. These early redemptions increase the expected return for bondholders and thus the cost of debt. Nonetheless, using the cost of debt obtained by the model seems to be a reasonable approximation in most cases.
Cost of debt obtained by the model compared to the actual cost of debt when an constant-leverage policy is conducted (upper graph) and resulting cash flow valuations (lower graph). The actual cost of debt is obtained by simulating the EBIT flow, where the debt ratio is re-adjusted in each period to retain its initial value. The lower graph show the results of a WACC-based valuation of a perpetual cash flow of 1, where the cost of equity is externally given. As a benchmark, also the value obtained by the approximation cost of debt = corporate interest rate is displayed. The basic parameters are the initial EBIT flow \(X_0 = 5\), EBIT growth rate \(g = 1\%\), relative bankruptcy costs \(\alpha = 50\%\), corporate tax rate \(\tau = 30\%\), risk-free interest rate \(r = 3\%\), market price of risk \(\theta = 0.25\), and correlation \(\rho = 0.6\). The model is calibrated (by means of volatility), so that the debt value equals its face value \(D = F = 30\)
The constant-leverage policy makes the WACC method an appropriate choice for the valuation of the firm or single projects of the firm. To analyze the effect of the approximation on the final outcome, the value of a cash flow, we consider a perpetual flow of 1 in each period to be discounted with the WACC. The perspective is thus internal, looking at a new project within the firm. The value of a different cash flow is easily obtained by a simple scaling. As argued, we take the cost of equity as given—without loss of generality, we use the value obtained by the model. Here, the textbook formula is directly applicable to calculate the WACC, once with the actual cost of debt and once with the cost of debt obtained by the model. The lower graph of Fig. 6 shows the resulting value of the perpetuity. Differences remain rather small—even in the extreme cases of very high corporate interest rates, they are below 5%. As a benchmark, the graph also displays the resulting values when the corporate interest rate itself is used as an approximation for the cost of debt, as sometimes recommended. With deviations of up to 15%, this approximation is considerably worse.
6 Conclusion
The cost of debt is an essential component of the cost of capital, which is a central figure in a number of applications, such as capital budgeting, performance measurement, and firm valuation. Using the yield to maturity of corporate debt is an inappropriate choice in the presence of substantial default risk. The expected return to bondholders, rather than the yield to maturity, is a correct value for the cost of debt. The expected return lies between the risk-free rate and the yield to maturity. It is the risk-free rate, plus the risk premium, which compensates the bondholders for bearing default risk. The relative proportion of the risk premium with respect to the total yield spread depends on the market price of risk.
We propose an EBIT-based model which allows a calculation of the cost of debt. The benefits of the model are the theoretical compatibility with multi-period applications and the applicability for private companies. We derive expressions for the cost of debt and the cost of equity which can be solved iteratively.
The model can easily be calibrated to input data that are readily observable or can be reasonably estimated. The unobservable parameters, EBIT growth rate and bankruptcy costs, prove to have a little impact on the model output. The most crucial parameter is the market price of risk. Instead of explicitly estimating this global parameter, one can alternatively calibrate the model to reflect an externally given cost of equity. With this approach, the model can be used to estimate the cost of debt relative to the cost of equity. However, it is assumed that the fair corporate interest rate for debt trading at par is known or can be reasonably estimated.
A decision maker who already has an estimation for the cost of equity can thus use the model to estimate the cost of debt. In a case where firm and project valuation with the weighted average cost of capital (WACC) is applicable (that is, under exogenous financing with constant leverage), the cost of debt obtained with the model can be used as a reasonable approximation, although the model actually assumes a time-varying leverage.
It can be shown that the textbook formula for the WACC is valid for an instantaneous time horizon with the additional condition that there are no bankruptcy costs. This is not surprising, as the financing condition, a constant-leverage ratio, is fulfilled by nature for an instantaneous horizon. For longer horizons, however, the actual cost of overall capital can substantially differ from the textbook WACC, as the debt-to-equity ratio is not constant in the model.
Notes
See, among others, Schönbucher (2003) for an overview of default risk modeling.
The approach has found its way into the popular textbook of Copeland et al. (2005).
The Merton model is also applied by Husmann and Schmidt (2008), who derive the “incremental borrowing rate” according to International Financial Reporting Standards (IFRS 36).
As a further difference, we consider earnings instead of cash flow. The difference is the net effect of depreciation, which lowers earnings but not cash flow, and capital expenditure, which lowers cash flow but not earnings, and changes in net working capital. We assume that these effects add up to zero; in other words, depreciation equals capital expenditure and net working capital is kept constant.
There are, however, some differences. In contrast to the Goldstein et al. (2001) approach, we do not model a dynamic capital structure. Furthermore, we refrain from modeling personal taxes raised on payments to investors.
Thus, EBIT cannot become negative. As a consequence, there is no bankruptcy risk for an all-equity firm. The approach of modeling EBIT as a geometric Brownian motion has become standard in the literature, see, for example, Hackbarth et al. (2007), Strebulaev (2007), Purnanandam (2008), and Riis Flor (2008).
We assume that, in line with Goldstein et al. (2001), the total EBIT flow is immediately distributed among the claimants.
In this sense, the asset value is a gross value, as bankruptcy costs are also covered, although there are no direct claimants to this part of the asset value.
Expectation under the risk-neutral measure is denoted \({\mathbb {E}}_Q\) in the following, while expectation under the physical measure is simply denoted \({\mathbb {E}}\).
Goldstein et al. (2001) assume that bondholders have to pay taxes in the event of a default, so they only receive \((1 - \tau ) \, (1 - \alpha )\) of the remaining asset value. As such an approach introduces some additional complexity (for example, Eq. (13) will no longer hold), we assume that government has no claim in the event of a default, in line with the classical Leland (1994) model and some more recent approaches such as Glover (2016).
As the company does not necessarily default at all, \(t^*\) can be infinite.
For the calibration of the model in Sect. 3, we will use \(D = F\) as an identifying assumption.
In practical applications, an average value over a few preceding years could be more appropriate.
In the Gordon growth model, the EBIT growth rate is constant over time.
See Welch (2017) for an overview.
Thus, the calibration requires knowledge of the current fair corporate interest rate (for debt issued at par value). In practice, when the company has several layers of debt raised at different times, one can use the latest negotiated interest rate as the best market proxy for a fair corporate interest rate.
This concave increase of the covariance with default risk can be explained in a stylized one-period setting. In this setting, the bond return \(r_\mathrm{D}\) is \(-1\) in case of default, and it is \(+i\) otherwise; default risk is totally systematic and linked to the market return \(r_M\). Without loss of generality, the distribution of \(r_M\) is standard normal. Thus, default occurs if \(r_M < N^{-1}(p)\), where p is the default probability and N is the standard normal distribution. The covariance of bond returns and market returns is then given by
$$\begin{aligned} \mathrm{Cov}(r_M, r_\mathrm{D}) = - \int _{-\infty }^{N^{-1}(p)} x \, \mathrm{d}N(x) + i \int _{N^{-1}(p)}^{\infty } x \, \mathrm{d}N(x) = \phi \left( N^{-1}(p)\right) (1 + i) , \end{aligned}$$where \(\phi\) is the normal density function. As can easily be verified, this covariance increases concavely with p.
Berg (2010) reports very similar figures based on the Merton model, calibrated to real-world data.
In a way, such a calibration is quite analogous to the “practitioners Black–Scholes approach” (An and Suo 2009) to option pricing: although practitioners know that the assumptions of the Black–Scholes model do not hold, they, nonetheless, use the model by estimating the implied volatilities from traded options data and calculating prices for non-traded, but similar options and other derivatives with these implied volatilities.
Note that the Goldstein et al. (2001)’s assumption that bondholders have to pay taxes upon default is equivalent to increased bankruptcy costs. Our deviation obviously has a negligible impact on the resulting cost of debt, which would increase from 3.69% to 3.70%. For the highly leveraged firm, the value would be 4.95% instead of 4.88%.
There might be slight deviations because of the coupon effect, but these deviations are small, in general.
Default rates are based on Moody’s statistics 1983–2013 provided by Ou (2014). The corresponding cost of debt estimate is the internal rate of return of expected payments of a fictitious 20-years-to-maturity bond and a (notional) yield to maturity of the actual corporate bond. For simplicity, recovery rates are assumed to be zero.
Equity and asset value are driven by the same risk factor, and hence, the instantaneous correlations with the market factor are identical.
This relation follows from Itô’s Lemma. See, e.g., Black and Scholes (1973).
This assumption is easily modeled by letting \(\alpha = 0\). In the appendix, we show how to incorporate non-zero bankruptcy costs. This involves calculating an instantaneous return on bankruptcy costs, which is analogous to the instantaneous returns on debt and equity, as shown below.
Note that this identity would be violated if government had a claim on bondholders in the event of a default.
It is different to the textbook WACC without bankruptcy costs because of the model calibration: with bankruptcy costs, debt is worth less and requires a higher interest rate, which increases the WACC.
Shortly speaking, the firm uses a biased model to estimate the cost of debt to be plugged into the correct WACC formula. As a second use case, one could also think of a firm with time-varying leverage consistent with the model, so it would calculate the correct cost of debt, but then to plugged into a biased WACC formula.
This redemption can be seen as a repurchase at market value. The market value is calculated at each simulation step based on the current conditions, assuming an infinite time horizon and the bankruptcy threshold B. Note that such a redemption policy at market value (in contrast to a call option at a fixed price) has no impact on the actual value of the bond.
As Gamba et al. (2008) point out, a continuous maintenance of a constant debt ratio would leave the firm without default risk, as it would have redeemed all the debt before bankruptcy was reached. Therefore, default must be modeled by an exogenous threshold, which we assume to be the ex-ante optimal threshold B.
References
An, Y., and W. Suo. 2009. An empirical comparison of option-pricing models in hedging exotic options. Financial Management 38: 889–914.
Berg, T. 2010. From actual to risk-neutral default probabilities: Merton and beyond. Journal of Credit Risk 6 (1): 55–86.
Black, F., and M. Scholes. 1973. The pricing of options and corporate liabilities. Journal of Political Economy 81: 637–654.
Brealey, R.A., S.C. Myers, and F. Allen. 2016. Principles of corporate finance, 12th ed. Singapore: McGraw-Hill.
Brennan, M.J. 2003. Corporate investment policy. In Handbook of the Economics of Finance, ed. G.M. Constantinides, M. Harris, and R.M. Stulz, 167–214. Amsterdam: Elsevier.
Cooper, I.A., and S.A. Davydenko. 2007. Estimating the cost of risky debt. Journal of Applied Corporate Finance 19: 90–95.
Copeland, T.E., J.F. Weston, and K. Shastri. 2005. Financial theory and corporate policy, 4th ed. Boston: Pearson.
Da, Z., R.J. Guo, and R. Jagannathan. 2012. CAPM for estimating the cost of equity capital: Interpreting the empirical evidence. Journal of Financial Economics 103: 204–220.
Damodaran, A. 2012. Investment valuation, 4th ed. New York: Wiley.
Gamba, A., G.A. Sick, and C.A. León. 2008. Investment under uncertainty, debt and taxes. Economic Notes 37 (1): 31–58.
Glover, B. 2016. The expected cost of default. Journal of Financial Economics 119: 284–299.
Goldstein, R., N. Ju, and H.E. Leland. 2001. An EBIT-based model of dynamic capital structure. Journal of Business 74: 483–512.
Grinblatt, M., and J. Liu. 2008. Debt policy, corporate taxes, and discount rates. Journal of Economic Theory 141: 225–254.
Hackbarth, D., C.A. Hennessy, and H.E. Leland. 2007. Can the trade-off theory explain debt structure? Review of Financial Studies 20: 1389–1428.
Hsia, C.C. 1981. Coherence of the modern theories of finance. Financial Review 16: 27–42.
Hsia, C.C. 1991. Estimating a firm’s cost of capital: An option pricing approach. Journal of Business Finance & Accounting 18: 281–287.
Husmann, S., and M. Schmidt. 2008. The discount rate: A note on IAS 36. Accounting in Europe 5 (1): 49–62.
Leland, H.E. 1994. Corporate debt value, bond covenants, and optimal capital structure. Journal of Finance 49: 1213–1252.
Löffler, A. 2004. Zwei Anmerkungen zu WACC. Zeitschrift für Betriebswirtschaft 74: 933–942.
Merton, R.C. 1973. An intertemporal capital asset pricing model. Econometrica 41: 867–887.
Merton, R.C. 1974. On the pricing of corporate debt: The risk structure of interest rates. Journal of Finance 29: 449–470.
Miles, J.A., and J.R. Ezzell. 1980. The weighted average cost of capital, perfect capital markets, and project life: A clarification. Journal of Financial and Quantitative Analysis 15: 719–730.
Ou, S. 2014. Annual default study: Corporate default and recovery rates, 1920–2013, moody’s Investors Service
Purnanandam, A. 2008. Financial distress and corporate risk management: Theory and evidence. Journal of Financial Economics 87: 706–739.
Riis Flor, C. 2008. Capital structure and assets: Effects of an implicit collateral. European Financial Management 14: 347–373.
Ross, S.A., R.W. Westerfield, J.F. Jaffe, and B.D. Jordan. 2016. Modern financial management, 11th ed. New York: McGraw-Hill.
Schönbucher, P.J. 2003. Credit derivatives pricing models: Models, pricing and implementation. Chichester: Wiley.
Strebulaev, I.A. 2007. Do tests of capital structure theory mean what they say? Journal of Finance 62: 1747–1787.
Welch, I. 2017. Corporate finance. Los Angeles
Acknowledgements
The author thanks the editor and two anonymous referees for valuable comments and suggestions. He furthermore thanks Olaf Korn for fruitful discussions, as well as Florian Borchard for capable research assistance.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
1.1 Implied asset volatility
Given the current debt value D, we can use (10) to calculate an implied value for \(\eta\):
Inserting \(D = F\) and the threshold B according to its definition (8) yields an expression for \(\eta\) with the yet unknown asset volatility \(\sigma\):
We can now use the definition (11) of \(\eta\) to iteratively calculate an implied value for the asset volatility:
1.2 Derivatives with respect to asset value
To calculate the derivatives of equity and debt value with respect to asset value, we first need the derivative of \(\eta\):
where, for simplicity of notation, \(\lambda = \lambda (\gamma , r, \sigma )\).
Regarding the equity value, we can write (13) explicitly to obtain
It follows
using the definition \(B = \frac{ \lambda }{ 1 + \lambda } \, \frac{ i }{ r } F\) (8).
Regarding the debt value, deriving Eq. (10) yields
1.3 Instantaneous WACC with bankruptcy costs
In Sect. 5.1, we have derived the textbook formula for the instantaneous WACC when bankruptcy costs are zero. In the general case, Eq. (27) becomes
where \({\mu }_{BC}\) is the instantaneous return on bankruptcy costs, that is, the expected instantaneous drift of their value. It is calculated analogously to the drifts of debt and equity in the intertemporal CAPM as
with
according to (23). The partial derivative is derived similar to \(\partial D / \partial A\) as
(Note that, technically, \(\sigma _{BC}\) becomes negative.)
With bankruptcy costs, the expected return on firm value after taxes is \(A \, {\mu } \, (1 - \tau ) - BC \, {\mu }_{BC} \, (1 - \tau )\) (as expected, bankruptcy costs also decrease the expected tax payments). Hence, the instantaneous WACC is given by
The textbook formula for the instantaneous WACC must, therefore, be extended by a component for bankruptcy costs:
To illustrate the effect, we consider the highly leveraged firm (see Sect. 3) with bankruptcy costs \(\alpha = 50\%\). Here, we have \({\mu }_E = 8.90\%\), \({\mu }_D = 4.37\%\), and \({\mu }_{BC} = 1.97\%\). The true instantaneous WACC calculated with Eq. (47) is \({\mu }_{\mathrm{WACC}} = 5.51\%\), whereas the textbook formula, ignoring bankruptcy costs, yields \(5.64\%\).
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Baule, R. The cost of debt capital revisited. Bus Res 12, 721–753 (2019). https://doi.org/10.1007/s40685-018-0070-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40685-018-0070-6