Discontinuous financing based on market values and the value of tax shields

Abstract

The tax shield as present value of debt-related tax savings plays an important role in firm valuation. Driving the risk of future debt levels, the firm’s strategy to adjust the absolute debt level to future changes of the firm value, labeled as (re-) financing policy, affects the value of tax shields. Standard discounted cash flow (DCF) models offer two simplified (re-) financing policies originally introduced by Modigliani and Miller (MM) as well as Miles and Ezzell (ME). In this paper, we introduce a discontinuous financing policy that refers to the refinancing intervals, i.e., the maturity structure of the firm’s debt. By deriving APV valuation and beta unlevering equations that allow for this discontinuous financing policy, we show the MM and ME policies to be special cases of the proposed extension. While we document the effect of discontinuous refinancing to be economically significant when leverage is high and refinancing periods are extremely long, our results suggest that for low-levered firms with short refinancing periods, the traditional continuous refinancing-based models (like the Miles/Ezzell model) produce relatively robust value estimates. Combining capital structure and maturity structure choices, our model extends the set of feasible financing policies in DCF valuation models.

1 Introduction

Due to the tax deductibility of interest payments, taxes are a major factor driving corporate capital structure decisions (see, e.g., Graham 2000). In the literature on firm valuation, the integration of debt-related tax savings into the pricing framework has been (and still is) subject of a lively debate: researchers have been concerned with the inclusion of default risk and costs of financial distress (see, e.g., Koziol 2014; Molnár and Nyborg 2013), personal income taxes (e.g., Sick 1990; Molnár and Nyborg 2013), and consequences of different “debt policies” or “financing policies”¹ (see, e.g., Fernandez 2004; Arzac and Glosten 2005; Cooper and Nyborg 2006; Massari et al 2007 and Dempsey 2013).

This paper analyzes the impact of a firm’s policy of adjusting future debt levels towards changes of its market value, labeled as (re-)financing policy, on the value of its tax shields. It does so by extending the well-known financing policy based on market values originally introduced by Miles and Ezzell (1980) by a discontinuous refinancing sequence. This sequence is defined by the firm’s timing of its debt level adjustments towards a target leverage ratio on changes of its economic environment, reflected by its market value. Between two adjustment dates, the firm’s debt levels are state independent and certain. The choice of the adjustment sequence closely relates to the maturity structure choice of corporate debt: choosing a certain time to maturity for corporate debt contractually fixes debt levels over this time frame. Renewing debt at the end of maturity will take into account the prevailing economic conditions reflected by the firm’s market value.²

The chosen refinancing policy has an impact on the risk properties of debt-related tax savings: while debt levels are certain between two adjustment/refinancing dates, the adjustment towards changes of the firm value itself exposes debt levels to the firm’s business risk at every refinancing date.

So far, firm valuation models capture the firm’s chosen refinancing/adjustment policy by offering two simple types of “debt policies” or “financing policies”.³ The first policy assumes future debt levels to be certain (non-stochastic) [(see, Modigliani and Miller 1958) and 1963 henceforth termed MM)], whereas the second policy rests on certain leverage ratios based on market values of debt and equity (see, e.g., Miles and Ezzell 1980 and 1985; Harris and Pringle 1985) henceforth termed ME). When assuming constant absolute debt levels (in case of MM) and constant leverage ratios (in case of ME), both policies reflect different frequencies for the adjustment of the level of outstanding debt towards future changes in firm value. Kruschwitz et al (2007) allow for a combination of the two policies and analyze a “hybrid” financing policy shifting one time from a MM policy towards a ME policy. As our model allows for shifts in both directions for several times, it offers a significantly higher flexibility for the firm’s financing policy.

We propose a generalized model allowing the firm to choose its capital structure and refinancing sequence and thus include discontinuous financing policies that extend the standard MM and ME setting in firm valuation. In addition, we show that the aforementioned standard financing policies are special polar cases of our model each assuming a particular refinancing sequence. Moreover, we derive closed-form pricing equations for the adjusted present value (APV) approach and a beta unlevering procedure consistent to the refinancing sequence of the introduced discontinuous financing policies. Finally, we briefly point to the applicability of the weighted average cost of capital (WACC) approach in combination with the proposed financing policy.

As our approach allows for a richer set of choices with respect to the corporate “financing policies”, it makes an important contribution to the literature on firm valuation: it introduces more realistic assumptions of the firms debt policies. Empirically, firms do not seem to follow either of the two simplified financing policies from above. In the corporate finance literature, there has been a long debate around the question if at all, and if so how frequently firms adjust their debt level and/or capital structure towards changes in firm value. Fischer et al (1989) showed that transaction costs play an important role for the adjustment of the debt level towards a certain target value determined by an optimal leverage ratio. Huang and Ritter (2009) found evidence that firms adjust half way towards a target leverage on book values at a moderate speed of 1.6–3.7 years. Leary and Roberts (2005) find a full adjustment of debt levels towards a target market leverage in 2–4 years after equity issues and equity shocks. Thus, by introducing the firm’s historic refinancing/adjustment policy or a policy representative for the respective industry, our model allows for more realistic estimates of the tax shield in firm valuation. While our results indicate a significant economic effect of discontinuous financing on the tax shield value for high debt levels and extremely long refinancing periods, we also find the traditional ME financing policy to generate relatively robust value estimates for low-levered firms with short refinancing intervals.

This paper is organized as follows. In Sect. 2, we discuss the basic assumptions and standard financing policies in discounted cash flow models. Section 3 introduces the framework of a discontinuous financing policy and derives the corresponding equations for tax shield pricing. In Sect. 4, we derive the unlevering relations for beta factors and discuss their implications. To highlight the potential deviation caused using the two simplified financing policies instead of a maturity structure matching, we provide a numerical example in Sect. 5. A conclusion and outlook for future research are given in Sect. 6.

2 The model

2.1 Basics

We assume a standard economic multi-period setting, with $t,~t+1,\ldots ,~T-1,~T$ points in time, where $T=\infty$ ⁴ is possible. The capital market is free of arbitrage and the spanning property holds for the subsequently discussed free cash flows, equity, and firm values. From this assumption, the fundamental theorem of asset pricing applies and there exists a risk-neutral probability measure $\mathbb {Q}$ that is equivalent to the subjective probability measure $\mathbb {P}$.⁵ The operator for the expected value under $\mathbb {P}$ contingent on the available information at time t is denoted by $\mathbb {E}_t[.]$ and under the risk-neutral probability measure $\mathbb {Q}$ by $\mathbb {E}^{\mathbb {Q}}_t[.]$. The risk-free rate $r_f$ and the corporate tax rate $\tau$ are assumed to be deterministic and constant.⁶

The firm realizes in every future period s uncertain, unlevered free cash flows $\widetilde{\text {FCF}}_s$, with $s={t+1}, {t+2}, ..., T$. The expected unlevered free cash flows are determined by

$$\begin{aligned} \mathbb {E}_t\left[ \widetilde{\text {FCF}}_{t+1}\right]&=\widetilde{\text {FCF}}_t (1+g), \end{aligned}$$

(1)

where g denotes the (expected) growth rate. In addition, we assume $FCF_0>0$ and $g>-1$ to hold implying $\widetilde{\text {FCF}}_t>0$. With this explicit modelling of auto-regressive free cash flows, the expected value in an arbitrary period s, with $s>t$, can be determined by $\mathbb {E}_t[\widetilde{\text {FCF}}_s]=\widetilde{\text {FCF}}_t(1+g)^{s-t}$.⁷

The value of an unlevered firm at time t, $\widetilde{V}_{t}^{\text {U}}$, whose assets generate a stream of cash flows $\widetilde{\text {FCF}}_s$, with $s=t+1,~...,~T$, is determined under $\mathbb {Q}$ by

$$\begin{aligned} \widetilde{V}_{t}^{\text {U}}&=\sum _{s=t+1}^T\frac{\mathbb {E}^{\mathbb {Q}}_t[\widetilde{\text {FCF}}_s]}{(1+r_f)^{s-t}}. \end{aligned}$$

(2)

The cost of capital of an unlevered firm $r_\mathrm{u}$ is assumed to be deterministic and constant in time. This assumption allows to write for the value of the unlevered firm under $\mathbb {P}$ ⁸

$$\begin{aligned} \widetilde{V}_{t}^{\text {U}}&=\sum _{s=t+1}^T\frac{\mathbb {E}_t[\widetilde{\text {FCF}}_s]}{(1+r_\mathrm{u})^{s-t}}. \end{aligned}$$

(3)

Note, we understand the one-period cost of capital in an arbitrary period t as deterministic conditional expected returns (see, e.g., Kruschwitz and Löffler 2006).

Now, consider an otherwise identical firm that partly finances its operations with debt. In every period, this levered firm has to pay interest on the total amount of debt outstanding $\widetilde{D}_s$ and possible principal payments. The possibly risk adjusted cost of debt is denoted as $r_D$.⁹

The value of the levered firm, $\widetilde{V}^{\text {L}}_t$, can be determined by the adjusted present value approach (APV) (see, e.g., Myers 1974) which combines the unlevered firm value and the tax shield $\mathrm{TS}_t$ comprising the present value of future tax savings due to the tax deductibility of interest payments:

$$\begin{aligned} \widetilde{V}^{\text {L}}_t&= \widetilde{V}_{t}^{\text {U}}+ \mathrm{TS}_t. \end{aligned}$$

(4)

In the next section, we quantify the tax shield, $\mathrm{TS}_t$, for the well-known financing policies following Modigliani and Miller as well as Miles and Ezzell.

2.2 Simplified financing policies

Equation (4) is generally valid without having imposed yet any assumptions with respect to the pursued financing policy of the firm. We start our analysis by looking at two standard financing policies proposed by Modigliani and Miller (1958) (MM policy or autonomous financing) and Miles and Ezzell (1980) (ME policy or financing based on market values):

• MM policy: the firm projects a certain, state independent, not necessarily constant total amount of debt $D_t$ for every future period t. Combined with random future firm values $\widetilde{V}^\mathrm{L}_s$, with $s>t$, this policy implies random leverage ratios $\widetilde{l}_s$ as $\widetilde{l}_s = D_s / \widetilde{V}^\mathrm{L}_s$. Assuming $D_s = D_t$ for all s, the firm will maintain its current level of debt for all future periods independently from the development of the firm value $\widetilde{V}^\mathrm{L}_s$. This can be interpreted as the choice of a refinancing policy assuming an adjustment interval tending to infinity; the firm never adjusts the level of debt according to potential changes in $\widetilde{V}^\mathrm{L}_t$. Given a constant debt level, the value of the tax shield is given by

  $$\begin{aligned} \mathrm{TS}^{MM}_t&= \sum _{s=t+1}^\infty \frac{\tau \cdot r_D\cdot D_t}{(1+r_D)^{s-t}} = \tau \cdot D_t. \end{aligned}$$

  (5)

• ME policy: the firm establishes a certain, state independent, not necessarily constant, leverage ratio $l_s$ in any future period $s > t$. Given that future firm values $\widetilde{V}^L_s$ are random, future debt levels $\widetilde{D}_s=l_s\cdot \widetilde{V}^\mathrm{L}_s$ are uncertain as well. In a discrete time setting, this policy implies that the absolute level of debt is following the development path of the uncertain future firm value $\widetilde{V}^\mathrm{L}_s$ if the leverage ratio is constant over time, i.e., $l_t = l$ $\forall$ t. The firm is adjusting its debt level every period according to the realized firm value. This debt policy can be interpreted as a choice of a refinancing/adjustment sequence of 1 period, i.e., the debt issued in period t, $D_t$, is redeemed in $t+1$ and new debt at an amount of $\widetilde{D}_{t+1}$ is issued. Since the leverage ratio ties the debt level to the levered firm value, the tax savings are subject to the same dynamics as the unlevered free cash flows (see, e.g., Arzac and Glosten 2005). Assuming a constant leverage ratio and perpetual free cash flows (i.e., $g = 0$), the tax shield according to the ME approach is determined by

  $$\begin{aligned} \mathrm{TS}^{ME}_t&=\sum _{s=t+1}^\infty \frac{\tau \cdot r_D\cdot \mathbb {E}_t[\widetilde{D}_{s-1}]}{(1+r_D)(1+r_\mathrm{u})^{s-t-1}}=\frac{\tau \cdot r_D\cdot D_t}{r_\mathrm{u}}\frac{1+r_\mathrm{u}}{1+r_D}. \end{aligned}$$

  (6)

Figure 1 depicts the debt structure of the two standard financing policies. The first line illustrates the classical MM assumption of a constant debt level $D_t$ for all periods $t+1,~t+2,~\ldots$. In every arbitrary period $s>t$, the firm realizes expected tax savings $\tau \cdot r_D\cdot D_t$ due to the tax deductibility of interest payments. The second line shows the assumption regarding the debt maturity structure implied by the ME approach. In an arbitrary future period s, with $t<s\le T$, the firm adjusts its debt level according to $\widetilde{D}_s=l\cdot \widetilde{V}^\mathrm{L}_s$. Without loss of generality, we regard only the net principal payments or change of the debt level, which is defined by $\Delta \widetilde{D}_s=\widetilde{D}_{s-1}-\widetilde{D}_s$. Positive net principal payments, $\Delta \widetilde{D}_s>0$, indicate a decrease in the debt level and vice versa. The ME approach implicitly assumes that the firm refinances and adjusts every single period its debt level, i.e., the debt issued in period t, $D_t$, is redeemed in $t+1$ and new debt with an amount of $\widetilde{D}_{t+1}$ is issued.

Fig. 1

Illustration of the different debt maturity structures underlying the approaches

3 A discontinuous financing policy based on market values

In this section, we introduce a discontinuous financing policy based on market values. According to this financing policy, the firm chooses to refinance its debt every k periods, i.e., at the points in time $t,~{t+k},~{t+2 k},~\ldots ,~t+n\cdot k$, where $n\in \mathbb {N}$. At any arbitrary refinancing date $t+nk$, the firm’s debt level is adjusted according to $\widetilde{D}_{t+nk}=l_{t+nk} \cdot \widetilde{V}^{\text {L}}_{t+nk}$, where $l_{t+nk}$ denotes the target capital structure at $t+nk$. In addition, we assume a bullet structure of the redemption payment implying a constant debt level between two arbitrary refinancing dates $t+nk$ and $t+(n+1)k$. Thus, at every period s, the firm’s debt level is¹⁰

$$\begin{aligned} \widetilde{D}_{s}&= {\left\{ \begin{array}{ll} l_s \cdot \widetilde{V}^{\text {L}}_s &{}\quad \text {~if~} \quad s=t+n\cdot k \quad \text {~for~} n\quad\in \mathbb {N},\\ \widetilde{D}_{s-1} &{}\quad \text {~else.} \end{array}\right. } \end{aligned}$$

(7)

Note that the first adjustment is observable at t. This financing policy combines a target leverage ratio $l_t$ with a certain refinancing policy and maturity structure: refinancing debt every k periods the firm adjusts the debt level according to the then prevailing market value of the firm.

Assuming that $T-t$ can be divided by k resulting in an integer, the value of the tax shield is given by¹¹

$$\begin{aligned} \mathrm{TS}_{t}^k&= \sum _{s=t+1}^{t+\frac{T-t}{k}} \sum _{j=1}^{k} \frac{\tau \cdot r^{(k)}_D\cdot \mathbb {E}_t\left[ \widetilde{D}_{t+(s-t)k-k}\right] }{(1+r^{(k)}_D)^{j} \cdot (1+r_{\mathrm{u}})^{(s-t)k-k}}. \end{aligned}$$

(8)

The valuation of the tax shield in an arbitrary year from $T-k+1$ to T has to take into account that the level of debt is certain since the last adjustment at $T-k$. This implies that the cost of debt for the debt issued in $T-k$ with a maturity of k, $r^{(k)}_D$, is the appropriate discount rate¹² for the tax savings up to the next refinancing point. From $T-k$ to the current point at time t, the appropriate discount rate is the unlevered cost of equity $r_\mathrm{u}$ as the present value of the tax shield depends on the future debt adjustments to the (stochastic) firm value.¹³

Assuming constant free cash flows ($g=0$) and a constant target leverage ratio at any future refinancing date, i.e., $l_s=l$ for any $s=t+k,~t+2k,~t+3k,~\ldots$, and an infinite lifetime of the firm Eq. (8) can be simplified¹⁴ for the case of $T=\infty$ ¹⁵ to

$$\begin{aligned} TS_{t}^k&= D_t \cdot \Lambda _t^k, \text { with } \Lambda _t^k = \frac{\tau \cdot r^{(k)}_D\cdot AF(r_\mathrm{u},k)}{AF(r^{(k)}_D,k) \cdot r_\mathrm{u}}, \end{aligned}$$

(9)

where $AF(r,k)=\frac{r \cdot (1+r)^k}{(1+r)^k-1}$ is the annuity factor for discount rate r and time to maturity k. Note that $\Lambda _t^k$ in (9) accounts for the maturity structure and refinancing frequency of debt chosen by the firm. The sensitivity of the tax shield with respect to k depends on the difference between $r^{(k)}_D$ and $r_\mathrm{u}$. For the standard case $r^{(k)}_D<r_\mathrm{u}$, the tax shield value increases with k.

By substituting Eq. (9) in (4), the relation between the unlevered and the levered firm value is

$$\begin{aligned} \widetilde{V}^{\text {L}}_t&= \frac{\widetilde{V}_{t}^{\text {U}}}{1-l \cdot \Lambda _t^k}. \end{aligned}$$

(10)

According to Eq. (10), we observe a constant relationship between the levered and the unlevered firm value if the leverage is set to $l_t=l$ on all refinancing dates $t,~{t+k},~{t+2 k}, \ldots$ and the parameters k and $\tau$ of $\Lambda _t^k$ are constants as well. Note that $r_\mathrm{u}$ is an expected return and $r^{(k)}_D$ denotes the “cost of debt” for a debt issue with time to maturity k. This results in a constant relationship between the unlevered firm value and the total amount of debt, $\widetilde{D}_{s}=l \cdot \widetilde{V}^{\text {L}}_s$, for all $s=t, t+k, {t+2k}, \ldots$.

The third line in Fig. 1 illustrates the maturity structure of the discontinuous financing policy. At time t, the firm issues debt with a fixed maturity structure of k periods. After k periods (e.g., years), the firm refinances this debt issue at time $t+k$ by redeeming the debt issued on the most recent refinancing date t, $\widetilde{D}_{t}$, and issuing new debt $\widetilde{D}_{t+k}$ according to its target leverage ratio applied to the prevailing market value of the firm.

By comparing our tax shield Eq. (8) against (6) and (5), we find the two debt policies to be special and polar cases of the proposed discontinuous financing policy: setting $k=1$ yields the ME policy Eq. (6) and letting k tends to infinity the MM-policy Eq. (5) (see Appendix 8 for the proof). Obviously, any value of k between the two polar cases results in a pricing equation that yields values between the MM- and ME-implied values.

The result derived in this section has an important implication for the practical relevant WACC approach. It is well known that cost of capital needs to be known with certainty at the timepoint of valuation t.¹⁶ Random future cost of capital cannot be used as discount rates to obtain present values of future expected cash flows.¹⁷ Given a refinancing policy with a fixed interval of k periods, the capital structure of the firm (in market values) is known with certainty every k periods, i.e., when the firm readjusts the debt level according to the target leverage ratio l. Thus, the firm’s WACC, defined as $wacc_{t+nk}=r_L~(1-l) ~+~ r_D~(1-\tau )~l$, at any arbitrary refinancing point $t+nk$ is also non-random. However, this is not true for any intermediate timepoint s between two arbitrary adjustment dates, with $t+nk<s<t+(n+1)k$. Between two refinancing dates, the financing policy described fixes the debt level to $D_{t+nk}$ and the leverage ratio $\widetilde{l}_{s}=D_{t+nk}/\widetilde{V}^L_s$ turns into a random variable. As a consequence, $\widetilde{wacc}_s$ is a random variable for any intermediate point in time s and thus does no longer meet the requirement from above to serve as cost of capital, implying that a WACC-based valuation for discontinuous financing is not possible. Only in one special case, WACC may be used as discount rate for every future period’s cash flow: if $k=1$, i.e., the ME policy applies, the firm’s debt level will be adjusted every period and l is known with certainty at any future point in time.

4 Unlevering beta

In the preceding section, we derived a pricing equation for a discontinuous financing policy. In this section, we analyze the impact of the discontinuous financing policy on the levered beta by deriving a relation between the levered, $\beta ^{(k)}_{L}$, and unlevered (asset) beta factor, $\beta _U$. Following the literature (e.g., Miles and Ezzell 1985), we start our analysis by obtaining a relation for the “weighted average” beta factor, $\beta _w$ based upon the increments of the APV equation incorporating the tax shield for the discontinuous financing policy, as given by Eq. (8). Second, we recognize the well-known fact that the leverage weighted average of the debt beta, $\beta ^{(k)}_D$, and the beta for levered equity, $\beta ^{(k)}_{L}$, yields the firm’s weighted average beta, $\beta _w$, and rearrange to obtain an equation relating $\beta ^{(k)}_{L}$, $\beta ^{(k)}_D$, and $\beta _U$:¹⁸

$$\begin{aligned} \beta ^{(k)}_{L}&=\left( \frac{1-\sum _{j=1}^{k}\frac{\tau \cdot r^{(k)}_D\cdot l }{(1+r^{(k)}_D)^j}}{1-l}\right) \cdot \beta _U+ \left( \frac{\sum _{j=1}^{k}\frac{\tau \cdot r^{(k)}_D\cdot l }{(1+r^{(k)}_D)^j}-l}{1-l}\right) \cdot \beta ^{(k)}_D. \end{aligned}$$

(11)

Equation (11) generally holds for a discontinuous financing policy and, therefore, includes the two special cases of the MM and ME approaches. Note that the superscript (MM) indicates the MM policy and (ME) the ME policy. Assuming risk-free debt, with $\beta ^{(k)}_D=0$ implying $r^{(k)}_D=r_f$, and letting $k \rightarrow \infty$, we find the unlevering relation for the MM model:

$$\begin{aligned} \beta ^{MM}_{L}&=\left( 1+(1-\tau )\frac{\widetilde{D}_t}{\widetilde{E}_t}\right) \cdot \beta _U. \end{aligned}$$

(12)

Setting $k=1$ results in the unlevering relationship of the standard ME model:

$$\begin{aligned} \beta ^{ME}_{L}&=\left( \frac{1-\frac{\tau \cdot r_f\cdot l}{1+r_f}}{1-l}\right) \cdot \beta _U. \end{aligned}$$

(13)

Table 1 Comparison of unlevering procedures

Now, we are interested in the potential effect of a given discontinuous financing policy with sequence k compared to the two standard financing policies by ME and MM when deriving a firm’s asset beta from a given levered equity beta. To illustrate this impact, we look at the standard setting of corporate valuation of a levered beta $\beta _L$ estimated based on empirical capital market data. Table 1 displays asset betas computed using the derived unlevering equations for a set of different financing policies [$k=1$ (ME policy), $k=3,~5,~10$ and $k=\infty$ (MM policy)], different leverage ratios ($l=0.4,~0.6~\text {and}~0.8$) and estimates for equity betas ($\beta _L=0.5,~1,~\text {and}~1.5$).¹⁹ In addition, the calculations assume a debt beta of zero, i.e., $r_D=r_f$ with $\beta _D=0$. The corporate tax rate is $\tau =35\%$ and the risk-free rate $r_f=2\%$.

We find unlevered betas to decline in value for increasing leverage ratios l and to increase with increasing k. The first result reflects the well-known (reverted) impact of financial leverage risk (e.g., Miles and Ezzell 1985). The second effect is a direct consequence of the tax savings’ risk properties: as increasing k reduces the risk of future debt levels and the tax savings attached to it, it also curbs the increase in financial leverage with increasing debt.

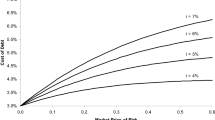
Finally, we derive percentage estimation errors for using the unlevering Eqs. (12) and (13) of the two simplified financing policies whenever a discontinuous financing policy with sequence k is actually pursued, i.e., Eq. (11) should be applied. For the MM policy, define the percentage estimation error by $\frac{\beta ^{MM}_U}{\beta ^{(k)}_U}-1$. Substituting Eqs. (12) and (11) as well as rearranging, we obtain

$$\begin{aligned} \frac{\beta ^{MM}_U}{\beta ^{(k)}_U}-1 = \frac{\tau l-\sum _{j=1}^{k}\frac{\tau r_fl}{(1+r_f)^j}}{1-\tau l}. \end{aligned}$$

(14)

For $\tau >0$ and $l>0$, we find percentage errors of the MM unlevering equation to increase in l and to decrease in k. The latter result is not surprising as a refinancing sequence with $k=\infty$ is equivalent to the MM policy.

For the ME policy, define the percentage estimation error by $1-\frac{\beta ^{ME}_U}{\beta ^{(k)}_U}$.²⁰ Combining (11) with (13) and rearranging yields²¹:

$$\begin{aligned} 1-\frac{\beta ^{ME}_U}{\beta ^{(k)}_U}=\frac{\sum _{j=1}^{k-1}\frac{\tau r_fl }{(1+r_f)^j}}{(1+(1-\tau l)r_f)}. \end{aligned}$$

(15)

Equation (15) suggests the estimation error to increase with l and k. Again, the latter reflects the result from above that $k=1$ is equivalent to the ME policy. While both simplified equations may produce significant errors in deriving unlevered asset betas, the percentage deviation to realistic (discontinuous) financing policies is smaller under the ME assumptions than under the ones of the MM model. One way to minimize errors is to estimate refinancing sequences for different industries empirically and transfer them into Eq. (11).

5 Relevance of discontinuous financing policies for the tax shield value

In the subsequent section, we highlight the impact of the chosen refinancing policy on the levered firm value. As we are also interested in the deviation caused using the two simplified models of ME and MM policies from the value given the “true” policy of the firm, we consider a levered firm with a refinancing frequency of $k=3$ years. This frequency is in line with the empirical findings of the studies from above (see, e.g., Leary and Roberts 2005). We concentrate on the effect of the refinancing sequence and thus assume for simplicity the firm’s cost of debt to be independent from its choice of k, i.e., $r^{(k)}_D=r_D=r_f$ for all k and equal to $2\%$. With this assumption, we consider debt to be risk free. The firm has a constant expected annual unlevered free cash flow of 100 over an infinite lifetime $(g=0)$. Moreover, the equity betafactor of an otherwise identical but unlevered firm with the same business risk is $\beta _U=1.1$. The corporate tax rate $\tau$ is set to $35\%$ and the return of the market portfolio $r_m$ to $7.5\%$. With these assumptions, the unlevered cost of equity according to the standard CAPM return equation:

$$\begin{aligned} r_\mathrm{u}&= r_f + (r_m-r_f)\cdot \beta _U \end{aligned}$$

(16)

is calculated as $r_\mathrm{u}=8.0805\%$ and in turn the unlevered firm value amounts to $\widetilde{V}_{t}^{\text {U}}=\frac{100}{0.0805}=1,242.24$.

The superscript (MM) indicates the MM policy (ME) the ME policy and $k=3$ the respective refinancing assumption within the discontinuous financing policy framework. Comparing the three different assumptions, we first determine the firm values using Eq. (10). Notice that, as firm values differ with respect to the assumed financing policy, a given leverage ratio of $40\%$ implies different absolute debt values for the three policies.²² Having derived the firm values $\widetilde{V}^{L}_t$ allows us to compute the absolute debt amount and the tax shield value $TS_t$.

• 1. ME policy

Starting with the ME policy ($k=1$), the basic parameter $\Lambda _t^{ME}$ is equal to 0.0921. Based on Eq. (10), the levered firm value is equal to

$$\begin{aligned} \widetilde{V}^{{\rm L},ME}_t&= \frac{1,242.24}{1-0.4\cdot 0.0921}= 1,289.76, \end{aligned}$$

(17)

and the absolute debt value $D^{ME}_t$ amounts to 515.9. The tax shield value is then

$$\begin{aligned} {\rm TS}^{ME}_t&= \frac{0.35 \cdot 0.02 \cdot 515.9}{0.0805-0}\cdot \frac{1+0.0805}{1+0.02} = 47.52. \end{aligned}$$

(18)

• 2. MM policy

$\Lambda _t^{MM}$ for the MM policy ($k=\infty$) is equal to 0.35 and the levered firm value amounts to

$$\begin{aligned} \widetilde{V}^{{\rm L},MM}_t&= \frac{1,242.24}{1-0.4\cdot 0.35}=1,444.46. \end{aligned}$$

(19)

With a leverage of $l = 0.4$, the absolute debt value $D^{MM}_t$ is equal to 577.78. In this case, the value of the debt related tax savings amounts to

$$\begin{aligned} {\rm TS}^{MM}_t&= 0.35 \cdot 577.78 = 202.22. \end{aligned}$$

(20)

• 3. Exemplary maturity structure of the firm ($k=3$)

$\Lambda _t^{k=3}$ for the chosen refinancing policy by the firm is equal to 0.0974 and the levered firm value amounts to

$$\begin{aligned} \widetilde{V}^{L,k=3}_t&= \frac{1,242.24}{1-0.4\cdot 0.0974}=1,292.59. \end{aligned}$$

(21)

This implies an absolute debt value $D^{k=3}_t$ of 517.04. Finally, the tax shield value amounts to

$$\begin{aligned} TS^{k=3}_t&= 0.0974 \cdot 517.04 =50.36. \end{aligned}$$

(22)

As the refinancing policy of the firm with $k=3$ is close to $k=1$ and far away from $k=\infty$, our example results in a moderate undervaluation when applying the simplified ME policy, but in a significant overvaluation when relying on the simplifying assumption of an MM policy.

In Fig. 2, we depict the levered firm value as a function of k. We vary the value of k between 1 and 30, for four different leverage ratios, $l=0$ (i.e., the unlevered firm value), 0.4 (the previously discussed example), 0.6, and 0.8. In general, we observe for the three cases $l>0$ the levered firm value to increase in k. All graphs increase with increasing values for k. To provide a concise and clear Fig. 2, we have abstained from depicting values tending towards a maximum value for $k=\infty$.²³ In particular, for $k=1$, Fig. 2 depicts the leverage dependent values for the ME case 1, 289.76 $(l=0.4)$, 1, 314.91 $(l=0.6)$, and 1, 341.06 $(l=0.8)$. Last but not least, it should be noted that for $k=\infty$, i.e., the MM case, we would obtain the levered firm values: 1, 444.46, 1, 572.45, and 1, 725.33, respectively.

Fig. 2

$V^L_t$ dependent on k for four different leverages

Summarizing, the refinancing sequence of the firm’s debt is a major factor influencing the tax shield value. Depending on the firm’s actual choice of k, using the ME or MM financing policy may result in significant deviations from the levered firm value that matches the actual refinancing sequence of the debt issue. While for shorter maturities, the difference to the ME case could be regarded as relatively small, an application of the MM policy would result in a significant overvaluation of the tax savings of debt.

The economic effect of the pricing discrepancy between the k-implied tax shields is a direct result of the discounting technique. For higher (lower) values of k, the number of years with a certain debt level increases (decreases). Correspondingly, the number of years where the debt value and in turn the interest tax savings are subject to the same risk as the unlevered cash flows decreases (increases). Respectively, an increasing (decreasing) number of annual tax savings are discounted by $r^{(k)}_D$ and a decreasing (increasing) number with the unlevered cost of capital $r_\mathrm{u}$.

6 Conclusion

In this paper, we develop a model to value debt related tax shields. This model allows for a discontinuous debt financing policy by giving the opportunity to choose the firm’s leverage ratio and a refinancing interval of corporate debt. We show how to include the refinancing policy into the well-known APV approach and derive a pricing equation adjusting the discounting procedure accordingly. Moreover, we derive general relations between the unlevered and the levered beta factor. For the tax shield valuation and the APV approach, we also show that the two simplified financing policies currently proposed by the valuation literature, the Modigliani/Miller and the Miles/Ezzell case can be regarded as polar cases of the discontinuous financing policy. Furthermore, we briefly discuss the general inapplicability of the textbook WACC approach in combination with discontinuous financing.

Finally, we have to point towards some limitations of our approach. Obviously, the presented financing policy does not capture all possible policies of firms choosing their capital structure and refinancing sequence. For instance, a policy including a dynamic adjustment towards a target leverage ratio including transaction costs as first suggested by Fischer et al (1989) is not captured by our approach. Moreover, as the standard ME and MM approaches, our model does not explicitly account for default and potential bankruptcy cost. We believe, however, that the model can be easily extended towards this feature. The cost of debt is currently exogenously given and does not relate to any properties of default triggers. Thus, as the firm’s refinancing sequence combined with the leverage choice has an impact on credit risk, endogenizing the cost of debt, depending on l and k, is an obvious next step in extending the model.

Appendices

The definition of the discounting rule

The tax shield pricing equation mapping a discontinuous financing policy based on market values with refinancing every k years can be obtained by

$$\begin{aligned} {\rm TS}_{t}^k&= \sum _{s=t+1}^{t+\frac{T-t}{k}} \sum _{j=1}^{k} \frac{\tau \cdot r^{(k)}_D\cdot \mathbb {E}_t\left[ \widetilde{D}_{t+(s-t)k-k}\right] }{(1+r^{(k)}_D)^{j} \cdot (1+r_\mathrm{u})^{(s-t)k-k}}. \end{aligned}$$

(23)

The following example highlights the derivation of the proposed discounting procedure for the valuation of the tax shield.

Example 1

We assume the current point in time to be $t=0$ and the lifetime of the project to end in $T=4$. The firm’s financing policy is to adjust the debt level every $k=2$ years. The tax shield is given by Eq. (8), in which we apply j times $r^{(k)}_D$ and $(s-t) \cdot k - k$ times $r_\mathrm{u}$ as a discount rate.

Table 2 displays the adjustment of the amount of debt according to the refinancing sequence and highlights the number of years in which a tax shield needs to be discounted using the cost of debt $r^{(k)}_D$ and unlevered cost of capital $r_\mathrm{u}$, respectively.

Table 2 Discount rates and debt amount per index s in (8)

To find a pricing equation for $(T-t)/k$ being not an integer, we simplify Eq. (8) by defining two operators.

Definition 1

Integers a (dividend) and k (divisor) are given with $k>0$, two unique integers q (quotient) and r (remainder) exist, such that $a=k\cdot q + r$ and $0 < r \le k$. Thus, we can write

$$a \; div\; k=q, \quad and \quad a \; cert \; k=r.$$

Note that this is not the Euclidian division (division based on a modulo operator), where q is the downward rounded quotient of a / k with the remainder or rest of r. This would be the case if $0 \le r < k$. In our definition, the number $a=8$ divided by $k=3$ results in a div $k=q=2$ with remainder a cert $k=r=2$ and the number $a=9$ divided by $k=3$ results in $q=2$ with remainder $r=3$.

With these two operators at hand, we rewrite Eq. (8) without the assumption of k being a divisor of $T-t$:

$$\begin{aligned} TS_{t}^k&= \sum _{s=t+1}^{T} \frac{\tau \cdot r^{(k)}_D\cdot \mathbb {E}_t\left[ \widetilde{D}_{s-(s-t)~\mathrm{cert}~ k}\right] }{(1+r^{(k)}_D)^{(s-t)~\mathrm{cert}~ k} \cdot (1+r_\mathrm{u})^{((s-t)~\mathrm{div}~k) \cdot k}}. \end{aligned}$$

(24)

The following example highlights the derivation of the correct discount rate per annual tax shield.

Example 2

We assume the current point in time to be $t=5$ and the lifetime of the project to end in $T=12$. The firm’s financing policy is to adjust the debt level every $k=3$ years. The tax shield is given by Eq. (24), in which we apply$(s-t)~\mathrm{cert}~ k$ times $r_D$ and $((s-t)~\mathrm{div}~k) \cdot k$ times $r_\mathrm{u}$.

Table 3 displays the denominator of (24) and highlights the number of years for which a tax shield needs to be discounted per cost of debt $r^{(k)}_D$ and unlevered cost of capital $r_\mathrm{u}$, respectively.

Table 3 Discount factors per index s in (24)

Finally, some specific cases might require to drop our assumption that the time point of valuation t is itself a refinancing point. Consider a setting in which t represents a point in time between two refinancing dates. The firm has debt outstanding amounting to $D_t$ which is held constant until the next refinancing date, $\Theta$. As above, the firm chooses to refinance its debt every k periods and T represents the end of the lifetime. In this case, the tax shield pricing equation extends to

$$\begin{aligned} TS_{t}^k&= \sum _{i=1}^{\Theta -t}\frac{\tau \cdot r^{(k)}_D\cdot D_t}{(1+r^{(k)}_D)^i} + \sum _{s=t+1}^{t+\frac{T-\Theta }{k}} \sum _{j=1}^{k} \frac{\tau \cdot r^{(k)}_D\cdot \mathbb {E}_t\left[ \widetilde{D}_{t+(s-t-1)k+\Theta -t}\right] }{(1+r^{(k)}_D)^{j} \cdot (1+r_\mathrm{u})^{(s-t-1)k+\Theta -t}}. \end{aligned}$$

(25)

Initially, focus on the first term representing the tax shield value based upon the certain debt level $D_t$ chosen at the last refinancing date. Since the debt level remains certain, the appropriate discount rate is $r^{(k)}_D$. Now, regard the second term in Eq. (25) mapping the value of all future tax savings incurred after the next refinancing date $\Theta$. Comparing the second term with Eq. (8) reveals only one difference: the tax shield value at time $\Theta$ needs to be discounted by the unlevered cost of capital from time $\Theta$ to t. Otherwise, the discounting procedure described in Sect. 3 holds here as well.

The following example highlights the aforementioned discounting procedure.

Example 3

We assume the current point in time to be $t=1$ and the lifetime of the project to end in $T=4$. The firm’s financing policy is to adjust the debt level every $k=2$ years. Time $\Theta =2$ represents the next refinancing date. The tax shield is given by Eq. (25), in which we apply in the second term j times $r^{(k)}_D$ and $(s-t) \cdot k + \Theta - t$ times $r_\mathrm{u}$ as a discount rate.

Table 4 displays the adjustment of the amount of debt according to the refinancing sequence and highlights the number of years in which the tax shield needs to be discounted using the cost of debt $r^{(k)}_D$ and the unlevered cost of capital $r_\mathrm{u}$. Panel A depicts the discounting procedure for the first term in Eq. (25). Notice that for the outlined example the current debt outstanding $D_t=D_1$ is a certain quantity chosen at the last refinancing date. Therefore, the tax savings based on $D_1$ and incurred at time $t+1=2$ need to be discounted once by the cost of debt. Panel B shows the discounting procedure for the time $\Theta$ to T. The firm refinances its debt in $\Theta$ and keeps it constant until the next refinancing date $\Theta +k=T$. Thus, the expected tax savings at time $T=4$, $\tau r^{(k)}_D\mathbb {E}_t[\widetilde{D}_{2}]$, need to be discounted twice by the cost of debt and once by the unlevered cost of capital. Accordingly, the tax savings incurred at time $t=3$ need to be discounted once by the cost of debt and once by the unlevered cost of capital.

Table 4 Discount rates and debt amount per period in (25)

The generalized pricing equation and the ME and MM policies as polar cases

Definition 2

We consider a loan $P_0$ with a lifetime of k years and we assume annual compounding. The annual payment c corresponding to interest and redemption payments for k years is given by

$$\begin{aligned} c=P_0 \cdot AF(r,k) \text {~, with~}\quad AF(r,k)=\frac{r \cdot (1+r)^k}{(1+r)^k-1} \end{aligned}$$

(26)

The present value of tax savings resulting from interest payments of a debt issue with k years time to maturity, where the debt levels are certain and constant thus can be written as

$$\begin{aligned} \sum _{s=t+1}^{t+k} \frac{\tau \cdot r^{(k)}_D\cdot D_t}{(1+r^{(k)}_D)^{(s-t)}} = \frac{\tau \cdot r^{(k)}_D\cdot D_t}{AF(r^{(k)}_D,k)}, \end{aligned}$$

(27)

Equation (8) can be simplified to

$$\begin{aligned} {\rm TS}_{t}^k&= \sum _{s=t+1}^{t+\frac{T-t}{k}} \frac{\tau \cdot r^{(k)}_D\cdot E_t\left[ \widetilde{D}_{t+(s-t) \cdot k-k}\right] }{AF(r^{(k)}_D,k)\cdot (1+r_\mathrm{u})^{(s-t) \cdot k-k}}. \end{aligned}$$

(28)

Equation (28) defines the total tax shield value as present value of a sequence of tax savings. Assuming a bullet redemption payment and a constant target leverage ratio, i.e., $l_s=l_t$ for all $s=t+k,~t+2k,~t+3k,~...$, and combining with $g=0$ and $T\rightarrow \infty$ results in expected tax shields of $\tau \cdot r^{(k)}_D\cdot \mathbb {E}_t\left[ \widetilde{D}_{s}\right] =\tau \cdot r^{(k)}_D\cdot \widetilde{D}_t$ for all periods. Multiplying the present value for every financing sequence with $AF(r_\mathrm{u},k)$ is turning the value of this sequence s into an annuity between s and $s+k$ and the total tax savings over all sequences into a perpetuity. The present value of the tax shields can thus be calculated by dividing this perpetual cash flow by $r_\mathrm{u}$ finally resulting in

$$\begin{aligned} {\rm TS}_t^k&= D_{t}\cdot \Lambda _t^k, \text {with}\; \Lambda _t^k = \frac{\tau \cdot r^{(k)}_D\cdot AF(r_\mathrm{u},k)}{AF(r^{(k)}_D,k) \cdot r_\mathrm{u}}. \end{aligned}$$

(29)

The two simplified financing policies defined by Modigliani and Miller (1958) and Miles and Ezzell (1980) imply tax shield pricing equations that are special cases of (29) and (9). First, from (28) and $k=1$, we simplify to the value of the tax shield according to the assumptions of Miles and Ezzell and risky debt, where the firm refinances every year:

$$\begin{aligned} TS^{ME}_t&= \sum _{s=t+1}^{T} \frac{\mathbb {E}_t\left[ \widetilde{D}_{s-1}\right] \cdot r_D\cdot \tau }{(1+r_D) \cdot (1+r_\mathrm{u})^{s-(t+1)}}. \end{aligned}$$

(30)

In Eq. (30), tax savings from interest payments are discounted with the cost of debt for one year and the cost of unlevered capital for the remaining number of years.²⁴

Choosing $k=1$ yields $\Lambda _t^{k=1} = \tau \cdot \frac{r_D\cdot (1+r_\mathrm{u})}{(1+r_D) \cdot r_\mathrm{u}}$ and in turn the tax shield equation implied by the ME policy:

$$\begin{aligned} {\rm TS}^{k=1}_t&=\sum _{s=t+1}^\infty \frac{\tau \cdot r_D\cdot \mathbb {E}_t[\widetilde{D}_{s-1}]}{(1+r_D)(1+r_\mathrm{u})^{s-t-1}}=\frac{\tau \cdot r_D\cdot D_t}{r_\mathrm{u}}\frac{1+r_\mathrm{u}}{1+r_D}=TS^{ME}_t. \end{aligned}$$

(31)

The levered firm value in (10) is then

$$\begin{aligned} \widetilde{V}^{\rm L}_t&= \frac{\widetilde{V}_{t}^{\text {U}}}{1-l_t \cdot \tau \cdot \frac{r_D\cdot (1+r_\mathrm{u})}{(1+r_D) \cdot r_\mathrm{u}}}, \end{aligned}$$

(32)

which is equal to the pricing equation for the levered firm value implied by the assumptions of Miles and Ezzell, $\widetilde{V}^{{\rm L},ME}_t$.

Second, in the case that the firm never refinances and the current debt level is assumed to be constant until infinity, choosing k tends to $\infty$, $\Lambda _t^{k=\infty } \rightarrow \tau$. Then, the value of the tax shield is determined by

$$\begin{aligned} {\rm TS}^{k=\infty }_t&= \sum _{s=t+1}^{T}\frac{r_D\cdot \tau \cdot \mathbb {E}_t[D_{s-1}]}{(1+r_D)^{s-t}} = \tau \cdot D_t=TS^{MM}_t. \end{aligned}$$

(33)

which is equal to the the tax shield pricing equation for the Modigliani and Miller case.

The levered firm value according to (10) is calculated by

$$\begin{aligned} \widetilde{V}^{L}_t&= \frac{\widetilde{V}_{t}^{\text {U}}}{1-l_t \cdot \tau } \leftrightarrow \widetilde{V}^{L}_t= \widetilde{V}_{t}^{\text {U}}+ \tau \cdot D_{t}= \widetilde{V}^{L,MM}_t. \end{aligned}$$

(34)

Again, Eq. (34) describes the MM case.

Proof of $r_\mathrm{u}$ as appropriate discount rate

This section proves $r_\mathrm{u}$ to be the appropriate discount rate for the tax shield value $TS_{n\cdot k}^k$ determined at an arbitrary refinancing point $n\cdot k$. In particular, we analyze the levered firm value at time $t=n\cdot k$, where n is an integer. The levered firm value at nk under the risk-neutral probability measure is given by

$$\begin{aligned} \widetilde{V}^{\rm L}_{nk}&=\sum _{s=1}^{k}\frac{\mathbb {E}^{\mathbb {Q}}_{nk}[\widetilde{FCF}^L_{nk+s}]}{(1+r_f)^s} + \frac{\mathbb {E}^{\mathbb {Q}}_{nk}[\widetilde{V}^L_{(n+1)k}]}{(1+r_f)^k}, \end{aligned}$$

(35)

where $\widetilde{FCF}^L_t$ denotes the levered free cash flow at an arbitrary time t. The levered free cash flow is the sum of the unlevered free cash flow and the tax savings at an arbitrary time t, i.e., $\widetilde{FCF}^L_t=\widetilde{\text {FCF}}_t+\tau r_D\widetilde{D}_{t-1}$. This allows to write

$$\begin{aligned} \widetilde{V}^L_{nk}&=\sum _{s=1}^{k}\frac{\mathbb {E}^{\mathbb {Q}}_{nk}[\widetilde{\text {FCF}}_{nk+s}]}{(1+r_f)^s} + \sum _{s=1}^{k}\frac{\mathbb {E}^{\mathbb {Q}}_{nk}[\tau r^{(k)}_D\widetilde{D}_{nk+s-1}]}{(1+r_f)^s} + \frac{\mathbb {E}^{\mathbb {Q}}_{nk}[\widetilde{V}^L_{(n+1)k}]}{(1+r_f)^k}. \end{aligned}$$

(36)

Equation (36) consists of three components. The first is the value of the unlevered free cash flows for all cash flows beyond time nk until $nk+k$. The second component determines the value of the tax shield for the same time frame. The third component is the value of all levered free cash flows beyond time $(n+1)k$. We focus on the second component and note that the debt amount has been adjusted at time nk according to the leverage ratio which implies $\widetilde{D}_{nk}=l\cdot \widetilde{V}^L_{nk}$. Thus, for all s, with $nk\le s<nk+k$, $\widetilde{D}_{nk}=l\cdot \widetilde{V}^L_{nk}$ which is a certain variable at time nk. Rearranging yields

$$\begin{aligned} \widetilde{V}^L_{nk}&=\sum _{s=1}^{k}\frac{\mathbb {E}^{\mathbb {Q}}_{nk}[\widetilde{\text {FCF}}_{nk+s}]}{(1+r_f)^s} + \tau r^{(k)}_Dl \widetilde{V}^L_{nk}\underbrace{\sum _{s=1}^{k}\frac{1}{(1+r_f)^s}}_{=:\lambda } + \frac{\mathbb {E}^{\mathbb {Q}}_{nk}[\widetilde{V}^L_{(n+1)k}]}{(1+r_f)^k}. \end{aligned}$$

(37)

Defining $\sum _{s=1}^{k}\frac{1}{(1+r_f)^s}=:\lambda$ and further rearranging yields

$$\begin{aligned} \widetilde{V}^L_{nk}(1-\tau r^{(k)}_Dl \Lambda )&=\sum _{s=1}^{k}\frac{\mathbb {E}^{\mathbb {Q}}_{nk}[\widetilde{\text {FCF}}_{nk+s}]}{(1+r_f)^s} + \frac{\mathbb {E}^{\mathbb {Q}}_{nk}[\widetilde{V}^L_{(n+1)k}]}{(1+r_f)^k} \end{aligned}$$

(38)

or

$$\begin{aligned} \widetilde{V}^L_{nk}&=\sum _{s=1}^{k}\frac{\mathbb {E}^{\mathbb {Q}}_{nk}[\widetilde{\text {FCF}}_{nk+s}]}{(1-\tau r^{(k)}_Dl \lambda )(1+r_f)^s} + \frac{\mathbb {E}^{\mathbb {Q}}_{nk}[\widetilde{V}^L_{(n+1)k}]}{(1-\tau r^{(k)}_Dl \lambda )(1+r_f)^k}. \end{aligned}$$

(39)

By solving Eq. (39) recursively, we obtain for any arbitrary refinancing date $t+n\cdot k$:

$$\begin{aligned} \widetilde{V}^L_{t}&= \sum _{j=t}^{\infty }\sum _{s=1}^{k}\frac{\mathbb {E}^{\mathbb {Q}}_{t}[\widetilde{\text {FCF}}_{j+s}]}{(1-\tau r^{(k)}_Dl \lambda )^{(j-t)+1}(1+r_f)^{(j-t)k+s}}. \end{aligned}$$

(40)

Equation (40) displays a linear relationship between $\widetilde{V}^{L}_{t}$ and the unlevered free cash flows. Both quantities only differ by a constant scalar factor and therefore have the same expected return.²⁵ It follows that the tax shield value at an arbitrary point in time $t=nk$ has to be discounted by $r_\mathrm{u}$ for all preceding periods. Applying the fundamental theorem of asset pricing (Kruschwitz and Löffler 2006, Theorem 2.3,p.39) allows to rewrite the pricing equation (40) under the subjective probability measure $\mathbb {P}$ by

$$\begin{aligned} \widetilde{V}^{\rm L}_{t}&= \sum _{j=t}^{\infty }\sum _{s=1}^{k}\frac{\mathbb {E}_t[\widetilde{\text {FCF}}_{j+s}]}{(1-\tau r^{(k)}_Dl \lambda )^{(j-t)+1}(1+r_\mathrm{u})^{(j-t)k+s}}. \end{aligned}$$

(41)

Again, the convergence to the Miles and Ezzell as well as the Modigliani and Miller equation is shown by setting $k=1$ and $k=\infty$. To start with the Miles and Ezzell case, we set $k=1$ and note $\lambda$ to converge to $\frac{1}{1+r_D}$. This allows to write

$$\begin{aligned} \widetilde{V}^{\rm L}_t&=\sum _{j=t}^{\infty }\frac{\mathbb {E}_t[\widetilde{\text {FCF}}_{j+s}]}{\left( 1-\frac{\tau r_Dl}{1+r_D}\right) ^{(j-t)+1}(1+r_\mathrm{u})^{(j-t)+1}}. \end{aligned}$$

(42)

Equation (42) is equivalent to the result of Miles and Ezzell (1980).²⁶

Setting $k=\infty$ implies $\lambda =\sum _{s=1}^{k}\frac{1}{(1+r_D)^s}$ to converge to $\lambda =\frac{1}{r_D}$. Thus, we arrive at

$$\begin{aligned} \widetilde{V}^{\rm L}_t&=\frac{\mathbb {E}_t[\widetilde{\text {FCF}}_{t+1}]}{(1-\tau l)r_\mathrm{u}}. \end{aligned}$$

(43)

Equation (43) corresponds to the Modigliani and Miller result.²⁷

Derivation of the beta relationships

To obtain the relation between the levered beta and the unlevered beta, we proceed equivalently as in the respective literature stream (e.g., Miles and Ezzell 1985) and begin by writing down the levered firm value at time t with refinancing every k periods:

$$\begin{aligned} \widetilde{V}^{L}_t&= \widetilde{V}^{\rm U}_{t} + TS^{k}_t \end{aligned}$$

(44)

$$\begin{aligned}&= \frac{\mathbb {E}_t[\widetilde{\text {FCF}}_{t+1}+ \widetilde{V}^U_{t+1}]}{(1+r_\mathrm{u})} +\sum _{j=1}^{k}\frac{\tau \cdot r^{(k)}_D\cdot l \cdot \widetilde{V}^{L}_t}{(1+r^{(k)}_D)^j} + \frac{\mathbb {E}_t[TS^{k}_{t+k}]}{(1+r_\mathrm{u})^k}, \end{aligned}$$

(45)

where $\widetilde{V}^U_{t+1}$ is the unlevered firm value at time $t+1$ and $TS^{k}_{t+k}$ is the $t+k$ value of tax savings beyond $t+k$. The first component of the aforementioned formula is simply the unlevered firm value. The second term represents the value of the tax savings until time $t+k$ and the third term represents the present value of all tax savings beyond the first refinancing at time $t+k$. Consistent to the literature stream, we define a beta factor, $\beta _w$, as the weighted average of the betas of these three terms. Since the discount rate for the first and third term is the unlevered cost of equity, for both terms, the unlevered beta factor, $\beta _U$, has to be used. Since $r^{(k)}_D$ is the rate of return of the second term, the beta factor of the debt issue, $\beta ^{(k)}_D$, should be used. In case of risk-free debt, the debt beta is zero, i.e., $\beta ^{(k)}_D=0$.

Using Eq. (44), we readily obtain the respective weights of the beta factors. The weight of the debt beta component is $\sum _{j=1}^{k}\frac{\tau \cdot r^{(k)}_D\cdot l }{(1+r^{(k)}_D)^j}$. This implies for the remaining components, i.e., the unlevered beta factor, $\beta _U$, to have a value weight of $1-\sum _{j=1}^{k}\frac{\tau \cdot r^{(k)}_D\cdot l }{(1+r^{(k)}_D)^j}$. Thus, we obtain for the relation between $\beta _w$ and $\beta _U$:

$$\begin{aligned} \beta _w&= \left( 1-\sum _{j=1}^{k}\frac{\tau \cdot r^{(k)}_D\cdot l }{(1+r^{(k)}_D)^j}\right) \cdot \beta _U+ \sum _{j=1}^{k}\frac{\tau \cdot r^{(k)}_D\cdot l }{(1+r^{(k)}_D)^j} \cdot \beta ^{(k)}_D. \end{aligned}$$

(46)

In addition, we retain the relation between the weighted average beta, $\beta _w$, the debt beta, $\beta ^{(k)}_D$, and the beta factor of levered equity , $\beta ^{(k)}_{L}$, a standard result of the capital budgeting literature stream, by

$$\begin{aligned} \beta _w&=l \cdot \beta ^{(k)}_D+ (1-l) \cdot \beta ^{(k)}_{L}. \end{aligned}$$

(47)

Equations (46) and (47) allow us to determine the relation between $\beta _U$ and $\beta ^{(k)}_{L}$:

$$\begin{aligned} \beta ^{(k)}_{L}&=\left( \frac{1-\sum _{j=1}^{k}\frac{\tau \cdot r^{(k)}_D\cdot l }{(1+r^{(k)}_D)^j}}{1-l}\right) \cdot \beta _U+ \left( \frac{\sum _{j=1}^{k}\frac{\tau \cdot r^{(k)}_D\cdot l }{(1+r^{(k)}_D)^j}-l}{1-l}\right) \cdot \beta ^{(k)}_D. \end{aligned}$$

(48)

To proof the validity of this unlevering procedure and to compare it to the standard formulas of MM and ME, we regard the cases $k\rightarrow \infty$ and $k=1$. For the MM case assuming risk-free debt, i.e., $\beta ^{(k)}_D=0$, we obtain

$$\begin{aligned} \lim \limits _{k\rightarrow \infty } \beta ^{(k)}_{L}&=\left( \frac{1-\frac{\tau \cdot r_f\cdot l}{r_f}}{1-l}\right) \cdot \beta _U\end{aligned}$$

(49)

$$\begin{aligned}&=\left( 1+(1-\tau )\frac{\widetilde{D}_t}{\widetilde{E}_t}\right) \cdot \beta _U. \end{aligned}$$

(50)

Equation (49) constitutes the classic MM beta adjustment equation.

For the ME case, $k=1$, we find the standard ME beta adjustment already proposed by Miles and Ezzell (1985):

$$\begin{aligned} \beta ^{ME}_{L}&=\left( \frac{1-\frac{\tau \cdot r_f\cdot l}{1+r_f}}{1-l}\right) \cdot \beta _U. \end{aligned}$$

(51)