Profit-oriented scheduling of resource-constrained projects with flexible capacity constraints

Abstract

We consider a novel generalization of the resource-constrained project scheduling problem (RCPSP). Unlike many established approaches for the RCPSP that aim to minimize the makespan of the project for given static capacity constraints, we consider the important real-life aspect that capacity constraints can often be systematically modified by temporarily assigning costly additional production resources or using overtime. We, furthermore, assume that the revenue of the project decreases as its makespan increases and try to find a schedule with a profit-maximizing makespan. Like the RCPSP, the problem is $\mathcal {NP}$-hard, but unlike the RCPSP, it turns out that an optimal schedule does not have to be among the set of so-called active schedules. Scheduling such a project is a formidable task, both from a practical and a theoretical perspective. We develop, describe, and evaluate alternative solution encodings and schedule decoding mechanisms to solve this problem within a genetic algorithm framework and we compare the solutions obtained to both optimal reference values and the results of a commercial local search solver called LocalSolver.

1 Introduction

Many models and procedures for resource-constrained project scheduling problems (RCPSPs) assume that the capacities of the renewable resources that are required to perform the project’s activities are exogenously given and that the objective is to find a (feasible) schedule with a minimal project makespan or duration. In reality, the renewable resources like human labor or machinery are often temporarily assigned to a project and decisions on additional resources or overtime are made to achieve a short project duration. A short project duration may be economically attractive for different reasons. Consider, for example, software development projects or construction projects for factories. In such cases, a shorter project duration may permit an earlier market entry. This desire to achieve a short project duration can, e.g., lead to contractual penalty clauses or other incentive schemes that relate actual payments to project durations. In such cases, the revenue from a project typically decreases as its duration increases. This immediately leads to the question how to use overtime and how to schedule such projects with flexible capacity constraints and makespan-dependent revenues in the most profitable way.

The remainder of this paper is organized as follows: in Sect. 2, we describe the assumptions of the resource-constrained project scheduling problem with makespan-specific revenues and option of overcapacity (RCPSP-ROC), give real-world examples, demonstrate basic problem and solution properties, and provide an overview of the related literature. In Sect. 3, we develop a formal mathematical decision model for the RCPSP-ROC and discuss properties of solutions that guide the development of solution procedures. The design rationales and detailed descriptions of different solution encodings for this problem are given in Sect. 4.2. On this basis, we propose various genetic algorithms and local search procedures in Sects. 4.3 and 4.4. Section 5 is devoted to the test design and the results from a numerical study to evaluate the different proposed methods to solve the RCPSP-ROC. Sect. 6 concludes this paper by giving a short summary of the results and suggestions for future research.

2 Problem and literature

2.1 Projects with flexible capacity constraints, makespan-dependent revenues, and overtime cost

The problem studied in this paper is a modification and extension of the well-established RCPSP, cf., e.g. Pritsker et al. (1969). In a project, there are given activities $j \in \mathcal {J}\,=\,\{0, 1,\ldots , J, J\,+\,1\}$ that have to be executed to complete the project. Activities 0 and $J\,+\,1$ denote the dummy start and the dummy end activity, respectively. Each activity has to be executed exactly once. Between activities, there can be precedence restrictions preventing an activity j to start unless all its predecessor activities $i \in \mathcal {P}_j$ have been completed. Activities and precedence relations can be visualized as an activity-on-node network like the one depicted in Fig. 1.

Fig. 1

Activity on node graph

Table 1 Activity durations and capacity requirements

During the duration $d_j$ of activity j, it requires $k_{jr}$ units of a renewable resource r, see the data in Table 1 for the example project in Fig. 1 using a single renewable resource $r\,=\,1$.

A feasible schedule for such a project is completely characterized by the starting times $\mathrm{ST}_j$ (or, due to non-preemption, alternatively by the finishing times $\mathrm{FT}_j\,=\,ST_j\,+\,d_j$) of all activities j, so that all precedence constraints are respected and that the project is feasible with respect to the capacities of the resources required to perform these activities. The capacity $K_r$ of resource r is often assumed to be exogenously given and constant over time, and one seeks a schedule that minimizes the project duration or makespan $\mathrm{ST}_{J+1}\,=\,\mathrm{FT}_{J\,+\,1}$.

We extend this well-known problem setting by adding the possibility to use overtime capacity $z_{rt}$ at resource r in period t, up to a limit $\overline{z}_r$, i.e., $z_{rt}\le \overline{z}_r$ in all periods, at a cost of $\kappa _r$ monetary units per period and capacity unit of overtime. If in some periods, overtime $z_{rt}$ is used, it may be possible to perform activities in parallel that would have to be scheduled sequentially if no overtime capacities were available. If overtime is used, it may hence be possible to achieve a shorter project makespan. A distinction between internal and external resources is not made.

We now further assume that a project’s economic value depends on the project’s makespan. This value is reflected, for example, by a customer’s willingness to pay. In particular, we assume that it is non-increasing as the makespan increases. In Table 2, we show the values for three such hypothetical customers for the project in Fig. 1. This directly leads to the question how to schedule the project in a profit-maximizing way and how to use overtime most efficiently, taking the individual customer’s perspective and sensitivities into account.

Table 2 Makespan-dependent willingness to pay (revenue) of different customers

For the example project in Fig. 1, we assume that the capacity of the single renewable resource amounts to $K_1=4$ units and that it is possible to use $\overline{z}_1\,=\,2$ units of overtime per period at an overtime cost of $\kappa _1\,=\,10$ monetary units per period and unit of overtime. For customer A in Table 2, the schedule presented in Fig. 2 with a makespan of 10 periods and no overtime is profit-maximizing.

Fig. 2

Optimal schedule without overtime usage for customer A

Note that in this special case of customer A, our problem setting bears a resemblance to the resource overload problem with “total overload cost function”, as stated in Neumann and Zimmermann (1999), p. 594, because in this special case, the objective is effectively reduced to minimizing the cost of overtime for a given deadline $\delta$, which is shown to be $\mathcal {NP}$-hard by Neumann et al. (2003), p. 242.

If, by contrast, there are more strongly decreasing revenues as for the time-sensitive customer B, then the schedule in Fig. 3 with a duration of only 8  periods is profit-maximizing. We use two units of the comparatively cheap overtime, but are able to decrease the makespan by two periods and, therefore, increase the revenue by 30  units and the profit from 15 to 25  units compared to the schedule in Fig. 2.

Fig. 3

Schedule with maximum amount of overtime utilized

For Customer C, it is neither optimal to minimize overtime as for Customer A nor to minimize the makespan as for Customer B. Instead, in this case, the schedule in Fig. 4 with a makespan of 9  periods, 1  unit of overtime and a resulting profit of 5 units is profit-maximizing.

Fig. 4

Schedule with some overtime usage

Fig. 5

Relationship between makespan, overtime cost, revenue and profit

In general, let $\underline{T}$ denote the shortest possible makespan making potentially ample use of overtime irrespective of overtime cost but within overtime bounds $\overline{z}_r$. In a similar way, let $\overline{T}$ denote the shortest possible makespan using only the regular capacity $K_r$, i.e., without any use of overtime. Then, the potentially optimal, i.e., profit-maximizing, project durations, should lie in the time interval $[\underline{T}, \overline{T}]$, since a makespan below $\underline{T}$ is impossible and a makespan exceeding $\overline{T}$ unnecessarily leads to possibly decreasing revenues. In other words, we assume that the cost and revenue structures are roughly, as shown in Fig. 5, to lead to a non-trivial problem.

Typical real-world examples for projects with these features include aircraft engine remanufacturing projects undertaken by a service contractor, software development projects, and construction projects. Jet engines of commercial aircraft are extremely valuable and durable goods that are routinely overhauled and remanufactured, often after significant wear and tear. Aircraft engine remanufacturing is executed by independent service contractors or original equipment manufacturers. In either case, this complex process typically has a project character, see Kellenbrink and Helber (2015) and Kellenbrink and Helber (2016), as the state of the engines as well as the chosen repair or replace options differ from case to case. The customers are typically airlines that are interested in short remanufacturing processes. For them, it is neither attractive to operate with a large number of reserve engines nor to reduce flight operations due to lengthy engine overhaul processes. The service provider may hence use overtime to increase his capacity for these overhaul processes. Similar situations can exist in software development projects when additional (freelance) programmers are temporarily hired to speed up software development processes. In construction projects, it is not unusual that companies obtain additional capacities by temporal hiring of additional manpower or by renting additional machinery to speed up projects. In many of these cases, the decision maker faces the fundamental problem outlined above to use these additional resources in the most profitable way. However, as far as we know, there is no solution approach available dealing with this problem setting in a systematic way.

2.2 Related literature

The problem described in Sect. 2.1 bears similarities to the well-known and widely researched single-mode single-project RCPSP without preemption, shortly characterized by $PS|prec|C_{max}$ using the notation introduced by Brucker et al. (1999). Recent overviews of the RCPSP and its extensions were given by Hartmann and Briskorn (2010) and Demeulemeester and Herroelen (2006). Additional literature surveying the state of the art in RCPSP research was published by Kolisch and Padman (2001), Brucker et al. (1999), Herroelen et al. (1998), and Özdamar and Ulusoy (1995). Kolisch and Hartmann (2006) evaluated and differentiated various heuristic solution approaches for the standard RCPSP. Artigues et al. (2015) provide a survey as well as a theoretical and experimental comparison of linear programming formulations for the RCPSP.

The trade-off between a shorter duration and lower costs may seem similar to the discrete-time–cost trade-off problem (DTCTP). However, unlike the RCPSP-ROC, the DTCTP is a multi-mode problem with modes defining activity durations and resource consumptions, as formulated by Hindelang and Muth (1979). In the RCPSP-ROC, activities can only be executed in a single mode and, therefore, with one specific value for duration and resource consumptions. Furthermore, the DTCTP minimizes total costs from resource usage and not the excess of a resource threshold. Therefore, unlike the RCPSP-ROC, it does not take into account the availability of “free” normal capacity.

The most important difference between the standard RCPSP and the variant treated in this paper is the objective function. An objective function is regular if and only if it is monotonically non-decreasing in the activity starting times, cf., e.g., Brucker and Knust (2012), p. 12. Minimizing the makespan is an example of such a regular objective function for the RCPSP. A detailed description and analysis of different objective functions for RCPSPs can be found in the extensive scheduling fundamentals book by Schwindt (2005).

In our paper, we consider a profit objective in which the project’s profit is the difference between the makespan-dependent revenue and the associated overtime cost. The objective function of this problem is a linear combination of both a regular part and a non-regular part. Minimizing the makespan is equivalent to maximizing the revenue, since the revenue function is assumed to be monotonically decreasing in the makespan, i.e., $u_t \ge u_{t+1} \; \forall \; t$. For any strictly decreasing revenue $u_t$, revenue maximization even matches the makespan minimization objective. Hence, this part is a regular function. However, minimizing overtime cost is a non-regular objective, since decreasing the overtime typically leads to longer project durations as fewer activities can be performed in parallel.

Focusing on this behavior of the revenue and the cost function, two decomposition approaches involving different RCPSP aspects known from the literature seem to suggest themselves. On the one hand, the makespan can be minimized for the (potentially extremely large) set of all possible fixed overtime profiles. The remaining problems of revenue maximization are similar to many makespan-oriented objective functions if we do not consider the possible difference between the given overtime profile and the actually used overtime in the resulting schedule. (This difference may lead to an overestimation of the overtime cost.) These subproblems are equivalent to the RCPSP with time-varying capacities, which was introduced in Hartmann (2012) and more elaborately described in Hartmann (2015). A more general RCPSP extension which also includes time-varying capacities was introduced by Klein (2000). This is a well-researched problem for which many powerful algorithms are available. Unfortunately, the set of all the possible overtime profiles can be extremely large.

On the other hand, the overtime cost can be minimized for the set of all possible fixed deadlines. This set of fixed deadlines can also be very large depending on the structure and size of the problem instance. The remaining problem for any given deadline resembles the following problems with resource-oriented objective functions, which are non-regular. For an overview, see Neumann et al. (2003).

• Resource investment problem: Peak resource utilization must be minimized without taking into account neither the threshold of free normal capacity nor the duration of utilization, cf., e.g., Drexl and Kimms (2001).

• Resource-leveling problems: Negative and positive deviations from a given resource usage threshold have to be minimized, cf., e.g., Easa (1989).

• Resource overload problem: Only positive deviations are minimized, but no upper bound for the total resource consumption is considered, cf., e.g., Neumann and Zimmermann (1999), p. 594, and Neumann et al. (2003), p. 242.

• Project scheduling problem with given deadline (PSPDL): This is similar to the resource overload problem, but overtime is limited to a percentage of normal capacity, cf., e.g., Kolisch (1995) and Deckro and Hebert (1989).

Of all the related scheduling problems with cost-based objective functions presented above, the PSPDL in the single-mode variant is the only one matching all key aspects of the remaining subproblems acquired when decomposing the RCPSP-ROC into cost-minimization problems with fixed deadlines. The percentage of normal capacity additionally available as overtime in the PSPDL can be derived from the upper bound of overtime in the RCPSP-ROC and vice versa. Unfortunately, if we treat the remaining problem for a given fixed deadline as a PSPDL, the issue arises that the practically required makespan of a resulting schedule may be shorter than the given deadline. (This difference may lead to an underestimation of the revenues.) As mentioned above, to solve the master problem, solving one PSPDL instance for each possible deadline is required.

Both ideas to relate our problem to those previously presented approaches in the literature appear to be problematic, given the potentially large number of subproblems that are themselves hard to solve. We are, therefore, not aware of any procedure to solve the problem type presented above. For this reason, we now state it formally and present newly developed algorithmic solution approaches.

3 Formal description and analysis of the RCPSP with revenues and overtime cost

3.1 Mathematical model

We now formally define the resource-constrained project scheduling problem with revenues and overtime cost, as described in Sect. 2.1. This linear programming formulation is based on the widely used discrete-time formulation with “pulse” end variables for the RCPSP, see Artigues et al. (2015). The use of this formulation is only valid if the starting times of all activities in an optimal schedule are integer. Therefore, we assume that all activity durations are integer and that overtime usage always affects entire (but potentially very small) time periods t.

We use the so-called dummy activities 0 and $J+1$ with a duration of 0 periods and no resource consumption to represent the distinct start and end of the project. In a preprocessing step, we compute for each activity j earliest finish times $EFT_j$ and latest finish times $LFT_j$ by standard forward and backward pass calculations, see, e.g., Demeulemeester and Herroelen (2006), p. 96ff. In this process, earliest possible finishing times $EFT_j$ can easily be determined by constructing an earliest start schedule, thereby ignoring any capacity constraints. In a similar way, a tight and efficient upper bound for the latest finishing time $LFT_{J+1}$ for the dummy ending activity $J+1$ can be determined by constructing a feasible schedule with regular capacity using any heuristic procedure for the RCPSP. From this latest finishing time $LFT_{J+1}$, the other latest finishing times can then be derived in a backward pass.

Table 3 Notation of the RCPSP-ROC

The central binary decision variable $x_{jt}$ of the discrete-time model equals one if activity j is finished at the end of period t and zero otherwise. The implied amount of overtime used in period t at resource r is tracked in the derived decision variable $z_{rt}$. Using the notation as given in Table 3, we now define the RCPSP-ROC as follows:

Model RCPSP-ROC

$$\begin{aligned}&\max \, F \,= \,\sum _{t=EFT_{J+1}}^{LFT_{J+1}} u_t \cdot x_{J+1,t}\, - \,\sum _{r \in \mathcal {R}} \sum _{t \in \mathcal {T}} \kappa _r \cdot z_{rt} \end{aligned}$$

(1)

subject to

$$\begin{aligned}\sum _{t\,=\,EFT_j}^{LFT_j} x_{jt}\, = \,1, \quad j \in \mathcal {J} \end{aligned}$$

(2)

$$\begin{aligned}\sum _{t\,=\,EFT_i}^{LFT_i} x_{it} \cdot t \,\le \,\sum _{t\,=\,EFT_j}^{LFT_j} x_{jt} \cdot t \,- \,d_j, \quad j \in \mathcal {J}, i \in \mathcal {P}_j \end{aligned}$$

(3)

$$\begin{aligned}\sum _{j\,=\,1}^{J} \sum _{\tau \,=\,t}^{t+d_j-1} k_{jr} \cdot x_{j\tau } \le K_r + z_{rt}, \quad r \in \mathcal {R}, t \in \mathcal {T} \end{aligned}$$

(4)

$$\begin{aligned}z_{rt} \,\le \, \overline{z}_r, \quad r \in \mathcal {R}, t \in \mathcal {T} \end{aligned}$$

(5)

$$\begin{aligned}x_{jt}\,\in \,\{0,1\}, \quad j \in \mathcal {J}, t \in \mathcal {T} \end{aligned}$$

(6)

$$\begin{aligned} z_{rt} \,\ge \, 0, \quad r \in \mathcal {R}, t \in \mathcal {T} \end{aligned}$$

(7)

The objective function (1) maximizes the contribution to the profit. It is the revenue related to the finishing period of the dummy-activity $J+1$ minus the total amount of overtime cost resulting from the schedule. Equations (2) enforce that each activity is finished exactly once between its earliest and latest finishing times. The precedence restrictions between activities are modeled via constraints (3). Capacity limits for the renewable resources are enforced and overtime usage is determined through constraints (4). An upper bound $\overline{z}_r$ for overtime usage is established via restrictions (5).

3.2 Complexity analysis, structural characteristics, and algorithmic considerations

The RCPSP-ROC is a generalization of the RCPSP, which itself has been proven to be an $\mathcal {NP}$-hard problem by Blazewicz et al. (1983). Since there is a polynomial time reduction for RCPSP instances to RCPSP-ROC instances (that is RCPSP  $\le _p$  RCPSP-ROC), it follows that RCPSP-ROC is also an $\mathcal {NP}$-hard problem. The reduction can be achieved by setting the revenue function to any strictly monotonically decreasing function (e.g., $u_t\,=\,-\,t$) and by preventing any usage of overtime by setting the overtime limit to zero, i.e., $\overline{z}_r\,=\,0, \, \forall \, r$. Given the $\mathcal {NP}$-hardness of the RCPSP-ROC, we do not expect to be able to develop an exact algorithm for the RCPSP-ROC that runs in polynomial time. We also observed that the computation time using the Gurobi MIP solver, see http://www.gurobi.com/, even for small RCPSP-ROC instances can be substantial. For this reason, we turned to heuristic methods to determine at least sub-optimal schedules in acceptable time.

To (hopefully) find good solutions of a scheduling problem in a systematic manner, the structural properties of good or even optimal solutions to this problem have to be identified. To this end, Schwindt (2005) introduced the term “characteristic points”. Characteristic points of a specific scheduling problem form a set of feasible schedules which is guaranteed to include at least one optimal schedule for that problem, see Neumann et al. (2000), who already described the underlying idea. For scheduling problems with regular objective functions, e.g., makespan minimization, this is the set of so-called active schedules $\mathcal {AS}$. A schedule is active if no activity can start earlier without delaying another one, i.e., no local or global left shift is possible in such a schedule. As a consequence, it is sufficient to consider “only” all active schedules to find the optimal solution. Many algorithmic approaches take this property into account. Unfortunately, for scheduling problems with objective functions that combine regular and non-regular components, such as the RCPSP-ROC with revenues and overtime cost, it is not sufficient to only consider the set of active schedules, see Ballestin and Blanco (2015), p. 418. It can be possible to improve a given schedule without changing its makespan by delaying an activity, thereby reducing overtime usage and cost. It is hence not sufficient or advisable to limit the search to the set of active schedules.

Fig. 6

Example of optimal schedule being outside of $\mathcal {QSS}$

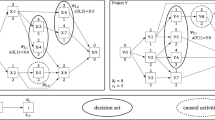
One might also consider to operate on the set of quasi-stable schedules $\mathcal {QSS}$ that have to be examined for problems in which resource usage deviations from a certain threshold are minimized, see Neumann et al. (2003), p. 210. However, one can find RCPSP-ROC instances for which none of the optimal schedules is quasi-stable, and hence, it is not even sufficient to limit the search to the set of quasi-stable schedules $\mathcal {QSS}$, see Fig. 6. For the problem instance with two interchangeable symmetric non-dummy activities depicted in Fig. 6a, with a revenue function shown in Fig. 6b and per-unit overtime cost of $\kappa =\frac{1}{2}$ monetary units, the schedule $\mathrm{ST}^{6c}_j\,=\,(1, 1)$ in Fig. 6c and the pair of schedules $\mathrm{ST}^{6e}_j\,=\,(1,3)\, \equiv \, (3,1)$ in Fig. 6e are quasi-stable but only the non-quasi-stable schedule pair $\mathrm{ST}^{6d}_j\,=\,(1,2)\, \equiv \, (2,1)$ in Fig. 6d is optimal.

As the set of quasi-stable schedules $\mathcal {QSS}$ is the largest set of characteristic points defined in the literature, we are not able to classify our problem class into any known class of schedules. This implies that optimal schedules for the RCPSP-ROC have other and so far unknown properties than optimal schedules of established RCPSP variants. For this reason, it is not at all obvious how to systematically construct potentially optimal schedules.

4 Heuristic algorithmic approaches

4.1 General considerations: genetic algorithms vs. LocalSolver

To develop algorithms for the RCPSP-ROC, two different approaches appear to be very promising. On the one hand, population-based genetic algorithms (see Holland (1975)) turned out to be very powerful to solve RCPSPs, in particular with respect to the makespan minimization objective, see, e.g., the results reported in Kolisch and Hartmann (2006). If one follows this approach, the central question is how solutions are encoded and how schedules are derived from this encoding, so that the operators of genetic algorithms can lead to new and still feasible schedules. (Note that a direct representation based on a possibly extremely large number of decision variables from the RCPSP-ROC model in Sect. 3 does not meet this fundamental requirement.) However, such a solution representation and corresponding schedule generation scheme can also be used within a (heuristic) local search algorithm. A commercial solver named LocalSolver, see http://www.localsolver.com, has recently gained attention as it offers a flexible modeling interface to define in particular combinatorial optimization problems, for example, vehicle routing problems. The solver is based on a hybrid approach combining local search, constraint propagation, and inference, see Benoist et al. (2011). It turned out to be relatively easy to use LocalSolver to solve our problem; given the solution representation and decoding mechanisms, we developed for the genetic algorithms. Furthermore, LocalSolver easily beat the Gurobi MIP solver operating on the RCPSP-ROC formulation in Sect. 3. For those reasons, we used a relatively lightweight LocalSolver implementation based on the solution representations for the genetic algorithms as a surprisingly strong benchmark.

4.2 Alternative solution encodings and corresponding schedule generation schemes

4.2.1 The serial schedule generation scheme based on an activity list $\lambda$

In the context of the RCPSP, the serial schedule generation scheme (SSGS) is widely used to decode a solution representation based on an activity list $\lambda$ into a schedule, see Kolisch and Hartmann (1999), p. 150ff. In an activity list $\lambda$, all jobs (including the dummy activities) are included once. If an activity i in the project has to precede another activity j, then this order has to be respected in the activity list as well. Hence, the first and last entries of the activity list are always the (dummy) start and end activities. Using the SSGS, one iteratively schedules activities in the order implied by the activity list. Starting with the first activity on this list $\lambda$, one determines its earliest starting point that is feasible both with respect to capacity constraints and activity precedence relations.

Consider, for example, the project depicted in Fig. 1 requiring a single resource $r\,=\,1$ with a period capacity of $K_1\,=\,4$ capacity units (and no overtime capacity, that is $\overline{z}_r\,=\,0, \forall \; r$). Then, the activity list

$$\begin{aligned} \lambda _1\, = \,\left( 0, 1, 3, 2, 5, 4, 6, 7 \right) \end{aligned}$$

(8)

is decoded into the schedule in Fig. 2. Note that the SSGS is not injective, meaning different activity lists can lead to the same schedule. For details on this established procedure, see Kolisch and Hartmann (1999).

This serial schedule generation scheme operating on an activity list $\lambda$ only generates active schedules $\mathcal {AS}$ which are a subset of the quasi-stable schedules, i.e., $\mathcal {AS} \subseteq \mathcal {QSS}$, when enumerating over all possible activity lists $\lambda$ as input data. As mentioned before, it is not even sufficient to consider (only) the set of $\mathcal {QSS}$ schedules to find an optimal solution for the RCPSP-ROC. We are hence not aware of any established construction rule operating on an activity list $\lambda$ and the SSGS to build promising schedules for the RCPSP-ROC, due to its specific objective function.

For this reason, we developed several extended solution representations and modified decoding mechanisms that can all be seen as generalizations of the established SSGS approach for the RCPSP. We describe these below in detail.

The basic reasoning is that when constructing a schedule, it is (with respect to revenues) essentially attractive to schedule activities as early as possible. This tends to be achieved by the SSGS. However, in the RCPSP-ROC, there is the additional question of when or for which activities overtime should be used. We present below three different approaches in which this decision is directly determined by the solution representation.

4.2.2 Solution encoding $(\lambda |{\hat{z}}_r)$

One possible solution encoding for the RCPSP-ROC is the representation $(\lambda |{\hat{z}}_r)$. Here, $\hat{z}_r$ denotes a column vector specifying the maximum permissible overtime usage for resource r. When decoding a solution via the SSGS, we hence operate on a modified and time invariant period capacity $K_{{rt}}^{{\bmod }}\,=\,K_r\,+\,\hat{z}_r$ for each resource r and period t.

For the project introduced in Fig. 1 requiring a single resource $r\,=\,1$ with a regular period capacity of $K_1\,=\,4$ capacity units, the representation

$$\begin{aligned} (\lambda |{\hat{z}}_r)\,=\,\begin{array}{cccccccc}(0&1&3&2&5&4&6&7\;|\;[0])\end{array} \end{aligned}$$

(9)

(without overtime permission) is decoded into the schedule in Fig. 2, whereas the representation

$$\begin{aligned} (\lambda |{\hat{z}}_r)=\begin{array}{cccccccc}(0&1&3&2&5&4&6&7\;|\;[2])\end{array} \end{aligned}$$

(10)

leads to the schedule in Fig. 3. In this case, the additional decision on a fixed upper bound $\hat{z}_1\,=\,2$ for overtime throughout the entire planning horizon is a component of the encoded solution. Please note that $\hat{z}_r$ only gives the maximum permissible overtime and that the amount of overtime actually used has to be derived from the schedule to compute the objective function value related to this schedule.

For a single resource r, the set of possible (integer) $\hat{z}_r$ values is rather small and contains $\overline{z}_r+1$ elements $\{0, \ldots , \overline{z}_r\}$. However, even a full state space enumeration for this representation does not necessarily yield an optimal schedule, since this representation only explores a subset of the entire set of all possible overtime profiles. An obvious advantage of this representation is that it is quite lean.

4.2.3 Solution encoding $(\lambda |\hat{z}_{rt})$

The $(\lambda |{\hat{z}}_{rt})$ representation is quite similar to the $(\lambda |{\hat{z}}_{r})$ representation. It generalizes the $(\lambda |{\hat{z}}_r)$ representation by deciding on a per-period basis on the allowed amount of overtime and, therefore, inducing a time-varying profile. Here $\hat{z}_{rt}$ denotes a matrix of permissible overtime capacities. When applying the SSGS, the modified and time-variant period capacity $K_{{rt}}^{{\bmod }}\,=\,K_r+\hat{z}_{rt}$ for each resource r and period t is considered.

For the project introduced in Fig. 1, the representation:

$$\begin{aligned} (\lambda |\hat{z}_{rt})\,=\,\begin{array}{cccccccccc}(0&1&3&2&5&4&6&7\;|\;\begin{bmatrix} 0&0&0&2&2&2&0&0&0&0 \end{bmatrix})\end{array} \end{aligned}$$

(11)

with permission of two units of overtime in periods four, five, and six is decoded into the schedule in Fig. 2 (in which no overtime is actually used), whereas the representation

$$\begin{aligned} (\lambda |\hat{z}_{rt})\,=\,\begin{array}{cccccccccc}(0&1&3&2&5&4&6&7\;|\;\begin{bmatrix} 0&0&1&1&0&0&0&0&0&0 \end{bmatrix})\end{array} \end{aligned}$$

(12)

with permission of one unit of overtime in periods three and four leads to the schedule in Fig. 4.

Since this representation can be used to explore the entire set of possible overtime profiles, it is in principle guaranteed to find an optimal solution when doing a full state space exploration. However, this is of course not practical, since it is still an $\mathcal {NP}$-hard problem and the matrix of permissible overtime capacities $\hat{z}_{rt}$ can get very large very quickly, requiring a high-dimensional search process in combination with all possible activity lists.

4.2.4 Solution encoding $(\lambda |\beta )$

In the $(\lambda | \beta )$ representation, the need to use overtime is tied to activities j as opposed to resources r as assumed in the $(\lambda | \hat{z}_r)$ representation or resource-period combinations (r, t) in the $(\lambda |\hat{z}_{rt})$ representation. The idea behind this representation is that some activities may be especially critical, for example, due to the fact that they have many successors or a long duration. The $(\lambda |\beta )$ representation hence explicitly contains the information whether an activity is allowed to be scheduled with or only without additional overtime usage. When the activity list $\lambda$ is being decoded and an activity j is being treated given a partial schedule, the original capacity $K_r$ is used with respect to resource r if $\beta _j \,=\, 0$, i.e., if activity j is not allowed to use overtime while being inserted into the partial schedule. However, if $\beta _j \,= \,1$, i.e., if activity j is allowed to use overtime, the modified capacity $K_{{rt}}^{{\bmod }}\,=\,K_r+\overline{z}_{r}$ is being used.

For the project depicted in Fig. 1 requiring a single resource $r\,=\,1$ with a regular period capacity of $K_1\,=\,4$ capacity units the representation

$$\begin{aligned} \left( \begin{array}{c} \lambda \\ \beta \end{array} \right) \, =\, \left( \begin{array}{cccccccc} 0 &{} 1 &{} 3 &{} 2 &{} 5 &{} 4 &{} 6 &{} 7\\ 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 1 &{} 0\end{array} \right) \end{aligned}$$

(13)

with permission of overtime for activities two and six is decoded into the schedule in Fig. 3, whereas the representation:

$$\begin{aligned} \left( \begin{array}{c} \lambda \\ \beta \end{array} \right) \, = \,\left( \begin{array}{cccccccc} 0 &{} 1 &{} 3 &{} 2 &{} 5 &{} 4 &{} 6 &{} 7\\ 0 &{} 0 &{} 1 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0\end{array} \right) \end{aligned}$$

(14)

with permission of overtime for activities three and five leads to the schedule in Fig. 2. Note that even a full state space enumeration along this representation is not guaranteed to yield an optimal solution as it may be optimal to use overtime during only a part of the execution of an activity (see Fig. 6d).

4.2.5 Iterative forward–backward improvement without cost increase

Since hybrid genetic algorithms incorporating a neighborhood search based additional improvement step are shown to be efficient for solving the RCPSP in the literature, see Kolisch and Hartmann (2006), we adapted the so-called iterative forward–backward improvement technique by Li and Willis (1992) for the RCPSP-ROC. In its original form, this technique tries to decrease the project duration by subsequently shifting and aligning all activities to the right and afterwards to the left. This is iteratively repeated until there is no improvement as opposed to the more widespread double justification variant with just two shifting passes. The approach tends to decrease makespan while maintaining the feasibility of the schedule. For a more detailed description of this procedure, see Valls et al. (2005). We modified the procedure by allowing only such shifts that do not increase overtime consumption, therefore, leading to schedules with possibly both decreased makespan and lowered overtime costs. We apply this improvement step to each given schedule for all decoding schemes introduced.

4.3 Genetic algorithms for the RCPSP-ROC

4.3.1 Basis solution approach of genetic algorithms

Genetic algorithms are nature-inspired meta-heuristics that have been successfully applied to many different combinatorial optimization problems. They were first presented by Holland (1975) and are now widely and successfully used in computer science and operations research. As shown in Kolisch and Hartmann (2006), they are the dominating heuristic method in the literature to solve the RCPSP as they can often find high-quality solutions for challenging problems very quickly.

Genetic algorithms for an optimization problem operate on a population of individuals or candidate solutions over a sequence of generations with reproduction and selection mimicking the “survival of the fittest”. A candidate solution can in principle contain a complete set of numerical values as assignment for the decision variables of an underlying optimization model as the binary $x_{jt}$ and the integer $z_{rt}$ variables in the RCPSP-ROC model presented in Sect. 3. However, it is often more convenient and efficient to use a more compact encoding like the activity list $\lambda$ introduced before. The objective function value of the schedule then serves as a fitness value for the particular activity list of that individual.

The individuals of one generation are taken as parents, combined in the so-called crossover operation, and potentially mutated to hopefully create better child individuals. Out of the set of parents and children, a new generation of parents for the next generation is selected. This process is repeated iteratively until a specified termination criterion is met.

To characterize our genetic algorithms, we hence have to specify the solution representation, the decoding scheme and the fitness computation as well as the structure of the initial population, the combination of solutions, and finally the mutation and selection operators. As representations, we use the encodings introduced in Sect. 4.2 together with their corresponding schedule generation schemes. For each of these considered representations, we specify the remaining elements of the genetic algorithm in the following subsections.

4.3.2 Generation of the initial population

All our solution representations contain activity lists as a substantial element. We construct each activity list in the initial population step by step, starting with the first position of that list. For each position, we determine the set of activities $j \in \mathcal {D}$ that have not yet been assigned to the activity list, while all immediate predecessor activities $i \in P_j$ have already been assigned to that particular list. Each such activity $j \in \mathcal {D}$ can hence be selected for the currently considered position of the activity list without violating any precedence constraint between activities. One of these activities $j \in \mathcal {D}$ is chosen randomly following a distribution, where the selection probability positively correlates with the priority value of that activity (biased sampling). The chosen activity is then appended to the activity list and this procedure repeats until all activities are included.

In our case, we are using the latest finishing times $LFT_j$ of the activities as priority values, so that the priority of activities decreases with increasing latest finishing times. This is a useful priority rule, since delaying an activity j with a small $LFT_j$ value is likely to postpone project completion. Based on these priorities, the weight $w_j\,=\,\max _{i \in \mathcal {D}} LFT_i \,- \,LFT_j$ is the relative regret of not selecting activity j, i.e., the difference between highest overall priority value for the assignable activities $i \in \mathcal {D}$ and priority value of activity j. To randomly select one of the schedulable activities $j\, \in \, \mathcal {D}$, we use non-uniform selection probabilities

$$\begin{aligned} Prob_j \,=\, \frac{(w_j+1)}{\sum _{i \,\in \,\mathcal {D}} (w_i\,+\,1)} \end{aligned}$$

in a regret-based biased random sampling (RBBRS) as proposed by Kolisch and Drexl (1996) and Tormos and Lova (2001).

In the $(\lambda |\hat{z}_r)$ representation, an additional initial limit on the permissible overtime $\hat{z}_r$ for each resource r has to be assigned for each individual. We draw it randomly from a uniform distribution over the integer values in the set $\{0, 1, 2, ..., \overline{z}_r \,-\, 1, \overline{z}_r\}$ for each resource r. In the case of the $(\lambda |\hat{z}_{rt})$ representation, we use this limit for resource r over all periods t, so that initially, we have $\hat{z}_{r,1}\,=\,\hat{z}_{r,2}\,=\,...=\hat{z}_{r,T}$ for each resource r of an individual. In the $(\lambda |\beta )$ representation, the binary parameter $\beta _j$ which indicates whether activity j may be scheduled using overtime is set to 0 or 1 with probabilities of 0.5 each.

4.3.3 Crossover

During each iteration of the genetic algorithm, we build pairs of individuals by randomly matching distinct individuals from the current parent set until each individual has been matched with one other individual from that set. Denote one individual from such a pair as the mother “M” and the other as the father “F”.

Let $\lambda ^\mathrm{M}$ be the mother’s activity list and $\lambda ^\mathrm{F}$ be the father’s activity list. Following Hartmann (1998), we perform a one-point crossover on those activity lists. We pick a random number q between 1 and J. A daughter is characterized by choosing the first q elements from the mother. The remaining elements, not yet chosen from the mother, are taken in the order of the father. The son is determined analogously by switching the roles of mother and father. With this approach, all precedence restrictions are always met, so that each activity list is feasible. For the $(\lambda |\beta )$ representation containing an additional overtime decision per job, the overtime decision for each job is linked to the overtime decision from the passing parent.

We describe this procedure using an example for the $(\lambda |\beta )$ representation of the sample project in Fig. 1 (considering only the non-dummy activities) with the crossover point $q=3$:

$$\begin{aligned} I^\mathrm{M} \,=\, \left( \begin{array}{ccc|ccc} 1 &{} 2 &{} 3 &{} 4 &{} 5 &{} 6 \\ 1 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0\end{array} \right) \quad I^\mathrm{F} \,= \,\left( \begin{array}{ccc|ccc} 1 &{}3&{} 5 &{} 2 &{} 4 &{} 6\\ 1 &{} 0 &{} 1 &{} 0 &{} 1 &{} 0\end{array} \right) \end{aligned}$$

$$\begin{aligned} I^\mathrm{D} \,=\, \left( \begin{array}{ccc|ccc} 1 &{} 2 &{} 3 &{} 5 &{} 4 &{} 6 \\ 1 &{} 1 &{} 0 &{} 1 &{} 1 &{} 0\end{array} \right) \quad I^\mathrm{S} \,= \,\left( \begin{array}{ccc|ccc} 1 &{} 3 &{} 5 &{} 2 &{} 4 &{} 6 \\ 1 &{} 0 &{} 1 &{} 1 &{} 0 &{} 0\end{array} \right) \end{aligned}$$

The first three positions on the activity list for the daughter “D” are taken in the sequence given by the mother. It is not possible to simply take the last three elements from the father as activity two would be implemented twice and activity five never. For this reason, we only take the sequence of the remaining activities from the father: five, four, and six. The $\beta _j$ values for the first three positions are inherited from the mother. For the other activities, the values are inherited from the father. The son “S” analogously inherits in the opposite direction.

In the $(\lambda |\hat{z}_{r})$ and $(\lambda |\hat{z}_{rt})$ representations, a second one-point crossover is performed. The crossover of the $\hat{z}_r$ and $\hat{z}_{rt}$ components is independent of the crossover of the activity lists. The reason is that there exists no direct relationship between the elements of an activity list and the entries of the matrix $\hat{z}_{rt}$ or vector $\hat{z}_r$. We show the procedure for the case of two resources r and six periods t and first assume that the crossover is performed periodwise between periods four and five. For clarity reasons, the activity lists as part of the complete $(\lambda |\hat{z}_{rt})$-genotypes were omitted in this example. Their crossover again follows the procedure from Hartmann (1998):

$$\begin{aligned} {\hat{z}_{rt}^\mathrm{M}} \,=\, \left( \begin{array}{cccc|cc} 3 &{} 3 &{} 3 &{} 3 &{} 3 &{} 3 \\ 1 &{} 1 &{} 4 &{} 4&{} 4 &{} 4\end{array} \right) \quad {\hat{z}_{rt}^\mathrm{F}}\, = \,\left( \begin{array}{cccc|cc} 2 &{}2&{} 2 &{} 2 &{} 6 &{} 6\\ 0 &{} 0 &{} 1 &{} 1 &{} 1 &{} 1\end{array} \right) \end{aligned}$$

$$\begin{aligned} {\hat{z}_{rt}^\mathrm{D}} \,=\, \left( \begin{array}{cccc|cc} 3 &{} 3 &{} 3 &{} 3 &{} 6 &{} 6 \\ 1 &{} 1 &{} 4 &{} 4 &{} 1 &{} 1\end{array} \right) \quad {\hat{z}_{rt}^\mathrm{S}} \,=\, \left( \begin{array}{cccc|cc} 2 &{} 2 &{} 2 &{} 2 &{} 3 &{} 3 \\ 0 &{} 0 &{} 1 &{} 1 &{} 4 &{} 4\end{array} \right) \end{aligned}$$

The result shows, e.g., for the son individual and resource $r\,=\,1$, that the permissible overtime is two units for the first four periods (as inherited from the father) and three units for the remaining two periods (as inherited from the mother). In a similar way, the crossover can be performed resourcewise between resources, in this case the only two resources one and two:

$$\begin{aligned} I^\mathrm{M}_{\hat{z}_{rt}}\, =\, \left( \begin{array}{cccccc} 3 &{} 3 &{} 3 &{} 3 &{} 3 &{} 3 \\ 1 &{} 1 &{} 4 &{} 4&{} 4 &{} 4\end{array} \right) \quad I^\mathrm{F}_{\hat{z}_{rt}}\, = \,\left( \begin{array}{cccccc} 2 &{}2&{} 2 &{} 2 &{} 6 &{} 6\\ 0 &{} 0 &{} 1 &{} 1 &{} 1 &{} 1\end{array} \right) \end{aligned}$$

$$\begin{aligned} I^\mathrm{D}_{\hat{z}_{rt}} \,= \,\left( \begin{array}{cccccc} 3 &{} 3 &{} 3 &{} 3 &{} 3 &{} 3 \\ 0 &{} 0 &{} 1 &{} 1 &{} 1 &{} 1\end{array} \right) \quad I^\mathrm{S}_{\hat{z}_{rt}} \,= \,\left( \begin{array}{cccccc} 2 &{} 2 &{} 2 &{} 2 &{} 6 &{} 6 \\ 1 &{} 1 &{} 4 &{} 4 &{} 4 &{} 4\end{array} \right) \end{aligned}$$

In the case of the $(\lambda |\hat{z}_{rt})$ representation, we either perform the crossover periodwise or resourcewise (with probabilities of 0.5 each). For the $(\lambda |\hat{z}_{r})$ representation, it can only be performed resourcewise.

4.3.4 Mutation

Mutation is only applied with a certain small mutation probability $P_{mutate}$. For activity lists, we apply a so-called adjacent pairwise interchange, see Hartmann (1999), p. 90, and Brucker and Knust (2012), p. 130. With probability $P_{mutate}$ an activity $j\,=\,\lambda _i$ on position i of list $\lambda$ is exchanged with the activity $\lambda _{i\,+\,1}$ on the next position $i\,+\,1$ (if available) unless this would result in an infeasible activity list. Therefore, feasibility-violating swaps are avoided.

In the case of the $(\lambda |\hat{z}_{r})$ or the $(\lambda |\hat{z}_{rt})$ representation, we mutate the overtime capacities $\hat{z}_{r}$ and ${z}_{rt}$ by randomly either increasing or decreasing all values by one capacity unit (unless this would violate the limits 0 and $\overline{z}_r$, respectively). For the $(\lambda |\beta )$ representation, we mutate by flipping a randomly selected bit, i.e., by setting $\beta _j \leftarrow 1\, -\, \beta _j$.

4.3.5 Selection

In the selection step, individuals with low fitness values get discarded. For our implementation, we chose to discard the 50% worst individuals out of the set of all parents and all children of the current generation, i.e., we use an elite selection scheme.

4.4 Central elements of the local search implementation using LocalSolver

The commercial general-purpose local search solver LocalSolver offers as its front end a descriptive modeling language. It can be used to declare and define the elements of an optimization model such as variables, parameters, objective function, and constraints. The exploration of the search space is completely done in a proprietary black-box fashion by LocalSolver.

In principle, it is possible to use a direct solution representation based on the binary $x_{jt}$ variables, as defined in the RCPSP-ROC. However, this representation is neither suitable for a local search algorithm nor for a genetic algorithm. Swapping two jobs in a schedule, for example, is conceptually rather simple and easily implemented in an activity list encoding, whereas in a direct binary encoding of a schedule, potentially, many different variables must be modified and it can be difficult to achieve feasibility again.

Fortunately, the descriptive LocalSolver language contains not only the modeling elements commonly used in MIP models like the RCPSP-ROC in Sect. 3, but also other language elements like if–then clauses, maximum or minimum operators, and so-called list variables that can be used to describe problems in a very compact way. In particular, this list variable can be used to directly model an activity list and perform a local search over this activity list using the black-box LocalSolver search engine, i.e., its back end.

Using a list variable to directly model, the activity list turned out to be very simple and effective. A list variable in LocalSolver holds a permutation of numbers in a certain range $[0, n-1] \cap \mathbb {N}_0$ of n elements. The upper limit $n-1$, and therefore, the cardinality n of this range can be externally specified. For our problem setting, we set $n=J\,+\,2$. LocalSolver explores possible solutions by permuting this list.

When using an indirect encoding via an activity list in a modeling language, a corresponding decoding procedure must be implemented. The current version of the LocalSolver language is well suited for descriptive programming but not yet suitable for highly efficient algorithmic procedural programming. However, the LocalSolver Software Development Kit (SDK) offers an Application Programming Interface (API) for implementing parts of the model as function callbacks written in another general-purpose programming language. With these so-called native functions, a custom algorithm can be integrated in a LocalSolver model and the respective search process. This allows us to reuse and plug in the schedule generation and decoding procedures described in Sect. 4.2 and already implemented in the genetic algorithm.

The additional effort to use LocalSolver within our C++  program is hence very limited. The main component for the case of the $(\lambda |\beta )$ representation is shown in Listing 1. This short code fragment is sufficient to declare the model’s data object (code lines 1 and 2), embed the native decoding function (code lines 5 and 6), and establish the activity list augmented by the binary $\beta _j$ vector (code lines 9–24) using a list variable. This way, additional data representing the decisions on overtime is integrated into LocalSolver.

Note that the list variable, i.e., the activity list, is not guaranteed to be topologically ordered after a position swap performed by LocalSolver. There are two ways to resolve this issue. First, one could add an additional constraint to the model, which enforces that list elements (i.e., activities) can only occur at a certain list position if all predecessors are at earlier positions on that list. In this case, the local search via the LocalSolver engine is forced to generate only feasible activity lists. Alternatively, one could omit this constraint and instead modify the decoding procedure to be usable with all possible permutations. To this end, it is sufficient to delay scheduling an activity on the list until all its immediate predecessors have been scheduled when decoding the activity list. Numerical experiments show that the second option is more efficient on average, because LocalSolver performs worse when using a model with order constraints. This negative effect overcompensates the advantage of the topologically ordered list.

In summary, LocalSolver only needs a trivial model consisting of the list variable, setting its length to the number of jobs and possible additional decision variables for overtime. LocalSolver decides on the assigned values of the decision variables and then passes these variables to the native function facilities of the LocalSolver API. The called decoding procedure maps the list and overtime decisions to a schedule and an objective function value, as described in Sect. 4.2. The local search stops when a pre-determined clock time has elapsed. Contrasting it with the genetic algorithm, we observe that we now operate on a single solution as opposed to a population of solutions and that all the modification and selection is done by a black-box engine as opposed to the crossover, mutation, and selection operators required in the genetic algorithms.

5 Numerical analysis of the different solution methods

5.1 Test design

We performed a set of numerical experiments to evaluate the relative quality of the different solution approaches, as presented in Sect. 4. To this end, the widely used PSPLIB problem library of heterogeneous and challenging RCPSP instances presented in Kolisch and Sprecher (1996) was used and modified to match the specific characteristics of our problem. In particular, we defined additional parameters not already included in the classical RCPSP. These are resource-specific overtime cost of $\kappa _{r}=\frac{1}{2}$ monetary units per capacity unit and period, upper bounds for overtime $\overline{z}_{r}=\frac{1}{2} K_r$, and the makespan-dependent revenue function $u_t$. The revenue function has to be constructed carefully to avoid that the optimal solutions either always have zero overtime or always use overtime whenever possible. In these two trivial cases, a standard RCPSP procedure to minimize the makespan would be sufficient after adjusting the capacities to $K_r^\prime = K_r + \overline{z}_r$ or $K_r^\prime =K_r$, respectively.

Thus, interesting problem instances have a certain structure with their optimal makespan being between those two extreme points $\underline{T}$ and $\overline{T}$, as shown in Fig. 5. Ideally, $\underline{T}$ should be the shortest possible makespan that can be achieved within the overtime limits $z_r$. In a similar way, $\overline{T}$ should be the shortest possible makespan that is possible without any overtime. However, to determine these two values, two $\mathcal {NP}$-hard problems would have to be solved, which is entirely impractical. In a fast and simple (but admittedly crude) approximation, we took advantage of the fact that in the PSPLIB, the activities for each project are always topologically ordered. For this reason, the SSGS can always be used to decode the canonical activity list $\lambda =(0, 1, 2, 3, 4,...,J-2, J-1, J, J+1)$ into a feasible schedule without overtime. The makespan of this schedule is an upper bound of the duration of the shortest feasible schedule without overtime. Furthermore, the makespan of the earliest start schedule delivers an efficiently computable lower bound for the shortest schedule with arbitrary legitimate amount of overtime. We call these the $\overline{T}$- and the $\underline{T}$-schedules, respectively. The makespans of those two schedules were then used as the $\underline{T}$ and $\overline{T}$ limits of the interesting makespan interval for the respective revenue function. To roughly match the structure of the profit curve in Fig. 5, the revenue function has to be determined in a suitable way. We decided to use a partially parabolic function defined as follows:

$$u_{t} = \left\{ {\begin{array}{*{20}l} {\overline{C} ,} \hfill & {{\text{if}}\;t < \underline{T} } \hfill \\ {\overline{C} - \frac{{\overline{C} }}{{\left( {\overline{T} - \underline{T} } \right)^{2} }} \cdot {{\left( {t - \underline{T} } \right)^{2} }},} \hfill & {{\text{if}}\;\underline{T} \le t \le \overline{T} } \hfill \\ {0,} \hfill & {{\text{if}}\;\overline{T} < t.} \hfill \\ \end{array} } \right.$$

(15)

Here, $\overline{C}$ denotes the actual cost of overtime associated with the earliest start schedule $\underline{T}$ as defined above, thus representing an upper bound for overtime cost. Note that the revenue function is concave and monotonically decreasing in the relevant makespan interval from $\underline{T}$ to $\overline{T}$. This decreasing marginal utility of makespan reductions is reasonable as penalty cost typically increase with advancing delay and tardiness. Due to the definition of the revenue function (15), we know that at least one schedule exists with a profit of at least 0 monetary units for each project.

We extended all 480 PSPLIB instances from the set j30 with 30 real activities and two dummy activities as described. We omitted 151 instances in which the makespan of the schedule computed using the SSGS with the canonical activity list and $K_r^\prime = K_r + \overline{z}_r$ equals the makespan of the schedule computed with $K_r^\prime =K_r$. This is a rough heuristic to decide whether overtime potentially has relevance for this instance. We, furthermore, excluded 59 instances for which the Gurobi MIP solver could not find a proven optimal solutions within 1800 s of CPU time on a single processor with a clock rate of 2.50 GHz and 32 GB of RAM. This resulted in 270 interesting problem instances with known optimal solutions. With this preparation, we were able to compute meaningful relative profit deviations when comparing our heuristic results to optimal solutions.

In a similar way, we examined j120 instances from the PSPLIB, where the total number of 600 instances got reduced to 585 projects relevant for our problem setting. We were unable to determine proven optimal solutions using Gurobi for this problem class of much larger project networks with 120 activities each. We hence evaluated the different heuristics against each other, using the best known solution per instance as a benchmark.

The activity list decoding schemes and the genetic algorithm were implemented in C++ to achieve computational performance and interoperability with the LocalSolver API. Based on numerical tests, we chose a mutation probability $P_{mutate}=5\%$ and population size (size of one generation) $N^I=80$. The results were obtained on a single processor with a clock rate of 3.40 GHz and 16 GB of RAM workstation using one thread.

5.2 Results

For the 270 comparatively small projects with 30 non-dummy activities in conjunction with a time limit of 30 s, we generated the results, as shown in Table 4.

Table 4 Numerical results over time for small projects with 30 non-dummy activities

This table shows the chronological progression of the relative gap of each solution method averaged over all instances. For each instance and method, the relative gap is a result of computing the deviation between the known optimal reference solution computed by Gurobi and the solution that method discovered up to that point in time. More precisely, this deviation is defined as $\frac{p^* - p}{p^*}$, where p is the profit considered and $p^*$ is the optimal profit. Please note that Gurobi is both used in a first run to compute optimal reference values, and in a second run with time limit of 30 s to benchmark, it as exact method against the heuristic methods.

The cells showing average gaps are colored using a palette between red for high gaps and green for low gaps. This helps following and discerning the comparative progression of gaps visually. All methods start from an initial seed solution with no profit and, therefore, a relative gap of 100% to the optimal solution.

The last three rows of Table 4 summarize further information for each method, again aggregated over all instances. These values reflect the results obtained when reaching the time limit. Consequently, they do not represent values averaged over time. The first of these rows is equal to the row containing the average gap for the time limit of 30 s. The remaining rows show the highest relative gap of any individual problem instance and the percentage of instances which were solved to optimality, respectively.

Overall, the gaps show that with a time limit of just 30 s, all heuristic solution methods are able to generate good solutions and are able to move towards them rather quickly with gaps of only $0.02\%$ to about $0.28\%$.

The table also includes the behavior of the MIP solver Gurobi. One can see that on average all heuristics outperform the exact reference method Gurobi during the considered timespan. Gurobi still has a gap of $1.46\%$ after computation is terminated in its time limited run. Even though Gurobi is outperformed by the heuristics, this still shows that the direct binary encoding $x_{jt}$ yields acceptable results for such small instances when used as encoding for a MIP solver. This is in accord with the results from the experimental comparison of different RCPSP formulations in Artigues et al. (2015).

When comparing the heuristic solution methods, it becomes apparent that the genetic algorithm yields very good results in short time and with a small amount of schedules, respectively. This behavior is due to the fact that the problem-specific configuration of the genetic algorithm enables very good results by selecting promising schedules and combining them in a constructive way. However, after a few seconds, there is no further improvement observable.

In contrast to this, LocalSolver is not able to find such good solutions in the beginning due to the initially quite arbitrary creation of new schedules. However, the results by LocalSolver improve steadily, so that they dominate the genetic algorithm for all representations after 9 s. The number of schedules visited at a certain point in time will be roughly the same in case of both LocalSolver and the genetic algorithms. The decoding procedures used in conjunction with LocalSolver might be even slightly slower due to being robust against non-topologically sorted lists, which are avoided as inputs of the fitness functions of the genetic algorithms. Hence, the superior performance of LocalSolver after a few seconds is caused by more flexible neighborhood movement rules of this generalized local search solver.

Table 5 Numerical results for small projects with 30 non-dummy activities

The number of schedules generated is a widespread termination criteria in the scheduling literature. In Table 5, average gaps towards optimal solutions are shown for limits of 1000, 5000, and 50,000 schedules. Thereby, each iteration of the forward–backward improvement is counted as one schedule both in the GA and LocalSolver. These results are in accord with the results obtained with a time limit of 30 s.

Table 6 Numerical results over time for largeprojects with 120 non-dummy activities

Table 7 Numerical results for large projects with 120 non-dummy activities

The results for the 585 large projects with 120 non-dummy activities with a time limit of 120 s and up to 50,000 schedules are shown in Tables 6 and 7, respectively. Since even for the simpler RCPSP there exist many j120 instances, which are not optimally solved yet, we did not attempt to compute optimal reference values for this set of large instances. Instead, the relative deviation is computed referencing the best known solution of all methods. These best known solutions represent lower bounds for the optimal profit. To tighten these bounds, we additionally computed profits using the most promising $(\lambda |\hat{z}_{rt})$ representation in a genetic algorithm on a computing cluster with a time limit of 30 min per instance.

For large projects with 120 activities, the exact method is not able to produce any reasonably useful results within a 2 min time limit. The heuristic methods still yield fairly good solutions with small gaps towards the best known solutions. The dominance of LocalSolver models using indirect solution encodings over the problem-specific genetic algorithm counterparts is now broken and flipped. The specific genetic algorithms clearly beat all other procedures considered when solving larger problem instances. Therefore, the low-effort solution method of using a standard solver is not advisable for large instances. In addition, it seems that the $(\lambda |\hat{z}_{rt})$ representation is not very well suited for solving large problem instances in conjunction with LocalSolver. This may be due to LocalSolver not being able to efficiently traverse different $\hat{z}_{rt}$ assignments, of which there are many.

In summary, the problem-specific procedures on average outperform the black-box generic methods for large problem instances. This relationship is reversed when considering small instances, though. A generalized standard software beating a custom heuristic may not be intuitive at first sight. Although algorithmically the problem-specific approach is very likely to be superior, the generalized local search implementation is a commercial software product with years of development and effort by a team of programmers, whereas the genetic algorithm was implemented in shorter time from scratch. This might explain why a black-box heuristic solver is able to outperform a problem-specific genetic algorithm for small problem instances. For large instances, the algorithmic advantages from problem knowledge in the genetic algorithms seem to dominate any implementation issues in comparison to a commercially developed and optimized general-purpose software.

6 Conclusion and outlook

In this paper, we presented an extension of the RCPSP with overtime cost and a revenue function monotonically decreasing with project duration. We formalized the scheduling problem as a mixed-integer linear program and designed encodings as preparation step for the development of efficient solution procedures. We then developed a genetic algorithm for the problem, computed and interpreted results for a problem library based on a widely used RCPSP test set. We further investigated the use of a general local search heuristic, thus offering numerical results for both problem specific as well as generic black-box heuristic solution methods. The results are very promising. For larger projects with many activities, heuristic problem-specific solution methods beat generic black-box inexact solvers. For small size projects, using a heuristic black-box method worked best.

For future research, it is promising to use modified operators of the genetic algorithm to achieve better results, for example, the peak crossover operator proposed by Valls et al. (2008). This operator considers the fitness of the individuals in the crossover.

In addition, the activity list as the core of all representations evaluated may be exchanged with another widespread encoding for inducing activity priorities, the so-called standardized random key representation, Debels et al. (2006).

However, it is expected that the general solution behavior remains the same even with such improvements. Therefore, it would be even more interesting to use entirely different solution procedures or representations. A suitable and ideally more compactsolution encoding may speed up the solution process by removing more redundant points in the solution space. One idea is to evaluate a representation based on quasi-stable schedules known for resource-leveling problems with a heuristically defined makespan. Again, the goal is to explore the smallest possible set guaranteed to contain an optimal solution. However, to this end and also to develop an exact algorithm, it would be extremely helpful to identify and formalize properties of optimal solutions.