1 Introduction

One of the basic functions of coolant in the grinding process is rinsing away chips in the work zone, along with cleaning the grinding wheel itself [1]. This function is crucially important in view of the fact that the grinding wheel active surface (GWAS) influences both the course and the effects of the grinding process determined, among other things, by the geometric structure of the surface, microhardness, as well as the state of stress in the workpiece surface layer [2,3,4]. In this context, one of the most undesirable phenomena occurring during grinding is the appearance of clogging of the intergranular spaces taking place on in the area of the active grinding surface. A proliferation of clogging causes a reduction in the cutting ability of the grinding wheel, a reduction in efficiency, an increase in grinding force, as well as an increase in friction and consequently temperature, which leads to premature wearing of the tool. A too-high temperature also encourages the occurrence of grinding defects, such as burns on the workpiece surface [5].

One of the most effective ways to remove chips from the grinding zone, as well as to clean the grinding wheel, is the application of the conventional flood method (WET) with the use of water oil emulsion. This method is still commonly used in industrial practice [6, 7]. Through appropriately selected conditions for the use of water oil emulsions, such as the nominal flow rate and the angular setting of the nozzle in regard to the GWAS, the flood method facilitates the effective removal of impurities from the grinding zone, significantly limiting the occurrence and increase of clogging on the grinding wheel active surface [8,9,10].

It should, however, be remembered that the high level of effectiveness of the WET method is connected with the necessity of delivering high rates of coolant into the grinding zone. From a technical point of view this is a fundamental disadvantage of this method, considering that only a small part of the volume of the emulsion reaches the area of contact between the grinding wheel and the material being machined [9]. Moreover, the necessity to buy, clean, regenerate and use coolant fluids significantly raises manufacturing costs [11,12,13].

Taking the above into account, it is aimed to completely eliminate or reduce expenditure on coolant fluids. During recent years, this aim has been further strengthened due to environmental reasons and the necessity of adhering to ever more strict rules related with environmental protection and workers’ health and safety [14, 15]

In this context, one of the most frequently used ways of significantly reducing the amount of coolant being delivered into the grinding zone is the employment of the minimum quantity lubrication method, known by the acronym MQL [7, 8, 16]. The MQL method is based on the continuous production of an oil mist and delivering it direct into the grinding zone, most often to the grinding wheel active surface. The flow of lubricating agent is facilitated by a transporting agent, namely a stream of compressed air [17], also fulfilling, to a small degree, the function of a coolant. The literature indicates that the MQL lubricating agent is delivered in the amount of 10–500 ml/h [7, 14, 18,19,20,21,22,23]. In comparison, water oil emulsions, when used in the flood method, are used in amounts of over 120,000 ml/h, although during grinding this amount, depending on the type of process, can reach from 300,000 to 1,200,000 ml/h. Synthetic esters or fatty alcohols are most often used as a lubricating agents. For some time now, due to environmental reasons, vegetable oils have also been used as a lubricating agent in the MQL method [15, 23,24,25]. However, a major limitation in the use of vegetable oils is their high cost in comparison with synthetic and mineral oils [26]. According to Madanhire and Mbohwa [27] vegetable oils are up to eight times more expensive when compared with machining fluids based on mineral oils.

One should remember that, alongside the advantages of the MQL method related with its good lubricating properties, it possesses the disadvantage of a lack of sufficient cooling properties over a broad range of variables in the grinding process when compared with the traditional flood method [28, 29]. The cause of this state of affairs is due to the small amount of coolant delivered into the grinding zone and, additionally, the low heat storage capacity of the oil and air [29, 30]. For this reason, during recent years intensive research has been conducted on improving the effectiveness of cooling and lubrication in the MQL method. In this regard, research on the use of nanofluids, as well as joining the MQL method with cryogenic cooling, along with delivering an additional stream of cooled air, is undergoing particularly intensive development [14, 15, 19, 20, 28, 31,32,33,34,35,36,37].

In the case of nanofluids, a serious limitation in industrial applications is the significant increase in viscosity in regard to the base oil [38,39,40]. A further obstacle in the common industrial use of nanofluids is the necessity to maintain a uniform and stable suspension of nanoparticles, as well as their even distribution throughout the base oil, along with the necessity to lower the quite high cost of using nanoparticles [41, 42]. In the case of employing cryogenic cooling, the disadvantage of such a solution is the cost of the special system delivering the cryogenic agent to the machining zone, greater than in the case of a conventional system, as well as the greater cost of purchasing LN2 in comparison with conventional coolant fluids.

Despite the disadvantages listed above, mainly those of a financial nature, the application of MQL methods, along with it various improvements (such as: vegetable oil, nanofluids, cryogenic cooling), is a desirable solution from an environmental point of view. Moreover, due to technological reasons, the MQL method, when used in appropriate machining conditions, produces results comparable with those gained from the flood method (WET), while, in particular machining conditions, the results gained from the MQL method are even better [13, 14]. Examples of such experiments concern, among other things: surface roughness [18, 28, 36]; microhardness [22, 33, 43, 44]; residual stress [21, 22, 44]; grinding forces [33, 45, 46]; grinding temperature [45, 47]; specific grinding energy and G ratio [33, 36, 37, 43, 46].

However, attention should be paid to the fact that up to now research studies have concentrated on ensuring the effective lubrication and cooling of the grinding zone and determining the impact of using the MQL method on the machined surface quality (roughness, microhardness, stress) and the parameters of the grinding process (grinding forces, grinding temperature). In the research studies available there is a lack of information on the subject of the ability of the MQL method to achieve a longer period of grinding wheel life, the cleaning of its active surface and removal of impurities from the grinding zone. In focusing on the high significance of this function of a coolant fluid on the course and results of the grinding process, the authors of this article present research on this question. This research was conducted during the grinding of the face surface of hob cutters. It was acknowledged that the basis for assessing and optimising the conditions for delivering the coolant in the MQL method would be first conducting and then analysing numerical simulations of air flow in the grinding zone.

It must be emphasised that carrying out flow simulations is a labour-intensive and time-consuming task, which results in, among other things, preparing a geometric model and computational grid, setting the boundary and initial conditions, as well as running simulations based on an appropriate flow model. The issues connected with this are described in the Sect. 2 of this work. In the numerical analysis, the SST k-ω model, available in the Ansys CFX program, was employed and Kato and Launder’s modifications applied to it. The results gained on the basis of the developed numerical model are presented in Sect. 3. On the basis of the results, the efficiency ηws of the system delivering air directly into the grinding zone was determined, meaning the parameter determining the relationship between the amount of air delivered by the nozzle into the grinding zone and the amount of air delivered directly into the contact zone of the grinding wheel with the hob cutter. In addition, the value of wall shear stress τw occurring on the conical surface in the area of the grinding wheel active surface was also determined, as well the area of wall shear stress Pτ on which these stresses have an impact.

With the aim of verifying the results of the simulation gained, experimental tests were conducted and which are described in Sect. 4. As a parameter verifying the effectiveness of air delivery into the grinding zone, the amount of clogging occurring on the GWAS was chosen. It was assumed that this amount would be defined as the percentage rate of grinding wheel clogging Z%. This rate was determined on the basis of GWAS microscopic image analysis. This method has also been used by other researchers in a similar way [48, 49], as well as by the authors [10].

It worth emphasising that in the scientific-technical literature there is a lack of complex research and studies concerning the use of coolant during the sharpening of hob cutters employing of the MQL method. The small number of works available only concentrate on describing experimental tests [35, 50]. Moreover, as the research studies in the field described in this article constitute something new and not dealt with until now, this work is important both for scientific and industrial reasons.

2 Numerical simulation of the flow of coolant fluid delivered by minimum quantity lubrication (MQL) in the process of grinding hob cutters’ face surface

2.1 CAD 3D models

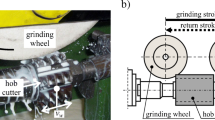
The numerical simulations described in this article were conducted with the use of a CAD 3D model of real elements occurring in the hob cutter sharpening process (Fig. 1). The process depends on grinding the face surface of the hob cutter on a special tool grinder. During the grinding of a hob cutter (1) it is: fixed in the cutter arbour (2); moves together with the grinder table at speed vw in regard to the grinding wheel (3); rotating at speed ns. The machining allowance is taken as a result of the reciprocal movement of the grinding wheel and the hob cutter in the following cycles which are comprised of alternating grinding and return strokes. The coolant is delivered into the grinding zone by a single nozzle, in this case by an MQL nozzle (4), spraying an oil-mist as part of the MQL method.

Fig. 1
figure 1

View of the machining area during the process of hob cutter sharpening

Full size image

The assumptions made in creating the CAD 3D model used for the requirements of the numerical simulation are presented in Table 1.

Table 1 Parameters of CAD 3D model
Full size table

The module value m of the hob cutter was chosen as an upper value in regard to the hob cutter modules most frequently employed in the motor industry in the production of cars. In practice, this allowed one to produce the toughest working conditions resulting in the longest maximum line of contact of the abrasive grains of the grinding wheel active surface with the machined surface.

In Fig. 2, a 3D geometric model is presented, as well as a way to generate the oil-mist in the MQL nozzle used in the described experiments. The oil and water are delivered to the nozzle outlet through separate channels. The stream of oil is sprayed at the nozzle outlet by a stream of air creating an oil-mist. The mist made in this way is directed into the machining area as a result of setting the spray nozzle appropriately.

Fig. 2
figure 2

Spray nozzle used in the MQL method. a CAD 3D model, b longitudinal cross-section of CAD 3D model

Full size image

2.2 CAD 3D model of system and delivery of cooling and lubrication agent in the MQL method

Before attempting to carry out numerical simulations, the created CAD 3D models were reciprocally placed in a way corresponding to the real settings of the reproduced parts during the sharpening process. A CAD 3D model of the system was created in this way (Figs. 3 and 4).

Fig. 3
figure 3

Placement of the area on the grinding wheel active surface onto which the oil-mist is directed (MQL area): 1–grinding wheel; 2–hob cutter; X—line of contact of apical cutting edge of the hob cutter with grinding wheel; Y—imaginary line parallel to line X

Full size image
Fig. 4
figure 4

Angular placement of the nozzle delivering the oil-air mist (MQL) in regard to the grinding wheel active surface. a general view, b setting of the MQL nozzle in regard to line A, c setting of the MQL nozzle in regard to line B; 1–grinding wheel; 2–hob cutter; 3–MQL nozzle; A–line indicated by tapering of the grinding wheel; B–line tangential to the grinding wheel active surface

Full size image

As shown in Fig. 3, the coolant fluid in the form of an oil-mist is delivered into the grinding zone with the aid of nozzle (3), on the right-hand side the hob cutter (2) on a piece of an MQL grinding wheel active surface (1). The MQL area is situated between line X comprising the line of contact of the apical cutting edge of the hob cutter with the grinding wheel and an imaginary line Y situated parallel to line X at a distance of 25 mm from it (Fig. 3). Such a location of the MQL area results from a review of the literature which indicated that the oil-mist should be sprayed onto the grinding wheel active surface (GWAS) as close as possible to the contact zone of the grinding wheel and the object being machined. The placement of this area in the manner shown in Fig. 3 takes into account the limitations (collisions) introduced by reciprocal movement of the grinding wheel and the hob cutter during machining.

The axis of the nozzle (Fig. 4) is inclined towards line A, indicated by the tapering of the grinding wheel at a degree of 90° (Fig. 4), and then at angle ε in relation to line B (Fig. 4c), tangential to the GWAS and simultaneously cutting line A at an angle of 90° (Fig. 4). As shown in Fig. 4, in the experiments four settings of angle ε were used, namely: 30°, 45°, 60° and 90°. Due to technical limitations regarding the settings, the angular inclination of the spray nozzle generating the oil-mist in regard of the grinding wheel active surface may be no less than 30°. In addition, the nozzle outlet (3) is placed at a distance of 15 mm from the GWAS. The grinding wheel, rotating in a clockwise direction, carries with it the oil-mist and directs it into the contact zone of the active abrasive grains with the hob cutter.

2.3 Numerical simulation of air flow in MQL method

2.3.1 Model and computational grid

The aim of the conducted simulation experiments was to determine the ability of the air used in the MQL method during hob cutter sharpening in cleaning the GWAS. Due to this, the numerical simulation of the cooling and lubrication agent was limited to the delivery of just air, without the involvement of oil. The remaining conditions for delivering machining fluids did not undergo any change.

The following should be listed as the most important particular aims of the numerical simulations conducted:

  1. (1)

    Indentifying the parameter determining the relationship between the amount of air delivered by the nozzle to the grinding zone with the amount of air delivered directly to the contact zone with the hob cutter. It is assumed that this parameter is to be defined as the effectiveness of the air delivery system by use of the MQL method;

  2. (2)

    identifying the value of wall shear stresses τw occurring on the surface of a tapered grinding wheel in the area of the grinding wheel active surface as result of delivering air by use of the MQL method;

  3. (3)

    determining the area of wall shear stress Pτ on which there is an impact of shear stresses τw.

During the course of the experiments the flow of compressed air was simulated which, following its exit from the nozzle, hit the grinding wheel active surface rotating at the grinding wheel rotational speed ns, and then, as a result of the rotation of the grinding wheel, was delivered into its contact zone with the hob cutter. The area in which the flow of air was simulated was determined by the fluid domain, placing it between the parts of the 3D model of the system and adapting it to the shape of the grinding wheel, hob cutter and nozzle ends (Fig. 5).

Fig. 5
figure 5

Location of fluid domain in 3D model of air delivery system in MQL method

Full size image

Before attempting to conduct the simulation, the fluid domain was optimised, creating hexagonal grid elements whose regular shape facilitate the obtaining of correct results in the numerical simulation. Particular emphasis is placed on grid integrity and the appropriate density of the inflation layer in the place where the air hits the surface of the rotating grinding wheel. The appearance of fluid domain grids optimised for the requirements of the simulation is shown in Fig. 6. Depending on the angle of the nozzle configuration, the number of nodes in the discrete model ranged from 1,082,908 to 1,599,846 and the number of elements from 1,085,411 to 1,552,138. Detailed values for each discrete model were shown in Table 2.

Fig. 6
figure 6

Discreet model of fluid domain. a General view, b cross-section

Full size image
Table 2 Characteristics of conditions of simulations
Full size table

2.3.2 Boundary and initial conditions

Numerical simulations for determining efficiency ηws, wall shear stresses τw, and areas of wall shear stress Pτ, were carried out for four angular settings of the nozzle. Angle ε was applied ranging through 30°, 45°, 60° and 90° (Fig. 4). It was assumed that the surface which served for determining which part of the nominal output of the air came through the outlet surface from the fluid domain would be located under the hob cutter tooth as indicated in Fig. 7.

Fig. 7
figure 7

Inlet and outlet surface from fluid domain (marked in red) (color figure online)

Full size image

It should be pointed out here that due to the requirements of the described simulations assumptions were made that the hob cutter and the grinding wheel were stationary in regard to each other, apart from the rotation of the grinding wheel with a rotational speed of ns = 2950 rpm. This simplification is a result of the fact that during machining the length of the line of contact between the grinding wheel and the hob cutter (rack shape) was changing in a continuous manner and, following on from this, the outlet surface from the fluid domain would have also undergone dimensional changes. In the view of the authors, the lack of this simplification would have led to an unnecessary lengthening of the duration of the numerical simulation.

Finally, it was assumed to determine efficiency ηws as the relationship of the mass flow ṁin of air on the inlet surface into the fluid domain with the mass flow ṁout of air on the outlet surface from the fluid domain, which is described by the Eq. (1):

$$\eta_{ws} = \frac{{\dot{m}_{{{\text{in}}}} }}{{\dot{m}_{{{\text{out}}}} }} .$$
(1)

The numerical simulation was conducted using the Ansys CFX 2019 program. The boundary and initial conditions were defined as:

  • Medium: air (in the CFX program the air model used – ideal gas);

  • Air temperature: 20 °C (ambient room temperature);

  • Inlet velocity: 30 m/s;

  • Rotational speed of the grinding wheel tapered surface:

  • ns = 2950 rpm,

  • rotating clockwise.

Due to the requirements of the simulation it was assumed that the absolute barometric pressure reached 1013 hPa. In regard to this, the pressure value on the surface of the fluid domain was defined as 0 Pa.

2.3.3 Turbulence model and modification of the production term

In this study, the SST k−ω model, available in the Ansys CFX program was employed [53]. Kato and Launder’s modifications were applied to the SST k−ω model itself [54]. This model is a hybrid combining the best properties of the k−ω and k-ε models, as well as making it possible to introduce a term that limits over-production of turbulence kinetic energy in the areas of high-pressure gradients. In addition, k−ω equation models are used modelling the turbulence flow in the boundary layer. Due to the fact that the k−ω model is highly sensitive to the turbulent values in the free flow, it is substituted with the k−ε model in the layers located further away from the wall. This model models turbulence in the free flow well and is also less sensitive to inlet conditions of a magnitude describing turbulence. The desired characteristics of both modules combine into one model, taking advantage of the fact that the standard k−ε model may be transformed into equations for k and ω due to the fact that ω is the appropriate dissipation of the kinetic energy of turbulence, thus ω = ε/k. The equations of this model are then multiplied by a function which has a value of 1 in free flow and 0 at the wall, while the standard k-ω model equation is multiplied by the function F1. The applied equation models are as follows:

  • Turbulent kinetic energy:

    $$\frac{{\partial \left( {\rho k} \right)}}{\partial t} + \frac{{\partial \left( {\rho u_{j} k} \right)}}{{\partial x_{j} }} = - P - \beta^{*} \rho \omega k + \frac{\partial }{{\partial x_{j} }}\left[ {\frac{{\left( {\mu + {\upsigma }_{k} \mu_{t} } \right)\partial k}}{{\partial x_{j} }}} \right] ;$$
    (2)

  • Dissipation of turbulent kinetic energy:

    $$\frac{{\partial \left( {\rho \omega } \right)}}{\partial t} + \frac{{\partial \left( {\rho u_{j} \omega } \right)}}{{\partial x_{j} }} = - \frac{\gamma }{{\upsilon_{t} }}P - \beta^{*} \rho \omega ^{2} + \frac{\partial }{{\partial x_{j} }}\left[ {\left( {\mu + \sigma_{\omega } \mu_{t} } \right)\frac{\partial \omega }{{\partial x_{j} }}} \right] + 2\left( {1 - F_{1} } \right)\frac{{\rho {\upsigma }_{\omega 2} }}{\partial \omega }\frac{\partial k}{{\partial x_{j} }}\frac{\partial \omega }{{\partial x_{j} }} ;$$
    (3)

    where:

  • Turbulent viscosity:

    $$\upsilon_{t} = \frac{{a_{1} k}}{{{\max}\left( {a_{1} \omega ,SF_{2} } \right)}} ;$$
    (4)

  • Production term:

    $$P = \mu_{t} SS ;$$
    (5)

    whereby:

    $$S = \sqrt {\frac{1}{2}\left( {\frac{{\partial u_{i} }}{{\partial x_{j} }} + \frac{{\partial u_{j} }}{{\partial x_{i} }}} \right)^{2} } ;$$
    (6)

  • Functions F1 and F2:

    $$F_{1} = {\text{ tanh}}\left( {\arg _{1}^{4} } \right),{\text{ arg}}_{1} = {\text{ min }}\left( {\max \left( {\frac{{\surd k}}{{0.09\omega y}},\frac{{500\nu }}{{\omega y^{2} }}} \right),\frac{{4\rho \sigma \omega ^{2} k}}{{{\text{CDk}}\omega {\text{y}}^{2} }}} \right);$$
    (7)
    $$F_{2} { } = {\text{ tanh}}\left( {{\arg}_{2}^{2} { }} \right),{\arg}_{2} { } = {\text{ max}}\left( {2{ }\frac{{\surd { }k}}{{0.09{\upomega }y{ }}}{ },{ }\frac{{500{\nu }}}{{y^{2} {\upomega }}}{ }} \right);$$
    (8)

  • Constant coefficients:

    $$\sigma _{{k1}} = 0.85~~\sigma _{{\omega 1}} = 0.5~~~\beta _{1} = 0.075~~~~\beta ^{*} = 0.09~~~\kappa = 0.41~~~~\gamma _{1} = ~\frac{{\beta _{1} }}{{\beta ^{*} }} - \sigma _{{\omega 1}} ~\kappa ^{2} ~\sqrt {\beta ^{*} };$$
    $$\sigma_{{{\text{k}}2}} = 1.0{ }\sigma_{{{\upomega }2}} = 0.856{ }\beta_{2} = 0.0828{ }\beta^{*} = 0.09,{ }\kappa = 0.41{ }\gamma_{2} = { }\frac{{\beta_{2} }}{{\beta^{*} }} - \sigma_{{{\upomega }2}} { }\kappa^{2} { }\sqrt {\beta^{*} } .{ }$$

Kato and Launder’s modification was applied to the SST k-ω model. The SST k-ω turbulence model has a tendency to overproduce artificially turbulence in the pile-up areas due to high S values generated in these regions. Kato and Launder suggest substituting tangential stresses S in the turbulence production equation with rotation Ω, thus:

$$P = \mu_{t} S\Omega { },$$
(9)

where:

$$\Omega = \sqrt {\frac{1}{2}\left( {\frac{{\partial u_{i} }}{{\partial x_{j} }} - \frac{{\partial u_{j} }}{{\partial x_{i} }}} \right)^{2} } .$$
(10)

2.3.4 Wall shear stresses on the grinding wheel surface

In view of the shear stresses in the boundary layer [55, 56] for a numerical simulation analysis focusing on the possibility of removing impurities from the grinding wheel active surface with a stream of air, wall shear stresses τw occurring on the tapering surface of the grinding wheel (wall) were used. This stress is described by the equation:

$$\tau_{w} = \mu \left( {\frac{\partial u}{{\partial y}}} \right)_{y = 0}$$
(11)

where:

τw: wall shear stress on tapering surface of the grinding wheel (wall),

µ: dynamic viscosity,

u: speed on tapered surface of the grinding wheel (wall),

y: distance from wall of the tapered surface of the grinding wheel.

Table 2 summarises the conditions of the numerical simulations performed.

3 Results of numerical simulation of air flow in the hob cutter blade grinding zone by use of the MQL method

3.1 Efficiency η ws of the air delivery system

Figure 8 shows the layout of the air flow streamlines in the fluid domain obtained as a result of numerical simulations for four angular settings of the nozzle, namely: 30°, 45°, 60°, 90°.

Fig. 8
figure 8

Layout of air flow streamlines in fluid domain obtained for angle of inclination of nozzle ε. a 30°, b 45°, c 60°, d 90°

Full size image

As may be observed in Fig. 8, decreasing the angle of inclination ε in regard to the grinding wheel active surface causes that the lines representing the air flow streamlines are more concentrated and arrange themselves in a direction ‘under the tooth’ of the hob cutter (in accordance with the rotational direction of the grinding wheel). This causes that the greater part of the air streams reach the contact zone of the hob cutter with the grinding wheel resulting in lower losses as a consequence of multi-directional spraying of air from the site where it hits the grinding wheel, which occurs, for example, when the inclination of the nozzle is at 90°.

Confirmation of the above-described character of the impact of changes to the angle of inclination ε on the directionality of the air streams are a result of efficiency ηws, defining the relationship between the amount of air delivered by the nozzle into the grinding zone and the amount of air delivered directly into the contact zone of the grinding wheel with the hob cutter. The results are tabulated in Table 3 and presented in Fig. 9.

Table 3 Efficiency ηws of air delivery system
Full size table
Fig. 9
figure 9

Efficiency ηws of air delivery system obtained for four angles of inclination of nozzle ε: 30°; 45°; 60°; 90°

Full size image

As the results from the data presented in Table 3 and Fig. 9 indicate, decreasing angle ε causes an increase in the effectiveness of delivering air into the grinding zone expressed as efficiency ηws. The greatest efficiency ηws, meaning the most beneficial from a viewpoint of cleaning (and cooling) the grinding zone, was achieved by setting the nozzle at an angle of ε = 30° in regard to the grinding wheel active surface. The numerical simulation indicated in this case that, although most of the stream of air, as a result of the occurrence of the air barrier phenomenon around the spinning grinding wheel, most of which did not reach the GWAS, was instead carried and directed straight into contact zone of the grinding wheel with the hob cutter.

Attention should be paid to a small difference between the efficiency rate obtained at the angles of 30° and 40°, reaching almost 2%. In practice, this means a large tolerance of the angular setting of the nozzle, which translates into easier installation and a shorter time in setting it in position. At the same time, further increasing the angle of tilt of the nozzle causes that the difference in efficiency increases significantly. Indeed, for an angle of ε = 60° the ηws value is approximately 8% greater in regard to the efficiency for an angle of ε = 30°, while this difference reaches 45% for an angle of ε = 90°.

3.2 Wall shear stresses τ w

Figure 10 presents layouts of wall shear stresses τw occurring on the surface of a tapering grinding wheel in the grinding wheel active surface area. Layouts are presented for four angular settings of the nozzle, namely: 30°, 45°, 60°, 90°.

Fig. 10
figure 10

Layouts of wall shear stresses τw obtained for four angles of inclination of nozzle ε: 30°; 45°; 60°; 90°

Full size image

In Table 4 and Fig. 11 maximum values of wall shear stresses τw-max obtained for four angles of inclination of nozzle ε are presented.

Table 4 Maximum wall shear stress τw-max
Full size table
Fig. 11
figure 11

Maximum wall shear stresses τw-max obtained for four angles of inclination of nozzle ε: 30°; 45°; 60°; 90°

Full size image

On the basis of the data presented in Table 4 and Fig. 11, it may be stated that the greatest value of wall shear stresses occurred at an angle of ε = 90°. At the same time, the maximum τw value decreases along with the angle of the spray nozzle in regard to the GWAS, reaching at an angle of ε = 30°, a value over twice as low as that in relation to the value obtained at an angle of ε = 90°. This results from the above-mentioned occurrence of the air barrier phenomenon around the spinning grinding wheel which carries the stream of air from the spray nozzle. The lower the value of the angle of inclination of the nozzle, the lower the amount of air reaching the GWAS, while more is delivered to the contact zone of the grinding wheel with the hob cutter.

3.3 Effect of wall shear stresses τ w on areas of wall shear stress P τ

Attention should be paid to the fact that apart from the shear stress value τw, the areas of wall shear stress Pτ on which these stresses operate also have an impact on the ability to clean impurities from the grinding wheel active surface. The greater the area of wall shear stress, the greater the ability to remove impurities from the surface of the grinding wheel. Table 5 presents the effects of wall shear stresses τw on areas of wall shear stress Pτ caused by the stream of air, and determined for four cases of angular settings of the nozzle, namely: 30°, 45°, 60°, 90°. For each of these four angles ε, an area of wall shear stress was selected for analysis determined by three ranges of wall shear stresses, namely: (1) 30–120 Pa, (2) 40–120 Pa and (3) 50–120 Pa.

Table 5 Areas of wall shear stress Pτ
Full size table

The shape and size of the area of wall shear stress Pτ, obtained depending on the angle of the inclination of the nozzle ε, is depicted in Fig. 12. On this image is shown areas of wall shear stress Pτ obtained for case 1, where the wall shear stresses were found to be in a range of 30 to 120 Pa. The areas of wall shear stress are shown in green.

Fig. 12
figure 12

Areas of wall shear stress Pτ showing occurrence of wall shear stresses τw in a range of 30–120 Pa obtained for angles of inclination of nozzle ε. a 30°, b 45°, c 60°,d 90°

Full size image

With the aim of analysing the results presented in Table 5, their values have been used to create the graph in Fig. 13.

Fig. 13
figure 13

Areas of wall shear stress Pτ showing occurrence of wall shear stresses τw obtained in a range of: a 30–170 Pa, b 40–170 Pa, c 50–170 Pa

Full size image

On the basis of Table 5 and Fig. 13 it may be observed that for all three ranges of wall shear stresses τwthe greatest areas of wall shear stress Pτ were obtained by setting the spray nozzle at an angle of ε = 90° in regard to the GWAS. It is worth noting that the second highest area of wall shear stress Pτ values occurred by setting the nozzle at an angle of ε = 60° and is, on average, about 40% lower than the highest.

The above-mentioned property results due to the character of the air flow and is caused by the occurrence of the air barrier phenomenon around the spinning grinding wheel, mostly blocking the air stream reaching the GWAS, a phenomenon already described in regard to the efficiency ηws graph (Fig. 10), as well as the maximum wall shear stresses τw-max (Fig. 11).

4 Experimental verification of numerical simulation results

4.1 Grinding the face surface of hob cutters

The aim of the experimental tests was to verify the results of numerical simulations of the air flow used in the grinding zone when employing the MQL method. Due to the fact that one of the functions of coolant is removing chips from the grinding zone, as well as cleaning the grinding wheel itself, the amount of clogging occurring on the grinding wheel active surface was chosen as a parameter verifying the effectiveness of air delivery. During the experimental tests, the face surface of hob cutters was ground, followed by the measurement of the proportion of surface clogging occurring on the grinding wheel active surface, with a grinding wheel clogging coefficient of Z% being determined on this basis. The obtained results allowed one to assess in a direct manner, the conditions for delivering air in the MQL method determined by the angle of inclination of the spray nozzle ε.

During grinding, the face surface of NMFc-3/20°/B solid hob cutters made of HS6-5-2 high speed uncoated steel was sharpened. These cutters are intended for the manufacture of spur cogwheels in accordance with ISO 53 and ISO 54 norms. Table 6 presents the grinding conditions applied during the described tests.

Table 6 Grinding conditions
Full size table

The hob cutters were sharpened on a special conventional hob grinding machine for sharpening using a Norton 38A60KVBE dish grinding wheel. This is a grinding wheel made of white fused alumina grains with a vitrified bond. The grinding wheel was dressed before each test with the use of a single point diamond dresser. The grinding parameters of the hob cutter blades were selected on the basis of the given literature [57, 58], as well as workshop practices.

During testing, coolant was delivered in the form of an oil-mist with the aid of the MQL-type system Micro-Jet MKS-G100, manufactured by MicroJet (Germany) with an output of QMQL = 50 ml/h. As a fluid, an ester-based synthetic oil was used, namely Biocut 3000 made by Molyduval (Germany) [59]. The nozzle was tilted in regard to the grinding wheel active surface applying a range of four angles ε, namely: 30°; 45°; 60°; 90°. As a reference, machining was also conducted using the flood method (WET), applying a water–oil emulsion by the use of Emulgol ES-12 (5%) oil made by Orlen Oil (Poland) [60]. The conditions for applying the oil were set on the basis of previous experiments [10]. A single nozzle was used, titled at an angle of ε = 30° in regard to the grinding wheel active surface, which delivered the emulsion into the grinding zone with a nominal output of QWET-IN = 7 l/min.

4.2 Measurement of grinding wheel clogging

The measurement of grinding wheel clogging was commenced from the recording of images of part of the grinding wheel active surface (GWAS) with the use of a DO Smart 5 MP PRO digital microscope, manufactured by Delta Optical (Poland) [61]. The images were recorded by using Optical Smart Analysis 1.0.5 software with 50 × magnification. The images, recorded in gray scale, were analysed with the aim of discovering clogging and then determining the degree to which chips had clogged the intergranular spaces of the grinding wheel. With this aim in mind, Met-Ilo v.5.1 software, developed at the Technical University of Silesia, was used [62]. This software allows one to discover chips accumulated among the grains of the grinding wheel on the basis of the intensity of light reflected from the chips and from the surface in which they are absent. This difference in the intensity of reflected light is used to separate out areas of the images, depending on setting the colour of pixels corresponding to chips as white and designating the remaining pixels red. As a result of dividing the number of black pixels by the total number of pixels, the grinding wheel clogging coefficient Z% is determined. The final value of the grinding wheel clogging coefficient Z% representative of single grinding tests were set as the arithmetical average value of the coefficients determined on the basis of five GWAS images taken in various locations on the circumference of the grinding wheel and occupying approximately 6% of the area of the GWAS in total [10].

4.3 Results and discussion

Table 7 and Fig. 14 present the measurement results for clogging of the grinding wheel active surface during grinding with delivery of coolant as part of the minimum quantity lubrication (MQL) method, as well as the flood methods using an oil–water emulsion. The proportion of clogging is described by applying the grinding wheel clogging coefficient Z%.

Table 7 Grinding wheel clogging coefficient Z%
Full size table
Fig. 14
figure 14

Grinding wheel clogging coefficient Z%

Full size image

As Table 7 and Fig. 14 show, the grinding wheel clogging coefficient Z% assumes the lowest (most beneficial) value for a nozzle inclination angle of ε = 90°. Here, it should be noticed that the value of the grinding wheel clogging coefficient Z% obtained for the remaining angles ε are similar. The difference in the extreme Z% values obtained for the angles of ε = 30° and ε = 90° reach barely 1.7 p.p. Therefore, one may state that a change in the angle ε does not have a significant impact on the effectiveness of chip removal from the intergranular spaces of the grinding wheel. This property may be explained by analysing the results of numerical simulations and assuming that the impact of air flow delivered into the workpiece/grinding wheel contact zone (expressed as efficiency ηws) on grinding wheel clogging is equivalent to the impact of wall shear stresses τw on the GWAS. At an angle of ε = 90°, wall shear stresses τw have a decisive influence on cleaning of the GWAS. With the decreasing the angle of inclination of the nozzle, the impact of shear stresses τw also decreases while the cleaning function is taken on by air delivered directly into the contact zone of the grinding wheel with the face surface of the hob cutter being sharpened.

A comparison of the coefficient Z% obtained during grinding by use of the flood method (WET), as well as the minimum use of machining fluid indicates an insufficient cleaning ability for the MQL method. The difference between the most advantageous coefficient Z% values obtained from both methods reaches 11.1 p.p., whereby the coefficient Z% value obtained for the MQL method is more than 7 times greater that the coefficient Z% value for the WET method.

5 Conclusions

The experimental research described in this article concerned determining the ability of air used in the MQL method to clean the grinding wheel active surface (GWAS) during the grinding of the face surface of hob cutters. In this regard, a numerical simulation of the cooling and lubrication agent was limited to only providing air, without the involvement of oil. On the basis of the results obtained in regard to the applied conditions of the numerical simulation, it may be seen that the SST k-ω turbulence model with Kato and Launder’s modifications allows one to conduct simulations of the air flow delivered into the grinding zone during sharpening of the hob cutters. However, a detailed analysis is possible to conduct under significantly simplified boundary and initial conditions.

On the basis of an analysis of the numerical simulation of the air flow, it may be stated that:

  1. (1)

    Decreasing the angle ε of nozzle inclination in regard to the GWAS increases the directionality of the stream of air causing most of it to be directed into the contact zone of the hob cutter with the grinding wheel. Therefore, the lower the angle ε, the greater the effectiveness of the stream of air from the MQL nozzle reaching the grinding zone, expressing itself as greater efficiency ηws. The greatest efficiency ηws was achieved by setting the nozzle at the lowest of the tested angles, namely ε = 30°.

  2. (2)

    Increasing the nozzle inclination angle ε in regard to the GWAS causes the greater part of the stream of air to reach the surface of the grinding wheel. Thus, the greater the angle ε, the greater the wall shear stresses τw on the grinding wheel active surface. The greatest value of maximum wall shear stresses τw-max was obtained for an angle of ε = 90°.

  3. (3)

    Increasing the nozzle inclination angle ε in regard to the GWAS causes the Pτ areas of wall shear stress on which wall shear stresses τwexert an impact, to take on the greatest value by setting the spray nozzle at an angle of ε = 90°.

The results of the experimental tests indicate that:

  1. (1)

    Changing the nozzle inclination angle ε did not have a significant impact of the effectiveness of chip removal in the intergranular spaces of the grinding wheel. The difference in the grinding wheel clogging coefficient Z% between the extreme angular settings of the nozzle (ε = 30° and ε = 90°) reached barely 1.7 p.p.

  2. (2)

    The ability of air used in the MQL method to clean the GWAS depends, to the same degree, both on wall shear stresses τw and on the amount of air being directed directly into the workpiece/grinding wheel contact zone (expressed as efficiency ηws). By setting the nozzle at an angle of ε = 90°, wall shear stresses τw have a significant impact on cleaning of the GWAS. At an angle of ε = 30°, the cleaning function is taken on by the air being delivered directly to the contact zone of the grinding wheel with the face surface of the hob cutter being sharpened, expressed quantitatively as efficiency ηws.

  3. (3)

    The value of the grinding wheel clogging coefficient Z% for the MQL method is over 7 times greater than the value of the coefficient value for the flood method (WET). This is indicated by the insufficient ability of the MQL cleaning method to remove impurities from the grinding wheel active surface. A solution to this problem may be the use of an additional nozzle cleaning by the use of compressed air (CA) or cold compressed air (CCA). The latter solution could also fulfil the additional function of cooling the grinding zone.

The conducted tests maybe constitute a basis for optimising the conditions for delivering coolant and lubrication fluids during the process of grinding the face surface of hob cutters applied both in the use of conventional grinding machines, as well as numerically controlled grinding centres.