Numerical analysis of coolant flow in the grinding zone

Abstract

The article presents results of research concerning computational fluid dynamics (CFD) of water oil emulsion in grinding zone during sharpening of hob cutter face surface. The numerical simulations made possible to determine the influence of different angular nozzle settings and nominal emulsion flow rate on the quantity of emulsion directly reaching the area of contact between the grinding wheel and the machined material. “SST k-ω” model, available in Ansys CFX program, was used in the numerical analysis; however, Kato and Launder’s modifications were used in the model. Experimental tests were carried out in order to verify results obtained on basis of the numerical simulations. The percentage rate of grinding wheel clogging was used as a verifying parameter. Analysis of the clogging made it possible to indirectly evaluate results of the numerical simulation. The clogging measurements were carried out using optical method by taking microscopic images of the grinding wheel active surface (GWAS), which were later analyzed using an image analysis program. As a result of the conducted numerical simulations, it was concluded that the greatest effectiveness of emulsion provision into the grinding zone was obtained when the nozzle was set at the smallest of the examined angles (30°) and greatest of the examined nominal flow rates (7 l/min). This conclusion was confirmed with results of experimental tests, where it was also observed that increasing the nominal flow rate over 5 l/min does not have significant influence on the amount of clogging on the grinding wheel active surface.

1 Introduction

Grinding is a process in material removal processing used in finishing operations in order to guarantee low-dimension shape tolerance of the parts and to obtain, respectively, low roughness of the machined surface [1,2,3]. The specifics of this process cause a considerable part of the mechanical grinding energy to be transformed into heat, where the heat sources are primarily plastic strains occurring in the chip formation process, as well as friction. As specified by Malkin et al. [4, 5], as much as 85% of the heat energy generated in the grinding process is transmitted to the workpiece. In these conditions, significant heat stress is created in the workpiece surface layer, which then contribute to creation of a network of cracks, often invisible upon examining the surface with naked eye. Temperature increase in the workpiece is the principal cause of changes in microhardness and internal stresses in relation to the input material. The increased heat strain on the surface layer causes occurrence of adverse tensile internal stresses that decrease the fatigue strength of the dynamically loaded machine parts, as well as decreasing of microhardness inside the surface layer [6, 7]. Structural changes can also occur as a result of the high temperature in the surface layer, which considerably decrease properties of the grinded surface [2]. The surface layer can be composed of double hardened layer and the below tempered area or just one double hardened area of minor thickness.

In order to remove the above-mentioned inconveniences, grinding processes are carried out using cooling liquids, which results directly from the functions they fulfill [1]. Usually, the cooling liquids are delivered into the grinding zone in generous amounts, using the flood method [8,9,10]. In this method, the coolant is pressed with a pump and directed through a nozzle or nozzles with an aperture slot to the area of contact between the grinding wheel and the machined material. The basic coolants used in the flood method are water oil emulsions which are obtained by diluting oil concentrate with water, where the oil content in the emulsion is usually between 2 and 5% [11].

From the available publications, it is known that one of the inconveniences of using the conventional flood method is occurrence of the so-called air barrier phenomenon. This phenomenon is caused by the rotational motion of the grinding wheel and manifests itself in the form of spinning air jet surrounding the grinding wheel around its circumference [12, 13]. The research presented in the work [8] indicate that with peripheral speed of v_s = 20 m/s, the emulsion jet is deviated and sprayed, which hinders its contact with the grinding wheel active surface and considerably limits access of the emulsion into the grinding zone. Therefore, only a minor part of the volume of the provided machining fluid actually reaches the area of contact between the grinding wheel and the workpiece. For this reason, such machining conditions are sought that the greatest possible amount of the emulsion delivered into the grinding zone directly reaches the area of contact between the active abrasive grains and the machined material.

Usually, experimental tests constitute basis for elaborating and optimizing coolant provision conditions in grinding processes. Effectiveness of the applied machining conditions can be evaluated on their basis [14,15,16]. Nevertheless, even if the experimental tests facilitate obtaining information about the effectiveness of the executed process, their great disadvantage is lack of the possibility of precise analysis of phenomena occurring during the liquid flow in the grinding process. For this reason, there are no detailed data that could contribute to optimizing the grinding process. Such information can only be obtained by conducting numerical simulations of emulsion flow in the grinding zone.

Overview of the literature revealed that publications concerning numerical simulations of flows in the grinding process are scarce. Moreover, they refer only to some aspects of the process and usually do not contain extensive information about the applied numerical model and its quality and present only general guidelines in the conclusions. Frequent studies concern the shape of the coolant delivery nozzle and its optimization [17,18,19,20,21]. In these studies, the character of coolant flow in the area of wheel-workpiece contact and the formation of an air barrier around the grinding wheel and its influence on the fluid flow behavior were also analyzed. The influence of grinding wheel velocity as well as air and fluid flow parameters on heat exchange [22] was also considered. Other studies undertaken concern the development of new wheel designs, as, e.g., with internal channels supplying coolant directly to the grinding zone [23]. It is worth noting that the authors of the research most frequently used Ansys CFX and FLUENT software to carry out the CFD analysis. Moreover, the RANS turbulence model based on the Navier-Stokes equation averaged by Reynolds and the “SST k-ω” model available in Ansys CFX [23,24,25] were used. An interesting approach to numerical simulations is described in the paper [26] on the flow of coolant in the grinding process of flat surfaces. The authors carried out the research using two models. The first general model, which covered the entire grinding wheel and the area around it, was used to determine the boundary conditions for the second model. The second detailed model included a section of the grinding wheel-workpiece zone, a nozzle, and a part of the domain surrounding the grinding zone.

Academic and technical subject literature lacks thorough research and works concerning application of coolants in hob cutter grinding. The scarce works that exist focus on describing experimental tests [10, 27], completely skipping numerical simulations, including analysis of the coolant flow in the grinding zone. It must be, however, highlighted that the process of grinding hob cutters face is conducted in specific machining conditions connected with the following: (1) shape of the grinding wheel whose active surface (GWAS) is part of a conic surface, (2) shape of the face surface which adopts the form of a rack, additionally placed along the helix with large traverse, and (3) kinematics of the grinding wheel and the workpiece which requires constant linear contact of both elements. Due to this, flow simulation is technically challenging and becomes highly work- and time-consuming. This involves, among others, preparing a geometric model and network, determining the edge and initial conditions, and conducting a simulation on basis of correct flow model.

The above issues, on basis of machining conditions applied in actual hob cutter grinding process, are described in Sections 2 and 3 of this work. The numerical analysis used “SST k-ω” model available in Ansys CFX program; however, the Kato and Launder modifications were used in the model. As a result, a numerical model was developed, used for determining the influence of various angular nozzle settings and the nominal flow rate Q_WET-IN of the emulsion onto the quantity of emulsion that actually directly reaches the area of contact of the grinding wheel with the machined material (Section 4). It was assumed that this quantity would be referred to as the effective flow rate Q_WET-OUT which reflect the effectiveness of emulsion provision. On basis of the obtained results, a parameter describing the ratio between the amount of emulsion provided with the nozzle to the grinding zone and the amount of emulsion provided directly into the area of contact between the grinding wheel and the hob cutter, was also established. It was assumed that the parameter would be determined as efficiency η_ws of the emulsion provision system.

In order to verify the obtained simulation results, experimental tests were conducted, as described in Section 5. Due to the fact that one of the coolant’s functions is flushing out chips from the grinding zone and dampening and cleaning the grinding wheel, the amount of clogging on GWAS was selected as the parameter verifying effectiveness of emulsion provision. It was assumed that this amount would be expressed in percentage terms as Z_% index of grinding wheel clogging. This index was established on basis of analysis of microscopic images of GWAS. This methodology was also used in a similar form by other researchers [28, 29].

2 Machining conditions during grinding of the hob cutters face surface

The process of grinding a hob cutter consists in grinding its face surface on specialist tool grinders. During grinding, the hob cutter mounted on tool arbor moves along with the grinder table with velocity v_w in relation to the grinding wheel rotating at the speed n_s (Fig. 1a). The machining allowance is removed as a result of mutual movement of the grinding wheel and the hob cutter in consecutive cycles which involve concurrent strokes—grinding and return (Fig. 1b).

Fig. 1

Process of hob cutter grinding. a Machining area [27]. b Work cycle [10]

The following assumptions necessary to make 3D models were made. The models were later used to perform simulation of the coolant flow during the grinding process:

• 1. Solid-state hob cutter for making cogwheels compliant with ISO 53 and ISO 54. Cutter parameters: module m = 3 mm, obliquity angle α = 20°, number of cutting edges z_h = 9, grinded outline, precision class B (according to PN-ISO 4468:1999). The m module value was selected as the top range value of hob cutter modules most commonly used in car industry in production of passenger cars;

• 2. Dish grinding wheel—type 12 according to PN-ISO 525:2001. Grinding wheel dimensions were selected on basis of catalog of Norton company and they are 200/90 × 20/2 × 32.

Coolant is provided into the grinding zone during hob cutter grinding. It was assumed that:

• 1) The coolant is in the form of water oil emulsion on basis of Emulgol ES-12 oil (5%);

• 2) The emulsion is provided into the grinding zone using the flood method.

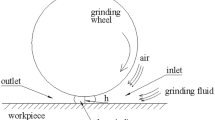
Figure 2 presents location of the zone on the grinding wheel active surface (GWAS), which the emulsion jet was directed onto, while Fig. 3 presents angular layout of the emulsion providing nozzle in relation to the grinding wheel active surface.

Fig. 2

Location of the zone on the grinding wheel active surface which the emulsion was directed onto. 1 Grinding wheel. 2 Hob cutter. X Line of contact between the apical cutting edges of the hob cutter with the grinding wheel. Y Conventional line collateral to line X

Fig. 3

Angular layout of emulsion providing nozzle in relation to the grinding wheel active surface. a General view. b Setup of the nozzle in relation to line A. c Setup of the nozzle in relation to line B. 1 Grinding wheel. 2 Hob cutter. 3 Nozzle. A Line determined by the generator of the grinding wheel cone. B Line tangential to the grinding wheel active surface

As presented in Fig. 2, the WET zone, onto which the emulsion is applied, is located on the grinding wheel active surface as close as possible to the area of contact of the grinding wheel and the hob cutter. The location of this zone takes into consideration the limitations imposed by mutual movement of the grinding wheel and the cutter during machining.

The coolant, in the form of oil emulsion, was provided into the grinding zone using nozzle 3, on the right side of the hob cutter 2 onto the WET fragment of grinding wheel active surface 1. The WET zone is situated between line X which constitutes line of contact between the apical hob cutter cutting edges and conventional line Y situated parallel to line X 25 mm away from it (Fig. 2). Axis of nozzle 3 ( Fig. 3) was tilted towards line A, determined by the generator of the grinding wheel cone, at an angle of 90° (Fig. 3b), and then at an angle ε in relation to line B ( Fig. 3c), tangential to the grinding wheel active surface and simultaneously intersecting line A at a 90° angle. As shown in Fig. 3c, four settings of angle ε were used in the research, respectively, 30°, 45°, 60°, and 90°. It should also be mentioned that the angular inclination of nozzle 3 in relation to line B can be no less than 30°, which results from technical limitations in the nozzle settings. Moreover, outlet of nozzle 3 was placed at a distance of 15 mm away from the grinding wheel active surface. Rotating clock-wise, the grinding wheel lifts the emulsion and introduces it into the area of contact between the active abrasive grains and the hob cutter.

3 Numerical simulation of water oil emulsion provided into the machining zone during grinding hob cutter face surface

3.1 Model and calculation grid

The purpose of the numerical simulations was to:

• 1. Determine the amount of emulsion that directly reaches the area of contact between the grinding wheel and the hob cutter. It was assumed that the amount would be referred to as effective flow rate Q_WET-OUT;

• 2. Establishing the parameter that determines the ratio between the amount of emulsion provided with the nozzle into the grinding zone and the amount of emulsion that directly reaches the area of contact between the grinding wheel and the hob cutter. It was assumed that the parameter would be referred to as η_ws efficiency of emulsion provision system.

Flow of water oil emulsion, which after exiting the nozzle hits the grinding wheel active surface and then, as a result of grinding when rotation at rotational speed n_s, is provided into the area of contact of the grinding wheel and the hob cutter, was simulated during the tests. A 3D model of the system, presented in Fig. 4, was constructed for the simulation. The system is composed of grinding wheel, hob cutter, nozzle end, and fluid domain.

Fig. 4

A 3D model of the system: grinding wheel, hob cutter, nozzle, and fluid domain

The 3D model was then used for a CFD simulation. The preparation involved optimizing the fluid domain in such a way so as to obtain possibly correct quality of the calculation grin in the entire domain. For this purpose, hexagonal elements of the grid were created, whose regular shapes facilitate obtaining correct results in the numerical simulation. Particular attention was paid to the grid integrity and relevant compaction of the inflation layer in the place where the emulsion hits the surface of the rotating grinding wheel. An image of the fluid domain grid optimized for the sake of the simulation is presented in Fig. 5.

Fig. 5

Discreet model of the fluid domain

The fluid domain size was selected in such a way that the boundary conditions at its borders did not affect the analyzed area being the outlet surface from the fluid domain. This area is described in Section 3.2. The verification of the fluid domain size carried out in this way allowed for its optimization in terms of calculation speed, correctness of results, and residual convergence.

3.2 Boundary and initial conditions

The numerical simulations to determine effectiveness η_ws and effective flow rate Q_WET-OUT were carried out for twelve variants described with the following variables:

• Four angular setups of the nozzle, for ε angle of 30°, 45°, 60°, and 90°, respectively,

• Three nominal flow rates Q_WET-IN of the emulsion upon outlet to the fluid domain, which were, respectively, 3, 5, and 7 l/min.

It was assumed that the surface that would be used to determine what part of nominal flow rate Q_WET-IN traverses the outlet surface from the fluid domain would be located under the hob cutter tooth indicated in Fig. 6. It should also be mentioned that for the needs of the described simulation, simplifications were made which involved assuming that the hob cutter and the grinding wheel are immobile towards one another, except for the grinding wheel rotation with rotational speed of n_s = 2950 rot./min. This simplification results from that fact that during machining the length of line of contact between the grinding wheel and the hob cutter face surface (rack shape) changes continuously, which would entail the outlet surface from the fluid domain changing as well. According to the authors, failing to adopt this simplification would unnecessarily prolong the duration of the numerical simulation.

Fig. 6

Surface of inlet and outlet from the fluid domain (red color)

In the end, η_ws efficiency was assumed as the ratio of the mass flow ṁ_in of the emulsion on the inlet surface into the fluid domain, to the mass flow ṁ_out of the emulsion on outlet surface from the fluid domain:

$$ {\eta}_{\mathrm{ws}}=\frac{{\dot{m}}_{\mathrm{in}}}{{\dot{m}}_{\mathrm{out}}} $$

(1)

The numerical simulations were conducted in Ansys CFX program. The fluid domain was simulated as interaction of two phases—emulsion phase and air phase. The phase parameters were defined as follows:

• air: ideal gas;

• emulsion: density ρ_WET = 960.7 kg/m³, absolute viscosity η_WET = 0.001488 Pa s;

• emulsion flow rate Q_{WET_IN} = 3, 5, and 7 l/min;

• rotational speed of the grinding wheel conic surface n_s = 2950 rot./min.

Due to interaction of the two phases—emulsion and air, the numerical calculations were made for non-stationary flow, assuming constant values of η_ws efficiency would be obtained after certain duration of the simulation.

For the sake of the simulation, it was assumed that the absolute barometric pressure was 1013 hPa. In reference to this, the pressure value on outlet surfaces from the fluid domain was determined as 0 Pa (Fig. 7).

Fig. 7

Inlet (black arrows) and opening (blue arrows) conditions of the discreet model

For each emulsion mass flow, separate numerical simulations were performed, each time changing the value of the flow rate. The functionality of the Ansys CFX numerical program was used for this purpose. The boundary condition of the flow rate was parameterized in the numerical software on the inlet surface into the fluid domain, which enabled numerical simulations to be performed for different flow values on the same model.

3.3 Multiphase model

In order to simulate interaction of two phases—air and emulsion, relevant model for multiphase flows was selected in Ansys CFX program. The emulsion (fluid) was defined as primary fluid (α), and the air (gas) as secondary fluid (β). A homogenous model which simplifies Euler’s description of interaction of two phases by the two-phase sharing, among others, velocity field, temperature, and pressure was used. Separation of phases and their interactions were modeled using surface tension. Surface tension is a force impacting the surface separating the phases so as to limit its field. The surface tension determines with which force per a unit of length the surface between the phases is intersected. In Ansys CFX program, the surface tension model is based on Brackbill’s constant surface force model [30]. The surface tension is modeled as volume force concentrated on the surface.

The surface tension force obtained from Brackbill’s model has the following form:

$$ {F}_{\upalpha \upbeta}={f}_{\upalpha \upbeta}{\delta}_{\upalpha \upbeta} $$

(2)

where:

$$ {f}_{\upalpha \upbeta}=-{\sigma}_{\upalpha \upbeta}{\kappa}_{\upalpha \upbeta}{n}_{\upalpha \upbeta}+{\nabla}_s\sigma $$

(3)

where:

σ - the surface tension coefficient,

n_αβ - the vector normal towards the plane separating the phases,

κ_αβ - the plane curve described as:

$$ {\kappa}_{\upalpha \upbeta}=\nabla {n}_{\upalpha \upbeta} $$

(4)

where:

δ_αβ - the term activating surface tension force solely near the phases border,

∇_s - the gradient on the surface.

Two terms on the right side of Eq. (3) represent, respectively, the normal and tangential components of the surface tension force. The normal component increases depending on the surface curve, while the tangential component depending on changed in the surface tension component.

3.4 Turbulence model

Properly selected RANS turbulence model based on the Navier-Stokes equations averaged by Reynolds should correctly anticipate the influence of small vortex structures onto the entire simulated flow and calculate the reliable averaged values of the simulated flow parameters.

In this study, the “SST k-ω” model, available in Ansys CFX program was used. The model is a hybrid combining the best properties of “k-ω” and “k-ε” models and makes it possible to introduce a term that limits over-production of the turbulence kinetic energy in the areas of high-pressure gradients. “k-ω” model equations are used to model the turbulence flow in the boundary layer. Due to the fact that “k-ω” model is highly sensitive to the turbulent values in the free flow, it is substituted with “k-ε” in the layers located further away from the wall. The latter model models turbulence in free flow very well and is less sensitive to inlet conditions for values that describe the turbulence. The desired features of both models are joined in one model, using the fact that the standard “k-ε” model can be transformed into equations on k and ω due to the fact that ω is the proper dissipation of the turbulence kinetic energy, therefore ω = ε/k. The equations of this model are then multiplied by the function whose value is 1 in the free flow and 0 by the wall, and the standard “k-ω” model equations are multiplied by function F₁. Through the turbulent viscosity equation, the model also limits values of the principal stresses of the flow. The applied model equations are as follows:

• turbulent kinetic energy:

$$ \frac{\partial \left(\rho k\right)}{\partial t}+\frac{\partial \left(\rho {\mathrm{u}}_jk\right)}{{\partial x}_j}=-P-{\beta}^{\ast}\rho \upomega k+\frac{\partial }{{\partial x}_j}\left[\frac{\left(\mu +{\upsigma}_k{\mu}_t\right)\partial k}{{\partial x}_j}\right] $$

(5)

• dissipation of the turbulent kinetic energy:

$$ \frac{\partial \left(\rho \omega \right)}{\partial t}+\frac{\partial \left(\rho {\mathrm{u}}_j\omega \right)}{{\partial x}_j}=-\frac{\gamma }{\upsilon_t}P-{\beta}^{\ast}\rho {\omega}^2+\frac{\partial }{{\partial x}_j}\left[\left(\mu +{\upsigma}_{\omega }{\mu}_t\right)\frac{\partial \omega }{{\partial x}_j}\right]+2\left(1-{F}_1\right)\frac{\rho {\upsigma}_{\omega 2}}{\partial \omega}\frac{\partial k}{\partial {x}_j}\frac{\partial \omega }{\partial {x}_j} $$

(6)

where:

• turbulent viscosity:

$$ {\upsilon}_t=\frac{a_1k}{\max \left({a}_1\omega, \mathrm{S}{\mathrm{F}}_2\right)} $$

(7)

• production term:

$$ P={\mu}_t\mathrm{SS} $$

(8)

where:

$$ S=\sqrt{\frac{1}{2}{\left(\frac{\partial {\mathrm{u}}_i}{{\partial x}_j}+\frac{\partial {\mathrm{u}}_j}{{\partial x}_i}\right)}^2} $$

(9)

• functions F₁ and F₂:

$$ {F}_1=\tanh \left({\arg}_1^4\ \right),{\arg}_1=\min\ \left(\max \left(\frac{\surd \mathrm{k}}{0.09\upomega \mathrm{y}},\frac{500\upnu}{\upomega {\mathrm{y}}^2}\right),\frac{4\uprho \upsigma {\upomega}^2\mathrm{k}}{\mathrm{CDk}\upomega {\mathrm{y}}^2}\right) $$

(10)

$$ {F}_2=\tanh \left({\arg}_2^2\ \right),{\arg}_2=\max \left(2\ \frac{\surd \mathrm{k}}{0.09\upomega \mathrm{y}}, \frac{500\upnu\ }{{\mathrm{y}}^2\upomega}\ \right) $$

(11)

• fixed coefficients:

$$ {\displaystyle \begin{array}{c}{\sigma}_{k1}=0.85,{\sigma}_{\omega 1}=0.5,{\beta}_1=0.075,{\beta}^{\ast }=0.09,\kappa =0.41,{\gamma}_1=\frac{\beta_1}{\beta^{\ast }}-{\sigma}_{\omega 1}\ {\kappa}^2\ \sqrt{\beta^{\ast }};\\ {}{\sigma}_{k2}=1.0,{\sigma}_{\omega 2}=0.856,{\beta}_2=0.0828\ {\beta}^{\ast }=0.09,\kappa =0.41,{\gamma}_2=\frac{\beta_2}{\beta^{\ast }}-{\sigma}_{\omega 2}\ {\kappa}^2\ \sqrt{\beta^{\ast }}.\end{array}} $$

3.5 Modification of the production term

Kato and Launder’s modification was used in the “SST k-ω” model. The “SST k-ω” turbulence model has a tendency to artificially overproduce turbulence in the pile-up areas due to high S values generated in these regions. Kato and Launder suggest to substitute tangential stresses S in the turbulence production equation with rotation Ω, then:

$$ P={\mu}_tS\Omega $$

(13)

where:

$$ \Omega =\sqrt{\frac{1}{2}{\left(\frac{\partial {\mathrm{u}}_i}{{\partial x}_j}-\frac{\partial {\mathrm{u}}_j}{{\partial x}_i}\right)}^2} $$

(14)

3.6 Adhesion of the conic surface of the grinding wheel

The roughness occurring on the actual grinding wheel surface was included in the conducted simulations by adopting adhesion on the grinding wheel conic surface and determining the contact angle. The contact angle is the angle between the border of the two phases and the grinding wheel surface, which is established on basis of the surface tension model. The contact angle of 80° was set in the hereby simulations. The 80° angle was adopted based on the analysis of the research work described in [31, 32]. Selection of the angle took into account filling the intergranular spaces with emulsion during operation and hydrodynamic impact of the emulsion on the grinding wheel surface.

4 Results of numerical simulations and their analysis

Figure 8 presents the spill of emulsion in the fluid domain obtained as a result of simulations of the flow with nominal flow rate Q_WET-IN = 5 l/min with four angular nozzle settings. The nature of the emulsion spill for the two remaining nominal flow rates Q_WET-IN is similar.

Fig. 8

Iso-surface obtained for the flow of 5 l/min and nozzle inclination angle ε: a 90°, b 60°, c 45°, and d 30°

What is worthwhile is the fact that the smaller the ε angle of nozzle inclination towards the grinding wheel active surface, the more directed the flow, in accordance with the grinding wheel rotation. As a result, a greater amount of the emulsion reaches the area of contact between the hob cutter and the grinding wheel as a result of smaller losses resulting from spill of the emulsion from the place of hitting the rotating grinding wheel surface. This is confirmed by values of the effective flow rate Q_WET-OUT obtained as a result of numerical simulations and then presented in Table 1 and illustrated in Fig. 9.

Table 1 Effective flow rate Q_WET-OUT in the grinding zone

Fig. 9

Effective flow rate Q_WET-OUT in the grinding zone obtained for four nozzle inclination angles—90°, 60°, 45°, and 30°, and three nominal flow rates Q_WET-IN—3 l/min, 5 l/min, and 7 l/min

What is noticeable when analyzing the above data is the fact that with the angle ε = 90°, when the nozzle is perpendicular to the grinding wheel active surface, Q_WET-OUT values of different nominal emulsion flow rates Q_WET-IN are the lowest. This can be explained by the fact that as the emulsion hits the rotating grinding wheel, it spills in multiple directions and only its small part is moved towards the area of contact between the grinding wheel and the hob cutter. Changing the nozzle location as a result of inclining it by angle ε causes the jet flowing out of the nozzle to be directed towards the area of contact of the hob cutter and the grinding wheel, which combined with the rotation of the grinding wheel increases the amount of the emulsion that reaches the grinding zone. The smaller the angle ε, the greater the effectiveness of the emulsion reaching the grinding zone manifested in greater effective flow rate Q_WET-OUT.

At the same time, it can be observed that as angle ε decreases, the influence of the applied nominal flow rate Q_WET-IN onto the obtained Q_WET-OUT values increases. Thus, for the angle ε = 90°, the difference between the extreme values of Q_WET-OUT is 0.066 l/min, for angle ε = 60°, 0.415 l/min, and for ε = 45°, 0.475 l/min, while for angle ε = 30°, the difference is 0.768 l/min.

The greatest effectiveness of provision of emulsion into the grinding zone expressed with flow rate Q_WET-OUT was obtained with setting the nozzle at the angle of ε = 30° and nominal flow rate Q_WET-IN = 7 l/min.

The nature of influence of ε inclination angle changes onto the effectiveness of provision of emulsion into the area of contact between the grinding wheel and the hob cutter is confirmed by results of efficiency η_ws summarized in Table 2 and presented in Fig. 10.

Table 2 Efficiency η_ws

Fig. 10

Efficiency η_ws obtained for four nozzle inclination angles—90°, 60°, 45°, and 30°, and three nominal flow rates Q_WET-IN—3 l/min, 5 l/min, and 7 l/min

As seen from Table 2 and Fig. 10, decreasing angle ε with fixed nominal flow rate Q_WET-IN of the emulsion causes efficiency of provision of the emulsion into the grinding zone, expressed with efficiency η_ws, to increase. For each nominal flow rate Q_WET-IN, the greatest efficiency η_ws was obtained by setting the nozzle at an angle ε = 30° in relation to the grinding wheel surface.

5 Experimental verification of numerical simulation results

5.1 Grinding hob cutters face surface

5.1.1 Research post and methodology

The purpose of the experimental tests was to verify the results obtained as a result of numerical simulations of the emulsion flow in the grinding zone. During the experimental tests hob cutters face surface was grinded, after which the amount of clogging on the grinding wheel active surface was measured and Z_% grinding wheel clogging coefficient was determined on this basis. Due to the fact that the value of this parameter depends on the effectiveness of emulsion provision into the grinding zone, results obtained from the measurements allowed the authors to indirectly evaluate the conditions of emulsion provision (nozzle inclination angle ε, nominal flow rate Q_WET-IN).

The face surface of solid-state hob cutters NMFc-3/20°/B, made from high-speed steel HS6-5-2 without anti-wear cover, was sharpened in the grinding process. These cutters are used in manufacturing cylindrical gears compliant with ISO 53 and ISO 54 norms. The cutters were grinded on a special conventional grinding wheel for grinding hob cutters, using dish grinding wheel 38A60KVBE by Norton Company. It is a grinding wheel made from alundum with ceramic bond. The grinding wheel was conditioned before each trial, using one-point diamond dresser. The parameters of grinding hob cutters edges were selected on basis of available literature data [33, 34] and workshop practice. The allowance a = 0.3 mm was removed in 10 work cycles composed of work and return stroke, using grinding depth of a_e = 0.03 mm for each cycle.

Water oil emulsion using Emulgol ES-12 oil (5%) was used as a coolant. The emulsion was provided into the grinding zone with flood method (WET), applying it through a single nozzle with three nominal flow rates Q_WET-IN of 3, 5, and 7 l/min. The nozzle was inclined in relation to the grinding wheel active surface at four angles ε of 30°, 45°, 60°, and 90°.

Table 3 presents grinding conditions applied in the described tests.

Table 3 Grinding conditions

5.1.2 Measurement of grinding wheel clogging

Measurements of the grinding wheel clogging were begun by taking images of a grinding wheel active surface (GWAS) fragment using digital microscope DO Smart by Delta Optical company. The microscope is equipped with CMOS matrix with a 2-Mpx resolution and inbuilt illumination using LED diodes. Images magnified × 50 were registered using Delta Optical Smart Analysis 1.0.5 program provided by the microscope producer (Fig. 11a, b). In the next step, the gray scale images were analyzed to detect clogging and then to determine the extent to which the chips filled up the intergranular spaces. Program for image analysis Met-Ilo v.5.1 developed in Silesian University of Technology (Fig. 11c) was used for this purpose. This program makes it possible to detect chips collected between the abrasive grains on basis of intensity of light reflected from the chips and the surface devoid of them. The difference in intensity of the reflected light is used for segmentation of the image area, which consists in setting the color of pixels corresponding to white-colored chips and coloring the remaining pixels red. Grinding wheel clogging coefficient Z_% was established as a result of dividing the number of black pixels by the total number of pixels.

Fig. 11

Measurements of grinding wheel clogging. a GWAS image after dressing, magnified × 50. b GWAS image after grinding, magnified × 50. c GWAS image processed to determine Z_%

For each of the twelve cases of variable emulsion provision conditions—ε, Q_WET-IN value of grinding wheel clogging coefficient Z_% was calculated as arithmetic mean of values of indexes determined on basis of five GWAS images taken in different places on the grinding wheel circumference.

5.2 Results and discussion of experimental tests

Table 4 and Fig. 12 present results of measuring the clogging of grinding wheel active surface represented by grinding wheel clogging coefficient Z_%.

Table 4 Grinding wheel clogging coefficient

Fig. 12

Grinding wheel clogging coefficient Z_%

As can be concluded from Table 4 and Fig. 12, for each of the three flow rates Q_WET-IN, coefficient Z_% adopts the lowest (most advantageous) value for nozzle inclination angle ε = 30° and increases its value as the angle increases. Such a nature of clogging occurrence is in line with efficiency values η_ws obtained on basis of numerical tests and previously presented in Table 2 and Fig. 10. Therefore, decreasing angle ε with constant nominal flow rate Q_WET-IN of the emulsion causes the efficiency of emulsion provision into the grinding wheel expressed with efficiency η_ws to increase and simultaneously Z_% coefficient value decreases.

Considering separately four cases of angular setting of the nozzle, it needs to be observed that for each of them the greatest (unfavorable) values of coefficient Z_% were obtained for the lowest nominal flow rate Q_WET-IN which was 3 l/min, while the lowest (most advantageous) values of coefficient Z_% were obtained for the greatest flow rate Q_WET-IN = 7 l/min. Such a nature of occurrence of clogging is in line with values of effective flow rate Q_{WET_OUT} obtained on basis of numerical research and presented earlier in Table 1 and in Fig. 9. Therefore, the greater the effective flow rate Q_WET-OUT, the lower the value of grinding wheel clogging coefficient Z_%. It is worth noticing that for flow rates Q_WET-IN = 5 l/min and Q_WET-IN = 7 l/min and with nozzle inclination by angles ε = 30° and ε = 45°, the grinding wheel clogging described with coefficient Z_% is similar, and the considerable differences appear between them for the two greatest angles ε 60° and 90°. This occurs even though, as illustrated in Fig. 9, the effective flow rate Q_WET-OUT obtained for nominal flow rate Q_WET-IN = 7 l/min is 40% greater than flow rate Q_WET-OUT obtained for flow rate Q_WET-IN = 5 l/min. It can be concluded that increasing the nominal flow rate over 5 l/min does not have significant influence on decreasing the amount of clogging on the grinding wheel active surface.

5.3 Analysis and comparison of the results of numerical simulations and experimental research

Based on the comparison of numerical simulations (Table 1) and experimental studies (Table 2), it can be concluded that there is a close relationship between the amount of effective emulsion flow rate Q_{WET_OUT} and the angle ε of emulsion providing nozzle inclination, and the Z_% index of grinding wheel clogging.

In the case of dependence of the Z_% index on the effective flow rate Q_{WET_OUT}, the comparison of the obtained results (Figs. 9 and 12) leads to the conclusion that the increase of the Q_{WET_OUT} index at a constant angle of ε results in obtaining smaller (more favorable) values of the Z_% index, decrease in the number of cloggings on the grinding wheel surface. It results from the fact that at a constant angle ε, the increase of effective flow rate Q_{WET_OUT} is obtained by increasing the nominal flow rate Q_{WET_IN} and as a result, more emulsions reach the contact zone of the hob cutter with the grinding wheel and more emulsion are involved in removing chips from the intergranular spaces of the grinding wheel active surface outside the contact zone.

The relation between the Z_% ratio and the effective flow rate Q_{WET_OUT} for a constant nominal flow rate Q_{WET_IN} is similar to the character described above. Comparison of the obtained results (Figs. 9 and 12) leads to the conclusion that the reduction of the angle ε of the nozzle inclination results in the obtaining of smaller (more favorable) Z_% index value, i.e., the reduction of the number of cloggings on the grinding wheel surface. This dependence results from the fact that, as described in Section 4, together with decreasing the angle ε value, the emulsion flow is more directed towards the contact of the hob cutter with the grinding wheel, which, together with the wheel rotation, consequently increases the amount of emulsion entering the grinding zone and flushing out the chips from it. This is also confirmed by the η_ws efficiency results given in Fig. 10.

6 Conclusions

On basis of the results obtained in relation to the applied results of numerical tests, it can be observed that the “SST k-ω” turbulence model with Kato and Launder’s modifications makes it possible to carry out a simulation of emulsion flow in grinding hob cutters face surface. Detailed analysis can, however, be conducted in considerable simplification of edge and initial conditions.

The numerical analysis of the flow allowed to formulate the following specific conclusions.

• 1. decreasing angle ε of nozzle inclination in relation to GWAS causes the emulsion stream flowing out of the nozzle to be directed towards the area of contact between the hob cutter and the grinding wheel, which combined with grinding wheel rotation increases the amount of emulsion that reaches the grinding zone. Therefore, the lower the angle ε with fixed nominal flow rate Q_WET-IN, the greater the effectiveness of the emulsion reaching the grinding zone expressed with greater effective flow rate Q_WET-OUT.

• 2. As angle ε of nozzle inclination towards GWAS decreases, the influence of the applied nominal flow rate Q_WET-IN onto the obtained Q_WET-OUT values increases. The greatest effectiveness of emulsion provision into the grinding zone expressed with effective flow rate Q_WET-OUT was obtained by setting the nozzle at the lowest of the examined angles, ε = 30°, and the greatest of the examined nominal flow rates, Q_WET-IN = 7 l/min.

• 3. Efficiency η_ws results confirm the nature of influence of inclination angle ε changes onto effectiveness of providing the emulsion to the area of contact between the grinding wheel and the hob cutter. Decreasing angle ε with fixed nominal flow rate Q_WET-IN of the emulsion causes the effectiveness of emulsion provision into the grinding zone expressed with efficiency η_ws to increase. For each nominal flow rate Q_WET-IN, the greatest efficiency η_ws was obtained by setting the nozzle at the smallest of the examined angles (ε = 30°).

Results of the experimental tests confirmed above-mentioned conclusions of simulation. On their basis, it can be concluded that:

• 1. Decreasing angle ε with fixed nominal flow rate Q_WET-IN of the emulsion causes the effectiveness of emulsion provision to the grinding zone to increase and the percentage rate of clogging on the grinding wheel active surface (GWAS) expressed with index Z_% decreases.

• 2. Increasing nominal flow rate Q_WET-IN with fixed nozzle inclination angle ε causes the percentage rate of clogging on GWAS to decrease (lowest Z_% value).

At the same time, results of experimental tests indicate that increasing the nominal flow rate over 5 l/min does not have significant influence on decreasing the amount of clogging on the grinding wheel active surface.

The conducted research can constitute basis for optimization of conditions of providing coolants during the process of grinding hob cutters face surface with both conventional grinders and numerically controlled grinding centers.