On the Sensing, Actuating and Energy Harvesting Properties of a Composite Plate with Piezoelectric Patches

Abstract

The paper investigates how the energy input/output of a composite plate with piezoelectric patches, acting as a sensor, actuator, or energy harvester, can be regulated by changing the parameters of the piezoelectric patches, the external vibrating frequency and the boundary conditions imposed on the host plate-layer. It is shown that for any size of the piezoelectric patches there is always one location where the energy input/output reaches a maximum, whether the process is very low frequency or higher frequency. Furthermore, for a dynamic vibrational loading the energy input/output is highly sensitive whether the operating frequency is below or above the system’s resonance frequency. For the operating frequency close to but below the resonance frequency, the location for the maximum energy input/output is considerably different from the optimal location when the operating frequency is just above the systems resonance frequency. That is to say, a slight change in the operating frequency around the resonance frequency can make a considerable difference to the optimal locations for the piezoelectric patches for maximum energy input/output.

1 Introduction

The ability of piezoelecric materials to convert mechanical stresses into an electric field, and vice versa has found extensive applications in sensors, actuators, and energy harvesters. For example, new developments in wireless and micro-electro-mechanical systems have increased the demand for portable electronics and wireless sensors, making power supply of these portable devices a crucial issue. Harvesting ambient energy from external sources by using piezoelectric materials can become one of the solutions of this problem [1,2,3]. Since piezoelectric devices have the highest energy density and more flexibility to be integrated into a system, energy harvesting, sensing and actuating with piezoelectric materials are the most widely used and investigated both theoretically [4,5,6,7,8] and experimentally [9,10,11].

There have been different approaches for maximizing the energy input/output including the choice of piezoelectric material and the configuration [12]. One of the solutions is frequency tuning of the piezoelectric element with the external source and maximizing the converted energy using the concept of resonance [13]. This can be achieved by changing the thickness ratio of the piezoelectric patch and the host element  [14].

The energy output/input can be extremely sensitive to the length and location of the piezoelectric patches. Optimal placement of piezoelectric material for cantilever beams for power harvesting efficiency are considered in [15, 16]. Controlling the shape of a laminated beam by an optimally placed piezo actuator for minimizing the maximum deflection is studied in  [17,18,19]. For thin plates the problem from various perspectives has been investigated in [20,21,22] and  [23]. A discussion of different optimization criteria used by researchers for optimal placement of piezoelectric sensors and actuators on a smart structure has been carried out in a comprehensive technical review [24].

It is known that energy input/output can be maximum/minimum when the structure is in the resonance condition [25, 26]. The patches length and location in this case can hugely affect the energy input/output depending on how close the external vibration frequency is to resonance frequencies corresponding to the length and position of the patches. This paper investigates the effect of the location and size of piezoelectric patches in a composite multilayer plate on the energy input/output around the resonance frequency when the plate acts as a sensor, actuator, or an energy harvester.

2 Statement of the Problem

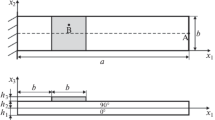
A composite piezoelectric structure is considered which consists of a plate-layer substrate of length $L$ in $x_1$ direction, a unit width in $x_2$ direction assuming that all the unknown functions are independent of $x_2$ and two piezoelectric patches of length $l_p<=L$ running the full width of the plate, perfectly bonded to its top and bottom surfaces (Fig. 1). The substrate can be a conductor for generating charge. The position of the patches is defined by $a$ and $b=a+l_p$ and ${h_p}/{2}$ and $h_m$ are the thicknesses of the piezoelectric patches and the substrate.

The top and bottom surfaces of the piezoelectric patches are metalized to form electrodes that can be wired in series. To achieve this they are poled in opposite directions so that they produce electric fields in the same direction (Fig. 1). In the case of a parallel connection, piezoelectric layers are poled in the same direction and produce electric fields in opposite directions. The electrodes covering the opposite faces of the piezoelectric layers are assumed to be thin compared to the overall thicknesses of the structure so that their contribution to the thickness can be neglected.

Fig. 1

Schematic of the plate-layer with two piezoelectric patches perfectly bonded to the top and bottom surfaces

The poling directions of the piezoelectric patches are perpendicular to the planar direction, which is the most convenient way to polarize piezoelectric elements when fabricated. Piezoelectric elements described above are operating in the (31) mode, where 3 is the polarization direction of the piezoelectric layer and 1 is the stress direction. This mode corresponds to the piezoelectric charge constant $d_{31}$, describing the induced polarization in the poled direction per unit stress applied in stress direction. Since in (31) mode the stress is not applied along the polar axis of the piezoelectric material $d_{31}$ is always smaller than $d_{33}$. However the system in $d_{31}$ mode is much more compliant and therefore larger strains can be produced with smaller input forces and also, the resonant frequency is much lower [3]. These make the use of a piezoelectric element operating in (31) mode preferable.

Assuming a driving harmonic force $q_0 \text {e}^{\text {i} \omega t}$, where $\omega$ is the frequency, the transverse displacements in the regions $0\le x_1\le a$, $a\le x_1\le b$ and $b\le x_1\le L$ can be written in the form $W_i(x_1,t)=W_i(x_1) \text {e}^{\text {i}\omega t}$, with $i=1,2,3$ corresponding to each region. Introducing dimensionless parameters $\displaystyle x=\frac{x_1}{L}$, $w_i=\displaystyle \frac{W_i}{L}$, $h_m=\displaystyle \frac{h_m}{L}$ and $h_p=\displaystyle \frac{h_p}{L}$ the equations describing forced vibrations of a mid-plane transverse deflections of a Kirchhoff plate-layer take the following form:

$$\begin{aligned}&\frac{d^4 w_1}{d x^4}-{{\bar{\lambda }}}_1^4\left( 1-\frac{\varepsilon _1 \text {i}}{2 \rho _1h_m L^3\omega }\right) w_1=\frac{q_0 }{D_1}, \quad \quad 0\le x\le \alpha \end{aligned}$$

(1)

$$\begin{aligned}&\frac{d^4 w_2}{d x^4}-{{\bar{\lambda }}}_2^4 \left( 1-\frac{\varepsilon _2 \text {i}}{2 \rho _2h_p L^3\omega }\right) w_2=\frac{q_0 }{D_2}, \quad \quad \alpha \le x\le \beta \end{aligned}$$

(2)

$$\begin{aligned}&\frac{d^4 w_3}{d x^4}-{{\bar{\lambda }}}_3^4\left( 1-\frac{\varepsilon _3 \text {i}}{2 \rho _3h_m L^3\omega }\right) =\frac{q_0 }{D_1}, \quad \quad \beta \le x\le 1, \end{aligned}$$

(3)

where $\text {i}=\sqrt{-1},$$\alpha =\displaystyle \frac{a}{L},$$\beta =\displaystyle \frac{b}{L},$${{\bar{\lambda }}}_{k}^4=\displaystyle \frac{2\rho _{k} h_{m,(p)} \omega ^2 L^2}{D_{k}},$$\rho _k$ are the mass densities, $\varepsilon _k$ the damping coefficients, $D_k$ the stiffness constants, ($k=1,2,3$), for regions $0\le x \le \alpha$, $\alpha \le x \le \beta$, $\beta \le x \le 1$, with $D_1=\displaystyle \frac{2}{3(1-\nu _1 ^2)}E_m \left( \frac{h_m}{2}\right) ^3$, $D_2=\displaystyle \frac{2}{3(1-\nu _2^2)}\left[ E_p\left( \left( h_p+\frac{h_m}{2}\right) ^3-\left( \frac{h_m}{2}\right) ^3\right) +E_m\left( \frac{h_m}{2}\right) ^3\right]$ and $\lambda _3\equiv \lambda _1$, $\rho _3\equiv \rho _1$. $E_m$ and $E_p$ are the Young’s moduli for the substrate and the piezoelectric patches, and $\nu _1\equiv \nu _3$ and $\nu _2$ the Poisson ratios.

The constitutive equations for the piezoelectric patches and the substrate are [13]

$$\begin{aligned} T_1^p=E_p(S_1^p-d_{31}E_3),\, D_3=d_{31}T_1^p+ \varepsilon _{33}^s E_3,\, S_1^p=-x_3\frac{d^2 w_2}{d x^2}, \end{aligned}$$

$$\begin{aligned} T_1^m=E_m S_1^m,\quad S_1^m=\displaystyle -x_3\frac{d^2 w_{1}}{d x^2}, \quad 0\le x \le \alpha ,\quad S_1^m=\displaystyle -x_3\frac{d^2 w_{3}}{d x^2},\quad \beta \le x \le 1, \end{aligned}$$

(4)

where the subscripts 1 and 3 represent the direction along which the corresponding parameter is measured, $T_1^p$ and $T_1^m$ are the stresses, $S_1^p$ and $S_1^m$ are the strains (superscripts $p$ and $m$ indicating the piezoelectric patches and the plate), $d_{31}$ is the piezoelectric constant coefficient, $E_3$ the electric field, $D_3$ the electric displacement and $\varepsilon _{33}^ s$ the permittivity at constant strain.

Three different boundary conditions will be considered at $x=0$ and $x=1$:

• 1. Simply supported:

  $$\begin{aligned} w_1(0)=0, \quad D_1 \displaystyle \frac{d^2w_1}{d x^2}=0, \qquad w_3(1)=0, \quad D_3 \displaystyle \frac{d^2w_3}{d x^2}=0. \end{aligned}$$

  (5)

• 2. Simply supported at one end and clamped on the other:

  $$\begin{aligned} w_1(0)=0, \quad D_1 \displaystyle \frac{d^2w_1}{d x^2}=0, \qquad w_3(1)=0, \quad \displaystyle \frac{d w_3}{d x}=0. \end{aligned}$$

  (6)

• 3. Cantilevered plate-layer:

  $$\begin{aligned} w_1(0)=0, \quad \displaystyle \frac{d w_1}{d x}=0, \qquad M_3^m(1)=0, \quad Q_3^m(1)=0. \end{aligned}$$

  (7)

Continuous bending moments and shear forces are assumed at $x=\alpha$ and $x=\beta$:

$$\begin{aligned} w_1(\alpha )= & {} w_2(\alpha ), \quad w_2(\beta )=w_3(\beta ), \qquad w_1'(\alpha )=w_2'(\alpha ),\quad w_2'(\beta )=w_3'(\beta ), \end{aligned}$$

(8)

$$\begin{aligned} M_1^m(\alpha )= & {} M_1^p(\alpha ), \quad M_2^m(\beta )=M_3^p(\beta ), \quad Q_1^m(\alpha )=Q_1^p(\alpha ), \quad Q_2^m(\beta )=Q_3^p(\beta ), \end{aligned}$$

(9)

where

$$\begin{aligned} M_{i}^m= & {} -D_1\displaystyle \frac{d^2 {w_{i}}}{d x^2}, (i=1,3),\quad \nonumber \\ M_2^p= & {} -D_2\frac{d^2w_{2}}{d x^2}-C_1E_0, \quad E_0=E_3,\nonumber \\ Q_{i}^m= & {} -D_i\displaystyle \frac{d^3w_{i}}{d x^3}, (i=1,3), \quad Q_2^p=-D_2\frac{d^3w_{2}}{d x^3},\quad \nonumber \\ C_1= & {} \displaystyle \frac{d_{31} E_p}{2}\left[ \left( h_p+\frac{h_m}{2}\right) ^2-\left( \frac{h_m}{2}\right) ^2\right] . \end{aligned}$$

(10)

Note that for the formulated boundary value problem there can be two sources of excitation. One is mechanical such as external wind and gas flow, which appears in the right hand side of Eqs.  (1)–(3). In this case the system will act as an energy harvester or a sensor. The second source of excitation can be through boundary conditions (9)–(10) due to an external applied voltage or an electrical field which appears in the expression of $M_2^p$ in (10). In this case the system can act as an actuator.

2.1 The Solution of the Problem

The solutions of (1)–(3) in three regions are

$$\begin{aligned} w_{i} \, = \, a_{i} \text {e}^{ {{\tilde{\lambda }}}_i^{(1)} x}+b_{i}\text {e}^{{{\tilde{\lambda }}}_i^{(2)} x}+c_{i}\text {e}^{{{\tilde{\lambda }}}_i^{(3)} x}+d_{i}\text {e}^{{{\tilde{\lambda }}}_i^{(4)} x}\nonumber \\&-\frac{q_0 }{D_i{{\tilde{\lambda }}}_i^4}, \qquad i=1,2,3, \end{aligned}$$

(11)

where for each value of $i$, ${{\tilde{\lambda }}}_{(i)}^{(j)}$ ($j=1,2,3,4$) are the four roots of ${{{\tilde{\lambda }}}_i^4}= {{{\bar{\lambda }}}_i^4 \left( 1-\displaystyle \frac{\varepsilon _i \text {i}}{2 \rho _ih_{m(p)} L^3\omega }\right) }$. Satisfying corresponding boundary conditions in (5)–(7) leads to the solution of the following system of equations for finding the unknown coefficients $a_i, b_i, c_i, d_i,$$(i=1,2,3)$

$$\begin{aligned} \mathbf{A } \mathbf{X }^T\,=\, \frac{1}{D_1 {{\tilde{\lambda }}}_1^4}\left( q_0 \mathbf{Y } _1^T+ C_1 E_0 B\mathbf{Y }_2^T\right) , \end{aligned}$$

(12)

where $B\, = \, \displaystyle \frac{D_1}{D_2}\frac{{{\tilde{\lambda }}}_1^4}{{{\tilde{\lambda }}}_2^2}$. The matrix $\mathbf{A }$ is given in the Appendix and $\mathbf{X }^T$ is the transpose of the vector $\mathbf{X }=(a_1, b_1, c_1, d_1, a_2, b_2, c_2, d_2, a_3, b_3, c_3, d_3).$

For boundary conditions (5) and (6) $\mathbf{Y }_1^T$ and $\mathbf{Y }_2^T$ are the transposes of the vectors

$$\begin{aligned} \mathbf{Y }_1\,= \,& {} \left( 1, 0, 1-\displaystyle \frac{{{\tilde{\lambda }}}_1^4}{{{\tilde{\lambda }}}_2^4}\frac{D_1}{D_2}, 0, 0, 0, -1+\displaystyle \frac{{{\tilde{\lambda }}}_1^4}{{{\tilde{\lambda }}}_2^4}\frac{D_1}{D_2}, 0, 0, 0, 0, 1\right) \end{aligned}$$

(13)

$$\begin{aligned} \mathbf{Y }_2 \,= \,& {} (0, 0, 0, 0, -1, 0, 0, 0, 1, 0, 0, 0), \end{aligned}$$

(14)

and for a cantilevered plate-layer (7) the vector $\mathbf{Y }_1$ changes to

$$\begin{aligned} \mathbf{Y }_1=\left( 1, 0, 1-\displaystyle \frac{{{\tilde{\lambda }}}_1^4}{{{\tilde{\lambda }}}_2^4}\frac{D_1}{D_2}, 0, 0, 0, -1+\displaystyle \frac{{{\tilde{\lambda }}}_1^4}{{{\tilde{\lambda }}}_2^4}\frac{D_1}{D_2}, 0, 0, 0, 0, 0\right) . \end{aligned}$$

(15)

After introducing vectors $\mathbf{X }_1(x_1^{(1)}, x_2^{(1)}, \ldots , x_{12}^{(1)})$ and $\mathbf{X }_2(x_1^{(2)}, x_2^{(2)}, \ldots , x_{12}^{(2)})$ such that $\mathbf{A } \mathbf{X }_1^T=\mathbf{Y }^T_1$ and $\mathbf{A } \mathbf{X }_2^T=\mathbf{Y }^T_2$ it follows from (12) that the solutions can be written in the following form

$$\begin{aligned} \left\{ \begin{array}{ccc} w_1(x) \\ w_2 (x)\\ w_3(x) \end{array} \right\}= & {} \displaystyle \frac{1}{D_1 {{\tilde{\lambda }}}_1^4} \left( q_0 \left\{ \begin{array}{ccc} v_{11}(x) \\ v_{21} (x) \\ v_{31}(x) \end{array} \right\} +C_1 E_0 B \left\{ \begin{array}{ccc} v_{12}(x) \\ v_{22} (x) \\ v_{32}(x) \end{array} \right\} \nonumber \right. \\&\left. -q_0\left\{ \begin{array}{ccc} 1 \\ \displaystyle \frac{D_1}{D_2}\frac{{{\tilde{\lambda }}}_1^4}{{{\tilde{\lambda }}}_2^4} \\ 1 \end{array} \right\} \right) , \end{aligned}$$

(16)

where

$$\begin{aligned} v_{11}(x) \,= \,& {} x_1^{(1)} \text {e}^{ {{\tilde{\lambda }}}_1^{(1)} x}+x_2^{(1)}\text {e}^{{{\tilde{\lambda }}}_1^{(2)} x}+x_3^{(1)} \text {e}^{{{\tilde{\lambda }}}_1^{(3)} x}+x_4^{(1)}\text {e}^{{{\tilde{\lambda }}}_1^{(4)} x}, \end{aligned}$$

(17)

$$\begin{aligned} v_{21}(x)=\, & {} x_5^{(1)} \text {e}^{ {{\tilde{\lambda }}}_2^{(1)} x}+x_6^{(1)}\text {e}^{{{\tilde{\lambda }}}_2^{(2)} x}+x_7^{(1)} \text {e}^{{{\tilde{\lambda }}}_2^{(3)} x}+x_8^{(1)}\text {e}^{{{\tilde{\lambda }}}_2^{(4)} x}, \end{aligned}$$

(18)

$$\begin{aligned} v_{31}(x)= \,& {} x_9^{(1)} \text {e}^{ {{\tilde{\lambda }}}_1^{(1)} x}+x_{10}^{(1)}\text {e}^{{{\tilde{\lambda }}}_1^{(2)} x}+x_{11}^{(1)} \text {e}^{{{\tilde{\lambda }}}_1^{(3)} x}+x_{12}^{(1)}\text {e}^{{{\tilde{\lambda }}}_1^{(4)} x}. \end{aligned}$$

(19)

The functions $v_{12}(x), v_{22}(x)$ and $v_{32}(x)$ in (16) are given by similar equations to (17), (18) and (19) with $x_{i}^{(1)}$ being replaced by $x_{i}^{(2)}$, ($i=1,2,\ldots , 12$).

The solutions written in the form (16) show the piezoelectric coupling in the middle term of the right hand side and are especially useful in investigating the total energy of the system:

$$\begin{aligned} U= & {} \frac{1}{2}\int \limits _0^1\int \limits _{-\frac{h_m}{2}}^\frac{h_m}{2}U^mdxdz\nonumber \\&+ \frac{1}{2}\int \limits _\alpha ^\beta \left[ \int \limits _{-\frac{h_m}{2}-h_p}^{-\frac{h_m}{2}}U^pdzdx+ \int \limits _{\frac{h_m}{2}}^{\frac{h_m}{2}+\frac{h_p}{2}}U^pdxdz \right] , \end{aligned}$$

(20)

where

$$\begin{aligned} U^m=\frac{1}{2} \text {Re}((S_1^m)^*T_1^m) \quad U^p=\frac{1}{2}\text {Re}((S_1^p)^*T_1^p)+\frac{1}{2}\text {Re}(D_3^*E_0), \end{aligned}$$

(21)

and $*$ indicates the complex conjugate. Using constitutive equations (4) the total energy of the system can be expressed via the displacements:

$$\begin{aligned} U= & {} \frac{D_1 L^2}{2}\left[ \theta +\frac{D_2}{D_1}\int _\alpha ^\beta \frac{d^2w_2}{d x^2}\frac{d^2w_2}{d x^2} dx+\int _0^\alpha \frac{d^2w_1}{d x^2} \frac{d^2w_1}{d x^2} dx\nonumber \right. \\&\left. +\int _\beta ^1\frac{d^2w_3}{d x^2}\frac{d^2w_3}{d x^2}dx \right] , \end{aligned}$$

(22)

where $\theta =\displaystyle \frac{\varepsilon _{33}E_0^2}{D_1}(1-k_1^2)h_p(\beta -\alpha )$ and $k_1^2={d_{31}^2}/{(S_{11}^p\varepsilon _{33})}$ is the dimensionless electro-mechanical coupling factor. For the following discussion expression (22) is more convenient to write as:

$$\begin{aligned} U=\displaystyle \frac{D_1 L^2}{2}\left( \frac{1}{D_1{{\tilde{\lambda }}}_1^4}\right) ^2 \left( E_0^2C_1^2 Q_1+q_0^2 Q_2+2 BC_1E_0q_0 Q_3 \right) . \end{aligned}$$

(23)

Note that $U$ is a function of parameters $\alpha$, $\beta$, the vibration frequencies ${{\tilde{\lambda }}}_1$, ${{\tilde{\lambda }}}_2$ and the material properties of the structure. Further, in (23)

$$\begin{aligned} Q_1= & {} \frac{\varepsilon _{33}D_1}{L^3C_1^2 }{{\tilde{\lambda }}}_1^8(1-k_1^2)h_p(\beta -\alpha ) \nonumber \\&+ B^2\left( \frac{D_2}{D_1}\int \limits _\alpha ^\beta \vert v_{22}''\vert ^2 dx+\int \limits _0^\alpha \vert v_{12}''\vert ^2dx+\int \limits _\beta ^1\vert v_{32}''\vert ^2dx\right) , \end{aligned}$$

(24)

$$\begin{aligned} Q_2= & {} \frac{D_2}{D_1}\int \limits _\alpha ^\beta \vert v_{21}''\vert ^2dx+\int \limits _0^\alpha \vert v_{11}''\vert ^2dx+\int \limits _\beta ^1 \vert v_{31}''\vert ^2dx, \end{aligned}$$

(25)

$$\begin{aligned} Q_3= & {} \frac{D_2}{D_1}\int \limits _\alpha ^\beta (E_0v_{21}''v_{22}''+E_0v_{21}''v_{22}'')dx\nonumber \\&+\int \limits _0^\alpha (E_0v_{11}''v_{12}''+E_0v_{11}''v_{12}'')dx\nonumber \\&+\int \limits _\beta ^1(E_0v_{31}''v_{32}''+E_0 v_{31}''v_{32}'')dx. \end{aligned}$$

(26)

In (23) following [4, 5] we define $Q_1$, $Q_2$ and $Q_3$ as the coefficients of actuating, sensing and energy harvesting respectively. Hence the expression for the total energy in (23) can be used to analyze the structure (Fig. 1) as an actuator, sensor and an energy harvester.

Analogous to a parallel plate capacitance the generated charge can be expressed as $Q(t)=\displaystyle \frac{\partial U(t)}{\partial V_0(t)},$ where $V_0(t)$ is the voltage, $Q(t)$ is the charge. Writing $E_0(t)=V_0(t)/h_p$ for the uniform electric field in terms of the electric potential difference, the generated charge can be calculated from (23) as follows:

$$\begin{aligned} Q(t)={D_1 L^2}\left( \frac{1}{D_1}\right) ^2\left( V\frac{C_1^2}{L^2}\frac{Q_1}{h_p^2{{\tilde{\lambda }}}_1^8}+q_0\frac{C_1}{L}\frac{B}{2h_p{{\tilde{\lambda }}}_1^8}Q_3\right) . \end{aligned}$$

(27)

The first term inside the brackets in (27) is the amplitude of the charge $Q_{gen}^{V}$ generated by the applied voltage $V_0=V \text {e}^{\text {i}\omega t},$ and the second term describes the amplitude of the charge $Q_{gen}^{q_0}$ generated by the applied force $q=q_0 \text {e}^{\text {i} \omega t}:$

$$\begin{aligned} Q_{gen}^{V}=\frac{1}{D_1}C_1^2 \frac{Q_1}{h_p^2 {{\tilde{\lambda }}}_1^8}V, \quad Q_{gen}^{q_0}=\frac{L^4}{D_1}C_1 \frac{B Q_3}{2h_p {{\tilde{\lambda }}}_1^8} q_0. \end{aligned}$$

(28)

The first expression in (28) can be used to investigate the sensing properties of the structure. In order words $Q_s(t)=\displaystyle \frac{\partial U(t)}{\partial V_0(t)}\bigg \vert _{q_0=0}$ describes the structure as a sensor. On the other hand the middle term in (23) with the coefficient $Q_2$ can be used for investigating the system as an actuator $\left( Q_a(t)=\displaystyle \frac{\partial U(t)}{\partial q_0(t)}\bigg \vert _{E_0=0}\right)$. In the following discussion we will focus on the second expression in (28) describing energy harvesting properties of the structure and investigate ${{\tilde{Q}}}_3=\text {max}_{(\alpha ,\beta ,\omega )\in D} Q_3$, where $D$ is the domain of $(\alpha , \beta , \omega )$.

3 Discussion

Piezoelectric ceramics are often chosen for energy harvesting devices because apart from good piezoelectric properties they have low cost and are easy to be built in into an energy harvesting structure. PZT is the most frequently used piezoelectric ceramic due to its excellent piezoelectric properties and high Curie temperature. It has been expanded into a large family of ceramics, including PZT-5H, able to exhibit a broad range of properties. Although piezoelectric ceramics are rigid and brittle and less capable of sustaining large strain, overall, they can provide a higher power output than naturally flexible piezoelectric polymers.

Fig. 2

Generated charge at very low frequencies ($\omega \rightarrow 0$) for different lengths of the piezoelectric patches ($h_m=h_p=0.01$) and boundary conditions on the host plate: a simply supported, b simply supported at one end and clamped on the other, c)cantilevered

Material parameters of silicon (Si) for the host plate ($E_m=1.6\times 10^{11} N/m^2,$$\rho _1=2.3\times 10^3kg/m^3$) and the piezoelectric PZT-5H ($E_p=2.3\times 10^{10} N/m^2,$$\rho _2=7.5\times 10^3kg/m^3,$$d_{31}=-274\times 10^{-12}C/N, \varepsilon _{33}=277\times 10^{-10}F/m$) have been used for numerical calculations. The Poisson’s ratios are taken $0.3,$$h_m+h_p=0.02$ and $L=1$, the dimensionless length of the parches is $l=\displaystyle \frac{b-a}{L}=\beta -\alpha .$ Mass proportional damping of 1% is taken. The numerical calculations have been carried out for the amplitudes of the generated charge which from the second equation in (28) can be written in the following dimensionless form:

$$\begin{aligned} \tilde{Q}_{gen}^{q_0}=\frac{D_1}{L^4}\frac{1}{C_1}\frac{1}{q_0}Q_{gen}^{q_0}=\frac{B}{2{{\tilde{\lambda }}}_1^8 h_p}Q_3. \end{aligned}$$

(29)

The dependence of the harvested charge on the position of the piezoelectric patches at very low frequencies ($\omega \rightarrow 0$) shows that there is always a position where the harvester generates a maximum charge (Fig. 2a, b). The increase between minimum and maximum harvested charge can be significant. For a simply supported host plate (Fig. 2a), when $l=0.2$ the increase can be up to $160\%$ depending on the position of the patches. For $l=0.4$ the increase can be up to $66\%$, and for $l=0.5$ up to $42\%$. For the host plate simply supported at one end and clamped on the other these differences are more dramatic, the energy output is declining rapidly as the patches move beyond the position of maximum harvesting (Fig. 2b). For a cantilevered host plate the stress induced during bending is always concentrated near the clamped edge [12]. Depending on the length of the piezoelectric patches the maximum harvested charge can change by up to $100\%$ increasing from $0.81$ for $l=0.2$ to $1.72$ for $l=0.8$ (Fig. 2c).

Fig. 3

Dimensionless displacements at very low frequencies $(\omega \rightarrow 0)$ for piezoelectric patches at different locations $x$ for $l=0.4$. Boundary conditions on the host plate are: a simply supported, b simply supported at one end and clamped on the other, c cantilevered

For a particular length of the piezoelectric patches, the dimensionless displacements (Fig. 3)

$$\begin{aligned} w(x,\alpha , \beta , \omega )=\left\{ \begin{array}{lll} w_1,&{} { 0\le x\le \alpha ,} \\ w_2, &{} { \alpha \le x\le \beta ,} \\ w_3, &{} { \beta \le x\le 1 } \end{array} \right. \end{aligned}$$

(30)

show that the maximum charge is not necessarily harvested when the patches are at the position where the maximum displacement has its highest value. For example, in the case of simply supported plate with $l=0.4,$ the maximum charge is harvested when the patches are located at $\alpha =0.3$ (Fig. 2a) whereas the maximum displacement has its highest value when $\alpha =0$ (Fig. 3a) as shown. A similar picture is observed when the host structure is simply supported at one end and clamped on the other (Fig. 3a) as shown. The maximum charge for the case $l=0.4$ is harvested at $\alpha =0.25$ but the maximum displacement is reached at $\alpha =0.5$. For a cantilevered plate (Fig.  3c) as it would be expected for any position of the piezoelectric patches the maximum displacement is reached at the free end of the host plate and the harvesting energy is maximum at the clamped end.

Thus even at off-resonance frequencies there is always a position for the piezoelectric patches where the system generates maximum charge. This means that the dependence of the harvested charge on the position of the piezoelectric patches exists even at off-resonance frequencies. However it is important to know resonance frequencies to estimate the distribution of dynamic stress more accurately. The main goal here is to calculate energy harvesting due to dynamic stresses arising from external excitations. The external excitations produce displacements (4) which have been used in (21) to calculate the total energy (22) of the system. Knowledge of the resonance frequencies allows one to calculate displacements more accurately. Figure 4 shows first resonance frequencies $\lambda (l, \alpha )$ for different positions and lengths of the piezoelectric patches.

The dependence of dynamic displacements on the frequency of the external excitation around the first resonance frequencies is shown in Fig. 5. It is clear that there is a sharp change in the shape of the displacements around resonance frequencies. It is well known that around higher resonance frequencies the amplitude of the change is at least an order of magnitude lower than around the first resonance.

In practice the mode shape will experience charge cancellation as some regions are in compression while others in tension. In applications there are very well-developed approaches to overcome this problem and maximise the energy achieved by energy harvesting performances. One effective approach is including diode-based components that can guarantee one directional voltage. For example, the Schottky diode offers low forward voltage and high switching speed and is considered as an ideal component for energy harvesting applications [27].

Fig. 4

First resonance frequencies for different positions and lengths of the piezoelectric patches, $h_p/h_m=1$, a simply supported host, b simply supported at one end and clamped on the other

Fig. 5

The dynamic displacements around first resonance frequencies a$\lambda =2.87$ for the piezoelectric patch with $l=0.4$,$\alpha =0.3$, b$\lambda =3.02$ for $l=0.7$, $\alpha =0.15$

Fig. 6

a The generated charge at two near-resonance frequencies. b The generated charge as a function of frequency and position of the piezoelectric patches ($l=0.4$)

For a simply supported host plate (Fig. 4a) and the piezoelectric patches of length $l = 0.4$ attached at $\alpha =0.3$ where the corresponding resonance frequency is $\lambda =2.87$, the generated charge has a well-defined maximum value for the external vibrating frequency $\lambda = 2.86$ just under the minimum resonance frequency (Fig. 6a). When the external vibrating frequency is $\lambda =2.90$, just above the corresponding resonance frequency, the generated charge at the same location $\alpha =0.3$ receives a minimum value, also well demonstrated in Fig. 6b. On the other hand this frequency is resonant for two locations (due to the symmetry of the boundary conditions in this case) of the patches hence there are two maximum peaks for the harvested charge.

Since the pattern of the first resonance frequencies (Fig.  4a) change for the piezoelectric harvesters with length $l\ge 0.5$, the effect of the change in vibrating frequency at the maximum of the harvested charge changes as well. For piezoelectric patches with $l=0.5$ (Fig. 7) the harvested charge is minimised when the vibrating frequency is just below the resonance frequency $\lambda =2.92$ corresponding to the location of patches $\alpha =0.26$. At this same location the harvested charge changes into maximum with slight change in the external vibrating frequency becoming just above the resonance frequency.

Fig. 7

a The generated charge for two near-resonance frequencies. b The generated charge as a function of frequency and position of the piezoelectric patches ($l=0.5$)

Figure 8a, b confirm the results for $l\ge 0.5$ in the case $l=0.7$. The first resonance frequency at $\alpha =0.15$ is $\lambda = 3.02$. When the vibrating frequency is below the resonance frequency ($\lambda =3$) the generated charge has a minimum value and when the vibrating frequency exceeds the resonance frequency ($\lambda =3.08$) the generated charge has a maximum value at the same location of the harvester $\alpha =0.15$.

Fig. 8

a The generated charge for two near-resonance frequencies. b The generated charge as a function of frequency and the position of the piezoelectric patches ($l=0.7$)

The dynamic displacements around second and third resonance frequencies in Fig. 9 show that there is no shape change around the second resonance frequency $\lambda =6.056$ but there is an abrupt shape change around the third resonance frequency $\lambda =11.02$. This means that only around odd resonance frequencies the generated charge will change from maximum to minimum or vice versa. It is also worth mentioning that compared to the displacements around the fundamental resonance frequency the displacements around higher resonance frequencies are two orders of magnitude smaller. This will obviously be reflected in the amount of generated charge around second and third resonance frequencies.

Fig. 9

The dynamic displacements for around a second and b third resonance frequencies for the piezoelectric patch with $l=0.4$, $\alpha =0.3$

Cantilevered plates and beams are more commonly used for energy harvesting with piezoelectric energy harvesters because of the much larger mechanical strains they produce within the piezoelectric harvester. Also, as can be seen by comparing Figs. 4 and 10a, the resonance frequencies of the fundamental flexural modes in this case are lower compared to the corresponding length and position of the piezoelectric patches in other vibration modes. Although as expected the maximum resonance frequencies are at $x=0$ regardless of the lengths of the piezoelectric patches, the value of the maximum resonance frequencies vary for different lengths of the harvester, reaching a maximum of around $l=0.45$ and minimum for $l=0.9$ (Fig. 10b).

Fig. 10

a First resonance frequencies of the cantilevered harvester for different positions and lengths of the piezoelectric patches, for $h_m=h_p=0.01$. b Maximum resonance frequencies for different lengths of the piezoelectric patches

3.1 The Effect of the Thickness Ratio on the Harvested Charge

The amount of the power produced by piezoelectric energy harvesters (between nano-watts to milli-watts) depends on both intrinsic features such as piezoelectric and mechanical properties of materials, the resonance frequency of the piezoelectric patches, the design of the piezoelectric element and the circuitry and extrinsic factors such as the input frequency and the amplitude of the excitation. Increasing the $h_p/h_m$ ratio adds stiffness and mass to the structure changing its intrinsic properties and thus changing the dynamic response.

As already mentioned power density of a piezoelectric vibrational energy harvesting device is strongly frequency dependent as the piezoelectric generates maximum power at its resonance frequency. Therefore, the fundamental frequency of the host determines the size of the piezoelectric element in a piezoelectric energy harvesting structure. Since most of the vibrations from commonly occurring sources are low frequency vibrations, low frequency fundamental mode are normally targeted when designing the energy harvesting structure. Figure 11 shows the fundamental resonance frequencies at different positions of the piezoelectric patches on a simply supported plate for different values of the thickness ratio. For $h_p/h_m < 1$ these frequencies decrease for longer piezoelectric patches and always have a minimum point (Fig.  11a). It is clear from the earlier discussion that the harvesting coefficient will have maximum values for operating frequencies below the resonance frequency and minimum value above the resonance frequencies (Fig. 6).

Fig. 11

First resonance frequencies for different positions and lengths of the piezoelectric patches for simply supported host for a$\displaystyle {h_p}/{h_m}=0.1$, b$\displaystyle {h_p}/{h_m}=2,$c$\displaystyle {h_p}/{h_m}=10$

For $h_p/h_m \ge 1$, although the overall resonance frequencies decrease, they increase with the length of the piezoelectric patches and have maximum values for $l\ge 0.5$ (Fig. 11b, c). This means that the qualitative picture of the outcome energy will be similar to that described in the previous section. The generated charge will have minimum values for operating frequencies below the maximum resonance frequency and maximum value above the maximum resonance frequencies (Fig.  7b).

4 Conclusion

The investigation carried out in this paper allows to determine a position for piezoelectric patches hosted by a non-piezoelectric plate-layer to maximize the performance of piezoelectric sensors, actuators and energy harvesters. The expression of the total energy has been derived investigating the converted energy for any length of the piezoelectric patches. The discussion carried out for energy harvesting can be extended for a piezoelectric sensor and an actuator.

It is shown that at very low frequencies for any specified size of the piezoelectric patches there is only one location on the host plate where the patches generate a maximum energy input/output. In a dynamic vibrational loading the same location corresponds to the piezoelectric patches’ location where the system’s resonance frequency reaches its extremum value as a function of the position of the patches on the host plate.

As expected in the case of a dynamic vibrational loading the maximum charge can be harvested at the resonance frequency, which varies for different positions and lengths of the piezoelectric patches. However in this case the energy input/output is extremely sensitive to the operating frequency. If the operating frequency is below the systems resonant frequency corresponding to the length and position of the patches, the location for maximum energy input/output is drastically different from the best location when the operating frequency is just above the systems resonant frequency. In other words, if the systems operating frequency is close to the resonant frequency the composite does not necessarily generate maximum energy input/output. Depending on the length of the piezoelectric patches the maximum energy output can be achieved if the operating frequency is just under or just above the corresponding resonance frequency.

The discussion carried out for energy harvesting can be extended for sensing and actuating properties of the structure. As expressions (24) and (25) for the sensing and actuating coefficients $Q_1$ and $Q_2$ suggest, the results are qualitatively similar to those for the harvesting coefficient $Q_3$ in (26) and the same discussion can be applied to sensing and actuating properties of the structure.

These theoretical results show that when tuning the energy harvesting structure to the ambient vibrating frequency care should be taken as to how to approach to the resonance frequency. The energy outcome will strongly depend on not only the length and position of the piezoelectric harvesters but to a very large extend how the resonance frequency is approached: from below or from above.

Appendix 1

Matrix $\mathbf{A }$ written in the block-matrix form has the following matrix entries:

$$\begin{aligned} A=\left( \begin{array}{ccc} A_{11} &{}A_{12} &{} 0 \\ A_{21} &{} A_{22} &{} A_{23} \\ 0 &{} A_{32} &{} A_{33} \\ \end{array} \right) , \end{aligned}$$

(31)

where for a simply supported plate-layer

$$\begin{aligned} A_{11}= & {} \left( \begin{array}{cccc} 1 &{} 1 &{} 1 &{} 1 \\ -1 &{} 1 &{} 1 &{} -1 \\ e_1^{-a \nu } &{} e_1^{-{ia} \nu } &{} e_1^{{ia} \nu } &{} e_1^{a \nu } \\ a \gamma e_1^{-a \nu } &{} i a \gamma e_1^{-{ia} \nu } &{} -i a \gamma e_1^{{ia} \nu } &{} -a \gamma e_1^{{ia} \nu } \\ \end{array} \right) , \nonumber \\ A_{12}= & {} \left( \begin{array}{cccc} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ -e_1^{-\nu } &{} -e_1^{-i \nu } &{} -e_1^{i \nu } &{} -e_1^{\nu } \\ -e_1^{-\nu } &{} -i e_1^{-i \nu } &{} i e_1^{i \nu } &{} e_1^{\nu } \\ \end{array} \right) , \nonumber \\ A_{21}= & {} \left( \begin{array}{cccc} -a^2 \xi e_1^{-a \nu } &{} a^2 \xi e_1^{\nu (-{ia})} &{} a^2 \xi e_1^{\nu {ia}} &{} -a^2 \xi e_1^{\nu {ia}} \\ -a^3 \tau e_1^{-a \nu } &{} i a^3 \tau e_1^{-a \nu } &{} -i a^3 \tau e_1^{\nu {ia}} &{} a^3 \tau e_1^{\nu {ia}} \\ 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ \end{array} \right) , \nonumber \\ A_{22}= & {} \left( \begin{array}{cccc} e_1^{-\mu } &{} -e_1^{-i \mu } &{} -e_1^{i \mu } &{} e_1^{\mu } \\ e_1^{-\mu } &{} -i e_1^{-i \mu } &{} i e_1^{i \mu } &{} -e_1^{\mu } \\ e_1^{-\frac{\beta \mu }{\alpha }} &{} e_1^{-\frac{i \beta \mu }{\alpha }} &{} e_1^{\frac{i \beta \mu }{\alpha }} &{} e_1^{\frac{\beta \mu }{\alpha }} \\ e_1^{-\frac{\beta \mu }{\alpha }} &{} i e_1^{-\frac{i \beta \mu }{\alpha }} &{} -i e_1^{\frac{i \beta \mu }{\alpha }} &{} -e_1^{\frac{\beta \mu }{\alpha }} \\ \end{array} \right) , \nonumber \\ A_{23}= & {} \left( \begin{array}{cccc} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ -e_1^{-\frac{a \beta \nu }{\alpha }} &{} -e_1^{-\frac{i a \beta \nu }{\alpha }} &{} -e_1^{\frac{i a \beta \nu }{\alpha }} &{} -e_1^{\frac{a \beta \nu }{\alpha }} \\ -a \gamma e_1^{-\frac{a \beta \nu }{\alpha }} &{} -i a \gamma e_1^{-\frac{i a \beta \nu }{\alpha }} &{} i a \gamma e_1^{\frac{i a \beta \nu }{\alpha }} &{} a \gamma e_1^{\frac{a \beta \nu }{\alpha }} \\ \end{array} \right) \end{aligned}$$

(32)

$$\begin{aligned} A_{32}= & {} \left( \begin{array}{cccc} -e_1^{-\frac{\beta \mu }{\alpha }} &{} e_1^{-\frac{i \beta \mu }{\alpha }} &{} e_1^{\frac{i \beta \mu }{\alpha }} &{} -e_1^{\frac{\beta \mu }{\alpha }} \\ -e_1^{-\frac{\beta \mu }{\alpha }} &{} i e_1^{-\frac{i \beta \mu }{\alpha }} &{} -i e_1^{\frac{i \beta \mu }{\alpha }} &{} e_1^{\frac{\beta \mu }{\alpha }} \\ 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ \end{array} \right) , \end{aligned}$$

(33)

$$\begin{aligned} A_{33}= & {} \left( \begin{array}{cccc} a^2 \xi e_1^{-\frac{\nu a \beta }{\alpha }} &{} -a^2 \xi e_1^{-\frac{i \nu a \beta }{\alpha }} &{} -a^2 \xi e_1^{\frac{i \nu a \beta }{\alpha }} &{} a^2 \xi e_1^{\frac{\nu a \beta }{\alpha }} \\ a^3 \tau e_1^{-\frac{\nu a \beta }{\alpha }} &{} -i a^3 \tau e_1^{-\frac{i \nu a \beta }{\alpha }} &{} i a^3 \tau e_1^{\frac{i \nu a \beta }{\alpha }} &{} -a^3 \tau e_1^{\frac{\nu a \beta }{\alpha }} \\ -e_1^{-\frac{a \nu }{\alpha }} &{} e_1^{-\frac{i a \nu }{\alpha }} &{} e_1^{\frac{i a \nu }{\alpha }} &{} -e_1^{\frac{a \nu }{\alpha }} \\ e_1^{-\frac{a \nu }{\alpha }} &{} e_1^{-\frac{i a \nu }{\alpha }} &{} e_1^{\frac{i a \nu }{\alpha }} &{} e_1^{\frac{a \nu }{\alpha }} \\ \end{array} \right) . \end{aligned}$$

(34)

For a plate-layer simply supported at one end and clamped on the other:

$$\begin{aligned} A_{33}=\left( \begin{array}{cccc} a^2 \xi e_1^{-\frac{\nu a \beta }{\alpha }} &{} -a^2 \xi e_1^{-\frac{i \nu a \beta }{\alpha }} &{} -a^2 \xi e_1^{\frac{i \nu a \beta }{\alpha }} &{} a^2 \xi e_1^{\frac{\nu a \beta }{\alpha }} \\ a^3 \tau e_1^{-\frac{\nu a \beta }{\alpha }} &{} -i a^3 \tau e_1^{-\frac{i \nu a \beta }{\alpha }} &{} i a^3 \tau e_1^{\frac{i \nu a \beta }{\alpha }} &{} -a^3 \tau e_1^{\frac{\nu a \beta }{\alpha }} \\ e_1^{-\frac{a \nu }{\alpha }} &{} i e_1^{-\frac{i a \nu }{\alpha }} &{} -i e_1^{\frac{i a \nu }{\alpha }} &{} -e_1^{\frac{a \nu }{\alpha }} \\ e_1^{-\frac{a \nu }{\alpha }} &{} e_1^{-\frac{i a \nu }{\alpha }} &{} e_1^{\frac{i a \nu }{\alpha }} &{} e_1^{\frac{a \nu }{\alpha }}\\ \end{array} \right) , \end{aligned}$$

(35)

For a cantilevered plate-layer

$$\begin{aligned}&A_{11}\left( \begin{array}{cccc} 1 &{} 1 &{} 1 &{} 1 \\ 1 &{} i &{} -i &{} -1 \\ e_1^{-a \nu } &{} e_1^{-{ia} \nu } &{} e_1^{{ia} \nu } &{} e_1^{a \nu } \\ a \gamma e_1^{-a \nu } &{} i a \gamma e_1^{-{ia} \nu } &{} -i a \gamma e_1^{{ia} \nu } &{} -a \gamma e_1^{{ia} \nu } \\ \end{array} \right) , \end{aligned}$$

(36)

$$\begin{aligned}&A_{33}=\left( \begin{array}{cccc} a^2 \xi e_1^{-\frac{\nu a \beta }{\alpha }} &{} -a^2 \xi e_1^{-\frac{i \nu a \beta }{\alpha }} &{} -a^2 \xi e_1^{\frac{i \nu a \beta }{\alpha }} &{} a^2 \xi e_1^{\frac{\nu a \beta }{\alpha }} \\ a^3 \tau e_1^{-\frac{\nu a \beta }{\alpha }} &{} -i a^3 \tau e_1^{-\frac{i \nu a \beta }{\alpha }} &{} i a^3 \tau e_1^{\frac{i \nu a \beta }{\alpha }} &{} -a^3 \tau e_1^{\frac{\nu a \beta }{\alpha }} \\ -e_1^{-\frac{a \nu }{\alpha }} &{} e_1^{-\frac{i a \nu }{\alpha }} &{} e_1^{\frac{i a \nu }{\alpha }} &{} -e_1^{\frac{a \nu }{\alpha }} \\ -e_1^{-\frac{a \nu }{\alpha }} &{} i e_1^{-\frac{i a \nu }{\alpha }} &{} -i e_1^{\frac{i a \nu }{\alpha }} &{} e_1^{\frac{a \nu }{\alpha }} \\ \end{array} \right) , \end{aligned}$$

(37)

and $\mu =\root 4 \of {\lambda ^2-i \epsilon _2 },$$\nu =\root 4 \of {\lambda ^2-i \eta \epsilon _1 },$$i=\sqrt{-1}$, $\gamma =\displaystyle \frac{\nu }{\mu },$$e_1=e^{\alpha \sqrt{\lambda }},$$\tau =\displaystyle \frac{D_1 \nu ^3}{D_2 \mu ^3},$$\xi =\displaystyle \frac{D_1 \nu ^2}{D_2 \mu ^2},$$a=\root 4 \of {\displaystyle \frac{D_2}{D1}\frac{\rho _1}{\rho _2} \left( \frac{2 h_{p}}{h_m}+1\right) }$, $\eta =\displaystyle \frac{D_2}{D_1 a^4}$.