On the existence of cycles with restrictions in the color transitions in edge-colored complete graphs

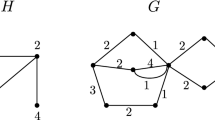
Abstract

Consider the following edge-coloring of a graph G. Let H be a graph possibly with loops, an H-coloring of a graph G is defined as a function $c : E(G) \rightarrow V(H).$ We will say that G is an H-colored graph whenever we are taking a fixed H-coloring of G. A cycle $(x_0,x_1,\ldots ,x_n,x_0),$ in an H-colored graph, is an H-cycle if and only if $(c(x_0x_1),c(x_1x_2),\ldots , c(x_nx_0),$ $c(x_0x_1))$ is a walk in H. Notice that the graph H determines what color transitions are allowed in a cycle in order to be an H-cycle, in particular, when H is a complete graph without loops, every H-cycle is a properly colored cycle. In this paper, we give conditions on an H-colored complete graph G,  with local restrictions, implying that every vertex of G is contained in an H-cycle of length at least 5. As a consequence, we obtain a previous result about properly colored cycles. Finally, we show an infinite family of H-colored complete graphs fulfilling the conditions of the main theorem, where the graph H is not a complete k-partite graph for any k in ${\mathbb {N}}.$

1 Introduction

For basic concepts, terminology and notation not defined here, we refer the reader to [5]. Throughout this work, we will consider finite simple graphs, unless otherwise is specified. Let G be a graph, V(G) and E(G) will denote the sets of vertices and edges of G,  respectively.

A k-edge-coloring of a graph G is defined as a function $f : E(G) \rightarrow \{1,2,\ldots ,k\}.$ We will say that G is a k-edge-colored graph whenever we are taking a fixed k-edge-coloring of G. Different kinds of walks have been studied in edge-coloring graphs, for example, monochromatic walks (that are walks with all the edges of the same color), properly colored walks (that are walks with no consecutive edges having the same color), rainbow walks (that are walks whose all edges have different color) and walks with a given color pattern, see [4, 6, 16, 20].

In particular, properly colored walks are of interest for theoretical reasons, for example, as a generalization of walk in undirected and directed graphs, see [3], as well as, in Graph Theory Application, for example, in Genetic and Molecular Biology [7, 8, 18, 21], Engineering and Computer Science [1, 19, 22], and Management Science [24, 25].

Several authors have studied the existence and the length of properly colored cycles and paths, see [2, 9, 15]. In particular, Grossman and Häggkvist [14] were the first to study the problem of the existence of properly colored cycles in k-edge-colored graphs, and they proved Theorem 1, for $k=2.$ Later, Yeo [26] proved it for $k\ge 2.$

Theorem 1

(Grossman and Häggkvist [14], and Yeo [26]) Let G be a k-edge-colored graph,  $k\ge 2,$ with no properly colored cycle. Then,  G has a vertex $z \in V(G)$ such that no connected component of $G-z$ is joined to z with edges of more than one color.

Let G be an edge-colored graph and v a vertex of G,  the color degree of v,  denoted by $\delta ^c(v),$ is the number of colors in the edges incident with v. Wang and Li [23] studied the existence of properly colored Hamiltonian cycles and conjectured that in any graph with at least three vertices such that $\delta ^c(v)\ge \frac{n}{2},$ for every vertex v,  the graph contains a properly colored Hamiltonian cycle. Fujita and Magnant [9] gave a counterexample for that conjecture and proposed a new conjecture by changing $\delta ^c(v)\ge \frac{n}{2}$ for $\delta ^c(v)\ge \frac{n+1}{2}.$ They observed that proving that conjecture seems difficult even for complete graphs, so they studied that case and proved Theorem 2.

Theorem 2

(Fujita and Magnant [9]) Let G be an edge-colored complete graph with at least 13 vertices. If $\delta ^c(v)\ge \frac{n+1}{2},$ for every vertex v in V(G),  then every vertex in G is contained in a properly colored cycle of length at least 5.

In this paper, we will work with a more general concept of edge-coloring defined as follows: Let H be a graph possibly with loops, an H-coloring of a graph G is defined as a function $c : E(G) \rightarrow V(H).$ We will say that G is an H-colored graph whenever we take a fixed H-coloring of G. A walk $W=(x_0,x_1,\ldots ,x_n),$ in an H-colored graph, is an H-walk if and only if for every $i\in \{0,\ldots ,n-2\},$ $c(x_ix_{i+1})$ and $c(x_{i+1}x_{i+2})$ are adjacent in H;  and whenever $x_0=x_n$ and $c(x_{n-1}x_n)$ and $c(x_nx_1)$ are adjacent in H,  we will say that W is a closed H-walk. A (closed) H-walk T is an H-path (H-cycle) if and only if T is a path (cycle). These definitions were introduced in the context of Kernel Theory in digraphs by Linek and Sands in [17].

A theoretical reason to study H-walks is that they generalize monochromatic walks and properly colored walks. To see that H-walks generalize properly colored walks, consider the following H-coloring. Let G be a k-edge-colored graph with color function f,  and H a complete graph with vertex set $\{v_1,\ldots ,v_k\}.$ Consider $G'$ the H-coloring of G such that $c(e)=v_{f(e)},$ it is easy to see that each properly colored walk in G corresponds to an H-walk in $G'$ and vice versa. If we replace the complete graph H by the graph $H'$ defined as $V(H')=V(H)$ and $E(H')=\{v_iv_i : i \in \{1,\ldots ,k\}\},$ then each monochromatic walk in G corresponds to an $H'$-walk in $G'$ and vice versa. Also, notice that if $W=(x_0,x_1,\ldots ,x_n)$ is an H-walk such that $(c(x_0x_1),c(x_1x_2),\ldots ,c(x_{n-1}x_n))$ is a path in H,  then W is a rainbow walk.

In [20], it can be found several applications on edge-colored graphs with restrictions in the color transitions. The following problem refers to the area of communication in networks: A company has multiple servers to send and receive information, where there is direct communication between some pairs of them. Sometimes, it is possible that a message cannot be received because of a failure in the connection between two consecutive servers in a route of communication. For different reasons (such as, external attacks or internal failures), the connection between two servers may fail. In order to have a robust network against communications faults, it is desired to have communications routes passing through two consecutive connections with a low mean probability of failure. We can represent this situation with the help of an H-colored graph defined as follows: we have one vertex in the graph G for every server in the network, and two different vertices A and B are adjacent in G if and only if A and B have a connection. Now, we construct the graph H that will determine what color transitions are allowed: the vertices of the graph H are the probability of failure in the different connections in the communication network (notice that the communication network if finite, so it has a finite number of connections), and two vertices x and y of H are adjacent if and only if $\frac{x+y}{2} <p,$ for a fixed p in [0, 1) (for example, we can consider $p=0.5$). Finally, we color the edges of the graph G with the probability of its failure.

In [12], Galeana-Sánchez, Rojas-Monroy, Sánchez-López and Villarreal-Valdés began the study of H-colorings by providing conditions implying the existence of Euler H-trails in H-colored graphs. Later, they gave in [13] an extension of Theorem 1 from which can be extracted an algorithm to determine in polynomial time whether an H-colored multigraph contains an H-cycle. The following auxiliary graph has proved to be an essential part in the writing and development of the previous results.

Definition 1

Let G be an H-colored graph and v a non-isolated vertex of G. We define the graph $G_v$ as follows

• 1. $V(G_v)=\{vx\in E(G):x\in N_G(v)\}.$

• 2. $ab\in E(G_v),$ with $a\ne b,$ if and only if $c(a)c(b)\in E(H).$

Note that $G_v$ is a simple graph for every non-isolated vertex v of G.

In [10], Galeana-Sánchez, Hernández-Lorenzana and Sánchez-López began the study of the existence of H-paths and H-cycles of certain lengths in an H-colored graph, and by considering the graph $G_v,$ they proved the following result.

Theorem 3

(Galeana-Sánchez et al. [10]) Let G be an H-colored graph. If $|V(G)|\ge 4$ and for every x in V(G),  $G_x$ is a complete $k_x$-partite graph,  for some $k_x$ in ${\mathbb {N}},$ with $k_x \ge \frac{|V(G)|}{2},$ then G has an H-cycle of length at least $\lceil \frac{|V(G)|}{2} \rceil +1.$

The main result in this work shows conditions on an H-colored complete graph G,  with restrictions given by the auxiliary graph $G_x,$ implying that every vertex of G is contained in an H-cycle of length at least 5. As a consequence of the main result we obtain Theorem 2. Moreover, for every odd natural number n,  we show an example of an H-colored complete graph of order n fulfilling the conditions of the main theorem, but the graph H is not a complete k-partite graph. Our aim with this and other similar results is to find conditions on an H-colored complete graph G,  implying that every vertex of G is contained in an H-cycle of length l for every l in $\{3,\ldots ,|V(G)|\},$ that is, G is a vertex H-pancyclic graph.

2 Terminology and notation

Let G be a graph. In the rest of paper, we will denote by: $N_G(u)$ the neighborhood of v,  $\delta _G(v)$ the degree of v,  for $X\subseteq V(G),$ G[X] the subgraph of G induced by X,  $G-X$ the subgraph of G induced by $V(G)-X,$ and if $X=\{a\},$ we write $G-a$ instead of $G-\{a\}.$ If the graph G is understood, we omit the subscript G.

A walk is a sequence $W=(v_0,v_1,\ldots ,v_k)$ such that $v_i v_{i+1}\in E(G)$ for every i in $\{0,1,\ldots ,k-1\}.$ The number k is the length of W,  denoted by $\ell (W).$ If $v_0=v_k,$ then we say that W is a closed walk. We say that the walk W is a path if and only if $v_i\ne v_j$ for every $\{i,j\}$ subset of $\{0,1,\ldots ,k\},$ with $i \ne j.$ A closed walk $(v_0,v_1,\ldots , v_k,v_0)$ is a cycle if and only if $k\ge 2$ and $(v_0,v_1,\ldots ,v_k)$ is a path. If $V=(u_0,\ldots ,u_n)$ and $W=(u_n,v_1,v_2,\ldots ,v_k)$ are two walks, the concatenation $(u_0,\ldots ,u_n,v_1,v_2\ldots ,v_k)$ of the walks V and W is denoted by $V\cup W,$ and the walk $(u_n,\ldots ,u_0)$ is denoted by $V^{-1}.$

A subset I of V(G) is independent if and only if the subgraph G[I] has no edges. For a fixed positive integer k,  we say that a graph G is a k-partite graph if and only if there exists a partition $\{V_1,\ldots ,V_k\}$ of V(G) where each $V_i$ is an independent set. Moreover, a k-partite graph with a partition $\{V_1,\ldots ,V_k\}$ of V(G) into independent sets, is said to be a complete k-partite graph if and only if for every x in $V_i$ and for every y in $V_j,$ x and y are adjacent in G,  for every $\{i,j\}$ subset of $\{1,\ldots ,k\},$ with $i\ne j.$

Let G be an H-colored graph, $W=(v_0,\ldots ,v_k)$ a walk in G and i in $\{1,\ldots ,k-1\}.$ We say that $v_i$ is an obstruction of W if and only if $c(v_{i-1} v_i)c(v_i v_{i+1})\notin E(H);$ and whenever $v_0=v_k,$ we say that $v_0$ is an obstruction if and only if $c(v_{k-1} v_k)c(v_k v_1)\notin E(H).$

For a better understanding for the reader, we include notation and observations which were introduced in [11].

Observation 4

Let G be an H-colored graph,  such that for every x in V(G),  $G_x$ is a complete $k_x$-partite graph for some $k_x$ in ${\mathbb {N}}.$ Suppose that $\{ux,vx\}$ is a subset of E(G). The following statements are equivalent : 

• 1. ux and vx are in different partite sets of the $k_x$-partition of $V(G_x).$

• 2. ux and vx are adjacent in $G_x.$

• 3. $c(ux)c(vx)\in E(H).$

• 4. x is not an obstruction of the path (u, x, v).

• 5. (u, x, v) is an H-path in G.

As a direct consequence of Observation 4 and the definition of H-cycle, we have the following observations:

Observation 5

Let G be an H-colored graph,  such that for every x in V(G),  $G_x$ is a complete $k_x$-partite graph for some $k_x$ in ${\mathbb {N}}.$ Suppose that $C=(u_1,\ldots ,u_{n-1},u_n,u_1)$ is a cycle in G. The following statements are equivalent : 

• 1. C is an H-cycle in G.

• 2. $(c(u_1 u_2),\ldots ,c(u_{n-1} u_n),c(u_n u_1),c(u_1 u_2))$ is a walk in H.

• 3. $u_1,\ldots ,u_{n}$ are not obstructions of the cycle C.

• 4. $u_{i-1}u_i$ and $u_{i+1}u_i$ are in different partite sets of the $k_{u_i}$-partition of $V(G_{u_i})$ for every i in $\{1,\ldots ,n\}$ (the subscripts are taken modulo n).

Observation 6

Let G be an H-colored graph,  such that for every x in V(G),  $G_x$ is a complete $k_x$-partite graph for some $k_x$ in ${\mathbb {N}}.$ If (u, v, w) is an H-path,  then for every x in $N_G(v)$ we have that (x, v, u) or (x, v, w) is an H-path.

Observations 4, 5 and 6 will be frequently used in the proof of the main result.

Observation 7

Let G be an H-colored graph without isolated vertices,  and D an induced (by V(D)) subgraph of G. If for every x in V(G),  $G_x$ is a complete $k_x$-partite graph for some $k_x$ in ${\mathbb {N}},$ then for every x in V(D),  $D_x$ is a complete $l_x$-partite graph for some $l_x$ in ${\mathbb {N}}.$ Moreover,  if $\{P_1^x,P_2^x,\ldots ,P_{k_x}^x\}$ is the $k_x$-partition of $V(G_x)$ into independent sets,  then $\{P_i^x\cap V(D_x): P_i^x\cap V(D_x)\ne \emptyset , i\in \{1,2,\ldots , k_x\}\}$ is the $l_x$-partition of $V(D_x)$ into independent sets.

If D is an induced subgraph of G without isolated vertices, then for every x in V(D), we write $k_x^D$ instead of $l_x,$ where $l_x$ is the one referred in Observation 7.

Let G be an H-colored complete graph, A a subset of V(G) and v in $V(G)-A.$ We say that A has the H-dependency property with respect to the vertex v if and only if for every subset $\{a,a'\}$ of A,  $(v,a,a')$ or $(v,a',a)$ is not an H-path in G.

Proposition 8

[11] Suppose that for every x in V(G),  $G_x$ is a complete $k_x$-partite graph for some $k_x$ in ${\mathbb {N}}.$ Let A be a subset of V(G) and v be a vertex in $V(G) - A.$ If A has the H-dependency property with respect to the vertex v,  then there exists some vertex a in A such that

• 1. $k_a^D \le \frac{|A|+1}{2},$ where $D=G[A],$ and

• 2. if $|A| \ge 2,$ then a is an obstruction of the walk $(v,a,a')$ for some $a'$ in $N_D(a).$

3 Main results

Theorem 9

Let H be a graph possibly with loops and G an H-colored complete graph of order n,  with $n \ge 13.$ Suppose that : 

• 1. For every x in V(G),  $G_x$ is a complete $k_x$-partite graph,  with $k_x \ge \dfrac{n+1}{2}.$

• 2. There is no cycle of length 3 in G with exactly 2 obstructions.

Then,  every vertex of G is contained in an H-cycle of length at least 5.

Proof

Suppose, by contradiction, that there is a vertex v in G that is not contained in any H-cycle of length at least 5.

Let $C=(x_1,x_2,\ldots ,x_l,x_1)$ be an H-cycle of maximum length in G. It follows by Theorem 3 that $l \ge \lceil \dfrac{n}{3} \rceil +1 \ge \lceil \dfrac{13}{3} \rceil +1 = 6.$ So, $v \not \in V(C).$

Case 1. $\{vx_1, vx_2, \ldots , vx_l\}$ is an independent set in $G_v,$ i.e., $\{vx_1, vx_2, \ldots , vx_l\} \subseteq P_i^v,$ for some $i \in \{1,\ldots , k_v\}.$

Without loss of generality, suppose that $\{vx_1, vx_2, \ldots , vx_l\} \subseteq P_1^v.$ Let $F= \{x \in V(G) - (V(C)\cup \{v\}) : xv \not \in P_1^v\}.$ Since $k_v \ge \dfrac{n+1}{2},$ we have that $|F| \ge \dfrac{n+1}{2} -1 = \dfrac{n-1}{2}.$ $\square$

Claim 1

Every vertex u in F is an obstruction of the H-path $T_i=(v,u,x_i),$ for every $i \in \{1,\ldots ,l\}.$

Proof of Claim 1

Assume, by contradiction, that there is a vertex u in F such that $T=(v,u,x_i)$ is an H-path, for some $i \in \{1,\ldots ,l\}.$

Case 1.1 $(u,x_i,x_{i+1})$ is an H-path.

If $(x_{i-2},x_{i-1},v)$ is an H-path, then $C'=(v,u,x_i)\cup (x_i,C,x_{i-1})\cup (x_{i-1},v)$ is an H-cycle. Otherwise, $x_{i-1}$ is an obstruction of the cycle $(v,x_{i-1},x_{i-2},v)$ and, by assumption of the Case 1, v is also a obstruction of the same cycle. So, by the hypothesis 2, $x_{i-2}$ is an obstruction of the cycle $(v,x_{i-1},x_{i-2},v).$ Hence, $(x_{i-3},x_{i-2},v)$ is an H-path and $C''=(v,u,x_i)\cup (x_i,C,x_{i-2})\cup (x_{i-2},v)$ is an H-cycle.

Case 1.2 $(u,x_i,x_{i+1})$ is not an H-path.

Then, $(u,x_i,x_{i-1})$ is an H-path.

If $(x_{i-2},x_{i-3},v)$ is an H-path, then $C'=(v,u,x_i,x_{i-1},x_{i-2},x_{i-3},v)$ is an H-path. Otherwise, $x_{i-3}$ is an obstruction of the cycle $(v,x_{i-2},x_{i-3},v)$ and, by assumption of the Case 1, v is also a obstruction of the same cycle. So, by the hypothesis 2, $x_{i-2}$ is an obstruction of the cycle $(v,x_{i-2},x_{i-3},v).$ Hence, $(x_{i-1},x_{i-2},v)$ is an H-path and $C''=(v,u,x_i,x_{i-1},x_{i-2},v)$ is an H-cycle.

In both cases, we have that v is contained in an H-cycle of length at least 5, a contradiction, and the claim holds. $\square$

Since $A=\{uy \in V(G_u): y \in V(C)\}$ is contained in the same partite set of the $k_u$-partition of $V(G_u)$ as uv in the graph $G_u,$ and $uv \not \in A,$ we have that $F_u= G_u - A$ is a complete $k_u^{G-V(C)}$-partite graph. Moreover, $n'=|V(G)-V(C)| \le n-l \le \dfrac{2n}{3},$ and for every vertex $u \in F,$ $k_u^{G-V(C)} \ge \dfrac{3n'}{4}.$

Claim 2

For every $u\in F,$ $k_u^{G[F\cup \{v\}]} \ge 3.$

Proof of Claim 2

Suppose, by contradiction, that $k_u^{G[F\cup \{v\}]} < 3.$

Let $E=V(G)-(F\cup V(C) \cup \{v\}).$ Notice that $|E| \le n-\dfrac{n-1}{2}-6-1 = \dfrac{n-13}{2}.$

Since every vertex $u \in F$ is an obstruction of the H-path $T_i=(v,u,x_i),$ then $k_u \le k_u^{G[F\cup \{v\}]} +|E|< 3 +\dfrac{n-13}{2}=\dfrac{n-7}{2} < \dfrac{n+1}{2},$ a contradiction, and the claim holds. $\square$

Since $k_u^{G[F \cup \{v\}]} \ge 3,$ for every $u \in F \cup \{v\},$ there is an H-path $P=(v,w_1,w_2,w_3)$ such that $w_i \in F,$ for every $i \in \{1,2,3\}.$ Let $X= \{x \in V(G)-(V(C)\cup V(P)): vx \text { and } vw_1 \text { are adjacent in } F_v\},$ i.e., a vertex x is in X if and only if $x \in V(G)-(V(C)\cup V(P))$ such that $T=(w_1,v,x)$ is an H-path in $G-V(C).$ Let $Y= \{y \in V(G)-(V(C)\cup V(P)): w_3y \text { and } w_2w_3 \text { are adjacent in } F_{w_3}\},$ i.e., a vertex y is in Y if and only if $y \in V(G)-(V(C)\cup V(P))$ such that $T=(w_2,w_3,y)$ is an H-path in $G-V(C).$

Since $k_v^{G-V(C)} \ge \dfrac{3n'}{4}$ and $k_{w_3}^{G-V(C)} \ge \dfrac{3n'}{4},$ we have that $|X| \ge \dfrac{3n'}{4} -1$ and $|Y| \ge \dfrac{3n'}{4} -1.$ Notice that $X\cup Y \subseteq V(G)-(V(C)\cup V(P)),$ and hence $|X\cup Y|=|X| + |Y| - |X \cap Y| \le n'-4,$ so $\dfrac{n'}{2} < |X\cap Y|.$ Moreover, $|X\cap Y| \le n'-4.$

Notice that for every $w \in X \cap Y,$ we have that vw and $ww_3$ are not adjacent in $F_w,$ otherwise $T=(w,v,w_1,w_2,w_3,w)$ is an H-cycle, contradicting that v is not contained in an H-cycle of length at least 5.

In addition, for every $\{y_1,y_2\} \subseteq X \cap Y,$ $y_1y_2$ and $vy_1$ are not adjacent in $F_{y_1}$ or $y_1y_2$ and $vy_2$ are not adjacent in $F_{y_2},$ otherwise, $T=(y_2,y_1,v,w_1,w_2,w_3,y_2)$ is an H-cycle of length 6 containing v,  a contradiction. Therefore, $X \cap Y$ has the H-dependency property with respect to the vertex v.

By Proposition 8, there is a vertex $y \in X\cap Y$ with $k_y^{G[X\cap Y]} \le \dfrac{|X\cap Y| +1}{2},$ and since $|X\cap Y|>\frac{n'}{2}\ge \frac{|F|}{2}\ge \frac{n-1}{4}\ge 2,$ there is a vertex a in $X\cap Y$ such that ya and vy are in the same partite set of the $k_y$-partition of $V(G_y).$

Recall that V(C),  $X\cap Y$ and $\{v,w_3\}$ have no vertices in common and $|V(G)-V(C)|=n'.$

Hence, $k_y \le k_y^{G[X\cap Y]} + |V(G)- (V(C) \cup (X\cap Y) \cup \{v,w_3\})| \le \dfrac{|X\cap Y| +1}{2} + (n'-|X\cap Y| -2) \le n' - \dfrac{|X\cap Y|}{2}-\dfrac{3}{2} \le n' - \dfrac{\dfrac{n'}{2}}{2}-\dfrac{3}{2} \le \dfrac{3n'}{4}\le \dfrac{n}{2},$ a contradiction.

Case 2. $\{vx_1, vx_2, \ldots , vx_l\}$ is not an independent set in $G_v.$

For the proof of this case, we will consider 2 cases depending on whether $(v,x_i,x_{i+1})$ and $(v,x_i,x_{i-1})$ are H-paths or not.

Case 2.a There exists $i\in \{1,\ldots ,l\}$ such that $(v,x_i,x_{i+1})$ is an H-path, and there exists $j\in \{1,\ldots ,l\}$ such that $(v,x_j,x_{j-1})$ is an H-path.

Suppose, without loss of generality, that $vx_1$ and $vx_2$ are in different partite sets of $V(G_v),$ i.e., $vx_1$ and $vx_2$ are adjacent in $G_v.$

For the proof of Case 2.a, we will consider 4 cases depending on whether $(v,x_1,x_l)$ and $(v,x_2,x_3)$ are H-paths or not.

Case 2.a.1 $(v,x_1,x_l)$ and $(v,x_2,x_3)$ are H-paths.

In this case, $C'=(v,x_2)\cup (x_2,C,x_1)\cup (x_1,v)$ is an H-cycle of length at least 5 containing v,  a contradiction.

Case 2.a.2 $(v,x_1,x_l)$ is an H-path and $(v,x_2,x_3)$ is not an H-path.

Since $(v,x_2,x_3)$ is not an H-path, then $(v,x_2,x_1)$ is an H-path.

Then, by hypothesis of the Case 2, there is $i \in \{3,\ldots ,l\}$ such that $(v,x_i,x_{i+1})$ is an H-path.

Notice that if $i \in \{3,\ldots ,l-2\},$ then $C'=(v,x_i)\cup (x_i,C,x_1)\cup (x_1,v)$ or $C''=(v,x_i)\cup (x_i,C,x_2)\cup (x_2,v)$ is an H-cycle of length at least 5 containing v,  a contradiction. So, $i \in \{l-1,l\}$ and, for every $j \in \{3,\ldots ,l-2\},$ $(v,x_j,x_{j-1})$ is an H-path.

Claim 3

$(v,x_{l-1},x_l)$ is not an H-path.

Proof of Claim 3

Proceeding by contradiction, suppose that $(v,x_{l-1},x_l)$ is an H-path.

Consider the cycle $T=(v,x_2,x_3,v).$ Since $x_2$ is an obstruction of T and $x_3$ is not an obstruction of T,  it follows by hypothesis that v is not an obstruction of T. Hence, $vx_2$ and $vx_3$ are in different partite sets of $V(G_v).$ Since $G_v$ is a complete $k_v$-partite graph, we have that $x_2v$ and $x_{l-1}v$ are adjacent in $G_v$ or $x_3v$ and $x_{l-1}v$ are adjacent in $G_v.$ Therefore, either $C'=(v,x_2)\cup (x_2,C^{-1},x_l,x_{l-1})\cup (x_{l-1},v)$ or $C''=(v,x_3)\cup (x_3,C^{-1},x_l,x_{l-1})\cup (x_{l-1},v)$ is an H-cycle of length at least 5 containing v,  a contradiction. Therefore, $(v,x_{l-1},x_l)$ is not an H-path and the claim holds. $\square$

Claim 4

$(v,x_l,x_1)$ is not an H-path.

Proof of Claim 4

Proceeding by contradiction, suppose that $(v,x_l,x_1)$ is an H-path.

Consider the cycle $T=(v,x_3,x_4,v).$ Since $x_3$ is an obstruction of T and $x_4$ is not an obstruction of T,  it follows by hypothesis that v is not an obstruction of T. Hence, $vx_3$ and $vx_4$ are in different partite sets of $V(G_v).$ Since $G_v$ is a complete $k_v$-partite graph, we have that $x_3v$ and $x_lv$ are adjacent in $G_v$ or $x_3v$ and $x_lv$ are adjacent in $G_v.$ Therefore, either $C'=(v,x_3)\cup (x_3,C^{-1},x_1,x_l)\cup (x_l,v)$ or $C''=(v,x_4)\cup (x_4,C^{-1},x_1,x_l)\cup (x_l,v)$ is an H-cycle of length at least 5 containing v,  a contradiction. Therefore, $(v,x_l,x_1)$ is not an H-path and the claim holds. $\square$

Claim 5

$(v,x_1,x_2)$ is not an H-path.

Proof of Claim 5

Proceeding by contradiction, suppose that $(v,x_1,x_2)$ is an H-path.

Consider the cycle $T=(v,x_1,x_l,v).$ It follows by the assumption of the Case 2.a and Claim 4 that $x_1$ is not an obstruction of T and $x_l$ is an obstruction of T. So, by hypothesis, v is not an obstruction of T. Hence, $(v,x_1)\cup (x_1,C,x_l)\cup (x_l,v)$ is an H-cycle of length at least 5 containing v,  a contradiction. Therefore, $(v,x_1,x_2)$ is not an H-path and the claim holds. $\square$

Therefore, for every $i \in \{3,\ldots ,l\},$ $(v,x_i,x_{i+1})$ is not an H-path, a contradiction. So this case is not possible.

Case 2.a.3 $(v,x_1,x_l)$ is not an H-path and $(v,x_2,x_3)$ is an H-path.

By symmetry, we have that this case is similar to the Case 2.a.2. Therefore, the Case 2.a.3 lead us to a contradiction.

Case 2.a.4 $(v,x_1,x_l)$ is not H-path and $(v,x_2,x_3)$ is not an H-path.

If there exists $k\in \{4,\ldots ,l-1\}$ such that $(x_k,v,x_1)$ and $(x_k,v,x_2)$ are H-paths, then either $C'=(v,x_k)\cup (x_k,C^{-1},x_1)\cup (x_1,v)$ or $C''=(v,x_k)\cup (x_k,C,x_2)\cup (x_2,v)$ is an H-cycle of length at least 5 containing v,  a contradiction. So, for every $k\in \{4,\ldots ,l-1\},$ $(x_k,v,x_1)$ is not an H-path or $(x_k,v,x_2)$ is not an H-path.

Observation A. If $(x_k,v,x_1)$ is an H-path, for some $k\in \{4,\ldots ,l-1\},$ then $(v,x_k,x_{k-1})$ is not an H-path. Otherwise, if $(x_k,v,x_1)$ is an H-path, for some $k\in \{4,\ldots ,l-1\},$ and $(v,x_k,x_{k-1})$ is an H-path, then $C'=(v,x_1)\cup (x_1,C,x_k)\cup (x_k,v)$ is an H-cycle of length at least 5 containing v,  a contradiction.

Observation B. If $(x_k,v,x_2)$ is an H-path, for some $k\in \{4,\ldots ,l-1\},$ then $(v,x_k,x_{k+1})$ is not an H-path. Otherwise, if $(x_k,v,x_2)$ is an H-path, for some $k\in \{4,\ldots ,l-1\},$ and $(v,x_k,x_{k+1})$ is an H-path, then $C'=(v,x_k)\cup (x_k,C,x_2)\cup (x_2,v)$ is an H-cycle of length at least 5 containing v,  a contradiction.

The rest of the proof of this case is divided into 4 cases according to whether $\{vx_j, vx_{j+1}, vx_1\}$ and $\{vx_j, vx_{j+1}, vx_2\}$ are independent sets in $G_v$ or not.

Case 2.a.4.1 There exists $j \in \{4,\ldots ,l-2\}$ such that $\{vx_j, vx_{j+1}, vx_1\}$ is an independent set in $G_v.$

In this case, v is an obstruction of $(x_j,v,x_{j+1}).$ Moreover, by Observation A, we have that $x_j$ is an obstruction of $(v,x_j,x_{j+1})$ and $x_{j+1}$ is not an obstruction of $(v,x_{j+1},x_j).$ Hence, the cycle $(v,x_j,x_{j+1},v)$ has two obstructions, a contradiction.

Case 2.a.4.2 There exists $j \in \{4,\ldots ,l-2\}$ such that $\{vx_j, vx_{j+1}, vx_2\}$ is an independent set in $G_v.$

In this case, v is an obstruction of $(x_j,v,x_{j+1}).$ Moreover, by Observation B, we have that $x_{j+1}$ is an obstruction of $(v,x_{j+1},x_j)$ and $x_j$ is not an obstruction of $(v,x_j,x_{j+1}).$ Hence, the cycle $(v,x_j,x_{j+1},v)$ has two obstructions, a contradiction.

Case 2.a.4.3 $l > 6$ and there is no $j \in \{4,\ldots ,l-2\}$ such that $\{vx_j, vx_{j+1}, vx_2\}$ and $\{vx_j, vx_{j+1}, vx_1\}$ are independent sets in $G_v.$

Notice that $\{vx_4, vx_6, vx_1\}$ and $\{vx_5, vx_2\}$ are independent sets in $G_v$ or $\{vx_4, vx_6, vx_2\}$ and $\{vx_5, vx_1\}$ are independent sets in $G_v.$

If $\{vx_4, vx_6, vx_1\}$ and $\{vx_5, vx_2\}$ are independent sets in $G_v,$ then by applying Observations A and B, we can conclude that $(v,x_4,x_3)$ and $(v,x_5,x_6)$ are H-paths. Therefore, $C'= (v,x_5)\cup (x_5,C,x_4)\cup (x_4,v)$ is an H-cycle of length at least 5 containing v,  a contradiction.

If $\{vx_4, vx_6, vx_2\}$ and $\{vx_5, vx_1\}$ are independent sets in $G_v,$ then by applying Observations A and B, we can conclude that $(v,x_6,x_7)$ and $(v,x_5,x_4)$ are H-paths. Therefore, $C'= (v,x_6)\cup (x_6,C,x_5)\cup (x_5,v)$ is an H-cycle of length at least 5 passing through v,  a contradiction.

Case 2.a.4.4 $l=6,$ $\{vx_4,vx_5,vx_2\}$ is not an independent set in $G_v$ and $\{vx_4,vx_5,vx_1\}$ is not an independent set in $G_v.$

Since for each $i\in \{4,5\},$ $(x_i,v,x_1)$ is not an H-path or $(x_i,v,x_2)$ is not an H-path, we have that $\{vx_4, vx_1\}$ and $\{vx_5, vx_2\}$ are independent sets in $G_v$ or $\{vx_4, vx_2\}$ and $\{vx_5, vx_1\}$ are independent sets in $G_v.$

Whenever $\{vx_4, vx_1\}$ and $\{vx_5, vx_2\}$ are independent sets in $G_v,$ then by applying Observations A and B, we can conclude that $(v,x_4,x_3)$ and $(v,x_5,x_6)$ are H-paths. Therefore, $C'= (v,x_5,x_6,x_1,x_2,x_3,x_4,v)$ is an H-cycle of length at least 5 containing v,  a contradiction.

Whenever $\{vx_4, vx_2\}$ and $\{vx_5, vx_1\}$ are independent sets in $G_v,$ then by applying Observations A and B, we can conclude that $(v,x_4,x_3)$ and $(v,x_5,x_6)$ are H-paths. Recall that $(v,x_1,x_2)$ and $(v,x_2,x_1)$ are H-paths.

If $(x_6,v,x_1)$ is an H-path, then $(x_6,v,x_5)$ is an H-path. Hence, $C'=(v,x_1,x_2,x_3,x_4,x_5,x_6,v)$ or $C''=(v,x_6,x_1,x_2,x_3,x_4,x_5,v)$ is an H-cycle, a contradiction.

If $(x_6,v,x_1)$ is not an H-path, then $(x_6,v,x_5)$ is not an H-path. Then, either $(v,x_5,x_6,v)$ or $(v,x_6,x_1,v)$ is a cycle of length 3 with 2 obstructions, a contradiction.

Case 2.b For every i in $\{1,\ldots ,l\},$ $(v,x_i,x_{i+1})$ is not an H-path, or for every j in $\{1,\ldots ,l\},$ $(v,x_j,x_{j-1})$ is not an H-path.

Without loss of generality, suppose that for every i in $\{1,\ldots ,l\},$ $(v,x_i,x_{i+1})$ is not an H-path. Since for every i in $\{1,\ldots ,l\},$ $(v,x_i,x_{i+1})$ is not an H-path and $(x_{i-1},x_i,x_{i+1})$ is an H-path, then we have that $(v,x_i,x_{i-1})$ is an H-path. Moreover, for every i in $\{1,\ldots ,l\},$ $(x_i,v,x_{i+1})$ is an H-path, otherwise, the cycle $(v,x_i,x_{i+1},v)$ would have 2 obstructions (namely v and $x_{i+1}$), which is impossible.

Claim 6

V(C) has the H-dependency property with respect to the vertex v.

Proof of Claim 6

Proceeding by contradiction, suppose that V(C) has not the H-dependency property with respect to the vertex v,  that is, there exists a subset $\{x_i,x_j\}$ of V(C),  with $i<j,$ such that $(v,x_i,x_j)$ and $(v,x_j,x_i)$ are H-paths. Given that $(v,x_i,x_j)$ is an H-path and $(v,x_i,x_{i+1})$ is not an H-path, thus we have that $(x_j,x_i,x_{i+1})$ is an H-path, and by a similar argument, $(x_i,x_j,x_{j+1})$ is an H-path. Hence $C'=(v,x_j,x_i)\cup (x_i,C,x_{j-1})\cup (x_{j-1},v)$ and $C''=(v,x_i,x_j)\cup (x_j,C,x_{i-1})\cup (x_{i-1},v)$ are H-cycles in G,  and moreover, $\ell (C')+\ell (C'')=\ell (C)+4\ge 10.$ Therefore, $C'$ or $C''$ is an H-cycle of length at least 5 containing v,  a contradiction.

$\square$

Let $W=\{x\in V(G)-V(C):\text{ there } \text{ exists }\ j\in \{1,\ldots ,l\}\ \text{ such } \text{ that }\ (x,x_j,x_{j+1}) \text{ is } \text{ an }\ H\text{-path } \}.$ Notice that $v\notin W$ and possibly $W=\emptyset .$ Also, the index j in $\{1,\ldots , l\}$ such that $(x,x_j,x_{j+1})$ is an H-path is not necessarily unique.

Claim 7

For every w in W and for every index j in $\{1,\ldots ,l\}$ such that $(w,x_j,x_{j+1})$ is an H-path,  w is an obstruction of the path $(v,w,x_{j}).$

Proof of Claim 7

Let $w\in W$ and $j\in \{1,\ldots ,l\}$ be an index such that $(w,x_j,x_{j+1})$ is an H-path. Proceeding by contradiction, suppose that w is not an obstruction of the path $(v,w,x_{j}).$ Since $(x_{j-2},v,x_{j-1})$ is an H-path, thus $(x_{j-2},v,w)$ or $(x_{j-1},v,w)$ is an H-path; and recall that $(v,x_{j-2},x_{j-3})$ and $(v,x_{j-1},x_{j-2})$ are H-paths. Hence, $C'=(x_{j-2},v,w,x_{j})\cup (x_{j},C,x_{j-2})$ or $C''=(x_{j-1},v,w,x_{j})\cup (x_{j},C,x_{j-1})$ is an H-cycle containing v,  where $\ell (C')=\ell (C)+1> 5$ and $\ell (C'')=\ell (C)+2>5,$ which is impossible. $\square$

Claim 8

W has the H-dependency property with respect to the vertex v.

Proof of Claim 8

Proceeding by contradiction, suppose that W has not the H-dependency property with respect to the vertex v,  that is, there exists a subset $\{w,w'\}$ of W such that $(v,w,w')$ and $(v,w',w)$ are H-paths. Since w is in W,  it follows that there exists $j\in \{1,\ldots ,l\}$ such that $(w,x_j,x_{j+1})$ is an H-path, and by Claim 7, we have that w is an obstruction of the path $(v,w,x_j),$ thus vw and $wx_j$ are in the same partite set of $V(G_w).$ In addition, as $(v,w,w')$ is an H-path, it follows that vw and $ww'$ are in different partite sets of $V(G_w).$ Hence $w'w$ and $wx_j$ are in different partite sets of $V(G_w),$ that is, $(w',w,x_j)$ is an H-path. Since $(x_{j-2},v,x_{j-1})$ is an H-path, we have that $(x_{j-2},v,w')$ or $(x_{j-1},v,w')$ is an H-path, hence $C'=(x_{j-2},v,w',w,x_{j})\cup (x_{j},C,x_{j-2})$ or $C''=(x_{j-1},v,w',w,x_{j})\cup (x_{j},C,x_{j-1})$ is an H-cycle containing v,  where $\ell (C')=\ell (C)+2>5$ and $\ell (C'')=\ell (C)+3>5,$ a contradiction. $\square$

Claim 9

$V(C)\cup W$ has the H-dependency property with respect to the vertex v.

Proof of Claim 9

Let $\{w,x\}$ be a subset of $V(C)\cup W.$ Since V(C) and W have the H-dependency property with respect to the vertex v,  we can suppose that $w\in W$ and $x\in V(C),$ that is, $x=x_j$ for some j in $\{1,\ldots ,l\}.$ We will prove that $(v,x_j,w)$ is not an H-path or $(v,w,x_j)$ is not an H-path.

Supposing that $(v,x_j,w)$ is an H-path, and it suffices to prove that $(v,w,x_j)$ is not an H-path, that is, w is an obstruction of $(v,w,x_j).$ Given that $(v,x_j,w)$ is an H-path, it follows that $vx_j$ and $wx_j$ are in different partite sets of $V(G_{x_j}).$ Also, recall that $(v,x_j,x_{j+1})$ is not an H-path, which implies that $vx_j$ and $x_{j+1}x_j$ are in the same partite set of $V(G_{x_j}).$ Hence, $wx_j$ and $x_{j+1}x_j$ are in different partite sets of $V(G_{x_j}),$ thus $(w,x_j,x_{j+1})$ is an H-path. Therefore, by Claim 7, we have that w is an obstruction of $(v,w,x_j).$ Claim 9 holds. $\square$

Given that $V(C)\cup W$ has the H-dependency property with respect to the vertex v,  we have by Proposition 8 that there exists a vertex u in $V(C)\cup W$ such that $k_u^{D}\le \frac{|V(D)|}{2}\le \frac{|V(C)|+|W|+1}{2},$ where $D=G[V(C)\cup W],$ and since $|V(C)\cup W|\ge |V(C)|>2,$ it follows that $u'$ is an obstruction of $(v,u,u')$ for some $u'\in N_D(u).$

Recall that $G_u$ is a complete $k_u$-partite graph for some $k_u$ in ${\mathbb {N}}$ and $D_u$ is a complete $k_u^D$-partite graph for some $k_u^D$ in ${\mathbb {N}},$ with $k_u^D\le k_u.$ Moreover, if $\mathcal {P}=\{P_1^u,\ldots ,P_{k_u}^u\}$ is the $k_u$-partition of $V(G_u)$ into independent sets, then we can suppose without loss of generality that $\mathcal {Q}=\{P_i^u\cap V(D_u):P_i^u\cap V(D_u)\ne \emptyset ,i\in \{1,2,\ldots ,k_u\}\}=\{P_1^u\cap V(D_u),\ldots ,P_{k_u^D}^u\cap V(D_u)\}$ is the partition of $V(D_u)$ into independent sets.

Since u is an obstruction of $(v,u,u')$ for some $u'\in N_D(u),$ it follows that vu and $uu'$ are in the same partite set of the $k_u$-partition of $V(G_u).$ Since $u'\in N_D(u),$ we have that $uu'\in P_i^{u}\cap V(D_u)$ for some i in $\{1,\ldots ,k_u^D\},$ without loss of generality suppose that $uu'\in P_1^{u}\cap V(D_u),$ where $P_1^{u}\cap V(D_u)\subseteq P_1^{u}.$ Thus, it follows that $vu\in P_1^{u}.$

Claim 10

$k_u^D=k_u.$

Proof of Claim 10

Proceeding by contradiction, suppose that $k_u^D<k_u,$ thus there exists $uv'\in P_{k_u}^{u},$ which implies that $uv'\in V(G_u)-V(D_u),$ and $v'\in V(G)-V(D),$ where $V(D)=V(C)\cup W.$ Notice that $v\ne v',$ because $uv\in P_1^{u}$ and $uv'\in P_{k_u}^{u}.$

Given that $v'\notin W,$ it follows by the definition of the set W that for every i in $\{1,\ldots ,l\},$ $(v',x_i,x_{i+1})$ is not an H-path, thus $x_iv'$ and $x_i x_{i+1}$ are in the same partite set of the $k_{x_i}$-partition of $V(G_{x_i}).$ We claim that $u\in W$ (recall that $u\in V(C)\cup W$). Otherwise, if $u\in V(C),$ then $u=x_i$ for some i in $\{1,\ldots ,l\},$ and $uv'$ and $ux_{i+1}$ are in the same partite set of the $k_u$-partition of $V(G_u),$ which is a contradiction since $ux_{i+1}\in P_j^{u}$ for some j in $\{1,\ldots ,k_u^D\}$ and $uv'\in P_{k_u}^{u},$ with $j\le k_u^D< k_u.$

Since $u\in W,$ we have by the definition of the set W that there exists $i_u$ in $\{1,\ldots ,l\}$ such that $(u,x_{i_u},x_{i_{u}+1})$ is an H-path. Now, since $(v',x_{_{i_u -1}}, x_{_{i_u}})$ is not an H-path and $(x_{_{i_u -2}},x_{_{i_u -1}},x_{_{i_u}})$ is an H-path, we have that $(v',x_{_{i_u -1}},x_{_{i_u -2}})$ is an H-path. Notice that $(x_{_{i_u -1}},v',x_{_{i_u -2}})$ is an H-path, otherwise the cycle $(v',x_{_{i_u -1}},x_{_{i_u -2}},v')$ would have 2 obstructions (namely $v'$ and $x_{_{i_u -2}}$), which is impossible. As $(x_{_{i_u -1}},v',x_{_{i_u -2}})$ is an H-path, it follows that $(x_{_{i_u -2}},v',u)$ or $(x_{_{i_u -1}},v',u)$ is an H-path. Hence $C'=(x_{_{i_u -2}},v',u,x_{_{i_u}})\cup (x_{_{i_u}},C,x_{_{i_u -2}})$ or $C''=(x_{_{i_u -1}},v',u,x_{_{i_u}})\cup (x_{_{i_u}},C,x_{_{i_u -1}})$ is an H-cycle, where $\ell (C')=\ell (C)+1>\ell (C)$ and $\ell (C'')=\ell (C)+2>\ell (C),$ which is impossible because C is an H-cycle of maximum length in G. $\square$

Finally, $k_u=k_u^D\le \frac{|V(C)|+|W|+1}{2}\le \frac{n}{2}<\frac{n+1}{2},$ a contradiction. $\square$

Recall that in an edge-colored graph G and for every vertex x in V(G),  we define the color degree of the vertex x,  denoted by $\delta ^c(x),$ as $|\{c(xv):v\in N_G(x)\}|.$

Proposition 10

If H is a complete graph without loops and G is an H-colored graph,  then

• 1. For every vertex x in V(G),  $G_x$ is a complete $k_x$-partite graph for some $k_x$ in ${\mathbb {N}},$ and moreover,  $k_x=\delta ^c(x),$

• 2. If W is a walk,  then W is an H-walk if and only if W is a properly colored walk. In particular,  W is an H-path (H-cycle) if and only if W is a properly colored path (cycle).

• 3. G has no cycles of length 3 with exactly 2 obstructions.

Proof

Let H be a complete graph without loops and G an H-colored graph.

1. Let x be a vertex of G,  and suppose that $\{c(xv):v\in N_G(x)\}=\{1,\ldots ,\delta ^c(x)\}.$ For every i in $\{1,\ldots ,\delta ^c(x)\},$ we define $V_i=\{xv \in E(G) :c(xv)=i\}.$ Since H is a complete graph without loops, we have that $ab\in E(G_x)$ if and only if $a\in V_i$ and $b\in V_j,$ for some $\{i,j\}$ subset of $\{1,\ldots ,\delta ^c(x)\},$ with $i\ne j.$ Therefore, $G_x$ is a complete $k_x$-partite graph, with $k_x=\delta ^c(x).$

2. It follows directly from the definitions.

3. Proceeding by contradiction, suppose that G has a cycle of length 3 with exactly 2 obstructions, say $C=(u,v,w,u)$ with u and v obstructions of C. Since u is an obstruction of C,  it follows that $c(uv)c(uw)\notin E(H),$ and as H is a complete graph without loops, $c(uv)=c(uw).$ Using a similar argument, $c(vu)=c(vw),$ which implies that $c(wu)=c(wv).$ Thus, $c(wu)c(wv)\notin E(H),$ that is, w is an obstruction of C,  which is impossible. $\square$

In the particular case when H is a complete graph without loops, we obtain Theorem 2 as a direct consequence of Theorem 9 and Proposition 10.

The following construction shows how to construct an H-coloring of a complete graph $K_n,$ with n an odd number, where H is not a complete k-partite graph and $K_n$ fulfills the hypotheses of Theorem 9.

Construction 1. Let $n=2k+1,$ $K_n$ be the complete graph of order n with set vertex $\{v_1,\ldots ,v_n\}$ and $H_n$ a graph defined as follows: $V(H_n)=\{x_1,x_2,\ldots ,x_n\},$ and $x_j$ is adjacent to $x_i,$ $i < j,$ if and only if $i=1$ or $j-i \le k.$ Color the edges of $K_n$ with the following H-coloring:

$$\begin{aligned} c(v_iv_j)= \left\{ \begin{array}{ll} x_1 &{} \quad \text {if}\ v_iv_j=v_1v_n \\ x_{\lceil \frac{i+j}{2} \rceil } &{}\quad \text {otherwise}. \end{array} \right. \end{aligned}$$

An example of this construction is illustrated in Fig. 1.

Fig. 1

Example of an H-coloring of a complete graph of order 13 that fulfills the hypothesis of Theorem 9

We think that Theorem 9 is still true if we remove the second hypothesis.

Conjecture 11

Let G be an H-colored complete graph of order n,  with $n \ge 13,$ such that for every x in V(G),  $G_x$ is a complete $k_x$-partite graph for some $k_x \ge 2.$ If for every x in V(G),  $k_x \ge \dfrac{n+1}{2},$ then every vertex of G is contained in an H-cycle of length at least 5.

If Conjecture 11 is true, then the following results follows immediately: Let G be an H-colored complete graph of order n,  with $n \ge 13.$ If for every x in V(G),  $G_x$ has a complete $k_x$-partite spanning subgraph, for some $k_x \ge \dfrac{n+1}{2},$ then every vertex of G is contained in an H-cycle of length at least 5.