On the spectra and spectral radii of token graphs

Abstract

Let G be a graph on n vertices. The k-token graph (or symmetric k-th power) of G, denoted by $F_k(G)$, has as vertices the ${n\atopwithdelims ()k}$ k-subsets of vertices from G, and two vertices are adjacent when their symmetric difference is a pair of adjacent vertices in G. In particular, $F_k(K_n)$ is the Johnson graph J(n, k), which is a distance-regular graph used in coding theory. In this paper, we present some results concerning the (adjacency and Laplacian) spectrum of $F_k(G)$ in terms of the spectrum of G. For instance, when G is walk-regular, an exact value for the spectral radius $\rho$ (or maximum eigenvalue) of $F_k(G)$ is obtained. When G is distance-regular, other eigenvalues of its 2-token graph are derived using the theory of equitable partitions. A generalization of Aldous’ spectral gap conjecture (which is now a theorem) is proposed.

1 Introduction

For a (simple and connected) graph $G=(V,E)$ with adjacency matrix $\varvec{A}$, its local spectrum at vertex u plays a role similar to the (standard adjacency) spectrum when the graph is ‘seen’ from vertex u. For instance, the local spectra of G, for every $u\in V$, were used by Fiol and Garriga [15] to prove the so-called ‘spectral excess theorem’, which gives a quasi-spectral characterization of distance-regular graphs. In turn, this result was the crucial tool for the discovery, by van Dam and Koolen [11], of the first known family of non-vertex-transitive distance-regular graphs with unbounded diameter. Besides, Fiol et al. [17] used the local spectra to define the local predistance polynomials, which were used to characterize a general kind of local distance regularity (intended for not necessarily regular graphs).

One of the most important parameters in spectral graph theory is the index or spectral radius of a graph, which corresponds to the largest eigenvalue of its adjacency matrix. This parameter has special relevance in the study of many integer-valued graph invariants, such as the diameter, the radius, the domination number, the matching number, the clique number, the independence number, the chromatic number, or the sequence of vertex degrees. In turn, this leads to studying the structure of graphs having an extremal spectral radius and fixed values of some of such parameters. See Brualdi et al. [5, Cap. 3].

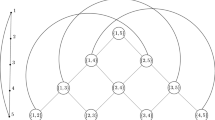
In this work, we use some information given by the local spectra to obtain new results about the spectral radius of an ample family of graphs, which are known as token graphs or symmetric kth powers, defined as follows. For a given integer k, with $1\le k \le n$ (where n is the order of G), the k-token graph $F_k(G)$ of G is the graph whose vertex set $V (F_k(G))$ consists of the ${n \atopwithdelims ()k}$ k-subsets of vertices of G, and two vertices A and B of $F_k(G)$ are adjacent whenever their symmetric difference $A \bigtriangleup B$ is a pair $\{a,b\}$ such that $a\in A$, $b\in B$, and $\{a,b\}\in E(G)$. In Fig. 1, we show the 2-token graph of the cycle $C_9$ on 9 vertices. In particular, if $k=1$, then $F_1(G)\cong G$; and if G is the complete graph $K_n$, then $F_k(K_n)\cong J(n,k)$, where J(n, k) denotes the Johnson graph; see Fabila-Monroy et al. [13].

The name ‘token graph’ also comes from the observation in [13] that vertices of $F_k(G)$ correspond to configurations of k indistinguishable tokens placed at distinct vertices of G, where two configurations are adjacent whenever one configuration can be reached from the other by moving one token along an edge from its current position to an unoccupied vertex. Such graphs are also called symmetric k-th power of a graph in Audenaert et al. [2]; and n-tuple vertex graphs in Alavi et al. [1]. They have applications in physics; a connection between symmetric powers of graphs and the exchange of Hamiltonian operators in quantum mechanics is given in [2]. Our interest is in relation to the graph isomorphism problem. It is well known that there are cospectral non-isomorphic graphs, where often the spectrum of the adjacency matrix of a graph is used. For instance, Rudolph [27] showed that there are cospectral non-isomorphic graphs that can be distinguished by the adjacency spectra of their 2-token graphs, and he also gave an example for the Laplacian spectrum. Audenaert et al. [2] also proved that 2-token graphs of strongly regular graphs with the same parameters are cospectral and also derived bounds on the (adjacency and Laplacian) eigenvalues of $F_2(G)$ for general graphs. For more information, see again [2] or [13].

What can be said about the spectrum of $F_k(G)$? The three main results that we want to recall are the following.

Theorem 1.1

(Audenaert et al. [2]) All the strongly regular graphs with the same parameters have cospectral symmetric squares (or 2-token graphs).

Theorem 1.2

(Dalfó et al. [9]) For any graph G on n vertices, the Laplacian spectrum of its h-token graph is contained in the Laplacian spectrum of its k-token graph for every $1\le h\le k\le n/2$.

Theorem 1.3

(Lew [23]) Let G have Laplacian eigenvalues $\lambda _1(=0)<\lambda _2\le \cdots \le \lambda _n$. Let $\lambda$ be an eigenvalue of $F_k(G)$ not in $F_{k-1}(G)$. Then

$$\begin{aligned} k(\lambda _2-k+1)\le \lambda \le k\lambda _n, \end{aligned}$$

(1)

and both bounds are tight.

In fact, the lower bound in (1) was first proved by Dalfó et al. in [26, Ths. 3.5-3.6].

Fig. 1

The 2-token graph $F_2(C_9)$ of the cycle graph with vertex set $V(C_{9})={\mathbb {Z}}_9$. The vertices inducing a circumference (in dashed line) of radius $r_{\ell }$, with $\ell =1,2,3,4$ and $r_1>r_2>r_3>r_4$ are ij with ${{\,\textrm{dist}\,}}(i,j)=\ell$ in $C_9$

In this paper, we mainly derive new results about the spectral radius of token graphs, and it is organized as follows. The next section begins with some basic concepts, definitions, and results. More precisely, we recall some known results about the local spectra and derive the basic tools for computing the spectral radius. In Sect. 3, we introduce the new concepts of k-algebraic connectivity and k-spectral radius. There, we study some of their properties and propose a generalization of Aldou’s spectral gap conjecture, already a theorem (see Caputo et al. [7]). In Sect. 4, we give both lower and upper bounds for the spectral radius of a token graph, which are shown to be asymptotically tight. In the same section, we present some infinite families in which the exact values of the spectral radius are obtained. Finally, in the last section, we deal with the case of distance-regular and strongly regular graphs, where two results are presented in the form of Audenaert et al.’s result [2] and Lew’s result [23].

2 Preliminaries

2.1 Graphs and their spectra

Let G be a (simple and connected) graph with vertex set $V(G)=\{1,2,\ldots ,n\}$ and edge set E(G). Let G have adjacency matrix $\varvec{A}$, and spectrum

$$\begin{aligned} {{\,\textrm{sp}\,}}G\equiv {{\,\textrm{sp}\,}}\varvec{A}=\{\theta _0^{m_0},\theta _1^{m_1},\ldots ,\theta _d^{m_d}\}, \end{aligned}$$

where $\theta _0>\theta _1>\cdots >\theta _d$. Thus, by the Perron–Frobenius theorem, G has spectral radius $\rho (G)=\theta _0$.

Let $\varvec{L}=\varvec{D}-\varvec{A}$ be the Laplacian matrix of G, with eigenvalues

$$\begin{aligned} \lambda _1(=0)<\lambda _2\le \cdots \le \lambda _n. \end{aligned}$$

Recall that $\lambda _2$ is the algebraic connectivity, and $\varvec{D}$ is the diagonal matrix whose diagonal entries are the vertex degrees of G.

2.2 The local spectra of a graph

Let G have different eigenvalues $\theta _0>\cdots >\theta _d$, with respective multiplicities $m_0,\ldots ,m_d$. If $\varvec{U}_i$ is the $n\times m_i$ matrix whose columns are the orthonormal eigenvectors of $\theta _i$, the matrix $\varvec{E}_i=\varvec{U}_i\varvec{U}_i^{\top }$, for $i=0,1,\dots ,d$, is the (principal) idempotent of $\varvec{A}$ and represents the orthogonal projection of ${\mathbb {R}}^n$ onto the eigenspace ${{\,\textrm{Ker}\,}}(\varvec{A}-\theta _i \varvec{I})$. The (u-)local multiplicities of the eigenvalue $\theta _i$ are defined as

$$\begin{aligned} m_u(\theta _i) = \Vert \varvec{E}_i\varvec{e}_u\Vert ^2 = \langle \varvec{E}_i\varvec{e}_u,\varvec{e}_u\rangle = (\varvec{E}_i)_{uu}\qquad \hbox {for }\, u\in V\, \hbox { and } \,i =0,1,\dots ,d, \end{aligned}$$

where $\varvec{e}_u$ is the n-dimensional vector with a 1 in the uth entry and zeros elsewhere. In particular, $m_u(\theta _0)=v_{u}^2>0$, where $\varvec{v}$ is the corresponding normalized Perron eigenvector, that is, the eigenvector that can be chosen to have strictly positive components. Although the local multiplicities are, of course, not necessarily integers, they have nice properties when the graph is studied from a vertex, so justifying their name. Thus, they satisfy $\sum _{i=0}^d m_u(\theta _i) = 1$ and $\sum _{u\in V} m_u(\theta _i) =m_i$, for $i=0,1,\dots ,d$. The number $a_{uu}^{(\ell )}$ of closed walks of length $\ell$ rooted at vertex u can be computed as

$$\begin{aligned} a_{uu}^{(\ell )}=\sum _{i=0}^d m_{u}(\theta _i) \theta _i^{\ell } \end{aligned}$$

(2)

(see Fiol et al. [17, Corollary 2.2]). By picking up the eigenvalues $\theta _i$ with non-null local multiplicities, $\mu _0(=\theta _0)>\mu _1>\cdots >\mu _{d_u}$, we define the (u-)local spectrum of G as

$$\begin{aligned} {{\,\textrm{sp}\,}}_u G:= \left\{ \mu _0^{m_{u}(\mu _0)},\mu _1^{m_{u}(\mu _1)},\ldots ,\mu _{d_u}^{m_{u}(\mu _{d_u})}\right\} , \end{aligned}$$

with (u-)local mesh, or set of distinct eigenvalues, ${{\,\textrm{ev}\,}}_u G:=\{\mu _0>\mu _1>\cdots >\mu _{d_u}\}$. The eccentricity of a vertex u satisfies an upper bound similar to that satisfied by the diameter of G in terms of its distinct eigenvalues. More precisely

$$\begin{aligned} {{\,\textrm{ecc}\,}}(u) \le d_u=|{{\,\textrm{ev}\,}}_u G|-1. \end{aligned}$$

(3)

In coding theory, $d_u$ corresponds to the so-called ‘dual degree’ of the trivial code $\{u\}$. For more information, see Fiol et al. [17].

We use the following lemma to prove the results of Sect. 4. Notice that this is just a reformulation of the power method in terms of the number of walks given by (2).

Lemma 2.1

Let G be a finite graph with different eigenvalues $\theta _0>\cdots > \theta _d$. Let $a^{(\ell )}_u$ be the number of $\ell$-walks starting from (any fixed) vertex u, and let $a^{(\ell )}_{uu}$ be the number of closed $\ell$-walks rooted at u. Then

$$\begin{aligned} \rho (G)=\lim _{\ell \rightarrow \infty } \root \ell \of {a^{(\ell )}_u}=\lim _{\ell \rightarrow \infty } {{\,\textrm{sup}\,}}\root \ell \of {a^{(\ell )}_{uu}}, \end{aligned}$$

where $`{{\,\textrm{sup}\,}}$’ denotes the supremum.

Proof

We only prove that $\rho (G)$ equals the second limit (the other equality proved similarly). Using (2)

$$\begin{aligned} a_{uu}^{(\ell )}&=\sum _{i=0}^d m_{u}(\theta _i) \theta _i^{\ell } = \theta _0^{\ell }\left( m_{u}(\theta _0) + m_{u}(\theta _1)\left( \frac{\theta _1}{\theta _0}\right) ^{\ell } +\cdots + m_{u}(\theta _d)\left( \frac{\theta _d}{\theta _0}\right) ^{\ell }\right) \\&\quad {\mathop {\longrightarrow }\limits ^{\ell \rightarrow \infty }} \left\{ \begin{array}{cl} 2\theta _0^{\ell } m_u(\theta _0) &{}\quad \hbox {if}\, G\, \hbox {is bipartite and}\, \ell \,\hbox {is even}, \\ 0 &{}\quad \hbox {if }\,G \,\hbox {is bipartite and}\, \ell \, \hbox {is odd,}\\ \theta _0^{\ell }m_u(\theta _0) &{}\quad \hbox {otherwise,} \end{array} \right. \end{aligned}$$

where we used that $m_u(\theta _0)>0$ and $\theta _0>|\theta _i|$ for every $i\ne 0$, except when G is bipartite, in which case $\theta _d=-\theta _0$ and $m_u(\theta _d)=m_u(\theta _0)$. Thus, the result holds by taking $\ell$-th roots. $\square$

2.3 Regular partitions and their spectra

Dealing with a regular partition is a useful method in graph theory, as it allows us to obtain some information about a graph considering a smaller version of it (the so-called ‘quotient graph’). Besides, if we consider a graph G and a group of automorphisms $\Gamma$, then a partition of the vertices of the graph into orbits by $\Gamma$ is a regular partition.

Let $G=(V,E)$ be a graph with vertex set $V=V(G)$, adjacency matrix $\varvec{A}$, and Laplacian matrix $\varvec{L}$. A partition $\pi$ of its vertex set V into r cells $C_1,C_2,\ldots ,C_r$ is called regular (or equitable) whenever, for any $i,j=1,\ldots ,r$, the intersection numbers $b_{ij}(u)=|G(u)\cap C_j|$ (where $u\in C_i$, and G(u) is the set of vertices that are neighbors of the vertex u) do not depend on the vertex u but only on the cells $C_i$ and $C_j$. In this case, such numbers are simply written as $b_{ij}$, and the $r\times r$ matrices $\varvec{Q}_A=\varvec{A}(G/\pi )$ and $\varvec{Q}_L=\varvec{L}(G/\pi )$ with entries $(\varvec{Q}_A)_{ij}=b_{ij}$ and

$$\begin{aligned} \textstyle (\varvec{Q}_L)_{ij}=\left\{ \begin{array}{ll} -b_{ij} &{}\quad \hbox {if }\, i\ne j,\\ b_{ii}-\displaystyle \sum _{j=1}^r b_{ij} &{}\quad \hbox {if }\, i=j, \end{array} \right. \end{aligned}$$

(4)

are, respectively, referred to as the quotient matrix and quotient Laplacian matrix of G with respect to $\pi$. In turn, these matrices correspond to the quotient (weighted) directed graph $G/\pi$, whose vertices representing the r cells, and there is an arc with weight $b_{ij}$ from vertex $C_i$ to vertex $C_j$ if and only if $b_{ij}\ne 0$. Of course, if $b_{ii}>0$, for some $i=1,\ldots ,r$, the quotient graph (or digraph) $G/\pi$ has loops. Given a partition $\pi$ of V with r cells, let $\varvec{S}$ be the characteristic matrix of $\pi$, that is, the $n\times r$ times matrix whose columns are the characteristic vectors of the cells of $\pi$. Then, $\pi$ is a regular partition if and only if $\varvec{A}\varvec{S}=\varvec{S}\varvec{Q}_A$ or $\varvec{L}\varvec{S}=\varvec{S}\varvec{Q}_L$. Moreover

$$\begin{aligned} \varvec{Q}_A=(\varvec{S}^{\top }\varvec{S})^{-1}\varvec{S}^{\top }\varvec{A}\varvec{S},\quad \hbox {and}\quad \varvec{Q}_L=(\varvec{S}^{\top }\varvec{S})^{-1}\varvec{S}^{\top }\varvec{L}\varvec{S}. \end{aligned}$$

Thus, there is a strong analogy with similar results satisfied by the Laplacian matrices of the h-token graph and k-token graph of G for $h\le k$. More precisely, we have the following statements (Those numbered with 1 can be found in Godsil [19, 20]. The statements in 2 are derived similarly to those in number 1 when we use the quotient Laplacian matrix, defined in (4), instead of the standard quotient matrix. Finally, the statements in 3 follow from the results given by Dalfó et al. in [9].):

• 1. If $\pi$ is a regular partition with characteristic matrix $\varvec{S}$ and quotient matrix $\varvec{Q}_A=\varvec{A}(G/\pi )$, then

  • (a) $\varvec{A}\varvec{S}=\varvec{S}\varvec{Q}_A$.

  • (b) $\varvec{Q}_A=(\varvec{S}^{\top }\varvec{S})^{-1}\varvec{S}^{\top }\varvec{A}\varvec{S}$.

  • (c) The column space (and its orthogonal complement) of $\varvec{S}$ is $\varvec{A}$-invariant.

  • (d) The characteristic polynomial of $\varvec{Q}_A$ divides the characteristic polynomial of $\varvec{A}$. Thus, ${{\,\textrm{sp}\,}}\varvec{Q}_A \subseteq {{\,\textrm{sp}\,}}\varvec{A}$.

  • (e) If $\varvec{v}$ is an eigenvector of $\varvec{Q}_A$ with eigenvalue $\lambda$, then $\varvec{S}\varvec{v}$ is an eigenvector of $\varvec{A}$ with the same eigenvalue. (The eigenvector $\varvec{v}$ of $\varvec{Q}_A$ ‘lifts’ to an eigenvector of $\varvec{A}$.)

  • (f) If $\varvec{v}$ is an eigenvector of $\varvec{A}$ with eigenvalue $\lambda$ and $\varvec{S}^{\top }\varvec{v}\ne \varvec{0}$, then $\varvec{S}^{\top }\varvec{v}$ is an eigenvector of $\varvec{Q}_A$ with the same eigenvalue.

• 2. If $\pi$ is a regular partition with characteristic matrix $\varvec{S}$ and quotient Laplacian matrix $\varvec{Q}_L=\varvec{L}(G/\pi )$, then

  • (a) $\varvec{L}\varvec{S}=\varvec{S}\varvec{Q}_L$.

  • (b) $\varvec{Q}_L=(\varvec{S}^{\top }\varvec{S})^{-1}\varvec{S}^{\top }\varvec{L}\varvec{S}$.

  • (c) The column space (and its orthogonal complement) of $\varvec{S}$ is $\varvec{L}$-invariant.

  • (d) The characteristic polynomial of $\varvec{Q}_L$ divides the characteristic polynomial of $\varvec{L}$. Thus, ${{\,\textrm{sp}\,}}\varvec{Q}_L \subseteq {{\,\textrm{sp}\,}}\varvec{L}$.

  • (e) If $\varvec{v}$ is an eigenvector of $\varvec{Q}_L$ with eigenvalue $\lambda$, then $\varvec{S}\varvec{v}$ is an eigenvector of $\varvec{L}$ with the same eigenvalue.

  • (f) If $\varvec{v}$ is an eigenvector of $\varvec{L}$ with eigenvalue $\lambda$ and $\varvec{S}^{\top }\varvec{v}\ne \varvec{0}$, then $\varvec{S}^{\top }\varvec{v}$ is an eigenvector of $\varvec{Q}_L$ with the same eigenvalue.

• 3. Let $\varvec{L}_h=\varvec{L}(F_h(G))$ and $\varvec{L}_k=\varvec{L}(F_k(G))$ be, respectively, the Laplacian matrices of the h-token and k-token graphs of G, for $h\le k$, and let $\varvec{S}_b$ be the (k, h)-binomial matrix. This is a ${n \atopwithdelims ()k}\times {n \atopwithdelims ()h}$ matrix whose rows are indexed by the k-subsets of $A\subset [n]$, and its columns are indexed by the h-subsets of $X\subset [n]$, with entries

  $$\begin{aligned} (\varvec{S}_b)_{AX}= \left\{ \begin{array}{ll} 1 &{} \hbox {if } \,X\subset A,\\ 0 &{} \hbox {otherwise.} \end{array} \right. \end{aligned}$$

  Then

  • (a) $\varvec{L}_k\varvec{S}_b=\varvec{S}_b\varvec{L}_h$.

  • (b) $\varvec{L}_h=(\varvec{S}_b^{\top }\varvec{S}_b)^{-1}\varvec{S}_b^{\top }\varvec{L}_k\varvec{S}_b$.

  • (c) The column space (and its orthogonal complement) of $\varvec{S}_b$ is $\varvec{L}_k$-invariant.

  • (d) The characteristic polynomial of $\varvec{L}_h$ divides the characteristic polynomial of $\varvec{L}_k$. Thus, ${{\,\textrm{sp}\,}}\varvec{L}_h \subseteq {{\,\textrm{sp}\,}}\varvec{L}_k$.

  • (e) If $\varvec{v}$ is an eigenvector of $\varvec{L}_h$ with eigenvalue $\lambda$, then $\varvec{S}_b\varvec{v}$ is an eigenvector of $\varvec{L}_k$ with eigenvalue $\lambda$.

  • (f) If $\varvec{v}$ is an eigenvector of $\varvec{L}_k$ with eigenvalue $\lambda$ and $\varvec{S}_b^{\top }\varvec{v}\ne \varvec{0}$, then $\varvec{S}_b^{\top }\varvec{v}$ is an eigenvector of $\varvec{L}_h$ with the same eigenvalue.

2.4 Walk-regular graphs

Let $a_u^{({\ell })}$ denote the number of closed walks of length ${\ell }$ rooted at vertex u, that is, $a_u^{({\ell })}=a_{uu}^{({\ell })}$. If these numbers only depend on ${\ell }$, for each $\ell \ge 0$, then G is called walk-regular, a concept introduced by Godsil and McKay in [21].

Notice that, as $a_u^{(2)}=\delta _u$, the degree of vertex u, a walk-regular graph is necessarily regular.

Moreover, a graph G is called spectrally regular when all vertices have the same local spectrum: ${{\,\textrm{sp}\,}}_u G={{\,\textrm{sp}\,}}_v G$ for any $u,v\in V$. The following result (in Delorme and Tillich [12], Fiol and Garriga [16], and also Godsil and McKay [21]) provides some characterizations of such graphs.

Lemma 2.2

[12, 16, 21] Let $G=(V,E)$ be a graph. The following statements are equivalent.

• (i) G is walk-regular.

• (ii) G is spectrally regular.

• (iii) The spectra of the vertex-deleted subgraphs are all equal: ${{\,\textrm{sp}\,}}\, (G{\setminus } u)={{\,\textrm{sp}\,}}\, (G{\setminus } v)$ for any $u,v\in V$.

3 The k-algebraic connectivity and k-spectral radius

In this section, we always consider the Laplacian spectrum. Let G be a graph on n vertices, and $F_k(G)$ its k-token graph for $k\in \{0,1,\ldots ,n\}$. Note that $F_k(G)\cong F_{n-k}(G)$, where, by convenience, $F_0(G)\cong F_n(G)=K_1$ (a singleton). Moreover, $F_1(G)\cong G$. From Dalfó et al. [9], it is known that the Laplacian spectra of the token graphs of G satisfy

$$\begin{aligned} \{0\}={{\,\textrm{sp}\,}}F_0(G)\subset {{\,\textrm{sp}\,}}F_1(G)\subset {{\,\textrm{sp}\,}}F_2(G)\subset \cdots \subset {{\,\textrm{sp}\,}}F_{\lfloor n/2\rfloor }(G). \end{aligned}$$

(5)

Let us denote $\alpha (G)$ and $\rho (G)$ the algebraic connectivity (see Fiedler [18]) and the spectral radius of a graph G, respectively. Then, from (5), we have

$$\begin{aligned} \alpha (G)&\ge \alpha (F_2(G))\ge \cdots \ge \alpha (F_ {\lfloor n/2\rfloor }(G)), \end{aligned}$$

(6)

$$\begin{aligned} \rho (G)&\le \rho (F_2(G))\le \cdots \le \rho (F_{\lfloor n/2\rfloor }(G)). \end{aligned}$$

(7)

The concepts of algebraic connectivity and spectral radius, together with (5)–(7) suggest the following definitions.

Definition 3.1

Given a graph G on n vertices and an integer k, such that $1\le k\le \lfloor n/2\rfloor$, the k-algebraic connectivity $\alpha _k=\alpha _k(G)$ and the k-spectral radius $\rho _k=\rho _k(G)$ of G are, respectively, the minimum and maximum eigenvalues of the multiset ${{\,\textrm{sp}\,}}F_k(G){\setminus } {{\,\textrm{sp}\,}}F_{k-1}(G)$.

Notice that, since ${n\atopwithdelims ()k}>{n\atopwithdelims ()k-1}$ for $1\le k\le \lfloor n/2\rfloor$, the parameters $\alpha _k$ and $\rho _k$ always exist.

For instance, with $G=P_6$, the path on 6 vertices, we have (approximately)

$$\begin{aligned} \alpha _1(P_6)=0.2679,\quad \alpha _2(P_6)=0.5727,\quad \alpha _3(P_6)=0.9302, \end{aligned}$$

and

$$\begin{aligned} \rho _1(P_6)=3.7320,\quad \rho _2(P_6)=6.504,\quad \rho _3(P_6)=7.4871, \end{aligned}$$

whereas for $G=C_7$, the cycle on 7 vertices, we get

$$\begin{aligned} \alpha _1(C_7)=0.7530,\quad \alpha _2(C_7)=1.1633,\quad \alpha _3(C_7)=1.2696. \end{aligned}$$

Moreover, from these definitions, the following facts hold:

• (i) $\rho _k(G)\ge \alpha _k(G)\ge 0$.

• (ii) $\alpha _1(G)=\alpha (G)$ (the standard algebraic connectivity of G) and $\rho _1(G)=\rho (G)$ (the standard spectral radius of G).

• (iii) Since $F_k(K_n)\cong J(n,k)$ (the Johnson graph), we have

  $$\begin{aligned} \alpha _k(K_n)=\rho _k(K_n)=k(n+1-k), \qquad k=1,\ldots ,\lfloor n/2\rfloor . \end{aligned}$$

  In particular, $\alpha _1(K_n)=\rho _1(K_n)=n$, $\alpha _2(K_n)=\rho _2(K_n)=2(n-1)$, and so on.

The equalities in (iii) come from the fact that the Johnson graph J(n, k) has different Laplacian eigenvalues $\lambda _j=j(n+1-k)$, with multiplicities $m_j={n\atopwithdelims ()j}-{n\atopwithdelims ()j-1}$ for $j=0,1,\ldots ,k$.

From what is known about token graphs, we can suggest some conjectures and state some results, as follows.

Conjecture 3.2

For any graph G

$$\begin{aligned} \alpha _1(G)\le \alpha _2(G)\le \cdots \le \alpha _{\lfloor n/2\rfloor }(G). \end{aligned}$$

Because of (6), if Conjecture 3.2 holds, also does the conjecture proposed in [9], that is, $\alpha (F_k(G))=\alpha (G)$ for any $k\le n/2$. In fact, the last equality follows from the proof of Aldous’ spectral gap conjecture given by Caputo et al. in [7]. By this result, what we can state is that $\min \{\alpha _2,\ldots , \alpha _{\lfloor n/2\rfloor }\}\ge \alpha _1.$

Conjecture 3.3

For any graph G

$$\begin{aligned} \rho _1(G)\le \rho _2(G)\le \cdots \le \rho _{\lfloor n/2\rfloor }(G). \end{aligned}$$

Notice that, from (7), if this conjecture holds, then $\rho _k(G)=\rho (F_k(G))$ for any $k\le n/2$.

Lemma 3.4

For any graph G and its complementary graph ${\overline{G}}$, the k-algebraic connectivity and k-spectral radius of ${\overline{G}}$ satisfy

$$\begin{aligned} \alpha _k(G)+\rho _k({\overline{G}})=k(n-k+1). \end{aligned}$$

Proof

It was proved in [9] that each eigenvalue of J(n, k) is the sum of one eigenvalue of $F_k(G)$ and one eigenvalue of $F_k({\overline{G}})$. Then, from (5), the eigenvalues of ${{\,\textrm{sp}\,}}F_k(G){\setminus } {{\,\textrm{sp}\,}}F_{k-1}(G)$ and ${{\,\textrm{sp}\,}}F_k({\overline{G}}){\setminus } {{\,\textrm{sp}\,}}F_{k-1}({\overline{G}})$ must be paired in such a way that their sums are all equal to the ‘new’ eigenvalue of ${{\,\textrm{sp}\,}}F_k(J(n,k)){\setminus } {{\,\textrm{sp}\,}}F_{k-1}(J(n,k))$, which is $k(n-k+1)$. In particular, this happens with the minimum eigenvalue of ${{\,\textrm{sp}\,}}F_k(G){\setminus } {{\,\textrm{sp}\,}}F_{k-1}(G)$, $\alpha _k(G)$ and the maximum eigenvalue of ${{\,\textrm{sp}\,}}F_k({\overline{G}}){\setminus } {{\,\textrm{sp}\,}}F_{k-1}(({\overline{G}})$, $\rho _k({\overline{G}})$. $\square$

Moreover, $\alpha (G)=n-\rho ({\overline{G}})$, as it is well known.

Corollary 3.5

For any graph G on n vertices

$$\begin{aligned}&\alpha _k(G)\le k(n-k+1),\qquad k=1,\ldots , \lfloor n/2\rfloor .\\&\rho _k({\overline{G}})\le k(n-k+1),\qquad k=1,\ldots , \lfloor n/2\rfloor .\\ \end{aligned}$$

From Lemma 3.4 and Proposition 5.2, we get the following result, which will be proved in Sect. 5.

Corollary 3.6

Let G be a bipartite distance-regular graph. Let $\varvec{L}(F_2/\pi )$ be the quotient matrix in (17) with spectral radius $\rho _L(F_2/\pi )$. Then

$$\begin{aligned} \alpha _2({\overline{G}})={n\atopwithdelims ()2}-\rho _L(F_2/\pi ). \end{aligned}$$

4 The spectral radius of token graphs

In contrast with the previous section, in this section, we always consider the spectral radius of the adjacency matrix of a (connected) graph. Consider a graph G with spectral radius $\rho (G)$ and vertex-connectivity $\kappa$ (that is, the minimum number of vertices whose suppression either disconnects the graph or results in a singleton). By taking the spectral radii of its U-deleted subgraphs, with $U\subset V$ and $|U|=k<\kappa$, we define the following two parameters:

$$\begin{aligned} \rho ^k_M(G)&=\max \{\rho (G{\setminus } U): U\subset V, \,|U|=k\},\\ \rho ^k_m(G)&=\min \{\rho (G{\setminus } U): U\subset V, \,|U|=k\}. \end{aligned}$$

Notice that, if G is walk-regular, then $\rho ^1_M(G)=\rho ^1_m(G) =\rho (G{\setminus } u)$ for every vertex u. If G is distance-regular with degree $\delta$, it is known that it has vertex-connectivity $\kappa (G)=\delta$ (see Brouwer and Koolen [4]). Moreover, Dalfó et al. [8] showed that ${{\,\textrm{sp}\,}}(G{\setminus } U)$ only depends on the distances in G between the vertices of U. Thus, for every $k\le \delta -1$, the computation of $\rho ^k_M(G)$ and $\rho ^k_m(G)$ can be drastically reduced by considering only the subsets U with different ‘distance-pattern’ between vertices. For instance, if G has diameter D

$$\begin{aligned} \rho ^2_M(G)&=\max _{1\le \ell \le D}\{\rho (G{\setminus } \{u,v\}): {{\,\textrm{dist}\,}}_G(u,v)=\ell \},\\ \rho ^2_m(G)&=\min _{1\le \ell \le D}\{\rho (G{\setminus } \{u,v\}): {{\,\textrm{dist}\,}}_G(u,v)=\ell \}. \end{aligned}$$

In general, using interlacing (see Haemers [22] or Fiol [14]), we have the following result.

Lemma 4.1

Let G be a graph with n vertices, vertex-connectivity $\kappa$, and eigenvalues $\lambda _1\ge \lambda _2\ge \cdots \ge \lambda _n$. Then, for every $k=1,\ldots ,\kappa -1$

$$\begin{aligned} \lambda _{k+1}&\le \rho ^k_M(G)\le \lambda _1, \end{aligned}$$

(8)

$$\begin{aligned} \lambda _{n}&\le \rho ^k_m(G)\le \lambda _{n-k}. \end{aligned}$$

(9)

From the above results, Lemma 2.1, and the bounds for the spectral radius of graph perturbations obtained in Dalfó et al. [10] and Nikiforov [24], we obtain the following main result.

Theorem 4.2

Let G be a graph with spectral radius $\rho (G)$ and vertex-connectivity $\kappa >1$. Given an integer k, with $1\le k<\kappa$, let $\rho ^k_M(G)$ and $\rho ^k_m(G)$ be the maximum and minimum of the spectral radii of the U-deleted subgraphs of G, where $|U|=k$.

• (i) The spectral radius of the k-token graph $F_k(G)$ satisfies

  $$\begin{aligned} k\rho ^{k-1}_m(G)\le \rho (F_k(G))\le k\rho ^{k-1}_M(G). \end{aligned}$$

  (10)

• (ii) If G is a graph of order n and diameter D, the spectral radius of the k-token graph $F_k(G)$ satisfies

  $$\begin{aligned} \rho (F_k(G))< k\left( \rho (G)-\frac{1}{n\rho (G)^{2D}}\right) . \end{aligned}$$

  (11)

• (iii) If G is walk-regular and $k=2$ (that is, $F_2(G)$ is the 2-token graph of G), then

  $$\begin{aligned} \rho (F_2(G))= 2\rho ^1_m(G)= 2\rho ^1_M(G). \end{aligned}$$

  (12)

Proof

(i) To prove the upper bound in (10) the key idea is the following: Given some integer $\ell$ large enough, every $\ell$-walk W in $F_k(G)$ from a given vertex A can be seen as $\ell _i$-walks in G for $i=1,\ldots , k$ such that $\sum _{i=1}^k \ell _i=\ell$. Each step of W corresponds to one step given by a token, say ‘1’, whereas the remaining tokens are ‘still’. Thus, the move of token ‘1’ is done in $G{\setminus } U$ for some vertex subset U, with $|U|=k-1$, and the same holds for every token. Thus, for $\ell$ great enough, W induces a number of walks of order ${\ell \atopwithdelims ()\ell _1,\ell _2,\ldots , \ell _k}$ since, in each step, one of the k tokens can be moved. For large $\ell$, the number of ‘conflicts’ (that is, two moves of tokens to the same vertex of G) is negligible with respect to the length of the $\ell$-walk. Then, the total number of $\ell$-walks $w_A^{(\ell )}$ in $F_k(G)$ starting from A is of order

$$\begin{aligned} w_A^{(\ell )}\sim \sum _{\ell _1+\cdots +\ell _k=\ell }{\ell \atopwithdelims ()\ell _1,\ell _2,\ldots , \ell _k}w_u^{(\ell )}=k^{\ell }w_u^{(\ell )}, \end{aligned}$$

(in which we applied the Multinomial Theorem to obtain the equality) and where, for some given vertex u in G, $w_u^{(\ell )}$ is the number of $\ell$-walks starting from u in $G{\setminus } U$. Consequently

$$\begin{aligned} \rho (F_k(G))=\lim _{\ell \rightarrow \infty }\root \ell \of {w_A^{(\ell )}}=k \lim _{\ell \rightarrow \infty }\root \ell \of {w_u^{(\ell )}}\le k\rho _M^{k-1}(G). \end{aligned}$$

The lower bound comes from $\lim _{\ell \rightarrow \infty }\root \ell \of {w_u^{(\ell )}}\ge k\rho _M^{k-1}(G)$.

(ii) This follows from (i) and a result of Nikiforov (see [25, Theorem 1]) stating that if G is a graph as in the conditions of the theorem, and $H(=G{\setminus } U)$ is a proper subgraph of G, then $\rho (H)<\rho (G)-\frac{1}{n\rho (G)^{2D}}$.

Finally, (iii) holds using (10), since, as commented above, in a walk-regular graph G, we have $\rho ^1_M(G)=\rho ^1_m(G) =\rho (G{\setminus } u)$ for every vertex u. $\square$

Notice that, if G is connected $(D<\infty$), (11) improves the upper bound $k \rho (G)$ of Lew [23] in Theorem 1.3. Moreover, as commented in Nikiforov [25], for large values of $\rho (G)$ and D, the right hand of (11) yields the correct order of magnitude of $\rho (H)$. Thus, we can say that, asymptotically, the spectral radius of $F_k(G)$ is k times the spectral radius of G. Moreover, in the case when G is regular, (ii) can be rewritten as

$$\begin{aligned} \rho (F_{k}(G))< k\left( \rho (G)-\frac{1}{n(D+1)}\right) \end{aligned}$$

(13)

(see again [25, Th. 4]).

Since the different eigenvalues of the path $P_n$ on n vertices are $\theta _i=2\cos \left( \frac{i\pi }{n+1} \right)$ for $i=1,\ldots ,n$, and the spectral radius of the complete bipartite graph is $\rho (K_{m,n})=\sqrt{mn}$, we get the following results.

Corollary 4.3

Let $P_n$ and $C_n$ be, respectively, the path and cycle graph on n vertices. Let $P_{\infty }$ and $C_{\infty }$ be, respectively, the infinite path and cycle graphs. Then, their spectral radii satisfy the following:

• (i) $\rho (F_2(P_n))\le 4\cos (\pi /n)$ and $\rho (F_2(P_{\infty }))= 4$.

• (ii) $\rho (F_2(C_n))= 4\cos (\pi /n)$ and $\rho (F_2(C_{\infty }))= 4$.

• (iii) $\rho (F_2(K_{n,n}))= 2\sqrt{n(n-1)}$.

Table 1 Spectral radii of the 2-token graphs of the cycles $C_n$ with respect to spectral radii of the paths graphs $P_{n-1}$

Let us show a pair of examples (1):

• $F_2(C_3)=C_3=K_3$ has spectrum $\{-1^{[2]},2\}$, whereas $P_2$ has $\{-1,1\}$.

• $F_2(C_4)=K_{2,4}$ has spectrum $\{-2\sqrt{2},0^{[6]},2\sqrt{2}\}$, whereas $P_3$ has $\{-\sqrt{2},0,\sqrt{2}\}$.

5 The case of distance-regular graphs

In this section, we adopt the terminology of Brouwer et al. [3] for distance-regular graphs. Furthermore, since we examine both the adjacency and Laplacian spectra, we denote their respective spectral radii as $\rho _A$ and $\rho _L$. In the following result, consider that G is a distance-regular graph with degree $\delta =b_0$, diameter d, intersection array

$$\begin{aligned} \iota (G)=\{ b_0, b_1, \ldots , b_{d-1}; c_1, c_2, \ldots , c_d\} \end{aligned}$$

(14)

or intersection matrix

$$\begin{aligned} \varvec{B}&=\left( \begin{array}{ccccc} 0 &{}\quad b_0 &{}\quad &{}\quad &{}\quad \\ c_1 &{}\quad a_1 &{}\quad b_1 &{}\quad &{}\quad \\ &{}\quad c_2 &{}\quad a_2 &{}\quad \ddots &{}\quad \\ &{}\quad &{}\quad \ddots &{}\quad \ddots &{}\quad b_{d-1} \\ &{}\quad &{}\quad &{}\quad c_d &{}\quad a_d \\ \end{array} \right) , \end{aligned}$$

(15)

where $a_i=\delta -b_i-c_i$, for $i=1,\ldots ,d$.

Lemma 5.1

Let $F_2(G)$ be the 2-token graph of a distance-regular graph G with degree $\delta =b_0$, diameter d, and intersection array $\iota (G)$ as in (14). Then, $F_2=F_2(G)$ has a regular partition $\pi$ with quotient matrix and quotient Laplacian matrix Then, $F_2=F_2(G)$ has a regular partition $\pi$ with quotient matrix and quotient Laplacian matrix

$$\begin{aligned} \varvec{A}(F_2/\pi )&=2\left( \begin{array}{ccccc} a_1 &{}\quad b_1 &{}\quad &{}\quad &{}\quad \\ c_2 &{}\quad a_2 &{}\quad b_2 &{}\quad &{}\quad \\ &{}\quad c_3 &{}\quad a_3 &{}\quad \ddots &{}\quad \\ &{}\quad &{}\quad \ddots &{}\quad \ddots &{}\quad b_{d-1}\\ &{}\quad &{}\quad &{}\quad c_d &{}\quad a_d \\ \end{array} \right) , \end{aligned}$$

(16)

$$\begin{aligned} \varvec{L}(F_2/\pi )&=2\left( \begin{array}{ccccc} b_1 &{}\quad -b_1 &{}\quad &{}\quad &{}\quad \\ -c_2 &{}\quad c_2+b_2 &{}\quad -b_2 &{}\quad &{}\quad \\ &{}\quad -c_3 &{}\quad c_3+b_3 &{}\quad \ddots &{}\quad \\ &{}\quad &{}\quad \ddots &{}\quad \ddots &{}\quad -b_{d-1} \\ &{}\quad &{}\quad &{}\quad -c_d &{}\quad c_d \\ \end{array} \right) , \end{aligned}$$

(17)

where $c_i+a_i+b_i=\delta$, for $i=0,1,\ldots ,d$.

Proof

Let us consider the partition $\pi$ with classes $C_1,C_2,\ldots ,C_d$, where $C_i$ is constituted by the vertices $\{u,v\}$ of $F_2(G)$, with $u,v\in V(G)$, such that ${{\,\textrm{dist}\,}}_G(u,v)=i\in \{1,\ldots ,d\}$. Note that $\varvec{A}(F_2/\pi )$ is a $d\times d$ matrix, since $\pi$ has d classes. Then, since $G(v)\cap G_{i-1}(u)=c_{i-1}$, $G(v)\cap G_{i}(u)=a_i$ and $G(v)\cap G_{i+1}(u)=b_{i+1}$ (and the same equalities hold when we interchange u and v), the vertex $\{u,v\}\in C_i$ is adjacent to $2c_{i-1}$, $2a_i$, and 2$b_{i+1}$ vertices in $C_{i-1}$, $C_i$, and $C_{i+1}$, respectively. Thus, since this holds for every vertex in $C_i$, the partition $\pi$ is regular with the quotient matrix in (16). From this and (4), we obtain the Laplacian quotient matrix of (17). $\square$

The following result shows that the quotient matrices of a regular partition can be used to find the spectral radius or Laplacian spectral radius of the 2-token graph of G.

Proposition 5.2

Let G be a distance-regular graph with adjacency and Laplacian matrices $\varvec{A}$ and $\varvec{L}$. Let $F_2=F_2(G)$ be its 2-token graph with adjacency and Laplacian matrices $\varvec{A}(F_2)$ and $\varvec{L}(F_2)$ with respective spectral radii $\rho _A(F_2)$ and $\rho _L(F_2)$. Let $\varvec{A}(F_2/\pi )$ and $\varvec{L}(F_2/\pi )$ be the quotient matrices in (16) and (17) with respective spectral radii $\rho _A(F_2/\pi )$ and $\rho _L(F_2/\pi )$. Then, the following holds:

• (a) $\rho _A(F_2)=\rho _A(F_2/\pi )$.

• (b) $\rho _L(F_2)\ge \rho _L(F_2/\pi )$, with equality if G is bipartite.

Proof

(a) This follows from Lemma 5.1 and the known fact that if G is a graph with regular partition $\pi$, then the spectral radius of G is equal to the spectral radius of $G/\pi$. (The reason is that the Perron vector of $G/\pi$ lifts to the Perron vector of G.)

(b) In this case, we know that the eigenvector $\varvec{v}$ of the spectral radius $\rho _L(F_2/\pi )$ satisfies $\varvec{v}^{\top } \varvec{1}=0$. Then, we only can conclude that $\rho _L(F_2)\ge \rho _L(F_2/\pi )$. If G is bipartite, all the closed walks rooted at a vertex u have even length. Then, the diagonal entries of $\varvec{L}(F_2)^{\ell }$ are the same as those of the $\ell$-th power of the signless Laplacian matrix. Therefore, as in case (a), we can apply the Perron–Frobenius Theorem, obtaining the equality between the Laplacian spectral radius of $F_2$ and that of its quotient. $\square$

In fact, the eigenvalues of $\varvec{A}(F_2/\pi )$ are 2 times the zeros of the so-called conjugate polynomial ${\overline{p}}_d$ of the distance polynomial $p_d$ of G (with $p_d(\varvec{A})=\varvec{A}_d$, where $\varvec{A}_d$ is the d-distance matrix of G). The conjugate polynomials were introduced by Fiol and Garriga in [15], and are defined on the mesh $\{\theta _0,\theta _1,\ldots ,\theta _d\}$ in terms of the distance polynomials $p_0,p_1,\ldots ,p_d$ as

$$\begin{aligned} {\overline{p}}_i(\theta _i)=\frac{p_{d-i}(\theta _i)}{p_d(\theta _i)}\quad \hbox {for}\quad i=0,1,\ldots ,d. \end{aligned}$$

Thus, in particular ${\overline{p}}_d(\theta _i)=p_d(\theta _i)^{-1}$ and, up to a constant, ${\overline{p}}_d$(x) equals the characteristic polynomial of $\frac{1}{2}\varvec{A}(F_2/\pi )$ (for more details, see Cámara et al. [6]).

Let us show an example.

Example 5.3

The Heawood graph H (which is the point/line incidence graph of the Fano plane) is a bipartite distance-regular graph with $n=14$ vertices, diameter three, and intersection array $\{b_0,b_1,b_2; c_1,c_2,c_3\}=\{3,2,2; 1,1,3\}$. The Laplacian spectral radius of H is $\rho _L(H)=6$, and the algebraic connectivity of ${\overline{H}}$ is $\alpha _1({\overline{H}})=n-\rho _L(H)=8$. By Proposition 5.2, the 2-token graph $F_2=F_2(H)$ has a regular partition $\pi$ with quotient matrix

$$\begin{aligned} \varvec{A}(F_2/\pi ) =2\left( \begin{array}{ccc} 0 &{}\quad 1 &{}\quad 0 \\ 2 &{}\quad 0 &{}\quad 3 \\ 0 &{}\quad 2 &{}\quad 0 \end{array} \right) , \end{aligned}$$

and quotient Laplacian matrix

$$\begin{aligned} \varvec{L}(F_2/\pi ) =2\left( \begin{array}{rrr} 1 &{}\quad -1 &{}\quad 0 \\ -2 &{}\quad 5 &{}\quad -3\\ 0 &{}\quad -2 &{}\quad 2 \end{array} \right) . \end{aligned}$$

The eigenvalues of $\varvec{A}(F_2/\pi )$ are $0,\pm 4\sqrt{2}$, whereas those of $\varvec{L}(F_2/\pi )$ are $0,8\pm 2\sqrt{7}$. Thus, we conclude that $\rho _A(F_2(H))=4\sqrt{2}$ and $\rho _{2}(H):=\rho _L(F_2(H))= 8+2\sqrt{7}$. From this and Lemma 3.4, we have that $\alpha _2({\overline{H}})=2(n-1)-\rho _{2}(H)=18-2\sqrt{7}$, which is greater than $\alpha _1({\overline{H}})=8$. Since the algebraic connectivity of $F_2({\overline{H}})$ also is 8, we get $\alpha _1(F_2({\overline{H}}))=\alpha _1({\overline{H}})$, as expected.

It is well known that the distance polynomials satisfy the three-term recurrence $xp_i=b_{i-1}p_{i-1}+a_i p_i+c_{i+1}p_{i+1}$ with $p_0=1$ and $p_1=x$. Then, the 3-distance polynomial of H is $p_3(x)=\frac{1}{3}(x^3-5x)$, so that the conjugate polynomial ${\overline{p}}_3$ must satisfy ${\overline{p}}_3(\pm 3)=p_3(\pm 3)^{-1}=\pm \frac{1}{4}$, and ${\overline{p}}_3(\pm \sqrt{2})=p_3(\pm \sqrt{2})^{-1}=\mp \frac{\sqrt{2}}{2}$. This results into ${\overline{p}}_3(x)=\frac{1}{12}x^3-\frac{2}{3}x$, with roots $0,\pm 2\sqrt{2}$, which correspond to the eigenvalues of $\frac{1}{2}\varvec{A}(F_2/\pi )$, as predicted (Fig. 2).

Fig. 2

The Heawood graph is the point-line incidence graph of the Fano plane

Other consequences of Lemma 5.1 and Proposition 5.2 are the following. First, from Theorem 1.1, we got the following result.

Corollary 5.4

Let ${{\mathcal {F}}}$ be the family of all distance-regular graphs with diameter d and the same parameters (or intersection array). Then, every graph $G\in {{\mathcal {F}}}$ has 2-token graph $F_2=F_2(G)$ with the d (adjacency or Laplacian) eigenvalues of $\varvec{A}(F_2/\pi )$ or $\varvec{L}(F_2/\pi )$ given in (16) and (17). In particular, $F_2$ has spectral radii $\rho _A(F_2)=\rho _A(F_2/\pi )$, and $\rho _L(F_2)=\rho _L(F_2/\pi )$ if it is bipartite (Proposition 5.2).

Thus, the natural question is if, as in the case of strongly regular graphs (see Godsil [19, 20]), all distance-regular graphs with the same parameters are also cospectral (with respect to the adjacency or Laplacian matrix). In fact, notice that since every graph $G\in {{\mathcal {F}}}$ has the same eigenvalues, the spectrum of its k-token graph $F_k(G)$ also has such eigenvalues (Theorem 1.2).

Moreover, from Theorem 1.3 and the interlacing theorem (see Haemers [22]), we get the following consequence.

Corollary 5.5

Let G be a distance-regular graph with (adjacency) eigenvalues $\theta _0>\theta _1>\cdots >\theta _d$. Then, the 2-token graph $F_2(G)$ has some eigenvalues $\mu _0>\mu _1>\cdots >\mu _{d-1}$ satisfying

$$\begin{aligned} 2\theta _{i+1}\le \mu _i \le 2\theta _i,\qquad i=0,\ldots ,d-1. \end{aligned}$$

Proof

Apart from the factor 2, the matrix $\varvec{A}(F_2/\pi )$ in (16) is a principal $d\times d$ submatrix of the intersection matrix $\varvec{B}$ in (15). Then, the result follows using interlacing (see Haemers [22]). $\square$

5.1 Strongly regular graphs

Let G be a (connected) strongly regular graph on n vertices, which is a distance-regular graph with diameter 2. Let G have parameters (n, d, a, c), that is, G is d-regular (with $b_0=d$), $a_1=a$, and $c_2=c$. Then, its intersection matrix is

$$\begin{aligned} \varvec{B}= \left( \begin{array}{ccc} 0 &{}\quad 1 &{}\quad 0 \\ d &{}\quad a &{}\quad c \\ 0 &{}\quad d-a-1 &{}\quad d-c \end{array} \right) . \end{aligned}$$

Then, the 2-token graph $F_2=F_2(G)$ has a regular partition $\pi$ with quotient matrix

$$\begin{aligned} \varvec{A}(F_2/\pi ) =\left( \begin{array}{cc} 2a &{}\quad 2c \\ 2d-2a-2 &{}\quad 2d-2c \\ \end{array} \right) . \end{aligned}$$

Such a regular partition was given by Audenaert et al. in [2], and noted that the adjacency eigenvalues of $\varvec{A}(F_2/\pi )$ are

$$\begin{aligned} \theta _{1,2}=d+(a-c)\pm \sqrt{[d-(a-c)]^2-4c}. \end{aligned}$$

They also commented that the positive eigenvalue $\theta _1$ has a positive eigenvector (Perron vector) and, so, it corresponds to the (adjacency) spectral radius $\rho _A(F_2(G))$.

In contrast, the quotient Laplacian matrix is

$$\begin{aligned} \varvec{L}(F_2/\pi ) =\left( \begin{array}{cc} 2c &{}\quad -2c \\ -2d+2a +2&{}\quad 2d-2a-2 \end{array} \right) , \end{aligned}$$

which has eigenvalues $\lambda _1=0$ and $\lambda _2=2(d-1)-2(a-c)$. Now, the eigenvector of $\lambda _2$ is orthogonal to $\varvec{1}$. Then, we can only conclude that the Laplacian spectral radius of $F_2(G)$ satisfies

$$\begin{aligned} \rho _L(F_2(G))\ge 2(d-1)-2(a-c). \end{aligned}$$

(18)

For instance, the cycle on five vertices $C_5$ is strongly regular with parameters (5, 2, 0, 1). Its Laplacian spectral radius is (approximately) $\rho _L(F_2(G))=6.2361$, whereas the lower bound in (18) gives 4.