On the algebraic connectivity of some token graphs

Abstract

The k-token graph $F_k(G)$ of a graph G is the graph whose vertices are the k-subsets of vertices from G, two of which are adjacent whenever their symmetric difference is a pair of adjacent vertices in G. It was proved that the algebraic connectivity of $F_k(G)$ equals the algebraic connectivity of G with a proof using random walks and interchange of processes on a weighted graph. However, no algebraic or combinatorial proof is known, and it would be a hit in the area. In this paper, we algebraically prove that the algebraic connectivity of $F_k(G)$ equals the one of G for new infinite families of graphs, such as trees, some graphs with hanging trees, and graphs with minimum degree large enough. Some examples of these families are the following: the cocktail party graph, the complement graph of a cycle, and the complete multipartite graph.

1 Introduction

Let G be a simple graph with vertex set $V(G)=\{1,2,\ldots ,n\}$ and edge set E(G). Let $\delta (G)$ denote the minimum degree of G. For a given integer k such that $1\le k \le n$, the k-token graph $F_k(G)$ of G is the graph whose vertex set $V (F_k(G))$ consists of the ${n \atopwithdelims ()k}$ k-subsets of vertices of G, and two vertices A and B of $F_k(G)$ are adjacent whenever their symmetric difference $A \bigtriangleup B$ is a pair $\{a,b\}$ such that $a\in A$, $b\in B$, and $(a,b)\in E(G)$. The naming ‘token graph’ comes from an observation in Fabila-Monroy et al. [7], that vertices of $F_k(G)$ correspond to configurations of k indistinguishable tokens placed at distinct vertices of G, where two configurations are adjacent whenever one configuration can be reached from the other by moving one token along an edge from its current position to an unoccupied vertex. Thus, the maximum degree of $F_k(G)$ satisfies

$$\begin{aligned} \Delta (F_k(G))\le k\Delta (G). \end{aligned}$$

(1)

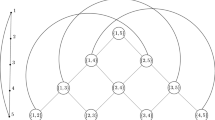
In Fig. 1, we show the 2-token graph of cycle $C_9$ on nine vertices.

Note that, for convenience, if $k=0$, then $F_0(G)$ is an only vertex; if $k=1$, then $F_1(G)\cong G$; and if G is the complete graph $K_n$, then $F_k(K_n)\cong J(n,k)$, where J(n, k) denotes the Johnson graph (see again [7]).

Fig. 1

The 2-token graph $F_2(C_9)$ of the cycle graph, with vertex set $V(C_9)=\{0,1,\ldots ,8\}$. The vertices on the circumference of radius $r_{\ell }$, with $\ell =1,2,3,4$ and $r_1>r_2>r_3>r_4$ are $\{i,j\}$ with ${{\,\textrm{dist}\,}}(i,j)=\ell$ in $C_9$

Token graphs have some applications in physics. For instance, a relationship between token graphs and the exchange of Hamiltonian operators in quantum mechanics is given in Audenaert et al. [1].

Recently, it was conjectured by Dalfó et al. [5] that the algebraic connectivity of $F_k(G)$ equals the algebraic connectivity of G. After submitting the first version of this paper, the authors learned (from Fabila-Monroy [6]) that this conjecture was already known as the Aldous’ spectral gap conjecture, and it was proved in 2010 by Caputo et al. [3]. Moreover, Ouyang [12] and Lew [11] also mentioned that this conjecture was actually solved. Besides, Cesi [4] provided a simpler proof of the so-called ‘octopus inequality,’ which is one of the main ingredients to prove Aldous’ conjecture. These results were obtained in completely different contexts and using distinct techniques. More precisely, they used the theory of continuous Markov chains of random walks and the so-called interchange of processes on a weighted graph. In this paper, we present an algebraic approach to this problem for trees and other graphs, and we give a new method that can be of interest, giving an alternative algebraic proof.

This paper is structured as follows. In Sect. 2, we present some of the known results on the algebraic connectivity. In Sect. 3, we prove that the algebraic connectivity of a graph and its k-token graph coincide

for new infinite families of graphs, such as trees, some graphs with hanging trees, and graphs with minimum degree large enough. Some examples of these families are the following: the cocktail party graph, the complement graph of a cycle, and the complete multipartite graph.

2 Known results

First, let us introduce some notation and known results used throughout the paper. The transpose of a matrix $\varvec{M}$ is represented by $\varvec{M}^\top$, the identity matrix by $\varvec{I}$, the all-1 vector $(1,..., 1)^{\top }$ by $\varvec{1}$, the all-1 (universal) matrix by $\varvec{J}$, and the all-0 vector and all-0 matrix by $\varvec{0}$ and $\varvec{O}$, respectively. Let $[n]:=\{1,\ldots ,n\}$, and ${[n]\atopwithdelims ()k}$ denote the set of k-subsets of [n], which is the set of vertices of the k-token graph.

For our purpose, it is convenient to indicate by $W_n$ the set of all column vectors $\varvec{v}$ such that $\varvec{v}^{\top }\varvec{1} = 0$. Recall that any square matrix $\varvec{M}$ with all zero row sums has an eigenvalue 0 with corresponding eigenvector $\varvec{1}$.

When $\varvec{M}=\varvec{L}(G)$, the Laplacian matrix of a graph G, the matrix is positive semidefinite, with eigenvalues $(0=)\lambda _1\le \lambda _2\le \cdots \le \lambda _n$. Its second smallest eigenvalue $\lambda _2$ is known as the algebraic connectivity of G (see Fiedler [8]), and we denote it by $\alpha (G)$. The spectral radius $\lambda _{\max }(G)=\lambda _n$ satisfies several lower and upper bounds (see Patra and Sahoo [14] for a survey). Here, we will use the following ones in terms of the maximum degree of G:

$$\begin{aligned} 1+\Delta (G)\le \lambda _{\max }(G)\le 2\Delta (G). \end{aligned}$$

(2)

The upper bound is due to Fiedler [8], whereas Grone and Merris proved the lower bound in [10], assuming that G has at least one edge.

In this paper, we want to study the algebraic connectivity of token graphs of trees and graphs with hanging trees, among others. As far as we know, this study was initiated by Dalfó et al. [5], where they proved the following results.

For some integers n, h, and k, with $1\le h<k<n$, we consider the (n; k, h)-binomial matrix $\varvec{B}$, with rows indexed by the k-subsets $A\subset [n]$, columns indexed by the h-subsets $X\subset [n]$, and entries $(\varvec{B})_{AX}=1$ if $X\subset A$, and $(\varvec{B})_{AX}=0$ otherwise. Note that the transpose of $\varvec{B}$ is the so-called set-inclusion matrix, denoted by $W_{h,k}(n)$ (see, for instance, Godsil [9].)

Lemma 2.1

([5]) Let G be a graph on n vertices. For some integers h, k such that $1\le h < k \le \lfloor \frac{n}{2}\rfloor$, let $F_h=F_h(G)$ and $F_k=F_k(G)$ be their h- and k-token graphs with respective Laplacian matrices $\varvec{L}_h$ and $\varvec{L}_k$. Then, the following holds:

• (i) If $\varvec{v}$ is a $\lambda$-eigenvector of $\varvec{L}_h$, then $\varvec{B}\varvec{v}$ is a $\lambda$-eigenvector of $\varvec{L}_k$. Thus, the Laplacian spectrum (eigenvalues and their multiplicities) of $\varvec{L}_h$ is contained in the Laplacian spectrum of $\varvec{L}_k$.

• (ii) If $\varvec{u}$ is a $\lambda$-eigenvector of $\varvec{L}_k$ such that $\varvec{B}^{\top }\varvec{u}\ne \varvec{0}$, then $\varvec{B}^{\top }\varvec{u}$ is a $\lambda$-eigenvector of $\varvec{L}_h$.

Given two integers n and k such that $k\in [n]$, the Johnson graph J(n, k) can be defined as the k-token graph of the complete graph $K_n$, that is, $F_k(K_n)\cong J(n,k)$. It is known that these graphs are antipodal (but not bipartite) distance-regular graphs, with degree $d=k(n-k)$, diameter $D=\min \{k,n-k\}$, and with Laplacian spectrum (eigenvalues and multiplicities)

$$\begin{aligned} \lambda _j=j(n+1-j)\qquad \text{ and } \qquad m_j={n\atopwithdelims ()j}-{n\atopwithdelims ()j-1},\qquad j=0,1,\ldots ,D. \end{aligned}$$

(3)

(See again [5]).

For example, $F_2(K_{4})\cong J(4,2)$ is a 2-regular graph with $n=6$ vertices, diameter $D=2$, and with Laplacian spectrum $S(F_2(K_{4}))=\{0^{[1]}, 4^{[3]}, 6^{[2]}\}$.

Let us consider a graph G and its complement $\overline{G}$, with respective Laplacian matrices $L_G$ and $L_{\overline{G}}$. Since $L_G+L_{\overline{G}}=n\varvec{I}-\varvec{J}$, the Laplacian spectrum of $\overline{G}$ is the complement of the Laplacian spectrum of G with respect to the Laplacian spectrum of the complete graph $K_n$. We represent this as

$$\begin{aligned} {{\,\textrm{sp}\,}}G \oplus {{\,\textrm{sp}\,}}\overline{G} = {{\,\textrm{sp}\,}}K_n, \end{aligned}$$

where each eigenvalue of G and each eigenvalue of $\overline{G}$ are used once. In [5], it was shown that a similar relationship holds between the Laplacian spectra of the k-token of G and the k-token of $\overline{G}$, but now with respect to the Laplacian spectrum of the Johnson graph.

Theorem 2.2

([5]) Let $G=(V,E)$ be a graph on $n=|V|$ vertices, and let $\overline{G}$ be its complement. For a given k, with $1\le k\le n-1$, let us consider the token graphs $F_k(G)$ and $F_k(\overline{G})$. Then, the Laplacian spectrum of $F_k(\overline{G})$ is the complement of the Laplacian spectrum of $F_k(G)$ with respect to the Laplacian spectrum of the Johnson graph $J(n,k)=F_k(K_n)$. That is, every eigenvalue $\lambda _J$ of J(n, k) is the sum of one eigenvalue $\lambda _{F_k(G)}$ of $F_k(G)$ and one eigenvalue $\lambda _{F_k(\overline{G})}$ of $F_k(\overline{G})$, where each $\lambda _{F_k({G})}$ and each $\lambda _{F_k(\overline{G})}$ is used once:

$$\begin{aligned} \lambda _{F_k({G})}+\lambda _{F_k(\overline{G})}=\lambda _J. \end{aligned}$$

(4)

Note that, in this result, it is not stated what the pairing of the eigenvalues of $F_k({G})$ and $F_k(\overline{G})$ is, giving the corresponding eigenvalue of J(n, k). In the following section, we improve this result by showing such a pairing, which is necessary for the proof of Theorem 3.7.

As a consequence of Lemma 2.1(i) and $F_k(G)=F_{n-k}(G)$, the fact that the algebraic connectivities of G and $F_k(G)$ coincide

only needs to be proved for the case $k=\lfloor n/2 \rfloor$. Moreover, it was noted that this result

also holds when the graph G is disconnected and for those graphs whose token graphs are regular, which are $K_n$ and $S_n$ (with even n and $k=n/2$), and their complements.

Besides, it is shown in [5] that this result

holds for the following infinite families of graphs.

Theorem 2.3

([5]) For each of the following classes of graphs, the algebraic connectivity of a token graph $F_k(G)$ equals the algebraic connectivity of G.

• (i) Let $G=K_n$ be the complete graph on n vertices. Then, $\alpha (F_k(G))=\alpha (G)=n$ for every n and $k=1,\ldots ,n-1$.

• (ii) Let $G=S_n$ be the star graph on n vertices. Then, $\alpha (F_k(G))=\alpha (G)=1$ for every n and $k=1,\ldots ,n-1$.

• (iii) Let $G=P_n$ be the path graph on n vertices. Then, $\alpha (F_k(G))=\alpha (G)=2(1-\cos (\pi /n))$ for every n and $k=1,\ldots , n-1$.

• (iv) Let $G= K_{n_1,n_2}$ be the complete bipartite graph on $n=n_1+n_2$ vertices, with $n_1\le n_2$. Then, $\alpha (F_k(G))=\alpha (G)=n_1$ for every $n_1$, $n_2$, and $k=1,\ldots ,n-1$.

3 New algebraic results

In this section, we provide an algebraic method to prove that the algebraic connectivities of G and $F_k(G)$ coincide for some infinite families of graphs.

In our proofs, we use the following concepts and results. As a consequence of Lemma 2.1, the spectrum of J(n, k) in (3), and Theorem 2.2, we can state the following lemma.

Lemma 3.1

Let G a graph on n vertices and $k\le n/2$. Let $\Lambda$ be the set of pairs $(\lambda ,\overline{\lambda })$ of eigenvalues of $F_k(G)$ and $F_k(\overline{G})$, with $k\le n/2$, sharing both the same eigenvector $\varvec{v}$ with J(n, k). Then, consider the partition of $\Lambda$ into the sets $\Lambda _0,\Lambda _1,\ldots ,\Lambda _k$ such that $\Lambda _0=\{(0,0)\}$, and

$$\begin{aligned} \Lambda _j=\{({{\,\textrm{sp}\,}}F_j(G)\!\setminus \! {{\,\textrm{sp}\,}}F_{j-1}(G),\ {{\,\textrm{sp}\,}}F_j(\overline{G})\!\setminus \! {{\,\textrm{sp}\,}}F_{j-1}(\overline{G}))\}\quad \text{ for } j=1,\ldots ,k. \end{aligned}$$

Let $m_j={n\atopwithdelims ()j}-{n\atopwithdelims ()j-1}$. Let $\lambda _1\le \lambda _2\le \cdots \le \lambda _{m_j}$ be the eigenvalues of ${{\,\textrm{sp}\,}}F_j(G)\!{\setminus }\! {{\,\textrm{sp}\,}}F_{j-1}(G)$ in non-decreasing order, and $\overline{\lambda }_1\ge \overline{\lambda }_2\ge \cdots \ge \overline{\lambda }_{m_j}$ the eigenvalues of ${{\,\textrm{sp}\,}}F_j(\overline{G})\!{\setminus }\! {{\,\textrm{sp}\,}}F_{j-1}(\overline{G})$ in non-increasing order. Then,

$$\begin{aligned} \lambda _j + \overline{\lambda }_{m_j-i+1}=j(n-j+1)\quad \text{ for } i=1,\ldots , m_j\text{. } \end{aligned}$$

(5)

Proof

Recall that every right value in (5) is an eigenvalue of J(n, j) with multiplicity $m_j$ for $j=1,\ldots ,k$. From Lemma 2.1, when we go from the spectra of $\{F_{j-1}(G)$, $F_{j-1}(\overline{G})\}$ to the spectra of $\{F_{j}(G)$, $F_{j}(\overline{G})\}$, all the eigenvalues of $\Lambda _0,\ldots ,\Lambda _{j-1}$ reappear (with eigenvectors $\varvec{v}$ such that $\varvec{B}^{\top }\varvec{v}\ne \varvec{0}$), together with ‘new’ eigenvalues belonging to $\Lambda _j$ (with eigenvectors $\varvec{v}$ such that $\varvec{B}^{\top }\varvec{v}= \varvec{0}$). Similarly, when we go from $J(n,j-1)$ to J(n, j), the new eigenvalue is $j(n-j+1)$ with multiplicity $m_j$ for $j=1,\ldots ,k$. Then, from Theorem 2.2, $m_j$ coincides with the number of pairs in $\Lambda _j$ and, moreover, each pair sums up to give the constant $j(n-j+1)$, that is,

$$\begin{aligned} \Lambda _j=\{(\lambda ,\overline{\lambda }):\lambda +\overline{\lambda }=j(n+1-j)\} \quad \text{ for } j=1,\ldots ,k, \end{aligned}$$

which proves (5).

$\square$

Let us show an example of Lemma 3.1.

Fig. 2

Graph G and its complement graph $\overline{G}$ of Example 3.2

Example 3.2

Consider graph G and its complement graph $\overline{G}$ of Fig. 2. The spectra of G, $\overline{G}$, and their k-tokens for $k=2,3$ are the following:

$$\begin{aligned} {{\,\textrm{sp}\,}}G&=\{0,2,4^{[3]},6\}\subset {{\,\textrm{sp}\,}}F_2(G) =\{0,2,4^{[5]},6^{[4]},8^{[3]},10\}\\&\subset {{\,\textrm{sp}\,}}F_3(G) =\{0,2,4^{[6]},6^{[4]},8^{[5]},10^{[3]}\}.\\ {{\,\textrm{sp}\,}}\overline{G}&=\{0^{[2]},2^{[3]},4\}\subset {{\,\textrm{sp}\,}}F_2(\overline{G}){=}\{0^{[3]},2^{[6]},4^{[4]},6^{[2]}\} \subset {{\,\textrm{sp}\,}}F_3(\overline{G}) {=}\{0^{[3]},2^{[8]},4^{[6]},6^{[2]}\}. \end{aligned}$$

Then, as shown in Table 1, there is a pairing between the eigenvalues of $F_3(G)$ and the eigenvalues of $F_3(\overline{G})$, satisfying Theorem 2.2. Namely,

$$\begin{aligned} {{\,\textrm{sp}\,}}F_3(G)\oplus {{\,\textrm{sp}\,}}F_3(\overline{G}) = {{\,\textrm{sp}\,}}J(6,3)=\{0, 6^{[5]}, 10^{[9]}, 12^{[5]}\}. \end{aligned}$$

Thus, the pairs of $\Lambda _0$, $\Lambda _1$, $\Lambda _2$, and $\Lambda _3$ add up to 0, 6, 10, and 12, respectively.

Table 1 For Example 3.2, the spectra of $F_1(G)$ and $F_1(\overline{G})$, $F_2(G)$ and $F_2(\overline{G})$, and $F_3(G)$ and $F_3(\overline{G})$ giving, respectively, the spectrum of J(6, 1), J(6, 2), and J(6, 3) by addition, according to Lemma 3.1

Given a graph $G=(V,E)$ of order n, we say that a vector $\varvec{v}\in \mathbb {R}^n$ is an embedding of G if $\varvec{v}\in W_n$ (that is, $\varvec{v}^{\top }\varvec{1}=0$). Note that if $\varvec{v}$ is a $\lambda$-eigenvector of G, with $\lambda >0$, then it is an embedding of G.

For a graph G with Laplacian matrix $\varvec{L}(G)$, and an embedding $\varvec{v}$ of G, let

$$\begin{aligned} \lambda _G(\varvec{v}):=\frac{\varvec{v}^{\top }\varvec{L}(G)\varvec{v}}{\varvec{v}^{\top }\varvec{v}}=\frac{\sum \limits _{(i,j)\in E}[\varvec{v}(i)-\varvec{v}(j)]^2}{\sum \limits _{i\in V}\varvec{v}^2(i)}, \end{aligned}$$

(6)

where $\varvec{v}(i)$ denotes the entry of $\varvec{v}$ corresponding to the vertex $i\in V(G)$. The value of $\lambda _G(\varvec{v})$ is known as the Rayleigh quotient. If $\varvec{v}$ is an eigenvector of G, then its corresponding eigenvalue is $\lambda (\varvec{v})$. Moreover, for an embedding $\varvec{v}$ of G, we have

$$\begin{aligned} \alpha (G)\le \lambda _G(\varvec{v}), \end{aligned}$$

(7)

and we have equality when $\varvec{v}$ is an $\alpha (G)$-eigenvector of G.

The following result, Lemma 3.4, describes a particular ‘rank-one perturbation’ of a symmetric matrix. Hence, the given inequality is a consequence of eigenvalue interlacing, as Bunch, Nielsen, and Sorensen described in [2]. In the case of trees, this result is also a consequence of the following theorem by Patra and Lal [13, Th. 3.1].

Theorem 3.3

([13]) Let $e=(u, v)$ be an edge of a tree T. Let $\widetilde{T}$ be the tree obtained from T by ‘collapsing’ the edge e (that is, deleting e and identifying u and v). Then, $\alpha (\widetilde{T})\ge \alpha (T)$.

However, for completeness, we here provide a direct proof by using Fiedler eigenvectors (that is, those corresponding to the algebraic connectivity).

Lemma 3.4

Let $G^+=(V^+,E^+)$ be a graph on the vertex set $V=\{1,2,\ldots ,n+1\}$, having a vertex of degree 1, say the vertex $n+1$ that is adjacent to n. Let $G=(V,E)$ be the graph obtained from $G^+$ by deleting the vertex $n+1$. Then,

$$\begin{aligned} \alpha (G)\ge \alpha (G^+), \end{aligned}$$

with equality if and only if the $\alpha (G)$-eigenvector $\varvec{v}$ of G has entry $\varvec{v}(n)=0$.

Proof

Let $\varvec{v}\in W_n$ be an eigenvector of G with eigenvalue $\alpha (G)$ and norm $\Vert \varvec{v}\Vert =1$, so that

$$\begin{aligned} \lambda (\varvec{v})=\sum \limits _{(i,j)\in E}[\varvec{v}(i)-\varvec{v}(j)]^2=\alpha (G). \end{aligned}$$

(8)

Let $\varvec{w}\in \mathbb R^{n+1}$ be the vector with components $\varvec{w}(i)=\varvec{v}(i)-\frac{\varvec{v}(n)}{n+1}$ for $i=1,\ldots ,n$ and $\varvec{w}(n+1)=\varvec{w}(n)=\frac{n\varvec{v}(n)}{n+1}$. Note that $\varvec{w}$ is an embedding of $G^+$ since

$$\begin{aligned} \sum _{i=1}^{n+1}\varvec{w}(i)=\sum _{i=1}^n \left( \varvec{v}(i)-\frac{\varvec{v}(n)}{n+1}\right) +\varvec{w}(n+1)=0-\frac{n\varvec{v}(n)}{n+1}+\varvec{w}(n)=0. \end{aligned}$$

Then, from (7),

$$\begin{aligned} \alpha (G^+)&\le \lambda (\varvec{w})=\frac{\sum \limits _{(i,j)\in E^+}[\varvec{w}(i)-\varvec{w}(j)]^2}{\sum \limits _{i\in V^+}\varvec{w}^2(i)} =\frac{\sum \limits _{(i,j)\in E}[\varvec{v}(i)-\varvec{v}(j)]^2}{\sum \limits _{i\in V}[\varvec{v}(i)-\frac{\varvec{v}(n)}{n+1}]^2+\varvec{w}(n+1)^2}\le \alpha (G), \end{aligned}$$

where the last inequality comes from (8) since, as $\varvec{v}$ is an embedding of G,

$$\begin{aligned} \sum \limits _{i\in V}\left[ \varvec{v}(i)-\frac{\varvec{v}(n)}{n+1}\right] ^2=\sum \limits _{i\in V}\left[ \varvec{v}(i)^2-2\varvec{v}(i)\frac{\varvec{v}(n)}{n+1}+\frac{\varvec{v}(n)^2}{(n+1)^2}\right] =1+n\frac{\varvec{v}(n)^2}{(n+1)^2}\ge 1. \end{aligned}$$

Finally, the equality $\alpha (G^+)=\alpha (G)$ holds if and only if $\varvec{v}(n)=0$. $\square$

Let G be a graph with k-token graph $F_k(G)$. For a vertex $a\in V(G)$, let $S_a:=\{A\in V(F_k(G)):a\in A\}$ and $S'_a:=\{B\in V( F_k(G)):a\not \in B\}$. Let $H_a$ and $H'_a$ be the subgraphs of $F_k(G)$ induced by $S_a$ and $S'_a$, respectively. Note that $H_a\cong F_{k-1}(G{\setminus } \{a\})$ and $H'_a\cong F_k(G{\setminus } \{a\})$.

Lemma 3.5

Given a vertex $a\in G$ and an eigenvector $\varvec{v}$ of $F_k(G)$ such that $\varvec{B}^{\top }\varvec{v}=\varvec{0}$, let

$$\begin{aligned} \varvec{w}_a:=\left. \varvec{v}\right| _{S_a} \text { and \quad } \varvec{w}'_a:=\left. \varvec{v}\right| _{S'_a}. \end{aligned}$$

Then, $\varvec{w}_a$ and $\varvec{w}'_a$ are embeddings of $H_a$ and $H'_a$, respectively.

Proof

Assume that the matrix $\varvec{B}^{\top }$ has the first row indexed by $a\in V(G)$. Then, we have

$$\begin{aligned}\varvec{0}= \varvec{B}^{\top }\varvec{v}= \left( \begin{array}{cc} \varvec{1}^{\top } &{} \varvec{0}^{\top }\\ \varvec{B}_1 &{} \varvec{B}_2 \end{array} \right) \left( \begin{array}{c} \varvec{w}_a \\ \varvec{w}'_a \end{array} \right) = \left( \begin{array}{c} \varvec{1}^{\top }\varvec{w}_a \\ \varvec{B}_1\varvec{w}_a+\varvec{B}_2\varvec{w}'_a \end{array} \right) , \end{aligned}$$

where $\varvec{1}^{\top }$ is a row ${n-1\atopwithdelims ()k-1}$-vector, $\varvec{0}$ is a row ${n-1\atopwithdelims ()k}$-vector, $\varvec{B}_1=\varvec{B}(n-1,k-1)^{\top }$, and $\varvec{B}_2=\varvec{B}(n-1,k)^{\top }$. Then, $\varvec{1}^{\top }\varvec{w}_a=0$, so that $\varvec{w}_a$ is an embedding of $H_a$. Furthermore, since $\varvec{v}$ is an embedding of G, we have $\varvec{1}^{\top }\varvec{v}=\varvec{1}^{\top }\varvec{w}_a+\varvec{1}^{\top }\varvec{w}'_a=0$ (with the appropriate dimensions of the all-1 vectors). Hence, it must be $\varvec{1}^{\top }\varvec{w}'_a =0$, and $\varvec{w}'_a$ is an embedding of $H'_a$. $\square$

Theorem 3.6

For each of the following classes of graphs, the algebraic connectivity of a token graph $F_k(G)$ satisfies the following.

• (i) Let $T_n$ be a tree on n vertices. Then, $\alpha (F_k(T_n))=\alpha (T_n)$ for every n and $k=1,\ldots ,n-1$.

• (ii) Let G be a graph such that $\alpha (F_k(G))=\alpha (G)$. Let $T_G$ be a graph where each vertex of G is the root vertex of some (possibly empty) tree. Then, $\alpha (F_k(T_G))=\alpha (T_G)$.

Proof

To prove (i), let $V(T_n)=[n]$. From previous comments, we can assume that $T_n$ is connected. Then, the result is readily checked for $n\le 4$ and $k=1,2$ and 3. Now, we proceed by induction. Suppose $n>4$ and $k>1$. To our aim, by Lemma 2.1(ii), it suffices to show that if $\varvec{v}$ with a given norm, say $\varvec{v}^{\top }\varvec{v}=1$, is an eigenvector of $F_k:=F_k(T_n)$, with $\varvec{B}^{\top }\varvec{v}=\varvec{0}$, then $\lambda (\varvec{v})\ge \alpha (T_n)$. Let $i\in [n]$. As defined before, let $S_i:=\{A\in V(F_k):i\in A \}$ and $S'_i:=\{B\in V(F_k):i\not \in B\}$. Let $H_i$ and $H'_i$ be the subgraphs of $F_k$ induced by $S_i$ and $S'_i$, respectively. We have $H_i\cong F_{k-1}(T_{n-1})$ and $H'_i\cong F_k(T_{n-1})$, where $T_{n-1}=T\setminus i$. Moreover, note that if vertex i is of degree 1 in $T_n$, then $T_{n-1}$ is also connected. Let $\varvec{w}_i:=\left. \varvec{v}\right| _{S_i}$ and $\varvec{w}'_i:=\left. \varvec{v}\right| _{S'_i}$, by Lemma 3.5, we know that $\varvec{w}_i$ and $\varvec{w}'_i$ are embeddings of $H_i$ and $H'_i$, respectively. By the induction hypothesis, we have

$$\begin{aligned} \lambda (\varvec{w}_i)=\frac{\sum \limits _{(A,B)\in E(H_i)} [\varvec{w}_i(A)-\varvec{w}_i(B)]^2}{\sum \limits _{A\in V(H_i)}\varvec{w}_i(A)^2}\ge \alpha (T_{n-1}), \end{aligned}$$

and

$$\begin{aligned} \lambda (\varvec{w}'_i)=\frac{\sum \limits _{(A,B)\in E(H'_i)}[\varvec{w}'_i(A)-\varvec{w}'_i(B)]^2}{\sum \limits _{A\in V(H'_i)}\varvec{w}'_i(A)^2}\ge \alpha (T_{n-1}). \end{aligned}$$

Since $V(H_i)\cup V(H'_i)=V(F_k)$ and $\varvec{v}^{\top }\varvec{v}=1$, we get

$$\begin{aligned} \lambda (\varvec{v})&=\sum \limits _{(A,B)\in E(F_k)}[\varvec{v}(A)-\varvec{v}(B)]^2 \nonumber \\&\ge \sum \limits _{(A,B)\in E(H_i)}[\varvec{w}_i(A)-\varvec{w}_i(B)]^2 + \sum \limits _{(A,B)\in E(H'_i)}[\varvec{w}'_i(A)-\varvec{w}'_i(B)]^2 \nonumber \\&\ge \alpha (T_{n-1})\Big [\sum \limits _{A\in V(H_i)}\varvec{w}_i(A)^2 + \sum \limits _{B\in V(H'_i)}\varvec{w}'_i(B)^2\Big ] \nonumber \\&= \alpha (T_{n-1})\Big [ \sum \limits _{A\in V(H_i)}\varvec{v}(A)^2 + \sum \limits _{B\in V(H'_i)}\varvec{v}(B)^2\Big ] \nonumber \\&= \alpha (T_{n-1}) > \alpha (T_n), \end{aligned}$$

(9)

where (9) follows from Lemma 3.4. (Notice that, since i has degree 1, collapsing the edge of which i is an end-vertex is equivalent to removing i, so obtaining $T_{n-1}$.)

Furthermore, since $\lambda (\varvec{v})>\alpha (T_n)$, we get that $\alpha (T_n)$ is an eigenvalue of both $T_n$ and $F_k(T_n)$ with the same multiplicity.

Regarding (ii), it could be seen as a generalization of (i). Thus, it is proved in the same way by induction on the number of vertices not in G (that is, the non-root vertices of the trees), and starting from G. (The other way around, proved (ii), the result in (i) is a corollary when we start with $G=K_1$ or $G=K_2$.) $\square$

Note that the result of Theorem 3.6(i) implies the ones of Theorem 2.3(ii) and (iii).

Theorem 3.7

Let G be a graph on n vertices satisfying $\alpha (F_{k-1}(G))=\alpha (G)$ and minimum degree

$$\begin{aligned} \delta (G)\ge \phi (k)=\frac{k(n+k-3)}{2k-1} \end{aligned}$$

(10)

for some integer $k=1,\ldots , \lfloor n/2\rfloor$. Then, the algebraic connectivity of its k-token graph equals the algebraic connectivity of G, that is,

$$\begin{aligned} \alpha (F_k(G))=\alpha (G). \end{aligned}$$

Proof

The hypothesis $\alpha (F_{k-1}(G))=\alpha (G)$ implies that, in ${{\,\textrm{sp}\,}}F_{k}(G)$, all the eigenvalues of $F_k(G)$ that are in $\Lambda _1,\ldots ,\Lambda _{k-1}$ must be greater than or equal to $\alpha (G)$. Reasoning by contradiction, if $\alpha (F_k(G))<\alpha (G)$, then the eigenvalue $\alpha (F_k(G))$ must belong to $\Lambda _k$. Then, by Lemma 3.1, the eigenvalue $\lambda _{F_k(G)}=\alpha (F_k(G))$ must be paired with the eigenvalue $\lambda _{\max }F_k(\overline{G})$ belonging also to $\Lambda _k$ (both eigenvalues sharing the same eigenvector $\varvec{v}$ with J(n, k)). Thus,

$$\begin{aligned} \alpha (G)+\lambda _{\max }F_k(\overline{G})>\alpha (F_k(G))+\lambda _{\max }F_k(\overline{G})=k(n-k+1). \end{aligned}$$

Thus, using that $\alpha (G)=n-\lambda _{\max }(\overline{G})$,

$$\begin{aligned} \lambda _{\max }(F_k(\overline{G}))> k(n-k+1)-\alpha (G)=k(n-k+1)-n+\lambda _{\max }(\overline{G}). \end{aligned}$$

However, from the upper and lower bounds in (2) for the (Laplacian) spectral radius of a graph, together with (1), we get

$$\begin{aligned} 2k\Delta (\overline{G})\ge \lambda _{\max }(F_k(\overline{G}))>k(n-k+1)-n+\lambda _{\max }(\overline{G})\ge (k-1)(n-k)+\Delta (\overline{G})+1, \end{aligned}$$

or, in terms of $\delta (G)$,

$$\begin{aligned} n-1-\delta (G)=\Delta (\overline{G})>\frac{(k-1)(n-k)+1}{2k-1}. \end{aligned}$$

Hence, $\delta (G)<n-1-\frac{(k-1)(n-k)+1}{2k-1}=\frac{k(n+k-3)}{2k-1}$, contradicting the hypothesis. $\square$

For the two extreme cases, $k=2$ and $k=n/2$, we get the following consequences.

Corollary 3.8

Let G be a graph on n vertices and minimum degree $\delta (G)$.

• (i) If $\delta (G)\ge \frac{2}{3}(n-1)$, then $\alpha (F_2(G))=\alpha (G)$.

• (ii) If $\delta (G)\ge \frac{3}{4}n$, then G satisfies $\alpha (F_k(G))=\alpha (G)$ for every $k=1,\ldots ,n-1$.

Proof

(i) With $k=2$, the condition (10) becomes $\delta (G)\ge \frac{3}{2}(n-1)$. Then, since $\alpha (F_1(G))=\alpha (G)$, Theorem 3.7 gives the result.

(ii) Assuming that n is even (the odd case is similar), it is enough to prove the result for $k=n/2$. In this case, the condition (10) becomes $\delta (G)\ge \phi (n/2)=\frac{n(3n-6)}{4(n-1)}$. It is readily checked that $\frac{3}{4}n>\phi (n/2)>\phi (k)$ for every $k=2,\ldots ,\frac{n}{2}-1$. So, we can use induction from case (i) to prove the hypotheses in Theorem 3.7 hold for every k. $\square$

Some examples of known graphs satisfying Corollary 3.8 are:

• With (minimum=maximum) degree $n-1$, the complete graphs (already mentioned).

• With degree $n-2$, the cocktail party (regular) graph (obtained from the complete graph with an even number of vertices minus a matching).

• With degree $n-3$, the complement (regular) graph $\overline{C_n}$ of the cycle with $n\ge 12$ vertices.

• The complete r-partite graph $G=K_{n_1,n_2,\ldots ,n_r}\ne K_r$ for $r\ge 2$, with number of vertices $n=n_1+n_2+\cdots +n_r$, for $n_1\le n_2\le \cdots \le n_r$, with minimum degree $\delta (G)=n_1+\cdots +n_{r-1}$ and $n\ge 3n_r-2$.

4 Conclusions

As explained in the Introduction, Caputo, Liggett, and Richthammer [3] proved the Aldous’ spectral gap conjecture, which includes the until then conjecture that states that the algebraic connectivity of a graph and its k-token graph coincide for any k. They used random walks and interchanges of processes on a weighted graph. However, some algebraic graph theory community researchers are looking for an algebraic proof. In this paper, we provide an algebraic proof for some families of graphs. We think that our techniques could be applied to other families and, perhaps, graphs in general.