Global behavior of a third order difference equation with quadratic term

Abstract

In this paper, we solve and study the global behavior of the admissible solutions of the difference equation

$$\begin{aligned} x_{n+1}=\frac{x_{n}x_{n-2}}{-ax_{n-1}+bx_{n-2}}, \quad n=0,1,\ldots , \end{aligned}$$

where $a, b>0$ and the initial values $x_{-2}$, $x_{-1}$, $x_{0}$ are real numbers.

1 Introduction

In [11], the author obtained the solutions and determined the forbidden sets of the two difference equations

$$\begin{aligned} x_{n+1}=\frac{x_{n}x_{n-1}}{x_{n}-x_{n-2}}, \quad n=0,1,\ldots , \end{aligned}$$

and

$$\begin{aligned} x_{n+1}=\frac{x_{n}x_{n-1}}{-x_{n}+x_{n-2}}, \quad n=0,1,\ldots , \end{aligned}$$

where the initial values $x_{-2}$, $x_{-1}$, $x_{0}$ are real numbers.

In [3], the author determined the forbidden set and discussed the global behavior of the solutions of the difference equation

$$\begin{aligned} x_{n+1}=\frac{ax_{n}x_{n-2}}{-bx_{n}+cx_{n-3}},\quad n=0,1,\ldots , \end{aligned}$$

where a, b, c are positive real numbers and the initial conditions $x_{-2}$,$x_{-1}$,$x_0$ are real numbers.

He also in [12] determined the forbidden sets and discussed the global behaviors of solutions of the two difference equations

$$\begin{aligned} x_{n+1}=\frac{ax_{n}x_{n-1}}{\pm bx_{n-1}+ cx_{n-2}},\quad n=0,1,\ldots , \end{aligned}$$

where a, b, c are positive real numbers and the initial conditions $x_{-2},x_{-1},x_0$ are real numbers.

Recently, there has been a great interest in studying properties of nonlinear and rational difference equations (see [1, 4,5,6,7,8,9,10, 12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37] and the references therein).

In this paper, we study the difference equation

$$\begin{aligned} x_{n+1}=\frac{x_{n}x_{n-2}}{-ax_{n-1}+bx_{n-2}}, \quad n=0,1,\ldots , \end{aligned}$$

(1)

where $a, b>0$ and the initial values $x_{-2}$, $x_{-1}$, $x_{0}$ are real numbers.

The transformation

$$\begin{aligned} y_n=\frac{x_{n-1}}{x_n},\ \text {with}\ y_{-1}=\frac{x_{-2}}{x_{-1}},\ y_{0}=\frac{x_{-1}}{x_{0}} \end{aligned}$$

(2)

reduces Eq. (1) into the difference equation

$$\begin{aligned} y_{n+1}=-\frac{a}{y_{n-1}}+b,\ n=0,1,\ldots \end{aligned}$$

(3)

The solution of (3) depends on the relation between a and b. By solving Eq. (3) and after some calculations, the solution of Eq. (1) can be obtained.

2 Case $b^2>4a$

In this section, we assume that $b^2>4a$. Suppose that

$$\begin{aligned} \theta _j=\frac{\lambda ^j_{+}-\lambda ^j_{-}}{\sqrt{b^2-4a}}, \end{aligned}$$

where $\lambda _{-}=\frac{b}{2}-\frac{\sqrt{b^2-4a}}{2}$ and $\lambda _{+}=\frac{b}{2}+\frac{\sqrt{b^2-4a}}{2}$, $j=0,1,\ldots$.

We give the following Lemma without proof:

Lemma 2.1

The following identities are true:

• (1)
  $$\begin{aligned} -a\theta _{j}+b\theta _{j+1}=\theta _{j+2},\quad j=0,1,\ldots \end{aligned}$$
• (2)
  $$ \begin{gathered} - a( - ax_{0} \theta _{j} + x_{{ - 1}} \theta _{{j + 1}} ) + b( - ax_{0} \theta _{{j + 1}} + x_{{ - 1}} \theta _{{j + 2}} ) \hfill \\ \quad = - ax_{0} \theta _{{j + 2}} + x_{{ - 1}} \theta _{{j + 3}} ,\quad j = 0,1, \ldots \hfill \\ \end{gathered} $$
• (3)
  $$ \begin{gathered} - a( - ax_{{ - 1}} \theta _{j} + x_{{ - 2}} \theta _{{j + 1}} ) + b( - ax_{{ - 1}} \theta _{{j + 1}} + x_{{ - 2}} \theta _{{j + 2}} ) \hfill \\ \quad = - ax_{{ - 1}} \theta _{{j + 2}} + x_{{ - 2}} \theta _{{j + 3}} ,\quad j = 0,1, \ldots \hfill \\ \end{gathered} $$

Theorem 2.2

Let $\{x_n\}_{n=-2}^\infty$ be an admissible solution of Equation (1). Then

$$ x_{n} = \left\{ {\begin{array}{*{20}l} {\frac{\nu }{{\gamma _{0} \left( {\frac{{n - 1}}{2}} \right)\gamma _{{ - 1}} \left( {\frac{{n + 1}}{2}} \right)}},} \hfill & {n = 1,3, \ldots ,} \hfill \\ {\frac{\nu }{{\gamma _{0} \left( {\frac{n}{2}} \right)\gamma _{{ - 1}} \left( {\frac{n}{2}} \right)}},} \hfill & {n = 2,4, \ldots ,} \hfill \\ \end{array} } \right. $$

(4)

where $\nu =x_{0}x_{-1}x_{-2}$, $\gamma _{-i}(n)=-ax_{-i}\theta _{n} +x_{-i-1}\theta _{n+1}$, $i=0,1$ and $j=0,1,\ldots$.

Proof

We can write the given solution (4) as

$$\begin{aligned} \begin{aligned}&x_{2m+1}=\frac{\nu }{\gamma _{0}(m)\gamma _{-1}(m+1)},\\&x_{2m+2}=\frac{\nu }{\gamma _{0}(m+1)\gamma _{-1}(m+1)}. \end{aligned} \end{aligned}$$

(5)

When $m=0$,

$$\begin{aligned} \begin{aligned} x_{1}&=\frac{\nu }{(-ax_0\theta _{0}+x_{-1} \theta _{1})(-ax_{-1}\theta _{1} +x_{-2}\theta _{2})}\\ {}&=\frac{x_{0}x_{-1}x_{-2}}{(x_{-1})(-ax_{-1}+bx_{-2})}=\frac{x_{0}x_{-2}}{-ax_{-1}+bx_{-2}}\\ {}&=x_1. \end{aligned} \end{aligned}$$

Similarly

$$\begin{aligned} \begin{aligned} x_{2}&=\frac{\nu }{(-ax_0\theta _{1}+x_{-1} \theta _{2})(-ax_{-1}\theta _{1} +x_{-2}\theta _{2})}\\ {}&=\frac{x_{0}x_{-1}x_{-2}}{(-ax_0+bx_{-1})(-ax_{-1}+bx_{-2})}=\frac{x_{1}x_{-1}}{-ax_{0}+bx_{-1}}\\ {}&=x_2. \end{aligned} \end{aligned}$$

Suppose that the result is true for $m>0$.

Then

$$\begin{aligned}&\frac{x_{2m+1}x_{2m-1}}{-ax_{2m}+bx_{2m-1}}\\&\quad =\frac{\frac{\nu }{\gamma _{0}(m)\gamma _{-1}(m+1)} \frac{\nu }{\gamma _{0}(m-1)\gamma _{-1}(m)}}{-a\frac{\nu }{\gamma _{0}(m)\gamma _{-1}(m)} +b\frac{\nu }{\gamma _{0}(m-1)\gamma _{-1}(m)}}\\&\quad = \frac{\nu }{\gamma _{-1}(m+1)(-a\gamma _{0}(m-1)+b\gamma _{0}(m))}. \end{aligned}$$

Using Lemma (2.1), we get

$$\begin{aligned}&\frac{x_{2m+1}x_{2m-1}}{-ax_{2m}+bx_{2m-1}} \\&\quad =\frac{\nu }{\gamma _{-1}(m+1)\gamma _{0}(m+1)}\\&\quad =x_{2m+2}. \end{aligned}$$

Similarly we can show that

$$\begin{aligned} \frac{x_{2m+2}x_{2m}}{-ax_{2m+1}+bx_{2m}} =x_{2m+3}. \end{aligned}$$

This completes the proof. $\square$

Consider the set

$$\begin{aligned} D_1=\left\{ (x,y,z)\in {\mathbb {R}}^3: \frac{x}{\lambda ^2_{+}/a^2} =\frac{y}{\lambda _{+}/a}=z\right\} \end{aligned}$$

and

$$\begin{aligned} D_2=\left\{ (x,y,z)\in {\mathbb {R}}^3: \frac{x}{\lambda ^2_{-}/a^2} =\frac{y}{\lambda _{+}/a}=z\right\} . \end{aligned}$$

Theorem 2.3

The two sets $D_1$ and $D_2$ are invariant sets for Equation (1).

Proof

Let $(x_0,x_{-1},x_{-2})\in D_1$. We show that $(x_n,x_{n-1},x_{n-2})\in D_1$ for each $n\in {\mathbb {N}}$. The proof is by induction on n. The point $(x_0,x_{-1},x_{-2})\in D_1$ implies

$$\begin{aligned} \frac{x_0}{\lambda ^2_{+}/a^2} =\frac{x_{-1}}{\lambda _{+}/a}=x_{-2}. \end{aligned}$$

Now for $n=1$, we have

$$\begin{aligned} x_{1}=\frac{x_0x_{-2}}{-ax_{-1}+bx_{-2}}= \frac{(\lambda _{+}/a)x_{-1}(a/\lambda _{+})x_{-1}}{-ax_{-1}+b(a/\lambda _{-})x_{-1}}= \frac{\lambda ^2_{+}}{a^2}x_{-1}. \end{aligned}$$

Then we have

$$\begin{aligned} \frac{x_1}{1/\lambda ^2_{-}} =\frac{x_{0}}{1/\lambda _{-}}=x_{-1}. \end{aligned}$$

This implies that $(x_1,x_{0},x_{-1})\in D_1$.

Suppose now that $(x_n,x_{n-1},x_{n-2})\in D_1$. That is

$$\begin{aligned} \frac{x_n}{\lambda ^2_{+}/a^2} =\frac{x_{n-1}}{\lambda _{+}/a}=x_{n-2}. \end{aligned}$$

Then

$$\begin{aligned} x_{n+1}=\frac{x_nx_{n-2}}{-ax_{n-1}+bx_{n-2}}= \frac{((\lambda _{+}/a))x_{n-1}(a/\lambda _{+})x_{n-1}}{-ax_{n-1}+b(a/\lambda _{+})x_{n-1}}= \frac{\lambda ^2_{+}}{a^2}x_{n-1}. \end{aligned}$$

Then $(x_{n+1},x_{n},x_{n-1})\in D_1$. Therefore, $D_1$ is an invariant set for Eq. (1).

By similar way, we can show that $D_2$ is an invariant set for Eq. (1).

This completes the proof. $\square$

Theorem 2.4

Assume that $\{x_n\}_{n=-2}^\infty$ is an admissible solution of Equation (1). The following statements are true:

• (1) If $b>a+1$, then the solution $\{x_n\}_{n=-2}^\infty$ converges to zero.

• (2) If $b=a+1$, then we have the following:

  • (a) If $b<2$, then the solution $\{x_n\}_{n=-2}^\infty$ converges to a finite limit.

  • (b) If $b>2$, then the solution $\{x_n\}_{n=-2}^\infty$ converges to zero.

• (3) If $b<a+1$, then we have the following:

  • (a) If $b<2$, then the solution $\{x_n\}_{n=-2}^\infty$ is unbounded.

  • (b) If $b>2$, then the solution $\{x_n\}_{n=-2}^\infty$ converges to zero.

Proof

We can write $\theta _j=\lambda ^j_{+}\frac{(1- (\frac{\lambda _{-}}{\lambda _{+}})^j)}{\sqrt{b^2-4a}}$.

• (1) If $b>a+1$, then $\lambda _{+}>1$. That is $\theta _m\rightarrow \infty$ as $m\rightarrow \infty$. Also both of $\gamma _{0}(m)$ and $\gamma _{-1}(m)$ are unbounded. This implies that

  $$\begin{aligned} x_{2m+1}=\frac{\nu }{\gamma _{0}(m)\gamma _{-1}(m+1)}\rightarrow 0\ \text {as}\ m\rightarrow \infty . \end{aligned}$$

  Similarly for $x_{2m+2}$.

• (2) Suppose that $b=a+1$, then either $\lambda _{-}=1$ or $\lambda _{+}=1$.

  • (a) If $b<2$, then $\lambda _{+}=1$. It follows that $\theta _m\rightarrow \frac{1}{\sqrt{b^2-4a}}$ as $m\rightarrow \infty$. This implies that

    $$\begin{aligned} x_{2m+1}\rightarrow \frac{\nu (b^2-4a)}{(-ax_0+x_{-1})(-ax_{-1}+x_{-2})}. \end{aligned}$$

    Similarly for $x_{2m+2}$.

  • (b) If $b>2$, then $\lambda _{-}=1$. It follows that $\theta _m\rightarrow \infty$ as $m\rightarrow \infty$. This implies that

    $$\begin{aligned} x_{2m+1}=\frac{\nu }{\gamma _{0}(m)\gamma _{-1}(m+1)}\rightarrow 0\ \text {as}\ m\rightarrow \infty . \end{aligned}$$

    Similarly for $x_{2m+2}$.

• (3) The proof is similar to that in (2) and is omitted.

This completes the proof. $\square$

Example (1)

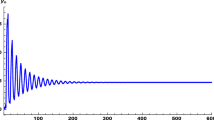
Figure 1 shows that, if $a=1.1,b=2.2$ ($b>a+1$), then a solution $\{x_n\}_{n=-2}^\infty$ of Eq. (1) with $x_{-2}=3$, $x_{-1}=-1$ and $x_{0}=2$ converges to zero.

Example (2)

Figure 2 shows that, if $a=0.7,b=1.7$ ($b=a+1$ and $b<2$), then a solution $\{x_n\}_{n=-2}^\infty$ of Eq. (1) with $x_{-2}=3$, $x_{-1}=-1$ and $x_{0}=2$ converges to

$$\begin{aligned} \frac{\nu (b^2-4a)}{(-ax_0+x_{-1})(-ax_{-1}+x_{-2})} \simeq 0.06081. \end{aligned}$$

Fig. 1

$x_{n+1}=\frac{x_{n}x_{n-2}}{-1.1x_{n-1}+2.2x_{n-2}}$

Fig. 2

$x_{n+1}=\frac{x_{n}x_{n-2}}{-0.7x_{n-1}+1.7x_{n-2}}$

Example (3)

Figure 3 shows that, if $a=0.2,b=1$ ($b<a+1$ and $b<2$), then a solution $\{x_n\}_{n=-2}^\infty$ of Eq. (1) with $x_{-2}=3$, $x_{-1}=-1$ and $x_{0}=2$ is unbounded.

Example (4)

Figure 4 shows that, if $a=3, b=3.7$ ($b<a+1$ and $b>2$), then a solution $\{x_n\}_{n=-2}^\infty$ of Eq. (1) with $x_{-2}=3$, $x_{-1}=-1$ and $x_{0}=2$ converges to zero.

Fig. 3

$x_{n+1}=\frac{x_{n}x_{n-2}}{-0.2x_{n-1}+x_{n-2}}$

Fig. 4

$x_{n+1}=\frac{x_{n}x_{n-2}}{-3x_{n-1}+3.7x_{n-2}}$

3 Case $b^2=4a$

During this section, we assume that $b^2=4a$.

Theorem 3.1

Let $\{x_n\}_{n=-2}^\infty$ be an admissible solution of Equation (1). Then

$$ x_{n} = \left\{ {\begin{array}{*{20}l} {\left( {\frac{2}{b}} \right)^{n} \frac{{4\nu }}{{\mu _{0} \left( {\frac{{n - 1}}{2}} \right)\mu _{{ - 1}} \left( {\frac{{n + 1}}{2}} \right)}},} \hfill & {n = 1,3, \ldots ,} \hfill \\ {\left( {\frac{2}{b}} \right)^{n} \frac{{4\nu }}{{\mu _{0} \left( {\frac{n}{2}} \right)\mu _{{ - 1}} \left( {\frac{n}{2}} \right)}},} \hfill & {n = 2,4, \ldots ,} \hfill \\ \end{array} } \right. $$

(6)

where $\nu =x_{0}x_{-1}x_{-2}$, $\mu _{-i}(n)=-bnx_{-i}+2(1+n)x_{-i-1}$, $i=0,1$ and $j=0,1,\ldots$.

Proof

It is sufficient to write the formula (6) as

$$\begin{aligned} \begin{aligned}&x_{2m+1}=\left( \frac{2}{b}\right) ^{2m+1}\frac{4\nu }{\mu _0(m) \mu _{-1}(m+1)},\\ {}&x_{2m+2}=\left( \frac{2}{b}\right) ^{2m+2}\frac{4\nu }{\mu _0(m+1) \mu _{-1}(m+1)}, \end{aligned} \end{aligned}$$

(7)

as well as noting that

$$\begin{aligned} \mu _{-i}(m-1)+\mu _{-i}(m+1)=2\mu _{-i}(m),\ i=0,1. \end{aligned}$$

$\square$

Theorem 3.2

Assume that $\{x_n\}_{n=-2}^\infty$ is an admissible solution of Equation (1). The following statements are true:

• (1) If $b\ge 2$, then the solution $\{x_n\}_{n=-2}^\infty$ converges to zero.

• (2) If $b<2$, then the solution $\{x_n\}_{n=-2}^\infty$ is unbounded.

Proof

Clear that both of $\mu _{0}(m)$ and $\mu _{-1}(m)$ are unbounded. Then (1) is satisfied directly. When $b<2$, then $(\frac{2}{b})^m\rightarrow \infty$ as $m\rightarrow \infty$.

Then using formulas (7) we can write

$$\begin{aligned} |x_{2m+1}|=|\left( \frac{2}{b}\right) ^{2m+1}\frac{4\nu }{m^2(-bx_{0} +2\left( \frac{1}{m}+1)x_{-1}\right) \left( -b\left( 1+\frac{1}{m}\right) x_{-1}+2\left( \frac{2}{m}+1\right) x_{-2}\right) }|. \end{aligned}$$

By applying L’Hospital’s rule, we get $|x_{2m+1}|\rightarrow \infty$ as $m\rightarrow \infty$.

Similarly for $|x_{2m+2}|$.

This completes the proof. $\square$

Example (5)

Figure 5 shows that, if $a=0.64,b=1.6$ ($b^2=4a$ and $b<2$), then a solution $\{x_n\}_{n=-2}^\infty$ of Eq. (1) with $x_{-2}=3$, $x_{-1}=-1$ and $x_{0}=2$ is unbounded.

Example (6)

Figure 6 shows that, if $a=2.25,b=3$ ($b^2=4a$ and $b>2$), then a solution $\{x_n\}_{n=-2}^\infty$ of Eq. (1) with $x_{-2}=3$, $x_{-1}=-1$ and $x_{0}=2$ converges to zero.

Fig. 5

$x_{n+1}=\frac{x_{n}x_{n-2}}{-0.64x_{n-1}+1.6x_{n-2}}$

Fig. 6

$x_{n+1}=\frac{x_{n}x_{n-2}}{-2.25x_{n-1}+3x_{n-2}}$

4 Case $b^2<4a$

In this section, we study the final case when $b^2<4a$ and provide the forbidden set of Eq. (1).

Theorem 4.1

Let $\{x_n\}_{n=-2}^\infty$ be an admissible solution of Equation (1). Then

$$\begin{aligned} x_{n}=\left\{ \begin{array}{rcc} \frac{\sin ^2\alpha }{a^{\frac{n}{2}}} \frac{\nu }{\beta _{0}\left( \frac{n-1}{2}\right) \beta _{-1}\left( \frac{n+1}{2}\right) },&{}n=1,3,\ldots ,\\ \frac{\sin ^2\alpha }{a^{\frac{n}{2}}} \frac{\nu }{\beta _{0}\left( \frac{n}{2}\right) \beta _{-1}\left( \frac{n}{2}\right) },&{}n=2,4,\ldots ,\\ \end{array}\right. \end{aligned}$$

(8)

where $\nu =x_{0}x_{-1}x_{-2}$, $\beta _{-i}(n)= \sqrt{a}x_{-i}\sin n\alpha -x_{-i-1}\sin (n+1)\alpha$,

$\alpha = \tan ^{-1}\frac{\sqrt{4a-b^2}}{b}\in ]0,\frac{\pi }{2}[$ and $i=0,1$.

Proof

We can write the given solution (8) as

$$\begin{aligned} \begin{aligned}&x_{2m+1}=\frac{\sin ^2\alpha }{a^{m+\frac{1}{2}}} \frac{\nu }{\beta _{0}(m)\beta _{-1}(m+1)},\\&x_{2m+2}=\frac{\sin ^2\alpha }{a^{m+1}} \frac{\nu }{\beta _{0}(m+1)\beta _{-1}(m+1)}. \end{aligned} \end{aligned}$$

(9)

When $m=0$,

$$\begin{aligned} \begin{aligned} x_{1}&=\frac{\sin ^2\alpha }{\sqrt{a}} \frac{\nu }{\beta _{0}(0)\beta _{-1}(1)}\\ {}&= \frac{\sin ^2\alpha }{\sqrt{a}} \frac{\nu }{(-x_{-1}\sin \alpha )(\sqrt{a}x_{-1}\sin \alpha -x_{-2}\sin 2\alpha )}\\ {}&= \frac{1}{\sqrt{a}} \frac{\nu }{(-x_{-1}) \left( \sqrt{a}x_{-1}-x_{-2}\frac{b}{\sqrt{a}}\right) } =\frac{x_{0}x_{-2}}{-ax_{-1}+bx_{-2}}\\ {}&=x_1. \end{aligned} \end{aligned}$$

Similarly

$$\begin{aligned} \begin{aligned} x_{2}&=\frac{\sin ^2\alpha }{a} \frac{\nu }{\beta _{0}(1)\beta _{-1}(1)}\\ {}&= \frac{\sin ^2\alpha }{a} \frac{\nu }{(\sqrt{a}x_{0}\sin \alpha -x_{-1}\sin 2\alpha ) (\sqrt{a}x_{-1}\sin \alpha -x_{-2}\sin 2\alpha )}\\ {}&= \frac{1}{a} \frac{\nu }{\left( \sqrt{a}x_{0}-x_{-1}\frac{b}{\sqrt{a}}\right) \left( \sqrt{a}x_{-1}-x_{-2}\frac{b}{\sqrt{a}}\right) }\\ {}&=\frac{\nu }{(-ax_{0}+bx_{-1}) (-ax_{-1}+bx_{-2})}\\ {}&= \frac{x_{1}x_{-1}}{-ax_{0}+bx_{-1}}=x_2. \end{aligned} \end{aligned}$$

Suppose that the result is true for $m>0$.

Then

$$\begin{aligned}&\frac{x_{2m+1}x_{2m-1}}{-ax_{2m}+bx_{2m-1}}\\&\quad =\frac{\left( \frac{\sin ^2\alpha }{a^{m+\frac{1}{2}}} \frac{\nu }{\beta _{0}(m)\beta _{-1}(m+1)}\right) \left( \frac{\sin ^2\alpha }{a^{m-\frac{1}{2}}} \frac{\nu }{\beta _{0}(m-1)\beta _{-1}(m)}\right) }{-a\frac{\sin ^2\alpha }{a^{m}} \frac{\nu }{\beta _{0}(m)\beta _{-1}(m)}+b \frac{\sin ^2\alpha }{a^{m-\frac{1}{2}}} \frac{\nu }{\beta _{0}(m-1)\beta _{-1}(m)}}\\&\quad = \frac{(\sin ^2\alpha ) \nu }{a^{m+\frac{1}{2}\beta _{-1}(m+1) (-\sqrt{a}\beta _{0}(m-1)+b\beta _{0}(m))}}. \end{aligned}$$

Using the identity

$$\begin{aligned} \sqrt{a}\beta _{0}(m-1)+\sqrt{a}\beta _{0}(m+1) =b\beta _{0}(m) \end{aligned}$$

we get

$$\begin{aligned}&\frac{x_{2m+1}x_{2m-1}}{-ax_{2m}+bx_{2m-1}}\\&\quad =\frac{\sin ^2\alpha }{a^{m+1}}\frac{\nu }{\beta _{0}(m+1)\beta _{-1}(m+1)}\\&\quad =x_{2m+2}. \end{aligned}$$

Similarly we can show that

$$\begin{aligned} \frac{x_{2m+2}x_{2m}}{-ax_{2m+1}+bx_{2m}} =x_{2m+3}. \end{aligned}$$

This completes the proof. $\square$

In the following result, we show the existence of periodic solutions for Eq. (1).

Theorem 4.2

Assume that $\{x_n\}_{n=-2}^\infty$ is an admissible solution of Equation (1) and let $a=1$. If $\alpha =\frac{l}{k}\pi$ is a rational multiple of $\pi$ (with $0<l<\frac{k}{2}$), then $\{x_n\}_{n=-2}^\infty$ is periodic with prime period 2k.

Proof

Suppose that $a=1$. Using formula (9), we can write

$$\begin{aligned} \begin{aligned}&x_{2m+2k+1}=\sin ^2\alpha \frac{\nu }{\beta _{0}(m+k)\beta _{-1}(m+1+k)} \end{aligned} \end{aligned}$$

(10)

But for each $i=0,1$ we have

$$\begin{aligned} \begin{aligned} \beta _{-i}(m+k)&=x_{-i}\sin (m+k)\alpha -x_{-i-1}\sin (m+1+k)\alpha \\ {}&=x_{-i}\sin (m\alpha +k\alpha ) -x_{-i-1}\sin ((m+1)\alpha +k\alpha )\\&=x_{-i}\sin (m\alpha +l\pi )-x_{-i-1}\sin ((m+1)\alpha +l\pi )\\ {}&=(-1)^l (x_{-i}\sin m\alpha -x_{-i-1}\sin (m+1)\alpha ))\\ {}&= (-1)^l\beta _{-i}(m). \end{aligned} \end{aligned}$$

(11)

Then

$$\begin{aligned} \begin{aligned} x_{2m+2k+1}&=\sin ^2\alpha \frac{\nu }{\beta _{0}(m+k)\beta _{-1}(m+1+k)}\\ {}&= \sin ^2\alpha \frac{\nu }{(-1)^{2l}\beta _{0}(m) \beta _{-1}(m+1)}\\ {}&=x_{2m+1}. \end{aligned} \end{aligned}$$

(12)

Similarly, we can show that $x_{2m+2k+2}=x_{2m+2}$.

This completes the proof. $\square$

Theorem 4.3

Assume that $\{x_n\}_{n=-2}^\infty$ is an admissible solution of Equation (1). The following statements are true:

• (1) If $a<1$, then the solution $\{x_n\}_{n=-2}^\infty$ is unbounded.

• (2) If $a>1$, then the solution $\{x_n\}_{n=-2}^\infty$ converges to zero.

Proof

The proof is a direct consequence using formulas (9). $\square$

Example (7)

Figure 7 shows that, if $a=1,b=\sqrt{\frac{3-\sqrt{5}}{2}}$ ($b^2<4a$ and $\alpha =\frac{2\pi }{5}$), then a solution $\{x_n\}_{n=-2}^\infty$ of Eq. (1) with $x_{-2}=3$, $x_{-1}=-1$ and $x_{0}=2$ is periodic with prime period 10.

Example (8)

Figure 8 shows that, if $a=1,b=\sqrt{3}$ ($b^2<4a$ and $\alpha =\frac{\pi }{6}$), then a solution $\{x_n\}_{n=-2}^\infty$ of Eq. (1) with $x_{-2}=3$, $x_{-1}=-1$ and $x_{0}=2$ is periodic with prime period 12.

Fig. 7

$x_{n+1}=\frac{x_{n}x_{n-2}}{-x_{n-1}+ \sqrt{\frac{3-\sqrt{5}}{2}}x_{n-2}}$

Fig. 8

$x_{n+1}=\frac{x_{n}x_{n-2}}{-x_{n-1}+\sqrt{3}x_{n-2}}$

In the remainder of this section, we give the forbidden set of Eq. (1) (which depends on the relation between a and b).

Clear that, if $x_0=0$ and $x_{-1}x_{-2}\ne 0$, then $x_{3}$ is undefined. If $x_{-1}=0$ and $x_{0}x_{-2}\ne 0$, then $x_{5}$ is undefined. If $x_{-2}=0$ and $x_{0}x_{-1}\ne 0$, then $x_{4}$ is undefined.

Therefore, the point $(x_{0},x_{-1},x_{-2})$ with $x_{0}x_{-1}x_{-2}=0$ belongs to the forbidden set of Eq. (1).

The following result gives the forbidden sets of Eq. (1) for all values of $a>0$ and $b>0$.

Theorem 4.4

The following statements are true:

• (1) If $b^2>4a$, then the forbidden set of equation (1) is

  $$\begin{aligned} \begin{aligned} F_1=&\bigcup _{i=0}^2\{(u_0,u_{-1},u_{-2})\in {\mathbb {R}}^3:u_{-i}=0\}\cup \\ {}&\bigcup _{m=1}^\infty \left\{ (u_0,u_{-1},u_{-2})\in {\mathbb {R}}^3:u_{0}=\frac{u_{-1}}{a}\frac{\theta _{m+1}}{\theta _{m}}\right\} \cup \\ {}&\bigcup _{m=1}^\infty \left\{ (u_0,u_{-1},u_{-2})\in {\mathbb {R}}^3:u_{-1}=\frac{u_{-2}}{a}\frac{\theta _{m+1}}{\theta _{m}}\right\} . \end{aligned} \end{aligned}$$

• (2) If $b^2=4a$, then the forbidden set of equation (1) is

  $$\begin{aligned} \begin{aligned} F_2=&\bigcup _{i=0}^2\{(u_0,u_{-1},u_{-2})\in {\mathbb {R}}^3:u_{-i}=0\}\cup \\ {}&\bigcup _{m=1}^\infty \left\{ (u_0,u_{-1},u_{-2})\in {\mathbb {R}}^3:u_{0}=2\frac{1+m}{m}u_{-1}\right\} \cup \\ {}&\bigcup _{m=1}^\infty \left\{ (u_0,u_{-1},u_{-2})\in {\mathbb {R}}^3:u_{-1}=2\frac{1+m}{m}u_{-2}\right\} . \end{aligned} \end{aligned}$$

• (3) If $b^2>4a$, then the forbidden set of equation (1) is

  $$\begin{aligned} \begin{aligned} F_3=&\bigcup _{i=0}^2\{(u_0,u_{-1},u_{-2})\in {\mathbb {R}}^3:u_{-i}=0\}\cup \\ {}&\bigcup _{m=1}^\infty \left\{ (u_0,u_{-1},u_{-2})\in {\mathbb {R}}^3:u_{0}=\frac{\sin (m+1)\alpha }{\sqrt{a}\sin m \alpha }u_{-1}\right\} \cup \\&\bigcup _{m=1}^\infty \left\{ (u_0,u_{-1},u_{-2})\in {\mathbb {R}}^3:u_{-1}=\frac{\sin (m+1)\alpha }{\sqrt{a}\sin m \alpha }u_{-2}\right\} . \end{aligned}\end{aligned}$$