Towards a classification of rigid product quotient varieties of Kodaira dimension 0

Dedicated to Fabrizio Catanese on the occasion of his 70th birthday with gratitude and admiration.

Abstract

In this paper the authors study quotients of the product of elliptic curves by a rigid diagonal action of a finite group G. It is shown that only for $G = {{\,\mathrm{He}\,}}(3), {\mathbb {Z}}_3^2$, and only for dimension $\ge 4$ such an action can be free. A complete classification of the singular quotients in dimension 3 and the smooth quotients in dimension 4 is given. For the other finite groups a strong structure theorem for rigid quotients is proven.

1 Introduction

A compact complex manifold is called rigid if it has no nontrivial deformations. In [2] several notions of rigidity have been discussed, the relations among them have been studied and many questions and conjectures have been proposed.

We state here only the part of [2, Definition 2.1], which will be relevant for our purposes:

Definition 1.1

Let X be a compact complex manifold of dimension n.

• 1. A deformation of X is a proper smooth holomorphic map of pairs $f :({\mathfrak {X}},X) \rightarrow (\mathcal {B}, b_0)$, where $({{\mathcal {B}}},b_0)$ is a connected (possibly not reduced) germ of a complex space.

• 2. X is said to be rigid if for each deformation of X, $f :({\mathfrak {X}},X) \rightarrow ({{\mathcal {B}}}, b_0)$ there is an open neighbourhood $U \subset {{\mathcal {B}}}$ of $b_0$ such that $X_t := f^{-1}(t) \simeq X$ for all $t \in U$.

• 3. X is said to be infinitesimally rigid if $H^1(X, \Theta _X) = 0$, where $\Theta _X$ is the sheaf of holomorphic vector fields on X.

Remark 1.2

• 1. If X is infinitesimally rigid, then X is also rigid. This follows by Kodaira-Spencer-Kuranishi theory, since $H^1(X, \Theta _X)$ is the Zariski tangent space of the germ of analytic space which is the base ${{\,\mathrm{Def}\,}}(X)$ of the Kuranishi semiuniversal deformation of X. So, if $H^1(X, \Theta _X) =0$, ${{\,\mathrm{Def}\,}}(X)$ is a reduced point and all deformations are induced by the trivial deformation. The other implication does not hold in general as it was shown in [4], compare also [18].

• 2. Observe that, as it is shown in [2, Theorem 2.3], a compact complex manifold is rigid if and only if the base of the Kuranishi family ${{\,\mathrm{Def}\,}}(X)$ has dimension 0.

• 3. The only rigid curve is ${\mathbb {P}}^1$; for $n=2$ it was shown in [2, Theorem 1.3] that a rigid compact complex surface has Kodaira dimension $- \infty$ or 2.

That the restriction on the Kodaira dimension is a phenomenon in low dimensions and that in higher dimensions rigid manifolds are much more frequent has already been observed in [2, Theorem 1.4] (cf. also [7] for Kodaira dimension 0, [3] for Kodaira dimension 1):

Theorem 1.3

For all $n \ge 3$ and $-\infty ,0 \le k \le n$ there is a infinitesimally rigid n-dimensional compact complex manifold $Z_{n,k}$ of Kodaira dimension k.

One idea to construct the infinitesimally rigid examples is to consider finite quotients of smooth compact complex manifolds (often products of curves) with respect to a (infinitesimally) rigid holomorphic group action (see Definition 2.1). If one considers non free actions, under mild assumptions it is still true that the quotient is infinitesimal rigid (in dimension at least three), but since we are interested in infinitesimally rigid manifolds, we have to compare the infinitesimal deformations of the singular quotient with those of a suitable resolution of singularities.

The aim of this paper is to give a classification of infinitesimally rigid quotients of a product of elliptic curves by a diagonal action of a finite group G as far as possible. We first prove the following:

Theorem 1.4

Let G be a finite group which admits a rigid free diagonal action on a product of elliptic curves $E_1 \times \cdots \times E_n$. Then:

• 1. $n\ge 4$,

• 2. $E_i$ is the Fermat elliptic curve for each $1 \le i \le n$,

• 3. $G = {\mathbb {Z}}_3^2$ or the Heisenberg group ${{\,\mathrm{He}\,}}(3)$ of order 27.

These two groups are part of four so-called exceptional groups, which are groups admitting a rigid action on an elliptic curve such that the translation part is not uniquely determined (cf. Proposition 4.4).

For the non exceptional case instead we have the following result:

Theorem 1.5

Assume that G is not exceptional and admits a rigid diagonal action on a product of elliptic curves $E_1 \times \cdots \times E_n$. Then the elliptic curves are isomorphic, i.e., $E_1 \cong \cdots \cong E_n = :E$. The quotient is isomorphic to $X_{n,d}:=E^n/{\mathbb {Z}}_d$, where ${\mathbb {Z}}_d$ acts by multiplication with $\zeta _d \cdot {{\,\mathrm{Id}\,}}$. Here $d =3,6$ and E is the Fermat elliptic curve, or $d=4$ and E is the harmonic elliptic curve.

Remark 1.6

• 1. Observe that for the non exceptional groups we have in each dimension exactly one case for d. Unfortunately these quotients are singular, the singularities are of type $\frac{1}{k}(1, \ldots , 1)$, where $k~ \big \vert ~ d$. For $n \ge d$ these singularities are canonical and it can be shown that there is a resolution of singularities which is infinitesimally rigid (cf. [3]).

• 2. For $n=d=3,4,6$ the variety $X_{n,d}$ is a singular Calabi-Yau variety (cf. [7]).

We finally completely classify rigid diagonal actions of the two exceptional groups ${\mathbb {Z}}_3^2$ and ${{\,\mathrm{He}\,}}(3)$ in dimensions 3 and the free ones in dimension 4. In fact, we prove the following:

Theorem 1.7

• 1. There is exactly one isomorphism class of quotient manifolds $E^4/{\mathbb {Z}}_3^2$ resp. $E^4/{{\,\mathrm{He}\,}}(3)$ obtained by a rigid free and diagonal action. They have non isomorphic fundamental groups.

• 2. For each exceptional group ${\mathbb {Z}}_3^2$ and ${{\,\mathrm{He}\,}}(3)$ there are exactly four isomorphism classes of (singular) quotients $X_i:=E^3/{\mathbb {Z}}_3^2$ and $Y_i:=E^3/{{\,\mathrm{He}\,}}(3)$ obtained by a rigid diagonal G-action:

  • (i) $X_4$ and $Y_4$ are isomorphic to Beauville’s Calabi-Yau threefold $X_{3,3}$.

  • (ii) $X_3$ and $Y_3$ are also Calabi-Yau, uniformized by $X_{3,3}$ and admit crepant resolutions, which are rigid.

  • (iii) $X_2$ and $X_3$, resp. $Y_2$ and $Y_3$, are diffeomorphic but not biholomorphic.

  • (iv) The eight threefolds $X_i$, $Y_j$ form five distinct topological classes.

Our paper is organized as follows:

In a short first section we recall some facts on rigid group actions on complex manifolds. In the second chapter we treat rigid actions on elliptic curves recalling that a finite group G admitting a rigid action on an elliptic curve E has to be of the form $G= A \rtimes _{\varphi _d} {\mathbb {Z}}_d$, where $d \in \{3,4,6\}$, and E is the Fermat or the harmonic elliptic curve. Moreover we show that if G admits a rigid action on a product of elliptic curves, these curves have all to be the same. In the following section we prove Theorems 1.4 and 1.5 .

The last section is dedicated to the classification of the actions of the exceptional groups in dimensions 3 and 4. The results on the isomorphism classes in Theorem  1.7 is done using a MAGMA algorithm [11], which is available on the website of the second author: http://www.staff.uni-bayreuth.de/~bt300503/publi.html.

To obtain the topological results we exploit the fact that the fundamental groups of the smooth quotients resp. the orbifold fundamental groups of the singular quotients in dimension three are crystallographic groups.

2 Rigid group actions on complex manifolds

In this short introductory section we recall the definition of rigid group actions on complex manifolds and give a criterion for the rigidity of the diagonal action on a product of such.

Since in all of this article we only discuss infinitesimal rigidity, we often drop the adverb infinitesimally and only talk about rigidity.

Definition 2.1

Let X be a compact complex manifold and G be a finite group acting holomorphically on X. We say that the G-action is infinitesimally rigid if and only if $H^1(X,\Theta _X)^G=0$, where $\Theta _X$ is the tangent sheaf of X.

Remark 2.2

• 1. If the action of G is not faithful, then, denoting the kernel by K, we obviously have that $H^1(X,\Theta _X)^G=H^1(X,\Theta _X)^{G/K}$, hence after replacing G by G/K we may assume that G acts faithfully.

• 2. If G acts freely in codimension one, then for all i there is an isomorphism

  $$\begin{aligned} H^i(X/G,\Theta _{X/G}) \simeq H^i(X,\Theta _X)^G. \end{aligned}$$

  In particular, since $H^1(X/G,\Theta _{X/G})$ classifies the infinitesimal equisingular deformations of X/G, we see that, if the action is rigid, the quotient X/G has no equisingular deformations.

• 3. Consider the low term exact sequence of the local-to-global ${{\,\mathrm{Ext}\,}}$-spectral sequence on $Z := X/G$:

  $$\begin{aligned} 0 \rightarrow H^1(Z, \Theta _Z) \rightarrow {{\,\mathrm{Ext}\,}}^1(\Omega ^1_Z, \mathcal {O}_Z) \rightarrow H^0(Z,\mathcal {E}xt^1(\Omega ^1_Z, \mathcal {O}_Z)) \rightarrow \cdots . \end{aligned}$$

  By Schlessinger’s result [20] isolated quotient singularities in dimensions at least 3 are infinitesimally rigid, i.e., ${\mathcal {E}}xt^1(\Omega ^1_Z, \mathcal {O}_Z) =0$. Therefore the above exact sequence shows that, if G has only isolated fixed points on X, then

  $$\begin{aligned} H^1(Z, \Theta _Z) \simeq {{\,\mathrm{Ext}\,}}(\Omega ^1_Z,\mathcal {O}_Z). \end{aligned}$$

  This means that for Z all infinitesimal deformations are equisingular. In particular, for showing that Z is an infinitesimally rigid variety, it suffices to show that $H^1(X, \Theta _X)^G = 0$.

• 4. If Z is singular, one has to make sure that there is a resolution of singularities ${\widehat{Z}} \rightarrow Z$ such that ${\widehat{Z}}$ is infinitesimally rigid, since primarily we are interested in rigid manifolds (cf. Proposition 5.17).

Let G be a finite group acting holomorphically on the compact complex manifolds $X_1, \ldots , X_n$, then the diagonal subgroup $\Delta _G \simeq G$ acts in a natural way on the product $X_1 \times \cdots \times X_n$, in fact setting:

$$\begin{aligned} g(x_1, \ldots , x_n):=(g x_1, \ldots , g x_n). \end{aligned}$$

It is natural to call this action the diagonal G-action on the product $X_1 \times \cdots \times X_n$. Künneth’s formula allows us to give a reformulation of the rigidity of the diagonal action in terms of the individual actions on the factors:

Proposition 2.3

Let G be a finite group acting holomorphically on the compact complex manifolds $X_1, \ldots , X_n$. Then, the diagonal action on $X:=X_1 \times \cdots \times X_n$ is (infinitesimally) rigid, if and only if:

• 1. the G-action on each $X_i$ is rigid and

• 2. $\big [H^0(X_i,\Theta _{X_i}) \otimes H^1(X_j,{\mathcal {O}}_{X_j})\big ]^G=0$ for all $i \ne j$.

Proof

Let $p_i :X \rightarrow X_i$ be the projection onto the i-th factor. Then

$$\begin{aligned} H^1(X,\Theta _{X})=\bigoplus _{i=1}^{n}H^1(X, p_i^{*}\Theta _{X_i}). \end{aligned}$$

For each $1 \le i \le n$ we have

$$\begin{aligned} H^1(X, p_i^{*}\Theta _{X_i})= H^1(X_i,\Theta _{X_i}) \oplus \bigg [H^0(X_i,\Theta _{X_i}) \otimes \bigg (\bigoplus _{{\mathop {j \ne i}\limits ^{j=1}}}^{n} H^1(X_j, {\mathcal {O}}_{X_j}) \bigg )\bigg ], \end{aligned}$$

according to Künneth’s formula. The claim follows, by taking the G-invariant part. $\square$

Remark 2.4

In the special case where the products $h^0(X_i,\Theta _{X_i}) \cdot h^1(X_j,{\mathcal {O}}_{X_j})$ vanish, a diagonal G-action is rigid if and only if the G-action on each factor $X_i$ is rigid. This happens for example if the complex manifolds $X_i$ are regular or of general type.

3 Rigid actions on elliptic curves

In this paragraph we study rigid diagonal G-actions on a product $E_1 \times \cdots \times E_n$ of elliptic curves under the additional assumption that G acts faithfully on each factor.

Recall that any holomorphic map between elliptic curves, or more generally between complex tori, is induced by an affine linear map. Since the tangent bundle of an elliptic curve is trivial, Proposition 2.3 has a particularly simple reformulation:

Proposition 3.1

Let G be a finite group acting holomorphically on the elliptic curves $E_1, \ldots , E_n$, then the following are equivalent:

• 1. the diagonal G-action on $E_1 \times \cdots \times E_n$ is rigid,

• 2. none of the quadratic differentials $dz_i \otimes dz_j$ is G-invariant.

Proof

By duality, the rigidity conditions in Proposition 2.3 are equivalent to

$$\begin{aligned} H^0(E_i,(\Omega _{E_i}^1)^{\otimes 2})^G =0 \qquad \text {and} \qquad \big [H^1\big (E_i, (\Omega _{E_i}^1)^{\otimes 2}\big ) \otimes H^0(E_j, \Omega _{E_j}^1)\big ]^G = 0. \end{aligned}$$

We use that $H^0(E_i,(\Omega _{E_i}^1)^{\otimes 2}) = \langle dz_i^{\otimes 2} \rangle$ and

$$\begin{aligned} H^1\big (E_i, (\Omega _{E_i}^1)^{\otimes 2}\big ) \simeq H_{\overline{\partial }}^{1,1}(E_i,\Omega _{E_i}^1) = \langle (dz_i \wedge d{\overline{z}}_i) \otimes dz_i \rangle , \end{aligned}$$

to rewrite the rigidity conditions as:

$$\begin{aligned} \langle dz_i^{\otimes 2} \rangle ^G =0 \qquad \text {and} \qquad \langle (dz_i \wedge d{\overline{z}}_i) \otimes dz_i \otimes dz_j \rangle ^G = 0. \end{aligned}$$

The claim follows since G acts trivially on each 2-form $dz_i \wedge d{\overline{z}}_i$. $\square$

Remark 3.2

• 1. A holomorphic G-action of a finite group on an elliptic curve E induces a natural one-dimensional representation

  $$\begin{aligned} \varphi _E :G \rightarrow {{\,\mathrm{GL}\,}}\big (H^0(E, \Omega _{E}^1) \big ), \qquad g \mapsto [dz \mapsto (g^{-1})^{*}dz ]. \end{aligned}$$

  It is called the canonical representation. As it is one dimensional we identify it with its character $\chi _E$. If the linear part of $g\in G$ is a, then the value of $\chi _E(g)$ is equal to ${\overline{a}}$.

• 2. In terms of the characters $\chi _{E_i}$ the statement on the quadratic differentials $dz_i\otimes dz_j$ in Proposition 3.1 translates to $\chi _{E_i} \cdot \chi _{E_j} \ne \chi _{triv}$, for all $1 \le i,j\le n$.

• 3. It is well known that a G-action on an elliptic curve E is rigid if and only if $E/G\simeq {\mathbb {P}}^1$ and the Galois cover $\pi :E \rightarrow E/G\simeq {\mathbb {P}}^1$ is branched in three points $p_1$, $p_2$ and $p_3$. In this case the branching signatures $m_i$, which are defined to be the orders of the (cyclic) stabilizer groups $G_{x_i}$ for some $x_i \in \pi ^{-1}(p_i)$, are up to permutation equal to:

  $$\begin{aligned}{}[m_1,m_2,m_3]=[3,3,3], \quad [2,4,4], \quad \text {or} \quad [2,3,6], \end{aligned}$$

  see [17, Chapter III, Lemma 3.8 b)].

Rigid group actions on compact Riemann surfaces can be described purely in terms of group theory by Riemann’s existence theorem. In our situation we only need the following (much weaker) version of this theorem for elliptic curves.

Proposition 3.3

A finite group G admits a rigid action on an elliptic curve E if and only if there are elements $g_1,g_2,g_3 \in G$ of order $m_i={{\,\mathrm{ord}\,}}(g_i)$, which generate G, fulfill the relation $g_1g_2g_3=1_G$ and $[m_1,m_2,m_3]=[3,3,3]$, [2, 4, 4] or [2, 3, 6].

We refer to [17, Chapter III] for details and mention only the following:

Remark 3.4

• 1. A triple of elements $V:=[g_1,g_2,g_3]$ like in the Proposition above is called a generating triple of G with (branching) signature $[m_1,m_2,m_3]$. Assume that E admits a rigid G-action, let $\pi :E \rightarrow E/G\simeq {\mathbb {P}}^1$ be the quotient map and let ${\mathcal {B}}:=\lbrace p_1, p_2, p_3 \rbrace$ be the set of branch points of $\pi$. The fundamental group of ${\mathbb {P}}^1\setminus {\mathcal {B}}$ is generated by three simple loops $\gamma _i$ around $p_i$ fulfilling a single relation $\gamma _1 *\gamma _2 *\gamma _3=1$. The elements $g_i$ are obtained as the images of $\gamma _i$ under the monodromy homomorphism

  $$\begin{aligned} \eta :\pi _1({\mathbb {P}}^1\setminus {\mathcal {B}}, p) \rightarrow G. \end{aligned}$$

• 2. The cyclic subgroups $\langle g_i \rangle$ and their conjugates provide the non-trivial stabilizer groups of the G-action on E. Let $x_i \in E$ be a point with stabilizer $G_{x_i}=\langle g_i \rangle$, then $g_i$ acts around $x_i$ as a rotation by

  $$\begin{aligned} \exp \bigg (\frac{2\pi \sqrt{-1}}{m_i} \bigg ). \end{aligned}$$

  This rotation constant is nothing else than the linear part of any affine transformation inducing $g_i$. In particular, the character $\chi _E$ (cf. Remark  3.2) can be read of directly from the generating triple.

• 3. The union of the non-trivial stabilizer groups will be denoted by $\Sigma _V$. Observe that $\Sigma _V$ consists of the identity and all group elements which are not translations.

The further discussion heavily relies on the structure of the automorphism group of an elliptic curve E. Recall that ${{\,\mathrm{Aut}\,}}(E)$ is a semidirect product

$$\begin{aligned} {{\,\mathrm{Aut}\,}}(E)=E \rtimes {{\,\mathrm{Aut}\,}}_0(E), \end{aligned}$$

where ${{\,\mathrm{Aut}\,}}_0(E) \simeq {\mathbb {Z}}_2$, ${\mathbb {Z}}_4$ or ${\mathbb {Z}}_6$.

Proposition 3.5

[17, Chapter III Proposition 1.12] An elliptic curve with ${{\,\mathrm{Aut}\,}}_0(E)\simeq {\mathbb {Z}}_4$ is isomorphic to ${\mathbb {C}}/ {\mathbb {Z}}[i]$. An elliptic curve with ${{\,\mathrm{Aut}\,}}_0(E)\simeq {\mathbb {Z}}_6$ is isomorphic to ${\mathbb {C}}/ {\mathbb {Z}}[\zeta _3]$. Here, ${\mathbb {Z}}[i]$ are the Gaussian and ${\mathbb {Z}}[\zeta _3]$ the Eisenstein integers.

Assume now that E admits a rigid faithful action of a finite group G. Then by Remark 3.2 (3), the group G has an element of order 3, 4 or 6 with a fixed point which up to translation is the origin of E. Whence ${{\,\mathrm{Aut}\,}}_0(E)\simeq {\mathbb {Z}}_4$ or ${\mathbb {Z}}_6$ and G must be also a semidirect product

$$\begin{aligned} G\simeq A\rtimes {\mathbb {Z}}_d, \end{aligned}$$

with $d \in \{3,4,6\}$. The normal subgroup A can be considered as a subgroup of the group of n-torsion points $E[n] \simeq {\mathbb {Z}}_n^2$ for a suitable integer n.

More precisely, we have the following:

Proposition 3.6

A finite group G admits a faithful rigid holomorphic action on an elliptic curve E, if and only if it is isomorphic to a semidirect product

$$\begin{aligned} A \rtimes _{\varphi _d} {\mathbb {Z}}_d, \end{aligned}$$

where $d=3,4$ or 6 and $A \le {\mathbb {Z}}_n^2$ is a subgroup for some n, invariant under the action

$$\begin{aligned} \varphi _d :{\mathbb {Z}}_d \rightarrow {{\,\mathrm{Aut}\,}}({\mathbb {Z}}_n^2), \end{aligned}$$

defined by:

• $\varphi _3(1)(a,b)=(-b,a-b)$,

• $\varphi _4(1)(a,b)=(-b,a)$ or

• $\varphi _6(1)(a,b)=(-b,a+b)$.

The possible branching signatures $[m_1,m_2,m_3]$ of the cover $\pi :E \rightarrow E/G$, the abelianisations of G and the isomorphism types of E are summarised in the table below:

	$d=3$	$d=4$	$d=6$
$[m_1,m_2,m_3]$	$\quad [3,3,3] \quad$	$\quad [2,4,4] \quad$	$\quad [2,3,6] \quad$
$G^{ab}$	$\quad {\mathbb {Z}}_3$ or ${\mathbb {Z}}_3^2 \quad$	$\quad {\mathbb {Z}}_4$ or ${\mathbb {Z}}_2 \times {\mathbb {Z}}_4 \quad$	$\quad {\mathbb {Z}}_6 \quad$
E	${\mathbb {C}}/{\mathbb {Z}}[\zeta _3]$	${\mathbb {C}}/ {\mathbb {Z}}[i]$	${\mathbb {C}}/ {\mathbb {Z}}[\zeta _3]$

Before we proof the above proposition we observe the following:

Remark 3.7

• 1. By Proposition  3.3 a group $G=A \rtimes _{\varphi _d} {\mathbb {Z}}_d$ with a rigid action on an elliptic curve E is a quotient of the triangle group

  $$\begin{aligned} {\mathbb {T}}(m_1,m_2,m_3)= \langle a,b,c ~ | ~ a^{m_1} = b^{m_2} =c^{m_3}= abc=1 \rangle , \end{aligned}$$

  where $[m_1,m_2,m_3]$, d, and E are according to the table above. Whence $G^{ab}$ is a quotient of ${\mathbb {T}}(m_1,m_2,m_3)^{ab}$. Since the canonical projection $p :G \rightarrow {\mathbb {Z}}_d$ induces a surjective homomorphism $p^{ab} :G^{ab} \rightarrow {\mathbb {Z}}_d$, the isomorphism types of $G^{ab}$ in the table follow from the well known formula ${\mathbb {T}}(m_1,m_2,m_3)^{ab} \simeq {\mathbb {Z}}/k_1 \times {\mathbb {Z}}/k_2$, where

  • $k_1:=\gcd (m_1,m_2,m_3)$,

  • $k_2:={{\,\mathrm{lcm}\,}}\big (\gcd (m_1,m_2), \gcd (m_2,m_3), \gcd (m_1,m_3)\big )$.

• 2. It follows immediately from the above table that if a finite group G admits a rigid action on an elliptic curve E, the isomorphism type of E as well as the branching signature of the cover $E\rightarrow E/G$ is uniquely determined already by the abelianisation of G.

An immediate geometric consequence of Remark 3.7 (2) is:

Corollary 3.8

Let G be a finite group with a rigid diagonal action on a product of elliptic curves $E_1 \times \cdots \times E_n$, then the curves are all isomorphic to ${\mathbb {C}}/{\mathbb {Z}}[i]$ or they are all isomorphic to ${\mathbb {C}}/{\mathbb {Z}}[\zeta _3]$.

Moreover, the branching signature $[m_1,m_2,m_3]$ is the same for each cover $\pi _i :E_i \rightarrow E_i/G$.

Proof of Proposition 3.6

The formulas for $\varphi _d$ are immediately derived from the semidirect product structure of ${{\,\mathrm{Aut}\,}}(E)\simeq E \rtimes {{\,\mathrm{Aut}\,}}_0(E)$. The claim about the abelianisations follows from Remark 3.7 (2).

We are left to show that any group $A \rtimes _{\varphi _d} {\mathbb {Z}}_d$ has a rigid action on $E={\mathbb {C}}/{\mathbb {Z}}[i]$ or ${\mathbb {C}}/{\mathbb {Z}}[\zeta _3]$. For this purpose, we consider the natural action

$$\begin{aligned} A \rtimes _{\varphi _d} {\mathbb {Z}}_d \rightarrow {{\,\mathrm{Aut}\,}}(E), \qquad (a,b,c) \mapsto \bigg [z \mapsto \zeta _d^cz + \frac{a + \zeta _d b}{n} \bigg ], \end{aligned}$$

which is clearly rigid, because $A \rtimes _{\varphi _d} {\mathbb {Z}}_d$ acts non trivially on the generator $dz^{\otimes 2}$ of $H^0(E,\omega _E^{\otimes 2})$. $\square$

We end the section by the following useful result.

Lemma 3.9

The order of an element of $A \rtimes _{\varphi _d} {\mathbb {Z}}_d$, which is not contained in A, is equal to the order of its image under the canonical projection $p :A \rtimes _{\varphi _d} {\mathbb {Z}}_d \rightarrow {\mathbb {Z}}_d$.

Proof

Let f be such an element. Then the order of p(f) divides the order of f and it suffices to show the following: let $\omega _k$ be a k-th primitive root of unity and $f(z)=\omega _kz+b$, then $f^k=id$. This claim follows immediately from the well known formula $\omega _k^{k-1}+ \cdots +\omega _k+1=0$ and the computation

$$\begin{aligned} f^k(z)=z+ (\omega _k^{k-1}+ \cdots +\omega _k+1)b=z. \end{aligned}$$

$\square$

4 Classifying rigid diagonal actions on products of elliptic curves

In this section we shall show that there are only four candidates of finite groups, which we will call exceptional groups that may allow a free rigid action on the product of (at least 4) elliptic curves, and on the other hand we shall see that all other groups admit in each dimension exactly one rigid (singular) quotient.

The following is a trivial but useful observation:

Remark 4.1

Since we assume the action of G on $E_1 \times \cdots \times E_n$ to be diagonal, it is free if and only if for each $g \in G$ there exists an index $1 \le j \le n$ such that g acts on $E_j$ as a translation.

This motivates the following definition:

Definition 4.2

Let $\psi :G \rightarrow {{\,\mathrm{Aut}\,}}(E)$ be a faithful action of a finite group on an elliptic curve. We define the translation group of $\psi$ to be

$$\begin{aligned} T_{\psi } :=\lbrace g \in G ~ \big \vert ~ \psi (g) ~\text {is a translation} \rbrace . \end{aligned}$$

Remark 4.3

Let G be a finite group.

• 1. The translation group T of an action $\psi :G \rightarrow {{\,\mathrm{Aut}\,}}(E)$ is a normal abelian subgroup of G. If the action is moreover rigid, then $G \simeq T \rtimes {\mathbb {Z}}_d$, where $d=3,4$ or 6.

• 2. Let G be a finite group, admitting a diagonal action on a product of elliptic curves $E_1 \times \cdots \times E_n$. Then the action is free if and only if

  $$\begin{aligned} G = T_1 \cup \cdots \cup T_n, \end{aligned}$$

  where $T_i$ is the translation group of the action on the i-th factor.

A necessary condition for a group $A \rtimes _{\varphi _d} {\mathbb {Z}}_d$ to allow a rigid and free action on a product of elliptic curves is the existence of more than one normal abelian subgroup with quotient ${\mathbb {Z}}_d$. It turns out that there are only four of them and in fact in all other cases the translation group of any rigid action is A.

Proposition 4.4

Let $G=A \rtimes _{\varphi _d} {\mathbb {Z}}_d$ be a finite group and $\psi :G \rightarrow {{\,\mathrm{Aut}\,}}(E)$ be a rigid action on an elliptic curve E. Then $T_{\psi } = A$ except if G is one of the following:

$$\begin{aligned} {\mathbb {Z}}_3^2, \quad {\mathbb {Z}}_3^2 \rtimes _{\varphi _3} {\mathbb {Z}}_3, \quad {\mathbb {Z}}_2 \times {\mathbb {Z}}_4 \quad \text {or} \quad {\mathbb {Z}}_2^2 \rtimes _{\varphi _4} {\mathbb {Z}}_4. \end{aligned}$$

These four groups we shall call exceptional. Before we give a proof of Proposition 4.4, we recall some structural properties of the exceptional groups:

Remark 4.5

(1) We denote the group ${\mathbb {Z}}_3^2 \rtimes _{\varphi _3} {\mathbb {Z}}_3$ by ${{\,\mathrm{He}\,}}(3)$, because it is isomorphic to the Heisenberg group of upper triangular matrices

$$\begin{aligned} \begin{pmatrix} 1 &{} a &{} c \\ 0 &{} 1 &{} b \\ 0 &{} 0 &{} 1 \\ \end{pmatrix} \in {{\,\mathrm{SL}\,}}(3,{\mathbb {F}}_3). \end{aligned}$$

The normal abelian subgroups $A_i \trianglelefteq {{\,\mathrm{He}\,}}(3)$ of index three are the preimages of the index three subgroups of ${\mathbb {Z}}_3^2$ under the surjective homomorphism

$$\begin{aligned} \alpha :{\mathbb {Z}}_3^2 \rtimes _{\varphi _3} {\mathbb {Z}}_3 \rightarrow {\mathbb {Z}}_3^2, \qquad (a,b,c) \mapsto (a+b,c). \end{aligned}$$

They are all isomorphic to ${\mathbb {Z}}_3^2$ and the intersection of two of them equals the kernel of $\alpha$. Moreover, the kernel, the center $C_3:=Z\big ({{\,\mathrm{He}\,}}(3)\big )\simeq {\mathbb {Z}}_3$ and the commutator subgroup $[{{\,\mathrm{He}\,}}(3),{{\,\mathrm{He}\,}}(3)]$ are all the same.

The groups $A_i$, together with the center $C_3$ are all non-trivial normal subgroups of ${{\,\mathrm{He}\,}}(3)$:

Since the center $C_3$ is contained in all $A_i$’s, Remark 4.3 (1) implies that it acts by translations with respect to any rigid action $\psi :{{\,\mathrm{He}\,}}(3) \rightarrow {{\,\mathrm{Aut}\,}}(E)$.

(2) There are two normal subgroups of ${\mathbb {Z}}_2^2 \rtimes _{\varphi _4} {\mathbb {Z}}_4$ with quotient ${\mathbb {Z}}_4$. They are isomorphic to ${\mathbb {Z}}_2^2$ and obtained as the preimages of the corresponding subgroups $\langle (1,0) \rangle$ and $\langle (1,2) \rangle$ of ${\mathbb {Z}}_2 \times {\mathbb {Z}}_4$ under the surjective homomorphism

$$\begin{aligned} \beta :{\mathbb {Z}}_2^2 \rtimes _{\varphi _4} {\mathbb {Z}}_4 \rightarrow {\mathbb {Z}}_2 \times {\mathbb {Z}}_4, \qquad (a,b,c) \mapsto (a+b,c). \end{aligned}$$

It follows immediately from Remark 4.3, (2) that none of these groups can admit a free diagonal action on the product of elliptic curves.

Proof of Proposition 4.4

Let B be a normal abelian subgroup of G such that G/B is cyclic of order d. Necessarily, the commutator subgroup [G, G] must be contained in B.

$\underline{d=6}$: by Proposition 3.6 [G, G] has index six in G, this implies $B =[G,G] = A$.

$\underline{d=4}$: here G is a quotient of the triangle group ${\mathbb {T}}(2,4,4)$ (cf. Remark 3.7) which has three normal subgroups of index four, one is abelian and isomorphic to ${\mathbb {Z}}^2$, the other two groups are non abelian with abelianisation ${\mathbb {Z}}_2^3$. If $|G|>16$, then $|B| >4$. The preimage of B under $\phi :{\mathbb {T}}(2,4,4) \rightarrow G$ is a normal subgroup of index four and since B is abelian, there is a surjection $\phi ^{ab} :\phi ^{-1}(B)^{ab} \rightarrow B$. Assume now that $\phi ^{-1}(B)^{ab} \simeq {\mathbb {Z}}_2^3$. Then $\phi ^{ab}$ is an isomorphism from ${\mathbb {Z}}_2^3$ to B. A contradiction, since we assume that B is a subgroup of $E[n] \simeq {\mathbb {Z}}_n^2$. Thus $\phi ^{-1}(B)^{ab} = \phi ^{-1}(B) \simeq {\mathbb {Z}}^2$ and $B=A$. Suppose that $|G| \le 16$ and $B \ne A$, then B is a quotient of ${\mathbb {Z}}_2^2$ and G is equal to ${\mathbb {Z}}_2 \times {\mathbb {Z}}_4$ or ${\mathbb {Z}}_2^2 \rtimes _{\varphi _4} {\mathbb {Z}}_4$.

$\underline{d=3}$: if $|G| >27$, then $|B| >9$. The preimage of B under $\phi :{\mathbb {T}}(3,3,3) \rightarrow G$ is a normal subgroup of index three. Since B is abelian, there is a surjection $\phi ^{-1}(B)^{ab} \rightarrow B$. It is known that ${\mathbb {T}}(3,3,3)$ has exactly four normal subgroups of index three. One of them is isomorphic to ${\mathbb {Z}}^2$ and the others are non-abelian, with abelianisation ${\mathbb {Z}}_3^2$. It follows that $\phi ^{-1}(B)^{ab} = \phi ^{-1}(B) \simeq {\mathbb {Z}}^2$ and $B=A$. Suppose that $|G| \le 27$ and $B \ne A$, then B is a quotient of ${\mathbb {Z}}_3^2$. We conclude that G has order 9 or 27 and is equal to ${\mathbb {Z}}_3^2$ or ${{\,\mathrm{He}\,}}(3)={\mathbb {Z}}_3^2 \rtimes _{\varphi _3} {\mathbb {Z}}_3$. $\square$

Corollary 4.6

Assume that G is not exceptional and admits a rigid diagonal action on $E^n$. Then:

• 1. the action is not free;

• 2. the maps $g(z_1), \ldots , g(z_n)$ have the same linear part for all $g \in G$.

Proof

We know that $G = A \rtimes _{\varphi _d} {\mathbb {Z}}_d$ with $d=3,4$ or 6.

• 1. By Proposition 4.4 we have $T_i = A$ for all i. The claim follows now from Remark 4.3 (2).

• 2. We denote the curve E at position i by $E_i$. According to Remark 3.2 the value of the character $\chi _{E_i}(g)$ is the complex conjugate of the linear part of $g(z_i)$. Proposition 4.4 implies that $\ker (\chi _{E_i}) =A$, i.e. we can regard $\chi _{E_i}$ as a faithful character of $G/A \simeq {\mathbb {Z}}_d$. Such a character is defined by multiplication with a d-th primitive root of unity. For $d=3,4$ and 6 there are only two primitive roots of unity, namely $\zeta _d$ and $\zeta _d^{-1}$. Since we assume that the action is rigid, by Remark  3.2 it holds that $\chi _{E_i} \cdot \chi _{E_j}\ne \chi _{triv}$ and it follows that all characters $\chi _{E_i}$ are the same. $\square$

The following result shows that for the non exceptional case the situation is quite simple, since for each n and each d there is only one possible quotient, namely $X_{n,d}:=E^n/{\mathbb {Z}}_d$.

Theorem 4.7

Assume that $G=A \rtimes _{\varphi _d} {\mathbb {Z}}_d$ admits a rigid diagonal action on $E^n$. If G is not exceptional, then the quotient $E^n/G$ is isomorphic to $X_{n,d}:=E^n/{\mathbb {Z}}_d$, where ${\mathbb {Z}}_d$ acts on $E^n$ by multiplication with $\zeta _d \cdot {{\,\mathrm{Id}\,}}$.

Proof

Since G is not exceptional, the normal subgroup A is the translation group $T_i$ of the action on each factor of the product $E^n$. In particular $E^n/A$ is an abelian variety and by construction ${\mathbb {Z}}_d \simeq G/A$ acts on $E^n/A$ by multiplication with $\zeta _d \cdot {{\,\mathrm{Id}\,}}$. This implies that $E^n/A$ is isomorphic to $E^n$, according to [10, Corollary 13.3.5]. $\square$

Remark 4.8

In [7] Beauville considered the varieties $X_{d,d}$ for $d=3,4$ and 6. He explains that these singular varieties admit rigid, simply connected Calabi-Yau d-folds as resolutions of singularities.

5 The exceptional groups

In contrast to Theorem 4.7 the situation for the exceptional groups is more involved. In this chapter we analyse it in dimensions three and four. In Proposition  5.2 we shall see that rigid, free diagonal actions do not exist in dimension three. However we can drop the freeness assumption and classify rigid non-free actions. It turns out that the quotients by the groups ${\mathbb {Z}}_2 \times {\mathbb {Z}}_4$ and ${\mathbb {Z}}_2^2 \rtimes _{\varphi _4} {\mathbb {Z}}_4$ have non canonical singularities and therefore we do not consider it further.

In case of the groups ${{\,\mathrm{He}\,}}(3)$ and ${\mathbb {Z}}_3^2$, the quotients will be singular, but as we shall see only canonical cyclic quotient singularities of type $\frac{1}{3}(1,1,1)$ and $\frac{1}{3}(1,1,2)$ occur.

We study this case in detail and discover besides Beauville’s example $X_{3,3}$, other interesting rigid canonical threefolds and relations among them. From dimension four on, the groups ${{\,\mathrm{He}\,}}(3)$ and ${\mathbb {Z}}_3^2$ allow rigid free diagonal actions. Their existence for ${\mathbb {Z}}_3^2$ has already been observed in [2, Theorem 3.4]. We show that each exceptional group gives precisely one isomorphism class of a smooth rigid quotient fourfold $E^4/{\mathbb {Z}}_3^2$ and $E^4/{{\,\mathrm{He}\,}}(3)$. We prove that these manifolds are non-isomorphic by showing that they are even topologically distinct, i.e. non homeomorphic.

Remark 5.1

If we consider rigid actions of the exceptional groups ${\mathbb {Z}}_2 \times {\mathbb {Z}}_4$ and ${\mathbb {Z}}_2^2 \rtimes _{\varphi _4} {\mathbb {Z}}_4$ on $E^4$, then as observed before the action cannot be free, hence we obtain singular quotients, which have canonical singularities. Classifying these quotients as well as suitable resolutions of singularities of those should yield new interesting examples.

5.1 Free rigid diagonal actions on $E^4$

We start with the following quite easy but useful Proposition

Proposition 5.2

Assume that $G={{\,\mathrm{He}\,}}(3)$ or ${\mathbb {Z}}_3^2$ admits a rigid diagonal action on a product $E^n$. Then the action is free, if and only if each of the four normal subgroups of G of index three is equal to the translation subgroup $T_i$ on at least one factor. In particular, $n\ge 4$.

Proof

By Remark 4.3 (2), the action is free if and only if

$$\begin{aligned} G=T_1 \cup \cdots \cup T_n. \end{aligned}$$

(5.1)

Recall that each $T_i$ is equal to one of the four normal subgroups $A_1, \ldots , A_4$ of G of index three. Clearly, for (5.1) to hold, all $A_i$ must appear in the union, because the union of less than four of the $A_i$’s consists of at most 7 elements if $G={\mathbb {Z}}_3^2$ and of at most 21 elements if $G={{\,\mathrm{He}\,}}(3)$.

$\square$

We need the following Proposition only in a special case but for further use we prefer to state it in greater generality:

Proposition 5.3

Let G be a finite group acting holomorphically on the compact complex manifolds $X_1, \ldots , X_n$, let $A\trianglelefteq G$ be a normal subgroup and $Y_i:=X_i/A$.

1. There is a commutative square of finite holomorphic maps:

where the degree of f is $\vert A \vert ^{n-1}$.

2. If $n\ge 2$ the covering f is Galois if and only if A is contained in the center of G. In this case the Galois group of f is isomorphic to $A^{n-1}$.

Proof

• 1. is obvious.

• 2. Consider the composition of covers

  $$\begin{aligned} h :X_1\times \cdots \times X_n \rightarrow Y_1 \times \cdots \times Y_n \rightarrow (Y_1\times \cdots \times Y_n)/(G/A). \end{aligned}$$

We claim that h is always Galois. Observe that the elements of the groups $\Delta _G$ and $A^n$ act as deck transformations of h and therefore in order to show that h is Galois, it suffices to show that the cardinality of $\langle \Delta _G, A^n \rangle$ equals $\deg (h) = |A|^{n-1}|G|$. Since A is a normal subgroup of G, also $A^n$ is a normal subgroup of $\langle \Delta _G, A^n \rangle$. Clearly the natural homomorphism

$$\begin{aligned} \Delta _G \rightarrow \langle \Delta _G, A ^n \rangle /A^n \end{aligned}$$

is surjective and its kernel is $\Delta _A \simeq A$. Thus we see that $\langle \Delta _G, A^n \rangle$ has $|A|^{n-1}|G|$ elements.

By the fundamental theorem of Galois theory, f is Galois if and only if $\Delta _G$ is a normal subgroup of $\langle \Delta _G, A^n\rangle$. This is certainly the case if $A\le Z(G)$. Conversely, assume that $\Delta _G$ is normal. Let $a\in A$, then for all $g\in G$ there exists an element $g'\in G$, such that

$$\begin{aligned} (a,1,\ldots ,1 ) \circ (g, \ldots ,g) \circ (a^{-1},1,\ldots ,1) =(g',\ldots ,g'). \end{aligned}$$

This implies $aga^{-1}=g'=g$ i.e. $a \in Z(G)$.

Assume now that f is Galois. Then its Galois group is $\langle \Delta _G, A^n \rangle /\Delta _G$, which is isomorphic to $A^{n-1}$. In fact, the surjective homomorphism

$$\begin{aligned} A^n \rightarrow \langle \Delta _G, A^n \rangle /\Delta _G \end{aligned}$$

has kernel $\Delta _A$ and induces an isomorphism $\langle \Delta _G, A^n \rangle /\Delta _G \simeq A^n/\Delta _A \simeq A^{n-1}$. $\square$

Now we are ready to show that for each of the groups ${{\,\mathrm{He}\,}}(3)$ and ${\mathbb {Z}}_3^2$, there is exactly one isomorphism class of rigid étale quotients $E^4 /G$.

Theorem 5.4

There is exactly one isomorphism class of quotient manifolds $Z_1:=E^4/{\mathbb {Z}}_3^2$ resp. $Z_2:=E^4/{{\,\mathrm{He}\,}}(3)$ obtained by a rigid free and diagonal action. These projective manifolds are infinitesimally rigid of Kodaira dimension zero and there is an unramified Galois cover $f :Z_2 \rightarrow Z_1$ with group ${\mathbb {Z}}_3^3$.

Proof

First we show the existence and unicity of $Z_1$ resp. $Z_2$. Let G be ${\mathbb {Z}}_3^2$ resp. ${{\,\mathrm{He}\,}}(3)$. By Riemann’s existence theorem the diagonal actions of G on $E^4$ correspond to quadruples of generating triples $[V_1,V_2,V_3,V_4]$. The action of G is free on $E^4$, if and only if $\Sigma _{V_1} \cap \cdots \cap \Sigma _{V_4} = \lbrace 1_G \rbrace$.

As explained e.g. in [5] the group ${\mathfrak {S}}_4 \times {\mathcal {B}}_3^4 \times {{\,\mathrm{Aut}\,}}(G)$ acts on the set of quadruples of generating triples $[V_1,V_2,V_3,V_4]$. Here ${\mathfrak {S}}_4$ permutes the generating triples $V_i$ of the quadruple, ${{\,\mathrm{Aut}\,}}(G)$ acts diagonally on $[V_1,V_2,V_3,V_4]$, and the Artin Braid Group ${\mathcal {B}}_3$ acts separately on each $V_i$ by so-called Hurwitz moves. By [5, Proposition 3.3] equivalent quadruples of generating vectors yield isomorphic quotients. With a MAGMA algorithm we check that for each of the two groups there is exactly one orbit corresponding to a free rigid action, corresponding therefore to unique isomorphism class of a rigid manifold $Z_1:=E^4/{\mathbb {Z}}_3^2$ resp. $Z_2:=E^4/ {{\,\mathrm{He}\,}}(3)$.

Let us now consider the ${{\,\mathrm{He}\,}}(3)$ action on $E^4$ yielding $Z_2$. The center $C_3=Z\big ({{\,\mathrm{He}\,}}(3)\big ) \simeq {\mathbb {Z}}_3$ acts on each copy of E by translations, such that $E/C_3\simeq E$. Using the identification ${{\,\mathrm{He}\,}}(3)/C_3 \simeq {\mathbb {Z}}_3^2$, it can be checked again by a MAGMA routine that the image of the quadruple $[V_1,V_2,V_3,V_4]$ representing $Z_2$ is a quadruple which lies in the orbit representing $Z_1$. This means that on each factor we have a commutative triangle

By Proposition 5.3 we have a finite Galois cover $f :Z_2 \rightarrow Z_1$ with group ${\mathbb {Z}}_3^3$. The cover f is unramified, because the other three maps of the diagram in Proposition 5.3 are unramified. $\square$

Remark 5.5

Note that the fourfold $Z_2$ can be realized as a double quotient, namely the quotient of the torus $E^4/C_3$ by the induced action of ${\mathbb {Z}}_3^2 \simeq {{\,\mathrm{He}\,}}(3)/C_3$. By construction, the linear part of the ${\mathbb {Z}}_3^2$-action on $E^4/C_3$ giving $Z_2$ is the same as the linear part of the action on $E^4$ giving $Z_1$. It can be determined from the generating triples, see Remark 3.4 (3). In our situation we have (up to an automorphism of ${\mathbb {Z}}_3^2$):

$$\begin{aligned} \rho (a,b):= \begin{pmatrix} \zeta _3^b &{} 0 &{} 0 &{} 0 \\ 0 &{} \zeta _3^{a+b} &{} 0 &{} 0 \\ 0 &{} 0 &{} \zeta _3^a &{} 0 \\ 0 &{} 0 &{} 0 &{} \zeta _3^{2a+b} \end{pmatrix}, \qquad \text {for all} \quad (a,b) \in {\mathbb {Z}}_3^2. \end{aligned}$$

In the literature $\rho$ is usually called the analytic representation of the group action.

With the above in mind, it is not hard to write down explicit models of $Z_1$ and $Z_2$:

Example 5.6

We consider the following lattices

$$\begin{aligned} \Lambda _1:={\mathbb {Z}}[\zeta _3]^4 \qquad \text {and} \qquad \Lambda _2 = {\mathbb {Z}}[\zeta _3]^4 + {\mathbb {Z}} \frac{1+2\zeta _3}{3} (1,1,1,1) \end{aligned}$$

and define the complex tori $T_i:={\mathbb {C}}^4/\Lambda _i$. By definition $T_1 \simeq E^4$ and $T_2 \simeq E^4/\langle t \rangle$, where E is the equianharmonic elliptic curve and

$$\begin{aligned} t :E^4 \rightarrow E^4, \qquad z \mapsto z+ \frac{1+2\zeta _3}{3} (1,1,1,1). \end{aligned}$$

The two actions $\psi _i$ of ${\mathbb {Z}}_3^2$ on $T_i$, that give the quotients $Z_i$ are the following:

$$\begin{aligned} \psi _1(1,0)(z)&:= {{\,\mathrm{diag}\,}}(1, \zeta _3, \zeta _3, \zeta _3^2)z + \frac{1+2\zeta _3}{3} (1, 2,0,1), \\ \psi _1(0,1)(z)&:={{\,\mathrm{diag}\,}}(\zeta _3, \zeta _3, 1, \zeta _3) z + \frac{1+2\zeta _3}{3} (0,0,2,0), \\ \psi _2(1,0)(z)&:={{\,\mathrm{diag}\,}}(1, \zeta _3, \zeta _3, \zeta _3^2)z + \frac{1}{3} (1, 0 , 0, 2), \\ \psi _2(0,1)(z)&:={{\,\mathrm{diag}\,}}(\zeta _3, \zeta _3, 1, \zeta _3) z + \frac{1}{3}(0, 2 \zeta _3, 1+ \zeta _3, 2). \end{aligned}$$

The cohomology of the manifolds $Z_i$ is easy to compute:

Proposition 5.7

The projective manifolds $Z_1$ and $Z_2$ have the same Hodge numbers:

$$\begin{aligned} h^{1,0}=h^{2,0}=h^{3,1}=h^{4,0}=0, \quad h^{1,1}=4, \quad h^{2,1}=3,\quad h^{3,0}=1, \quad h^{2,2}=6. \end{aligned}$$

Moreover, $\mathcal {O}(K_{Z_i}) \ne \mathcal {O}_{Z_i}$ and $\mathcal {O}(K_{Z_i}) ^{\otimes 3} \simeq \mathcal {O}_{Z_i}$.

Proof

For any complex torus $T={\mathbb {C}}^n/\Lambda$ the Dolbeault groups have the description

$$\begin{aligned} H^{p,q}(T)= \Lambda ^p \Omega \otimes \Lambda ^q \overline{\Omega }, \quad \text {where} \quad \Omega :=\langle dz_1, \ldots , dz_n \rangle . \end{aligned}$$

Since the manifolds $Z_i$ are quotients of tori by free actions, the groups $H^{p,q}(Z_i)$ are isomorphic to the invariant parts of $\Lambda ^p \Omega \otimes \Lambda ^q \overline{\Omega }$ under the ${\mathbb {Z}}_3^2$ action induced by $\psi _i$. Since the derivative of a constant is zero, it suffices to act with the linear part of $\psi _i$ i.e. with the analytic representation. Since both actions $\psi _i$ have the same analytic representation $\rho$, both quotients $Z_1$ and $Z_2$ have isomorphic Dolbeault groups and in particular, the same Hodge numbers. To compute these groups explicitly we take the standard basis

$$\begin{aligned} {\mathcal {B}}:=\lbrace dz_{i_1} \wedge \cdots \wedge dz_{i_p} \otimes d{\overline{z}}_{j_1} \wedge \cdots \wedge d{\overline{z}}_{j_q} ~ \big \vert ~ i_1< \cdots< i_p \le 4, ~ j_1< \cdots < j_q \le 4 \rbrace \end{aligned}$$

of $\Lambda ^p \Omega \otimes \Lambda ^q \overline{\Omega }$. The fact that $\rho$ acts by diagonal matrices implies that a basis of $H^{p,q}(Z_i)$ is given by the invariant basis vectors of ${\mathcal {B}}$. The non-zero Dolbeault groups are:

$$\begin{aligned} H^{3,0}(Z_i)&\simeq \langle dz_1\wedge dz_2 \wedge dz_4 \rangle , \\ H^{1,1}(Z_i)&\simeq \langle dz_i\otimes d{\overline{z}}_i ~ \big \vert ~ i \le 4 \rangle , \\ H^{2,1}(Z_i)&\simeq \langle dz_1 \wedge dz_3 \otimes d{\overline{z}}_2, dz_2 \wedge dz_3 \otimes d{\overline{z}}_4, dz_3 \wedge dz_4 \otimes d{\overline{z}}_1 \rangle , \\ H^{2,2}(Z_i)&\simeq \langle dz_i \wedge dz_j \otimes d{\overline{z}}_i \wedge d{\overline{z}}_j ~ \big \vert ~ i < j \le 4 \rangle . \end{aligned}$$

To prove the statement about $\mathcal {O}(K_{Z_i})$, we note that the differential form

$$\begin{aligned} \big ( dz_1 \wedge \cdots \wedge dz_4)^{\otimes 3} \end{aligned}$$

is ${\mathbb {Z}}_3^2$-invariant. Thus it descends to $Z_i$ and provides a trivialization of $\mathcal {O}(K_{Z_i})^{\otimes 3}$.

$\square$

The remaining part of the subsection is devoted to prove that the manifolds $Z_1$ and $Z_2$ are not homeomorphic. More precisely, we shall show that they have non isomorphic fundamental groups.

Remark 5.8

The fundamental group of $Z_i$ is isomorphic to the group of deck transformations $\Gamma _i$ of the universal cover ${\mathbb {C}}^4 \rightarrow T_i \rightarrow Z_i$. It consists of the lifts of the automorphisms $\psi _i(a,b)$ for all $(a,b) \in {\mathbb {Z}}_3^2$ and is therefore a group of affine transformations. Since the linear parts $\rho (a,b)$ of the maps $\psi _i(a,b)$, viewed as real $8\times 8$ matrices, are orthogonal we can more precisely say that $\Gamma _i$ is a cocompact free discrete subgroup of the Euclidean group of isometries ${\mathbb {E}}(8):= {\mathbb {R}}^8 \rtimes {{\,\mathrm{O}\,}}(8)$.

Because the action of ${\mathbb {Z}}_3^2$ on $T_i$ does not contain translations, the lattice $\Lambda _i$ of the torus $T_i$ is equal to the intersection $\Gamma _i \cap {\mathbb {R}}^8$ i.e. the translation subgroup of $\Gamma _i$.

Definition 5.9

• 1. A discrete cocompact subgroup of ${\mathbb {E}}(n)$ is called a crystallographic group.

• 2. A Bieberbach group is a torsion free crystallographic group.

As a modern reference for Bieberbach groups we use [13], for the original results see [8, 9].

Remark 5.10

• 1. It is worth observing that the underlying ${\mathcal {C}}^{\infty }$-manifold of $Z_i$ admits a flat Riemannian metric i.e., a metric such that the curvature tensor

  $$\begin{aligned} R(X,Y)Z:=\nabla _X \nabla _YZ - \nabla _Y \nabla _XZ - \nabla _{[X,Y]}Z \end{aligned}$$

  with respect to the Levi-Civita connection is identically zero. Vice versa each compact flat Riemannian n-manifold is isometric to a quotient ${\mathbb {R}}^n /\Gamma$, where $\Gamma$ is a Bieberbach group (cf. [13, Chapter II]). Moreover, the quotient $\Gamma / \Lambda$ by the translation subgroup is isomorphic to the holonomy group of ${\mathbb {R}}^n /\Gamma$.

• 2. Obviously not every quotient of ${\mathbb {R}}^{2n}$ by a Bieberbach group has a complex structure. If there is a complex structure, then the complex manifold is an étale torus quotient and is called a generalized hyperelliptic manifold. These have been studied and classified in dimension 2 by Bagnera and de Franchis and in dimension 3 by Uchida-Yoshihara [21], Lange [16] and Catanese-Demleitner in [12]. In his PhD thesis [14] Demleitner gave a complete list of holonomy groups of generalized hyperelliptic 4-folds. The manifolds $Z_1$ and $Z_2$ are two distinct rigid examples, with holonomy group ${\mathbb {Z}}_3^2$. The second author and Demleitner work on a complete classification of rigid generalized hyperelliptic 4-folds.

In order to distinguish the fundamental groups $\Gamma _1$ and $\Gamma _2$ of $Z_1$ and $Z_2$ we will use the first and second of the following three theorems of Bieberbach (cf. [13, Chapter I]):

Theorem 5.11

(Bieberbach’s three theorems)

• 1. The translation subgroup $\Lambda :=\Gamma \cap {\mathbb {R}}^n$ of a crystallographic group $\Gamma \le {\mathbb {E}}(n)$ is a lattice of rank n and $\Gamma /\Lambda$ is finite. All other normal abelian subgroups of $\Gamma$ are contained in $\Lambda$.

• 2. Let $\Gamma _1, \Gamma _2 \le {\mathbb {E}}(n)$ be two crystallographic groups and $f :\Gamma _1 \rightarrow \Gamma _2$ be an isomorphism. Then there exists an affine transformation $\alpha \in {{\,\mathrm{Aff}\,}}(n)$, such that $f(g)=\alpha \circ g \circ \alpha ^{-1}$ for all $g\in \Gamma _1$.

• 3. In each dimension there are only finitely many isomorphism classes of crystallographic groups.

Remark 5.12

• 1. Assume that $Z_1$ and $Z_2$ are homeomorphic. Then, by Bieberbach’s second theorem, there exists an affine transformation $\alpha (x)=Ax+b$ such that $\alpha \circ \Gamma _2 \circ \alpha ^{-1}=\Gamma _1$. Bieberbach’s first theorem implies that $\alpha \circ \Lambda _2 \circ \alpha ^{-1}=\Lambda _1$. In other words, $\alpha$ induces diffeomorphisms

  $$\begin{aligned} {\widehat{\alpha }} :Z_2 \rightarrow Z_1 \qquad \text {and} \qquad {\widetilde{\alpha }} :{\mathbb {R}}^8/\Lambda _2 \rightarrow {\mathbb {R}}^8/\Lambda _1 \end{aligned}$$

  which make the following diagram commutative:

  

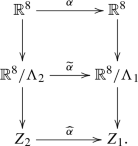
  In particular, Bieberbach’s theorems imply that $Z_1$ and $Z_2$ have isomorphic fundamental groups if and only if they are diffeomorphic, even by an affine diffeomorphism.

• 2. Recall that the actions $\psi _1$ and $\psi _2$ have the same analytic representation $\rho$, which we now view as a real representation:

  $$\begin{aligned} \rho _{{\mathbb {R}}}(a,b) := \begin{pmatrix} B^b &{} 0 &{} 0 &{} 0 \\ 0 &{} B^{a+b} &{} 0 &{} 0 \\ 0 &{} 0 &{} B^a &{} 0 \\ 0 &{} 0 &{} 0 &{} B^{2a+b} \end{pmatrix}, \quad B:=-\frac{1}{2} \begin{pmatrix} 1 &{} \sqrt{3} \\ -\sqrt{3} &{}1 \end{pmatrix}. \end{aligned}$$

  By the commutativity of the diagram in (1), there exists an automorphism $\varphi \in {{\,\mathrm{Aut}\,}}({\mathbb {Z}}_3^2)$, such that

  $$\begin{aligned} A \rho _{{\mathbb {R}}}(a,b) A^{-1} =\rho _{{\mathbb {R}}}\big (\varphi (a,b)\big ), \ \forall \ (a,b) \in {\mathbb {Z}}_3^2. \end{aligned}$$

  In other words, $\rho _{{\mathbb {R}}}(a,b)$ and $\rho _{{\mathbb {R}}}\big (\varphi (a,b)\big )$ are isomorphic as representations over ${\mathbb {R}}$.

Proposition 5.13

The representation $\rho _{{\mathbb {R}}}$ is the sum of four disctinct irreducible two-dimensional representations over ${\mathbb {R}}$.

Proof

The representations $B^b, B^{a+b}, B^a$ and $B^{2a+b}$ are indeed irreducible, because B is not diagonalizable over ${\mathbb {R}}$. Obviously they are distinct. $\square$

Remark 5.14

• 1. The group ${\mathbb {Z}}_3^2$ has precisely 5 irreducible real representations: the trivial representation and the four two dimensional representations from above. This can be verified with the help of the formula

  $$\begin{aligned} |G| = \sum _{\chi \in {{\,\mathrm{Irr}\,}}_{{\mathbb {R}}}(G)} \frac{\chi (1)^2}{\langle \chi , \chi \rangle } , \end{aligned}$$

  which holds for any finite group G.

• 2. By Schur’s Lemma the endomorphism algebra ${{\,\mathrm{End}\,}}_G(V)$ of an irreducible real representation V of a finite group G is a finite dimensional division algebra. As it is clearly associative, it is isomorphic to ${\mathbb {R}}$, ${\mathbb {C}}$ or the quaternions ${\mathbb {H}}$, according to Frobenius’ theorem [15].

Proposition 5.15

• 1. The ${\mathbb {R}}$-algebra of matrices H which commute with B is:

  $$\begin{aligned} \bigg \lbrace \begin{pmatrix} \lambda &{} -\mu \\ \mu &{} \lambda \end{pmatrix} ~ \bigg \vert ~ \lambda ,\mu \in {\mathbb {R}} \bigg \rbrace \simeq {\mathbb {C}}. \end{aligned}$$

• 2. The ${\mathbb {R}}$-vectorspace of matrices H with $HB=B^2H$ is

  $$\begin{aligned} \bigg \lbrace \begin{pmatrix} \lambda &{} \mu \\ \mu &{} -\lambda \end{pmatrix} ~ \bigg \vert ~ \lambda ,\mu \in {\mathbb {R}} \bigg \rbrace \simeq {\mathbb {R}}^2. \end{aligned}$$

The matrices in 1) define ${\mathbb {C}}$-linear maps and the matrices in 2) ${\mathbb {C}}$-antilinear maps. In complex coordinates $z=x+ i y$ we may identify them with

$$\begin{aligned} h_{\lambda + i \mu } :{\mathbb {C}} \rightarrow {\mathbb {C}}, \quad z\mapsto (\lambda +i\mu )z \qquad \text {and} \qquad {\overline{h}}_{\lambda + i \mu } :{\mathbb {C}} \rightarrow {\mathbb {C}}, \quad z\mapsto (\lambda +i\mu ){\overline{z}}. \end{aligned}$$

Proof

An Ansatz with a general $2\times 2$ matrix H yields a system of linear equations. The solutions are the displayed matrices. $\square$

Now we are ready to prove the following:

Theorem 5.16

The fundamental groups of the manifolds $Z_1$ and $Z_2$ are not isomorphic.

Proof

Assume that $\pi _1(Z_1) \simeq \pi _1(Z_2)$ then, as explained in Remark 5.12, Bieberbach’s theorems imply that there exists an affine transformation $\alpha (x)=Ax+b$ inducing diffeomorphisms

$$\begin{aligned} {\widehat{\alpha }} :Z_2 \rightarrow Z_1 \qquad \text {and} \qquad {\widetilde{\alpha }} :{\mathbb {R}}^8/\Lambda _2 \rightarrow {\mathbb {R}}^8/\Lambda _1. \end{aligned}$$

In particular,

$$\begin{aligned} A\cdot \Lambda _2=\Lambda _1. \end{aligned}$$

(5.2)

Our aim is to show that equation 5.2 leads to a contradiction.

As a first step, we prove that A has a very special form: we subdivide A into 16 blocks $A_{i,j}$ of $2\times 2$-matrices

$$\begin{aligned} A= \begin{pmatrix} A_{1,1} &{} A_{1,2} &{} A_{1,3} &{} A_{1,4} \\ A_{2,1} &{} A_{2,2} &{} A_{2,3} &{} A_{2,4} \\ A_{3,1} &{} A_{3,2} &{} A_{3,3} &{} A_{3,4} \\ A_{4,1} &{} A_{4,2} &{} A_{4,3} &{} A_{4,4} \end{pmatrix}. \end{aligned}$$

As we have seen in Remark 5.12 (2), there is an automorphism $\varphi \in {{\,\mathrm{Aut}\,}}({\mathbb {Z}}_3^2)$, such that

$$\begin{aligned} A \rho _{{\mathbb {R}}}(a,b) A^{-1} =\rho _{{\mathbb {R}}}\big (\varphi (a,b)\big ), \qquad \text {for all} \qquad (a,b) \in {\mathbb {Z}}_3^2. \end{aligned}$$

(5.3)

This means that A defines an equivalence of the representations $\rho _{{\mathbb {R}}}$ and $\rho _{{\mathbb {R}}}\circ \varphi$. By Proposition 5.13 the representation $\rho _{{\mathbb {R}}}$ is the direct sum of of all four distinct irreducible two-dimensional representations of ${\mathbb {Z}}_3^2$:

$$\begin{aligned} B^b, B^{a+b}, B^a, B^{2a+b} \ , \quad \text {where} \quad \quad B:=-\frac{1}{2} \begin{pmatrix} 1 &{} \sqrt{3} \\ -\sqrt{3} &{}1 \end{pmatrix}. \end{aligned}$$

Thus also $\rho _{{\mathbb {R}}}\circ \varphi$ consists of all four irreducible two-dimensional representations of ${\mathbb {Z}}_3^2$, possibly in a different order. By Schur’s lemma non-zero maps exist only between isomorphic irreducible representations hence, up to a permutation, A is a block diagonal matrix: to be more precise, there exists $\tau \in {\mathfrak {S}}_4$ such that for each i the block $A_{\tau (i),i}$ is invertible, while the other 12 blocks are identically zero.

The non-zero $2\times 2$ - blocks are those described in Proposition 5.15. Indeed, as B has order three, equation 5.3 implies that each non-zero block $A_{\tau (i),i}$ either commutes with B, or fulfills the equation $A_{\tau (i),i} B=B^2A_{\tau (i),i}$. Whence up to a permutation of blocks, A is a direct sum of ${\mathbb {C}}$-linear and ${\mathbb {C}}$-antilinear maps:

$$\begin{aligned} h_{w_i}(z)=w_i z \qquad \text {or} \qquad {\overline{h}}_{w_i}(z)=w_i {\overline{z}} \qquad \text {where} \quad w_i \in {\mathbb {C}}^{*}. \end{aligned}$$

Now we use equation  5.2 to derive a contradiction. As $e_i$ belongs to $\Lambda _2$ for all $1\le i \le 4$, we have $A(e_i) \in \Lambda _1 = {\mathbb {Z}}[\zeta _3]^4$. This shows that all $w_i$ belong to ${\mathbb {Z}}[\zeta _3]$. Similarly, since $A^{-1}(e_i)$ is a vector with just one non-zero entry, it must be contained in the sublattice

$$\begin{aligned} {\mathbb {Z}}[\zeta _3]^4 \subset \Lambda _2= {\mathbb {Z}}[\zeta _3]^4 + {\mathbb {Z}} \frac{1+2\zeta _3}{3} (1,1,1,1). \end{aligned}$$

Thus, $w_{i}^{-1}$ or its conjugate is also an Eisenstein integer and we conclude that $w_i$ is a unit in ${\mathbb {Z}}[\zeta _3]$, for all $1\le i \le 4$. On the other hand, the product of A and the lattice vector $\frac{1+2\zeta _3}{3} (1,1,1,1) \in \Lambda _2$ belongs to $\Lambda _1$, which means that

$$\begin{aligned} w_i \frac{1+2\zeta _3}{3} \in {\mathbb {Z}}[\zeta _3] \qquad \text {or} \qquad w_i \frac{1+2\zeta _3^2}{3} \in {\mathbb {Z}}[\zeta _3]. \end{aligned}$$

A contradiction, because $w_i$ is a unit for each i. $\square$

5.2 Rigid quotients of $E^3$ by the exceptional groups

Let $X := E^3 / G$ be a quotient of $E^3$ by a rigid diagonal action of one of the four exceptional groups G. Then according to Proposition 5.2 and Remark 4.5, (2) the action is not free and X has singular points. The singular points of X are precisely the images of the finitely many points $p=(p_1,p_2,p_3)$ in $E^3$ with non trivial stabilizer group. The stabilizer of a point $p\in E^3$ is the intersection of the cyclic groups $G_{p_i}$ and therefore cyclic (cf. Remark 3.4). We show that if $G = {\mathbb {Z}}_2 \times {\mathbb {Z}}_4$ or ${\mathbb {Z}}_2^2 \rtimes _{\varphi _4} {\mathbb {Z}}_4$, then X always has non canonical singularities of type $\frac{1}{4}(1,1,1)$. Therefore we shall restrict ourselves to the two remaining exceptional groups ${\mathbb {Z}}_3^2$ or ${{\,\mathrm{He}\,}}(3)$. Since a non trivial cyclic subgroup of ${\mathbb {Z}}_3^2$ or ${{\,\mathrm{He}\,}}(3)$ is isomorphic to ${\mathbb {Z}}_3$, the threefold X has only cyclic quotient singularities of type $\frac{1}{3}(1,1,1)$ and $\frac{1}{3}(1,1,2)$. We point out that these singularities are canonical, more precisely $\frac{1}{3}(1,1,2)$ is terminal by the Shepherd-Barron-Tai criterion (see [19, p. 376 Theorem]) and $\frac{1}{3}(1,1,1)$ is Gorenstein. In particular, for any resolution of singularities $\rho :{\widehat{X}} \rightarrow X$ it holds $\kappa ({\widehat{X}})=\kappa (X)= \kappa (E^3)=0$.

In terms of infinitesimal deformation theory these singularities are also well behaved in the following sense:

Proposition 5.17

Let X be a threefold with only isolated singularities of type $\frac{1}{3}(1,1,1)$ and $\frac{1}{3}(1,1,2)$, then X is canonical and there is a resolution of singularities $\rho :{\widehat{X}} \rightarrow X$, such that $H^1({\widehat{X}}, \Theta _{{\widehat{X}}}) \simeq H^1(X, \Theta _X)$.

In particular, if X is rigid, then also ${\widehat{X}}$ is rigid.

Proof

In [3, Corollary 5.9, Proposition 5.10] the authors showed that a germ $(U,p_0)$ of a singularity of type $\frac{1}{3}(1,1,1)$ or $\frac{1}{3}(1,1,2)$ has a resolution $\rho :{\widehat{U}} \rightarrow U$ such that

$$\begin{aligned} \rho _{*} \Theta _{{\widehat{U}}}= \Theta _U \qquad \text {and} \qquad R^1 \rho _{*} \Theta _{{\widehat{U}}}=0. \qquad \qquad (*) \end{aligned}$$

These resolutions can be glued to obtain a resolution $\rho :{\widehat{X}} \rightarrow X$ with the same property $(*)$. The low term exact sequence of the Leray spectral sequence

$$\begin{aligned} 0 \rightarrow H^1(X,\rho _{*} \Theta _{{\widehat{X}}}) \rightarrow H^1({\widehat{X}},\Theta _{{\widehat{X}}}) \rightarrow H^0(X,R^1\rho _{*} \Theta _{{\widehat{X}}}) \rightarrow \cdots \end{aligned}$$

gives us an isomorphism $H^1({\widehat{X}},\Theta _{{\widehat{X}}}) \simeq H^1(X,\Theta _X)$. $\square$

Remark 5.18

Since canonical singularities are rational (see e.g. [19, p. 363 (3.8)]), Leray’s spectral sequence implies that for any resolution of singularities $\rho :{\widehat{X}} \rightarrow X$ the irregularities

$$\begin{aligned} q_i({\widehat{X}}) := h^i({\widehat{X}},\mathcal {O}_{{\widehat{X}}}) \qquad \text {and} \qquad q_i(X):= h^i(X, \mathcal {O}_X) \end{aligned}$$

coincide. Since $H^{i,0}({\widehat{X}}) \simeq H^{i,0}(E^3)^G$, we can compute the irregularities $q_i$ in terms of invariant holomorphic differential forms:

$$\begin{aligned} q_i(X)=q_i({\widehat{X}})=\dim _{{\mathbb {C}}}\big (H^{i,0}(E^3)^G\big ). \end{aligned}$$

It is common to denote the top irregularity $q_3$ by $p_g$ and call it the geometric genus X or ${\widehat{X}}$, respectively.

Remark 5.19

Let $X:=E^3/G$, where G is a finite group acting diagonally on $E^3$.

• 1. According to Proposition  3.1 rigidity means that none of the quadratic differentials $dz_i \otimes dz_j$ is G- invariant. This implies that $q_2(X)=0$, since none of the 2-forms $dz_i \wedge dz_j$ can then be invariant either. By the same reason, we have $q_1(X)=0$.

• 2. If $dz_1 \wedge dz_2 \wedge dz_3$ is G-invariant, then the canonical sheaf of X is trivial, hence X is Gorenstein and $p_g(X)=1$. Otherwise, $p_g(X)=0$, and in this case $\mathcal {O}(3K_X) \simeq \mathcal {O}_X$.

• 3. If $p_g(X)=1$, then X is a Gorenstein Calabi-Yau threefold and its singularities must be of type $\frac{1}{3}(1,1,1)$. If the G-action is moreover rigid, none of the quadratic differentials $dz_i \otimes dz_j$ is G- invariant and an easy calculation using the invariance of $dz_1 \wedge dz_2 \wedge dz_3$ shows that there are no invariant forms of type (1, 2) on $E^3$. In particular, the topological Euler number is given by $e(X)=2 \dim _{{\mathbb {C}}}\big ( H^{1,1}(E^3)^G\big )$, because $H^i(X,{\mathbb {C}}) \simeq H^i(E^3,{\mathbb {C}})^G$ for all i.

• 4. Similarly, if $p_g(X)=0$ and X is rigid, then we have

  $$\begin{aligned} e(X)=2 \big [1+ \dim _{{\mathbb {C}}}\big ( H^{1,1}(E^3)^G\big ) - \dim _{{\mathbb {C}}}\big ( H^{1,2}(E^3)^G\big )\big ]. \end{aligned}$$

We show now that for the groups $G={\mathbb {Z}}_2 \times {\mathbb {Z}}_4$ and $G={\mathbb {Z}}_2^2 \rtimes _{\varphi _4} {\mathbb {Z}}_4$ the quotient $X:=E^3/G$ necessarily has non canonical singularities. Therefore in the sequel we do not consider these groups anymore.

Proposition 5.20

Let X be a quotient of $E^3$ by a rigid diagonal action of $G={\mathbb {Z}}_2 \times {\mathbb {Z}}_4$ or ${\mathbb {Z}}_2^2 \rtimes _{\varphi _4} {\mathbb {Z}}_4$, then X has a singularity of type $\frac{1}{4}(1,1,1)$. In particular, X is not canonical.

Proof

We show that $\rho (g)=\zeta _4 \cdot {{\,\mathrm{Id}\,}}$, for some $g\in G$, which implies the existence of a singularity of type $\frac{1}{4}(1,1,1)$. As above, we may consider X as a quotient by $G={\mathbb {Z}}_2 \times {\mathbb {Z}}_4$. The analytic representation $\rho$ is a sum of three characters $\chi _i$ of G of order 4, such that $\chi _i \ne \overline{\chi _j}$ for $i \ne j$. The order 4 characters of G are:

$$\begin{aligned} \zeta _4^b, \quad \zeta _4^{3b}, \quad (-1)^a \zeta _4^b \quad \text {and} \quad (-1)^{a} \zeta _4^{3b}. \end{aligned}$$

Since they come in pairs of conjugates, we conclude that two of the three characters $\chi _i$ in the analytic representation must be the same. Without loss of generality $\chi _1=\chi _2=\zeta _4^b$ and $\rho$ is equal to

$$\begin{aligned} {{\,\mathrm{diag}\,}}(\zeta _4^b,\zeta _4^b,\zeta _4^b), \quad {{\,\mathrm{diag}\,}}(\zeta _4^b,\zeta _4^b,(-1)^a \zeta _4^b ) \quad \text {or} \quad {{\,\mathrm{diag}\,}}(\zeta _4^b ,\zeta _4^b,(-1)^{a} \zeta _4^{3b}). \end{aligned}$$

$\square$

Lemma 5.21

Let X be a quotient of $E^3$ by a rigid diagonal action of ${\mathbb {Z}}_3^2$ or ${{\,\mathrm{He}\,}}(3)$. Let $N_{gor}$ be the number of singularities of type $\frac{1}{3}(1,1,1)$ and $N_{ter}$ be the number of singularities of type $\frac{1}{3}(1,1,2)$, then

$$\begin{aligned} e(X)=\frac{2}{3}(N_{gor}+N_{ter}). \end{aligned}$$

Proof

The quotient map $\pi :E^3 \rightarrow X$ restricts to an unramified cover

$$\begin{aligned} \pi :E^3\setminus \pi ^{-1}(S) \rightarrow X\setminus S \end{aligned}$$

of degree $d=9$ or 27, where $S:={{\,\mathrm{Sing}\,}}(X)$. Since the Euler number is additive and $e(E^3)=0$, we obtain:

$$\begin{aligned} -\vert \pi ^{-1}(S) \vert = e\big (E^3\setminus \pi ^{-1}(S)\big )=d e\big (X\setminus S\big ) = d\big (e(X) - \vert S \vert \big ). \end{aligned}$$

We conclude the proof, because the fibre of $\pi$ over each singularity consists of d/3 points. $\square$

Proposition 5.22

Let X be a quotient of $E^3$ by a rigid action of ${\mathbb {Z}}_3^2$ or ${{\,\mathrm{He}\,}}(3)$.

• 1. If $p_g=0$ then X has 9 terminal singularities of type $\frac{1}{3}(1,1,2)$.

• 2. If $p_g=1$ then ${{\,\mathrm{Sing}\,}}(X)$ consists of 9 or 27 Gorenstein singularites of type $\frac{1}{3}(1,1,1)$. The latter happens if and only if X is isomorphic to Beauville’s threefold $X_{3,3}$.

Proof

• 1. Thanks to the orbifold Riemann-Roch formula (see e.g. [19, p. 412 Corollary 10.3]) it is possible to express $\chi ({\mathcal {O}}_X)$ in terms of the intersection of Chern classes of a resolution $\rho :{\widehat{X}} \rightarrow X$ and local data coming from the singularities. In fact, it reads

  $$\begin{aligned} 24\chi ({\mathcal {O}}_X) = - c_1(\rho ^*K_X) \cdot c_2({\widehat{X}}) + \sum _{x \in {{\,\mathrm{Sing}\,}}(X)_{ter}} \frac{n_x^2-1}{n_x}, \end{aligned}$$

  where the sum runs over all terminal singularities $\frac{1}{n_x}(1,a_x,n_x-a_x)$ of X. Since $\mathcal {O}(3K_X) \simeq \mathcal {O}_X$, the first summand is zero. Moreover, all terminal singularities of X are of type $\frac{1}{3}(1,1,2)$ and $\chi (\mathcal {O}_X) = 1$. Hence the formula implies $N_{ter}=9$.

• 2. According to Lemma 5.21 and Remark 5.19 3), we have

  $$\begin{aligned} N_{gor}=3 \dim _{{\mathbb {C}}}\big ( H^{1,1}(X)^G\big ). \end{aligned}$$

  As in the proof of Proposition 5.7 we consider X as a ${\mathbb {Z}}_3^2$-quotient of a three dimensional torus und use the analytic representation $\rho$ to compute the dimension of the space of invariant (1, 1)-forms. The analytic representation $\rho$ is easy to describe, because it is a sum of three non-trivial characters $\chi _i$ of ${\mathbb {Z}}_3^2$. The invariance of $dz_1 \wedge dz_2 \wedge dz_3$ imposes the condition $\chi _1 \chi _2 \chi _3 =\chi _{triv}$. Moreover, we have $\chi _1 \ne \chi _2^2$, because $dz_1 \otimes dz_2$ is not invariant. Whence there are two cases:

Case 1: $\chi _1=\chi _2$, then $\chi _3$ is also equal to $\chi _1$ and up to an automorphism of ${\mathbb {Z}}_3^2$ it holds $\rho (a,b)={{\,\mathrm{diag}\,}}\big (\zeta _3^{a},\zeta _3^{a}, \zeta _3^{a} \big )$. In this case all (1, 1) forms are invariant i.e., $\dim _{{\mathbb {C}}}\big ( H^{1,1}(X)^G\big )=9$ and we conclude $N_{gor}=27$. The argument we used in the proof of Theorem 4.7 i.e. [10, Corollary 13.3.5] tells us that $X \simeq X_{3,3}$.

Case 2: $\chi _1 \ne \chi _2$, then since $\chi _1 \ne \chi _2^2$ there exists an automorphism of ${\mathbb {Z}}_3^2$ such that $\chi _1(a,b)=\zeta _3^{a}$ and $\chi _2(a,b)=\zeta _3^{b}$. This implies that $\chi _3(a,b)=\zeta _3^{2a+2b}$ and shows that the analytic representation is $\rho (a,b)={{\,\mathrm{diag}\,}}\big (\zeta _3^{a},\zeta _3^{b}, \zeta _3^{2a+2b} \big )$. We compute $\dim _{{\mathbb {C}}}\big ( H^{1,1}(X)^G\big )=3$ and obtain $N_{gor}=9$. $\square$

Recall that Beauville’s threefold $X_{3,3}$ is simply connected, see Remark 4.8. This allows us to show:

Proposition 5.23

Let X be a quotient of $E^3$ by a rigid diagonal action of ${\mathbb {Z}}_3^2$ or ${{\,\mathrm{He}\,}}(3)$ with $p_g=1$ and 9 singularities. Then X is uniformized by Beauville’s threefold $X_{3,3}$ by a degree three map. In particular, $\pi _1(X)$ is isomorphic to ${\mathbb {Z}}_3$.

Proof

We assume that X is a quotient of $E^3$ by ${\mathbb {Z}}_3^2$. The case where X is a quotient of $E^3$ by ${{\,\mathrm{He}\,}}(3)$, or equivalently X is a quotient of $E^3/C_3$ by ${\mathbb {Z}}_3^2$ is handled exactly in the same way.

In the proof of Proposition 5.22 2), we saw that up to an automorphism of ${\mathbb {Z}}_3^2$, the analytic representation is $\rho (a,b)={{\,\mathrm{diag}\,}}\big (\zeta _3^{a},\zeta _3^{b}, \zeta _3^{2a+2b} \big )$. The restriction to the subgroup $H:=\langle (1,1) \rangle \le {\mathbb {Z}}_3^2$ is generated by $\zeta _3 \cdot {{\,\mathrm{Id}\,}}$, which implies that $E^3/H$ is isomorphic to $X_{3,3}$, again using [10, Corollary 13.3.5]. We show that the map u fitting in the diagram

is a local biholomorphism. Then, since u is proper, it is an unramified cover. Clearly, u maps ${{\,\mathrm{Sing}\,}}(E^3/H)=\lbrace 27 \times \frac{1}{3}(1,1,1) \rbrace$ to ${{\,\mathrm{Sing}\,}}(X)=\lbrace 9 \times \frac{1}{3}(1,1,1) \rbrace$. More precisely, since u has degree three, the fibre of u over each point $p \in X$ consists either of three singular or three smooth points, depending if p is singular or not. Take a point $q \in E^3/H$ such that $u(q)=p$ and a point $x \in E^3$ such that $p_ 2(x) =q$, then $p_1(x)=p$ and the diagram of local rings commutes:

By definition of the sheaf of holomorphic functions on a quotient, the maps $p_1^{*}$ resp. $p_2^{*}$ are isomorphisms onto the subrings ${\mathcal {O}}_{E^3,x}^{G_x}$ resp. ${\mathcal {O}}_{E^3,x}^{H_x}$ of ${\mathcal {O}}_{E^3,x}$. The inclusion ${\mathcal {O}}_{E^3,x}^{G_x} \subset {\mathcal {O}}_{E^3,x}^{H_x}$ is an equality, since the stabilizers $H_x \subset G_x$ are equal. Indeed both groups $H_x$ and $G_x$ are either trivial or of order 3, depending if p and q are smooth or singular. $\square$

Remark 5.24

Let X be a quotient of $E^3$ by a rigid diagonal action of ${\mathbb {Z}}_3^2$ or ${{\,\mathrm{He}\,}}(3)$ uniformized by $X_{3,3}$. Then there is a crepant resolution $\rho :{\widehat{X}} \rightarrow X$ of singularities, such that ${\widehat{X}}$ is uniformized by the crepant resolution ${\widehat{X}}_{3,3}$ of Beauville’s threefold.

Theorem 5.25

For each exceptional group ${\mathbb {Z}}_3^2$ and ${{\,\mathrm{He}\,}}(3)$ there are exactly four isomorphism classes of quotients

$$\begin{aligned} X_i:=E^3/{\mathbb {Z}}_3^2 \qquad \text {and} \qquad Y_i:=E^3/{{\,\mathrm{He}\,}}(3) \end{aligned}$$

obtained by a rigid diagonal G-action. Some of the invariants are listed in the following table:

The threefolds $X_4$ and $Y_4$ are isomorphic to Beauville’s threefold.

		$p_g$	$b_3$	$b_2$	${{\,\mathrm{Sing}\,}}$
$X_1$	$Y_1$	0	0	5	$9 \times \frac{1}{3}(1,1,1)$, $9 \times \frac{1}{3}(1,1,2)$
$X_2$	$Y_2$	0	2	3	$9 \times \frac{1}{3}(1,1,2)$
$X_3$	$Y_3$	1	2	3	$9 \times \frac{1}{3}(1,1,1)$
$X_4$	$Y_4$	1	2	9	$27 \times \frac{1}{3}(1,1,1)$

Proof

In analogy to the proof of Theorem 5.4 we consider for each group $G={\mathbb {Z}}_3^2$ resp. ${{\,\mathrm{He}\,}}(3)$ the set of triples of generating triples $[V_1,V_2,V_3]$ which correspond to a diagonal rigid group action on $E^3$. Then we determine the orbits of the action of ${\mathfrak {S}}_3 \times {\mathcal {B}}_3^3 \times {{\,\mathrm{Aut}\,}}(G)$ on this set. We obtain 4 orbits for each group. The invariants are then computed as explained in Remark 5.19 and Lemma 5.21. $\square$

Remark 5.26

• 1. In the sequel we shall investigate the relations among the threefolds in the table. By looking at the Betti numbers, it is obvious that $X_i$ is not homeomorphic to $X_j$ or $Y_j$ for $j\ne i$, except for $i=2$ and $j=3$ or vice versa.

• 2. Using as in the proof of Theorem  5.4 the identification ${{\,\mathrm{He}\,}}(3)/C_3 \simeq {\mathbb {Z}}_3^2$, it can be checked again by a MAGMA routine that the image of the triple $[W_{i,1}, \ldots , W_{i,3}]$ representing $Y_i$ is a triple $[V_{i,1}, \ldots ,V_{i,3}]$ which lies in the orbit representing $X_i$. Therefore there are ramified Galois covers $f_i :Y_i \rightarrow X_i$ with group ${\mathbb {Z}}_3^2$, thanks to Proposition 5.3.

Proposition 5.27

The threefolds $X_2$ and $X_3$ are diffeomorphic in the orbifold sense. Likewise $Y_2$ and $Y_3$ are also diffeomorphic.

Remark 5.28

By Proposition 5.23 it follows that $\pi _1(X_2)$ and $\pi _1(Y_2)$ are isomorphic to ${\mathbb {Z}}_3$. Therefore we know all fundamental groups of the threefolds $X_i, Y_i$ in the above table, except for $i = 1$.

Using the description of the fundamental group of a product quotient given in [6], see also [1], a short MAGMA routine shows that $X_1$ and $Y_1$ are simply connected.

Proof of Proposition 5.27

We may realize $X_3$ as the quotient of $E^3$ by the ${\mathbb {Z}}_3^2$-action:

$$\begin{aligned} \psi _3(a,b)(z)={{\,\mathrm{diag}\,}}(\zeta _3^a,\zeta _3^b,\zeta _3^{2a+2b})z+ \frac{1+2\zeta _3}{3}(b,a,a). \end{aligned}$$

Indeed the action is faithful on each factor and, according to the argument in the proof of Proposition 5.22, Case 2, the quotient has 9 singularities of type $\frac{1}{3}(1,1,1)$.

Now we modify this action by replacing the third component of $\psi _3$ with the following action:

$$\begin{aligned} \psi _2(a,b)(z)={{\,\mathrm{diag}\,}}(\zeta _3^a,\zeta _3^b,\zeta _3^{a+b})z+ \bigg ( \frac{1+2\zeta _3}{3}b, \frac{1+2\zeta _3}{3}a, \frac{1+2\zeta _3^2}{3}a\bigg ). \end{aligned}$$

The action is still faithful on each factor, rigid and the invariants of the quotient are $p_g=0$, $b_3=2$ and $b_2=3$. Whence the quotient with respect to this action is $X_2$. By construction, the diffeomorphism

$$\begin{aligned} F:E^3 \rightarrow E^3, \qquad (z_1,z_2,z_3) \mapsto (z_1,z_2,{\overline{z}}_3) \end{aligned}$$

descends to the quotients ${\widehat{F}} :X_3 \rightarrow X_2$. An affine diffeomorphism between $Y_3$ and $Y_2$ is established in the same way. $\square$

The rest of the section is devoted to show the following:

Theorem 5.29

The threefolds in the table consist of five distinct topological types:

$$\begin{aligned} X_1, \quad Y_1, \quad X_2 \simeq _{\text {{diff}}} X_3, \quad Y_2\simeq _{\text {{diff}}} Y_3 \quad \text {and} \quad X_4\simeq _{\text {{bihol}}} Y_4 \end{aligned}$$

To prove the theorem it remains to show that the threefolds $X_i$ and $Y_i$ are not homeomorphic for $1 \le i \le 3$. Albeit we cannot use the fundamental groups to distinguish them, our argument is still analogous to the one that we gave in the previous section i.e., based on Bieberbach’s theorems. As a substitute for the fundamental group, we use:

Definition 5.30

Let $T={\mathbb {C}}^n/\Lambda$ be a complex torus and G be a finite group of automorphisms acting on T without translations. Let $\pi :{\mathbb {C}}^n \rightarrow T$ be the universal cover, then we define the orbifold fundamental group as

$$\begin{aligned} \Gamma :=\lbrace \gamma :{\mathbb {C}}^n \rightarrow {\mathbb {C}}^n ~ \big \vert ~ \exists ~ g \in G, ~~ s.t. ~ \pi \circ \gamma = g \circ \pi \rbrace . \end{aligned}$$

Remark 5.31

• 1. By definition $\Gamma$ is a cocompact discrete subgroup of the group of affine transformations. The subgroup of translations of $\Gamma$ is the lattice $\Lambda$. If G acts freely in codimension at least two, then $\Gamma$ is isomorphic to the fundamental group of the smooth locus of T/G.

• 2. We point out that $\Gamma _{X_i}$ and $\Gamma _{Y_i}$ can be described in terms of the triples $[V_{i,1}, \ldots ,V_{i,3}]$ and $[W_{i,1}, \ldots , W_{i,3}]$ of generating triples, which correspond to $X_i$ and $Y_i$ (cf. [6, Section 3]): let ${\mathbb {T}}$ be the triangle group ${\mathbb {T}}(3,3,3)$ and consider the homomorphisms

  $$\begin{aligned} \phi _{V_{i,j}} :{\mathbb {T}} \rightarrow {\mathbb {Z}}_3^2 \qquad \text {and} \qquad \phi _{W_{i,j}} :{\mathbb {T}} \rightarrow {{\,\mathrm{He}\,}}(3). \end{aligned}$$

  Then the groups $\Gamma _{X_i}$ and $\Gamma _{Y_i}$ are isomorphic to the fibred products:

  $$\begin{aligned} \Gamma _{X_i}&\simeq \lbrace t \in {\mathbb {T}}^3 ~ \big \vert ~ \phi _{V_{i,1}}(t_1)= \cdots = \phi _{V_{i,3}}(t_3) \rbrace , \\ \Gamma _{Y_i}&\simeq \lbrace t \in {\mathbb {T}}^3 ~ \big \vert ~ \phi _{W_{i,1}}(t_1)= \cdots = \phi _{W_{i,3}}(t_3) \rbrace . \end{aligned}$$

Lemma 5.32

The groups $\Gamma _{X_i}$ and $\Gamma _{Y_i}$ are not isomorphic for $1\le i \le 3$.

Proof

We only treat the case $i=1$. The strategy in the other cases is the same, even easier.

Assume that $\Gamma _{X_1}$ and $\Gamma _{Y_1}$ are isomorphic then, by Bieberbach’s second theorem 5.11, there exists an affine transformation

$$\begin{aligned} \alpha :{\mathbb {R}}^6 \rightarrow {\mathbb {R}}^6, \quad x \mapsto Ax+b, \end{aligned}$$

such that $\alpha \circ \Gamma _{X_1} \circ \alpha ^{-1}= \Gamma _{Y_1}$. As explained above, the analytic representations of the ${\mathbb {Z}}_3^2$ actions giving the quotients $X_1$ and $Y_1$ coincide. We view this representation $\rho =\rho _1$ as a real representation in the orthogonal group of $6\times 6$ matrices:

$$\begin{aligned} \rho _{{\mathbb {R}}}(a,b) := \begin{pmatrix} B^{a+b} &{} 0 &{} 0 \\ 0 &{} B^{a+b} &{} 0 \\ 0 &{} 0 &{} B^b \end{pmatrix}, \quad B=-\frac{1}{2} \begin{pmatrix} 1 &{} \sqrt{3} \\ -\sqrt{3} &{}1 \end{pmatrix}. \end{aligned}$$

In analogy to Remark 5.12 (2), there exists an automorphism $\varphi \in {{\,\mathrm{Aut}\,}}({\mathbb {Z}}_3^2)$, such that

$$\begin{aligned} A \rho _{{\mathbb {R}}}(a,b) A^{-1} =\rho _{{\mathbb {R}}}\big (\varphi (a,b)\big ), \quad \ \forall \ (a,b) \in {\mathbb {Z}}_3^2. \end{aligned}$$

The representation $\rho _{{\mathbb {R}}}$ consists of two copies of $B^{a+b}$ and one copy of $B^{b}$. Thus $\rho _{{\mathbb {R}}} \circ \varphi$ is also the sum of two copies of an irreducible two-dimensional real representation and another (distinct) irreducible two dimensional real representation. Schur’s Lemma implies that A is a block matrix:

$$\begin{aligned} A= \begin{pmatrix} A_1 &{} 0 \\ 0 &{} A_2 \end{pmatrix}, \quad \text {where} \quad A_1 \in {{\,\mathrm{GL}\,}}(4,{\mathbb {R}}) \quad \text {and} \quad A_2 \in {{\,\mathrm{GL}\,}}(2,{\mathbb {R}}). \end{aligned}$$

As in the proof of Theorem 5.16 we conclude that $A_2$ has to be ${\mathbb {C}}$-linear or ${\mathbb {C}}$-antilinear and we obtain a contradiction for the same reasoning. $\square$

Remark 5.33

We can use the description of the groups $\Gamma _{X_i}$ and $\Gamma _{Y_i}$ from Remark 5.31 (2) to compute, with the help of MAGMA, the number of their index three normal subgroups:

This is provides another argument that the groups $\Gamma _{X_i}$ and $\Gamma _{Y_i}$ cannot be isomorphic for $1 \le i \le 3$. Note that Proposition 5.27 implies $\Gamma _{X_2} \simeq \Gamma _{X_3}$ and $\Gamma _{Y_2}\simeq \Gamma _{Y_3}$, a fact that can be also verified using the MAGMA command SearchForIsomorphism.

	$\Gamma _{X_1}$	$\Gamma _{Y_1}$	$\Gamma _{X_2}$	$\Gamma _{Y_2}$	$\Gamma _{X_3}$	$\Gamma _{Y_3}$
# subgrps	41	14	41	5	41	5

Proof of Theorem 5.29

It remains to show that the threefolds $X_i$ and $Y_i$ are not homeomorphic for $1 \le i \le 3$. Assume the converse. We claim that a homeomorphism $f_i :X_i \rightarrow Y_i$ maps smooth to smooth and singular to singular points. In particular, it restricts to a homeomorphism between the regular loci $f_i :X_i^{\circ } \rightarrow Y_i^{\circ }$ and therefore induces an isomorphism between $\Gamma _{X_i}$ and $\Gamma _{Y_i}$, see Remark 5.31 (1). A contradiction. To verify the claim, we point out that the local fundamental group of a singularity of type $\frac{1}{3}(1,1,1)$ or $\frac{1}{3}(1,1,2)$ is isomorphic to ${\mathbb {Z}}_3$, while the local fundamental group of a smooth point is trivial. We conclude the proof, because f induces an isomorphism between $\pi _1^{loc}(X_i,p)$ and $\pi _1^{loc}\big (Y_i,f_i(p)\big )$, for all $p \in X_i$.

$\square$