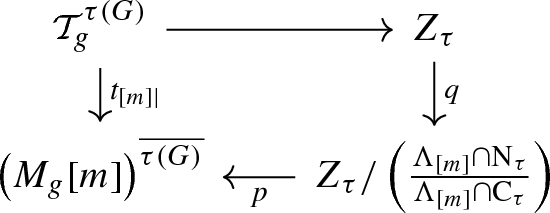Smooth covers of moduli stacks of Riemann surfaces with symmetry

Abstract

We construct explicitly a finite cover of the moduli stack of compact Riemann surfaces with a given group of symmetries by a smooth quasi-projective variety.

1 Introduction

For a finite group G, the locus $M_g(G)$ (in the moduli space $M_g$) of curves that have an effective action by G plays an important role in the study of the geometry of $M_g$ (for example its singularities [1, 2]), in the study of Shimura varieties (see e.g. [3,4,5] and the references therein), of totally geodesic subvarieties of $M_g$ [6], and also in the classification of higher dimensional varieties (see e.g. [7,8,9,10]). Similar loci in the moduli space of higher dimensional varieties have been studied in [11].

To investigate the geometry of $M_g(G)$ it is more natural to introduce the moduli stack ${\mathcal {M}}_g(G)$ of genus g compact Riemann surfaces with an effective action by G. Then we can obtain $M_g(G)$ as the image of a finite morphism ${\mathcal {M}}_g(G) \rightarrow M_g$. In this paper we study some geometric properties of ${\mathcal {M}}_g(G)$. If $g\ge 2$, ${\mathcal {M}}_g(G)$ is a complex orbifold, whose connected components are in bijection with the set ${\mathbb {T}}$ of topological types of the G-actions. For any $\tau \in {\mathbb {T}}$, let ${\mathcal {M}}_g(G, \tau )$ be the corresponding connected component. It is known that ${\mathcal {M}}_g(G, \tau )$ is isomorphic to the stack quotient $\left[ {\mathcal {T}}_g^{\tau (G)} / \mathrm{C}_{\Gamma _g}(\tau (G)) \right]$, where ${\mathcal {T}}_g^{\tau (G)}$ is the locus of points, in the Teichmüller space ${\mathcal {T}}_g$, that are fixed by $\tau (G)$, and $\mathrm{C}_{\Gamma _g}(\tau (G))$ is the centralizer of $\tau (G)$ in the mapping class group $\Gamma _g$. Using the theory of level structures we define a smooth quasi-projective variety $Z_\tau$ such that ${\mathcal {M}}_g(G, \tau ) \cong \left[ Z_\tau / \bar{\mathrm{C}}_\tau \right]$, where $\bar{\mathrm{C}}_\tau$ is a finite group. Hence ${\mathcal {M}}_g(G, \tau )$ is a smooth Deligne–Mumford stack and $Z_\tau \rightarrow {\mathcal {M}}_g(G, \tau )$ is a finite Galois cover. The disjoint union of the $Z_\tau$’s is a finite smooth cover of ${\mathcal {M}}_g(G)$, since ${\mathbb {T}}$ is finite (see e.g. [12]). Notice that the existence of a smooth quasi-projective variety Z and a finite flat morphism $Z\rightarrow {\mathcal {M}}_g(G)$ follows also from [13].

2 Moduli spaces of curves with symmetry

Throughout the article G is a finite group and g is an integer greater or equal than 2. Let ${\mathcal {M}}_g(G)$ be the stack, in the complex analytic category, whose objects are pairs $(\pi :{\mathcal {C}} \rightarrow B, \alpha )$, where $\pi :{\mathcal {C}} \rightarrow B$ is a family of compact Riemann surfaces of genus g and $\alpha :G \times {\mathcal {C}} \rightarrow {\mathcal {C}}$ is an effective (holomorphic) action of G on ${\mathcal {C}}$ such that, for any $a\in G$, $\pi \circ \alpha (a, \_)=\pi$. A morphism $(\Phi , \varphi ):(\pi :{\mathcal {C}} \rightarrow B, \alpha ) \rightarrow (\pi ' :{\mathcal {C}}' \rightarrow B', \alpha ')$ is a Cartesian diagram

such that, for any $a\in G$, $\Phi \circ \alpha (a, \_) \circ \Phi ^{-1}= \alpha '(a, \_)$.

Using the Teichmüller space ${\mathcal {T}}_g$, we are going to define a complex orbifold structure on ${\mathcal {M}}_g(G)$. Given a compact, connected, oriented topological surface of genus g, $\Sigma _g$, recall that a Teichmüller structure on a Riemann surface C is the isotopy class of an orientation preserving homeomorphism $f:C \rightarrow \Sigma _g$, it will be denoted with [f]. Two Riemann surfaces with Teichmüller structures $(C, [f]), (C',[f'])$ are isomorphic, if there exists an isomorphism $F :C \rightarrow C'$ such that $[f]= [f' \circ F]$. We will denote with [C, [f]] the class of (C, [f]). Then, ${\mathcal {T}}_g$ is the set of isomorphism classes [C, [f]] of compact Riemann surfaces of genus g with Teichmüller structures. The mapping class group of $\Sigma _g$, denoted by $\Gamma _g$, is the group of all isotopy classes of orientation preserving homeomorphisms of $\Sigma _g$. There is a natural action of $\Gamma _g$ on ${\mathcal {T}}_g$, given by

$$\begin{aligned}{}[\gamma ] \cdot [C,[f]] = [C, [\gamma \circ f]] \, , \quad \forall [\gamma ] \in \Gamma _g , \, [C, [f]] \in {\mathcal {T}}_g \, . \end{aligned}$$

Furthermore, for any $[C,[f]] \in {\mathcal {T}}_g$, the homomorphism

$$\begin{aligned} \sigma _{[f]} :\mathrm{Aut}(C) \rightarrow \Gamma _g \, , \quad \Phi \mapsto [f\circ \Phi \circ f^{-1}] \end{aligned}$$

is injective and its image is the stabilizer of [C, [f]] in $\Gamma _g$, that we denote by $\mathrm{Stab}_{\Gamma _g}([C,[f]])$. We collect in the following theorem several results about the Teichmüller space, for a proof and for more details we refer to [14, 15].

Theorem 2.1

${\mathcal {T}}_g$ has a natural structure of a complex manifold which is homeomorphic to the unit ball in ${\mathbb {C}}^{3g - 3}$. The action of $\Gamma _g$ on ${\mathcal {T}}_g$ is holomorphic and properly discontinuous. The map

$$\begin{aligned} {\mathcal {T}}_g \rightarrow M_g \, , \quad [C, [f]] \mapsto [C] \, , \end{aligned}$$

to the coarse moduli space of compact Riemann surfaces of genus g yields an isomorphism ${\mathcal {T}}_g/\Gamma _g \cong M_g$.

Furthermore there is a universal family of Riemann surfaces of genus g with Teichmüller structure

$$\begin{aligned} \eta :{\mathcal {X}}_g \rightarrow {\mathcal {T}}_g \, . \end{aligned}$$

Let $\alpha$ be an effective action of G on C, viewed as an injective group homomorphism $\alpha :G \rightarrow \mathrm{Aut}(C)$. Let us choose an orientation preserving homeomorphism $f :C \rightarrow \Sigma _g$. Then we have an injective homomorphism

$$\begin{aligned} \rho := \sigma _{[f]} \circ \alpha :G \rightarrow \Gamma _g \, \end{aligned}$$

(1)

such that $\rho (G) \subset \mathrm{Stab}_{\Gamma _g}([C, [f]])$. Notice that, if $f' :C \rightarrow \Sigma _g$ is another orientation preserving homeomorphism, we obtain a different homomorphism $\rho ' :G \rightarrow \Gamma _g$. However [C, [f]] and $[C,[f']]$ belong to the same $\Gamma _g$-orbit, so there exists $[\gamma ]\in \Gamma _g$ such that $[\gamma ] \cdot [C, [f]] = [C, [f']]$ and $\rho ' = [\gamma ] \cdot \rho \cdot [\gamma ]^{-1}$. This motivates the following definitions (that are already present in the literature, in slightly different forms, see e.g. [12] and the references therein).

Definition 2.2

Let $\alpha :G \rightarrow \mathrm{Aut}(C)$ be an injective homomorphism. Let $\rho$ be defined in (1). The topological type of the G-action $\alpha$ is the class of $\rho$ in $\mathrm{Hom}^\mathrm{inj} (G, \Gamma _g)/\Gamma _g$, where $\mathrm{Hom}^{\mathrm{inj}} (G, \Gamma _g)$ is the set of injective group homomorphisms from G to $\Gamma _g$, $\mathrm{Hom}^{\mathrm{inj}} (G, \Gamma _g)/\Gamma _g$ is the quotient under the action of $\Gamma _g$ by conjugation.

Definition 2.3

The Teichmüller space of compact Riemann surfaces of genus g with G-actions is the set

$$\begin{aligned} {\mathcal {T}}_g(G) = \{([C, [f]], \rho ) \in {\mathcal {T}}_g \times \mathrm{Hom}^{\mathrm{inj}} (G, \Gamma _g) \, | \, \rho (G) \subseteq \mathrm{Stab}_{\Gamma _g}([C, [f]])\} \, . \end{aligned}$$

Notice that, if $\mathrm{Hom}^{\mathrm{inj}} (G, \Gamma _g)\not = \emptyset$, then ${\mathcal {T}}_g(G)\not = \emptyset$ by Nielsen realization problem [16] and that it carries the following action by $\Gamma _g$:

$$\begin{aligned}{}[\gamma ] \cdot ([C, [f]], \rho ) = ([\gamma ] \cdot [C, [ f]], [\gamma ] \cdot \rho \cdot [\gamma ]^{-1}) \, , \end{aligned}$$

(2)

for $[\gamma ]\in \Gamma _g$ and $([C, [f]], \rho ) \in {\mathcal {T}}_g(G)$.

Proposition 2.4

${\mathcal {T}}_g(G)$ is a complex manifold. Moreover there is an object of ${\mathcal {M}}_g(G)$, $(\eta (G) :{\mathcal {X}}_g(G) \rightarrow {\mathcal {T}}_g(G), \alpha )$, such that the associated classifying morphism ${\mathcal {T}}_g(G) \rightarrow {\mathcal {M}}_g(G)$ induces an isomorphism

$$\begin{aligned} \left[ {\mathcal {T}}_g(G) / \Gamma _g \right] \cong {\mathcal {M}}_g(G) \, , \end{aligned}$$

where $\left[ {\mathcal {T}}_g(G) / \Gamma _g \right]$ is the stack quotient associated to the action (2). In particular ${\mathcal {M}}_g(G)$ has a structure of complex orbifold in the sense of [17, 15, XII, §4.].

Proof

It follows directly from Definition 2.3 that

$$\begin{aligned} {\mathcal {T}}_g (G) = \bigsqcup _{\rho \in \mathrm{Hom}^{\mathrm{inj}} (G, \Gamma _g)} {\mathcal {T}}_g^{\rho (G)} \, , \end{aligned}$$

where ${\mathcal {T}}_g^{\rho (G)}$ is the locus of points fixed by $\rho (G)$. Since $\rho (G)$ is a finite group, ${\mathcal {T}}_g^{\rho (G)}$ is a complex submanifold of ${\mathcal {T}}_g$, so the first claim follows.

For any $\rho \in \mathrm{Hom}^{\mathrm{inj}} (G, \Gamma _g)$, let $\eta (\rho ) :{\mathcal {X}}_g (\rho ) \rightarrow {\mathcal {T}}_g^{\rho (G)}$ be the restriction of the universal family. There is a natural effective action, $\alpha (\rho )$, of G on ${\mathcal {X}}_g (\rho )$ such that $(\eta (\rho ):{\mathcal {X}}_g (\rho ) \rightarrow {\mathcal {T}}_g^{\rho (G)}, \alpha (\rho ))$ is an object of ${\mathcal {M}}_g(G)$. Then we define $(\eta (G) :{\mathcal {X}}_g(G) \rightarrow {\mathcal {T}}_g(G), \alpha )$ as the disjoint union of these objects.

To prove the last statement recall that the objects of $\left[ {\mathcal {T}}_g(G) / \Gamma _g \right]$, over a base B, are pairs $(p:P\rightarrow B, f:P \rightarrow {\mathcal {T}}_g(G))$, where $p:P\rightarrow B$ is a principal $\Gamma _g$-bundle and f is a $\Gamma _g$-equivariant holomorphic map. Let $f^*(\eta (G))$ be the pull-back of the family $\eta (G)$. The action of $\Gamma _g$ on P extends to a free action on $f^*(\eta (G))$. So $f^*(\eta (G))$ descends to a family $\pi :{\mathcal {C}}\rightarrow B$ over B. By construction there is a G-action, $\alpha$, on ${\mathcal {C}}$, in such a way that $(\pi :{\mathcal {C}}\rightarrow B, \alpha )$ is an object of ${\mathcal {M}}_g(G)$. Similarly one associates to every arrow of $\left[ {\mathcal {T}}_g(G) / \Gamma _g \right]$ an arrow of ${\mathcal {M}}_g(G)$ obtaining an equivalence of categories. $\square$

Furthermore we have the following result.

Theorem 2.5

${\mathcal {M}}_g(G)$ is a smooth algebraic Deligne–Mumford stack with quasi-projective coarse moduli space.

A proof of this theorem will be given in Sect. 4, where we define a groupoid presentation of ${\mathcal {M}}_g(G)$, $X_1 {\mathop {t}\limits ^{[}}]{s}{\rightrightarrows } X_0$, with $X_0$ and $X_1$ smooth quasi-projective algebraic varieties, and such that $X_0 \rightarrow {\mathcal {M}}_g(G)$ is finite étale.

2.1 On the homology of $M_g(G)$

Let ${\mathbb {T}}\subset \mathrm{Hom}^{\mathrm{inj}} (G, \Gamma _g)$ be a set of representatives of topological types of G-actions (see Definition 2.2). Notice that, for any $\tau \in {\mathbb {T}}$,

$$\begin{aligned} \mathrm{Stab}_{\Gamma _g}(\tau ) = \mathrm{C}_{\Gamma _g}(\tau (G)) \, , \end{aligned}$$

where $\mathrm{C}_{\Gamma _g}(\tau (G))$ is the centralizer of $\tau (G)$ in $\Gamma _g$. Therefore we have an homeomorphism

$$\begin{aligned} {\mathcal {T}}_g(G) / \Gamma _g \cong \bigsqcup _{\tau \in {\mathbb {T}}} {\mathcal {T}}_g^{\tau (G)}/\mathrm{C}_{\Gamma _g}(\tau (G)) \, . \end{aligned}$$

Definition 2.6

Let $\tau \in {\mathbb {T}}$. The moduli space of compact Riemann surfaces of genus g with G-action of topological type $\tau$ is defined as ${\mathcal {T}}_g^{\tau (G)}/\mathrm{C}_{\Gamma _g}(\tau (G))$ and will be denoted by $M_g(G,\tau )$.

We have the following theorem from [18, 19] (see also [20] and the references therein).

Theorem 2.7

${\mathcal {T}}_g^{\tau (G)}$ is bi-holomorphic to ${\mathcal {T}}_{g',d}$ where $g'$ is the genus of C/G, $[C,[f]] \in {\mathcal {T}}_g^{\tau (G)}$, and d is the number of branch points of the quotient map $C \rightarrow C/G$. In particular ${\mathcal {T}}_g^{\tau (G)}$ is homeomorphic to the unit ball in ${\mathbb {C}}^{3g'-3+d}$.

Let us give an interpretation of the previous theorem. Given a point $[C, [f]] \in {\mathcal {T}}_g^{\tau (G)}$, let $\alpha :\sigma _{[f]}^{-1} \circ \tau :G \rightarrow \mathrm{Aut}(C)$. Then $f:(C, \alpha ) \rightarrow (\Sigma _g, f\circ \alpha \circ f^{-1})$ is G-equivariant, so it yields an orientation-preserving homeomorphism of $\theta :C'/G \rightarrow \Sigma _g'/G$, where $C'\subseteq C$ and $\Sigma _g' \subseteq \Sigma _g$ are the loci of points with trivial stabilizer. The bi-holomorphism in Theorem 2.7 sends [C, [f]] to $\left[ \Sigma _g'/G, [\theta ] \right] \in {\mathcal {T}}_{g',d}$.

We describe now the map ${\mathcal {T}}_{g', d} \rightarrow M_g(G,\tau )$, which is the composition of the inverse of the previous one, ${\mathcal {T}}_{g',d} \rightarrow {\mathcal {T}}_g^{\tau (G)}$, with the quotient ${\mathcal {T}}_g^{\tau (G)} \rightarrow {\mathcal {T}}_g^{\tau (G)}/\mathrm{C}_{\Gamma _g}(\tau (G))$. Let $p :\Sigma _g \rightarrow \Sigma _g/G$ be the quotient map, let $y\in \Sigma _g'/G$, and let $x \in p^{-1}(y)$. Let $\mu :\pi _1\left( \Sigma _g'/G, y \right) \rightarrow G$ be the monodromy of the covering p restricted to $\Sigma _g'$. For any $[D', [\theta ]] \in {\mathcal {T}}_{g',d}$ the composition

$$\begin{aligned} \mu \circ \theta _* :\pi _1(D', \theta ^{-1}(y)) \rightarrow G \, \end{aligned}$$

gives a G-cover $C' \rightarrow D'$, hence a point $[C, \alpha ] \in M_g(G,\tau )$. Then the map ${\mathcal {T}}_{g', d} \rightarrow M_g(G,\tau )$ sends $[D', [\theta ]]$ to $[C, \alpha ]$.

Notice that the class of $\mu$,

$$\begin{aligned}{}[\mu ] \in \mathrm{Hom}(\pi _1\left( \Sigma _g'/G, y \right) , G)/G \, , \end{aligned}$$

where G acts by conjugation, does not depend from the choice of y, and that $\Gamma _{g',d}$ acts on $\mathrm{Hom}(\pi _1\left( \Sigma _g'/G, y \right) , G)/G$.

It follows from this that

$$\begin{aligned} M_g(G, \tau ) \cong {\mathcal {T}}_{g',d}/\mathrm{Stab}_{\Gamma _{g',d}}([\mu ]) \, . \end{aligned}$$

In particular the homology of $M_g(G,\tau )$ with rational coefficients can be computed as the homology of the group $\mathrm{Stab}_{\Gamma _{g',d}}([\mu ])$:

$$\begin{aligned} H_n(M_g(G,\tau ) ; {\mathbb {Q}}) \cong H_n(\mathrm{Stab}_{\Gamma _{g',d}}([\mu ]); {\mathbb {Q}}) \, . \end{aligned}$$

Let now $(\alpha _1, \beta _1, \ldots , \alpha _{g'}, \beta _{g'}, \gamma _1, \ldots , \gamma _d)$ be a geometric basis of the fundamental group $\pi _1(\Sigma _{g'} {\setminus } \{ y_1, \ldots , y_d\}, y)$ (here we follow the notation of [12]). Setting $a_i = \mu (\alpha _i), b_i= \mu (\beta _i), c_j=\mu (\gamma _j)$, we obtain an element

$$\begin{aligned}{}[(a_1, b_1, \ldots , a_{g'}, b_{g'}, c_1, \ldots , c_d)] \in G^{2g'+d}/G \, , \end{aligned}$$

where G acts diagonally by conjugation. This yields an injective correspondence between classes $[\mu ]$ of monodromies and elements of $G^{2g'+d}/G$. $\Gamma _{g', d}$ acts on $G^{2g'+d}/G$ (see e.g. [12, Sec 2.]) and the homology of $\mathrm{Stab}_{\Gamma _{g',d}}([\mu ])$ is isomorphic to the equivariant homology of the orbit of $[(a_1, b_1, \ldots , a_{g'}, b_{g'}, c_1, \ldots , c_d)]$ under the action of $\Gamma _{g',d}$. This motivates the following

Question 2.8

[21] Let $n, d \in {\mathbb {N}}$. Are there constants a, b such that the dimension of $H_n^{\Gamma _{g',d}}(G^{2g'+d}/G ; {\mathbb {Q}})$ is independent of $g'$, in the range $g' > an+b$?

We proved in [12] that the previous question has an affermative answer in the case where $n=0$.

3 Level structures and Teichmüller structures

In this section we recall some basic results and we fix the notation, for the proofs and for more details we refer to [15, Chapter XVI]. Given two groups $G_1$ and $G_2$ we denote with $\mathrm{Hom}(G_1, G_2)$ the set of homomorphisms from $G_1$ to $G_2$. Notice that there is an action of $G_2$ on $\mathrm{Hom}(G_1, G_2)$, which is induced by the action of $G_2$ on itself by conjugation ($(g,h)\mapsto g^{-1}hg$). An exterior group homomorphism from $G_1$ to $G_2$ is an element of the quotient set $\mathrm{Hom}(G_1, G_2)/G_2$. For any $\varphi \in \mathrm{Hom}(G_1, G_2)$ we denote with $\hat{\varphi }$ its class in $\mathrm{Hom}(G_1, G_2)/G_2$. We will say that $\hat{\varphi }$ is an exterior group monomorphism (respectively epimorphism, isomorphism) if $\varphi$ is a monomorphism (respectively epimorphism, isomorphism).

Let X be a path connected topological space. For any pair of points $x, y \in X$ and for any continuous path $\gamma$ from x to y, let $\varphi _{\gamma } :\pi _1(X,x) \rightarrow \pi _1(X,y)$ be the isomorphism that sends any $[c]\in \pi _1(X,x)$ to $[\gamma ^{-1}\cdot c \cdot \gamma ]$, where c is a loop in X based at x and [c] is its homotopy class.

Let H be a group. We will identify two exterior homomorphisms $\hat{\alpha }\in \mathrm{Hom}(\pi _1(X,x), H)/H$ and $\hat{\beta }\in \mathrm{Hom}(\pi _1(X,y), H)/H$ if $\hat{\alpha }= \widehat{\beta \circ \varphi _{\gamma }}$. Notice that this definition does not depend on the choice of $\gamma$ and yields an equivalence relation on the disjoint union

$$\begin{aligned} \bigsqcup _{x\in X} \mathrm{Hom}(\pi _1(X,x), H)/H \, . \end{aligned}$$

The class of $\hat{\alpha }$ will be denoted with $[\alpha ]$.

Definition 3.1

A Teichmüller structure of level H on X is the class $[\alpha ]$ of an exterior epimorphism $\hat{\alpha }\in \mathrm{Hom}(\pi _1(X,x), H)/H$, for $x\in X$.

Let now C and $C'$ be two compact Riemann surfaces. Let $[\alpha ]$ and $[\alpha ']$ be two Teichmüller structures of level H on C and $C'$, respectively. We say that the pairs $(C, [\alpha ])$ and $(C', [\alpha '])$ are isomorphic if there exists an isomorphism $F:C \rightarrow C'$ such that $[\alpha ]=[\alpha ' \circ F_*]$, where $F_* :\pi _1 (C, x) \rightarrow \pi _1 (C', F(x))$ is the homomorphism induced by F, $\alpha :\pi _1 (C, x) \rightarrow H$ and $\alpha ' :\pi _1 (C', F(x)) \rightarrow H$ are representatives of $[\alpha ]$ and $[\alpha ']$, respectively. The isomorphism class of $(C,[\alpha ])$ will be denoted $[C; \alpha ]$. The set of isomorphism classes of compact Riemann surfaces of genus g with Teichmüller structures of level H will be denoted ${}_HM_g$. When $g\ge 2$ it is possible to define a structure of complex analytic space on ${}_HM_g$, called the moduli space of genus g curves with Teichmüller structure of level H. We refer to [15] for more details.

3.1 Level structures and Teichmüller structures

Let $[\psi ]$ be a Teichmüller structure of level H on $\Sigma _g$. The following map defines a morphism of complex analytic spaces:

$$\begin{aligned} t_{[\psi ]} :{\mathcal {T}}_g \rightarrow {}_HM_g \, , \quad [C, [f]] \mapsto [C; \psi \circ f_*] \, , \end{aligned}$$

where f is a representative of [f] and $\psi :\pi _1 (\Sigma _g, f(x)) \rightarrow H$ is a representative of $[\psi ]$.

Remark 3.2

As explained in [15], the mapping class group $\Gamma _g$ acts on the set of Teichmüller structures of level H on $\Sigma _g$ as follows: $[\psi ] \cdot [\gamma ] = [\psi \circ \gamma _*]$. Moreover every connected component of ${}_H M_g$ coincides with $t_{[\psi ]}({\mathcal {T}}_g)$, for some $[\psi ]$, we denote $t_{[\psi ]}({\mathcal {T}}_g)$ by $M_g[\psi ]$. Hence we have the following decomposition,

$$\begin{aligned} {}_H M_g = \coprod _{[\psi ] \, \mathrm{mod} \, \Gamma _g} M_g[\psi ] \, . \end{aligned}$$

Let $\Lambda _{[\psi ]} : = \{ [\gamma ] \in \Gamma _g \, | \, [\psi ] \cdot [ \gamma ] = [\psi ] \}$. Then

$$\begin{aligned} M_g[\psi ] = {\mathcal {T}}_g / \Lambda _{[\psi ]} \, . \end{aligned}$$

Furthermore, if $\Lambda _{[\psi ]}$ is a normal subgroup of $\Gamma _g$ and $\Gamma _g[\psi ]:= \Gamma _g/\Lambda _{[\psi ]}$, then

$$\begin{aligned} M_g = M_g[\psi ] / \Gamma _g[\psi ] \, . \end{aligned}$$

We report the following result from [15], where a characteristic subgroup of $\pi _1(\Sigma _g, x)$ is a subgroup that is mapped to itself by every automorphism of $\pi _1(\Sigma _g, x)$.

Lemma 3.3

If $\ker (\psi )$ is a characteristic subgroup, then $\Lambda _{[\psi ]}$ is a normal subgroup of $\Gamma _g$.

Proof

Under our hypotheses any automorphism $\gamma$ of $\pi _1(\Sigma _g)$ induces an automorphism ${\bar{\gamma }}$ of H such that $\psi \circ \gamma = {\bar{\gamma }} \circ \psi$. This yields a group homomorphism $\mathrm{Out}^+(\pi _1(\Sigma _g)) \rightarrow \mathrm{Out}(H)$, $[\gamma ] \mapsto [{\bar{\gamma }}]$, whose kernel is $\Lambda _{[\psi ]}$, under the identification of $\mathrm{Out}^+(\pi _1(\Sigma _g))$ with $\Gamma _g$. $\square$

In the case where $\ker (\psi )$ is a characteristic subgroup we can describe the action of $\Gamma _g$ on $M_g[\psi ]$ as follows [15].

Lemma 3.4

Let $\ker (\psi )$ be a characteristic subgroup of $\pi _1(\Sigma _g)$. Then $\Gamma _g$ acts on $M_g[\psi ]$ as follows:

$$\begin{aligned}{}[\gamma ] \cdot [C; \alpha ] = [C; {\bar{\gamma }} \circ \alpha ] \, , \end{aligned}$$

where ${\bar{\gamma }}$ is the automorphism of H defined in the proof of Lemma 3.3.

Let now $m\in {\mathbb {Z}}_{\ge 1}$ and let $\chi _m :\pi _1(\Sigma _g) \rightarrow H_1(\Sigma _g, {\mathbb {Z}}/m{\mathbb {Z}})$ be the composition of the natural morphism $\pi _1(\Sigma _g)\rightarrow H_1(\Sigma _g, {\mathbb {Z}})$ with the reduction modulo m. Then $H_1(\Sigma _g, {\mathbb {Z}}/m{\mathbb {Z}})$ is a strongly characteristic quotient of $\pi _1(\Sigma _g)$ (i.e. there is only one subgroup K of $\pi _1(\Sigma _g)$ such that $\pi _1(\Sigma _g)/K$ is isomorphic to $H_1(\Sigma _g, {\mathbb {Z}}/m{\mathbb {Z}})$), in particular $\ker (\chi _m)$ is a characteristic subgroup of $\pi _1(\Sigma _g)$. In this situation we use the following notation:

$$\begin{aligned} M_g[m] := M_g[\chi _m] \, , \quad \Gamma _g[m] := \Gamma _g[\chi _m] \, , \quad \Lambda _{[m]}:= \Lambda _{[\chi _m]} \, , \quad t_{[m]}:= t_{[\chi _m]} . \end{aligned}$$

Furthermore we have that

$$\begin{aligned} \Gamma _g[m] \cong \mathrm{Sp}_{2g} ({\mathbb {Z}}/ m{\mathbb {Z}}) \end{aligned}$$

and moreover $M_g[m]$ coincides with the set of isomorphism classes of pairs $(C, \rho )$, where $\rho :H_1(C, {\mathbb {Z}}/m{\mathbb {Z}}) \rightarrow ({\mathbb {Z}}/m{\mathbb {Z}})^{2g}$ is a symplectic isomorphism, with respect to the intersection form on $H_1(C, {\mathbb {Z}}/m{\mathbb {Z}})$ and the standard symplectic form on $({\mathbb {Z}}/m{\mathbb {Z}})^{2g}$.

4 Smooth covers of ${\mathcal {M}}_g(G, \tau )$

Let $\tau :G \rightarrow \Gamma _g$ be an injective homomorphism, we denote with $\mathrm{C}_\tau$ the centralizer of $\tau (G)$ in $\Gamma _g$, and with $\mathrm{N}_\tau$ the normalizer of $\tau (G)$ in $\Gamma _g$. For any subgroup $H\le \Gamma _g$, its image under the quotient morphism $\Gamma _g \rightarrow \Gamma _g[m]=\Gamma _g/\Lambda _{[m]}$ will be denoted by ${\bar{H}}$.

Proposition 4.1

Let $m\ge 3$ be an integer and $Z_\tau :={{\mathcal {T}}_g^{\tau (G)}}/({\Lambda _{[m]} \cap \mathrm{C}_\tau })$. Then $Z_\tau$ is a complex manifold and, for $M_g(G, \tau )$ defined in Definition 2.6, the quotient morphism ${\mathcal {T}}_g^{\tau (G)} \rightarrow M_g(G, \tau )$ induces a finite morphism

$$\begin{aligned} Z_\tau \rightarrow M_g(G, \tau ) \, , \end{aligned}$$

(3)

which gives an isomorphism between $M_g(G, \tau )$ and $Z_\tau /\bar{\mathrm{C}}_\tau$.

Proof

The first claim follows from the fact that $\Lambda _{[m]}$ acts freely on ${\mathcal {T}}_g$, since $m\ge 3$. To see this, let $[\gamma ] \in \Lambda _{[m]}$ and let $[C,[f]] \in {\mathcal {T}}_g$ such that $[\gamma ] \cdot [C,[f]] = [C,[f]]$. Then $[\gamma ] \in \mathrm{Aut}(C)$. Let ${{\bar{\gamma }}}_*$ be the induced automorphism of $H_1(C,{\mathbb {Z}}/m{\mathbb {Z}})$. Since $[\gamma ] \in \Lambda _{[m]}$, ${{\bar{\gamma }}}_* =\mathrm{Id}$, then $[\gamma ] = \mathrm{Id}_C$ [15, Prop. (2.8), p. 512].

The last claim follows from the fact that $\Lambda _{[m]}$ is a normal subgroup of $\Gamma _g$ (Lemma 3.3) and ${\bar{\mathrm{C}}_\tau } = \frac{\mathrm{C}_\tau }{\mathrm{C}_\tau \cap \Lambda _{[m]}}$, so

$$\begin{aligned} M_g(G, \tau ) = {\mathcal {T}}_g^{\tau (G)}/\mathrm{C}_\tau = Z_\tau /{\bar{\mathrm{C}}_\tau } \, . \end{aligned}$$

$\square$

Now we prove that $Z_\tau$ is a quasi-projective algebraic variety. Although this fact can be deduced from [20] or [2], we give here, for completeness, an elementary proof by showing that there is a finite morphism $Z_\tau \rightarrow \left( M_g[m]\right) ^{\overline{\tau ( G )}}$, where $\left( M_g[m]\right) ^{\overline{\tau ( G )}}$ is the set of points of $M_g[m]$ fixed by the action of $\overline{\tau ( G )}$. By a finite morphism of complex analytic spaces we mean a proper morphism with finite fibers.

Proposition 4.2

Let $t_{[m]} :{{\mathcal {T}}}_g \rightarrow M_g[m]$ be the morphism defined in Sect. 3.1, $m\ge 3$. Then the following statements hold true:

• 1. $t_{[m]}({{\mathcal {T}}}_g^{\tau (G)}) = \left( M_g[m]\right) ^{\overline{\tau ( G )}}$;

• 2. let $t_{[m]|}$ be the restriction of $t_{[m]}$ to ${{\mathcal {T}}}_g^{\tau (G)}$, then the following diagram is commutative:

  

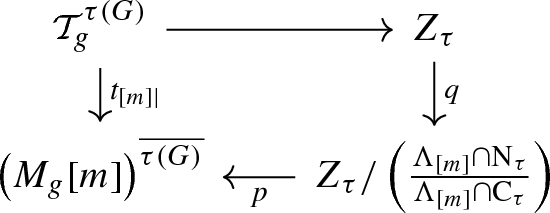
  where the horizontal arrow to the top is the quotient map by $\Lambda _{[m]}\cap \mathrm{C}_\tau$, q is the quotient map by $\frac{\Lambda _{[m]} \cap \mathrm{N}_\tau }{\Lambda _{[m]} \cap \mathrm{C}_\tau }$ and p sends any equivalence class of the $(\Lambda _{[m]} \cap \mathrm{N}_\tau )$-action to the corresponding equivalence class of the $\Lambda _{[m]}$-action (under the identification of $Z_\tau / \left( \frac{\Lambda _{[m]} \cap \mathrm{N}_\tau }{\Lambda _{[m]} \cap \mathrm{C}_\tau } \right)$ with $\frac{{\mathcal {T}}_g^{\tau (G)}}{\Lambda _{[m]} \cap \mathrm{N}_\tau }$);

• 3. the morphism $p\circ q$ is finite, therefore $Z_\tau$ has a structure of complex quasi-projective algebraic variety and $p\circ q$ is algebraic.

Proof

• 1. Since $\Lambda _{[m]}$ is normal in $\Gamma _g$ (Lemma 3.3), $t_{[m]}$ is G-equivariant, therefore $t_{[m]}({\mathcal {T}}_g^{\tau (G)}) \subseteq \left( M_g[m]\right) ^{\overline{\tau ( G )}}$. On the other hand, for any given $[C, \chi _m \circ f_*]\in \left( M_g[m]\right) ^{\overline{\tau ( G )}}$ and $[\gamma ] \in \tau (G)$, from the equality

  $$\begin{aligned}{}[C, \chi _m \circ f_*] = \overline{[\gamma ]} \cdot [C, \chi _m \circ f_*] \end{aligned}$$

  it follows that [C, [f]] and $[\gamma ]\cdot [C,[f]]$ map to the same point of $M_g[m]$. So, if $[\gamma ] \not \in \mathrm{Stab}_{\Gamma _g}([C,[f]])$, it would be an element of finite order of $\Lambda _{[m]}$, but this contradicts the fact that $\Lambda _{[m]}$ acts freely on ${\mathcal {T}}_g$. The statement in 2) follows from the fact that $M_g[m] =t_{[m]} ({\mathcal {T}}_g) = {\mathcal {T}}_g/\Lambda _{[m]}$ and from 1). To prove 3), we show that $p\circ q$ is closed and has finite fibers. Let us first show that q has finite fibers, equivalently that $\Lambda _{[m]} \cap \mathrm{C}_\tau$ has finite index in $\Lambda _{[m]} \cap \mathrm{N}_\tau$. Notice that, for $\tau (G) = \{ h_1, \ldots , h_{|\tau ( G )|} \}$, $\mathrm{C}_\tau$ is the stabilizer of $(h_1, \ldots , h_{|\tau ( G )|}) \in \prod _{h\in \tau (G)} \tau (G)$ with respect to the action of $\mathrm{N}_\tau$ given by conjugation on each factor. So $[ \mathrm{N}_\tau \, : \, \mathrm{C}_\tau ]< \infty$, hence also $[\Lambda _{[m]}\cap \mathrm{N}_\tau \, : \, \Lambda _{[m]}\cap \mathrm{C}_\tau ]< \infty$. To see that p has finite fibers, notice that for any $[C,[\chi _m \circ f_*]] \in \left( M_g[m]\right) ^{\overline{\tau ( G )}}$

  $$\begin{aligned} p^{-1}([C,[\chi _m \circ f_*]]) = \frac{\left( \Lambda _{[m]} \cdot [C,[f]] \right) \cap {\mathcal {T}}_g^{\tau (G)}}{\Lambda _{[m]} \cap \mathrm{N}_\tau } \, , \end{aligned}$$

  and, since $\Lambda _{[m]}$ acts freely on ${\mathcal {T}}_g^{\tau ( G )}$ (see the proof of Proposition 4.1), $p^{-1}([C,[\chi _m \circ f_*]])$ is in bijection with

  $$\begin{aligned} \frac{ \{\lambda \in \Lambda _{[m]} \, | \, \lambda ^{-1}\tau ( G) \lambda \subseteq \mathrm{Stab}_{\Gamma _g}([C,[f]]) \} }{\Lambda _{[m]} \cap \mathrm{N}_\tau } \, . \end{aligned}$$

  (4)

  The claim follows since the map from the quotient set in (4) to the set of subgroups of $\mathrm{Stab}_{\Gamma _g}([C,[f]])$, induced by $\lambda \mapsto \lambda ^{-1}\tau ( G) \lambda$, is injective.

  The fact that $p\circ q$ is closed follows from the fact that, for any closed subset $A \subseteq {\mathcal {T}}_g^{\tau (G)}$, the union of all $[\gamma ]\cdot A$, $[\gamma ] \in \Gamma _g$, is closed in ${\mathcal {T}}_g$ (see e.g. [20, proof of Theorem 1]). Finally, $Z_\tau$ and $p\circ q$ are algebraic by the Generalized Riemann Existence Theorem of Grauert-Remmert [22] (see [23], Theorem 3.2, Appendix B]), $Z_\tau$ is quasi-projective since $\left( M_g[m]\right) ^{\overline{\tau ( G )}}$ is so.

$\square$

Proof of Thm. 2.5

From the proof of Proposition 2.4 we have that

$$\begin{aligned} {\mathcal {M}}_g (G) = \bigsqcup _{\tau \in {\mathbb {T}}} \left[ {\mathcal {T}}_g^{\tau (G)}/\mathrm{C}_\tau \right] , \end{aligned}$$

where we use the notation of Sect. 2.1. Since ${\Lambda _{[m]} \cap \mathrm{C}_\tau }$ acts freely on ${\mathcal {T}}_g^{\tau (G)}$ the stack quotient $[{\mathcal {T}}_g^{\tau (G)}/({\Lambda _{[m]} \cap \mathrm{C}_\tau })]$ is represented by the variety $Z_\tau = {\mathcal {T}}_g^{\tau (G)}/({\Lambda _{[m]} \cap \mathrm{C}_\tau })$, hence

$$\begin{aligned} {\mathcal {M}}_g (G) = \bigsqcup _{\tau \in {\mathbb {T}}} \left[ Z_\tau /{\bar{\mathrm{C}}}_\tau \right] \, . \end{aligned}$$

The claim follows from the fact that the stack quotient of the algebraic variety $Z_\tau$ (Proposition 4.1) by the finite group ${\bar{\mathrm{C}}}_\tau$ is a Deligne–Mumford stack (see e.g. [24, (4.6.1)]). $\square$