Predicting the rutting behaviour of asphalt concrete in the modified wheel tracking test using DEM and a cohesive viscoelastic–elastoplastic-damage contact model

Abstract

This study used an advanced modelling approach capable of capturing the complex behaviour of asphalt concrete to model the modified wheel tracking test using a recent advanced experimental test set-up in accordance with ASTM D8292-20. The modelling approach uses the discrete element method (DEM) to naturally produce the heterogeneous internal structure and governs the behaviour of asphalt concrete at the grain level by an interparticle contact model. The contact model used is capable of characterising the rate and time dependency, viscoelastic-damage, and plastic-damage behaviour of asphalt concrete utilising the coupling of an elastoplastic-damage law with a viscoelastic-damage law. Unlike the conventional wheel tracking tests run in a fixed boundary condition (fully confined), the modified wheel tracking test considers the effect of boundary conditions on the rutting behaviour of asphalt mixes. Through comparisons and verifications with laboratory data of the rutting test at different boundary conditions (fully confined and unconfined), the modelling approach shows its capability of capturing the rutting behaviour of asphalt concrete in the modified wheel tracking test. Micromechanics analysis shows that the third (tertiary) stage of rutting behaviour is due to the weakening of the internal structure of the asphalt samples with contact bond breaks over time, which is found in the unconfined test. Meanwhile, the tertiary stage hardly occurs in the fully confined test once densification leads to contact of the aggregate–aggregate skeleton, forming a rigid structure to resist the load with lateral support from the fixed boundary condition. Finally, a parametric study was also conducted to provide further insight into the current testing set-up, including the effect of the sample size and boundary condition on the rutting behaviour of asphalt concrete.

1 Introduction

Rutting is one of the main distresses in asphalt concrete pavements [13, 33]. Rutting is associated with high temperatures, slow loading, or a combination of high temperatures and slow loading [11, 31]. The rutting mechanism in asphalt concrete includes compaction, also known as densification, due to the volume change underneath the wheel path and the lateral movement of asphalt concrete due to shear or distortion [13, 33]. The occurrence of rutting in asphalt pavements can greatly affect the riding quality of road pavement, increase the possibility of accidents, and lower the speed of vehicles [7, 29]. High rut depth requires pavement excavation, rehabilitation, or reconstruction, affecting economic and sustainable development [1, 7]. To control the quality of asphalt concrete subjected to rutting, wheel tracking tests for rutting resistance are required for heavy and medium loading traffic pavements in the design stage of asphalt mixtures [1]. Among the rutting tests, wheel tracking is the most popular for characterising the rutting resistance of asphalt mixes for quality control and quality management [1, 33]. Typically, the rut depth of asphalt samples from the experiment must be lower than a prescribed limit to satisfy the rutting resistance requirement for an asphalt mix [25]. Although the experimental wheel tracking test for rutting evaluation can provide the macro-behaviour of the asphalt mix, the micromechanism of the rutting behaviour is not clear [8, 26]. In addition, the various current testing devices of the wheel tracking test, such as the Asphalt Pavement Analyser, French Wheel Tracker, or Hamburg Wheel Tracking device, require running the test in a fixed boundary condition (e.g. samples are fully confined inside the mold) in which the damage and tertiary stage of rutting is hardly achieved and thus might not be able to characterise the difference in rutting resistance of asphalt mixes [21, 33]. To date, several experimental works have examined the new testing set-up of the wheel tracking test and utilised it to successfully characterise the rutting performance ranking of asphalt materials [21, 31, 32]. However, no numerical simulation has been performed to examine the micromechanism of the rutting behaviour of asphalt concrete under the new testing set-up.

This study aims to investigate the rutting behaviour of asphalt concrete under different boundary and geometry conditions using a current modified experimental set-up by an advanced numerical modelling approach. The work makes use of the DEM as the numerical platform to incorporate an advanced constitutive model capable of capturing the complex behaviour of asphalt concrete in the permanent deformation test utilising the modified wheel tracker rutting test. Numerical modelling using DEM was applied to illustrate its advantages in presenting the microstructural features of granular-based materials [5, 14, 20, 23]. The DEM considers a body as an assembly of particles in which particles interact via contact points; thus, the method is able to present the heterogeneity and interaction of particles at the grain scale [12, 15, 24, 35]. DEM can represent a body with an explicit description of grain size distribution and only requires proper constitutive models to govern the contact behaivour between two grains as well as the behaviour of bonding bridges between two grains. Thus, different materials can be flexibly modelled by adjusting the contact laws [18, 22, 27]. The DEM model in this study will be calibrated and validated using various tests for rutting under different boundary conditions of lateral confinement before being used for parametric studies. The study aims to provide insights into the rutting mechanism and rutting development in asphalt concrete, as well as the effects of microstructural features, boundary conditions, and sample geometry on rutting behaviour.

2 Experiment

The experimental test was conducted using a laboratory-produced dense graded hot-mix asphalt AC10, which has a nominal maximum aggregate size (NMAS) of 10 mm based on the Australian/New Zealand standard [2, 3]. The asphalt mix production, sample preparation, and testing were conducted at a pavement engineering laboratory at the University of Canterbury, Christchurch, New Zealand. The binder grade is PG64-16, which is equivalent to penetration grade 80/100 bitumen and was used for the asphalt mix. The viscosities of the binder measured at temperatures of 100 °C to 160 °C with 15 °C intervals were 4454, 1690, 728, 363, and 198 mPa.s, respectively. The optimum binder content was designed at 5.1% by the total mass of the asphalt mixture. The asphalt mixture was mixed at a temperature of 142 °C, and the loose asphalt mixture was compacted at the same temperature after the loose mix was conditioned in an oven (immediately after mixing) for one hour, as per the Australian/New Zealand standard [2, 3]. Slab samples with dimensions of 305 × 305 × 50 mm were prepared using a laboratory steel roller compactor. All samples were prepared with an air void target of 5.0 ± 1%. Before the test, samples were conditioned in a temperature controlled chamber for 7 h to ensure that the slabs reached a constant temperature of 60 °C. After conditioning, the test was started at the same temperature. The experimental wheel tracking test was conducted under different boundary conditions known as fully confined and unconfined. In the fully confined condition test, the sample was restrained and not allowed to move laterally, whereas the unconfined test allowed the sample to freely deform in the lateral direction. An illustration of the fully confined test and unconfined test is shown in Fig. 1. It should be noted that the movement of the slab sample is always constrained at both ends of the travel direction of the wheel in both the fully confined and unconfined cases. During the unconfined test, the rut depth (vertical deformation), the lateral deformation measured by two digital gauges, as shown in Fig. 1b, and the corresponding number of cycles were recorded. In the fully confined test, only the vertical deformation and the corresponding number of cycles were recorded.

Fig. 1

Schematic of the experimental wheel tracking test in the a fully confined, b unconfined test, and c sample dimensions

3 Numerical modelling

3.1 Modelling approach

Asphalt concrete is a bound material consisting of bitumen (bonding agent) and aggregates with different sizes and shapes that are randomly distributed in the mix or in the modelling designated as the material domain. The material domain in DEM simulations can be represented by replacing aggregates with idealised circular particles connected by contact bonds of simple geometry. This approach of simplifying the aggregate geometry aims to overcome the high computational cost of using real shape aggregates [17, 28], especially in the case of using a personal desktop. Since the number and size of particles significantly affect the computational cost of DEM simulations [4, 28], only reasonable aggregate sizes are considered (see Fig. 2). Given the simplification in the aggregate size, actual shapes of aggregate, and the mastic matrix’s geometry, the contact bond presenting the constitutive relation between particles would need to account for such simplified assumptions. This approach aims to enable the simplified DEM model to capture the essential behaviour of asphalt concrete. In this section, the general concept of DEM is presented, and subsequently, a summary of the contact model applied in the study is presented.

Fig. 2

Aggregate gradation curve in the experiment and aggregate size reproduced in the DEM

A computational domain in DEM is featured by an assembly of particles interacting with each other at their contact points and undergoes both translational and rotational motions. Every two particles (contact pair) interact via an interparticle contact law (i.e. contact model). Each particle features translational and rotational motions following the standard Newton’s second law and the Euler equation as follows, respectively:

$$ m{\ddot{\mathbf{x}}} = {\Sigma }{\mathbf{F}} - \alpha \left| {{\Sigma }{\mathbf{F}}} \right|sign\left( {{\dot{\mathbf{x}}}} \right) $$

(1)

$$ I{\ddot{\boldsymbol{\theta }}} = {\Sigma }{\mathbf{M}} - \alpha \left| {{\Sigma }{\mathbf{M}}} \right|sign\left( {{\dot{\boldsymbol{\theta }}}} \right) $$

(2)

In Eqs. 1 and 2, ${\Sigma }{\mathbf{F}}$ and ${\Sigma }{\mathbf{M}}$ are the total force and moment acting on the particle, respectively; ${\mathbf{x}}\user2{ }$ and ${{\varvec{\uptheta}}}$ are the translational and rotation displacement of the particle, respectively; single dot and double dot above variables indicate the first- and second-time derivatives, respectively; m is the particle mass; I is the moment of inertia of particle; $sign\left( {{\dot{\mathbf{x}}}} \right)$ and $sign\left( {{\dot{\boldsymbol{\theta }}}} \right)$ indicate the direction of particle translational and rotational velocities, respectively; and α is the nonviscous damping coefficient. This damping coefficient is used in the DEM to ensure that the assembled particles reach a state of equilibrium under all conditions [10]. For quasistatic analyses using DEM, α is often chosen as 0.7 [30]. In addition to the nonviscous damping coefficient, the stability of the system can also be treated by using a viscous damping coefficient, which is represented by the viscous dashpot in the contact model between two particles [9, 16]. In this study, a number of dashpots were used in the contact model to capture the viscoelastic behaviour of the asphalt concrete. Thus, a high nonviscous damping value is not needed. In fact, several studies have investigated this effect of nonviscous damping α and noted that when modelling brittle materials such as concrete, α values as small as 0.08 do not significantly differ from the higher values of α [28]. A preliminary study in this work as well as previous work [19] also showed that an α = 0.05 can be effectively used for asphalt concrete considering its highly viscoelastic behaviour. Thus, the value of α = 0.05 is adopted in this study while still ensuring the stability of DEM simulations considering dynamic simulations.

Once the particle accelerations are determined using Eqs. 1 and 2, the particle velocities and displacements can be obtained from the standard leapfrog time-integration scheme as described in Eqs. 3–6:

$$ {\dot{\mathbf{x}}}_{t + \Delta t/2}^{i} = {\dot{\mathbf{x}}}_{t - \Delta t/2}^{i} + {\ddot{\mathbf{x}}}_{t}^{i} \Delta t $$

(3)

$$ {\dot{\boldsymbol{\theta }}}_{t + \Delta t/2}^{i} = {\dot{\boldsymbol{\theta }}}_{t - \Delta t/2}^{i} + {\ddot{\boldsymbol{\theta }}}_{t}^{i} \Delta t $$

(4)

$$ {\mathbf{x}}_{t + \Delta t}^{i} = {\mathbf{x}}_{t}^{i} + {\dot{\mathbf{x}}}_{t + \Delta t/2}^{i} \Delta t $$

(5)

$$ {{\varvec{\uptheta}}}_{t + \Delta t}^{i} = {{\varvec{\uptheta}}}_{t}^{i} + {\dot{\boldsymbol{\theta }}}_{t + \Delta t/2}^{i} \Delta t $$

(6)

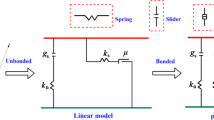
In Eqs. 3–6, $\Delta t$ is the time step, which must be chosen to be small enough so that during a single time step, disturbances affect only the particle’s intermediate neighbours [30]. Finally, a constitutive model (or contact model) presenting the relationship between the interparticle contact force and particle displacements is required to complete the description of particle motions. To simulate the nondamage viscoelastic behaviours of asphalt concrete, general viscoelastic models such as the general Maxwell model (Fig. 3a) can be used effectively. However, for damage-related issues, damage behaviour needs to be taken into account in the model. This study used a bond contact model that couples viscoelastic-damage elements (i.e. viscoelastic-damage section) and an elastoplastic-damage element (Fig. 3b). The contact model was proposed in a previous work [19]; thus, for the research in this paper, only key concepts are reintroduced. The total contact stress $({{\varvec{\upsigma}}}_{{{\mathbf{vep}}}} )$ developed in the contact bond connecting two particles is the sum of the viscoelastic contact stress (${{\varvec{\upsigma}}}_{{{\mathbf{ve}}}}$) and elastoplastic contact stress $({{\varvec{\upsigma}}}_{{{\mathbf{ep}}}} )$ (Eq. 7), and the total contact displacement ${\mathbf{u}}_{{{\mathbf{vep}}}} \user2{ }$ is equivalent to the displacement of each section (Eq. 8).

$$ {{\varvec{\upsigma}}}_{{{\mathbf{vep}}}} = {{\varvec{\upsigma}}}_{{{\mathbf{ve}}}} + {{\varvec{\upsigma}}}_{{{\mathbf{ep}}}} $$

(7)

$$ {\mathbf{u}}_{{{\mathbf{vep}}}} = {\mathbf{u}}_{{{\mathbf{ve}}}} = {\mathbf{u}}_{{{\mathbf{ep}}}} $$

(8)

where ${\mathbf{u}}_{{{\mathbf{ep}}}}$ is the displacement vector of the elastoplastic-damage section and ${\mathbf{u}}_{{{\mathbf{ve}}}}$ is the displacement vector of the viscoelastic-damage section. Note that the contact stress ${{\varvec{\upsigma}}}$ is a vector stress of the normal and shear tractions ${{\varvec{\upsigma}}} = \left( {{\varvec{\tau}}_{n} ,{\varvec{\tau}}_{s} } \right)$, acting on the contact plane normal to the contact bond between two particles.

Fig. 3

Contact bond model of two bonding particles featuring the nondamage behaviour of asphalt concrete (a) to the complex behaviour accounting for damage induced by plastic and viscoelastic behaviours (b) [19]

The viscoelastic-damage section consists of several viscoelastic elements (Maxwell elements) connected in parallel, in which each viscoelastic element is composed of a spring and a dashpot connected in series (Fig. 3b). Accordingly, the stress vector (${{\varvec{\upsigma}}}_{ve}^{i}$) of each Maxwell element is equivalent to either the stress vector in the spring (${{\varvec{\upsigma}}}_{{{\mathbf{mk}}}}^{i}$) or the stress vector in the dashpot (${{\varvec{\upsigma}}}_{{{\mathbf{mc}}}}^{i}$). Meanwhile, the displacement vector of a Maxwell element (${\mathbf{u}}_{ve}^{i}$) is the sum of the displacement vector of the spring (uⁱ_mk) and that of the dashpot (uⁱ_mc). The stress‒displacement relationship for the viscoelastic-damage element in the normal and shear directions is formulated as follows:

$$ \sigma_{ve}^{n} = \left( {1 - D_{ve} } \right)\mathop \sum \limits_{i} K_{m}^{i,n} u_{mk}^{i,n} - D_{ve} \langle - \mathop \sum \limits_{i} K_{m}^{i,n} u_{mk}^{i,n}\rangle $$

(9)

$$ \sigma_{ve}^{n} = \left( {1 - D_{ve} } \right)\mathop \sum \limits_{i} K_{m}^{i,n} u_{mk}^{i,n} - D_{ve} \langle \mathop \sum \limits_{i} K_{m}^{i,n} u_{mk}^{i,n} \rangle$$

(10)

In Eq. 9, the Macaulay bracket $\left\langle \cdot \right\rangle$ is used to describe that there is no damage developed in pure compression but still can occur in compression‒shear mode; the subscripts $n$ and $s$ present the normal and shear directions, respectively; $K_{m}^{i,n} , K_{m}^{i,s}$ are the stiffnesses in the normal and shear directions of Maxwell element i; $u_{mk }^{i,n} ,u_{mk}^{i,s}$ are the displacements in the normal and shear directions of Maxwell element i; $D_{ve}$ is the scalar rate-dependent damage variable in the viscoelastic-damage section, formulated as in Eq. 11:

$$ \dot{D}_{ve} = T\left( {\frac{{\langle\left( {1 - D_{ve} } \right)\mathop \sum \nolimits_{i} {\mathbf{C}}_{m}^{i,n} {\dot{\mathbf{u}}}_{mc}^{i,n} - D_{ve} \langle- \mathop \sum \nolimits_{i} {\mathbf{C}}_{m}^{i,n} {\dot{\mathbf{u}}}_{mc}^{i,n}\rangle - \sigma_{{{\text{max}}}}^{n}\rangle }}{{\sigma_{{{\text{max}}}}^{n} }} + \frac{{\langle\left( {1 - D_{ve} } \right)\mathop \sum \nolimits_{i} {\mathbf{C}}_{m}^{i,s} {\dot{\mathbf{u}}}_{mc}^{i,s} - \sigma_{{{\text{max}}}}^{s}\rangle }}{{\sigma_{{{\text{max}}}}^{s} }}} \right)^{B} $$

(11)

The damage evolution occurs when the stress exceeds the maximum stress $\sigma_{{{\text{max}}}}^{n}$ and $\sigma_{{{\text{max}}}}^{s}$ in the normal and shear directions, respectively. The material constants T and B are introduced to describe the evolution of the damage rate in each time step.

On the other hand, the stresses in the elastoplastic-damage element in the normal and shear directions ($\sigma_{ep}^{n} , \sigma_{ep}^{s}$) are formulated in the normal and shear directions as follows:

$$ \sigma_{ep}^{n} = k_{0}^{n} \left( {1 - D_{ep} } \right)\left( {u_{ep}^{n} - u_{p}^{n} } \right) - D_{ep} k_{0}^{n} \left\langle- \left( {u_{ep}^{n} - u_{p}^{n} } \right) \right\rangle$$

(12)

$$ \sigma_{ep}^{s} = k_{0}^{s} \left( {1 - D_{ep} } \right)\left( {u_{ep}^{s} - u_{p}^{s} } \right) $$

(13)

where $k_{0}^{n}$ and $k_{0}^{s}$ are the initial contact stiffness in the normal and shear directions, respectively, and $D_{ep}$ is a scalar damage variable of the elastoplastic-damage element. When the stress state reaches its yielding criterion, as formulated in Eq. 14, plastic displacement occurs and evolves.

$$ F\left( {\sigma_{ep}^{n} ,\sigma_{ep}^{s} ,D_{ep} } \right) = \left( {\beta \sigma_{ep}^{s} } \right)^{2} - [C_{0} \left( {1 - D_{ep} } \right) - \sigma_{ep}^{n} tan\varphi ]^{2} + \left[ {C_{0} \left( {1 - D_{ep} } \right) - \sigma_{0}^{t} \left( {1 - D_{ep} } \right)tan\varphi } \right]^{2} $$

(14)

The initial tensile strength and cohesion, describing the strength of the elastoplastic element in the normal and shear directions, are presented by $\sigma_{0}^{t} {\text{ and }}C_{0}$, respectively; $\varphi$ is the friction angle; and $\beta$ (formulated in Eq. 15) is a parameter used to adjust the intersection between the parabolic yield surface and shear stress axis to the original cohesion defined by the linear Drucker‒Prager yield surface:

$$ \beta = \frac{{\sqrt {2C_{0} \left( {1 - D_{ep} } \right)\sigma_{0}^{t} \left( {1 - D_{ep} } \right){\text{tan}}\left( \varphi \right) - \left[ {\sigma_{0}^{t} \left( {1 - D_{ep} } \right){\text{tan}}\left( \varphi \right)} \right]^{2} } }}{{C_{0} \left( {1 - D_{ep} } \right)}} $$

(15)

The increment of the plastic displacement vector is calculated based on the standard plastic flow rule (Eq. 16), in which $\delta \lambda \ge 0$ is the plastic multiplier, ${{\varvec{\upsigma}}}_{ep} = \left( {\tau_{ep}^{n} ,\user2{ }\tau_{ep}^{s} } \right)$ is the contact stress, and $G$ is the plastic potential function defined as per Eq. 17:

$$ \delta {\mathbf{u}}_{p} = \delta \lambda \frac{\partial G}{{\partial {{\varvec{\upsigma}}}_{ep} }} $$

(16)

$$ \begin{aligned}G\left( {\sigma_{ep}^{n} ,\sigma_{ep}^{s} ,D_{ep} } \right) = &\,\left( {\sigma_{ep}^{s} } \right)^{2} - [C_{0} \left( {1 - D_{ep} } \right) \\ &- \sigma_{ep}^{n} {\text{tan}}\left( \psi \right)]^{2}\\ & + [C_{0} \left( {1 - D_{ep} } \right)\\ & - \sigma_{0}^{t} \left( {1 - D_{ep} } \right){\text{tan}}\left( \psi \right)]^{2} \end{aligned}$$

(17)

The dilatancy angle $\psi$ in Eq. 17 is introduced to present the dilation effect occurring at the grain scale of the contact bond. Finally, the damage variable of the elastoplastic-damage section, $D_{ep} ,$ is expressed by an exponential function of plastic displacements as per Eq. 18. The softening parameters in normal and shear displacements $u_{c}^{n} {\text{ and }}u_{c }^{s}$ describe the softening behaviour of the contact bond at the grain level when either the bond changes its shape or microcracks occur in the bond, or both happen at the same time. The exponential evolution law allows a smooth transition between cohesive (bonded) and frictional behaviour (unbonded) in the simulation without ad hoc treatment when the contact bond is totally damaged (damage due to plastic $D_{ep}$ approaches one $(D_{ep} \to 1)$.

$$ D_{ep} = 1 - e^{{ - \left( {\frac{{u_{p}^{n} }}{{u_{c}^{n} }} + \frac{{u_{p}^{s} }}{{u_{c}^{s} }}} \right)}} $$

(18)

Finally, the stress‒displacement relationship of the viscoelastic–elastoplastic-damage contact model can be calculated as per Eqs. 19 and 20, in which $\sigma_{vep}^{n}$ and $\sigma_{vep}^{s}$ are the total stresses in the normal and shear directions of the contact, respectively.

$$ \sigma_{vep}^{n} = \left( {1 - D_{ve} } \right)\mathop \sum \limits_{i} K_{m}^{i,n} u_{mk}^{i,n} - D_{ve} \langle - \mathop \sum \limits_{i} K_{m}^{i,n} u_{mk}^{i,n} \rangle+ k_{0}^{n} \left( {1 - D_{ep} } \right)\left( {u_{ep}^{n} - u_{p}^{n} } \right) - D_{ep} k_{0}^{n} \langle- \left( {u_{ep}^{n} - u_{p}^{n} } \right)\rangle $$

(19)

$$ \sigma_{vep}^{s} = \left( {1 - D_{ve} } \right)\mathop \sum \limits_{i} K_{m}^{i,s} u_{mk}^{i,s} + k_{0}^{s} \left( {1 - D_{ep} } \right)\left( {u_{ep}^{s} - u_{p}^{s} } \right) $$

(20)

Note that the introduction of the two local damage variables $D_{ve}$ and $D_{ep}$ in the contact bond presents the damage that can occur and lead to the breakage of the contact bond induced either by dynamic viscoelastic stress under high loading rates or due to plastic deformation under static and low load rates. Furthermore, note that the development of $D_{ve}$ and $D_{ep}$ is independent and can occur simultaneously. This approach features the complex and realistic damage behaviour of asphalt concrete. Finally, the normal and shear stresses $(\sigma_{{{\text{vep}}}}^{n} \;{\text{and}}\;\sigma_{{{\text{vep}}}}^{s} )$ are converted to the corresponding contact forces $({\mathbf{F}}_{{{\text{vep}}}} )\user2{ }$ to update the motions of each individual particle as per Eq. 21. $A_{c}$ presents the contact area, which is equivalent to $2R$ in 2D or $\pi R^{2}$ in 3D simulation, with R being the minimum radius among the two particles in the contact pair. Further details of the stress update algorithms for the model implementation of each constitutive component are provided in previous work [19].

$$ {\mathbf{F}}_{vep} = {{\varvec{\upsigma}}}_{vep} A_{c} $$

(21)

3.2 Numerical sample creation

The DEM numerical simulation was conducted using a commercial software package named PFC from Itasca International. A workstation with a Core (TM) i7-6700 processor and a 3.2 GHz CPU and 16 GB of installed memory (RAM) was used for the simulation. The numerical test is performed in the 2D DEM simulation using circular particles. The choice of using 2D instead of 3D is due to two main reasons. First, 3D DEM simulation of the wheel tracking test considering the loading conditions in this study (see Sect. 3.3 for more detail) will take several months for one simulation to complete. Second, the main target of investigating the modified wheel tracker test is the difference in the lateral boundary conditions compared to those of the conventional test method [33]. Thus, 2D numerical modelling can still achieve the study target. Combining these two reasons, the choice of 2D is reasonable for the purpose of the study.

An illustration of the change from the 3D experimental test to the 2D numerical set-up is shown in Fig. 4. The gradation of aggregate in the experiment is replicated in the numerical simulation by creating samples with real aggregate gradation down to 2 mm diameter. No aggregates with a diameter of less than 2 mm are generated in the model to save computational cost. Rather, particles with a diameter of 2 mm are filled into the samples until a predefined porosity is reached. The missing information on aggregate creation (e.g. particle shapes, fine aggregate) is considered to be addressed by the advanced contact models. The circular particles are created by inputting the same portion of aggregate obtained on each sieve size as in the experiment, producing a smooth cumulative particle gradation curve based on the Rosin‒Rammler formulation [16]. The internal microstructure and heterogeneity are created by random distributions of aggregates at the sample creation stage along with the contact bond between particles, the diameter of which is equivalent to that of the smaller particle in an intact pair. The porosity of the sample is selected as 0.12, which is considered to be sufficiently dense to avoid excessive overlap between particles while still ensuring that the particles are well connected. In this manner, the system will eliminate the potential of the localised effect due to the inefficiency of contact bond connection [30]. For a numerical sample that is too dense, it could cause high overlap between particles. Overlap samples can cause simulation issues when compression is present where the particle overlap is large [28, 30], especially in this case study with permanent deformation in the compression-related direction.

Fig. 4

A 2D numerical set-up for the rutting test

In the numerical simulation of the wheel tracking test, particles with a diameter of 2.2 mm or greater are assigned as aggregates, while particles with a diameter from 2 mm to 2.2 mm are assigned as mastic. Accordingly, the contact model used for aggregate–aggregate pairs was the linear model (unbonded), and the viscoelastic–elastoplastic-damage model (bonded) was used for the aggregate-to-mastic and mastic-to-mastic contacts. The linear model (unbonded) contact model was also used for the aggregate wall and mastic wall. Note that the loading wheel of the experiment was a rubber wheel, and the boundary walls were metal. Using different contact properties that cannot be directly measured in this study would complicate the simulation. Furthermore, the deformation form in the experiment shows asphalt materials exhibit compliance during deformation. Thus, for the sake of removing the complexity while still achieve the main investigation target of the study, the assumption used in this case is deemed reasonable.

Several trials on assigning particles with a diameter of 2 mm for mastic resulted in a lack of bonding between aggregates, leading to localised failures in the samples due to insufficient bonding between adjacent aggregates. The assignment of mastic particles from 2 to 2.2 mm assures a reasonable bond of the particles in the numerical sample. Due to the high computational cost in the DEM simulation of the wheel tracking test, samples of 50 mm height and 203.3 mm width (equivalent to two-thirds of the full width of the real sample) were used in the numerical simulation for calibration and validation processes. Note that with the computer configuration and the numerical design, the actual time to complete one numerical test for a confined test of samples of 203.3 mm width was approximately 80 h, with the time step chosen at 4.0e − 6. The simulation of larger samples, such as 253 mm or 305 mm, required approximately 5 and 10 days, respectively. In this study, the time step was chosen to be smaller than the critical time step $t_{{{\text{critical}}}} = {\text{min}}\left( {0.2\sqrt {m^{i} /k^{i} } } \right)$ (where mⁱ is the mass of particle i, and $k^{i}$ is the spring stiffness) to ensure the numerical stability. Because there are several values of spring stiffness (e.g. $K_{m}^{i,n} ,k_{0}^{n}$) in the numerical domain, the critical time step $t_{{{\text{critical}}}}$ was determined based on the smallest particle size (e.g. 2 mm) and using that particle’s highest stiffness value in the contact. This approximation approach aims to estimate the upper bound of the time step, thus reducing the computational effort.

Typical test samples with a random aggregate distribution can be seen in Fig. 5. The random distribution of aggregates creates samples with different internal structures, reflecting the realistic case of aggregate and mastic distribution in asphalt samples.

Fig. 5

Random aggregate distribution of the numerical wheel tracking test samples

3.3 Boundary and loading condition

The boundary condition in the numerical simulation was set to be similar to the experiment, as illustrated in Fig. 6. The bottom plate in the experiment was represented by a wall at the bottom of the sample in the numerical simulation. The width of the wall is greater than the sample’s width to allow the lateral movement of the sample in the unconfined test. On the other hand, two lateral walls were set up in the fully confined test, which stopped the lateral movement of the sample during the test. The loading wheel was represented by a rectangle with a width of 50 mm, similar to the width of the wheel in the experimental test.

Fig. 6

Numerical testing set-up for a the unconfined test and b the confined test

In the experimental test, the loading wheel travels back and forth in the direction shown in Fig. 4 at a rate of 26.5 cycles per minute. Since each cycle consists of one pass moving backwards and one moving forwards, the loading wheel passes a cross section at the middle of the sample twice in a cycle. Thus, for each minute, the wheel passes a cross section in the centre of the sample 53 times. Because the DEM simulation of the wheel tracking test incurs high computational costs and cannot be conducted on a personal or desktop computer, an equivalent loading time method was applied for the numerical wheel tracking test. By using the loading scheme calculated as in the work of Saleh and Ebrahimi [34], the loading duration of each pass on a cross section is equivalent to 0.0837 s. The total loading duration on a cross section in the centre of the testing sample is equivalent to the number of total passes multiplied by the loading duration of each pass. The relationship between dynamic testing time and cycles and the accordingly equivalent static loading time is described in Fig. 7. In total, two samples with different boundary conditions (unconfined and confined) composed of four samples were used for the calibration and prediction processes.

Fig. 7

Relationship between the real dynamic testing time in the experiment and the equivalent static loading time in the numerical simulation (a) and between the number of cycles in the experiment and the equivalent static loading time in the numerical simulation (b)

4 Results and discussion

4.1 Calibration and prediction

This study adopted the deformability method to remove the size dependence on contact behaviour. Accordingly, the normal stiffness $k_{n}$ of contacts is expressed via the effective modulus E (Eq. 22), and the shear stiffness $k_{s}$ is calculated via the normal-to-shear stiffness ratio $\left( {k_{{{\text{ratio}}}} } \right)$ (Eq. 23). In Eq. 22, L = R_i + R_j in the particle-to-particle contact or L = R_i in the particle-to-wall contact. The parameter $k_{{{\text{ratio}}}}$ is linked with Poisson’s ratio υ, and $k_{{{\text{ratio}}}}$ is kept constant for all cases and is equal to 2.4. This value is equivalent to a Poisson’s ratio of approximately 0.42, which is within the typical range of Poisson’s ratios used for asphalt concrete.

$$ k_{n} = \frac{E}{L} $$

(22)

$$ k_{{{\text{ratio}}}} = \frac{{k_{n} }}{{k_{s} }} = 2\left( {1 + \vartheta } \right) $$

(23)

The model parameters are calibrated using two randomly distributed aggregate samples with the same grain size distribution as in Fig. 5. First, the linear contact model was used for the aggregate-to-aggregate contacts and aggregate/mastic-wall contacts with the model parameters chosen as in Table 1. This contact model features the unbonded interaction of two aggregate particles in the material domain under shear, compression, and shear‒compression modes, while the contact model does not sustain a tensile load. Regarding the particles-walls contact, the loading wheel of the experiment is a rubber wheel; thus, the stiffness is much lower than that of the aggregate. Furthermore, the rut surface of experimental samples is not perfectly flat but bumpy due to the greater densification of the mastic than the aggregate. Thus, the chosen stiffness for particles-wall contact is reasonable. Furthermore, in the experimental test, a piece of paper was placed at the bottom and at the side of the test sample to reduce friction between the slab and the bottom plate of the mould and to avoid sticking the asphalt slab at 60 °C to the mould (see Fig. 9); thus, the friction of the sample with the blade is smaller than that of the aggregate–aggregate contact considering interlocking.

Table 1 Model parameters for the linear contact model in the wheel tracking test

Next, the confined test was used to calibrate the nondamage parameters of the viscoelastic–elastoplastic-damage contact model, and then, the unconfined test was used to calibrate the damage parameters of the contact bond model. Due to the complex nature of asphalt concrete behaviour at the grain level in rutting tests, assumptions are necessary during calibration and validation. These assumptions help simplify the complex interactions between various deformation modes and compensate for the lack of fundamental tests to determine model parameters accurately. Despite these simplifications, the model can still provide valuable insights and predictions for asphalt concrete behaviour at the grain scale level in rutting tests.

The mastic–aggregate bond strength was assumed to be 1.5 times higher than the mastic–mastic bond strength, and the viscoelastic stiffness of the mastic–aggregate contact was two times stiffer than the stiffness of the mastic–mastic contact. Note that the elastic and viscoelastic stiffnesses (i.e. $E_{f}^{0} ,$ $E_{km}^{i}$, $E_{cm}^{i}$) greatly affect the first stage (densification) and the second stage (steady stage) of the rutting behaviour, while the elastoplastic and viscoelastic-damage-related parameters have a substantial effect on the rutting behaviour in the second and third stages (damage development and failure stage). In addition, to simplify the calibration process, the friction angle and the dilatant angle in the elastoplastic-damage section were fixed; the cohesive and tensile strengths were assumed to be equal, and the normal softening parameter $u_{c}^{n}$ was similar to the shear softening parameter $u_{c}^{s}$. Similarly, the tensile and shear thresholds in the viscoelastic-damage section were also assumed to be equal. The final calibrated parameters are summarised in Table 2.

Table 2 Model parameters for mastic-to-mastic and mastic-to-aggregate contacts in the wheel tracking test

The results of calibration and validation of the rutting test (rut depth by time) are shown in Fig. 8. The numerical simulation reasonably captured the rutting behaviour of the confined and unconfined tests, which includes the densification stage, the secondary (steady) stage of the confined test, and three different stages of rutting behaviour (densification, steady, and tertiary stages) in the unconfined experiment.

Fig. 8

Results of experiments and numerical simulations in the unconfined and confined wheel tracking tests

There are some differences in the rutting results compared to the experiment in the case of the unconfined test, which might be constituted by the simplification of the numerical approach (e.g. reasonable aggregate size chosen for mastic and aggregate to reduce the computation cost and simplified assumptions in the model during calibration, simplified loading scheme from cyclic to monotonic). Visual comparison of the samples between the experiment and the simulation after the test (Figs. 9 and 10) shows that the numerical tests captured the damage in test samples in the experiments quite well. In particular, the unconfined test shows cracks under the wheel load, especially large deformation cracking under the edge of the wheel load, which is captured as seen from the bottom of the test. Similar visualisation can also be seen in the case of the numerical test. For the confined case, the sample is intact with only notice of the deformation clearly seen at the edge and right under the wheel load position on the sample, which is also seen in the case of the numerical experiment. Overall, the calibration and validation show that the set of calibrated parameters produced reasonable results compared with the experiment and thus is used for further investigation of the rutting behaviour of asphalt concrete in the wheel tracking test under different conditions.

Fig. 9

Visualisation of experimental sample and numerical sample after the unconfined test

Fig. 10

Experimental sample (a) and numerical sample (b) after the confined test

4.2 Micromechanics of the rutting behaviour

The macro-rutting behaviour is mainly driven by the material micromechanics, in particular the interactions of particles (aggregate and mastic) at the grain level and the boundary conditions. The micromechanics investigation provides insight into the rutting development mechanism in asphalt concrete, especially when changing the boundary conditions of the testing set-up. Overview, changing aggregate distribution resulted in variation of the rutting test results (Fig. 8). The rutting behaviour in the unconfined test is more sensitive to the grain size distribution than that in the confined test. The results feature the advantages of the DEM, which naturally captures the heterogeneity of graded aggregate materials such as asphalt concrete.

4.2.1 Unconfined test

Visual examination of particle displacement shows that the rutting development mechanism in the test starts with the densification of aggregates near the top of the samples (see Fig. 11). Until 200 s of loading, the aggregate under the wheel load, from the top to the middle of the sample, shows significant displacement compared to the rest of the sample. It is also found that the movement is dominant in the vertical direction. In the later stage of the rutting mechanism, the aggregate from the top to the middle of the samples still shows dominant displacement, but notably, the horizontal movement becomes significant with the cracks clearly seen in the later stage (see loading time of 480 s in Fig. 11). This phenomenon is also in agreements with the experimental findings in a previous work [33].

Fig. 11

a Visual of sample displacement change over time and b displacement magnitude of particles by time in the unconfined test

Regarding the internal stress state (presented via the contact force between particle pairs), the stress is mainly distributed vertically in the area under wheel load between the two vertical edges of the wheel, as shown in Fig. 12. The stress is also distributed diagonally from the edge of the wheel to the bottom of the sample, creating a shear angle. This angle tends to shrink when damage (crack) occurs in the sample (see Fig. 12 at 480 s loading time). The normal stress in the internal sample is noticeably higher than the shear stress (Fig. 13), and the normal stress is dominated by the compression stress (Fig. 14), creating a complex mode of stress due to the random aggregate and mastic distribution in the internal structure of asphalt concrete. Among the contact types, the stress in the aggregate–aggregate contact is significantly higher than the stress in mastic–mastic and mastic–aggregate contacts, indicating that the load is mainly carried by the aggregate–aggregate skeleton, while the mastic system is responsible for bonding aggregates together, resisting the movement of the aggregates and providing cracking resistance.

Fig. 12

Internal contact force magnitude distribution at different stages of testing (a) and corresponding sample displacements (b)

Fig. 13

Normal and shear force distributions in the sample

Fig. 14

Tension–compression force distribution and tension–compression force magnitude of the internal sample in the unconfined test

When the rut depth increases, cracks can be seen in the samples, which are linked to the reduction in contact bonds due to contact bond breakage over time (Fig. 15). These cracks were formed due to the complex behaviour at the grain level of the internal structure due to the randomness of the aggregate distribution and different phases of the materials. The failures can be seen to be due to the tensile stress and strain, the shear stress and strain, and the combination of normal and shear stress and strain. When the rut depth shifted from the second stage to the third stage, the number of broken contact bonds started to increase sharply (Fig. 15), and rutting developed much more quickly than in the previous steady stage. The sharp increase in the rut depth is the result of weakening the internal structure of the sample due to contact bond loss, resulting in the lateral movement of the internal material structure and the reduction in load resistance of the test sample.

Fig. 15

Number of particle–particle contact over time in the unconfined tests

Investigation of the micromechanism of damage development in the unconfined test shows that damage due to viscoelasticity has a negligible role in the rutting development mechanism (Fig. 16). On the other hand, plastic damage controls rutting development. Incremental number of contact bonds with plastic damage as well as greater plastic damage over time when the samples change from densification to steady and finally ramp up the rutting. The edge of the sample with the wheel load and the bottom of the samples have more plastic damage than the top middle part of the sample, which is mainly subjected to densification. The results of damage analysis also indicate that while the viscoelastic properties affect the rutting process, the plastic damage (in the complex model of tension-shear and compression‒shear) controls the development of rutting mainly in the steady and tertiary stages. Note that the rut depth in the tertiary stage of the simulation rutting test increases faster than in the experiment due to the simplified loading method of using monotonic rather than cyclic loading in the experiment. Once the contact bonds decrease due to the cracks, the internal structure of the numerical samples becomes weaker, and with monotonic loading (without resting time), the deformation develops faster. On the other hand, cyclic loading allows the resting time of the samples and recovery after the loading moves from one position to another, elongating the damage development and resulting in elongation of the internal cracking process of the contact bonds in the sample over time. Therefore, the experimental tests have less steep rut depth development in the tertiary stage than the numerical tests. Finally, the cracks of the sample in the unconfined test involve large deformation (both experimental and numerical tests), indicating the advantage of the DEM in naturally capturing the phenomenon compared to the small deformation approach for cracking, such as in the case of FEM simulations normally applied for asphalt concrete.

Fig. 16

Damage development due to viscoelastic and plastic effects in the unconfined test

4.2.2 Confined test

The particle movement in the confined test is similar to the confined test at the beginning of the test up to 50 s loading time (Fig. 17). Densification is seen focused on the top part of the sample under the loading wheel. With rut depth developed, the densification goes deeper to the bottom and shows the lateral moving direction of particles. Investigation of the stress matrix distribution shows that the contact force under the load wheel and horizontal towards the confined wall is dominant in the sample (Fig. 18).

Fig. 17

a Visual view of sample displacement change over time and b displacement magnitude of particles over time in the confined test

Fig. 18

Internal force distribution at each stage of testing (a) and its corresponding displacement of the confined test (b)

The stress state at different loading times indicates that normal stress is still the dominant stress in the internal structure of the sample, and shear stress is also seen in the stress state (Fig. 19). Similar to the unconfined case, there are also tension forces found in the system, but they are also much smaller than the compression forces (Fig. 20). Furthermore, the tension force in the confined test is also found to be not as high as in the unconfined test due to smaller movement of the particles in the internal structure of the samples compared to the unconfined test. This indicates that in the confined test, the tension has less contribution to the rutting resistance of the asphalt sample compared to the compression constituted by the aggregate–aggregate skeleton. Similar to the unconfined test, the confined case also showed that the stresses in the mastic-to-mastic and mastic-to-aggregate contacts were much lower than those in the aggregate-to-aggregate contacts (see Fig. 20). The results also show that the mastic system in the confined test mainly affects the speed of rutting development in the densification and a part of the steady stage. Meanwhile, the aggregate structure is the main factor in resisting rutting development.

Fig. 19

Normal and shear force distributions in the confined test sample

Fig. 20

Tension–compression force distribution and tension–compression force magnitude of the confined test sample

The confined test samples show fewer bond contacts broken after the densification stage compared to the unconfined test (Fig. 21). Furthermore, the cracks did not significantly affect the rutting behaviour of the sample because the movement of the sample was confined. This leads to the initiation of new frictional contacts of aggregate–aggregate to resist the applied load even when the internal structure reduces its bonding ability to keep aggregate in place to resist tension force due to bonds broken. With this mechanism, the stress was redistributed in the sample, in which the horizontal stress increased due to the further lateral movement of the particles towards the lateral walls, creating resistance to vertical deformation. However, when stress redistribution moves towards greater reliability to the frictional aggregate–aggregate skeleton, it would reduce the sensitivity of the rutting test when comparing the material due to frictional resistance rather than bonded structure, as seen in reality.

Fig. 21

Number of particle–particle contact over time in the confined test in comparison with unconfined test

The micromechanism of damage development in the confined test has a phenomenon similar to that in the unconfined test, in which the damage due to viscoelasticity has a very negligible role in the rutting development mechanism (Fig. 22). On the other hand, plastic damage developed over time in terms of severity and number of damage contacts due to the movement of the particles. The plastic damage also developed much slower compared to the unconfined test due to the lateral confinement of the sample. In the confined test, the damage mechanism for the confined test considering the viscoelastic damage and plastic damage may have little effect on the rutting development when only densification and steady stage are considered. This is because both stages can be simulated by the movement and the retardance of the system due to the viscoelastic properties. However, this feature actually reduces the sensitivity of the confined test to characterise the rutting resistance, which is constituted by the skeleton structure of the aggregate as well as the tension and shear properties of the bond (bitumen and bitumen bond with aggregate). Considering materials with similar aggregate structures, the confined test is more likely to consider the compression resistance ability of the binder, while the tensile and shear strength may have little effect on the test. Note that the binder film in asphalt concrete is very thin (e.g. typically from 7 to 10 µm). Thus, when the deformation between the two coarse aggregates is more than the bitumen film (coating the aggregates), they would have aggregate–aggregate contact. This method was also argued by a work in the past [6]. The mastic system also deforms beside the inside structure of the mastic, and aggregate structures have voids. This deformation allows the material to be denser, can also carry out the load, but at the same time can be the obstacle between aggregate–aggregate, and for that the rutting keeps increasing in the test. Note that once the aggregate–aggregate contact is met, rutting seems to no longer develop or very little development. In other words, the confined test is less sensitive to rutting development due to the dominant aggregate–aggregate structure contribution compared to the shear and tension properties contribution of the mastic system. This could result in less sensitive rutting ranking when comparing asphalt mixes.

Fig. 22

Damage development due to viscoelastic and plastic effects in the confined test

4.3 Effect of the lateral confinement

The investigation into the lateral movement (i.e. horizontal deformation) shows that the horizontal deformation did not show a clear densification stage, as in the case of vertical deformation (Fig. 23). This indicates that the first stage of densification mainly involved vertical deformation rather than lateral deformation. This is because the densification did not cause the contact bonds to be broken, and thus, there was no significant lateral movement. However, the horizontal deformation shows a similar pattern as in the case of vertical deformation in the failure mode. The lateral and vertical deformations show similar flow numbers (see Fig. 8). Thus, in the unconfined case, the flow number of a sample in the rutting test can be obtained by either the vertical or horizontal deformation. The results in the numerical simulations confirm the conclusion in the unconfined test experiment in the literature [33].

Fig. 23

Horizontal deformation and vertical deformation versus loading time in the unconfined wheel tracking tests of the numerical simulation

In terms of the confinement, there was a swift development of the horizontal force applied on the lateral walls at the beginning of the test (Fig. 24). The jumps in the horizontal reaction force on the two walls were rather similar. After that, the horizontal reaction force on the confinement walls increased with time or according to the development of the rutting depth. The increase in the rut depth compacted the aggregate and mastic system and forced them to move laterally. The increase in the reacting force was not steady but showed fluctuation due to the change in the internal structure of the sample during the development of the vertical deformation as well as the effect of the stress–relaxation behaviour of the system caused by the contacts involving mastic. The results of the simulation also showed that the reaction forces were different between the left and right confinement walls, reflecting the effect of the nonhomogeneity of the internal structure due to the random distribution of aggregates in the sample.

Fig. 24

Horizontal reaction force exerted on the two lateral walls in the confined wheel tracking test as a function of time of numerical simulation

4.4 Effect of sample geometry

This section investigates the effect of the sample width on the rutting behaviour of asphalt concrete in both unconfined and confined tests. In particular, two samples with a width of 254 mm were numerically simulated to compare with the samples with a width of 203 mm, which was presented in the previous sections. The change in the width of the sample resulted in a change in the rutting behaviour of the mixtures in the unconfined test. The samples with a larger size tend to have greater rutting resistance than the smaller samples (Fig. 25), which could be because larger samples provide more surface area and thus greater friction force to resist the lateral movement of the samples, resulting in a higher rutting resistance. However, because the number of numerical samples tested is small and the results in the unconfined test are greatly affected by the random particle distribution, the results presented here might not be able to quantify the difference when comparing the rutting resistance of samples with different widths. Thus, more testing should be conducted in both numerical modelling and experiments to provide a more robust conclusion. In terms of rutting development in the test, the results show a similar pattern for rut depth for both cases (Fig. 26). Similar to the case for the 203 mm samples, either the horizontal deformation or the vertical deformation of the wider samples of 254 mm can be used to determine the failure of the sample in the unconfined wheel tracking test (Fig. 26). The result shows that the smaller sample can also be used to characterise the rutting behaviour of asphalt concrete in the unconfined test. However, due to the number of numerical simulations being limited in this section, a larger number of simulations should be carried out to check the conclusion.

Fig. 25

Numerical results of vertical deformation when changing the sample’s width as a function of time

Fig. 26

Horizontal deformation and vertical deformation vs loading time in the unconfined wheel tracking tests with different sample widths in the numerical simulation

In terms of the confined test, the results showed that the rutting behaviour and the rut depth of the wider samples are rather similar to those of the smaller samples (Fig. 27). This could be due to the lateral boundary conditions. In addition, the limitation in the testing time of numerical tests could contribute to the effect, so a longer testing time should be used to check the conclusion. In terms of the confinement walls, the horizontal reaction forces in the case of the smaller samples tend to be greater than those in the case of the larger samples (Fig. 27). This indicates that the area nearer to the loading wheel contributes more to the resistance of lateral movement of asphalt concrete in rutting deformation.

Fig. 27

Confinement force of samples during the numerical confined wheel tracking test

5 Conclusion

This study applies a newly developed DEM contact model, which features the viscoelastic‒plastic and damage behaviour of asphalt concrete at the grain scale, to investigate the rutting behaviour of asphalt concrete in different boundary conditions and sample sizes of the wheel tracking test. The results show that the DEM approach captures reasonably well the rutting behaviour of asphalt concrete under different boundary conditions. The DEM approach is also capable of capturing the effect of random aggregate distribution. Lateral confinement was found to significantly affect the rutting behaviour of asphalt concrete in the wheel tracking test. The unconfined test clearly shows three stages of rutting, and the flow number of the test sample could be determined. Furthermore, rutting failure can be determined using either vertical deformation or lateral deformation. Meanwhile, the fully confined test constrained the development of damage, resulting in only two first stages of rutting being captured, and the failure of the sample is not clear. Investigation of samples with different widths suggests that the smaller sample could also be used in the wheel tracking test to investigate the rutting behaviour of asphalt concrete. Overall, this study examines an important topic of asphalt concrete, and the findings in this study are important for the modification of the wheel tracking test, aiming to provide more mechanical sound and the efficiency of the test for quality assessment and quality control.