1 Introduction

Nano-indentation is a hardness test method frequently applied to small volumes of materials. To date, it has become one of the most common techniques for the quantitative characterization of mechanical properties of materials. However, nano-indentation tests provide little insight into indentation phenomena, such as dislocation nucleation, phase transformation, microstructure evolution and other related key features. Besides, such tests alone cannot predict the material response when conducted under varying experimental conditions, such as varying strain rate, for instance. As a result, finding a valid simulation approach to model the nano-indentation process has been an important research focus for over two decades.

So far, a variety of simulation approaches have been developed for nano-indentation. These include molecular dynamics (MD) simulation, finite element method (FEM), quasi-continuum (QC) method, discrete dislocation dynamics (DDD) simulation and crystal plasticity finite element method (CPFEM). A comprehensive review of modeling approaches adopted by the research community for nano-indentation can be found in Huang and Zhou [1]. Among the above-mentioned methods, MD simulation is one of the most widely employed computational techniques for modeling and predicting material behavior on the nanoscale. For example, researchers performed MD simulations to investigate underlying deformation mechanisms during nano-indentation [2,3,4] and factors affecting the mechanical response in terms of indentation force, strain, hardness and dislocation evolution [5, 6]. Although MD simulations can be used to study nano-indentation phenomena, many of the presented results are restricted to a very small length scale, i.e., < 20 nm [7], in most studies. The time interval for simulation steps and overall simulation time are also often on the order of picoseconds (i.e., < 20 ps in [4]), which may not be large enough to capture the macroscopic deformation characteristics of materials.

To overcome the limitations encountered in MD simulations, Tadmor and coworkers [8] established a quasi-continuum method by successfully coupling the FEM and MD methods. The basic idea is that the majority of the solid undergoing a slowly varying deformation at the atomic scale is described by the continuum approximation, via FEM, while discrete atoms are only employed near defects, interfaces and surfaces. Quasi-continuum simulations have also been performed to investigate microscopic mechanical properties during nano-indentation such as critical indentation load/depth [9], nano-hardness [10] and distance effect of the surface defects and surface roughness on elastic–plastic transition [11], as well as to study the incipient plasticity during nano-indentation in terms of incipient yield [12]. Although the quasi-continuum method has proven effective in dealing with nano-indentation problems, it has an inherent numerical limitation, that is, the introduction of non-physical forces due to imbalances between local and nonlocal environments [13].

Discrete dislocation dynamics simulation is a microscale method which demonstrates the potential to address some challenges encountered by MD simulation. This method uses dislocations as the simulated units and offers a way to extend time (i.e., microsecond timescale) and length scales (i.e., the defect scale). Bai et al. [14] conducted discrete dislocation dynamics simulations for nano-indentation on single crystal copper to investigate the dislocation evolution mechanisms and the influence of initial dislocation density on the plastic deformation. Song et al. [15] explored the indentation size effect at the nanometer scale through extensive discrete dislocation dynamics simulations of nano-indentation on a single FCC crystal. They focused on the behavior of the hardness and pop-in statistics during nano-indentation under various tensile loadings, which is related to the dislocation microstructure. Although the discrete dislocation dynamics simulation approach can provide useful insights into the evolution of the microstructure at larger length scales, it can only provide limited information (such as nucleation of dislocations and their subsequent activities) on the development of initial plasticity during nano-indentation compared to MD simulations due to the dependence on dislocations as its simulated entities.

As a macroscale method, the mesh-based finite element method (FEM) has also been used to study nano-indentation. Sarris et al. [16] employed FEM to quantify the effect of material properties and contact friction on the nano-indentation response of C–S–H phases. Fu et al. [17] used FEM to simulate nano-indentation tests on C–S–H and obtained force–displacement curves. However, there is an inherent limitation with FEM when modeling nano-indentation. In particular, FEM typically uses isotropic and macroscopic constitutive models to describe nanocrystalline materials, which neglect indentation scale effects and different grains and phases in crystalline materials. Therefore, FEM provides little information on microscopic material behavior during nano-indentation. As a result, its accuracy for simulating this process can be limited.

To address the above shortcomings of the standard FEM approach, researchers developed the crystal plasticity finite element method (CPFEM) which combines crystal plasticity theory [18] and FEM. This method was first introduced by Peirce et al. [19] in 1982 to study nonuniform deformations of rate-dependent single crystals and was subsequently applied to nano-indentation by Nix et al. [20] to study the effect of indentation size. Compared to standard FEM, CPFEM considers information of individual grains such as grain shape, grain orientation, and interaction among adjacent grains in crystalline materials. Thus, the technique is more effective in modeling anisotropic material behaviors and is closely related to the physical nature of microscopic deformation during nano-indentation. Various CPFEM-based models have investigated pop-in event observed in spherical nano-indentation [21], microstructure evolution [22] and pile-up patterns [23], for instance. The challenging task in CPFEM is the model formulations and definition of parameters which determine the deformation mechanism. Similar to the role of the interatomic potential in MD simulations, the nature and accuracy of empirical model formulations have significant influence on simulation results for nano-indentation in CPFEM.

In order to obtain a deeper understanding in the mechanics of plastic nano-indentation, researchers have also carried out multiscale simulations by combining the advantages of the above modeling approaches at different length scales. For example, Chang et al. [24] investigated multiscale simulations of nano-indentation on copper from atomic scale to continuum scale. In their study, MD simulations provided details of the dislocation nucleation mechanism at the atomic scale. This information was then incorporated as sets of local rules and passed on to discrete dislocation dynamics models that could simulate dislocation propagation. At the continuum scale, DDD simulations were used to compute coefficients in constitutive equations for crystal plasticity finite element models, which were performed and directly compared with AFM observations. Tsuru et al. [25] studied the nanoscale displacement burst phenomenon of single-crystalline aluminum by using multiscale simulation approaches. In their study, the nucleation mechanism of dislocations in the defect-free region was first investigated by using atomistic models. Subsequently, discrete dislocation dynamics simulations were performed to study the influence of collective motion of dislocations on the nano-scale plastic deformation. Wang et al. [26] also performed multiscale simulations of nano-indentation on Ni (100) thin film by coupling MD and finite element method. Such multiscale modeling approaches can overcome the barriers of individual simulation techniques and bridge the gap between these methods at different length scales. Thus, it is a promising research area for the study of nano-indentation. It is important to note that at the higher length scale of such multiscale approaches, FEM is currently the main technique employed by researchers studying nano-indentation. However, it could be argued that an alternative approach to FEM, that is typically more suited to the simulation of large strains and strain rates, could also be of interest for the study of nano-scale deformation phenomena, while still relying on constitutive models informed by atomistic-based, dislocation-based and/or microstructure-based effects.

For this reason, this paper focuses on the simulation of nano-indentation using a meshless numerical method known as smooth particle hydrodynamics (SPH). SPH is a Lagrangian particle-based method that can be applied to problems ranging from macro-scale, such as fracture of brittle solids, to atomistic-scale simulations [27,28,29,30]. The objective of the research reported here is not to implement a multiscale simulation approach that relies on SPH, as this would be the focus of further research. Instead, and as a first step toward this future goal, the objective here is to demonstrate the potential of SPH to simulate the material response during nano-indentation using relatively simple constitutive models. In particular, an SPH-based nano-indentation study found in the literature is firstly reproduced in Sect. 2 to establish the accuracy of the chosen SPH numerical model. Next, in Sect. 3, the implemented SPH model for nano-indentation is then validated and compared with FEM and experimental results, also available in the literature.

2 Methods

2.1 Basic principles of the SPH method

The SPH method was originally developed for hydrodynamics and solid mechanics problems which are basically described in the form of partial differential equations of field variables, such as the displacement, density, and stress.

The formulation of the SPH method is often divided into two steps, as described in Fig. 1. The first step consists in the kernel approximation of field functions. The second step is concerned with the particle approximation. In detail, since an arbitrary function can be represented in an integral form, the field functions are first rewritten in the form of integral representation by introducing a smoothing kernel function. Next, the problem domain where the field functions are defined is discretized by a set of arbitrarily distributed particles. The kernel approximation is then performed by summing up the values of the nearest neighboring particles in a local domain called the support domain, which yields the particle approximation of the function at a given point. Therefore, the formulation of SPH method can be expressed by Eq. (1).

$$\langle f\left( {{\varvec{x}}_{i} } \right)\rangle = \sum\limits_{j = 1}^{N} {\frac{{m_{j} }}{{\rho_{j} }}f({\varvec{x}}_{j} )W\left( {{\varvec{x}}_{i} - {\varvec{x}}_{j} ,h} \right)}$$
(1)

where f is a function of the three-dimensional vector x, N is the number of particles within the support domain of particle i, m and ρ represent the mass and density of particle j, W(xi-xj, h) is the smoothing kernel function, h is the smoothing length which defines the influence area of W. This influence area is called the support domain of W of point xi.

Fig. 1
figure 1

Particle approximation and kernel function in SPH method

Full size image

For consistency and completeness, the smoothing kernel function W should satisfy a number of conditions. The first one is the unity condition, which means that the integration of W over the integration domain should be 1. The second one is the delta function condition, which means the kernel function W(x-xʹ, h) approaches delta function δ(x-xʹ) when the smoothing length h approaches zero. The third condition is the compact condition, which can be described by the following equation.

$$W(\varvec{x} - \varvec{x}^{\prime } ,h) = 0\;{\text{when}}\left| {\varvec{x} - \varvec{x}^{\prime } } \right| > \kappa h$$
(2)

where κ is a constant which also defines the support domain of W of point x. Using the compact condition, integration over the entire problem domain is localized as integration over the support domain of W. This is very important considering the computation effort because problems with large deformation usually require a very large number of particles to discretize the entire problem domain.

Equation (1) implies that the value of a function at particle i can be approximated by summing up the average values of function at all the particles within the support domain weighted by the kernel function. In other words, the particle approximation in Eq. (1) converts the integral form of a function to the discretized summation over an arbitrary set of particles. This makes SPH method simple without using a background mesh for numerical integration. It can also be seen from Eq. (1) that the particle approximation introduces the mass and density of particles, which makes the SPH method particularly convenient and popular for hydrodynamic problems and solid mechanics problems in which the density is a key field variable.

2.2 SPH modeling of the nano-indentation process

In this research, the ANSYS/LS-DYNA software was used to model the nano-indentation process using the SPH method. To confirm the validity of the implemented model, its outcomes were first compared with the results reported by Guo and co-workers [31], who also simulated nano-indentation with SPH and is the only study of this kind to the best knowledge of the authors. In this section, we report the reproduction of their SPH model for nano-indentation. This initial study was also necessary to determine the appropriate particle numbers and indentation speed of the SPH model presented in [31], as these details were not available in the published study and thus required to carry out further SPH simulations in Sect. 3.

In the work of Guo and co-workers [31], nano-indentation experiments on a potassium dihydrogen phosphate crystal (KDP) specimen were conducted, and SPH simulations were carried out. The nano-indentation experiments included loading and unloading. For the loading part, a linearly increasing load was exerted on the top surface of the Berkovich indenter. A maximum load of 8 mN and a load increment of 100 μN/s were set at the beginning. The loading process ended when it reached the maximum load. However, the details of unloading process are not provided in [31].

For the SPH reproduction of these experiments, in this paper, the Berkovich indenter was discretized by FE meshes and employed as a rigid diamond with a density 3.515 g/cm3, Young’s modulus 1141 GPa and Poisson’s ratio 0.07. The KDP workpiece was represented by SPH particles and had a density 2.338 g/cm3, Young’s modulus 38.7 GPa, Poisson’s ratio 0.23 and yield stress 120 MPa. The material model 24 *Mat_Piecewise_Linear_Plasticity in LS-DYNA was employed to represent the plastic behavior of the KDP workpiece, and four data pairs (0.0, 0.12 GPa), (0.042, 0.76 GPa), (0.35, 1.2 GPa), (0.744, 1.565 GPa) are picked up from Fig. 5 in [31] to define the effective stress vs. effective plastic strain curve. The dimension of the Berkovich indenter can be found in Fig. 3 in [31], and the dimension of the workpiece was 8 × 8 × 6 µm3 (Fig. 2). The loading and unloading speeds were chosen as 100 m/s. In the SPH simulations presented in this paper, a constant speed rather than a linearly increasing force was exerted on the Berkovich indenter. This was done to reduce the computational time to a realistic level without sacrificing the accuracy of material responses.

Fig. 2
figure 2

SPH modeling of the nano-indentation process

Full size image

The contact model employed in all simulations in this paper was chosen as the type a5 contact in LS-DYNA, *Contact_Automatic_Nodes_to_Surface. In this algorithm, the penalty method has been implemented to treat sliding and impact along interfaces. In the case of the penalty-based contact, each slave node is checked for penetration through the master surface. When a penetration is found a force proportional to the penetration depth is applied to resist, and ultimately eliminate, the penetration. The term “automatic” means that this contact is non-oriented and can detect penetration coming from either side of an element, which makes this contact type better-suited for large deformation problems, such as the nano-indentation with a relatively large speed in this paper. In addition, the indication of “nodes_to_surface” is to couple the nano-indenter which was defined with finite elements and the workpiece which was defined with SPH elements. This term is a one-way treatment of contact and indicates that only the slave nodes on the nano-indenter are checked for penetration of the master segments on the workpiece. While in a two-way treatment of contact, a second time to check the master nodes for penetration through the slave segments is required. Therefore, the “nodes_to_surface” contact algorithm is effective and can reduce cost in the context of SPH simulation of nano-indentation. These factors contributed toward the choice of *Contact_Automatic_Nodes_to_Surface as the contact type in this paper.

2.3 Convergence study of the reproduced SPH model

Before the reproduced SPH model was used to investigate the indentation process, a convergence study was necessary to ensure that the simulation results were not influenced by the model itself. To investigate whether the maximum Von Mises stress converges to a certain value, a set of simulations with different particle densities were carried out, as illustrated in Fig. 3. It can be seen that the maximum Von Mises stress converges as the particle density increases. Therefore, the number of particle was chosen as 150 × 150 × 120 (which approximates to a particle density of 7000 1/µm3) to conduct subsequent SPH simulations as reported in the next section.

Fig. 3
figure 3

The effect of particle density on maximum Von Mises stress during nano-indentation process

Full size image

3 Results and discussion

3.1 Validation examination of the reproduced SPH model

Since the implemented SPH model was confirmed to be convergent, further simulations on the KDP workpiece were carried out. Figure 4 shows the force–displacement curve of the reproduced model with particle numbers of 150 × 150 × 120 and an indentation velocity of 100 m/s. It can be seen that the force between indenter and workpiece remains zero until the indentation depth reaches 25 nm. This can be attributed to the fact that there is an initial gap between the indenter and workpiece in the reproduced model, whose value equals to the radius of SPH particles (25 nm). Therefore, the initial contact occurs when the indentation depth reaches 25 nm. To compare the effective force–displacement curve with that reported in [31], the indentation depth of 25 nm is considered as the initial contact point between indenter and workpiece. Figure 5 shows the comparison of force–displacement responses from [31] and the simulation reproduced here. It can be seen that the force–displacement response obtained with the reproduced SPH model agrees well with that in [31].

Fig. 4
figure 4

Force–displacement curve in the reproduced model (without shift)

Full size image
Fig. 5
figure 5

Comparison of force–displacement curves from Guo et al. [31] and reproduced model

Full size image

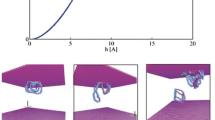
Figure 6 shows the distribution of Von Mises stress at indentation depth of 198 nm and 418 nm. It can be noted that the stress concentration always exists during the indentation process, and the influence area of the Von Mises stress increases as the indentation depth increases. A zoomed-in image of the indented area is illustrated in Fig. 7, which further clarifies the stress distribution and surface deformation in the indented area. The distribution patterns of Von Mises stress obtained are in good agreement with those reported in Fig. 7 in Guo et al. [31].

Fig. 6
figure 6

The distribution of Von Mises stress at different indentation depth (h)

Full size image
Fig. 7
figure 7

The zoomed-in image of the indented region during nano-indentation

Full size image

To measure the extent to which the maximum values of Von Mises stress and plastic strain are close to the simulation results in [31], the percentage differences between them were calculated. As shown in Fig. 8, these calculation results show that the percentage differences of the maximum Von Mises stress at the indentation depths of 88 nm, 198 nm, 308 nm and 418 nm are 9.27%, 3.34%, 1.95% and 2.66%, respectively. This indicates that the reproduction of the SPH model in [31] is more satisfactory when the indentation depth is relatively large. The large percentage difference of the maximum Von Mises stress with a small indentation depth may be attributed to the contact model between the indenter and workpiece, which needs to be refined in future work. In addition, comparison of the percentage differences in the maximum plastic strain at the end of loading and unloading process is 1.25% and 2.35% respectively, which also confirms the reliability of the reproduced SPH model.

Fig. 8
figure 8

Comparison of maximum Von Mises stress from Guo et al. [31] and reproduced simulation

Full size image

Figure 9 shows how the influence depth, i.e., the depth of the region where indentation-induced stress or strain exists, changes during the nano-indentation process. In Fig. 9, the variable k means the ratio between the indentation depth (m) and influence depth of Von Mises stress (n). It can be seen that k remains approximately constant during the indentation process, which indicates that the influence depth of Von Mises stress is nearly proportional to the indentation depth. This observation is also very similar to that initially made in [31].

Fig. 9
figure 9

Comparison of ratio between the indentation depth and influence depth of maximum Von Mises stress

Full size image

There are two ways to provide quantified evidence about the extent to which the variable k is close to that reported in [31]. One way is to compare the average value of variable k. The average value of variable k is 0.152 in the reproduced simulation, a percentage difference of 2.01% compared to the value of 0.149 in [31]. Another way is to compare the ratio between the standard deviation and averaged value of k. This ratio is 4.90% in the reproduced simulation, a percentage difference of 18.36% compared to the ratio of 4.14% in [31]. These observations show that the predictions of the influence depth in the reproduced model are consistent compared to the model presented in [31].

3.2 Comparison of the SPH model with FEM and experimental results

The aim of this section is to further establish and refine the accuracy of the implemented SPH model. For this purpose, following its validation in Sect. 3.1, the model was first used in the context of micro-indentation [32] in order to compare and benchmark the accuracy of SPH modeling of indentation with FEM and experimental results.

In [32], Dao and co-workers constructed axisymmetric two-dimensional and full three-dimensional finite element models to simulate the micro-indentation response of two aluminum alloys: 7075-T651 and 6061-T6511. A diamond Berkovich indenter was also employed in their work. Therefore, the implemented SPH model could be directly used to compare with the FEM implementation of Dao and co-workers [32]. The chosen material parameters of the diamond indenter for the SPH micro-indentation model can be found in Table 3 in [32]. The chosen stress–strain relationship of the two aluminum alloys was obtained by extracting data points from Fig. 4 in [32] using the Engauge Digitizer software, which accepts image files containing graphs and recovers the data points from those graphs. The detailed process is that Fig. 4 in [32] was imported and then digitized within the Engauge Digitizer software by placing points along axes and stress–strain curves. The resulting data points were then transferred to LS-DYNA directly via copy and paste. The curve of effective stress vs. effective plastic strain of the two aluminum alloys can be defined by these data points in LS-DYNA using the material model 24, *Mat_Piecewise_Linear_Plasticity, which has the capability of approximating a realistic non-linear stress–strain behavior by a sequence of linear segments. The formulations for calculating and updating the deviatoric stresses and plastic strain can be found in Material Model 3 and Material Model 24 in LS-DYNA Theory Manual. The loading and unloading speeds were also initially chosen as 100 m/s to be consistent with the values established in Sect. 3.1. However, speed values of 10 m/s, 1 m/s and 0.1 m/s were also investigated to understand their influence on the simulation results.

Figure 10 shows the comparison of micro-indentation responses on 7075-T651 aluminum specimen using SPH, FEM simulation and the experimental results also available from [32]. The red curve in Fig. 10 is the indentation response when using SPH with loading and unloading speeds of 100 m/s. It is clear that the loading curve matches well the FEM prediction and the experimental results when using a speed of 100 m/s; however, there is an obvious discrepancy in unloading curves between the SPH prediction with FEM and experimental results. The slope of the unloading curve obtained with SPH is larger than those reported for the FEM predictions and the experimental results. To further investigate these observations, the SPH model-based micro-indentation responses were obtained under different loading and unloading speeds. These results are also displayed in Fig. 10. The red, purple, orange and gray curve in Fig. 10 represent the SPH simulation with loading/unloading speeds of 100 m/s, 10 m/s, 1 m/s and 0.1 m/s, respectively. It can be seen that the residual depth decreases with the decrease in unloading speed. These observations in unloading curves may be related to the different elastic recovery of aluminum alloys under different unloading speeds. Figure 11 shows similar observation in SPH modeling of micro-indentation for 6061-T6511 aluminum specimen. From Figs. 10 and 11, it can be seen that the SPH prediction of micro-indentation compares very well with FEM prediction and experimental results for the loading part. Regarding the unloading part of the process, the SPH outcome becomes closer to the FEM and experimental results with the decrease in unloading speed used during the simulation.

Fig. 10
figure 10

Comparison of micro-indentation responses of 7075-T651 aluminum specimen between results from Dao et al. [32] and the SPH model in this paper. The green and black curve represent FEM and experimental results in the paper from Dao and co-workers, respectively. The red, purple, orange and gray curve represent the SPH simulation with loading and unloading speeds of 100 m/s, 10 m/s, 1 m/s and 0.1 m/s, respectively

Full size image
Fig. 11
figure 11

Comparison of micro-indentation responses of 6061-T6511 aluminum specimen between results from Dao et al. [32] and the SPH model in this paper. The green and black curve represent FEM and experimental results in the paper from Dao and co-workers, respectively. The red, purple, orange and gray curve represent the SPH simulation with loading and unloading speeds of 100 m/s, 10 m/s, 1 m/s and 0.1 m/s, respectively

Full size image

Another important observation which should be highlighted here is that the influence of indenter speed on the unloading response is more obvious than that on the loading response, as illustrated in Figs. 10 and 11. Since the same contact model and variation in speed (i.e., 100 m/s, 10 m/s, 1 m/s, 0.1 m/s) for loading and unloading processes are used in the simulations presented in both figures, the discrepancy between the sensitivity of loading and unloading process could be related to the variations in material behavior during compressive and tensile phases of loading. During the SPH modeling of micro-indentation reported in [32], the material constitutive models of aluminum alloys were obtained by extracting discrete data from stress–strain curves and then directly used as input data for the LS-DYNA simulations. Further information is needed to understand how the LS-DYNA software processes the extracted discrete data to obtain the material model and whether this material model has any influence on material behavior during compressive and tensile loading phases. The aforementioned information on the description of material model based on discrete input data is not readily available within the LS-DYNA software or related documents.

3.3 Investigation of effect of indenter tip on nano-indentation response

In Sect. 3.2, the validated SPH nano-indentation model was used to simulate micro-indentation to compare the accuracy of the SPH outcome against published FEM simulation and experimental results. In this section, the validated SPH nano-indentation model is directly used to reproduce a nano-indentation study reported by Karimzadeh et al. [33]. This study originally focused on investigating the effect of the indenter tip shape on the nano-indentation response.

In [33], an axisymmetric finite element model was employed to simulate the elasto–plastic behavior of an aluminum 1100 workpiece during nano-indentation, and the FEM outcomes were compared with experimental results. Two Berkovich indenters with tip radius of 0 nm and 200 nm were used in the work presented in [33]. Therefore, the established SPH model could also be directly used here to study the feasibility of the SPH method to investigate the effect of the shape of indenter tip on nano-indentation. The 3D Berkovich indenter with a tip radius of 200 nm was obtained by creating a rounded-tip indenter using the Solidworks software first (as illustrated in Fig. 12) and then by importing it into ANSYS/LS-DYNA. The material parameters of aluminum 1100 were extracted from Fig. 4 in [33] also using the Engauge Digitizer software. It should be noted that the stress–strain relationship Fig. 4 in [33] was obtained from uniaxial tensile test of aluminum 1100 and not using compression testing as was the case in the benchmark study considered in the previous section. The loading and unloading speeds were chosen as 10 m/s. The obtained SPH simulation results with different tip shapes and comparison with the results from the literature are shown in Fig. 13.

Fig. 12
figure 12

Nano-indenter with a tip radius of 200 nm established in Solidworks

Full size image
Fig. 13
figure 13

Load–displacement curves obtained from nano-indentation experiments and SPH simulation with loading and unloading speed of 10 m/s

Full size image

It can be seen that for both sharp indenter and rounded-tip indenter, the SPH simulation results compare well with those in [33]. The experimental data agree well with the SPH simulation results obtained here for a rounded-tip indenter. This is because in practice, the Berkovich indenter has an average tip radius of about 150–200 nm [34], which was also highlighted by Karimzadeh et al. [33]. In addition, the resultant force between indenter and workpiece is noted to be larger when using a rounded-tip indenter than when using a sharp indenter. This should be caused by the increase in contact area with blunt indenters for a given indentation depth. This may also be attributed to the increase in friction coefficient and friction force between the indenter and specimen surface when using a rounded-tip indenter. It can also be noted from Figs. 5, 10, 11 and 13 that the validated SPH nano-indentation model appears to have higher accuracy when used for nano-scale simulation compared to micro-scale simulation in the context of this study.

Based on the results obtained, it is suggested that the implemented SPH model of nano-indentation can be used in the prediction of nano-indentation response, especially during the loading process, on a metallic workpiece; however, the influence of speed on unloading process in LS-DYNA software needs to be further clarified. In reality, the unloading process may not always be considered as highly important when it comes to the simulation and prediction of nanoscale material deformation processes. Therefore, for all intents and purposes, it can be said that the above-described SPH model can predict nano-indentation processes with reliable accuracy.

4 Conclusions

In summary, a SPH model for nano-indentation was implemented using the ANSYS/LS-DYNA software. Predictions obtained with the model were compared with existing FEM and experimental results published in the literature with the aim of exploring the feasibility of applying SPH-based simulations of the nano-indentation process. The conclusions drawn from this study are summarized as follows:

  • The prediction reached with the implemented SPH model for nano-indentation matched well with that reported by Guo and co-workers in [31]. For example, the percentage errors between the SPH predictions and experimental results at various indentation depths were mostly within 5%. The reproduced SPH model in Fig. 5 also simulated results which were much closer to the published experimental data when the indentation depth exceeded 400 nm.

  • The SPH predictions for micro-indentation agreed well with the FEM outcome and experimental results obtained during the loading phase from the study reported by Dao et al. in [32]. For the unloading part, the response was seen to be influenced by the unloading speed. In particular, the SPH prediction gained in accuracy as the simulated unloading speed decreased. Further studies should be conducted to investigate the factors in the LS-DYNA software leading to this observation.

  • The SPH simulation results were also in good agreement with FEM predictions and experimental results of the nano-indentation study reported by Karimzadeh and co-workers in [33] on an aluminum 1100. The load–displacement curve simulated with the SPH model established here was also generally closer to the experimental results compared to the FEM-generated data reported in [33]. These observations provide enhanced confidence on the feasibility of the SPH method to simulate nano-indentation tests and to further investigate factors that influence the indentation response, such as the shape of indenter tip.

Collectively, the results obtained in the present feasibility study suggest that the SPH method can be a potential candidate for the accurate simulation of nano-indentation processes and as such it may also be further exploited in the prediction and simulation of more complex nanoscale deformation processes, such as nanomachining which employs nanoscale cutting tools such as the tip of an atomic force microscope probe.