Implicit or explicit time integration schemes in the PFEM modeling of metal cutting processes

Abstract

This work presents the development of an explicit/implicit particle finite element method (PFEM) for the 2D modeling of metal cutting processes. The purpose is to study the efficiency of implicit and explicit time integration schemes in terms of precision, accuracy and computing time. The formulation for implicit and explicit time marching schemes is developed, and a detailed study on the explicit solution steps is presented. The PFEM remeshing procedures for insertion and removal of particles have been improved to model the multiple scales of time and/or space of the solution. The detection and treatment of the rigid tool contact are presented for both, implicit and explicit schemes. The performance of explicit/implicit integration is studied with a set of different two-dimensional orthogonal cutting tests of AISI 4340 steel at cutting speeds ranging from 1 m/s up to 30 m/s. It was shown that if the correct selection of the time integration scheme is made, the computing time can decrease up to 40 times. It allows us to affirm that the computing time of the PFEM simulations can be excessive due to the used time marching scheme independently of the meshing process. As a practical result, a set of recommendations to select the time integration schemes for a given cutting speed are given. This is intended to minimize one of the negative constraints pointed out by the industry when using metal cutting simulators.

1 Introduction

The description of a metal cutting process can be defined by the interaction of two physical elements. A tool cutting edge penetrates into the a metal workpiece which material is thus plastically deformed and slides of along the rake face of the cutting edge. Large plastic strains, mainly located within the primary and the secondary shear zones, produce the detachment the material and create metal chips. Machining analysis focuses on the study of chip formation, which is associated with large deformations, high strain rates and high temperatures. Even if new manufacturing techniques, such as additive manufacturing [1], have recently been developed for metal processing, machining continues to be the most used manufacturing operation in terms of volume and expenditure. This process contributes to around 5% of the GDP of industrialized countries, representing a significant part of the wealth of these economies [2, 3]. The use of cutting edge technology such as numerical simulation can help to find the optimal cutting parameters and to visualize variables that are difficult to measure (e.g., the temperature and the strain rate field) without the need for costly experiments, thereby increasing the financial profitability of manufacturing companies.

Most of the time, the numerical modeling of metal cutting processes is based on continuum mechanics (CM) [4,5,6,7,8], where the linear momentum, energy equations and constitutive model are expressed as a set of nonlinear partial differential equations (PDE). This set of equations depends on space and time; thus, it is necessary to discretize these equations on space and time to obtain an approximate solution of a variable of interest at a time t.

The most used method for spatial discretization of the PDE for the problem of interest is based on finite element method (FEM) [9], including the FEM in their different descriptions: Lagrangian [4, 6], Eulerian and arbitrary Lagrangian–Eulerian formulations [5]. Other techniques have been developed like the multi-material Eulerian method [10], the volume of solid [11], the material point method or point in cell [12], which extend the FEM by applying other spatial mesh-based discretizations, showing some advantages in comparison with the FEM. The new methods based on a fixed mesh (background mesh) eliminate the problem of mesh distortion, using elements that are filled and unoccupied with material as it moves along the fixed mesh. However, they present limited possibilities for the modeling of some cutting conditions that needs for and accurate boundaries representation (e.g., segmented chip formation). The modeling is difficult if not impossible with these techniques when a fixed mesh is used [11].

Another set of methods based on continuum mechanics (CM) use the concept of particle methods and mesh-free methods, including the constrained natural element method [13], smoothed particle hydrodynamics [7, 14,15,16], the maximum entropy meshfree [17], the finite point method [18], stabilized optimal transportation meshfree method [19] and the particle finite element method (PFEM) [9].

Techniques not based on CM have been developed; among them are: the discrete element method (DEM) [20, 21] and molecular dynamics (MD) [22, 23] with a focus on the nanometric scale. In DEM, the workpiece is represented as a bulk of identical spheres arranged at random [20] or in a face-centered cubic lattice organization [20]. The motion of DEM particles is modeled using Newton’s second law, and the interparticle contact forces are modeled using springs and a damper approach. In contrast with FEM and other meshless methods, which are mainly designed to solve partial differential equations that describe the physical phenomena, DEM accounts for the simulations of particle interactions. The main challenge of DEM is to find appropriate force laws and parameters in order to synthesize the solid with correct physical properties [24]. MD is a method for analyzing the physical movements of atoms and molecules. In the most common version, the trajectories of atoms and molecules are determined by numerically solving second Newton’s law of motion for a system of interacting atoms/molecules, where forces between the particles and their potential energies are often calculated using interatomic potentials or molecular mechanics force fields [22, 23]. Though molecular dynamics is very closely related to DEM, however, DEM is generally distinguished by considering rotational degrees of freedom for particles as well as using complex geometries for the geometrical description of particles (e.g., polyhedra) [25]. MD has been used to model the cut of pieces at nanoscale [22, 23] while DEM models the cut of pieces with a size of the order of a few millimeters [24]. The main disadvantage of DEM is that the parameters of the model need to be adjusted for each case depending on the number, arrangement and size of particles [24] and for MD is the high number of particles needed to carried out a realistic numerical simulation [22, 23].

Since particle-based methods and meshless methods do not depend on a mesh, they do not have a mesh distortion problem. Therefore, they have an inherent advantage when modeling problems with large deformations such as machining [9]. However, the main disadvantage of these methods comes from the needed spatial searches, for instance, the search of particles neighbors and patches (updating the data base of neighbor particles takes usually a long time in comparison with other calculations needed during each time step [9]). This can be the most time-consuming computational operation for some of these techniques when it is used with explicit time integration schemes. It means that computational time used by the integration of the governing equations changes the relevance of the auxiliary techniques used in particle methods. More information about the advantages and disadvantages of the particles and meshless methods for the numerical modeling of metal cutting processes can be found in [9].

The time integration of the differential equations has been carried out with implicit [5, 6, 8, 17, 18] or explicit [4, 7, 10, 13, 14, 19] integration schemes. The selection of the scheme is usually based on its availability and recommendation of the computer software used and not based on the criterion of minimizing the computing time. Most commercial software is developed and specialized in the use of one type of time marching scheme, although some others offer different alternatives. Some top commercial software packages used in industry for the numerical simulation of metal cutting processes are: Abaqus (Implicit/Explicit)[9], Comsol (Implicit) [9], ANSYS (Implicit/Explicit) [9], AdvantEdge (Explicit) [26], Deform (Implicit) [27] and MSC. Marc (Implicit) [9]. Most of them use FEM to discretize in space the balance equations governing the physics of the problem. Abaqus also includes a SPH formulation able to model machining processes.

In the literature or in the manuals of commercial software, the following suggestions are made regarding the use of an implicit or explicit scheme: Explicit scheme must be used for applications of short duration, where high frequencies are relevant, such impact problems and explosions [28], Implicit schemes are appropriate for low velocity dynamics where the phenomena is dominated by low frequencies, such as for earthquake engineering with significant damping or for metal forming processes [28].

Following this recommendations, we can identify examples of cutting mechanics (processes including high speed cutting) where explicit schemes can be more efficient than implicit schemes. These examples define the term of High-Speed Machining (HSM), which conditions are complex and difficult fulfill by the available machine tools. It demands high precision ranges of cutting feeds and speeds, suitable tools and materials [29]. Furthermore, there is also no speed that defines the limits between low- and high-speed machining, arising the following question: At what cutting speed, are explicit schemes more efficient than implicit schemes? In the literature, there is no comparison between explicit and implicit time integration schemes of the numerical modeling of cutting process using the same spatial discretization and numerical method. Therefore, the conditions under which one scheme is better than the other have not been identified.

The main reason to develop numerical methods to simulate metal cutting processes is to observe and predict variables that are difficult to measure, with the goal to increase knowledge and understanding of the cutting process. The previous developments of the PFEM have shown its capacity to predict forces, strain, stress and to predict the transition from continuous to serrated chips with the increase in cutting speed [9]. The second reason to simulate cutting is to determine what processes parameters give the best cutting conditions, i.e., cutting speed, cutting depth and tool material. This analysis needs for expensive computing resources and large computing times, thus preventing the massive use of simulation by the industry.

The main goal of this work is to contribute to the second reason and develop criteria that allow the user of metal cutting simulations to select the most efficient time integration scheme according to their cutting conditions based in the spatial discretization. The modeling and the presented developments will be based on the Particle Finite Element Method (PFEM). The selection of time integration algorithm should not be based concerning only on computing time; it should also take into account the robustness and the convergence of the method. For example, when chip shapes or contact conditions are complex, the implicit algorithms use to present some convergence difficulties.

In order to analyze the robustness and the accuracy of the results, we will also show how to avoid the locking phenomena of linear triangle finite elements for implicit and explicit time integration by using stabilized mixed linear displacement–linear pressure finite elements. This work also shows that the excessive computing time of numerical simulations of metal cutting processes is not only due to the remeshing scheme typical of the PFEM, but it is due the incorrect selection of the time integration scheme of the balance equations.

The article is organized in eight sections starting with Sect. 2, where the strong and the weak form of the balance equations is presented and the spatial and time discretization of these equations explained. Section 3 develops the transient solution of the discretized equations used in the PFEM for solid mechanics, which is briefly explained in Sect. 4. In Sect. 5, a regularized Johnson–Cook constitutive model that represents the material behavior at different temperatures, strains and strain rates is proposed. This model allows to face a large range of cutting speeds and conditions. In Sect. 6, we describe the contact phenomena at the workpiece–tool interface with a rigid cutting tool for both implicit and explicit schemes. The numerical modeling of AISI 4340 steel with implicit and explicit schemes at different cutting speeds is presented in Sect. 7. The set of results coming from a comparative analysis will allow us to determine how to select the time integration in order to minimize the computing time. The discussion about it and some recommendations are presented in Sect. 8.

2 The irreducible and mixed formulation

2.1 Governing equations in strong form

Let us consider the body $\mathcal B$ that due to the applied loads undergoes large deformations, which occupies a region $\Omega$ of the two-dimensional Euclidean space $\mathcal E$ with a regular boundary $\Gamma$ of its reference configuration, with material particles labeled $\mathbf {X}$. A deformation of $\mathcal B$ is defined by a one-to-one mapping:

$$\begin{aligned} \varphi : \Omega \rightarrow \mathcal E \end{aligned}$$

(1)

that maps each particle $\mathbf {X}$ of the body $\mathcal B$ into a spatial point $\mathbf {x}$:

$$\begin{aligned} \mathbf {x} = \varphi (\mathbf {X},t) \end{aligned}$$

(2)

which represents the location of particle $\mathbf {X}$ of the deformed configuration of $\mathcal B$. The region of $\mathcal E$ occupied by $\mathcal B$ in its deformed configuration is denoted as $\varphi (\Omega )$.

The problem is governed by linear momentum and energy balance equations

$$\begin{aligned} \rho \mathbf {a} =&\nabla \cdot {\pmb \sigma } + \rho \mathbf {b} \text{ in } \varphi (\Omega ) \times [0, T] \end{aligned}$$

(3a)

$$\begin{aligned} \rho c_p \dot{ \theta } =&\nabla \cdot (k \nabla \theta ) + r \text{ in } \varphi (\Omega ) \times [0, T] \end{aligned}$$

(3b)

where $\rho$ is the mass density, $c_p$ is the specific heat, $\mathbf {a}$ is the acceleration (also known as the material derivative of the velocity), $\theta$ is the temperature, $\dot{ \theta }$ is the time derivative of the temperature, $\sigma$ is the symmetric Cauchy stress tensor, k is the thermal conductivity, $\mathbf {b}$ is the body force, and r is the heat source due to plasticity per unit of volume.

Mathematically, the heat source due to plasticity can be expressed as

$$\begin{aligned} r={{\eta }_{p}}({{\sigma }_{y}}+\beta )\dot{\varepsilon } \end{aligned}$$

(4)

where $\sigma _y+\beta$ is the equivalent stress, $\dot{\varepsilon }$ is the equivalent plastic strain rate, and ${{\eta }_{p}}$ is the fraction of the inelastic work. As usual for metal cutting simulations, the value ${\eta }_{p}$ is set to 0.9 [4, 30].

To deal with quasi-incompressibility due to $J_2$ plasticity, the Cauchy stress tensor is decomposed into its deviatoric and volumetric components as

$$\begin{aligned} {\pmb \sigma } = \mathrm{dev}({\pmb \sigma }) + p\mathbf {I} \end{aligned}$$

(5)

where $\mathrm{dev}({\pmb \sigma })$ is the deviatoric part of the Cauchy stress tensor, p is the pressure and $\mathbf {I}$ is the second order identity tensor. The pressure is assumed to be positive for a tension state.

As in the present work, a Neo-Hookean material [31] with free energy given in Appendix A is used, the continuity equation can be expressed as

$$\begin{aligned} p- \frac{\partial \overset{\scriptscriptstyle \frown }{U}(J)}{\partial J}=p -\kappa \frac{\mathrm{ln}(J)}{J} = 0 \text{ in } \varphi (\Omega ) \times [0, T] \end{aligned}$$

(6)

where $\kappa$ is the bulk modulus, J is the determinant of the deformation gradient $\mathbf {F} = \mathrm{d}\mathbf {x}/\mathrm{d}\mathbf {X}$ and the term $\kappa \frac{\mathrm{ln}(J)}{J}$ comes from the derivative of the volumetric component of the free energy function $\overset{\scriptscriptstyle \frown }{U}(J)$ of a Neo-Hookean material with respect to J. The reason to introduce the decomposition of the Cauchy stress in its deviatoric and hydrostatic components in Eq. (5) and the introduction of the continuity equation, Eq. (6), is because in this work we use a mixed formulation with linear triangle finite elements able to handle the incompressibility constraint due to $J_2$ plasticity. The details about the finite element discretization are presented in Sect. 2.3 .

The balance equations are solved numerically for a two-dimensional region $\Omega \subseteq {\mathbb {R}}^2$, for the time range $t \in [0, T]$, given the following boundary conditions on the Dirichlet ($\varphi (\Gamma _\mathbf {u})$ and $\varphi (\Gamma _{\varvec{\theta }})$) and Neumann boundaries ($\varphi (\Gamma _\mathbf {t})$ and $\varphi (\Gamma _\mathbf {q})$), respectively

$$\begin{aligned}&\mathbf {u} = \hat{\mathbf {u}} \text{ on } \Gamma _\mathbf {u} \end{aligned}$$

(7a)

$$\begin{aligned}&\mathbf {t} = {\pmb \sigma } \mathbf {n} =\hat{\mathbf {t}} \text{ on } \Gamma _\mathbf {t} \end{aligned}$$

(7b)

$$\begin{aligned}&\theta = \hat{\theta } \text{ on } \Gamma _\theta \end{aligned}$$

(7c)

$$\begin{aligned}&(k \nabla \theta )\centerdot \mathbf {n} =\hat{q} \text{ on } \Gamma _\mathbf {q} \end{aligned}$$

(7d)

where $\hat{\mathbf {u}},\hat{\mathbf {t}}, \hat{\theta }$ and $\hat{\mathbf {q}}$ are the prescribed displacements, tractions, temperatures and heat fluxes, respectively, and $\mathbf {n}$ is the unit outward normal to the boundaries of the solid body (the workpiece). In Eq. (7), the boundary $\Gamma = \Gamma _\mathbf {u} \cup \Gamma _\mathbf {t} = \Gamma _\theta \cup \Gamma _\mathbf {q}$ and $\Gamma _\mathbf {u} \cap \Gamma _\mathbf {t} = \Gamma _\theta \cap \Gamma _\mathbf {q} = \emptyset$.

Additionally, we assume that the following initial data is specified for the mechanical and thermal fields

$$\begin{aligned}&\mathbf {u}(\mathbf {x},0) = \mathbf {u}_0(\mathbf {x}) \text{ on } \Omega \end{aligned}$$

(8a)

$$\begin{aligned}&\dot{\mathbf {u}}(\mathbf {x},0) = \dot{\mathbf {u}}_0(\mathbf {x}) \text{ on } \Omega \end{aligned}$$

(8b)

$$\begin{aligned}&\theta (\mathbf {x},0) = \theta _0(\mathbf {x}) \text{ on } \Omega \end{aligned}$$

(8c)

where $\mathbf {u}_0(\mathbf {x})$, $\dot{\mathbf {u}}_0(\mathbf {x})$ and $\theta _0(\mathbf {x})$ are the initial displacement, velocity and temperature of the workpiece, respectively.

A constitutive equation for the evaluation of the stress–strain relation that includes the strain hardening, the strain rate hardening and the thermal softening is also needed to fully define the boundary value problem (BVP).

2.2 The weak form of the governing equations

Following the standard FEM procedure, the weak form of the momentum balance and energy equation is obtained in the following way: the $L_2$ inner product of Eqs. (3) is derived using arbitrary test functions $\mathbf {w}$ and $\zeta$, such that $\mathbf {w} = \{\mathbf {w} \in V | \mathbf {w} = \mathbf {0} \text{ on } \varphi (\Gamma _\mathbf {u})\}$, where V is the space of virtual displacements and $\hat{w} = \{\zeta \in T | \zeta = 0 \text{ on } \varphi (\Gamma _\theta )\}$, where T is the space of virtual temperatures. By using the divergence theorem, the weak forms of momentum balance and energy equation can be obtained and expressed as

$$\begin{aligned}&G_\mathrm{dyn}(\mathbf {u},\mathbf {w}) =\int \limits _{\varphi (\Omega )}{{\pmb \sigma } : \nabla ^S \mathbf {w} \mathrm{d}v } - \int \limits _{\varphi (\Omega )}{ \rho (\mathbf {b} - \mathbf {a})\cdot \mathbf {w} \mathrm{d}v } \nonumber \\&\quad -\int \limits _{\varphi (\Gamma _\mathbf {t})}{ \bar{\mathbf {t}}\cdot \mathbf {w} \mathrm{d}a =0} \end{aligned}$$

(9a)

$$\begin{aligned}&G_\mathrm{therm}(\theta ,\zeta ) = \int \limits _{\varphi (\Omega )}{ \zeta \rho c_p \dot{\theta } \mathrm{d}v } + \int \limits _{\varphi (\Omega )}{ \nabla \zeta \cdot (\kappa \nabla \theta ) \mathrm{d}v }\nonumber \\&\quad - \int \limits _{\varphi (\Omega )}{ \zeta r \mathrm{d}v } + \int \limits _{\varphi (\Gamma _\mathbf {q})}{ \zeta \hat{q} \mathrm{d}a =0} \end{aligned}$$

(9b)

where $\nabla ^S \mathbf {w}$ represents the symmetric part of the tensor $\nabla \mathbf {w}$, $\mathrm{d}v$ denotes the infinitesimal volume for the current configuration and $\mathrm{d}a$ denotes the infinitesimal area for the current configuration. The weak form of the pressure constitutive equation can be obtained and expressed as

$$\begin{aligned} G_\mathrm{press}(p,q) =\int \limits _{\varphi (\Omega )}{q\left( \frac{p}{\kappa } - \frac{\mathrm{ln}(J)}{J}\right) \frac{\mathrm{d}v}{J}} = 0 \end{aligned}$$

(10)

where q is the test function, such that $q = \{q \in Q | q = 0 \text{ on } (\Gamma _\mathbf {u})\}$, where Q is the space of virtual pressures.

For the treatment of the incompressibility constraint, the Polynomial Pressure Projection (PPP), introduced by Dohrmann and Bochev [32, 33] is used. The PPP modifies the weak form of the pressure constitutive equation as

$$\begin{aligned} G_\mathrm{press}(p,q)= & {} \int \limits _{\varphi (\Omega )}{q\left( \frac{p}{\kappa } - \frac{\mathrm{ln}(J)}{J}\right) \frac{\mathrm{d}v}{J}}\nonumber \\&+ \frac{\alpha }{G}\int \limits _{\varphi (\Omega )}{(qp - \tilde{q}\tilde{p})\frac{\mathrm{d}v}{J}} = 0 \end{aligned}$$

(11)

where $\alpha$ is a stabilization parameter ($\alpha$ is constant and equal to 1 for all the numerical simulations carried out in this work), G the shear modulus, $\tilde{p}$ the best approximation of $\tilde{p}$ in $(Q_0)$ and $\tilde{q} \in Q_0$ an arbitrary test function, where $Q_0$ is the space of polynomial functions with zero degree in each coordinate direction.

The best approximation $\tilde{p}$ of p of $Q_0$ is obtained through the following integral

$$\begin{aligned} \int \limits _{\varphi (\Omega )}{\tilde{q}\left( p - \tilde{p} \right) \frac{\mathrm{d}v}{J}} = 0 \end{aligned}$$

(12)

The previous integral represents the $L_2$ projection of the pressure with linear shape function in a discontinuous space (zero degree polynomial).

The main advantage of PPP compared to other stabilization techniques is that the pressure stabilization is accomplished without the use of the residual of the momentum equation; thus, the calculation of higher-order derivatives and the specification of a mesh size dependent stabilization parameter are avoided. Furthermore, the addition of the second term in Eq. (11) in a FEM context is performed at the elementary level.

2.3 Spatial discretization using FEM

Following a standard Galerkin approach, the displacements, the pressure, the temperature and the test functions are interpolated with linear shape functions $\mathbf {N}$:

(13)

where the upper symbol $\left( \bar{\cdot } \right)$ denotes a vector containing the nodal variables. The same order interpolation functions are used for scalar and vector fields: $\mathbf {N}$ and $\mathbf {N}_\mathbf {u}$.

The matrix form of the Galerkin expression of Eq. (9) is obtained introducing the previous approximations to the weak form,

$$\begin{aligned}&\mathbf {M}_\mathbf {u} \bar{\mathbf {a}} = \mathbf {f}_{\mathbf {u},\mathrm{ext}} - \mathbf {P}_{\mathbf {u}} (\bar{\mathbf {u}}) \end{aligned}$$

(14a)

$$\begin{aligned}&\mathbf {M}_\theta \bar{\dot{\theta }} = \mathbf {f}_{\theta ,\mathrm{ext}} - \mathbf {P}_{\theta } (\bar{\theta }) \end{aligned}$$

(14b)

The explicit form of each matrix of the system above can be written as

$$\begin{aligned} \mathbf {P}_{\mathbf {u}} ({\mathbf {u}})= & {} \int \limits _{\varphi (\Omega )}{\mathbf {B}_{\mathbf {u}}^T \bar{{\pmb \sigma }} \mathrm{d}v} \end{aligned}$$

(15)

$$\begin{aligned} \mathbf {P}_{\theta } (\bar{\theta })= & {} \int \limits _{\varphi (\Omega )}{ k \mathbf {B}_{\theta }^T\mathbf {B}_{\theta } \bar{\theta } \mathrm{d}v} \end{aligned}$$

(16)

$$\begin{aligned} \mathbf {f}_{\mathbf {u},\mathrm{ext}}= & {} \int \limits _{\varphi (\Omega )}{ \mathbf {N}_\mathbf{u }^T \cdot \mathbf {b} \mathrm{d}v} + \int \limits _{\varphi (\Gamma _\mathbf {t})}{ \mathbf {N}_\mathbf{u }^T \cdot \bar{\mathbf {t}} \mathrm{d}a } \end{aligned}$$

(17)

$$\begin{aligned} \mathbf {f}_{\theta ,\mathrm{ext}}= & {} \int \limits _{\varphi (\Omega )}{ {\mathbf {N}}^T r \mathrm{d}v} + \int \limits _{\varphi (\Gamma _\mathbf {t})}{ {\mathbf {N}}^T \hat{q} \mathrm{d}a } \end{aligned}$$

(18)

$$\begin{aligned} \mathbf {M}_\mathbf {u}= & {} \int \limits _{\varphi (\Omega )}{\rho \mathbf {N}_\mathbf{u }^T {\mathbf {N}_\mathbf{u }} \mathrm{d}v} \end{aligned}$$

(19)

$$\begin{aligned} \mathbf {M}_\theta= & {} \int \limits _{\varphi (\Omega )}{\rho c_p {\mathbf {N}}^T {\mathbf {N}} \mathrm{d}v} \end{aligned}$$

(20)

where $\mathbf {B}_{\mathbf {u}}$ is the small deformation strain displacement matrix, $\mathbf {B}_{\theta }$ is gradient temperature matrix, respectively, and $\bar{{\pmb \sigma }}$ corresponds to the Voigt notation of the Cauchy stress tensor.

The discrete counterpart of the stabilized pressure constitutive equation is given by

$$\begin{aligned} \mathbf {M}_{p}\bar{p}-\mathbf {F}_{p,\mathrm{vol}}({\bar{\mathbf{u}}})+\mathbf {F}_{p,\mathrm{stab}}(\bar{p})=0 \end{aligned}$$

(21)

where

$$\begin{aligned}&\mathbf {M}_{p} = \int _{\varphi (\Omega )}\dfrac{1}{\kappa }\mathbf {N}^T\mathbf {N} \,\frac{\mathrm{d}v}{J} \end{aligned}$$

(22)

$$\begin{aligned}&\mathbf {F}_{p,\mathrm{vol}}({\bar{\mathbf{u}}}) = \int _{\varphi (\Omega )} \mathbf {N}^T \left( \ \frac{\mathrm{ln}(J)}{J}\right) \,\frac{\mathrm{d}v}{J} \end{aligned}$$

(23)

$$\begin{aligned}&{\mathbf {F}_{p,\mathrm{stab}}}(\bar{p})= \int _{\varphi (\Omega )}\dfrac{\alpha }{G}\,\bar{p}\left( {\mathbf {N}}^{T}{\mathbf {N}}-{\tilde{\mathbf{N}}^{T}\tilde{\mathbf{N}}}\right) \,\frac{\mathrm{d}v}{J} \end{aligned}$$

(24)

As $\mathbf {N}$ contain the set of polynomials of order 1, $\tilde{\mathbf{N}}$ contain the set of polynomials of order 0.

The above global force vectors are obtained as the assemblies of element vectors as it is standard of finite elements theory. Given a nodal point, each component of the global force associated with a particular global node is obtained as the sum of the corresponding contributions from the element force vectors of all elements that share the node. In this work, the element force vectors are evaluated using Gaussian quadratures.

2.4 Time-integration schemes for the mechanical problem

We present subsequently the main steps for solving nonlinear dynamics problem presented in Eq. (14) (a) by using Newmark time integration schemes. To that end, the time interval of interest [0, T] is subdivided in the chosen number of time steps, which will specify the time instants where the selected time integration scheme should deliver the solution:

$$\begin{aligned} 0<t^1<t^2<\cdots<t^{n+1}<\cdots <T \end{aligned}$$

(25)

the solution at time $t^n$ is defined as:

$$\begin{aligned} \begin{matrix} {\bar{\mathbf{u}}}^n ={\bar{\mathbf{u}}}(t^n);&{\bar{\mathbf{v}}}^n ={\bar{\mathbf{v}}}(t^n);&{\bar{\mathbf{a}}}^n ={\bar{\mathbf{a}}}(t^n) \end{matrix} \end{aligned}$$

(26)

The time integration algorithm implemented in this work belongs to the family of Newmark methods. The method seeks the solution of linear momentum at time $t^{n+1}$ starting with the solution a time $t^{n}$ in a the step-by-step basis.

Equation (14) (a) is re-written as

$$\begin{aligned} \mathbf {M}_\mathbf {u}^{n+1} \bar{\mathbf {a}}^{n+1} = \mathbf {f}_{\mathbf {u},\mathrm{ext}}^{n+1} - \mathbf {P}_{\mathbf {u}}^{n+1} (\bar{\mathbf {u}}^{n+1} ) \end{aligned}$$

(27)

The problem consists of finding a displacement function that satisfies Eq. (27) and the corresponding initial conditions; the set of equations for the Newmark method defines the displacement and velocity fields at $t^{n+1}$ as an interpolation of the displacements and velocities a $t^n$, and acceleration field at $t^n$ and $t^{n+1}$ , which for the displacement fields reads:

$$\begin{aligned} {\bar{\mathbf{u}}}^{n+1} = {\bar{\mathbf{u}}}^{n} + h{\bar{\mathbf{v}}}^n + h^2 \left[ \left( \frac{1}{2} -\beta \right) {\bar{\mathbf{a}}}^{n} + \beta {\bar{\mathbf{a}}}^{n+1} \right] \end{aligned}$$

(28)

and velocity

$$\begin{aligned} {\bar{\mathbf{v}}}^{n+1} = {\bar{\mathbf{v}}}^{n} + h \left[ (1 -\gamma ){\bar{\mathbf{a}}}^{n} + \gamma {\bar{\mathbf{a}}}^{n+1} \right] \end{aligned}$$

(29)

Hence, by choosing $\beta = 0$ and $\gamma = 1/2$ we obtain the central difference scheme (called explicit scheme in this work), whereas for $\beta = 1/4$ and $\gamma = 1/2$ the general expression will reduce to the trapezoidal rule approximation (called implicit scheme in this work). In Eqs. (28) and (29), h represents time increment between $t^n$ and $t^{n+1}$, defined as: $h = t^{n+1} - t^{n}$. The time increment is also know as the time step.

2.4.1 Trapezoidal rule with displacement formulation (Implicit)

From Eqs. (28) and (29), and using the trapezoidal rule, the velocity ${\bar{\mathbf{v}}}^{n+1}$ and acceleration ${\bar{\mathbf{a}}}^{n+1}$ at $t^{n+1}$ reads as

$$\begin{aligned}&{\bar{\mathbf{v}}}^{n+1} = -{\bar{\mathbf{v}}}^{n} +\frac{2}{h}({\bar{\mathbf{u}}}^{n+1} - {\bar{\mathbf{u}}}^{n}) \end{aligned}$$

(30)

$$\begin{aligned}&{\bar{\mathbf{a}}}^{n+1} = -{\bar{\mathbf{a}}}^{n} -\frac{4}{h}{\bar{\mathbf{v}}}^{n} + \frac{4}{h^2}({\bar{\mathbf{u}}}^{n+1} - {\bar{\mathbf{u}}}^{n}) \end{aligned}$$

(31)

The last two equations are implicit in the sense that they depend upon the displacement value at $t^{n+1}$. As Newton–Raphson method is employed for the iterative solution of the set of nonlinear algebraic equations with displacements as main unknowns, the consistent linearization of momentum equation is necessary, which can be written as:

$$\begin{aligned} \left[ \frac{4}{h^2} \mathbf {M}_\mathbf {u} + \mathbf {K}_{\mathbf {uu},(i)}^{n+1} \right] \Delta \bar{\mathbf {u}}_{(i)}^{n+1} = -\mathbf {R}_{\mathbf {u},(i)}^{n+1} \end{aligned}$$

(32)

where the subscript (i) refers to the iteration number of the Newton–Raphson method and $\mathbf {K}_{\mathbf {uu}}^{n+1} =\frac{\partial \mathbf {P}_{\mathbf {u}}^{n+1} (\bar{\mathbf {u}}_{(i)}^{n+1} )}{\partial \bar{{\mathbf {u}}^{n+1}}}$ is the tangent stiffness matrix. In Eq. (32), $\mathbf {R}_{\mathbf {u}}^{n+1}$ is given by

$$\begin{aligned} \mathbf {R}_{\mathbf {u}}^{n+1,(i)} = \mathbf {M}_\mathbf {u}^{n+1} \bar{\mathbf {a}}_{(i)}^{n+1} + \mathbf {P}_{\mathbf {u}}^{n+1} (\bar{\mathbf {u}}_{(i)}^{n+1} ) -\mathbf {f}_{\mathbf {u},\mathrm{ext}}^{n+1} \end{aligned}$$

(33)

As is usual for nonlinear FEM, the tangent matrix is evaluated as the sum of the material stiffness matrix and the geometric stiffness matrix (see [31, 34]).

Equation (32) is completed with the update of displacement according to

$$\begin{aligned} \bar{\mathbf {u}}_{(i+1)}^{n+1} = \bar{\mathbf {u}}_{(i)}^{n+1} + \Delta \bar{\mathbf {u}}_{(i)}^{n+1} \end{aligned}$$

(34)

where $\Delta \bar{\mathbf {u}}_{(i)}^{n+1}$ is the increment of displacement during one Newton–Raphson iteration.

2.4.2 Trapezoidal rule with mixed formulation for the mechanical problem (Implicit)

The mixed formulation is based on linear interpolation finite elements for both displacement and pressure. In case of a mixed formulation with trapezoidal rule Eqs. (14) (a) and (21) should be solved in a coupled way. The time discretization of the previous equations is written as

$$\begin{aligned}&\mathbf {M}_\mathbf {u}^{n+1} \bar{\mathbf {a}}^{n+1} + \mathbf {P}_{\mathbf {u}}^{n+1} (\bar{\mathbf {u}}^{n+1} ) - \mathbf {f}_{\mathbf {u},\mathrm{ext}}^{n+1} = 0 \end{aligned}$$

(35a)

$$\begin{aligned}&\mathbf {M}_{p}\bar{p}^{n+1}-\mathbf {F}_{p,\mathrm{vol}}({\bar{\mathbf{u}}}^{n+1})+\mathbf {F}_{p,\mathrm{stab}}(\bar{p}^{n+1})=0 \end{aligned}$$

(35b)

where $\bar{\mathbf {a}}^{n+1}$ is given by Eq. (31).

The consistent linearization of Eqs. (35)(a) and (35)(b) is expressed in matrix form as

$$\begin{aligned} \begin{bmatrix} \frac{4}{h^2} \mathbf {M}_\mathbf {u} + {}^\mathrm{mix}\mathbf {K}_{\mathbf {uu},(i)}^{n+1} &{} \mathbf {K}_{\mathbf {u}p,(i)}^{n+1} \\ \mathbf {K}_{p\mathbf {u},(i)}^{n+1} &{} \mathbf {K}_{{pp},(i)}^{n+1} \end{bmatrix} \begin{bmatrix} \Delta \bar{\mathbf {u}}_{(i)}^{n+1} \\ \Delta \bar{\mathbf {p}}_{(i)}^{n+1} \end{bmatrix} = \begin{bmatrix} -\mathbf {R}_{\mathbf {u},(i)} \\ -\mathbf {R}_{p,(i)} \end{bmatrix} \end{aligned}$$

(36)

where

$$\begin{aligned}&\mathbf {K}_{\mathbf {u}p,(i)}^{n+1} = \int _{\varphi (\Omega )}\mathbf {B}^T\mathbf {m}\mathbf {N} \,\mathrm{d}{v} \end{aligned}$$

(37)

$$\begin{aligned}&\mathbf {K}_{p\mathbf {u},(i)}^{n+1}=\int _{\varphi (\Omega )}\frac{(1-ln(J))}{J^2}\mathbf {N}^T\mathbf {m}^T\mathbf {B} \,\mathrm{d}{v}\end{aligned}$$

(38)

$$\begin{aligned}&\mathbf {K}_{pp,(i)}^{n+1} = \mathbf {M}_{p} + \mathbf {M}_\mathrm{stab}\end{aligned}$$

(39)

$$\begin{aligned}&\mathbf {M}_\mathrm{stab} = \int _{\varphi (\Omega )}\dfrac{\alpha }{G}\,\left( {\mathbf {N}}^{T}{\mathbf {N}}-{\tilde{\mathbf{N}}^{T}\tilde{\mathbf{N}}}\right) \,\frac{\mathrm{d}v}{J}\end{aligned}$$

(40)

$$\begin{aligned}&\mathbf {R}_{\mathbf {u},(i)}^{n+1} = \mathbf {M}_\mathbf {u}^{n+1} \bar{\mathbf {a}}_{(i)}^{n+1} + \mathbf {P}_{\mathbf {u}}^{n+1} (\bar{\mathbf {u}}_{(i)}^{n+1},\bar{p}_{(i)}^{n+1} ) -\mathbf {f}_{\mathbf {u},\mathrm{ext}}^{n+1}\end{aligned}$$

(41)

$$\begin{aligned}&\mathbf {R}_{p,(i)}^{n+1} = \mathbf {M}_{p}\bar{p}_{(i)}^{n+1}-\mathbf {F}_{p,\mathrm{vol}}({\bar{\mathbf{u}}}^{n+1})+\mathbf {F}_{p,\mathrm{stab}}(\bar{p}_{(i)}^{n+1}) \end{aligned}$$

(42)

where $\mathbf {m}$ represent the second order identity tensor in Voigt notation. It is important to remark that ${}^\mathrm{mix}\mathbf {K}_{\mathbf {uu},(i)}^{n+1} \ne \mathbf {K}_{\mathbf {uu},(i)}^{n+1}$, the mathematical expressions for both matrices are given for Appendix B. Details about how to obtain the matrices are given in nonlinear finite element books like [31, 34]. Like $\mathbf {K}_{\mathbf {uu},(i)}^{n+1}$, ${}^\mathrm{mix}\mathbf {K}_{\mathbf {uu},(i)}^{n+1}$ is the sum of the material stiffness matrix and the geometric stiffness matrix. Furthermore, in the mixed formulation the Cauchy stress in Eq. (41) is evaluated with Eq. (5).

Equation (36) is completed with the update of displacement and pressure according to

$$\begin{aligned} \bar{\mathbf {u}}_{(i+1)}^{n+1} =&\bar{\mathbf {u}}_{(i)}^{n+1} + \Delta \bar{\mathbf {u}}_{(i)}^{n+1} \end{aligned}$$

(43a)

$$\begin{aligned} \bar{\mathbf {p}}_{(i+1)}^{n+1} =&\bar{\mathbf {p}}_{(i)}^{n+1} + \Delta \bar{\mathbf {p}}_{(i)}^{n+1} \end{aligned}$$

(43b)

where $\Delta \bar{\mathbf {u}}_{(i)}^{n+1}$ and $\Delta \bar{\mathbf {p}}_{(i)}^{n+1}$ are the increment of displacement and pressure during one Newton–Raphson iteration, respectively.

2.4.3 Central difference scheme with mixed formulation (Explicit)

In the central difference scheme, the displacement and velocity are updated at $t^{n+1}$ as

$$\begin{aligned} {\bar{\mathbf{u}}}^{n+1}= & {} {\bar{\mathbf{u}}}^{n} + h{\bar{\mathbf{v}}}^n + \frac{h^2}{2} {\bar{\mathbf{a}}}^{n} \end{aligned}$$

(44)

$$\begin{aligned} {\bar{\mathbf{v}}}^{n+1}= & {} {\bar{\mathbf{v}}}^{n} + \frac{h}{2}({\bar{\mathbf{a}}}^{n} + {\bar{\mathbf{a}}}^{n+1} ) \end{aligned}$$

(45)

The last two equations are explicit in the sense that they depend upon the displacement, velocity and acceleration at $t^{n}$. In Eq. (45), the acceleration at $t^{n+1}$ is obtained from the momentum equation evaluated in a special way as follows

$$\begin{aligned} \mathbf {M}_\mathbf {u}^{n+1} \bar{\mathbf {a}}^{n+1} + \mathbf {P}_{\mathbf {u}}^{n+1} (\bar{\mathbf {u}}^{n+1},\bar{p}^{n} ) -\mathbf {f}_{\mathbf {u},\mathrm{ext}}^{n+1} = 0 \end{aligned}$$

(46)

To decrease computational cost for the central difference scheme, $\mathbf {M}_\mathbf {u}^{n+1}$ is approximated by its diagonal form (lumped mass matrix).

The pressure at $t^{n+1}$ is obtained with the implicit solution of the pressure from Eq. (21) in the following way

$$\begin{aligned} (\mathbf {M}_{p}+\mathbf {M}_\mathrm{stab}) \bar{p}^{n+1} = \mathbf {F}_{p,\mathrm{vol}}({\bar{\mathbf{u}}}^{n+1}) \end{aligned}$$

(47)

The consecutive solution of Eqs. (44), (45), (46) and (47) represents a typical solution of a time step from time $t^n$ to time $t^{n+1}$ using the central difference scheme with mixed formulation. One way to avoid the implicit calculation of the pressure field (Eq. (47)) is the use of the displacement/irreducible formulation but with the locking problems due to incompressibility as it is shown for some examples presented in Sect. 7.

A formulation similar to the one presented in this section and stabilized using finite calculus has been presented in [35]. The previous formulation has the advantage that the pressure calculation is done explicitly, as a result a decrease of the computing time is expected. Another fully explicit formulation that solves the problem of locking of linear triangle finite elements that does not need the calculation of a implicit pressure have been developed; among them are F-bar [36] and average nodal strain/stresses [37]. The exploration of explicit formulations for both displacement and pressure that uses linear triangles finite elements will allow to find new finite element formulations that obtain the same results but with a lower computing cost. The study of the previous formulations as well as their computational efficiency will be investigated in future works.

2.5 Time-integration schemes of the thermal problem

To solve the thermal problem, it is necessary to approach the time derivative of the temperature $\dot{\theta }$. The forward Euler scheme approximates the time derivative of ${\theta }$ at time $t^n$ as

$$\begin{aligned} \dot{\theta }^{n} \approx \frac{\theta ^{n+1}-\theta ^{n}}{h}; \end{aligned}$$

(48)

meanwhile, the backward Euler scheme approximates the time derivative of ${\theta }$ at time $t^{n+1}$ as

$$\begin{aligned} \dot{\theta }^{n+1} \approx \frac{\theta ^{n+1}-\theta ^{n}}{h} \end{aligned}$$

(49)

Solving for $\theta ^{n+1}$ in Eq. (48), we obtain

$$\begin{aligned} \theta ^{n+1} = \theta ^{n} + \dot{\theta }^{n} h; \end{aligned}$$

(50)

the last equation is an explicit update because it depends on the values at time $t^{n}$.

Solving for $\theta ^{n+1}$ in Eq. (49), we find

$$\begin{aligned} \theta ^{n+1} = \theta ^{n} + \dot{\theta }^{n+1} h \end{aligned}$$

(51)

the last equation is an implicit update because it depends on the values at time $t^{n+1}$.

The time discretization of heat equation (Eq. (14)) is given by:

$$\begin{aligned} \mathbf {M}_\theta ^{n+1} \bar{\dot{\theta }}^{n+1} + \mathbf {P}_{\theta }^{n+1} (\bar{\theta }^{n+1}) - \mathbf {f}_{\theta ,\mathrm{ext}}^{n+1} = 0 \end{aligned}$$

(52)

For the solution of Eq. (52) using Backward Euler scheme, the consistent linearization is necessary; the linearization is given by:

$$\begin{aligned} \left[ \frac{1}{h} \mathbf {M}_\theta + \mathbf {K}_{\theta \theta ,(i)}^{n+1} - \mathbf {K}_{\mathrm{plast},(i)}^{n+1} \right] \Delta \bar{\theta }_{(i)}^{n+1} = -\mathbf {R}_{\theta ,(i)}^{n+1} \end{aligned}$$

(53)

where the subscript i refers to the iteration number of the Newton–Raphson method and where

$$\begin{aligned} \mathbf {K}_{\theta \theta }= & {} \int \limits _{\varphi (\Omega )}{ k \mathbf {B}_{\theta }^T\mathbf {B}_{\theta } \mathrm{d}v} \end{aligned}$$

(54)

$$\begin{aligned} \mathbf {K}_{\mathrm{plast}}= & {} \int \limits _{\varphi (\Omega )}{ \frac{\partial r}{\partial \theta } \mathbf {N}^T \mathbf {N} \mathrm{d}v} \end{aligned}$$

(55)

$$\begin{aligned} \mathbf {R}_{\theta ,(i)}^{n+1}= & {} \mathbf {M}_\theta ^{n+1} \bar{\dot{\theta }}_{(i)}^{n+1} + \mathbf {P}_{\theta }^{n+1} (\bar{\theta }_{(i)}^{n+1}) - \mathbf {f}_{\theta ,\mathrm{ext}}^{n+1} \end{aligned}$$

(56)

Equation (56) is completed with the update of temperature according to

$$\begin{aligned} \bar{\theta }_{(i+1)}^{n+1} = \bar{\theta }_{(i)}^{n+1} + \Delta \bar{\theta }_{(i)}^{n+1} \end{aligned}$$

(57)

For the Forward Euler time integration scheme, we evaluate the heat equation (Eq. (14)) at time $t_n$ as

$$\begin{aligned} \mathbf {M}_\theta ^{n} \bar{\dot{\theta }}^{n} + \mathbf {P}_{\theta }^{n+1} (\bar{\theta }^{n}) - \mathbf {f}_{\theta ,\mathrm{ext}}^{n} = 0 \end{aligned}$$

(58)

Solving for $\bar{\dot{\theta }}^{n}$, we obtain

$$\begin{aligned} \bar{\dot{\theta }}^{n} = (\mathbf {M}_\theta ^{n})^{-1}(\mathbf {f}_{\theta ,\mathrm{ext}}^{n} - \mathbf {P}_{\theta }^{n+1} (\bar{\theta }^{n})) \end{aligned}$$

(59)

After getting $\bar{\dot{\theta }}^{n}$, the temperature at $t^{n+1}$ is calculated using Eq. (51). It is important to remark that for computational efficiency the lumped mass matrix approximation will be used for the calculations.

3 Transient solution of the discretized equations

The thermo-mechanical problem will be solved using a staggered approach with a mechanical phase with the temperature held constant, followed by a thermal phase at a fixed configuration. The isothermal split solves the mechanical problem with a predicted value of temperature equal to the temperature of the last converged time step $t^{n}$ and, then, solves the thermal problem using the configuration obtained as a solution of the mechanical problem at $t^{n+1}$.

In Sects. 3.1 and 3.2, the transient solution of the thermo-mechanical problem using the trapezoidal rule with mixed formulation (implicit) and central difference scheme with mixed formulation (explicit) is presented, respectively.

3.1 Implicit schemes

Equations (35) and (52) are solved in time with two implicit Newton–Raphson type iterative schemes, one for the mechanical problem and one for the thermal problem [28, 31, 34]. The basic steps within a time increment $\left[ n, n + 1\right]$ are:

Initialize variables:

$$\begin{aligned}&\left( \bar{\mathbf {u}}_{(1)}^{n+1} = 0,\right. {\bar{\mathbf {p}}_{(1)}^{n+1} = \bar{\mathbf {p}}^{n}}, \bar{\theta }_{(1)}^{n+1} = \bar{\theta }^{n}, \bar{\mathbf {x}}_{(1)}^{n+1} = \bar{\mathbf {x}}^{n},\nonumber \\&\bar{\mathbf {v}}_{(1)}^{n+1} = \bar{\mathbf {v}}^{n}, \bar{\mathbf {b}}_{(1)}^{e,n+1} = \bar{\mathbf {b}}^{e,n}, \left. \bar{e}_{(1)}^{p,n+1} = \bar{e}^{p,n} \right) \end{aligned}$$

where $\bar{\mathbf {b}}^{e,}$ is volumetric preserving part of the elastic left Cauchy–Green tensor, $\bar{e}^{p}$ is the equivalent plastic strain and $\bar{\mathbf {x}}_{(i)}^{n}$ is the position of the particles a time $t^n$ and iteration i.

• Iteration loop for the mechanical problem: $i = 1,\ldots , N_{\mathrm{iter,mech}}$, where $N_{\mathrm{iter,mech}}$ is the maximum number of iterations.

  • 1. Compute the nodal displacement and pressure increments (It is important to remark that the term $\mathbf {R}_{\mathbf {u},(i)}$ includes the contribution of the contact forces as it is shown in Sect. 6)

    $$\begin{aligned} \begin{bmatrix} \frac{4}{h^2} \mathbf {M}_\mathbf {u} + {}^\mathrm{mix}\mathbf {K}_{\mathbf {uu},(i)}^{n+1} &{} \mathbf {K}_{\mathbf {u}p,(i)}^{n+1} \\ \mathbf {K}_{p\mathbf {u},(i)}^{n+1} &{} \mathbf {K}_{{pp},(i)}^{n+1} \end{bmatrix} \begin{bmatrix} \Delta \bar{\mathbf {u}}_{(i)}^{n+1} \\ \Delta \bar{\mathbf {p}}_{(i)}^{n+1} \end{bmatrix} = \begin{bmatrix} -\mathbf {R}_{\mathbf {u},(i)} \\ -\mathbf {R}_{p,(i)} \end{bmatrix} \end{aligned}$$

    (60)

    The solution of the linear systems is carried out using a LU factorization.

  • 2. Update the nodal displacements and pressures

    $$\begin{aligned} \bar{\mathbf {u}}_{(i+1)}^{n+1} =&\bar{\mathbf {u}}_{(i)}^{n+1} + \gamma \Delta \bar{\mathbf {u}}_{(i)}^{n+1} \end{aligned}$$

    (61a)
    $$\begin{aligned} \bar{\mathbf {p}}_{(i+1)}^{n+1} =&\bar{\mathbf {p}}_{(i)}^{n+1} + \gamma \Delta \bar{\mathbf {p}}_{(i)}^{n+1} \end{aligned}$$

    (61b)

    where $\gamma$ is a parameter between 0 and 1, $\gamma$ is given by the line search strategy. The line search strategy implemented in this work is presented in [31].

  • 3. Update the nodal coordinates, velocities and accelerations

    $$\begin{aligned} \bar{\mathbf {x}}^{n+1}&= \bar{\mathbf {x}}^{n} + \bar{\mathbf {u}}_{(i+1)}^{n+1} \end{aligned}$$

    (62a)
    $$\begin{aligned} {\bar{\mathbf{v}}}^{n+1}&=-{\bar{\mathbf{v}}}^{n} +\frac{2}{h}\left( {\bar{\mathbf{u}}}_{(i+1)}^{n+1} - {\bar{\mathbf{u}}}^{n}\right) \end{aligned}$$

    (62b)
    $$\begin{aligned} {\bar{\mathbf{a}}}^{n+1}&= -{\bar{\mathbf{a}}}^{n} -\frac{4}{h}{\bar{\mathbf{v}}}^{n} + \frac{4}{h^2}\left( {\bar{\mathbf{u}}}_{(i+1)}^{n+1} - {\bar{\mathbf{u}}}^{n}\right) \end{aligned}$$

    (62c)

  • 4. Calculate the relative deformation gradient measured between the current configuration $\mathbf {x}_n$ and the updated configuration $\mathbf {x}_{n+1}$: $\mathbf {F}$ = $\mathrm{d}\mathbf {x}_{n+1}/\mathrm{d}\mathbf {x}_n$, the Jacobian $J=\mathrm{det}(\mathbf {F})$ and the area of all elements of the mesh

  • 5. Calculate the Cauchy Stress $\pmb \sigma$, $\bar{\mathbf {b}}^{e}$ and $\bar{e}^\mathrm{p}$ at $n+1$ using an implicit stress update presented in Chapter 9 of [38]. Also, calculate the tangent constitutive matrix.

  • 6. Calculate the residuals $\mathbf {R}_{\mathbf {u},(i)}$ and $\mathbf {R}_{p,(i)}$

  • 7. Check convergence of the mechanical problem

    $$\begin{aligned}&\left\| \bar{\mathbf {u}}_{(i+1)}^{n+1} - \bar{\mathbf {u}}_{(i)}^{n+1} \right\| \le \mathrm{TOL}_{\mathbf {u}} \left\| \bar{\mathbf {u}}^{n} \right\| \nonumber \\&\left\| \bar{\mathbf {p}}_{(i+1)}^{n+1} - \bar{\mathbf {p}}_{(i)}^{n+1} \right\| \le \mathrm{TOL}_{p}\left\| \bar{\mathbf {p}}^{n} \right\| \end{aligned}$$

    (63)
    $$\begin{aligned}&\left\| \mathbf {R}_{\mathbf {u},(i)} \right\| \le \mathrm{TOL}_{\mathbf {u}} \text { max}\left( \left\| \mathbf {M}_\mathbf {u}^{n+1} \bar{\mathbf {a}}^{n+1} \right\| , \left\| \mathbf {P}_{\mathbf {u}}^{n+1} (\bar{\mathbf {u}}^{n+1} ) \right\| ,\right. \nonumber \\&\quad \left. \left\| \mathbf {f}_{\mathbf {u},\mathrm{ext}}^{n+1} \right\| \right) \nonumber \\&\left\| \mathbf {R}_{p,(i)} \right\| \le \mathrm{TOL}_{p} \text { max} \left( \left\| \mathbf {M}_{p}\bar{p}^{n+1} \right\| , \left\| \mathbf {F}_{p,\mathrm{vol}}({\bar{\mathbf{u}}}^{n+1}) \right\| ,\right. \nonumber \\&\quad \left. \left\| \mathbf {F}_{p,\mathrm{stab}}(\bar{p}^{n+1}) \right\| \right) \end{aligned}$$

    (64)

    where $\mathrm{TOL}_{\mathbf {u}}$ and $\mathrm{TOL}_{p}$ are prescribed error norms. In the set of examples presented in the paper we have set $\mathrm{TOL}_{\mathbf {u}}$ = $\mathrm{TOL}_{p}$ = $10^{-4}$.

  If conditions (63) and (64) are satisfied proceed to the thermal problem. Otherwise, make the iteration counter $i \leftarrow i + 1$ and repeat Steps 1–7.

• Iteration loop for the thermal problem: $i = 1,\ldots , N_{\mathrm{iter,therm}}$, where $N_{\mathrm{iter,therm}}$ is the maximum number of iterations.

  • 1. Compute the nodal temperature increments using a LU factorization of the linear system.

    $$\begin{aligned} \left[ \frac{1}{h} \mathbf {M}_\theta + \mathbf {K}_{\theta \theta ,(i)}^{n+1} - \mathbf {K}_{\mathrm{plast},(i)}^{n+1} \right] \Delta \bar{\theta }_{(i)}^{n+1} = -\mathbf {R}_{\theta ,(i)}^{n+1} \end{aligned}$$

    (65)

  • 2. Update the nodal temperatures

    $$\begin{aligned} \bar{\theta }_{(i+1)}^{n+1} = \bar{\theta }_{(i)}^{n+1} + \Delta \bar{\theta }_{(i)}^{n+1} \end{aligned}$$

    (66)

  • 3. Calculate $\bar{\mathbf {b}}^{e}$, $\bar{e}^\mathrm{p}$, the heat source due to plasticity r and the derivative of r with respect to temperature

  • 4. Calculate the residual $\mathbf {R}_{\theta ,(i)}^{n+1}$

  • 5. Check convergence of the thermal problem

    $$\begin{aligned} \left\| \bar{\theta }_{(i+1)}^{n+1} - \bar{\theta }_{(i)}^{n+1} \right\|\le & {} \mathrm{TOL}_{\theta } \left\| \bar{\theta }^{n} \right\| \end{aligned}$$

    (67)
    $$\begin{aligned} \left\| \mathbf {R}_{\theta ,(i)}^{n+1} \right\|\le & {} \mathrm{TOL}_{\theta } \text { max} \left( \left\| \mathbf {M}_\theta ^{n+1} \bar{\dot{\theta }}^{n+1} \right\| ,\right. \nonumber \\&\left. \left\| \mathbf {P}_{\theta }^{n+1} (\bar{\theta }^{n+1}) \right\| ,\left\| \mathbf {f}_{\theta ,\mathrm{ext}}^{n+1} \right\| \right) \end{aligned}$$

    (68)

    where $\mathrm{TOL}_{\theta }$ is the prescribed error norms of temperatures. In the set of examples presented in the paper, we have set $\mathrm{TOL}_d{\theta } = 10^{-4}$.

If conditions (67) and (68) are satisfied, then make $n \leftarrow n + 1$ and proceed to the next time step. Otherwise, make the iteration counter $i \leftarrow i + 1$ and repeat Steps 1–5.

3.2 Explicit schemes

Equations (35) and (52) are solved in time with two explicit schemes, one for the mechanical problem and one for the thermal problem [28, 31, 34]. The basic steps within a time increment $\left[ n, n + 1\right]$ are:

Given: $\left( \bar{\mathbf {u}}^{n}, \bar{\theta }^{n}, \bar{\mathbf {x}}^{n}, \bar{\mathbf {v}}^{n}, \bar{\mathbf {b}}^{e,n}, \bar{e}^{p,n} \right)$

• Loop for the mechanical problem.

  • 1. Calculate the time step

    $$\begin{aligned} h = C\frac{l}{\sqrt{\frac{E}{\rho }}} \end{aligned}$$

    (69)

    where l is the minimum distance between two particles of the mesh, $0 < C \le 1$ is a constant (0.8 used for all the numerical simulations), $\rho$ is the density and E is the elastic modulus of the material. As explicit scheme are only conditionally stable, the maximum size of the time step allowed is given by the well known Courant–Friedrichs–Lewy (CFL) criterion (Eq. (69)).

  • 2. Update the nodal displacements and positions

    $$\begin{aligned}&{\bar{\mathbf{u}}}^{n+1} = {\bar{\mathbf{u}}}^{n} + h{\bar{\mathbf{v}}}^n + \frac{h^2}{2} {\bar{\mathbf{a}}}^{n} \end{aligned}$$

    (70)
    $$\begin{aligned}&{\bar{\mathbf{x}}}^{n+1} = {\bar{\mathbf{x}}}^{n} + {\bar{\mathbf{u}}}^{n+1} \end{aligned}$$

    (71)

  • 3. Calculate the relative deformation gradient measured between the current configuration $\mathbf {x}_n$ and the updated configuration $\mathbf {x}_{n+1}$: $\mathbf {F}$ = $\mathrm{d}\mathbf {x}_{n+1}/\mathrm{d}\mathbf {x}_n$, the Jacobian $J=\mathrm{det}(\mathbf {F})$ and the area of all elements of the mesh

  • 4. Calculate the Cauchy Stress $\pmb \sigma$, $\bar{\mathbf {b}}^{e}$ and $\bar{e}^\mathrm{p}$ at $n+1$ using a implicit stress update presented in Chapter 9 of [38].

  • 5. Calculate nodal accelerations

    $$\begin{aligned} \bar{\mathbf {a}}^{n+1} = ({\mathbf {M}_\mathbf {u}^{n+1}})^{-1} \left( \mathbf {f}_{\mathbf {u},\mathrm{ext}}^{n+1} - \mathbf {P}_{\mathbf {u}}^{n+1} (\bar{\mathbf {u}}^{n+1},\bar{p}^{n} ) \right) \end{aligned}$$

    (72)

    where ${\mathbf {M}_\mathbf {u}^{n+1}}$ is the lumped mass matrix.

  • 6. Update the particle/nodal velocities

    $$\begin{aligned} {\bar{\mathbf{v}}}^{n+1} = {\bar{\mathbf{v}}}^{n} + \frac{h}{2}({\bar{\mathbf{a}}}^{n} + {\bar{\mathbf{a}}}^{n+1} ) \end{aligned}$$

    (73)

  • 7. Correct the nodal/particle positions, displacements, velocities and accelerations of the nodes that are in contact with the tool.

  • 8. Calculate implicitly the nodal/particle pressures.

    $$\begin{aligned} (\mathbf {M}_{p}+\mathbf {M}_\mathrm{stab}) \bar{p}^{n+1} = \mathbf {F}_{p,\mathrm{vol}}({\bar{\mathbf{u}}}^{n+1}) \end{aligned}$$

    (74)

  The linear system is solved using LU factorization.

• Loop for the thermal problem.

  • 1. Calculate the heat source due to plasticity r.

  • 2. Calculate the nodal temperatures.

    $$\begin{aligned} \bar{{\theta }}^{n+1} = \bar{{\theta }}^{n} + (\mathbf {M}_\theta ^{n+1})^{-1} \left( \mathbf {f}_{\theta ,\mathrm{ext}}^{n} - \mathbf {P}_{\theta }^{n+1} (\bar{\theta }^{n}) \right) \end{aligned}$$

    (75)

    where ${\mathbf {M}_\theta ^{n+1}}$ is the lumped mass matrix.

Make $n \leftarrow n + 1$ and proceed to the next time step. The step 8 of the loop for the mechanical problem is not necessary for the irreducible formulation.

4 The particle finite element method

The particle finite element method (PFEM) is a numerical method based on the followings ingredients: (1) an updated Lagrangian formulation, (2) the finite element method with displacement/velocity and pressures as main variables, (3) the Delaunay triangulation and (4) the alpha shape method [39, 40]. The combination of the four ingredients has allowed to model with great success fully and quasi incompressible free-surface flows using a Lagrangian framework, solving the mesh distortion limitation of the use of Lagrangian FEM formulations. As PFEM uses a Lagrangian formulation no convective terms and their inherent numerical difficulties are present in the balance equations. Since its original development, the application of PFEM has spread to problems in solid mechanics [41], thermo-mechanics [9, 42], granular materials [43,44,45,46,47], fluid–structure interaction [43, 48], contact of deformable bodies [49] and additive manufacturing processes [50]. Both explicit and implicit time integration schemes can be used for PFEM, although most of the times an implicit time integration has been preferred [51]. The PFEM has been used with an explicit time integration schemes, for example, in [52,53,54] while in [55,56,57] implicit schemes were proposed.

The boundary of the set of particles for the original PFEM is identified with the alpha shape method [58]; in this work the boundary is preserved using a constrained Delaunay triangulation to guarantee mass conservation and to avoid nonphysical increase in the flexural strength of the chip (see Fig. 1 where the purple elements represent the unphysical mass added by the alpha shape). In this work, the internal variables that describe the plastic phenomena are projected from old integration points to the new integration points using a minimum distance criteria to minimize the diffusion of this variables of the mapping from mesh to mesh (see Fig. 2). This is another difference with respect to the original PFEM. The previous ingredients improves the performance of the PFEM when it is applied to the numerical modeling of metal cutting processes as it is shown in [8].

The basics steps of the PFEM used in this work are:

Given a set of particles with a boundary that represent the workpiece at the beginning of the simulation

Set tool incremental displacement = 0.

• 1. Generate a constrained Delaunay triangulation using the particles as nodes.

• 2. Explicitly or implicitly solve the Lagrangian form of the mechanical problem.

• 3. Explicitly or implicitly solve the thermal problem.

• 4. Update particle position, velocities, accelerations. pressures and temperatures.

• 5. Set tool incremental displacement = tool incremental displacement + time step tool displacement.

• 6. If the tool incremental displacement is greater than a critical value (0.002 mm for all the numerical simulations) remesh the workpiece with the insertion of particles at the Gauss point of the mesh whose plastic power is greater than a given tolerance or remove particles that are closer than a critical distance, otherwise go to step 2. Set tool incremental displacement = 0.

Fig. 1

Exterior elements accepted by a non-uniform alpha-shape criterion

Fig. 2

Closest point projection for variables belonging to integration points

The minimum distance between particles is based on the following heuristic criteria:

$$\begin{aligned} {{h}_{\min }}=\max \left\{ \frac{d}{100},\frac{\pi r}{2*20} \right\} \end{aligned}$$

(76)

where ${h}_{\min }$ is the minimum distance between particles, d is the cutting depth, and r is the tool radius. The previous criteria was designed to avoid the use of very small mesh size when tool radius is close to 0 (sharp tool).

5 Johnson–Cook strength model

The constitutive model used for the modeling of metal cutting process should describe the behavior of the material at low and high strain rates. The Johnson–Cook (JC) material model describes the behavior of the metal in a wide ranges of temperatures, strains and strain rates.

The JC strength model [59] is a phenomenological model that describes the flow of the material as the product of three mathematical terms with A being the initial yield strength of the material at room temperature and a reference strain rate.

$$\begin{aligned} \sigma _y+\beta =A\left( 1+\frac{B}{A}\,\varepsilon ^{n} \right) \left( 1+C\ln {\dot{\varepsilon }^{'}} \right) \left( 1-{\theta ^{'}}^{m} \right) \end{aligned}$$

(77)

Here, $\varepsilon$ is the equivalent plastic strain, $\dot{\varepsilon }^{\prime }$ is the strain rate non-dimensionalized by the reference strain rate, $\sigma _y$ denotes the flow stress, $\beta$ the isotropic nonlinear hardening modulus, and B, C, m and n are fitting constants. In Eq. (77), ${\theta }^{\prime }$ is given by

$$\begin{aligned} {{\theta }^{'}}=\frac{\theta -{{\theta }_{0}}}{{{\theta }_\mathrm{melt}}-{{\theta }_{0}}} \end{aligned}$$

(78)

where ${\theta }_{0}$ is the room temperature, ${\theta }_\mathrm{melt}$ is the melt temperature and $\theta$ is the workpiece temperature. The non-dimensionalized plastic strain rate $\dot{\varepsilon }^{'}$ is given by:

$$\begin{aligned} \dot{\varepsilon }^{'} = \frac{\dot{\bar{e}}^\mathrm{p}}{\dot{\varepsilon }_{0}} \end{aligned}$$

(79)

$\dot{\bar{e}}^\mathrm{p}$ is the effective plastic strain rate, $\dot{\varepsilon }_{0}$ is the reference strain rate.

The JC model assumes an independent effect of the strains, strain rates and the temperatures. The expression for the first bracket of Eq. (77) represents the nonlinear hardening law, the expressions of the second terms model the strain rate hardening, and third bracket represents thermal softening, respectively.

Table 1 presents the JC parameters for the AISI 4340 steel used for the numerical simulations.

Table 1 Parameters of the Johnson–Cook constitutive equation for AISI 4340

The non-dimensionalized strain rate $\dot{\varepsilon }^{'}$ of the JC is modified to increase the robustness of the numerical method in the following way:

$$\begin{aligned} \dot{\varepsilon }^{'} = \frac{\dot{\bar{e}}^\mathrm{p} + \dot{\varepsilon }_{0}}{\dot{\varepsilon }_{0}} \end{aligned}$$

(80)

with the previous modification the problem of the convergence of the Newton–Raphson algorithm due to the change of $\ln {\dot{\varepsilon }^{'}}$ from positive to negative when $\dot{\varepsilon }^{'}$ is close to 1 is avoided with a minimum effect on the stress–strain curve.

Details about the implementation of an implicit backward Euler time integration scheme of the JC model are presented in [60, 61] and also included as an Annex A for completeness. For the present study, only a minor modification to the time integration presented in [60, 61] is necessary to include the new non-dimensionalized strain rate.

6 Contact modeling

In this work, the cutting tool moves along the horizontal direction from right to left with a specific cutting speed and cutting depth. The tool is rigid and represented by three curves: one line that represents the rake face, one line that represents the flank face and a circle that represents the tool tip. So the tool is defined by the rake angle $\theta _\mathrm{r}$, the flank angle $\theta _\mathrm{f}$, the tool radius R and the center of the tool tip $(x_\mathrm{c},y_\mathrm{c})$ as shown in Fig. 3.

Fig. 3

Tool regions to identify the contact surface

To identify which surface a particle is in contact with, the tool is divided in 3 regions, as it is shown in Fig. 3. Mathematically, the three region can be represented by the following inequalities:

Region I

$$\begin{aligned}&y-{{y}_{\mathrm{f}}}-\tan ({{\theta }_\mathrm{f}})\left( x-{{x}_{\mathrm{f}}} \right) >0 \end{aligned}$$

(81a)

$$\begin{aligned}&y-{{y}_{\mathrm{c}}}-\tan \left( \frac{\pi }{4}\right) (x-{{x}_{\mathrm{c}}})<0 \end{aligned}$$

(81b)

$$\begin{aligned}&y-{{y}_{\mathrm{c}}}+\tan \left( \frac{\pi }{2}-{{\theta }_\mathrm{f}}\right) (x-{{x}_{\mathrm{c}}})>0 \end{aligned}$$

(81c)

Region II

$$\begin{aligned}&{{\left( x-{{x}_{\mathrm{c}}} \right) }^{2}}+{{\left( y-{{y}_{\mathrm{c}}} \right) }^{2}}< {{R}^{2}} \end{aligned}$$

(82a)

$$\begin{aligned}&y-{{y}_{\mathrm{c}}}+\tan \left( \frac{\pi }{2}-{{\theta }_\mathrm{f}}\right) (x-{{x}_{\mathrm{c}}})<0 \end{aligned}$$

(82b)

$$\begin{aligned}&y-{{y}_{\mathrm{c}}}+\tan ({{\theta }_\mathrm{r}})(x-{{x}_{\mathrm{c}}})<0 \end{aligned}$$

(82c)

Region III

$$\begin{aligned}&y-{{y}_{\mathrm{r}}}-\tan ({{\theta }_\mathrm{r}})\left( x-{{x}_{\mathrm{r}}} \right) <0 \end{aligned}$$

(83a)

$$\begin{aligned}&y-{{y}_{\mathrm{c}}}-\tan \left( \frac{\pi }{4})(x-{{x}_{\mathrm{c}}}\right) >0 \end{aligned}$$

(83b)

$$\begin{aligned}&y-{{y}_{\mathrm{c}}}+\tan ({{\theta }_\mathrm{r}})(x-{{x}_{\mathrm{c}}})>0 \end{aligned}$$

(83c)

where

$$\begin{aligned}&{{x}_{\mathrm{f}}}={{x}_{\mathrm{c}}}+R\sin (\theta _{\mathrm{f}} ) \end{aligned}$$

(84a)

$$\begin{aligned}&{{y}_{\mathrm{f}}}={{y}_{\mathrm{c}}}-R\cos (\theta _{\mathrm{f}} ) \end{aligned}$$

(84b)

and

$$\begin{aligned}&{{x}_{\mathrm{r}}}={{x}_{\mathrm{c}}}-R\cos (\theta _{\mathrm{r}} ) \end{aligned}$$

(85a)

$$\begin{aligned}&{{y}_{\mathrm{r}}}={{y}_{\mathrm{c}}}+R\sin (\theta _{\mathrm{r}} ) \end{aligned}$$

(85b)

For the implicit time integration scheme, a penalty-based approach is used. That approach allows the penetration of workpiece particles inside the tool surface. When a penetration is detected, a force perpendicular to the closest tool surface is added to Eq. (35)(a) as an external force. Mathematically, the contact force using a penalty formulation is represented as

$$\begin{aligned} {{\mathbf {F}}_{\mathrm{N}}}=\kappa {{g}_{\mathrm{N}}}\mathbf {n} \end{aligned}$$

(86)

where $\kappa$ is the penalty parameter, ${g}_{\mathrm{N}}$ is the normal gap and $\mathbf {n}$ is the normal to the contact surface. The penalty parameter used here is:

$$\begin{aligned} \kappa =\frac{m}{{{h}^{2}}} \end{aligned}$$

where m is the mass of the node that is in contact and h is the time interval.

In the case of the explicit time integration scheme, a predictor–corrector strategy (PCS) is used. The PCS allows the penetration of the workpiece particles inside the tool. When the predicted position Eq. (70) of boundary particle penetrates the tool, an acceleration along the normal direction of the closest tool surface is imposed to that particle such that the particle stays over the tool surface for the beginning of the next time step [4, 62], eliminating the unwanted penetration. The PCS was preferred over a penalty approach to avoid that the contact penalty factor puts a narrower restriction on the time step [63].

The normal acceleration correction can be expressed as:

$$\begin{aligned} a_{j}^\mathrm{corr}=\frac{g_{N,j}}{{{h}^{2}}}{{\mathbf {n}}_{j}} \end{aligned}$$

where j represents one of the nodes that penetrates the tool, h is the time interval and ${\mathbf {n}}_{j}$ is the normal vector to the contact surface related to node j. The previous acceleration is added to the acceleration obtained in Eq. (72) for the Step 7 of Sect. 3.2.

7 Examples

Fig. 4

Linear cutting test model

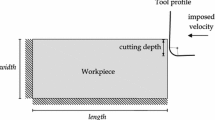
The PFEM with plane strain assumption is applied to the modeling of continuous chip formation process of orthogonal cutting of a rectangular block with cutting depth of 0.1 mm with both implicit and explicit time integration schemes of the balance equations. The workpiece is represented with a rectangle of height 0.5 mm and length 2 mm (see Fig. 4). The strain hardening, strain rate hardening and thermal softening of the AISI-4340 steel are described with the Johnson–Cook flow stress model. The material properties of the flow model and the thermo physical properties are listed in Tables 1 and 2, respectively. The cutting tool is assumed to be rigid and isothermal with a rake angle of 0$^{\circ }$, a flank angle of 5$^{\circ }$ and a tool radius of 0.025 mm. There is no friction for the contact zone between the workpiece and the chip. The melting temperature and the temperature at the beginning of the simulation are set to 1648 K and 293 K, respectively. The cutting speed varies between 1 and 30 m/s.

Table 2 Thermo physical properties of the workpiece

The results obtained will be analyzed and compared in the following sections for terms of computing time, chip shapes, stresses, temperature and cutting forces. Also, a comparison with the displacement/irreducible formulation as a possible form to avoid the implicit calculation of pressures is presented at the end of this section.

7.1 Computing time

Traditionally, most of the research of numerical modeling of metal cutting processes has been carried out with implicit or explicit commercial FEM codes. In some works, a comparison of the numerical simulations of cutting using different commercial simulation codes with implicit and explicit time integration schemes has been carried out in [64]. However, the comparison of the efficiency of the time integration schemes for the previous works is very difficult or has not been carried out, because the FEM formulation, the finite element used, the programming language of the simulation code and the computer where the simulations were run are very different. For example, some simulation programs have a flow formulation (negligible elastic strains) and others an elastoplastic formulation. The comparison of the two previous formulations does not make much sense as the flow formulation cannot predict residual stresses while the elastoplastic can predict residual stresses.

All the numerical simulations presented in this work were run on a Dell computer with an Intel Xeon(R) CPU E5-1660 v3 @ 3.00GHz x 16 processor and 32 GB of RAM (Located in Luleå, Norrbotten. Sweden). The PFEM was programmed using vectorized MATLAB programming for both explicit and implicit schemes. The routines used for explicit and implicit codes used for the calculation of the stresses, mechanical internal forces, mechanical external forces, thermal internal forces, thermal external forces, the inertial forces and the remeshing are exactly the same (see Sect. 3). The differences arise for the update of nodal position and temperatures as shown in Sect. 3.

Table 3 Selection of the optimal number of time steps for the implicit scheme (A cutting speed 20 m/s was used)

Table 4 Computing time at different cutting speeds using a tool displacement of 1 mm

Table 5 Computing time at higher cutting speeds using a tool displacement of 0.5 mm

A total of 34 simulations were performed, 17 with the implicit scheme and the other 17 with the explicit scheme (see Tables 4 and 5 ). In all the simulations, the number of particles varies between 787 at the beginning of the simulations and around 5706 at the end of the simulation, corresponding to a minimum distance between particles of 0.004 mm. The remeshing scheme ensures that the element size is never smaller that 0.004 mm, avoiding that a very small finite element can jeopardize the efficiency of the entire code for explicit simulation. All the implicit simulations need 2500 time steps for a tool advance of 1 mm, such that for a time step the tool advance a distance of 1/2500 mm. The implicit simulations were carried out using 2500 time steps because with that number of time steps corresponds a minimum computing time as it is shown in Table 3 and also corresponds to the minimum number of time steps with which the iterative Newton–Raphson scheme converges. Each mechanical implicit time step needs in average three Newton–Raphson iterations to reach a convergence of forces of $1\times {{10}^{-4}}$, and each thermal implicit time step needs two iterations to reach the same tolerance. The remeshing frequency of the PFEM takes place each 5 implicit time steps where particles are inserted and removed; the frequency of remeshing corresponds to a tool displacement of 0.002 mm. The average computing time of the implicit simulations is 0.89 h, being more or less the same for all cutting speeds (see Table 4). In explicit simulations, the remeshings were carried out after the tool had advanced a distance of 0.002 mm, such that a given simulation implies the same number of remeshings for both implicit and explicit schemes (each of the simulations presented in Table 4 required 500 calls to the remeshing scheme). The computing time for explicit simulations varies between 1.7 h for a cutting speed of 20 m/s up to 37.47 h for a cutting speed of 1 m/s, requiring 110.751 time steps for 20 m/s and 2.199.931 time steps for 1 m/s (see Table 4). Table 5 shows that for velocities greater than around 27 m/s the explicit scheme outperforms the implicit scheme. The results in Tables 4 and 5 show that the correct selection of the implicit or explicit time integration scheme can generate savings of computing of up to 40 times. One way to make the explicit scheme competitive at low speeds is the use of mass scaling, although it should be used with care because it can change the results completely due to the significant increase in the chip inertia. For that reason, mass scaling was not used in this work.

Table 5 presents a comparison at higher cuttings speeds but using a tool displacement of 0.5 mm keeping the other parameters equal to the ones used for the simulations presented in Table 4. The results presented in Table 5 verify that for velocities greater than 27 m/s the explicit schemes outperform the implicit schemes. The reason why higher cuttings speeds were run with a tool displacement of 0.5 mm is to avoid the contact of the chip with the top surface of the piece (self-contact) that take place if the simulations at higher cuttings speeds are run using a tool displacement of 1 mm.

In the following section, we present a comparison of the predicted chip shapes at different cuttings speeds with both implicit and explicit schemes.

7.2 Predicted chip shapes

Figure 5 shows the predicted chip shapes at different cutting speeds using the explicit and implicit scheme, respectively. The curvature of the chip is larger at a higher speed, resulting in the chip coming into contact with the workpiece at a smaller tool displacement. This is due to the fact that at higher cutting speeds the effect of heat diffusion is lower, generating locally higher temperatures and a significant thermal softening of the workpiece material.

The comparison in Fig. 5 shows that the tendency of predicted chip shape of both schemes seems to be the same. A detailed comparison of the chip shapes is presented in Fig. 6 for cutting speeds of 1 m/s and 10 m/s, respectively. Figure 6a shows that at 1 m/s there is a small difference between the predicted deformed chip thickness for close proximity to the primary shear zone. The other difference occurs at the highest point reached by the chip (see Fig. 6a). A comparison of the chip shape made with a smaller mesh size shows that these small differences become smaller. When comparing the shape of the chip predicted at 10 m/s (see Fig. 6b), differences are observed in the neighborhood of the highest point of both internal and external surfaces of the chip. In the same way as for the 1 m/s case, that small difference of the shape of the chip disappears with a small decrease in the size of the mesh (distance between particles). The distance between the particles (mesh size) for all the numerical simulations was the same as the distance used in Fig. 6 because, with that mesh size, the convergence of the cutting and feed forces is obtained as it is shown in Sect. 7.4.

Fig. 5

Chip shapes at different cutting speeds using the explicit (a) and the implicit (b) schemes

Fig. 6

Comparison of the chip shapes at 1 m/s (a) and 10 m/s (b) using implicit and explicit schemes

7.3 Predicted fields

Figures 7 and 10 show the predicted von Mises contour field at 1 m/s and 10 m/s using both implicit and explicit schemes. The maximum value of von Mises stress at 1 m/s is around 1377 MPa (see Fig. 7) and at 10 m/s is around 1344 MPa (see Fig. 10). The difference of the maximum von Misses stress between the numerical schemes is 4 MPa at 1 m/s and 2 MPa at 10 m/s (the same scales and ranges are used in Figs. 7 and 10 to simplify the comparison). These results show the similarities of the prediction between numerical schemes and the thermal softening arises at higher cutting speeds (smaller value of maximum von Mises stress at high cutting speeds).

In Figs. 8 and 11, the predicted contour field of temperature at 1 m/s and 10 m/s using implicit and explicit schemes is shown. At 1 m/s, the maximum value of the temperature is around 686 K and at 10 m/s is around 920 K. As expected, the highest temperature occurs at 10 m/s, due to the shorter time allowed for heat conduction take place, during the generated local heating. The difference between the maximum temperature predicted with implicit and explicit schemes at 1 m/s is 3 K and the difference at 10 m/s is around 30 K. The last measurement is not an indication that the two integration schemes give different results because with a small decrease in the mesh size the temperature differences between the schemes disappear. In addition, the similarity between the results obtained by both schemes can be verified by comparing global variables such as the force as it is presented in Sect. 7.4.

The strain rate field is shown in Figs.  9 and 12 for 1 m/s and 10 m/s, respectively. The strain rate reaches a value of around $5\times {{10}^{4}}$ and $7\times {{10}^{5}}$ 1/s for cutting speeds of 1 m/s and 10 m/s, showing higher strain rates at higher cutting speeds. According to Figs. 9 and 12, the predictions of the strain rate field for the implicit and explicit schemes are very similar, only showing a small difference near the tool tip.

Fig. 7

von Mises stress at 1 m/s: a implicit b explicit

Fig. 8

Temperature field at 1 m/s: a implicit b explicit

Fig. 9

Strain rate field at 1 m/s: a implicit b explicit

Fig. 10

von Mises stress at 10 m/s: a implicit b explicit

Fig. 11

Temperature field at 10 m/s: a implicit b explicit

Fig. 12

Strain rate field at 10 m/s: a implicit b explicit

7.4 Predicted forces

In Figs. 13, 16, 14 and 17, the predicted cutting and feed forces are shown for cutting speeds of 1 and 10 m/s for both implicit and explicit schemes. In Figs. 13, 16, 14 and 17, both the implicit and explicit schemes tend to the same value for both cuttings speeds; the only difference between the schemes is the noise which is typical of explicit integration schemes (No damping was used to attenuate noise for explicit simulations). In Fig. 15, a comparison of the prediction of the cutting force at 10 m/s with both explicit and implicit scheme is presented; a low-pass filter was used for the explicit signal to remove the nonphysical noise as it is suggested in [65]. The previous figure shows clearly that both schemes predict exactly the same cutting force.

Table 6 shows the predicted cutting and feed forces for the cutting speeds shown in Table 4 using implicit and explicit schemes. The value presented in Table 6 corresponds to the average value at the steady state. Table 6 shows that the cutting force decreases slightly with increasing speed and then remains constant. Meanwhile, the same table shows that the feed force increases with increasing cutting speed up to a speed of 13 m/s and then remains almost constant. The difference between the predictions with implicit and explicit simulations is always less than 3.5 N and in terms of percentage is less than 3% as it is shown in Table 6 . This comparison shows that the two schemes yields equivalent results. However, the advantage of implicit scheme over the explicit is clearly seen in terms of computational time at velocities smaller than 27 m/s as is shown in Sect. 7.1. At velocities higher that 27 m/s the explicit schemes is a better option in terms of computing time.

7.5 Locking with the irreducible formulation

In the following section, results with the irreducible/displacement based formulation are presented. The goal of an irreducible formulation is to avoid the implicit calculation of the pressure field of the explicit scheme developed in Sect. 2.4.3. and as a result decrease the computing time of the explicit scheme.

In Figs. 18 and 19, a comparison of the predicted cutting and feed forces using the mixed and the irreducible/displacement formulation is shown with an explicit time integration scheme. The irreducible formulation over-predicts the cutting force with around 10 N (6% higher); meanwhile, the feed forces are correctly predicted. The previous effect is the well-known volumetric locking problem due to plasticity of a finite element formulation with linear triangle finite elements. The previous results show the importance of the correct selection of the finite element when modeling metal cutting, since a wrong selection of the element can generate large prediction errors of important variables for cutting such as forces. If an implicit formulation with the irreducible formulation is used, an over-prediction in the cutting of around 6% similar to the ones obtained with the explicit one is obtained.

Figures 20 and 21 show pressure contours for a cutting speed of 10 m/s after a cutting length of 1mm, where the serious deficiencies of the standard formulations and the huge improvement achieved with the stabilized mixed formulation are evident [66]. Numerical examples in Fig. 21 show that the mixed formulation is free of pressure oscillations; meanwhile, in Fig. 20 the irreducible formulation shows the typical nonphysical spurious oscillations of the pressure field.

Fig. 13

Predicted cutting forces at 10 m/s

Fig. 14

Predicted feed forces at 10 m/s

Fig. 15

Predicted cutting forces at 10 m/s. The explicit force was filtered to remove the noise

Fig. 16

Predicted cutting forces at 1 m/s

Fig. 17

Predicted feed forces at 1 m/s

The motivation of this section is to quantity the error of the prediction of variables like cutting forces, pressure among others made when an irreducible formulation is used as some researchers [67,68,69,70] continue to use linear triangle finite elements to model metal cutting processes knowing that this finite element is prone to locking phenomena due to plasticity.

8 Discussion and conclusions

Metal cutting or machining is a process in which a thin layer of metal, the chip, is removed by a wedge-shaped tool from a large body. Cutting is a complex physical phenomena where adiabatic shear bands, excessive heating, large strains and high strain rates are present. Cutting speed plays an important role for chip morphology, cutting forces, energy consumption and tool wear. Due to the complex physical process of cutting, machining processes is one of the most challenging industrial problems to be analyzed from the numerical simulation point of view. To optimize and predict industrial machining an accurate, robust and efficient numerical simulation tool is needed. Here implicit and explicit numerical integration schemes for machining simulations are investigated with the goal to give insight of the best choices for accuracy and efficiency. Two time integration schemes of the balance equations were implemented within the PFEM framework and applied to the numerical modeling of metal cutting processes. Each of the schemes was tested at 17 cutting speeds, such that a total of 34 numerical simulations were carried out. The results presented here show that both schemes predicted the same value of stresses, temperature, strain rates and forces. The difference between the numerical schemes is evident when a comparison of the computing times is carried out. The results show that a selection of the implicit time integration scheme saves 40 times regarding computing time at a cutting speed of 1 m/s (low speed machining). Meanwhile, at 30 m/s the computing time with the explicit scheme is 75% of the time needed for the implicit scheme. As such, the excessive computing time attributed to the numerical simulation of cutting is not only attributed to the remeshing, but also to an incorrect selection of the time integration scheme. This results can be used as a guide that allows people who simulate cutting to select the time integration scheme that results in a minimum computing time. For example, for cutting under similar conditions to the ones presented in this work, the implicit scheme is recommend for cutting speeds lower than 27 m/s and the explicit one is recommend for velocities higher than 27 m/s.

At the same time, the results show how harmful it is to use a displacement/irreducible formulation with linear triangular finite elements for the numerical simulations of metal cutting in terms of the over-prediction of cutting forces and the nonphysical spurious oscillations of the pressure field. For example, the spurious oscillations of the pressure field of the irreducible formulation would not allow the use of a failure criteria that depends on the pressure-deviatoric stress ratio. The previous results allow to quantify the error that some researchers [67,68,69,70] are committing when they use linear triangle finite elements to model metal cutting processes knowing that this finite element is prone to locking phenomena due to plasticity. The problem is that for some regions of the chip the irreducible formulation will predict compression pressures while in reality they are in tension thus predicting no damage where damage should develop. The previous situation will invalidate the application of the irreducible formulation with linear triangle finite elements to the numerical modeling of segmented chip, where fracture criteria are of paramount importance. The stabilized mixed formulation with linear displacement and linear pressure for both the explicit and implicit time integration solves the problems of the irreducible formulation mentioned above. The previous results show the relevance of the selection of the finite element formulation used for the numerical modeling of metal cutting process.

The results presented here show that the PFEM solves the problems of mesh distortion and diffusion, typical of standard FEA, placing the PFEM in a competitive position with the FEM. A literature overview allows us to conclude that, among the new numerical methods developed for orthogonal cutting simulations, the only one that has been tested to model cutting with implicit and explicit time integration schemes is the PFEM. The other numerical methods have only implement one of the time integration schemes [30, 71]. The development of a code with both implicit and explicit integration schemes will allow the activation of an explicit scheme when an implicit scheme is not able to converge, increasing in this way the robustness of the numerical code.

Table 6 Predicted cutting and feed forces using implicit and explicit formulations. Average difference for cutting forces: 0.52% and feed forces 2.45%

Fig. 18

Comparison of cutting forces at 10 m/s using a mixed and a irreducible formulations

Fig. 19

Comparison of feed forces at 10 m/s using a mixed and a irreducible formulations

Fig. 20

Pressure field at a cutting speed of 10 m/s using the irreducible formulation

Fig. 21

Pressure field at a cutting speed of 10 m/s using the mixed formulation

In summary, the research carried out in this work allows to conclude that the implicit scheme is recommend to be used at velocities lower than 27 m/s for metal cutting problems with similar mesh size, number of finite elements, contact parameters and material model to the ones used in this work because its computational efficiency is better compared to the explicit scheme; meanwhile, the explicit is the option to choose for velocities higher than 27 m/s.

Appendices

Thermo-elastoplasticity model at finite strains

1.1 Constitutive thermo-hyperelastoplastic model

In Box 1, we present the main equations of the thermo-mechanical $J_2$ flow model for rate-dependent plasticity that will be used in this work.

Box 1 Coupled thermo-mechanical $J_2$ flow theory. Rate-dependent plasticity

COUPLED THERMO-MECHANICAL $J_2$ FLOW THEORY

RATE DEPENDENT PLASTICITY

1. Free energy function.

$\hat{\psi } = \hat{U}(J^e)+\hat{W}(\bar{\mathbf{b}}^e)+\hat{K}({{\bar{e}}\,}^p,\theta )$

2. Kirchhoff stress.

$\pmb {\tau } = J^e\,p\,{\mathbb {1}}+\mathbf {s}$

$p \,{:=}\, \kappa \, \ln (J^e)$

$\mathbf {s} \,{:=}\, \mu \,\mathrm{dev}({\bar{\mathbf{b}}}^e)$

3. Von Mises yield criterion.

$\Phi (\tau ,{{\bar{e}}\,}^p,\theta )=\Vert \mathrm{dev}(\tau )\Vert -\sqrt{\dfrac{2}{3}}\left( \sigma _y+\beta \right) (1+g({{\overset{.}{\mathop {{\bar{e}}}}\,}^{p}})\le 0$

4. Evolution equations $\lambda >0,\;\;\Phi \le 0,\;\;\lambda \,\Phi =0$

$\mathcal {L}_v\mathbf {b}^e = -2\,\lambda \,J^{-\frac{2}{3}}\dfrac{1}{3}{} tr (\bar{\mathbf{b}}^e)\mathbf {n}$

${\dot{\bar{ e}}\,}^p = -\lambda \,\partial _{\beta }\Phi (\tau ,{{\bar{e}}\,}^p,\theta )$

The definition of the variables that appear in this box

are explained in references [38, 72, 73].

In Box 1, the free energy is uncoupled into volumetric, deviatoric and isotropic hardening potential described by the functions $\hat{U}(J)$, $\hat{W}(\mathbf {b}^e)$ and $K({{\bar{e}}^{p}},\theta )$, respectively.

$$\begin{aligned} \hat{U}(J)= & {} \dfrac{1}{2}\kappa \ln ^2(J) \nonumber \\ \hat{W}(\mathbf {b}^e)= & {} \dfrac{1}{2}\,\mu \left[ tr(\bar{\mathbf{b}}^e)-3 \right] = \dfrac{1}{2}\,\mu \left[ tr(\bar{\mathbf{C}}^e)-3 \right] \nonumber \\ K({{\bar{e}}^{p}},\theta )= & {} \frac{B{{({{{\bar{e}}}^{p}})}^{n+1}}}{n+1}\left[ 1-{{\left( \frac{\theta -{{\theta }_{0}}}{{{\theta }_\mathrm{melt}}-{{\theta }_{0}}} \right) }^{m}} \right] \end{aligned}$$

(87)

where $\mu >0$ and $\kappa >0$ can be interpreted as the shear modulus and the bulk modulus. The function $K({{\bar{e}}\,}^p,\theta )$ is a nonlinear function of the equivalent plastic strain ${{\bar{e}}\,}^p$ and temperature $\theta$ which describes the isotropic strain hardening via the relation $\beta =-\partial _{{{\bar{e}}\,}^p}K({{\bar{e}}\,}^p,\theta )$. The K presented in Eq. (87) corresponds to the isotropic hardening potential of the Johnson–Cook material model presented in Sect. 5.

The g function presented in Box 1 represents the rate dependency of the Johnsoon–Cook material model. The g function is given by

$$\begin{aligned} g({{\overset{.}{\mathop {{\bar{e}}}}\,}^{p}})=1+C\ln (\frac{{{{\dot{\bar{e}}}}^{p}}+{{{\dot{e}}}_{0}}}{{{{\dot{e}}}_{0}}}) \end{aligned}$$

1.2 Implicit backward Euler integration scheme

In Box 2, the integration flowchart for the backward Euler method is presented.

Box 2 Implicit backward Euler integration flowchart for thermo-elastoplastic models

BACKWARD EULER INTEGRATION FLOWCHART

1. Thermoelastic trial state:

Initial data: $\;\bar{\mathbf{b}}^e_n,\,{{\bar{e}}\,}^p_n$

Current values of $\mathbf {F}_{n,n+1},\, \theta _{n+1}, \;$ where $\;\bar{\mathbf{F}}_{n,n+1}=J^{-\frac{1}{3}}\mathbf {F}_{n,n+1}$

Let $\;\; f^{trial}_{n+1} = \left\| \mathbf {s}^{trial}_{n+1}\right\| -\sqrt{\dfrac{2}{3}}\left( \sigma _{y,n+1}+\beta _{n+1}({{\bar{e}}}^{\,p}_n)\right)$

IF $f^{trial}_{n+1}\le 0\,: \;\;$ Set $\;\;(\bar{\mathbf{b}}^e_{n+1},\,{{\bar{e}}\,}^p_{n+1},) = (\bar{\mathbf{b}}^{e,trial}_n,\,{{\bar{e}}\,}^p_n)\;$ and EXIT

ELSE:

2. Consistency parameter:

Set $\bar{\mu } = \dfrac{\mu }{3}{} tr (\bar{\mathbf{b}}^{e,trial}_{n+1})$

Compute $\Delta \lambda _{n+1}$ by solving:

$g(\Delta \lambda _{n+1}) = f^{trial}_{n+1} - 2\,\Delta \lambda _{n+1}\,\mu \,\dfrac{1}{3} tr (\bar{\mathbf{b}}^{e,trial}_{n+1})$

$+ \sqrt{\dfrac{2}{3}}\left( \sigma _{y,n}+\beta _{n}({{\bar{e}}}^{\,p}_n)\right) *{{g}_{n}}(\dot{\bar{e}}_{n}^{p})$

$-\sqrt{\dfrac{2}{3}}\left( \sigma _{y,n+1}+\beta _{n+1}({{\bar{e}}}^{\,p}_{n+1})\right) {{g}_{n+1}}(\dot{\bar{e}}_{n+1}^{p}) = 0$

Return mapping:

Set $\mathbf {n}_{n+1} = \dfrac{\mathbf {s}^{trial}_{n+1}}{\Vert \mathbf {s}^{trial}_{n+1}\Vert }$ and update

$\mathbf {s}_{n+1} = \mathbf {s}^{trial}_{n+1} - 2\,\Delta \lambda _{n+1}\,\mu \,\dfrac{1}{3} tr (\bar{\mathbf{b}}^{e,trial}_{n+1})\mathbf {n}_{n+1}$

${\bar{e}\,}^{p}_{n+1} = {\bar{e}\,}^p_n - \lambda _{n+1}\Delta t\sqrt{\dfrac{2}{3}}$

3. Update the intermediate configuration by the closed form formula:

$\bar{\mathbf{b}}^e_{n+1} = \bar{\mathbf{b}}^{e,trial}_{n+1} - 2\,\Delta \lambda _{n+1}\,\dfrac{1}{3}{} tr (\bar{\mathbf{b}}^{e,trial}_{n+1})\mathbf {n}_{n+1}$

END

The definition of the variables that appear in this box are

explained in references [38, 72, 73].

Stiffness matrix

In this section, the formulas for the stiffness matrix for the standard and mixed formulations are presented.

1.1 Stiffness matrix irreducible formulation

The element stiffness matrix related to node I and J is given by (omitting the $n+1$ subscript and the iteration superscript (i))

$$\begin{aligned} \mathbf {K}_{IJij}^{(e)}=\mathbf {K}_{\mathbf {uu},IJij}^{geo,(e)}+\mathbf {K}_{\mathbf {uu},IJij}^{\mathrm{mat},(e)} \quad i,j=1,2 \end{aligned}$$

(88)

where the first term is the geometric stiffness matrix, $\mathbf {K}_{\mathbf {uu},IJij}^{\mathrm{geo},(e)}$, and the second, $\mathbf {K}_{\mathbf {uu},IJij}^{\mathrm{mat},(e)}$, the material tangent stiffness matrix.

The material tangent stiffness term is given by

$$\begin{aligned} \mathbf {K}_{\mathbf {uu},abij}^{\mathrm{mat},(e)}=\int \limits _{{{v}^{(e)}}}{\sum \limits _{k,l=1}^{2}{\left( \frac{\partial {{N}_{a}}}{\partial {{x}_{j}}}{{\mathbf {c}}_{ijkl}}\frac{\partial {{N}_{b}}}{\partial {{x}_{l}}} \right) }\mathrm{d}v}\quad i,j=1,2 \end{aligned}$$

(89)

and the geometric part of the tangent matrix is given by

$$\begin{aligned} \mathbf {K}_{\mathbf {uu},abij}^{geo,(e)}=\int \limits _{{{v}^{(e)}}}{\sum \limits _{k,l=1}^{2}{\left( \frac{\partial {{N}_{a}}}{\partial {{x}_{k}}}{{\sigma }_{kl}}\frac{\partial {{N}_{b}}}{\partial {{x}_{l}}} \right) }{{\delta }_{ij}}\mathrm{d}v}\quad i,j=1,2 \end{aligned}$$

(90)

In Eqs. (89) and (90), $N_a$ is the shape function in node a, $N_b$ is the shape function in node b, $\mathbf {c}_{ijkl}$ is the consistent (algorithmic) moduli, ${\sigma }_{kl}$ is the Cauchy stress tensor obtained with the irreducible formulation and ${\delta }_{ij}$ is the Kroneker delta. The consistent moduli for an elastic element are

$$\begin{aligned} \mathbf {c}=\mathbf {c}^{\mathrm{ela}} = \kappa \frac{\ln (J)}{J}\left[ \mathbf {I}\otimes \mathbf {I}-2\mathbf {i} \right] +\kappa \frac{\left( 1-\ln (J) \right) }{J}\mathbf {I}\otimes \mathbf {I}+\bar{\mathbf {C}} \end{aligned}$$

where $\mathbf {I}$ is the second-order identity tensor, $\mathbf {i}$ is the fourth-order identity tensor and $\bar{\mathbf {C}}$ is the deviatoric component of the spatial elasticity tensor (see [38]).

For a plastic element, the consistent moduli are

$$\begin{aligned} \mathbf {c}={{\mathbf {c}}^{pl}}={{\mathbf {c}}^\mathrm{ela}}-{{\beta }_{1}}{{\mathbf {c}}^\mathrm{ela}}-2\bar{\mu }{{\beta }_{3}}\mathbf {n}\otimes \mathbf {n}-2\bar{\mu }{{\beta }_{4}}\mathbf {n}\otimes \mathrm{dev}({{\mathbf {n}}^{2}}) \end{aligned}$$

where ${\beta }_{1}$, ${\beta }_{3}$, ${\beta }_{4}$, $\bar{\mu }$ and $\mathbf {n}$ has the same meaning as in [38].

1.2 Stiffness matrix mixed formulation

For a mixed finite element, the material and geometric stiffness matrix are given by:

$$\begin{aligned} {}^\mathrm{mix}\mathbf {K}_{\mathbf {uu},IJij}^{\mathrm{mat},(e)}=\int \limits _{{{v}^{(e)}}}{\sum \limits _{k,l=1}^{2}{\left( \frac{\partial {{N}_{I}}}{\partial {{x}_{j}}}\mathbf {c}_{ijkl}^\mathrm{mix}\frac{\partial {{N}_{J}}}{\partial {{x}_{l}}} \right) }\mathrm{d}v}\quad i,j=1,2 \end{aligned}$$

(91)

and

$$\begin{aligned} ^\mathrm{mix}\mathbf {K}_{\mathbf {uu},IJij}^{geo,(e)}=\int \limits _{{{v}^{(e)}}}{\sum \limits _{k,l=1}^{2}{\left( \frac{\partial {{N}_{I}}}{\partial {{x}_{k}}}{{\sigma }_{kl}}\frac{\partial {{N}_{J}}}{\partial {{x}_{l}}} \right) }{{\delta }_{ij}}\mathrm{d}v}\quad i,j=1,2 \end{aligned}$$

(92)

where $\mathbf {c}^\mathrm{mix}$ for an elastic is given by

$$\begin{aligned} \mathbf {c}^\mathrm{mix}=\mathbf {c}^{\mathrm{ela,mix}} = p\left[ \mathbf {I}\otimes \mathbf {I}-2\mathbf {i} \right] +\bar{\mathbf {C}} \end{aligned}$$

where p is the pressure obtained from the mixed formulation, and for a plastic element $\mathbf {c}^\mathrm{mix}$ is

$$\begin{aligned}&\mathbf {c}^\mathrm{mix}={{\mathbf {c}}^{\mathrm{pl,mix}}}={{\mathbf {c}}^{\mathrm{ela,mix}}}-{{\beta }_{1}}{{\mathbf {c}}^{\mathrm{ela}}}-2\bar{\mu }{{\beta }_{3}}\mathbf {n}\otimes \mathbf {n}\\&\quad -2\bar{\mu }{{\beta }_{4}}\mathbf {n}\otimes \mathrm{dev}({{\mathbf {n}}^{2}}) \end{aligned}$$

In Eq. (92), the Cauchy stress ${\sigma }_{kl}$ is calculated with the pressure obtained from the mixed formulation.