Waterfall Algorithm as a tool of investigation the geometrical features of granular porous media

Abstract

The paper describes the so-called Waterfall Algorithm, which may be used to calculate a set of parameters characterising the spatial structure of granular porous media, such as shift ratio, collision density ratio, consolidation ratio, path length and minimum tortuosity. The study is performed for 1800 different two-dimensional random pore structures. In each geometry, 100 individual paths are calculated. The impact of porosity and the particle size on the above-mentioned parameters is investigated. It was stated in the paper, that the minimum tortuosity calculated by the Waterfall Algorithm cannot be used directly as a representative tortuosity of pore channels in the Kozeny or the Carman meaning. However, it may be used indirect by making the assumption that a unambiguous relationship between the representative tortuosity and the minimum tortuosity exists. It was also stated, that the new parameters defined in the present study are sensitive on the porosity and the particle size and may be therefore applied as indicators of the geometry structure of granular media. The Waterfall Algorithm is compared with other methods of determining the tortuosity: A-Star Algorithm, Path Searching Algorithm, Random Walk technique, Path Tracking Method and the methodology of calculating the hydraulic tortuosity based on the Lattice Boltzmann Method. A very short calculation time is the main advantage of the Waterfall Algorithm, what meant, that it may be applied in a very large granular porous media.

1 Introduction

It is obvious that the length of a path in a non-empty space is usually higher than the length of this space measured in the same direction. The importance of this fact increases in relation to the decrease in the available free space and to the increase in the degree of geometry complication of the considered space. Different effects resulting from the increase in the relative path lengths are known in geodesy [1], transport [2], logistic [3], robotics [4], fluid mechanics [5], thermodynamics [6], energetics [7], electrochemist [8], physic and astronomy [9], medicine [10], ecology [11] and other areas. The relative elongation of a path in a limited space is known as the tortuosity. This parameter is defined as follows:

$$\begin{aligned} \tau =\frac{L_p}{L_0} \end{aligned}$$

(1)

where $\tau$ it the tortuosity (–), $L_p$ is the path length (m) and $L_0$ is a distance, for which the path is calculated (m).

Fig. 1

Application of the tortuosity concept in the theory of fluid flows through porous media: correction the piezometric head (a), correction the filtration velocity (b)

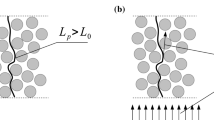
The tortuosity idea (but not the name of this parameter) was introduced by Kozeny [12], to correct the way of calculating the piezometric head occurring during fluid flows through porous media (Fig. 1a). Kozeny stated that the unitary piezometric head (or pressure drop) is in fact smaller when it is calculated for a real path length, and not for the total thickness of the porous body. In turn, Carman [13] used the same parameter to calculate the real velocity in pore channels. He stated that this velocity is higher than the filtration velocity (Fig. 1b). The investigations performed by these two researchers resulted in the so-called Kozeny–Carman equation

$$\begin{aligned} -\frac{{{d}}p}{{{d}}x} = C_{KC} \tau _f S_{0,Carman}^2 \frac{(1-\phi )^2}{\phi ^3}, \end{aligned}$$

(2)

where p is the pressure (Pa), x is a coordinate along which the pressure drop occurs (m), $\tau _f$ is the tortuosity factor (–) defined as the square of the tortuosity $\tau$ (–), $C_\mathrm{KC}$ is a pore shape factor (–) (a model constant, usually equal to 5.0 [13]), $S_{0,Carman}$ is the specific surface of the porous body in Carman meaning (1/m) (it is the inner surface of the solid body divided by the total volume of the solid part), $\phi$ is the porosity (–). If the tortuosity is directly calculated on the basis of the shapes of pore channels, than it is called the geometric or geometrical tortuosity. Note that the tortuosity factor is not the same than the tortuosity. In some papers, this issue is not underlined well enough and the Reader may be confused. Moreover, quite often both of these parameters are denoted by the same symbol, usually $\tau$ (like, e.g. in works [14] and [15]).

The tortuosity concept was very quickly applied in the theories related to the processes having a diffusional character (overall in meaning of Fourier’s law, Fick’s law, laws describing Markov processes or other). Knudsen (1928) proposed a following relationship (cited after [16] and [17]):

$$\begin{aligned} D_\mathrm{eff}=D \frac{\varepsilon }{\tau _f}, \end{aligned}$$

(3)

where $D_\mathrm{eff}$ is the effective diffusivity (m$^2$/s), D is the intrinsic diffusivity of the conductive phase (m$^2$/s), $\varepsilon$ is the volume fraction of the conductive phase (–). The concept of the effective diffusivity gave rise to a new group of methods serving to calculate the tortuosity (in this context called the diffusion tortuosity). Currently, different numerical methods are usually applied to investigate diffusion processes [15, 18]. The main advantages of this approach are the mathematical simplicity of the diffusion equation, relatively simple implementation and low demand of computational power in comparison with other methods, particularly with the Lattice Boltzmann Method mentioned below.

After the popularization of modern computational methods, new possibilities to calculate the tortuosity appeared. Koponen et al. [19, 20] proposed a methodology based on the Lattice Boltzmann Method (LBM). In this approach, the tortuosity (called usually the hydraulic tortuosity) is defined as follows

(4)

where $\left| v\right|$ is the absolute value of local flow velocity obtained for a creeping flow, $v_x$ is the X-component of velocity (where X is the direction of main flow), is spatial average over the pore space. The LBM-based methodology is usually applied in different, randomly generated pore structures consisting of rectangles (in 2D) or cuboids (in 3D) [21,22,23]. Other shapes of obstacles are taken into account relatively seldom (e.g. spherical particles like in [24]), mainly due to high requirements of lattice quality. The main disadvantage of the described methodology is a huge computational cost required to perform a LBM simulation, what limits its application to relatively small scale systems. In general, the velocity field needed to applicate Eq. (4) may be obtained with the use of a few other numerical techniques, like the Finite Volume Method (FVM), the Immersed Boundary Method (IBM), the Finite Element Method (FEM) or even the Finite Difference Method (FDM). However, the level of difficulty is even greater due to the requirements related to the quality of numerical grids. The methodology based on LBM simulations was also used in a previous work of the author (2019) [25]. The main result of those investigations was a new function serving to calculate tortuosity on the basis of the porosity and the size of a structural element forming the solid part of the porous body. It should be noted that if a velocity field is available, than the streamlines may be also calculated. Consequently, because they represent directly the paths lengths, a new kind of tortuosity may be obtained, the so-called streamline tortuosity.

More information can the Reader find in the review paper [26], in which 203 publications about tortuosity were analysed and summarized. All the available methods were divided into group having similar features and clearly compared in tables and figures.

Summarising the basic information, the tortuosity may be obtained as follows:

• (a) By the use of experimental-based methods. Here, the Computed Tomography and Image Analysis (CT/IA) is usually applied [15, 27]. Sometimes other methods are proposed, e.g. those based on acoustic [28], electrical [29] or optical [30] phenomena.

• (b) By the analysis of the pore channels geometry and the application of Eq. (1). The computational space may be expressed directly in a form of the vector geometry, or indirectly, by a grid of nodes, cells, elementary volumes, pixels or voxels. Algorithms may have analytical origins or may be based on different discrete techniques. Different methods based of the Random Walk technique developed by Pearson in 1905 [31] are here quite often applied.

• (c) By the analysis of diffusional properties of porous media and the application of Eq. (3).

• (d) By the analysis of transportation properties of fluids flowing through pore channels and the application of Eq. (4). Alternatively, lengths of streamlines may be calculated to obtain the streamline tortuosity.

• (e) By the use of hybrid methods combining different approaches described in previous items, e.g. CT/IA techniques needed to obtain the geometry with Random Walk algorithm serving to calculate lengths of particular paths.

• (f) By the use of empirical formulas available in the literature (but usually obtained from methodologies mentioned above), it is assumed that the tortuosity is a direct function of the porosity [32]. The impact of other factors is rarely taken into account. A short review of such formulas dedicated for granular beds was presented in a previous work [33] and because of that is not repeated here.

The hereby paper is related to geometrical methods, particularly these in which lengths of pore channels are calculated on the basis of different iterative numerical algorithms. The main area of interest is the granular beds, that is the porous media consisting of circular (in 2D) and spherical particles (in 3D). A short review of the most interesting works is presented below.

Nakashima and Watanabe [34] applied the Random Walk Method to calculate the tortuosity in a granular bed consisting of spherical particles with the average diameter equal to 2.11 mm and the standard deviation of 0.06 mm. The geometry of the porous medium is described by a discrete lattice of voxels. The walker executes a random jump to one of the six nearest unoccupied sites. If the randomly selected site or voxel is occupied by an obstacle or solid, the jump is not performed.

Delarue and Jeulin [35] analysed the morphological structure of six composite materials containing aggregates of spherical inclusions based on the data obtained by X-ray microtomography. The tortuosity was calculated in every space direction on the basis of paths consisting of linear sections (in the space between spheres) and arcs (on sphere surfaces). These calculations were performed for three-dimensional numerical grids consisting of voxels. Authors stated that the tortuosity calculated in such a way is very low, usually between 1.03 and 1.05. The idea presented by Delarue and Jeulin is very similar in character to the Waterfall Algorithm presented in the hereby paper. However, their description of the method is very short and quite general. It consists only of few sentences within which neither details nor features or properties are commented on.

Boudreau and Meysman [36] proposed a geometrical tortuosity model for predicting the tortuosity in marine muds represented by randomly located and arranged in layers, nonoverlapping disks. In their model, a virtual walker is defined the one which attempts to move through the pore space in a direction parallel to the cylindrical axis of the disks. According to the model, if the walker is in the pore space between the disks, it will simply move along the main direction. If the walker encounters a disk, it will choose a random direction and walk a straight line along the disk surface, until it reaches the edge of the disk and the movement in the main direction will be again possible. The model is analytical and is destined only for obstacles having one shape.

Huang et al. [37] propose the so-called Random Walking Particle Tracking (RWPT) method. The random walk of a particle in an advection velocity field is modelled by a stochastic differential equation containing terms responsible for the particle displacement, the advection displacement and a random walk displacement. The geometry is saved in a form of structural grid, in which each cell represents the pore space or the solid part of the porous medium. Walkers follow straight trajectory and change this trajectory only as a result of collisions with walls.

Amien et al. [38] used the Simple Neurite Tracer (SNT) to analyse the tortuosity in four kinds of digital samples of porous rock model of the 256$\times$256 pixels size. NST is a plugin of ImageJ software designed to allow easy semi-automatic tracing of neurons or other filament-like structures (e.g. microtubules, blood vessels) through either 2D images or 3D image stacks [39]. The details related to the used method are not supplied, but on the home page of the used software we can read that the A-Star algorithm is implemented in this code.

Cao et al. [40] presented an analytical model of calculating the tortuosity in cement-based materials containing aggregates with spherical or quasi-spherical shape. Paths are expressed as straight lines. However, when the path meets an obstacle, it bypasses it and returns to the original trajectory. Their results seem to be debatable, because the obtained tortuosity values are very high (between 20 and 50) and this does not correspond with the schemas presented in this work, in which paths are relatively straight.

Gong et al. [41] used micro-CT techniques and Image Analysis to calculate different parameters characterising the geometrical features of several kinds of sandstones. Some of them were defined by Authors. The pore topological properties were analysed with the use of a pore network model with various voxel sizes.

Usseglio-Viretta et al. [42] calculated the tortuosity using a graph analogy: graph nodes are the pore segments’ centres of mass, while graph edges connect nodes that correspond to adjacent pore segments in contact. The paths lengths were calculated with the Dijkstra algorithm. Authors investigated different 2D and 3D pore structures representing the material of battery electrodes with a wide range of porosity. It is the most complicated algorithm from all the presented here.

The hereby paper is a part of a larger investigation, in which various methods that may be used to calculate the tortuosity in porous media, particularly in granular beds, are tested or developed. In 2009, the so-called Path Tracking Method [43] was developed by the author. In this method, it is assumed that in a 3D bed tetrahedral structures formed by neighbouring particles can be always found. Having established the locations and sizes of particles which form subsequent tetrahedrons, different geometrical parameters (such as the local length of a path) may be calculated. The sum of all these local lengths gives the path length ($L_p$), which can be used to calculate the tortuosity. A comparison of approaches based on the Path Tracking Method and the other one in which the LBM simulations are used was presented in paper [44]. In paper [25], the hydraulic tortuosity based on a velocity field obtained by LBM simulations was calculated. A new function for calculating the tortuosity on the basis of porosity and the normalized size of a structural element forming the solid part of the porous body was proposed. In paper [33], two algorithms acting on a matrix of zeros and ones represented the porous body geometry were tested: A-Star Algorithm and the Path Searching Algorithm developed by the author. It was stated that the tortuosity established with the A-Star Algorithm is underestimated in comparison with the tortuosity (hydraulic or geometric) calculated by alternative numerical techniques; the tortuosity established by the Path Searching Algorithm is overestimated in comparison with the tortuosity calculated by alternative numerical techniques; the results obtained with the use of the Path Searching Algorithm are in a good agreement with the values calculated with the use of different, popular empirical formulas. In the hereby paper, the so-called Waterfall Algorithm is described. The algorithm was developed by the author in 2019. The main aim of the investigations presented here is to recognize the features and possibilities of this algorithm as well as its potential.

The discussion about the Waterfall Algorithm is divided into two parts. In the first stage, a comparison with binary algorithms described in paper [33] as well as with the Radom Walk technique is presented (Sec. 3.1). Additionally, the number of paths needed to obtain a representative value of the tortuosity for a 2D geometry is studied (Sec. 3.3). In this part, a comparison with the results obtained in the paper [44] is also shown (Sec. 3.2). After this stage, a set of new geometry indicators of ratios is proposed (Sec. 3.4). In the second part of the paper, a parametric study is described, in which 1800 pore structures with different porosities and particle size are analysed (Sect. 3.5). In that part, the relationships between porosity, particle size and geometry indicators as well as the tortuosity are shown.

2 Materials and methods

2.1 Materials

In the investigations, randomly generated porous beds with different porosity and particle size are used. It is assumed that the domain length is equal to 1 m in each direction. The particles are non-overlapping, and the minimum distance equals zero. In the main part of investigations, a set of 1800 pore structures with porosities between 0.5 and 0.9 was used. The particle sizes vary from 0.005 to 0.09 m. The geometry is generated by the use of a software written in the Fortran programming language.

2.2 Waterfall Algorithm

The Waterfall Algorithm is the author’s algorithm for searching as short as possible paths in granular beds consisting of spherical or circular particles, saved in the form of a vector geometry (Fig. 2). The geometry may be generated by appropriate random algorithms or by the use of the Discrete Element Method. Both ways were tested, and it was stated that there is no difference in acting the algorithm proposed. Only one condition is that particles forming a bed should not overlapping each other.

Fig. 2

The main idea of the Waterfall Algorithm

The algorithm covers the following steps:

• (a) Determining the location of the so-called Start Point.

• (b) Drawing a line from the Start Point parallel to the chosen direction of the Cartesian coordinate system (here to X direction).

• (c) Searching for the first sphere or circle having the common point with the line.

• (d) Calculating coordinates of the point ($P_\mathrm{in}$), in which the line enters into the current sphere or circle.

• (e) Calculating coordinates of the point ($P_\mathrm{out}$), in which the path leaves the current sphere or circle. This point is always located on a plane perpendicular to the main direction and passing through the centre of the current sphere or circle.

• (f) Calculating coordinates of intermediate points linking $P_\mathrm{in}$ and $P_\mathrm{out}$ located on the sphere surface or the circumference of the circle.

• (g) Repeating the algorithm starting with step (b). This time the subsequent lines (here called the current lines) are drawn from $P_\mathrm{out}$ points. In the paper, all points from which new lines are drawn (namely, Start Point in the 1st iteration and then all $P_\mathrm{out}$ points) are called the Current Points (CP). Analogically, each sphere or circle for which $P_\mathrm{in}$ and $P_\mathrm{out}$ points are calculated is called the Current Sphere or the Current Circle.

• (h) Finishing the algorithm if the current line does not cross any sphere or circle. In such a case, the last path point is added and the current path is completed.

The Waterfall Algorithm operates on a set of non-overlapping spherical or circular particles, for which the coordinates of the centres of all particles and their diameters or radii are known. In the implementation, it is assumed that such a set is prepared in advance, e.g. with the use of the random number generator and then saved in a file with an appropriate format. Optionally, the geometry of the system can be rotated by changing the X and Y, X and Z or Y and Z coordinates. At this stage, the geometry can be also scaled to other sizes according to any adopted scale factor, under the condition that the factor is the same for all space directions. Different scale factors would cause the particles to deform and, as a result, they would no longer be spherical or circular.

An important feature of the Waterfall Algorithm is that it works in the exactly same way for 2D and 3D geometries. The only difference is that in two-dimensional systems the value of the Z coordinate of all particles, as well as the Z coordinate of points $P_\mathrm{in}$ and $P_\mathrm{out}$, is reset to zero.

At the beginning of the program operation, the bed geometry is read from a file. At that stage, each particle is being assigned an identification number ranging from 1 to $n_s$, where $n_s$ is the total number of particles in the bed. This number is used to indicate which particle in the bed is the Current Sphere or the Current Particle.

The identification number of the current particle can be determined by an analytical or numerical method. Due to the simplicity of the operation, in the implementation described here, a numerical approach is used. It consists of iteratively shifting additional control point $P_i$ which moves along the current line by a certain, assumed, spatial step (dx), until it is inside some particle (Fig. 3).

Fig. 3

The idea of iterative searching the sphere which has a contact with the current line

The value of the spatial step is determined from the diameter of the smallest particle in the bed

$$\begin{aligned} {\mathrm{d}}x = \frac{d_\mathrm{min}}{d_r}, \end{aligned}$$

(5)

where ${\mathrm{d}}x$ is the spatial step in X direction (m), $d_\mathrm{min}$—minimum particle diameter (–), $d_r$—searching resolution (assumed to 1000) (–).

Fig. 4

Schema of the main elements of the Waterfall Algorithm

Location of $P_\mathrm{in}$ point (Fig. 4) may be calculated analytically from the sphere equation in Cartesian coordinates (here, the 3D space is assumed)

$$\begin{aligned} (x-x_0)^2 + (y-y_0)^2 + (z-z_0)^2 = r_0^2, \end{aligned}$$

(6)

where $x_0, y_0$ and $z_0$ are coordinates of the centre of the current sphere (m), $r_0$ is the radius of the current sphere (m). Since it is known that the $y_\mathrm{in}$ and $z_\mathrm{in}$ coordinates of the point $P_\mathrm{in}$ are the same as the coordinates of the Current Point, then to determine the $x_\mathrm{in}$ coordinate of this point it is enough to solve the following quadratic equation (where the lower value is the searched solution)

$$\begin{aligned} ax^2 + bx + c = 0, \end{aligned}$$

(7)

where

$$\begin{aligned} a = 1, b = -2x_0, c = x_0^2 - r^2 +(y_c-y_0)^2 + (z_c-z_0)^2. \end{aligned}$$

(8)

In the implementation of the algorithm, the task of determining the coordinates of the points $P_\mathrm{in}$ and $P_\mathrm{out}$ is performed in two separate external procedures. The first one (called “find_in”) requires variables $x_0, y_0, z_0, r_0, y_c$ and $z_c$ and returns the $x_\mathrm{in}, y_\mathrm{in}$ and $z_\mathrm{in}$ coordinates. The second procedure (called “find_out”) requires the values of $x_0, y_0, z_0, r_0, y_\mathrm{in}$ and $z_\mathrm{in}$ and returns the $x_\mathrm{out}$, $y_\mathrm{out}$, and $z_\mathrm{out}$ coordinates.

Coordinates of the $P_\mathrm{out}$ point are calculated on the basis of the knowledge of the $\alpha$ angle between the ${OP}_\mathrm{out}$ section and the Z axis (Fig. 5):

$$\begin{aligned} \alpha = acos \left( \frac{z_c - z_0}{\sqrt{(y_c - y_0)^2 + (z_c - z_0)^2}} \right) . \end{aligned}$$

(9)

These coordinates are calculated as follows:

$$\begin{aligned}&x_\mathrm{out} = x_0, \end{aligned}$$

(10)

$$\begin{aligned}&y_\mathrm{out} = \left\{ \begin{array}{ll} y_0 + 0.5 d_0 sin (\alpha ) &{} \quad \mathrm{for} y_\mathrm{in}>y_0 \\ y_0 - 0.5 d_0 sin (\alpha ) &{} \quad \mathrm{for} y_\mathrm{in} \le y_0 \end{array} \right. , \end{aligned}$$

(11)

$$\begin{aligned}&z_\mathrm{out} = \left\{ \begin{array}{ll} z_0 + 0.5 d_0 cos (\alpha ) &{} \quad \mathrm{for} z_\mathrm{in}>z_0 \\ z_0 - 0.5 d_0 cos (\alpha ) &{} \quad \mathrm{for} z_\mathrm{in} \le z_0 \end{array} \right. . \end{aligned}$$

(12)

Fig. 5

Schema of elements serving to calculate intermediate path points

Fig. 6

Visualisation of the Starting Point and $P_\mathrm{in}$ and $P_\mathrm{out}$ points obtained for the first iteration of the first path

Fig. 7

Visualisation of the first path and all current spheres belonging to this path

Fig. 8

Visualisation of all 16 paths obtained for the exemplary 3D geometry

The intermediate points ($Q_i$) lying on the surface of the current sphere between points $P_\mathrm{in}$ and $P_\mathrm{out}$ are determined in two steps within one calculation loop. In the first step, the $y_Q$ and $z_Q$ coordinates of the ith intermediate point are calculated:

$$\begin{aligned}&y_{Q,i} = \left\{ \begin{array}{ll} y_\mathrm{in} + {\mathrm{d}}y(i-1) &{} \quad \mathrm{for} y_\mathrm{in} > y_0 \\ y_\mathrm{in} - {\mathrm{d}}y(i-1) &{} \quad \mathrm{for} y_\mathrm{in}\le y_0 \end{array} \right. , \end{aligned}$$

(13)

$$\begin{aligned}&z_{Q,i} = \left\{ \begin{array}{ll} z_\mathrm{in} + {\mathrm{d}}z(i-1) &{} \quad \mathrm{for} z_\mathrm{in} > z_0\\ z_\mathrm{in} - {\mathrm{d}}z(i-1) &{} \quad \mathrm{for} z_\mathrm{in} \le z_0 \end{array} \right. , \end{aligned}$$

(14)

where

$$\begin{aligned} {\mathrm{d}}y = \frac{y_\mathrm{out} - y_\mathrm{in}}{n_Q}, {\mathrm{d}}z = \frac{z_\mathrm{out} - z_\mathrm{in}}{n_Q}. \end{aligned}$$

(15)

The $n_Q$ means the assumed number of intermediate points (100 in next considerations).

At the second stage, the “find_in” subroutine with $y_{Q,i}$ and $z_{Q,i}$ variables inserted instead of $y_c$ and $z_c$ is applied. Repeating this procedure $n_Q$ times, a poly-line linking $P_\mathrm{in}$ and $P_\mathrm{out}$ points is obtained.

The path length ($L_p$) is calculated as the sum of the lengths of straight sections lying between successive points on the path. Once the domain length ($L_0$) is known, the tortuosity may be calculated. Figure 6 shows the key elements of the Waterfall Algorithm for an exemplary 3D geometry. The visualisation covers the elements specified in the first iteration of the first path. The Start Point is marked with a black cube, point $P_\mathrm{in}$ is in blue, and point $P_\mathrm{out}$ in green. In order not to impair the visibility, the drawing does not take into account the intermediate points lying on the surface of the sphere.

In Fig. 7, the full trajectory of the first path for the same geometry is shown. This figure also shows all the spheres which became successive current spheres during the calculations. The number of “collisions” of lines originating from consecutive Current Points is relatively small, which results from the relatively high porosity of the system, equal in this case to 0.735.

Because one single path may not represent the features of a granular bed in a proper way, a regular grid of Start Points is applied in each case. In Fig. 8, an example of such a grid consisting of 16 Start Points is presented.

Fig. 9

A comparison between acting the Waterfall Algorithm, the A-Star Algorithm and the Path Searching Algorithm (the number of paths is limited to 10)

Fig. 10

A comparison between acting the Waterfall Algorithm and Random Walk Method (the number of paths is limited to 10)

3 Results and discussion

3.1 Waterfall Algorithm versus binary algorithms

In paper [33], an idea to calculate tortuosity based on geometry expressed in a form of binary matrix was studied. In this approach, the geometry of a granular bed is represented by a grid of nodes which are regularly arranged in the space. Each node is assigned with a binary value : zero, when the node is located in the pore space, and one, when the node is located inside the solid part of the porous body. Once such a space is specified, a path connecting subsequent zero nodes may be calculated with the use of appropriate algorithms. This section refers to the paper cited above. A comparison with the popular Random Walk Method is additionally presented.

Figure 9 shows a comparison of results obtained by: (a) the Waterfall Algorithm (black lines), (b) the A-Star Algorithm with the Euclidean heuristic function in the static variant (blue lines), (c) the A-Star Algorithm with the Euclidean heuristic function in the dynamic variant (red lines), (d) the Path Searching Algorithm (green lines). In the static (classical) variant of the A-Star Algorithm, the target node (the so-called Stop Point) remains motionless during calculations. In turn, in the dynamic variant the target node changes dependent of the location of the current node of the path. In this test, an exemplary 2D geometry is used. Before calculating, the input geometry was converted to a grid of nodes with resolution $500 \times 500$. The mean tortuosity value (average value from 50 individual paths) for the algorithms mentioned here is 1.0972 (a), 1.1847 (b), 1.1891 (c) and 1.8248 (d), respectively. It is noticeable that despite the qualitative similarity of all types of paths, the lowest (minimum) values were obtained when the Waterfall Algorithm was applied.

Figure 10 shows an analogous comparison of results for the same geometry obtained by: (a) the Waterfall Algorithm (black lines), (b) the Random Walk Method with D3Q26 grid model (red lines), (c) the Random Walk Method with D3Q6 grid model (blue lines). The grid model means here the number of possible directions of path movement. In D3Q26 variant, the path may move in perpendicular directions as well as in diagonal directions in the relation to the current grid node. In D3D6 variant, the diagonal directions are forbidden. The Random Walk Method gives quite chaotic paths shapes, and their lengths are much higher than in the other methods. The average tortuosity in the D3Q26 and D3Q6 variants is equal to 2.5477 and 2.5303, respectively.

Note, that the Waterfall Algorithm does not contain random elements, like in the case of the Path Searching Algorithm [33] or Random Walk Method. Each run of the program with the same geometry and the same search settings results in the same path trajectory and the same tortuosity. In this context, the Waterfall Algorithm is similar to the A-Star Algorithm which has the same feature.

It should be underlined that in all the so-called binary algorithm the result depends on the grid resolution. Here, only one resolution was used, but that is enough to catch similarities and differences between all approaches.

On this stage, a new general idea may be presented: since different algorithms give different tortuosity values even at the same conditions, maybe we should always base on the minimum tortuosity, which is always only one? This question remains open.

In Fig. 11, a relative comparison of calculation times (on the same computer) for all above described approaches is presented. As may be seen, the Waterfall Algorithm works very fast. The calculation time is about 100 times shorter compared to the Random Walk Method and about 100000 times shorter than the Path Searching Algorithm or the A-Star Algorithm. It means that the Waterfall Algorithm may be used for very large granular beds, what is its high advantage.

3.2 Waterfall Algorithm versus hydraulic and geometric tortuosity

In paper [44], a comparison of hydraulic tortuosity calculated by the use of the Lattice Boltzmann Method and the geometric tortuosity obtained by the Path Tracking Method was presented. The study was performed for a set of exemplary 3D granular beds generated by the Discrete Element Method. The porosity, the number of particles, the average diameter and the standard deviation were equal to 0.41 (–), 5000 (–), 6.072 mm, 0.051 mm, respectively. The number of fractions used to reconstruct the diameters distribution curve varied from 3 to 25. Each case was repeated 3 times. The representative hydraulic tortuosity for the case with 25 particles fractions was equal to 1.2314, 1.2331 and 1.2340 for repetitions 1, 2 and 3, respectively. In turn, the geometric tortuosity calculated from 25 independent paths in the same samples was equal to 1.2128, 1.2127 and 1.2148.

Figure 12 shows 25 paths obtained by the Waterfall Algorithm for the bed sample No. 1. The average values for repetition 1, 2 and 3 were equal to 1.06, 1.06 and 1.0605, respectively. After making an assumption, that there is a direct unambiguous relation between a representative tortuosity (e.g. hydraulic or geometric) and the minimum tortuosity, the following formula may be proposed

$$\begin{aligned} \tau = s_f \tau _\mathrm{min}, \end{aligned}$$

(16)

where $\tau$—the representative tortuosity (–), $s_f$—a scale factor (–), $\tau _\mathrm{min}$—the minimum tortuosity (calculated with the Waterfall Algorithm) (–).

Fig. 11

Comparison of the computation time

Fig. 12

Visualization of paths determined by the Waterfall Algorithm (bed sample No. 1)

For the given data, $s_f \approx 1.163$ for calculating the hydraulic tortuosity and $s_f \approx 1.144$ for calculating the geometric tortuosity. Similar scale factors may be calculated for other methods of calculating the tortuosity, e.g. of binary algorithms mentioned in the previous section. This issue remains open and needs further investigation.

The time needed to obtain the hydraulic tortuosity by the use of the Lattice Boltzmann Method reached hours, dependent on the grid resolution used. The Path Tracking Method turned out to be much faster. The average time of calculating a single paths was equal to about 6 s. The average time for calculating one single paths with the Waterfall Algorithm for the same porous media was equal to 0.64 s.

3.3 The needed number of Start Points

Figure 13 shows the impact of the number of Start Points on the average tortuosity value. The calculations were performed 100 times, starting with 10 Start Points. Then, the number of Start Points was increased by 10 in each repetition. In this test, the same geometry as in the Sect. 3.1 was used. Assuming that the exact value is the mean tortuosity obtained for 1000 paths (which is only an approximation as the mean value fluctuates all the time), the relative error can be calculated for any other number of Start Points. For example, the tortuosity for 50 paths, which was determined in Sect. 3.1, differs from the above-mentioned exact value by 0.17%. Such a difference may be neglected. The performed test shows that accepting several dozen Start Points is practically as good as accepting hundreds or thousands of such points. The same conclusion comes from other 2D and 3D tests which are, not, however, shown in the paper.

Fig. 13

Tortuosity as a function of the number of Start Points

Fig. 14

Schema for visualisation proposed geometry ratios

Fig. 15

The number of particles in function of $\phi$ and s

It should be added that an excessive increase in the number of Start Points does not have much justification for a couple of reasons. First, it causes a linear increase in computation time. Second, the high density of the Start Points causes that many neighbouring paths have the same shape besides the part located between the Start Point and the first $P_\mathrm{out}$ point (see paths $s_3$ and $s_4$ in Fig. 14). Consequently, certain groups of paths generate a very similar tortuosity value.

3.4 Proposition of new geometry indicators

The data obtained during the acting of the Waterfall Algorithm may be used to define several new parameters or indicators that can be used in a direct or comparative analysis of the geometrical features of different granular porous media. They may be defined as follows (Fig. 14):

• global shift ratio—an indicator describing the relative displacement of the first and the last point of a path in the plane perpendicular to the main direction:

  $$\begin{aligned} I_\mathrm{shift} = \frac{\sqrt{{\mathrm{d}}y_\mathrm{global}^2 + {\mathrm{d}}z_\mathrm{global}^2}}{l_x}, \end{aligned}$$

  (17)

  where ${{\mathrm{d}}y}_\mathrm{global}$ is the distance between the first and the last point of the current path in the Y direction (m), ${{\mathrm{d}}z}_\mathrm{global}$ is the distance between the first and the last point of the current path in the Z direction (m), $l_x$ is the length of the granular bed in X direction (m).

• collision density ratio—an indicator describing the number of contact points between the current lines and current spheres per unit length

  $$\begin{aligned} I_\mathrm{col} = \frac{n_\mathrm{col}}{l_x}, \end{aligned}$$

  (18)

  where $n_\mathrm{col}$ is the number of current spheres in the path (–).

• consolidation ratio—an indicator describing the consolidation degree of paths beginning from different Start Points

  $$\begin{aligned} I_\mathrm{con} = \frac{n_\mathrm{stop}}{n_\mathrm{start}}, \end{aligned}$$

  (19)

  where $n_\mathrm{start}$ is the number of Start Points defined in the current calculation (–), $n_\mathrm{stop}$ is the number of last path points with independent coordinates (–).

Fig. 16

Paths obtained for $\phi =0.5$, first repetition and $s=0.02$ (a), 0.04 (b), 0.06 (c) and 0.08 (d)

Fig. 17

Distribution of the global shift ratio for $\phi =0.5$ (a) and for all porosities (b)

Fig. 18

Distribution of the collision density ratio for $\phi =0.5$ (a) and for all porosities (b)

In the next investigation, the idea of the so-called structural element is used. It is a single object (here a circle) constituting an independent fragment of the skeleton of a porous medium [25]. The size of the structural element in the dimensionless form is defined as follows

$$\begin{aligned} s = \frac{d}{l_x}, \end{aligned}$$

(20)

where d is a characteristic length (here, it is the particle diameter) (m). Since in the test the unit size of 1 m by 1 m of the computational domain is assumed, the value of s is always the same as the particle diameter. For the same reason, the value of the collision ratio may be here directly interpreted as the number of $P_\mathrm{in}$ points.

3.5 Investigation of geometry indicators

In order to investigate whether and how the values of the indicators described in previous subsection change, 1800 porous structures were randomly generated in two-dimensional space with the size of $1\times 1$ m for ten porosities (from 0.5 to 0.95, every 0.05) and eighteen particle diameters (from 0.005 to 0.09 m, every 0.005 m). Tries of generating structures with porosity of 0.45 or less failed despite the fact, that the minimum theoretical porosity of uniform particles is equal to 0.339 [45]. The geometry was created with the use of an Author’s algorithm based on the random number generator. The minimum distance between particles was set to zero. It means that the particle could touch each other, but they could not overlap. The number of particles needed to obtain an assumed porosity for a chosen normalised size of the structural element varied from 8 (for $\phi =0.9$ and $s=0.09$) to 25461 (for $\phi =0.5$ and $s=0.005$). Each variant was repeated ten times. Due to the analytical approach, the number of particles in each repetition was the same (Fig. 15), but the particles had different locations. For every geometry, 100 Start Points was defined. In consequence, the obtained data set contained 180,000 individual paths.

Figure 16 shows selected examples of paths obtained for the lowest porosity and different normalized sizes of structural elements. It can be seen that despite the same porosity, the obtained patterns differ qualitatively. The same effect occurs in all other porosities. This shows that more than just porosity is required to understand or describe the properties of such porous media.

Fig. 19

Distribution of the consolidation ratio for $\phi =0.5$ (a) and for all porosities (b)

Fig. 20

Tortuosity in function of porosity: compilation of all data (a) and comparison with selected formulas (b)

In Fig. 17a, values of the global shift ratio for all structures with the porosity equal to 0.5 are visible. A single point on the graph represents the average value obtained from 100 independent paths. It was stated that the relationship is nonlinear. The proposed fit the $I_\mathrm{shift}(s)=as^b$ function, where $a=0.187$ and $b=0.517$. Note, that the range of global shift coefficient decreases in a significant way when the normalized size of the structural element decreases. Such a result was expected, but without appropriate investigations, it was impossible to predict the character of the function. In Fig. 17b, the average values of global shift ratio for all data are compared. It may be seen that the impact of the normalized size of the structural element is more noticeable for smaller porosities.

In Fig. 18a, the collision density ratio for all pore structures with porosity 0.5 is shown. As expected, the number of collisions decreases if the size of the structural element increases. The proposed fit the $I_\mathrm{col}=\frac{a}{s^b}$ function, where $a=0.666$ and $b=1.013$. The same function type was used to fit the data representing the consolidation ratio (Fig. 19a). Values of a and b coefficients are in this case equal to 0.032 and 0.456, respectively. Interestingly, the collision density ratio is very stable for both, the chosen porosity and the normalized size of the structural element. The collision density may be a very good indicator characterising the geometrical features of granular media. The consolidation ratio has similar features; however, the range of values is higher for each case. The collision density ratio grows when both, the porosity and the normalized size of the structural element, decrease (Fig. 18b). In turn, the consolidation ratio decreases for low porosity and high values of the normalized size of the structural element (Fig. 19b). Such relationships were expected, but the character of changes was unknown.

In Fig. 20a, the porosity-tortuosity relation for the obtained data is presented. As previously, a single point on the graph represents the average value obtained from 100 independent paths. In Fig. 20b, a comparison with two empirical formulas presented in the literature is shown [19, 46]. Both of them refer to hydraulic tortuosity obtained from LBM simulations. It may be seen that the general trend is correct; however, Waterfall Algorithm significantly underestimates the tortuosity values. Amien noted [38] that when compared to hydraulic tortuosity, geometrical tortuosity has smaller values. The reason is that hydraulic tortuosity is calculated on the basis of the flow path which lies precisely along the streamline and thus, its line is practically smooth. The obtained results are in agreement with this remark. Note also that the scope of the data corresponds well with the results obtained by Delarue and Jeulin [35] (recall: tortuosity between 1.03 and 1.05), who applied an algorithm which was very similar to the Waterfall Algorithm. The data visible in Fig. 20a may be described by a linear function with the slope equal to − 0.14 and the intercept of 1.14.

Fig. 21

Tortuosity in function of normalized size of the structural element for $\phi =0.5$

In Fig. 21, the tortuosity in the function of the normalized size of the structural element for the lowest porosity is shown. The tortuosity decreases when this size grows. At the same time, the scope of possible values increases significantly. The results show that the confidence level of tortuosity is higher in systems with small values of the s parameter. The relationship between porosity and the normalized size of the structural element may be expressed as follows:

$$\begin{aligned} \tau (s) = \frac{a}{s^b} + \frac{c}{s^d}, \end{aligned}$$

(21)

where $a = 0.54, b=-0.05, c=0.536$ and $d=0.041$.

In Fig. 22, the tortuosity is presented as a function of both parameters, namely the porosity and the normalized size of the structural element. A specific feature of this function is that the data range grows if porosity decreases and the normalized size of the structural element increases. The obtained relationship may be fitted with the following function:

$$\begin{aligned} \tau (\phi ,s) = \frac{1}{\phi ^a s^b}, \end{aligned}$$

(22)

where $a=0.096, b=0.0012$.

Fig. 22

Tortuosity for different porosities and normalized sizes of the structural elements

Fig. 23

Comparison of formulas (22) and (23)

In paper [25], a formula for calculating the tortuosity for a specific porosity and normalized size of the structural element was proposed. This function has the following form:

$$\begin{aligned} \tau (\phi ,s) = \frac{1}{\phi ^b s^c} + \frac{d}{\phi ^e s^f}, \end{aligned}$$

(23)

where $a=1.1, b=0.33, c=-0.01, d=5.3e-08, e=6.8, f=2.86$.

In Fig. 23, a comparison between Eq. (22) denoted by blue colour and Eq. (23) marked by red colour is presented. It may be seen that the tortuosity obtained from the Waterfall Algorithm is not as sensitive to the porosity and the normalized size of the structural element as the tortuosity calculated by the Path Tracking Method or the hydraulic tortuosity obtained from LBM simulations. Eq. (22) gives much smaller values than Eq. (23). Although such a result was expected, it turned out that the shape of the surface obtained from Eq. (22) has a different qualitative character than the surface representing Eq. (23). It means that the earlier mentioned scale factor $s_f$ is a function of porosity and the normalized size of the structural element.

4 Summary

The following remarks and conclusions can be formulated based on the results of the present study:

• The Waterfall Algorithm may be used in porous media consisting of non-overlapping circular or spherical particles. Such virtual beds may be generated by appropriate random algorithms or by the use of the Discrete Element Method. The compatibility with DEM models may by a significant advantage of the proposed approach.

• The Waterfall Algorithm may be used to calculate the lower range of the geometric tortuosity for granular porous media. The obtained values of the tortuosity cannot represent the tortuosity of pore channels in Kozeny or Carman meaning.

• There is a possibility to recalculate the minimum tortuosity to a representative tortuosity, but the knowledge about function $s_f(\phi ,s)$ is needed. On this stage, the theory of the so-called sensitivity analysis can be applied [47].

• The Waterfall Algorithm may be used to calculate different parameters which characterize the geometrical structure of granular porous media, such as the global shift ratio (in a similar way the local shift ratio may be defined, in which the shift on a single sphere or circle will be calculated), the collision density ratio and the consolidation ratio.

• The application of the proposed parameters is not limited to the Waterfall Algorithm and may be also used in the relation to other algorithms serving to calculate paths lengths in porous media. The kind of the porous body as well as the used algorithm does not matter.

• The applications of the parameters proposed in the paper remain open. However, it seems that the parameters can be used to define new models which could serve to predict the pressure losses in fluid flows through porous media. In particular, there is a potential to use the collision density ratio to estimate the beta factor responsible for the inertial effects in the Forchheimer equation. To propose such a model, a new study based on experimental data is needed. In turn, the shift ratio and the consolidation ratio may be applied to the issues related to mixing processes or chemical reactors.

• The Waterfall Algorithm do not need a grid of nodes, cells, pixels or voxels and works very fast. In the consequence may be used in a very large systems, in which other methods cannot be applied sue the limitation of the available computational power. It is the main advantage of this algorithm and can justify the need of further investigations.

• The Waterfall Algorithm is limited by the assumption about the shape of the particles. However, the idea can be understood as a more general: the path goes straight and if it will touch a body, than slides over its surface until it can go straight again. In such a context, the particle shape may by freely defined. Nevertheless, the implementation of this idea would require a modification of the algorithm.

• Since different algorithms give different tortuosity values even at the same conditions, maybe we should always base on the minimum tortuosity, which is always only one. This question remains open.

• The Waterfall Algorithm may be understood as a result of some kind of evolution. In Random Walk techniques, the path moves randomly on all stages of acting the algorithm. In additional, the space has to be expressed by a grid of nodes. In the algorithm described by Boudreau and Meysman, such a grid of nodes is unnecessary and the path moves randomly only if the main direction is not available. In the Waterfall Algorithm, a grid is also not needed. The next change is that the path shape is determined only by the geometry and random procedures are not in use at all.