Abstract
The effect of grid coarsening on the predicted total drag force and heat exchange rate in dense gas–particle flows is investigated using Euler–Lagrange (EL) approach. We demonstrate that grid coarsening may reduce the predicted total drag force and exchange rate. Surprisingly, exchange coefficients predicted by the EL approach deviate more significantly from the exact value compared to results of Euler–Euler (EE)-based calculations. The voidage gradient is identified as the root cause of this peculiar behavior. Consequently, we propose a correction algorithm based on a sigmoidal function to predict the voidage experienced by individual particles. Our correction algorithm can significantly improve the prediction of exchange coefficients in EL models, which is tested for simulations involving Euler grid cell sizes between \(2d_p\) and \(12d_p\). It is most relevant in simulations of dense polydisperse particle suspensions featuring steep voidage profiles. For these suspensions, classical approaches may result in an error of the total exchange rate of up to \(30\%\).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Particle–gas systems are extensively used in various processes such as chemical, petrochemical and pharmaceutical industries. Due to the complexity of such systems, as well as their opaqueness, numerical tools have been widely exploited. This includes simulations to better understanding phenomena originating from (i) particle–particle interactions (e.g., cohesive forces), as well as (ii) particles and the interstitial flow (e.g., elutriation of fines from fluidized beds). This insight can be achieved through detailed local information from two- or three-dimensional simulations, which have become valuable tools for engineers and researchers.
In simulations of particle–gas flow, usually two methodologies can be used to calculate interphase coupling forces: (i) a direct calculation of the coupling force via a particle-resolve (PR) flow simulation or (ii) using a drag closure that relies on average flow information only (i.e., the so-called particle unresolved method, PU). In the first methodology, the boundary between particles and fluid is discretized, and fluid flow is simulated in all detail. The PR method necessitates a comparably fine computational mesh to capture the boundaries and the flow accurately. Consequently, the computation time is high, and the application is typically limited to small particle ensembles in the order of \(\hbox {O}(10^{3})\) to \(\hbox {O}(10^{6})\) particles. Studies that have adopted the PR method are, for example, Avci and Wriggers [1], or the early work of Johnson and Tezduyar [2].
For numerical investigations of gas–particle flow using the PU approach, i.e., employing a closure for the drag force, generally two approaches can be employed: (i) the Euler–Euler (EE) approach, in which gas and particles are treated as interpenetrating continua. The kinetic theory of granular flow (KTGF), together with stress closures for enduring particle–particle contacts, is typically applied in order to close the set of equations when using the EE approach; or (ii) the Euler–Lagrange (EL) approach, in which gas phase is considered as continuous phase, while particles are treated individually by solving Newton’s equation of motion. Attractive for a number of engineering applications is the so-called particle unresolved EL approach (PU-EL), in which flow details around individual particles are not resolved. PU-EL avoids the need for the often prohibitively substantial number of fluid grids and offers comparably fast predictions that can account for, for example, intra-particle effects (e.g., diffusion and chemical reactions within porous particles).
It should be noted that when using a PU-EL approach, the CFD cell size (on which the transport equations for the fluid phase are solved) varies between approximately 2 and 15 times the particle diameter. Most importantly, the CFD cell size typically cannot be strictly enforced, since a complex-shaped unstructured fluid grid has to be used. Nowadays, such grids are built with fully automated gridding techniques and commonly used in many industrial applications of PU-EL. Thus, the voidage (i.e., the relative amount of void space) reconstructed on a typical fluid grid is blurred, with the degree of blurring depending on the local CFD cell size. As we will show, this blurring results in substantial errors when predicting fluid–particle transfer coefficients, and hence it is unwanted.
To obtain accurate distribution of key quantities in such gas–particle systems, both the EE approach and the (PU-)EL approach require a suitable CFD cell size to reduce blurring. Depending on the spatial distribution of the particles, which is dictated by the underlying flow physics, this size is typically in the order of a few particle diameters. The root cause for this need is that the relative void space between the particles can have nonlinear effect on exchange coefficients of momentum, heat and mass. This is especially true for moderately dense to dense gas–particle flows frequently encountered in chemical engineering applications. Hence, EE and EL models that claim to resolve all flow phenomena in this field necessitate so-called fine-grid simulations to resolve the voidage field.
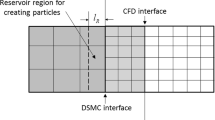
Despite the fast increase in the availability of computational resources, such a fine-grid simulation makes the numerical investigation of industrial scales system computationally very expensive or sometimes impossible. This is especially the case when using the (PU-)EL approach. To overcome such a limitation, a large number of research studies have been devoted to improving the reliability of so-called coarse-grid simulations in predicting the system behavior and performance. To provide a better understanding of such “coarse-grid” simulations, a typical schematic representation of a packed bed with fine and coarse grids is depicted in Fig. 1. It can be easily discerned from this figure that coarsening the CFD (fluid) grid leads the voidage being blurred over a larger region. We note in passing that this blurring is different from numerical diffusion caused by discretization schemes that are employed in solving the governing equations. In contrast, blurring has its origin in the mapping of particle-related information to a finite fluid grid.
1.1 Classical closures for coarse-grid simulations
In a pragmatic approach, as extensively performed by Sundaresan’s research group [3,4,5,6,7], the results of fine-grid simulations are filtered considering various grid sizes to obtain so-called filtered models. More precisely, these models are closures that focus on adjusting exchange coefficients (e.g., for the drag), or define a new constitutive model that is needed for coarse-grid simulations (e.g., for the particle-phase stress). For example, via this filtering approach, an average correction factor between zero and unity is developed to establish a “filtered” drag coefficient. This average filtered counterpart is hence predicted to be always smaller than the original drag coefficient, i.e., the one would use in a fine-grid simulation (see Schneiderbauer [8]). Note that average here refers to a particle ensemble average. This is important since none of the approaches for coarse-grid simulations presented above is currently able to predict the true distribution of filtered exchange coefficients.
An alternative concept is that of Parmentier et al. [9], who introduced an (average) subgrid drift velocity to reduce the fluid–particle relative velocity. This drift velocity is defined as the difference between the filtered gas–particle–fluid velocity seen by the particle phase and the resolved filtered gas velocity. In effect, the drift velocity concept leads to a similar modification of the filtered drag coefficient that is smaller than one in fine-grid counterpart. Yet another alternative is to consider the effect of unresolved structures in a more analytical fashion as done by Schneiderbauer [8]. One more example of analytically based coarse-grid corrections uses the energy minimization multi-scale (EMMS) method, originally developed by Li [10]. In this approach, the local heterogeneity is described in terms of decomposed dense and dilute phases. This method was integrated by Wang et al. [11] into an Euler description of gas–solid flow to include subgrid-scale model for drag force. Although the application of such a methodology is rather limited, e.g., by the fact that it is limited to a certain type of fluid–particle systems, it has attracted a significant research [12, 13].
1.2 The need to account for coherent structures
Most of the filtered models discussed in the previous paragraph depend on the relative grid size, the filtered particle concentration, as well as sometimes a third marker (e.g., the filtered slip velocity or a subgrid-scale particle agitation [8]). Most importantly, these corrections can only account for a certain phenomenon in an average sense (e.g., the spontaneous clustering of particles [14]) and use a primitive [8] or no information on the heterogeneous structure of the suspension. Consequently, regions featuring large voidage gradients, e.g., structures near the interface of particle clusters, are expected to be a problem for these filtered models. This is simply because these structures are averaged out in the above-discussed approaches, but certainly cause extrema in filtered exchange coefficients. Hence, they are inadequately modeled by currently available models that rely on average exchange coefficients. This is also supported by the study of Fullmer and Hrenya [15] that probed the effect of the local voidage on the mean-slip velocity in a comparably dilute fluidized bed \((\varphi _{p,\max } =0.25)\) using the EE approach. The predicted slip velocity was in a good agreement with the corresponding values from the EL-based simulations of Radl and Sundaresan [16]. However, Fullmer and Hrenya [15] demonstrated that the main reason for the deviation of the slip velocity in coarse-grid simulation of cluster can be associated with the voidage gradient at the boundary of the cluster[17,18,19]. Specifically, Fullmer and Hrenya [15] conclude that higher (mean) particle concentrations induce sharper voidage gradients, which necessitate a higher spatial grid resolution to capture these gradients.
To include the effect of coherent structures that lead to extrema in filtered exchange coefficients, new parameters, e.g., the gradient of flow variable, are required. The work of ten Cate and Sundaresan [20] followed such a thought and systematically analyzed the effect of voidage gradients on the momentum exchange coefficients. Similarly, corrections to the drag coefficient based on the “structure of the flow“ were proposed by Yang et al. [21]. They modified the drag coefficient through correlating the structure parameters with the solids concentration only, though. Only recently their work was followed by Zhou et al. [22] through direct numerical simulation of heterogeneous gas–solid flow. The results of their simulation proved the dependency of the drag force on the local heterogeneity. The latter was quantified in terms of solid concentration and, most importantly, by the magnitude and the angle of the voidage gradient. The latest work following such a chain of thoughts is that of Li et al. [23] who investigated the effect of the local heterogeneity in the particle distribution using an EE approach. They obtained a correction factor for this local heterogeneity with reference to homogenous distribution of particle in a cell as a pre-tabulated correction factor. The local heterogeneity in their study has been defined based on a linear voidage distribution in a computational cell. The model of Li et al. [23] has some limitations, e.g., it is only valid for the Euler–Euler approach and assumes a linear variation of the voidage. Furthermore, it was assumed that the velocity component normal to the flow is zero. This is problematic, since in case that a voidage gradient is present in a computational (Eulerian) cell, the velocity field can deviate from the main direction. The gas prefers to flow in the region with higher voidage, drastically changing the effective drag force in this computational cell.
1.3 Decoupling the effect of nonresolved structures and insufficient grid resolution
The above-mentioned studies focus on the correction of exchange coefficients which lump the effect of (i) nonresolved structures and (ii) numerical parameters (e.g., the grid resolution) into a single correction factor. In our present study, we follow the thought that the correction of the exchange coefficients must be split based on the source of the deviation. For instance, coarsening the grid size artificially introduces a more homogeneous voidage distribution, as depicted in Fig. 1, which drastically reduces the voidage gradient (see the left panel). As it will be explained later, the voidage distribution can be fitted to the sigmoidal function with model parameter a. In fact, as demonstrated by Fullmer and Hrenya [15] as well as Ozel et al. [4], the (Eulerian) grid size mainly influences the exchange coefficient through its effect on the particle volume fraction calculated in the cell. Thus, even in case one would be able to resolve heterogeneous structures in an EL-based simulation, the local particle concentration at each particle’s position cannot be probed accurately on a finite-sized Eulerian grid in general.
1.4 Goals
Hence, it is clear that classical (PU-)EL approaches mainly suffer from the inability in the reliable prediction of the local voidage as also reported by Lu et al. [24] through direct numerical simulation (DNS) of gas–solid flow. Since the voidage is the most important contributor—next to the fluid–particle relative speed—to predict exchange coefficients, we expect that even minute mispredictions of the local voidage lead to significant errors in the exchange coefficients. It is clear that the effect of a finite grid size on the voidage profile is not related to discretization schemes used for approximating, e.g., convective terms in the governing transport equations. The misprediction of the voidage distribution is associated with the mapping procedure and the subsequent interpolation of the voidage at the particle position. Specifically, when using coarse grids, a larger number of particles reside in a specific fluid cell. Consequently, particles in the same fluid cell will experience a similar voidage, followed by a similar flow speed. Therefore, in the present study, the main effort will be put on the correction of the voidage to eradicate the effect of voidage misprediction due to mapping and interpolation. It is worth mentioning that the corrected voidage will be only used for computing per-particle exchange coefficients (e.g., for drag and heat exchange)—the voidage on the fluid grid will be not modified. Hence, our proposed correction algorithm does not interfere with the conservation of total mass or volume on the fluid grid.
While our correction algorithm is novel in the field of PU-EL simulation models, one may compare it with “interface-sharpening” algorithms [25, 26]. The latter are frequently used in the so-called volume of fluid (VoF) method for modeling two phase flows of incompressible fluids and similar in spirit to our algorithm. However, there is a substantial difference between them: In the VoF method blurring of the phase fraction (a quantity that is similar to the voidage in our work) is related to the numerical diffusion introduced via discretization schemes. In contrast, in the gas–particle flows, blurring is connected to mapping the data from particles to fluid grid cells and subsequent interpolation at the particle position. Also, in interface-sharpening algorithms an additional transport equation (i.e., some kind of an anti-diffusion equation) needs to be solved [25, 26]. This is computationally expensive and in contrast to our study which relies on a pure algebraic correction approach (i.e., not transport equation needs to be solved).
In the present study, the correction model will be developed specifically for dense gas–particle flows that feature large voidage gradients. Typical examples of such flows include bubbling fluidized beds, packed bed reactors or clustered suspensions (e.g., flows of cohesive powders and granular materials).
One can criticize the approach adopted in our present study by the fact that subfluid cell information (i.e., the arrangement of particles) is ignored. However, using information on the arrangement of particles which would enable, for example, Voronoi tessellation [27] is avoided on purpose in our present study, using such particle-based information typically greatly increases the computational expense for computing the voidage. Thus, the main motivation behind our study is using information available on the fluid grid for the sake of computational efficiency.
The main goals of our present study can be summarized as follows:
-
1.
Examining the influence of fluid coarsening on the total drag force and heat exchange rate in dense gas–particle flows.
-
2.
Improving the prediction of hydrodynamics and heat transfer rates in bubbling fluidized beds, as well as packed beds. Here our focus is on systems that feature large voidage gradients.
-
3.
Developing a straight-forward, easy-to-implement method to correct the voidage (for the calculation of exchange coefficients) and consequently a source of error in PU-EL.
1.5 Outline
The main objective of the present work is developing a voidage correction model based on the local heterogeneity for PU-EL simulations of dense particulate systems. Specifically, we follow a chain of thoughts that is summarized by the following structure of our study: First, the validity of the filtered drag model developed by Radl and Sundaresan [16] is examined in a packed bed (Sect. 3.1). Second, the influence of fluid coarsening on the total predicted drag force, as well as the heat exchange rate, is investigated in a packed and a fluidized bed (Sect. 3.2). In addition, based on an assumed particle distribution the contribution of the voidage distribution on the deviation of drag force in coarse-grid simulation for both the EE approach and EL approach is revealed. An analysis of this deviation is then used to postulate an algorithm that maps the voidage distribution in a coarse-grid PU-EL simulation to the corresponding local value that would be obtained in a hypothetical fine-grid simulation (Sect. 3.3). Afterward, the reliability of the developed correction function is examined for the prediction of the total drag force through analytical considerations, as well as CFD-DEM simulations (see Sect. 3.4). Furthermore, the accuracy of this voidage correction function is assessed for predictions of the fluid–particle heat exchange rate. Afterward, the proposed model is extended to cover different regimes of voidage gradients. Finally, a brief discussion will be performed to take the effect of different angles between the velocity and the voidage gradient field into account for future study.
2 Mathematical modeling
In the present study, simulations were performed utilizing an extended version of the \(\hbox {CFDEM}^{\circledR }\) code [28]. This code is based on an open-source CFD–DEM framework to simulate coupled fluid–particle systems. The motion of the particles is resolved by means of the DEM and simulated using the \(\hbox {LIGGGHTS}^{\circledR }\) code [29]. The interstitial fluid flow is predicted via a classical (unresolved) CFD approach and simulated using the \(\hbox {OpenFOAM}^{\circledR }\) software package [30].
2.1 Flow
The equation of motion for fluid phase and individual particles can be derived based on Navier–Stokes equation and Newton’s equation of motion, respectively.
2.1.1 Fluid phase
Momentum equation for the fluid phase is solved based on the well-known Navier–Stokes equation:
The term \({\varvec{\varPhi }}_d\) is the force exerted by particles on fluid phase per unit volume, excluding buoyancy effects. As generally accepted, we assume that the drag force is the main force contributing to the momentum exchange rate between gas and particles. These drag forces can be computed using the correlation developed by Beetstra et al. [31] as follows:
where Re is the particle Reynolds number, which is calculated based on the superficial fluid velocity and the particle individual speed. The equations for the filtered drag model are reported in “Appendix A”. The adopted discretization and interpolation schemes are reported in Table 1.
2.1.2 Particles
The motion of individual spherical particles is predicted using Newton’s equation of translational and rotational motion:
where the forces exerted on each particle, shown on the right-hand side of Eq. (5), include (i) contact, (ii) drag, (iii) far-field pressure and (iv) gravity contributions, respectively. The contact law is based on a Hertzian interaction model with tangential history tracking to model stick-slip transitions correctly. The contact forces in the normal and tangential direction are given by
Here \(\delta _p\) denotes the particles overlap; k and \(\eta \) represent the stiffness coefficient and damping factor, respectively. These parameters can be calculated as a function of the Young modulus, the Poisson ratio and the coefficient of restitution. The values of these parameters, as well as of the friction coefficient, are reported in Table 1. The torque on the right-hand side of Eq. (6), \(t_i\), denotes the torques due to (i) particle–particle collisions (i.e., the tangential force component calculated via Eq. (8)) and (ii) fluid–particle interactions. It should be noted that the latter was assumed to be negligible in the present study. This is in line with the common assumption in the literature that only accounts for fluid flow-induced torque in case of nonspherical particles (e.g., the work of Ouchene et al. [32]).
To calculate the voidage in each fluid grid cell, particle data were mapped to the CFD cell via the “divided scheme.” This scheme is based on the division of each particle’s volume to 14 satellite points. The contribution of a specific particle to the voidage of fluid cells nearby the particle center is then defined based on a weighting factor. The latter is defined as the number fraction of satellite points (for each particle) in the fluid cell. As reported by Radl et al. [33] this algorithm is very robust—even for the case of particles residing near walls, or complex unstructured fluid grids with polyhedral cells. More details regarding the adopted models are available on the \(\hbox {LIGGGHTS}^\circledR \) online documentation [34] (http://www.cfdem.com/media/DEM/docu/Manual.html)
2.2 Heat transfer
The conservation equation for the thermal energy of the fluid phase can be derived as:
The term on the right-hand side of Eq. (9) is the volume-specific rate of heat exchange between the gas phase and the particles.
2.2.1 Closure for the heat transfer rate
Parameter h in Eq. (9) is the heat transfer coefficient, which can be evaluated from \(Nu=\left( {h\,d_p } \right) /\lambda _f\). Nu is the Nusselt number, which was obtained using the correlation developed by Deen et al. [35] for the fluidized beds:
More details about the implementation and verification of heat transfer equations in CFDEM can be found somewhere else [36].
3 Results and discussion
3.1 Assessment of filtered drag model for dense gas–particle flows
The validity of the filtered drag model developed by Radl and Sundaresan [16] was examined for a packed bed setup (see Fig. 2a) having a minimum voidage of 0.5. An array of Eulerian grid resolutions was probed to investigate grid effects. The packed bed setup features two regions characterized by steep voidage profiles and hence is ideally suited to investigate voidage gradient effects.
As shown in Fig. 2b, application of the filtered model deteriorates the prediction of the total drag force. Specifically, enlarging the grid size reduces the total drag force in a dense gas–particle flow that features voidage gradients. However, in all classical filtered drag closure models (e.g., that of Radl and Sundaresan [16]) the correction factor for the drag coefficient is smaller than unity. Therefore, employing the filtered model brings about even more reduction of the filtered drag coefficients. We note in passing that the closure of Radl and Sundaresan [16] ensures no correction in the dense packing limit. However, in regions featuring steep voidage profiles, the voidage is somewhat larger than that in the close packing limit. This causes the erroneous reduction of the drag correction in classical filtered drag models if applied to packed beds.
As a consequence, the total drag force is drastically underpredicted by classical filtered models, even though a correction of the exchange coefficients has been considered. Specifically, in the fine-grid simulation of comparably dilute flows, i.e., the ones used to establish classical filtered models, the clusters are sufficiently resolved. Gas prefers to bypass dense particle regions that are chaotically oriented for the sake of lower flow resistance. This fact enforces a correction factor smaller than unity for the drag coefficient in comparably dilute flow of chaotically oriented particle clusters.
Note that it is difficult to quantify the orientation of clusters in clustered suspensions, and that a significant level of anisotropy might be present. We have adopted the wording “chaotically” to reflect that the cluster orientation originates from a fluid mechanical instability that leads to a chaotic system behavior as discussed by Fullmer and Hrenya [37].
Clearly, a correction for chaotically oriented particle clusters cannot account for the effect of regions with a well-defined voidage gradient or suspensions with distinctly oriented particle clusters. The latter are suspensions that feature a large voidage gradient into one direction, e.g., as this in the packed bed depicted in Fig. 2a. For suspensions with distinctly oriented particle clusters a finitely sized Eulerian grid smears out the voidage distribution. Thus, particles are predicted to experience a (on average) higher voidage, and consequently a smaller drag force when using coarse Eulerian grids would be predicted. Hence, a correction factor larger than unity would be required for the exchange coefficients to correct for this error.
An alternative view on the difference between chaotically and distinctly oriented particle clusters is obtained when considering the angle between the main flow direction and the voidage gradient. Particularly, in a clustered suspension, the main flow direction has in general a certain angle relative to the local voidage gradient direction. This necessitates a correction factor of smaller than unity for the drag coefficient, as suggested by Li et al. [23]. However, in a packed bed, i.e., a prototype of a distinctly oriented particle suspension, fluid always flows parallel to the voidage gradient. Thus, a correction factor of larger than unity is needed. In short, utilization of a classical filtered model decreases the exchange coefficient even more, which is due to the incorrect assumption of a chaotically oriented particle suspension.
3.2 Systematic evaluation of the effect of fluid coarsening
We now aim on proving that smearing out the voidage distribution in a dense gas–particle flow is responsible for the deviation of the total drag force in coarse-grid simulations. Specifically, a calculation of the total drag force was performed for a packed bed considering the three situations depicted in Fig. 3:
-
(i)
A fine grid, in which the grid is aligned with the jump in the voidage profile. This case reflects the “perfect” solution, i.e., the analytically correct drag force (Fig. 3a).
-
(ii)
A “coarse Eulerian grid” with the same particle population as in case (i), but the jump in voidage profile is located at the center of the interface cell (Fig. 3b), as shown as dashed line in Fig. 3a for base case;
-
(iii)
A “coarse Lagrangian grid” with the same particle population and grid as in case (ii), but the voidage is linearly interpolated at each particle position (Fig. 3c). This corresponds to methodology which is typically used in PU-EL simulations.
Schematic representation of voidage distribution in the packed bed for a an extremely fine grid and for which the grid cell is aligned with the voidage jump, b a coarse Euler grid and c coarse Lagrangian grid. Gray circles indicate particles that are influenced by the voidage gradient in the interface cell
The profiles for the voidage and the drag force corresponding to these three situations are presented in Fig. 4. As shown in Fig. 4a, the drag force follows the same qualitative trend of the voidage distribution along the bed. Hence, the prediction of the total drag force can be improved if the voidage is corrected to the corresponding value in the fine-grid one. Upon increasing the cell size/bed length ratio, i.e., decreasing the mesh resolution or considering thinner packed beds, the total drag force calculated in Euler and Lagrangian grid drops. Surprisingly, for the latter the deviation from fine-grid results is higher (see Fig. 4b). This is since the sharp gradient of voidage cannot be accurately captured due to interpolation at the particle position. As discerned from Fig. 4b, the deviation of the total drag force will be drastically increased in case the maximum packing limit increases from 0.5 to 0.8 due to particle concentration effect on the drag force. Thus, the maximum particle volume fraction has a significant effect on the error in the predicted drag force. Such extremely dense beds are observed for strongly polydisperse granular materials, for which the calculated error can, in extreme cases, be as high as 60%.
As mentioned before, coarsening the grid size reduces the voidage experienced by individual particles on average. This is followed by a reduction of the drag coefficient, which is especially pronounced for densely packed systems. This effect is strong when using a PU-EL approach due to the linear interpolation of the voidage at particle position. In contrast, in the EE approach the porosity is lower, but the region that is used for the calculation of drag force is larger than that when using a fine grid. As shown in Fig. 3c, in the PU-EL approach a larger number of particles (shown in gray color) are influenced by the blurred voidage profile that occurs near the interface cell. Hence, the deviation of the total drag force when using the EE approach is lower than the one for a PU-EL approach.
In summary, it can be concluded that unreliable prediction of voidage distribution and its gradient is responsible for the failure of coarse-grid simulation in accurately predicting the drag force. Therefore, it is clear that a correction of the voidage can eradicate the main source of such deviations to some extent.
To generalize this finding to heat transfer and more complex flow situations, a set of simulations was performed to examine the effect of fluid coarsening on the total heat exchange rate in a bubbling fluidized bed. The corresponding results are summarized in Fig. 5, which illustrate the effect of CFD cell coarsening on the predicted thermal performance of the fluidized bed. As shown in this figure, coarsening the grid underpredicts the total heat exchange rate. Therefore, the time evolution of temperature is slowed down in the fluidized bed.
3.3 Voidage correction model
As demonstrated in the previous section, to improve the prediction of the drag force, a correction of the voidage before computing the exchange coefficients is required. To do so, the typical flowchart for CFD-DEM coupling was slightly modified to take the correction of the voidage for the calculation of drag force into account, as depicted in Fig. 6. It should be highlighted that in the modified approach (i.e., when using the voidage correction), the voidage experienced by each particle is only corrected for calculation of the drag force. This means that the voidage distribution in the fluid grid cells is not corrected. Therefore, the conservation of the voidage is not problematic. This can be also supported by the fact that the voidage experienced by each particle is individually calculated and corrected.
3.3.1 Simple algorithm for voidage jumps
We next aim on correcting for grid size effects in a situation in which the voidage changes within one computational (Eulerian) cell from unity to some minimum values. Thus, we consider a situation near the front row of particles in a packed bed or near the interface of a dense particle cluster. Specifically, we seek a correction function that has the interpolated voidage \(\varphi _f\) from a coarse grid as input and yields the correct voidage jump once a particle is outside of the dense region (i.e., the packed bed or the cluster). The latter is denoted as the corrected voidage \(\varphi _{f,\mathrm{corr}}\) in what follows. In such a way, regions with voidage jumps can be correctly handled, even when using comparably coarse grids.
It is clear from geometrical arguments that the correction function must be a step function at \(\varphi _f =1-\varphi _{p,\max } /2\) in case a linear interpolation of the voidage to the particle location is used (see Fig. 4 for an illustration). Unfortunately, the stability of the overall numerical algorithm is deteriorated in case a step function is used. Similarly, relying on cell-based values of the voidage, i.e., not using a linear interpolation to the particle position, is problematic when using the PU-EL approach due to stability reasons. As a compromise, we find that a piecewise function, such as the one shown in Fig. 7a, improves the prediction of the voidage jump without leading to a significant loss in stability.
As shown in Fig. 7b, employing this correction function can improve the prediction of the total drag force by 15% for \(\Delta _\mathrm{cell} /d_p=12\). Another point discerned from this figure is a \(5\%\) overprediction observed for a fine-grid simulation when using the simple correction model detailed in Eq. (11). This is due to the way that voidage has been corrected in the range \(0.4<\varphi _f <0.6\). In detail, based on the correction function, particles experience a lower corrected voidage (see Fig. 7a) and consequently a higher drag force, in this range. However, the particle volume fraction should remain unchanged for highly resolved simulation even after correction. This deficiency proves that the correction function should be developed in such a way that the voidage distribution does not change upon using fine grids. Clearly, grid size must be accounted for in the correction function, which is not the case in the simply algorithm detailed in the previous paragraph. Furthermore, the overprediction observed in Fig. 7b can be partially attributed to the inability to obtain the correct superficial fluid speed in \(\hbox {CFDEM}^{\circledR }\). This is due to the fact that in the underlying CFD tool (i.e., \(\hbox {OpenFOAM}^{\circledR }\)) the voidage is discretized at the cell centroid, while the fluid velocity is discretized at the face center. While the error associated with this problem of obtaining consistent superficial speeds appears to be fundamental, it is small and hence not discussed in greater detail.
It can be concluded that the robustness of the above simple algorithm depends on the lower and upper threshold value chosen for voidage. In addition, the implemented correction model can overpredict the total drag force in fine-grid simulation that may resolve a finite voidage gradient. Consequently, we next seek a more systematic development that can be applied for wide range of grid sizes.
3.3.2 Generalized algorithm for high voidage gradients
The voidage distribution in the packed bed, as well as near the bubble interphase in a bubbling fluidized bed, was investigated next. Therefore, different cases with a wide range of particle sizes, grid resolutions and bed geometries were considered. It should be noted that near the bubble interphase, the voidage profile was probed in the direction aligned with the voidage gradient. As shown in Fig. 8, our preliminary results for the voidage distribution prove that in the regions with a high voidage gradient, the voidage distribution can be approximated using a sigmoidal function. This is true for both packed and fluidized beds, as shown in Figs. 8 and 9. Therefore, a scaled voidage can be introduced, which is most naturally represented by
where x represents the distance from the interface position \(x_0\).
Comparison of a the voidage distribution and b the fitted sigmoidal distribution in a packed bed with dimension of \(54d_p \times 54d_p \times 96d_p\) for various grid sizes and c dependency of the scaled exponent \(a_\delta \) on grid size \(\left( a_\delta =\frac{a}{\Delta _\mathrm{cell} /d_p }\right) \)
To generalize the function fitted to the voidage distribution, a set of simulations was performed for a wide range of particle diameters, cell sizes and bed dimensions for the packed bed. As shown in Fig. 10a, b, the voidage distribution can be well approximated with a sigmoidal function for various cell sizes. As shown in Fig. 10c, the scaled model parameter \(a_\delta \), i.e., \(\frac{a}{\Delta _\mathrm{cell} /d_p}\), can be fitted using a harmonic function with the three parameters \(a_0=0.57,\,a_1 =0.033\) and \(a_2=-\,0.041\).
Consequently, the scaled voidage distribution in a coarse-grid simulation can be mapped to the corresponding distribution in a fine-grid simulation. The corresponding mapping function is shown in Fig. 11 and is given by
where \(a_{\delta _f } \) and \(a_{\delta _c}\) are the scaled model parameters for the fine- and coarse-grid simulations, respectively, which can be evaluated from Eq. (13). Note, in most practical situations, it is reasonable to use \(\delta _f =1\), i.e., correct the voidage to a fluid grid with a cell spacing that equals the particle diameter. Also, it will be necessary to limit \(a_{\delta _c}\) to some positive nonzero value for very large cell sizes \(\Delta _{cell}/d_p\) to avoid division by zero in Eq. (14).
After finding the correlation for the model parameters, the remaining challenge is calculating the minimum and maximum value of the voidage in the neighboring grid cells. This is necessary to calculate the voidage from the scaled voidage via Eq. (12). A straight-forward, but not necessarily the most efficient, algorithm would simply loop over the neighboring cells and calculate these limiting values for the voidage. Such a loop is generally computationally expensive, especially in case of multi-processor simulations where mesh information is residing on a distributed memory. Therefore, we propose an alternative approach in which we compute the minima as follows (more details about the method of calculation of these quantities can be found in “Appendix B”):
where \(\gamma \) is given by
These equations necessitate a calculation of the voidage gradient when correcting the voidage at the particle position, which is typically computationally more affordable. Furthermore, we note that the curvature of the voidage field can be considered when calculating \(\gamma \), meaning that the proposed correction is valid even on coarse grids for which the voidage profile is no longer linear.
3.3.3 Weighted generalized algorithm for arbitrary voidage gradients
The generalized sigmoidal correction function discussed in the previous section is strictly valid only for situations that feature high voidage gradients. Our preliminary work showed that utilizing such a correction for voidage fields that are characterized by relatively low gradients yields an artificial increase in the total drag force. For such fields, the scaling shown in Eq. (12) is no longer meaningful, since \(\varphi _{f,\max }\)–\(\varphi _{f,\min }\) approaches zero. Consequently, our assumption of a distinctly oriented particle cluster, which forms the basis of our correction, is no longer valid.
To enable our generalized algorithm to also handle low voidage gradients, we next propose a weighted correction algorithm. This algorithm is based on a degree of heterogeneity factor \(D_h\) that quantifies whether a distinctly oriented particle cluster is present or not in a computational cell. In case the voidage gradient is close to the maximum value possible in a computational cell, the contribution of the sigmoidal correction function outweighs. In contrast, in case the distribution of particles is almost uniform, no correction is needed and the sigmoidal distribution has a marginal contribution. The postulated weighted correction function is
Here the value for \({\varphi ^{\prime }}_{f,\mathrm{sigm}}\) is determined via the generalized sigmoidal correction function shown in Eq. (14). We will show in the section that the simple expression in Eq. (18) is indeed suitable to account for situations with low to high voidage gradients. The degree of heterogeneity is calculated based on the ratio of the local voidage gradient to the corresponding maximum possible value \(\left( {\frac{\varphi _{p,\max } }{\Delta _\mathrm{cell} }} \right) \) in the cell. It is hence defined by
Effect of employing the correction algorithm for a packed bed with a length of \(72d_p\) a voidage distribution versus bed height for the uncorrected case, as we as the case with generalized voidage correction; b total drag for different mesh resolutions; c total drag force analytically calculated for the voidage distribution predicted by \(\hbox {CFDEM}^{\circledR }\); “standard model” refers to using no correction
Effect of employing the correction algorithm for the system shown in Fig. 2c a voidage distribution versus bed height for the uncorrected case, as we as the case with generalized voidage correction; b total drag for different mesh resolutions
3.4 Benchmarking the voidage correction algorithms
3.4.1 Drag force in case of voidage jumps
The fidelity of the proposed correction algorithms for predicting the total drag force is examined next. To do so, after successful implementation of the proposed voidage correction model in \(\hbox {CFDEM}^{\circledR }\), a set of simulations was performed for various grid sizes, i.e., \(2d_p\)–\(10d_p \), for the generalized algorithm (denoted as “generalized algorithm,” see Sect. 3.3.2). In a fluidized bed the angle between the flow field and voidage gradient contributes to the exchange coefficients [23]. As discussed in Sect. 3.4.4, our correction algorithm will be evaluated for packed beds in the present work—the evaluation for fluidized bed (and hence arbitrary angles between flow field and the voidage gradient) will be left for future work. The benchmark case is a packed bed with a length of \(72d_p\) that features two voidage jumps at the inlet and outlet of the particle packing. (More details can be found in Table 1.)
The main criterion for the reliability of the simulation results was that the total drag force in a coarse-grid simulation compared favorably with that in a highly resolved simulation. As shown in Fig. 12a, upon employing the correction model, the voidage distribution can be more accurately predicted in the packed bed at the studied range of cell size and for the region with a sharp gradient of the voidage. As discerned in Fig. 12b, the improved prediction of the voidage distribution through the proposed correction function reduces the effect of a coarse computational grid on the total predicted drag force. However, due to the interpolation of the velocity field at the particle positions (note that the fluid velocity is evaluated at the cell faces), there is still a remaining error when using the generalized algorithm. Unfortunately, this amount of deviation (typically up to 7%) is inevitable since the used interpolation scheme cannot guarantee a correct superficial fluid speed at the particle location. To quantify the effect of this incorrect superficial speed, the total drag force was analytically calculated based on a corrected velocity field and the generalized sigmoidal voidage distribution. As depicted in Fig. 12c, when using a correct velocity field, the total drag force can be accurately predicted with less than 2 % relative error when using the generalized algorithm.
The proposed voidage correction function was also examined for situations with a linear decrease in the voidage in the interface cell as schematically illustrated in Lagrangian case of Fig. 3. The results are depicted in Fig. 13a and show that the voidage correction improves the predicted value for the voidage in the bed to a great extent. However, small deviations from the corresponding value in the fine-grid simulation can be still observed. Therefore, it is expected that the predicted total drag force shows some deviations even after the voidage correction. As shown in Fig. 13b, by correction of the voidage, the total drag force in the bed will be improved by 7.7% for an Eulerian cell size of \(10\,d_p\). The maximum error in case the corrected voidage is used is below 5% for all grid resolutions studied.
3.4.2 Drag force in case of finite voidage gradients
In order to check the generality of the proposed voidage correction model to situations with different voidage gradients \(\nabla \varphi _f\), an additional array of simulations was performed. To generate a defined voidage gradient, and as proposed by ten Cate and Sundaresan [20], an original particle bed (indicated with the subscript 0) having a uniform volume fraction \(\varphi _{p,0} \) was stretched. Thus, the original particle positions \(x_{p,0} \) were stretched to new particle position \(x_{p,\mathrm{new}}\) as follows:
Here we require \(\varphi _{p,new} =C_\varphi x+b\), i.e., we realize a linear voidage distribution. Consequently, \(\nabla \varphi _{p,\mathrm{new}}=C_\varphi \). Particles were initialized in \(\hbox {LIGGGHTS}^{\circledR }\), compacted to form a random bed, and then the position of each particle was modified based on Eq. (20). An illustration of the resulting particle bed is shown in Fig. 14.
As shown in Fig. 15a, application of the sigmoidal correction model (i.e., the generalized correction algorithm) for a constant voidage gradient of \(0.3\frac{\varphi _{p,\max } }{\Delta _\mathrm{cell} }\) worsens the prediction of total drag force. This is due to the artificial underprediction of the voidage as already discussed in “Sect. 3.3.3.”
However, as shown in Fig. 15a, b, using the weighted generalized correction algorithm significantly improves the prediction of the total drag force. This is true for various values of the voidage gradient and cell sizes up to \(10d_p\). While the need for a correction is not justified for low values of the voidage gradient (see Fig. 15a), the weighted generalized algorithm greatly improves the predictions for the larger value of \(0.5\varphi _{p,\max } /\Delta _\mathrm{cell} \) as shown in Fig. 15b.
3.4.3 Validity of the algorithm for heat transfer predictions
The rate of heat transfer in the gas–particle flow is mainly influenced by the particle volume fraction via the heat transfer coefficient and the slip velocity. Hence, unreliable prediction of voidage can influence the accuracy of heat transfer rate and temperature distribution as well. Consequently, the application of the voidage correction, as suggested in the present work for particle–fluid momentum exchange, can be extended to PU-EL simulation of heat and/or mass transfer in gas–solid flows. To assess the fidelity of the proposed voidage correction algorithms for prediction of heat transfer, a set of simulations of gas–solid system with fixed particles and sharp voidage gradient was performed considering various cell sizes. It should be noted that the simulation setup is the same as one used for Fig. 12. To compare the total rate of heat transfer in a steady-state condition, the particles’ temperature was kept constant, and the length of the bed chosen in such a way that the gas experiences insignificant heating when flowing through the bed.
The results of simulation for standard (i.e., no correction) and the generalized sigmoidal model are depicted in Fig. 16. As discerned from this figure, increasing the grid size reduces the total heat transfer rate in the system. Similar to its effect on the drag force, coarsening the grid smears out the voidage and consequently decreases the average heat transfer coefficient. This trend demonstrates the role of the voidage in prediction of system thermal performance. However, as depicted in Fig. 16, employing the voidage correction model can only partially improve the prediction of the total heat transfer rate in coarse-grid simulations. This is surprising, since the correction factor for the Nusselt number, \(\frac{Nu_{p,\mathrm{corr}}}{Nu_\mathrm{p}}\), at a cell/particle size ratio of 8 falls into the range of 0.86–1.28 (see Fig. 16c). This is a lower degree of correction in comparison with the drag coefficient \((0.71<\frac{\beta _\mathrm{corr} }{\beta }<1.4\), see Fig. 17a in the following paragraph). The observed more significant deviation for the heat transfer rate can hence be related to the interpolation of fluid quantities in the CFD cell. In other words, the fluid–particle heat exchange rate is influenced not only by the interpolation of the voidage and the fluid velocity field, but also by the fluid temperature interpolation. The predicted deviation can be associated with the weak sensitivity of the Nusselt number to the particle volume fraction and the strong influence of the fluid–particle relative speed which is analyzed. Indeed, the used drag law [31] features a more significant dependency on the voidage, but a lower sensitivity to the relative speed when compared to the used Nusselt number correlation [35]. Therefore, the fidelity of the proposed voidage correction function is eroded by the interpolated fluid velocity and temperature. This is since fluid velocity and temperature affect the heat transfer coefficient and the heat transfer rate. To isolate the effect of these two sources of error (i.e., interpolation of velocity and temperature), two sets of simulation were performed with constant values of: (i) gas–particle relative velocity and (ii) gas and particle temperatures + relative velocity. Comparing Fig. 16a, b demonstrated that upon using constant relative velocity, the deviation of total exchange rate in the standard model decreases to around six percent. The prediction of the corrected model improves to approximately five percent. When using a constant gas–particle temperature difference the deviation decreases especially for the generalized correction model. Therefore, it can be concluded that the fidelity of the proposed voidage correction function is mainly governed by the relative contribution of flow quantities, such as temperature and velocity field compared to that of the solid volume fraction on the predicted exchange rate. In short, the closure law employed for the computation of exchange coefficients must be considered. For instance, when applying the correlation of Deen et al. [35], the dependency of exchange coefficient is dominated by the flow speed rather than the solid concentration.
Assessment of developed voidage correction algorithm for predicting heat transfer rates in a packed bed for a generalized correction model and b enforcing constant relative velocity and/or temperature difference and c dependency of correction factor for the Nusselt number on solid particle volume fraction
As it can be concluded from this section, the correction model presented in this study is not limited to the hydrodynamics and can be used for heat and mass transfer without modification.
3.4.4 Discussion on the future extension of the algorithm to consider the relative voidage gradient angle
The proposed algorithms have been tested for situations in which the voidage gradient is aligned with the flow field. Also, our algorithm can be potentially useful for more complex situations in which the angle \(\theta \) between the voidage gradient and the main flow direction is nonzero, e.g., as encountered in fluidized beds. With “main flow” we hereby refer to the fluid–particle relative speed. To do so, the following approach was adopted
-
(i)
The correction function proposed in the current work was used for situations in which the fluid–particle relative speed is aligned with the voidage gradient (see Fig. 17a). Thus, based on the corrected voidage a corrected drag coefficient \(\beta _\mathrm{corr}\) can be calculated, and one can define:
$$\begin{aligned} \frac{\beta _\mathrm{corr} }{\beta }\left( {\theta =0} \right) =C_\varepsilon \end{aligned}$$(21) -
(ii)
The filtered drag model proposed by Radl and Sundaresan [16] for clustered flows, i.e., chaotically oriented particle clusters, was used for situations in which the voidage gradient is perpendicular to the fluid–particle relative speed (see Fig. 17b):
$$\begin{aligned} \frac{\beta _\mathrm{corr} }{\beta }\left( {\theta =\frac{\pi }{2}} \right) =C_f \end{aligned}$$(22) -
(iii)
Following the work of Li et al. [23], and as shown in Fig. 17c, a cosine function was fitted to calculate the correction factor for the drag coefficient for intermediate angles:
$$\begin{aligned} \frac{\beta _\mathrm{corr} }{\beta }=\frac{C_\varepsilon +C_f }{2}+\frac{C_\varepsilon -C_f }{2}{\cos }\left( {2\theta } \right) \end{aligned}$$(23)
As shown in Fig. 17c, the proposed algorithm will hence account for the voidage, the Eulerian grid cell size, as well as the orientation of the voidage gradient when correcting for the drag coefficient. While the magnitude of the voidage gradient is accounted for in the limit of \(\theta =0\), it is not considered when blending between distinctly and chaotically oriented particle clusters. Most importantly, for particle volume fractions \(\varphi _p\) near the close-packing limit, the proposed algorithm would suggest a much stronger positive drag correction compared to the negative correction proposed by Radl and Sundaresan [16]. This remarkable finding may explain the nonmonotonic behavior of the data for \(\varphi _p >0.5\) in Fig. 3 of Radl and Sundaresan [16], i.e., the strong increase in the drag correction near the close-packing limit.
4 Conclusion
In the present work, the effect of grid coarsening and hence that of unresolved property profiles on the predicted flow and thermal behavior of dense fluid–particle systems were investigated. Initially, the validity of filtered drag models developed for dilute flow was evaluated; it was shown that these filtered models cannot be reliably used for dense particulate flows with a coherent particle ordering. Specifically, we presented that available filtered models worsen the prediction for such systems on comparably coarse computational grids. In fact, while chaotically oriented particle clusters result in a reduction of the effective drag coefficient, the opposite is true for distinctly oriented particle clusters: Due to the nonlinear dependency of the drag coefficient on the voidage, distinctly oriented particle clusters necessitate a positive drag correction when performing coarse-grid simulations.
To systematically evaluate the influence of unresolved voidage fluctuations in dense flows, a set of simulations was performed considering packed and fluidized beds using the software \(\hbox {CFDEM}^{\circledR }\). The result of PU-EL simulations demonstrated that coarsening the CFD grid size reduces not only the total drag force, but also the total heat exchange rate in these flows. Therefore, in contrast to comparably dilute flows, a correction factor of larger than unity is required for all exchange coefficients, i.e., the drag and heat or mass transfer coefficients. Another interesting finding is that the deviation of the total drag force when using the EE approach is lower than the one when using a PU-EL approach. This is in contradiction with the results of simulations presented by Cloete et al. [38]. Specifically, these authors claimed that a discrete phase method (similar to the PU-EL approach considered in our present work) provides a better prediction of solid fluxes in coarse-grid simulation of a circulating fluidized bed. This disagreement can be explained by the comparison of the fluidization regime and the criterion chosen for judging the reliability of the simulation approach. In detail, in the case simulated by Cloete et al. [38], i.e., risers, the particles flow in form of clusters. Thus, the flow is comparably dilute, and as mentioned before, the effect of the grid size on the drag force arises due to unresolved voidage fluctuations and chaotically oriented particle clusters. In addition, Cloete et al. [38] used macroscopic bed characteristics as the measure for judging the reliability of the simulation. Particularly, they compared solid fluxes, while—as reported in their publication—the granular temperature could not be held constant. Since the latter has a fundamental effect on the voidage distribution, the peculiar behavior of the discrete simulation could not be fully revealed. The latter was the case in our present study, and hence we were able to identify this important shortcoming of the PU-EL approach.
We ultimately demonstrate that when adopting an algorithm to map the voidage in a coarse-grid simulation to the corresponding value in a fine-grid simulation, one can improve the prediction of exchange coefficients. Specifically, the voidage distribution in a particle system with voidage jumps was approximated using a sigmoidal function for different grid sizes. This allowed us constructing a voidage correction function that yields stable and accurate results. This correction of the voidage is of high importance to exclude the numerical artifacts from CFD-DEM predictions as reported by Lu et al. [24]. Considering DNS results as a reference, they proved that the coarse-grid simulation of gas–particle flow using EE and EL approach fails to predict the voidage distribution accurately. After successful implementation of the voidage correction function in \(\hbox {CFDEM}^{\circledR }\), a grid resolution study considering a packed bed proved the fidelity of the proposed correction function. To generalize the proposed correction function for various voidage gradients, the correction model was extended through a weighting function. Our simulation results prove the validity of such an approach for various values of the voidage gradient. Finally, the proposed correction function was applied for the prediction of heat transfer rates in a packed bed. An improvement of the total predicted heat transfer rate could be demonstrated for coarse-grid simulations. However, we show that this improvement is small compared to that for the drag force. This indicates that the functional form of the closure employed, specifically the relevance of the fluid–particle relative speed compared to that of the voidage, affects the overall fidelity of the proposed correction concept. Thus, while a voidage correction helps to improve the prediction of heat and mass transfer rates, more work is needed to account for grid effects on the fluid speed and temperature (or concentration) seen by individual particles.
Ultimately, an algorithm was proposed that blends the correction developed in this study with classical filtered drag models for chaotically oriented particle clusters. The remaining challenge is to systematically investigate whether the proposed blending function, inspired by the work of Li et al. [23], is indeed suitable for a wide range of applications. Along the same line of thoughts, the magnitude of the voidage gradient may be a suitable candidate to further improve the proposed blending between distinctly and chaotically oriented particle clusters. However, such an improvement first necessitates a more profound understanding of the role of voidage gradients on the drag in chaotically oriented particle clusters.
References
Avci B, Wriggers P (2012) A DEM–FEM coupling approach for the direct numerical simulation of 3D particulate flows. J Appl Mech 79:010901
Johnson AA, Tezduyar TE (1997) 3D simulation of fluid-particle interactions with the number of particles reaching 100. Comput Method Appl Mech Eng 145:301–321
Igci Y, Andrews AT, Sundaresan S, Pannala S, O’Brien T (2008) Filtered two-fluid models for fluidized gas-particle suspensions. AIChE J 54:1431–1448
Ozel A, Kolehmainen J, Radl S, Sundaresan S (2016) Fluid and particle coarsening of drag force for discrete-parcel approach. Chem Eng Sci 155:258–267
Ozarkar SS, Yan X, Wang S, Milioli CC, Milioli FE, Sundaresan S (2015) Validation of filtered two-fluid models for gas-particle flows against experimental data from bubbling fluidized bed. Powder Technol 284:159–169
Milioli CC, Milioli FE, Holloway W, Agrawal K, Sundaresan S (2013) Filtered two-fluid models of fluidized gas-particle flows: New constitutive relations. AIChE J 59:3265–3275
Girardi M, Radl S, Sundaresan S (2016) Simulating wet gas-solid fluidized beds using coarse-grid CFD-DEM. Chem Eng Sci 144:224–238
Schneiderbauer S (2017) A spatially-averaged two-fluid model for dense large-scale gas-solid flows. AIChE J 63:3544–3562
Parmentier JF, Simonin O, Delsart O (2012) A functional subgrid drift velocity model for filtered drag prediction in dense fluidized bed. AIChE J 58:1084–1098
Li J (1994) Particle-fluid two-phase flow: the energy-minimization multi-scale method. Metallurgical Industry Press, Beijing
Wang J, Ge W, Li J (2008) Eulerian simulation of heterogeneous gas-solid flows in CFB risers: EMMS-based sub-grid scale model with a revised cluster description. Chem Eng Sci 63:1553–1571
Zhang J, Ge W, Li J (2005) Simulation of heterogeneous structures and analysis of energy consumption in particle-fluid systems with pseudo-particle modeling. Chem Eng Sci 60:3091–3099
Wang J, Van der Hoef M, Kuipers J (2010) Coarse grid simulation of bed expansion characteristics of industrial-scale gas-solid bubbling fluidized beds. Chem Eng Sci 65:2125–2131
Sundaresan S (2003) Instabilities in fluidized beds. Ann Rev Fluid Mech 35:63–88
Fullmer WD, Hrenya CM (2016) Quantitative assessment of fine-grid kinetic-theory-based predictions of mean-slip in unbounded fluidization. AIChE J 62:11–17
Radl S, Sundaresan S (2014) A drag model for filtered Euler–Lagrange simulations of clustered gas-particle suspensions. Chem Eng Sci 117:416–425
Agrawal K, Loezos PN, Syamlal M, Sundaresan S (2001) The role of meso-scale structures in rapid gas-solid flows. J Fluid Mech 445:151–185
Wang J (2009) A review of Eulerian simulation of Geldart A particles in gas-fluidized beds. Ind Eng Chem Res 48:5567–5577
Andrews AT IV, Loezos PN, Sundaresan S (2005) Coarse-grid simulation of gas-particle flows in vertical risers. Ind Eng Chem Res 44:6022–6037
ten Cate A, Sundaresan S (2006) Analysis of the flow in inhomogeneous particle beds using the spatially averaged two-fluid equations. Int J Multiph Flow 32:106–131
Yang N, Wang W, Ge W, Li J (2003) CFD simulation of concurrent-up gas-solid flow in circulating fluidized beds with structure-dependent drag coefficient. Chem Eng J 96:71–80
Zhou G, Xiong Q, Wang L, Wang X, Ren X, Ge W (2014) Structure-dependent drag in gas-solid flows studied with direct numerical simulation. Chem Eng Sci 116:9–22
Li T, Wang L, Rogers W, Zhou G, Ge W (2017) An approach for drag correction based on the local heterogeneity for gas-solid flows. AIChE J 63:1203–1212
Lu L, Liu X, Li T, Wang L, Ge W, Benyahia S (2017) Assessing the capability of continuum and discrete particle methods to simulate gas-solids flow using DNS predictions as a benchmark. Powder Technol 321:301–309
Cassidy DA, Edwards JR, Tian M (2009) An investigation of interface-sharpening schemes for multi-phase mixture flows. J Comput Phys 228:5628–5649
So K, Hu X, Adams N (2011) Anti-diffusion method for interface steepening in two-phase incompressible flow. J Comput Phys 230:5155–5177
Rycroft C (2009) “Voro++: A three-dimensional Voronoi cell library in C++.”
Kloss C, Goniva C, Hager A, Amberger S, Pirker S (2012) Models, algorithms and validation for opensource DEM and CFD-DEM. Progress Comput Fluid Dyn Int J 12:140–152
Kloss C, Goniva C (2011) LIGGGHTS-open source discrete element simulations of granular materials based on Lammps. Suppl Proc Mater Fabr Prop Charact Model 2:781–788
Jasak H, Jemcov A, Tukovic Z (2007) OpenFOAM: A C++ library for complex physics simulations. International workshop on coupled methods in numerical dynamics. Croatia, IUC Dubrovnik, pp 1–20
Beetstra R, Van der Hoef M, Kuipers J (2007) Drag force of intermediate Reynolds number flow past mono-and bidisperse arrays of spheres. AIChE J 53:489–501
Ouchene R, Khalij M, Arcen B, Tanière A (2016) A new set of correlations of drag, lift and torque coefficients for non-spherical particles and large Reynolds numbers. Powder Technol 303:33–43
Radl S, Gonzalez B, Goniva C, Pirker S (2014) State of the art in mapping schemes for dilute and dense Euler-Lagrange simulations. In: Johansen ST, Olsen JE (eds) Proceedings of 10th international conference on CFD in oil & gas, metallurgical and process industries. SINTEF, Norway, Trondheim, Norway, pp 1–9
Kloss C LIGGGHTS-PUBLIC Documentation, Version 3.X
Deen NG, Kriebitzsch SH, van der Hoef MA, Kuipers J (2012) Direct numerical simulation of flow and heat transfer in dense fluid-particle systems. Chem Eng Sci 81:329–344
Salehi M-S, Askarishahi M, Radl S (2017) Analytical solution for thermal transport in packed beds with volumetric heat source. Chem Eng J 316:131–136
Fullmer WD, Hrenya CM (2017) Are continuum predictions of clustering chaotic? Chaos: An Interdisciplinary. J Nonlin Sci 27:031101
Cloete S, Johansen S, Braun M, Popoff B, Amini S (2010) Evaluation of a Lagrangian discrete phase modeling approach for resolving cluster formation in CFB risers, In: 7th International Conference on Multiphase Flow
Acknowledgements
Open access funding provided by University of Graz University of Technology.
Funding
Funding was provided by Die Österreichische Forschungsförderungsgesellschaft FFG.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Appendices
Appendix A
Filtered drag model equations
Functions a and f in Eq. (A.1) are piece continuous algebraic functions having the form in Eq. (A.4) and can be obtained through filtering the data from highly resolved CFD-DEM simulation. More details about the model can be found in Ref. [16]
Appendix B
The scaled voidage distribution can be approximated by calculation of minimum and maximum voidage in neighboring cells
The first and second derivative of this function with respect to the position x can be obtained as follows:
After dividing Eq. (B.3) by Eq. (B.2), we arrive at
where \(\gamma =e^{a\left( {x/d_p } \right) }\). Rearranging Eq. (B.4) leads to the expression for the parameter \(\gamma \) that reads:
By dividing Eq. (B.1) with (B.2) an expression for \(\varphi _{f,\min } \) is obtained:
Finally, after substitution of Eq. (B.6) in Eq. (B.1), the parameter \(\varphi _{f,\max } \) can be calculated:
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Askarishahi, M., Salehi, MS. & Radl, S. Voidage correction algorithm for unresolved Euler–Lagrange simulations. Comp. Part. Mech. 5, 607–625 (2018). https://doi.org/10.1007/s40571-018-0193-8
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40571-018-0193-8