1 Introduction

In general, Discrete Element Method (DEM) simulations need to start from a realistic initial particle configuration (called particle packing, or just packing), and the volume of the containing geometry usually needs to be filled as much as possible with particles. The ratio of volume of the particles over the containing geometry volume is called volume fraction (VF). If this initial particle configuration is not realistic, for example not dense enough, it is common to allow it to relax under the influence of gravity into a denser random packing, requiring computation time of the simulation, so in general there is an incentive to have high initial VFs.

Different methods have been proposed to generate particle packings. In [1] they have been classified into dynamic and constructive methods. Dynamic methods are based on a DEM simulation (according to [1]). They are very expensive in terms of computational cost, because the motion of each particle has to be simulated. On the other hand, constructive methods are only based on pure geometric calculations and are therefore a more efficient approach. The constructive methods can be further classified into advancing front methods and non-advancing front. In advancing front methods, particles are sequentially generated in their final positions, in contact with two (2D case) or three (3D case) other particles.

Regarding dynamic methods, wall compression [2], particle expansion [2, 3] and gravity deposition [2] can be mentioned. Constructive methods include sequential inhibition [4], triangulation [5], dropping [6] and advancing front [1, 2, 7, 8]. The above mentioned particle packing methods are briefly explained in the next paragraphs. More detailed reviews on packing methods can be found in [1, 2, 4, 7, 9].

The wall compression method consists of a DEM simulation, at which the domain walls are moved towards the particles so as to reduce the domain volume. This makes that the particles occupy relatively more space inside the containing domain, thus increasing the VF. The YADE software [10–12] has this method implemented.

The particle expansion method is somewhat analogous to the wall compression, but in this case, during the DEM simulation, the domain walls are fixed and particles sizes are expanded using a scale factor \(\alpha >1,\) every certain number of timesteps. Every time particles are expanded, several DEM iterations are required for the system to reach a state of equilibrium. The process terminates when the particles are jammed, usually after having been expanded several times.

In order to obtain a packing with gravity deposition, particles are initially regularly placed on top of a container. After that, a gravity field is applied to all the particles until they fill the container.

The sequential inhibition is one of the less effective packing methods, because it yields zero coordination number and a low VF. In each step of this method, a new particle is generated, and then several successive random positions inside the domain are calculated until the particle, placed in one of them, does not overlap with any existing particle, or until a large number of such random positions has been generated.

Particle packings can also be obtained from triangulations. In this case, the domain is first partitioned into a tetrahedral mesh, and then particles (usually spheres) are inscribed inside the tetrahedra. The main disadvantage of this method is that it is difficult to impose any prescribed distribution on particles sizes.

The dropping method is similar to the previously explained gravity deposition, but does not consist on a DEM simulation, having therefore a lower computational cost. The essential difference of the dropping method with respect to gravity deposition is that when a particle moves, it is directly placed in contact with its closest neighbor in a given direction. That’s why this method is purely geometrical.

It was previously mentioned that, in advancing front methods, particles are sequentially generated in their final positions in contact with one particle of the advancing front, and one (2D case) or two (3D case) additional particles, that are not necessarily in the advancing front. Such advancing front comprises the particles that are generally surrounding the others, and determines all the possible positions where new particles can be placed. The whole advancing front is subdivided into fronts whose definition varies from algorithm to algorithm. For example, in [7] the fronts are triplets of pairwise tangent spheres, while in the algorithm of Sect. 2 each front is a single sphere. The flow diagram of Fig. 1 based on [13] summarizes the basic steps of a generic advancing front algorithm. Such steps are not always the same and can have variations in different specific algorithms.

Fig. 1
figure 1

General steps that are common to all advancing front packing algorithms

Full size image

The problem of disk packing has been efficiently solved using an advancing front approach [1, 2]. The previously cited results allow to obtain high density disk packings in very short times. However, the 3D extension of these algorithms is not trivial. As a matter of fact, the authors of [2], instead of extending their own 2D advancing front algorithm to the case of spheres, proposed an efficient multilayer compaction algorithm [6]. This is because the algorithm itself and the implementation of such 3D extension is difficult because the line segment joining two tangent circles is always covered by these circles in the 2D case, but in 3D the triangle formed by the centers of three non-overlapping spheres can never be completely covered by the spheres.

Despite the previously mentioned difficulty for making the 3D extension of advancing front algorithms, there exists indeed such an extension [7, 8], which is briefly described in the following paragraphs. The main goal of this paper is to present another extension to 3D of 2D advancing front packing algorithms, in such a way that it is possible to obtain high VF packings in linear times.

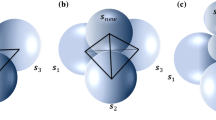
In Benabbou et al.’s algorithm [7, 8], the whole advancing front is comprised by fronts that are triangles whose vertices are centers of already generated spheres (Fig. 2a). Each new sphere \(s_{new}\) is placed tangent to three other \(s_{1},\,s_{2}\) and \(s_{3}\) comprising a front \(s_{1} s_{2} s_{3}.\) After that, the front \(s_{1} s_{2} s_{3}\) is deactivated and three new fronts \(s_{1} s_{2} s_{new},\,s_{1} s_{3} s_{new}\) and \(s_{2} s_{3} s_{new}\) are created by connecting \(s_{new}\) with \(s_{1}\) and \(s_{2},\) with \(s_{1},\) and \(s_{3},\) and with \(s_{2}\) and \(s_{3},\) respectively (Fig. 2b).

Fig. 2
figure 2

Example of an advancing front in Benabbou et al.’s algorithm. a Front \(s_{ 1}s_{ 2}s_{ 3}\) formed by spheres \(s_{ 1},\,s_{ 2}\) and \(s_{ 3},\) and b when the new sphere \(s_{new}\) is placed in contact with \(s_{ 1},\,s_{ 2}\) and \(s_{ 3},\) the front \(s_{ 1} s_{ 2}s_{ 3}\) is deactivated and the three new fronts \(s_{ 1} s_{ 2}s_{new},\,s_{ 1} s_{ 3}s_{new}\) and \(s_{ 2} s_{ 3} s_{new}\) are created

Full size image

This way of defining fronts leads to short computing times and potentially high VFs. It is, however, very restrictive, because a new sphere cannot be in touch with spheres from different fronts. Higher VFs could be obtained if this restriction is removed.

Once a packing has been obtained, it is necessary to evaluate its quality. Most of the existing packing quality indicators can be found in the book [4]. From those indicators, some of the most commonly used are the already mentioned VF, the coordination number, the homogeneity, the angular distribution of contacts and the fabric tensor.

The homogeneity of a packing can be quantified in several ways. Some authors [14] prefer to quantify it in terms of the variance of the void ratio (defined as the ratio of the volume of voids to the sum of particles’ volumes) calculated in several subdomains, while others prefer to quantify it by checking the spatial distribution of the particles’ centers. For example, He et al. [15] subdivide the domain in identical cubic cells, count the number of particle centers in each cell, and finally check if those numbers come from the uniform distribution. This approach has the disadvantage that different cell sizes may yield different results, so it is necessary to determine what cell size is most convenient.

For any given particle in a packing, its coordination number is defined as the number of contacts that such particle has with other particles in the packing. Moreover, the coordination number of the whole packing can be defined as the arithmetic mean of the coordination numbers of particles comprising it. Such number is an indicator of the connectivity of the system.

In a packing of unequal spheres, the angular distribution of contacts can be evaluated by examining the distributions of the relative projections on the Cartesian coordinate axes of the center-to-center lines between touching spheres [15]. Let \(s_{1}\) and \(s_{2}\) be any two touching spheres, of radii \(r_{1}\) and \(r_{2},\) respectively. Let \(x_{12},\,y_{12}\) and \(z_{12}\) be the projection on the x, y and z axis, respectively, of the line joining the centers of \(s_{1}\) and \(s_{2}.\) Then the relative projections of the center-to-center line between \(s_{1}\) and \(s_{2}\) on the x, y and z axis are defined by the expressions \(x_{12}^{\prime }=\frac{x_{12}}{r_{1}+r_{2}},\,y_{12}^{\prime }=\frac{y_{12} }{r_{1} +r_{2}}\) and \(z_{12}^{\prime }=\frac{z_{12} }{r_{1}+ r_{2}},\) respectively. According to [15], a packing of spheres can be considered isotropic if the relative projections obtained for all pairs of contacting spheres follow a uniform distribution in the interval [0, 1].

Another indicator of the isotropy of a packing is the fabric tensor. Like the relative projections of center-to-center lines explained in the previous paragraph, it also describes the distribution of contact orientations [1]. The fabric tensor is defined by the expression

$$\begin{aligned} \varphi _{ij} =\frac{1}{N}\mathop \sum \limits _{p=1}^{N} \frac{\mathop \sum \nolimits _{p_{c} =1}^{M_{p}} n_{i}^{p_{c}} n_{j}^{p_{c}} }{M_{p}}, \end{aligned}$$
(1)

for \(i,\,j\in \{{1,\,2,\,3}\},\) where N is the number of particles in the packing, index p runs through all particles, \(M_{p}\) is the number of contacts of particle p, index \(p_{c}\) runs through all contacts of particle p, and \(n^{pc}=({n_{1}^{p_{c}},\,n_{2}^{p_{c}},\,n_{3}^{p_{c}} })\in {\mathbb {R}}^{3}\) is the unit vector obtained by normalizing the vector with origin at the center of particle p and end at contact \(p_{c}\) of particle p. The sum of the eigenvalues of \(\varphi _{ij} \) always equals 1. The more different they are, the more anisotropic the packing is. In a perfectly isotropic packing, these eigenvalues are all equal to 1/3.

2 New improved advancing front packing algorithm

In this section we present a new advancing front algorithm for packing spheres with any radii distribution D into any arbitrarily complex geometry. The only restriction for distribution D is that its values must be contained within an interval \([a,\,b]\subset {{\mathbb {R}}},\) where a and b are known positive real numbers.

The algorithm proposed here is based on the idea of keeping a set F that contains the spheres comprising the advancing front (in the whole paper, the symbol F will be used to denote the advancing front, and must not be confused with the symbol f defined further in this section). Such spheres are usually the ones surrounding the packing (see Fig. 4). The set F is completely defined by the two following rules:

  1. (1)

    Each new generated sphere is automatically added to F.

  2. (2)

    Each time it is not possible to place a sphere tangent to an element \(s_{0} \in F\) and two of its neighbors (not necessarily members of F), \(s_{0}\) is removed from F.

Let \(s({{{\mathbf {c}}},\,r})\) denote a sphere (or disk, for the analogous 2D case) of center \({{\mathbf {c}}}\) and radius r. In each iteration, a new sphere of radius r is added to the packing (r can be different in each iteration), in contact with a sphere \(s_{0}=s( {{{\mathbf {c}}}_{0},\,r_{0}})\in F\) randomly chosen, and two other neighboring spheres of \(s_{0},\) not necessarily belonging to F. In this case, a sphere \(s_{i} =s({{{\mathbf {c}}}_{i},\,r_{i} })\) is considered to be a neighbor of \(s_{0}\) if and only if their separation is smaller than 2r, i.e., if and only if \(d({{{\mathbf {c}}}_{0},\,{{\mathbf {c}}}_{i}})\le r_{0} +r_{i} +2r,\) where the notation \(d({{{\mathbf {p}}},\,q})\) means the Euclidean distance between \({{\mathbf {p}}}\) and \({{\mathbf {q}}},\) for \({{\mathbf {p}}},\,{{\mathbf {q}}}\in {\mathbb {R}}^{3}.\) We call V the set of such neighbors of \(s_{0}.\) It can be proven that set V can also be defined as the set of all spheres in the packing that overlap with \(s_{V} =s({{{\mathbf {c}}}_{0},\,r_{0}+2r}).\) Two examples of set V can be seen in Fig. 4b, c, respectively, for the analogous case of disks in 2D.

Let \({\tilde{s}}_{1},\,{\tilde{s}}_{2}\) and \({\tilde{s}}_{3}^{~}\) be any three spheres, \(G\subseteq {\mathbb {R}}^{3}\) any subset of \({\mathbb {R}}^{3},\) V a set of spheres and \(r\in {\mathbb {R}}{\text {:}}\,r>0.\) We define \(f({\tilde{s}}_{1},\,{\tilde{s}}_{2},\,{\tilde{s}}_{2},\,G,\,V,\,r)\) as a set of spheres (or the empty set) such that they have radius r, are in outer contact with \({\tilde{s}}_{1},\,{\tilde{s}}_{2}\) and \({\tilde{s}}_{3}\) simultaneously, are completely contained in G and do not overlap with any element of V. The set \(f({\tilde{s}}_{1},\,{\tilde{s}}_{2},\,{\tilde{s}}_{3},\,G,\,V,\,r)\) has at most two elements, because there exist at most two spheres with radius r in outer contact with \({\tilde{s}}_{1},\,{\tilde{s}}_{2}\) and \({\tilde{s}}_{3}\) simultaneously. The expression \(f({\tilde{s}}_{1},\,{\tilde{s}}_{2},\,G,\,V,\,r)\) can be defined for the analogous 2D case, where \({\tilde{s}}_{1}\) and \({\tilde{s}}_{2}\) are disks, \(G\subseteq {\mathbb {R}}^{2}\) and V a set of disks. An example in 2D where \(f({s_{0},\,s_{i},\,G,\,V,\,r})=\{{s_{new}}\}\) can be observed in Fig. 4c.

The proposed method currently still has the disadvantage of remaining gaps between the spheres and the domain boundary \(\bar{G}.\) A new version at which the spheres, whenever possible, are tangent to \(\bar{G}\) is being developed. For the moment, we are making a relaxed use of the definition of function f, and considering that a particle is completely contained in G if its center is contained in G.

Pseudocode 1 contains the steps of our sphere packing algorithm, which is also represented by a flowchart (Fig. 3). In order to use the algorithm with other types of particles, the main required change is in the procedure to place one particle in contact with other three. Although for shapes other than spheres such procedure can be non trivial, the algorithm remains essentially the same.

Fig. 3
figure 3

Flowchart corresponding to Pseudocode 1

Full size image

Step 2 of the algorithm is illustrated in Fig. 4, using the simplified case of disks in 2D. In Fig. 4a, a new radius r is generated, and no other radius will be generated until a disk of radius r is added to the packing. This allows to respect the predefined distribution for radii. In Fig. 4b, a disk \(s_{0} \in F\) is selected at random. It is removed from F, since it is not possible to place a disk \(s_{new}\) of radius r tangent to \(s_{0}\) and one of its neighbors (such neighbors do not have to be necessarily in F), in such a way that \(s_{new}\) is completely contained in the domain and does not overlap with any existing disks. In Fig. 4c, a new disk \(s_{0} \in F\) is selected at random. In this case, it is possible to place a disk \(s_{new}\) of radius r in contact with \(s_{0}\) and one of its neighbors \(s_{i},\) and \(s_{0}\) is not removed from F at this time. Although in this example of Fig. 4d we have that \(s_{i} \in F,\) the case when the neighbor of \(s_{0}\) is not an element of F is also possible.

Fig. 4
figure 4

Example iterations of step 2 of our sphere packing algorithm, for the analogous simplified case of disks. Disks belonging to F are in dark, and disks belonging to V (in b, c) are the ones overlapping with disk \(s_{V}.\) a Radius generation of next disk (in the lower right corner of the square), b selection of element \(s_{ 0}\in F\) (pointed by the arrow), c \(s_{ 0}\) is removed from F and a new element \(s_{ 0} \in F\) is selected (pointed by the arrow), and d new disk \(s_{new}\) is placed in contact with \(s_{ 0}\) and one of its neighbors \(s_{i}\)

Full size image

In each attempt to place a new disk \(s_{new}\) in contact with a disk \(s_{0} \in F\) and one of its neighbors, elements of the set V (defined in Pseudocode 1) of neighbors of \(s_{0}\) are checked until finding one which is suitable in case it exists. The algorithm terminates when \(F=\emptyset .\) It is important to note that the only essential difference between the 2D and 3D cases of our algorithm lies in the fact that for the 2D case, each new particle is placed in contact with an element \(s_{0} \in F\) and a neighbor of \(s_{0},\) while in the 3D case each new particle is placed in contact with an element \(s_{0} \in F\) and two neighbors of \(s_{0}.\)

figure a

The algorithm is guaranteed to terminate in a finite number of steps. This is because only a finite number of spheres of bounded radii can be contained into a finite volume geometry without overlapping.

3 Comparison to constructive methods and packing quality analysis

Our packing algorithm was compared with the constructive algorithms [6] (one of the constructive algorithms with highest VF) and [7] (the only 3D advancing front packing method found in the literature) with respect to VF (Table 1). In order to do so, two cubic domains with side equal to 90 and 266 units were filled with spheres that have the same radii distributions of [6, 7], respectively. For the case of [6], the distribution is the continuous uniform distribution in the interval [0.01, 0.02] \((U[0.01,\,0.02]).\) The radii distribution \(D_{B}\) used in [7] is obtained from a histogram contained in the interval [2, 8] with a mean value approximately equal to 3.53. The VF was calculated using a reference sphere whose radius length is equal to half the size of the cube containing the spheres (see details in Sect. 5). In both cases, our algorithm shows a better performance in VF, which is more than 6 % points higher than [6] and more than 10 % points higher than [7].

Table 1 Comparison between our packer and [6, 7] with respect to VF
Full size table

Packings of Table 1 generated with our code can be seen in Fig. 5. They were generated at the average speeds of 148 (see packing 2 of Table 1) and 296 (see packing 4 of Table 1) particles per second, respectively, using an i3-3110M 2.4 GHz PC. Packing 1 (packing 3) of Table 1 was generated at an average speed of 148 particles per second (33,404 particles per second) with a 1.4-GHz PC (with an Intel Core 2 2.8 GHz PC). The previous values of generation speed are purely indicative and should not be used for any fair comparison. The comparison of our algorithm to other constructive methods was only with respect to VF, given that the time performance comparison of the different methods was not trivial, since the other codes could not be benchmarked on the same PC. An implementation of other methods in order to make a comparison in the same computational platform, is out of the scope of this work.

Fig. 5
figure 5

Packings obtained with our code. a Cube of side 90 filled with spheres with radii distributed \(U[{0.01,\,0.02}]\) and b cube of side 266 filled with spheres with radii distribution \(D_{B}\)

Full size image

Besides comparing our algorithm with others with respect to VF, we also analyzed its quality with other indicators. In order to check the homogeneity, the Kolmogorov–Smirnov (K–S) test to check the goodness of fit to the uniform distribution [16] was applied to the coordinates of centers of particles of Fig. 5. The values of the K–S statistic for the x, y and z coordinates of the centers of particles in both packings of Fig. 5 were 0.785883, 0.881239, 0.691313, 0.848386, 0.95004 and 0.816167, respectively. All these six values lie below the critical threshold of 1.358, calculated for a confidence level of 95 %. This indicates that both packings can be considered homogeneous with a 95 % confidence. For these packings, the distribution of the coordination number c of their particles can be seen in Fig. 6. The coordination number \(\bar{c}\) for both packings, expressed with two decimal digits, is the same and equal to 6.31.

Fig. 6
figure 6

Frequency distribution of the coordination number c of particles of packings of Fig. 5a (continuous line) and b (dashed line). The coordination number \(\bar{c}=6.31\) expressed with two decimal digits is the same for both packings

Full size image

The relative projections of center-to-center lines of contacting particles in packings of Fig. 5 don’t obey an uniform distribution. However, for both packings, the eigenvalues of the fabric tensor (which is another indicator of isotropy and angular contact distribution), are very close to 1/3. These eigenvalues are equal to 0.335, 0.334 and 0.331, for the case of Fig. 5a, and equal to 0.335, 0.333 and 0.332 for the case of Fig. 5b.

4 Comparison to dynamic methods

Theoretically, the highest possible VF, for any random (non-constant) radii distribution, cannot be determined. We have used other packing methods such as gravity deposition and wall compression in order to have an idea of how good the VFs achieved with our packer are.

For the case of radii with distribution \(U[0.01,\,0.02],\) two gravity deposition simulations were carried out. The results are shown in Fig. 7, the first with the DEMeter software [17] and the second with the YADE software [10–12]. In both simulations, 28,000 spheres were compressed gravitationally. VFs were 67.7 % for DEMeter and 65.1 % for YADE, respectively. A third simulation consisting of wall compression with YADE was done using the triaxial test provided by YADE with zero friction, yielding 66.1 % of VF (Fig. 7, right). Therefore, constructive sphere packing algorithms are still about more than 7 percent points below the density obtained by dynamic methods.

Fig. 7
figure 7

Gravity deposition of 28,000 spheres with DEMeter (left, with 67.7 % of VF) and YADE (center, with 65.1 % of VF). To the right, final state of the wall compression simulation with YADE (with 66.1 % of VF)

Full size image

5 Calculation of the VF

If the VF of a packing is calculated according to the definition of the first paragraph of the Sect. 1, it may not be a realistic result (lower VFs would be obtained), especially if there is a gap between the particles and the boundary of the containing geometry. In that case, it is better to calculate VF with respect to a reference volume sphere \(s_{ref}=s({{\mathbf {c}}}_{{{\mathbf {ref}}}},\,r_{ref})\) whose center usually coincides with that of the containing geometry (see example at Fig. 8), and the VF would be in that case the sum of volume intersections of spheres of the packing with \(s_{ref},\) divided by the volume of \(s_{ref}.\) It is important to notice that \(s_{ref}\) does not belong to the packing and is only used to calculate VF. This is the procedure we have used in the previous two sections to calculate VFs. Given any two spheres with radii \(r_{1}\) and \(r_{2},\) respectively, whose centers are separated by a distance d, the volume \(v_{int}\) of their intersection is given by:

$$\begin{aligned} v_{int} \!=\!\left\{ {{\begin{array}{ll} {0},&{} {\mathrm{if}\,d>r_{1} +r_{2} }, \\ {\frac{4\pi }{3}\min \{{r_{1},\,r_{2}}\}^{3},}&{} {\mathrm{if}\,d<|{r_{1} \!-\!r_{2} }|}, \\ {\frac{\pi ({r_{1} +r_{2} -d})^{2}({d^{2}-3({r_{1} \!-\!r_{2}})^{2}+2d({r_{1} +r_{2} })})}{12d}},&{} \mathrm{otherwise}. \\ \end{array} }} \right. \end{aligned}$$
(2)

The VF is never the same for different random packings, but has a statistical deviation. In order to determine how random the VF is in the packings of Figs. 5 and 7, we assigned 31 equispaced values to \(r_{ref}\) (see Fig. 8, right) in the interval \([{r_{max},\,a}],\) where a is half the side of the containing cube and \(r_{max}\) is the maximum radius of the spheres in the packing. The results are shown in Figs. 9 and 10 and commented in the next paragraph. Moreover, the packing of Fig. 5a, b was replicated 10 times and, with the obtained VFs calculated with \(r_{ref} =a,\) the 95 % confidence interval I obtained for the mean density was \(I=[{59.2,\,59.3}](I=[{59.8,\,59.9}]).\)

Fig. 8
figure 8

To the left, packing of Fig. 5. To the right, same packing with a reference volume sphere \(s_{ref}\) inside used to measure VF

Full size image
Fig. 9
figure 9

VF versus \(r_{ref} /a\) curves of packings obtained with our code. a Packing of Fig. 5a, b packing of Fig. 5b and c packing of spheres with radii distributed \(U[{0.01,\,0.02}]\) within a cube of side equal to 1.64

Full size image
Fig. 10
figure 10

VF versus \(r_{ref} /a\) curves of packings obtained with DEM simulations. a Wall compression with YADE, b gravity deposition with YADE and c gravity deposition with DEMeter

Full size image

Points forming apparently continuous smooth VF versus \(r_{ref}/a\) curves can be observed in Fig. 9 (for packings obtained with our code) and Fig. 10 (for packings obtained by DEM simulations). In Fig. 9a, b the curves are decreasing in the interval \(r_{ref}/a<1.\) This is due to the fact that our algorithm starts filling the cubes from their center, and the position and size of the first three particles (whose radii are equal to \(r_{max})\) have a big influence in the VF, especially when \(r_{ref}\) is small (the VF calculated with respect to \(s_{ref}\) only makes sense when \(r_{ref}\) is large with respect to the spheres radii). As a matter of fact, the curve in Fig. 9c is non-decreasing in the region \(r_{ref}/a<1,\) because in that case \({{\mathbf {c}}}_{{{\mathbf {ref}}}}\) was chosen far from the center of the cube containing the spheres. Also, for all plots in Figs. 9 and 10, the VF varies in less than 1 % in the region delimited by lines A and B. In this region, \(r_{ref}\) is less than a but large with respect to \(r_{max}.\) The VF corresponding to \(r_{ref}/a=1\) in the region, which is usually the lowest in such region, is the one we always use to report the VF of a cubic packing. For example, the VF values of packings 2 and 4 of Table 1 correspond to \(r_{ref}/a=1\) in Fig. 9a, b.

6 Temporal performance

The execution time of the algorithm of Sect. 2 (see Pseudocode 1) with respect to the number n of generated spheres is analyzed in this section. We first prove that each step by itself takes an \(O(1)\) time each time it is executed, and then we prove that each step takes a total of \(O(n)\) in the whole execution of the algorithm. This implies that the algorithm takes \(O(n)\) time in total, since those steps are not nested.

The algorithm requires an input of a lower and upper bound \(r_{min}\) and \(r_{max},\) respectively for the sphere’s radii. The existence of the interval \(I=[{r_{min},\,r_{max} }]\) that contains the radii of all the spheres implies that there exists an upper bound \(n_{p} \in {\mathbb {N}}\) for the number of spheres that can be tangent to any generated sphere. It also implies that there exists an upper bound \(n_{V} \in {\mathbb {N}}\) for the number of elements that set V (see step 2.1 of Pseudocode 1) can have. Both numbers \(n_{p}\) and \(n_{V}\) only depend on I.

Since we use a regular grid to find spheres’s neighbors, and the cell size of such grid only depends on I, each calculation of V in step 2.1 takes \(O(1)\) time. This fact, together with the existence of \(n_{V}\) implies that each calculation of \(f({s_{0},\,s_{i},\,s_{j},\,G,\,V,\,r})\) in step 2.2 takes \(O(1)\) time. The existence of \(n_{V}\) also implies that each time the for loop of step 2.2 is executed, its body is executed at most \(n_{V}({n_{V} +1})/2\) times, because \(n_{V}({n_{V} +1})/2\) is the highest number of possible pairs of different elements of V. Since the constant \(n_{V}({n_{V} +1})/2\) only depends on I and the calculation of \(f({s_{0},\,s_{i},\,s_{j},\,G,\,V,\,r})\) takes \(O(1)\) time, it can be affirmed that step 2.2 takes \(O(1)\) time each time it is executed. It can also be seen that steps 1 and 2.3 take \(O(1)\) time each time they are executed. Therefore, each step of the algorithm takes \(O(1)\) time each time such step is executed.

It can be seen that step 1 takes \(O(1)\) time in the whole execution of the algorithm. Step 2.2 is executed exactly n times, since each sphere is added exactly once to the packing. It takes therefore \(O(n)\) time in total. Step 2.3 is also executed exactly n times, since each sphere is removed exactly once from F. It takes \(O(n)\) time in total as well. Step 2.1 is executed exactly 2n times, since each time it is executed, either 2.2 or 2.3 are executed, but not both. So, it takes \(O(n)\) time in total as well. Therefore, the whole algorithm takes \(O(n)\) time in total. Figure 11 shows results of some experiments that confirm this.

Fig. 11
figure 11

Time required to generate a packing as function of the number of generated spheres. The continuous line is for packings with radii distribution \(U[{0.01,\,0.02}].\) The dashed line is for particle radii distribution \(D_{B}\)

Full size image

7 Preliminary applications

Pseudocode 1 can be used to generate packings for a wide range of DEM applications. Figures 12 and 13 show two of these applications. All these packings were obtained with spheres whose radii are uniformly distributed. Here, the issue of defining the problem boundaries has to be addressed before packing the particles. For such complex shapes, the surface may be approximated by a mesh of triangles similar to those adopted in the Finite Element Method.

Figure 12 shows the model of a human skull. The surface was approximated by a mesh comprising 28,684 triangular elements (Fig. 12a).Then the void space was filled with a dense packing of spheres with diameters in the interval [0.3, 0.5]. A total of 1,101,921 spheres were necessary for such packing. This model can eventually be used in Biomechanics to study the fractures due to shocks and penetrating objects.

Fig. 12
figure 12

Bioengineering application. Human skull mesh (a) filled with 1,101,921 spheres (b). This model can eventually be used in Biomechanics to study the fractures due to shocks and penetrating objects

Full size image
Fig. 13
figure 13

Mechanical application. Cutting tool mesh (a) filled with 352,203 spheres (b). This model can be used in tool wear studies

Full size image

Packings like the cutting tool of Fig. 13 can be used in tool wear studies. The surface comprised 180 triangles and the packing took 352,203 spheres with diameters in the interval [4, 5]. Applications of this model are described in [18], where a thermomechanical Discrete Element model is used to simulate the mechanical and thermal phenomena associated with the tool wear in the rock cutting process. There also exists research about soil and tillage–tool interaction using DEM [19]. Discrete Element simulations of tool wear phenomena can help improve the tool design process.

8 Conclusion

An advancing front algorithm for obtaining highly dense sphere packings, filling arbitrarily complex geometries, has been presented. It is simpler than other advancing front packing methods and can also be extended to other types of particles. When compared with other state of the art algorithms (excluding dynamic simulations), it shows a higher VF. The packings obtained were also successfully evaluated with other packing quality analysis techniques. Regarding temporal performance, the number of generated particles is linear with respect to time. Another finding is that the VF of packings generated with not only our code, but also with other constructive codes, is still several percent points below the dynamic initialization methods, for some radii distributions. One of the drawbacks of the algorithm is that the quality of the packings near the domain boundary has to be improved.