Granular gas of ellipsoids: analytical collision detection implemented on GPUs

Abstract

We present a hybrid GPU–CPU implementation of an accurate discrete element model for a system of ellipsoids. The ellipsoids have three translational degrees of freedom, their rotational motion being described through quaternions and the contact interaction between two ellipsoids is described by a force which accounts for the elastic and dissipative interactions. Further we combine the exact derivation of contact points between ellipsoids (Wang et al. in Computing 72(1–2):235–246, 2004) with the advantages of the GPU-NVIDIA parallelization strategy (Owens et al. in Comput Graph Forum 26:80–113, 2007). This novelty makes the analytical algorithm computationally feasible when dealing with several thousands of particles. As a benchmark, we simulate a granular gas of frictionless ellipsoids identifying a classical homogeneous cooling state for ellipsoids. For low dissipative systems, the behavior of the granular temperature indicates that the cooling dynamics is governed by the elongation of the ellipsoids and the restitution coefficient. Our outcomes comply with the statistical mechanical laws and the results are in agreement with previous findings for hard ellipsoids (Bereolos et al. in J Chem Phys 99:6087, 1993; Villemot and Talbot in Granul Matter 14:91–97, 2012). Additionally, new insight is provided namely suggesting that the mean field description of the cooling dynamics of elongated particles is conditioned by the particle shape and the degree of energy equipartition.

1 Introduction

Computer simulations facilitate the mathematical modeling of many systems in physics and engineering. In such numerical algorithms the physical problem is often reduced to a system of differential equations which cannot be solved analytically [4]. Implementing these algorithms has a computational time-cost that for many complex problems is not feasible. Therefore, in recent years several parallelization strategies have been developed [1, 5, 6].

One common option for parallelization is the so-called message passing interface (MPI), which is a standardized communication protocol which is used to coordinate many processes mapped on different nodes. MPI provides a language-specific syntax allowing the process to synchronize and communicate [5]. Although MPI can produce good benchmarks, there are huge differences between serial and parallel implementation of the same algorithm, due to one has to deal explicitly with the message passing. A more immediate option is Open Multi-Processing (OpenMP), which is an application program interface (API) consisting in a set of compiler directives, libraries and environment variables that notably improve the run-time benchmarks [6].

In the last years, graphics processing units (GPUs) have experienced a huge increase in number of cores and flip-flop rate to improve the rendering of more realistic video games. Moreover, GPUs are also becoming a powerful tool in many scientific projects because of its high computing throughput and memory bandwidth [7]. In this way, general-purpose computation on graphics hardware (GPGPU) [1, 8, 9] has become a promising alternative for parallel computing on clusters or supercomputers.

One important field in physics where parallel computing and efficient algorithms are required, due to its computational demands, is granular matter. Discrete element modeling (DEM) is widely accepted as an effective method in addressing physical and engineering problems concerning dense granular media [10]. Using DEM, particle shapes have been numerically identified from digitized images [11], represented either by superquadrics [12], polygons [13–15], ellipsoids [16–22], spheropolygons or spheropolyhedra [23] or by clumps of disks or spheres [24]. Moreover, advanced models that consider contact geometry and particle geometry have been developed by combining DEM with finite element formulations [25].

Nevertheless, the main disadvantages of DEM algorithms are the maximum number of particles and the computing time of the simulation. When examining spherical particles the contact search is the most time consuming part of the computation. Moreover, the computing time in notably enhanced when determining the interaction of non-spherical particles like ellipsoids, whose mathematically rigorous treatment is notably non-trivial [26, 27].

In the past, exact methods of contact detection for ellipsoids based on algebraic conditions have been proposed [26, 27]. However, those procedures generally involve the solution of characteristic polynomial equations, which made them infeasible for most applications, where thousands of particles are modeled. Thus, to achieve fast execution time, a number of approximated contact detection algorithms have been developed [16–19, 22]. For instance, intersection strategies [16], curvature simplifications [17] and geometric potential algorithms, have been introduced [19]. In general, those approximations have captured interlocking, the resistance to rolling; and have reproduced realistic statistics of orientation and stress transmission.

In the present work, we present a step forward in the development of such algorithms. Namely, we introduce an analytical description of an arbitrary number of polydisperse ellipsoids, which is computationally feasible, fast and accurate. Given the algebraic complexity of the interaction problem and its computational cost, we have taken advantage of the GPU-NVIDIA architecture [1] as a parallelization strategy. To validate the accuracy of the hybrid CPU-GPU algorithm, we have examined the free cooling process of a granular gas of frictionless ellipsoids, comparing our results with previous works, where other methodologies are used.

The paper is organized as follows: in Sect. 2 we describe the specific DEM, reviewing the algebraic conditions, which are later involved explaining the contact detection procedure. In Sect. 3 the implementation on GPU architecture is detailed. The homogeneous cooling state of a system of non-friction ellipsoids (Sect. 4) is then used to validate our GPU implementation, namely showing several situations where our implementation reproduces previous results in the literature. At the end, the conclusions and outlooks are presented in Sect. 5.

2 DEM model for ellipsoids

2.1 Relative position between two ellipsoids

An ellipsoid is a geometric object enclosed in a quadratic surface. The algebraic description of an ellipsoid centered at the origin and aligned with the axes in the three-dimensional Euclidean space is given by:

$$\begin{aligned} {x^2\over a^2} + {y^2\over b^2} + {z^2\over c^2}=1 \end{aligned}$$

(1)

where the positive numbers $a, b$ and $c$ are the lengths of the three semi-axis, as it is shown in Fig. 1. For convenience, we then introduce a scale factor ${\mathcal {W}}$ such that $a = a_0 {\mathcal {W}}, \,b = b_0 {\mathcal {W}}$ and $c = c_0 {\mathcal {W}}$, which reduces Eq. (1) to

$$\begin{aligned} {x^2\over a_0^2} + {y^2\over b_0^2} + {z^2\over c_0^2}={\mathcal {W}}^2. \end{aligned}$$

(2)

Fig. 1

Sketch of an ellipsoid, defined by the semi-axis lengths $a,\, b$ and $c$, the center of mass $(x_0,y_0,z_0)$ and $q=[q_0,q_1,q_2, q_3]$ is its quaternion (see text)

Therefore, we embed the three-dimensional Euclidean space in a four-dimensional space, rewriting Eq. (2) in the form

$$\begin{aligned} XSX^T = 0 \end{aligned}$$

(3)

where $X=(x,y,z,1)$ and

$$\begin{aligned} S=\begin{pmatrix} {1\over a_0^2} &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad {1\over b_0^2} &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad {1\over c_0^2} &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad -{\mathcal {W}}^2\\ \end{pmatrix}. \end{aligned}$$

(4)

More generally, an arbitrarily oriented ellipsoid centered at $(x_0,y_0,z_0)$ (see Fig. 1) is defined by a quadratic expression with the form of

$$\begin{aligned}&\alpha _0 x^2 + \alpha _1 y^2 + \alpha _2 z^2 + \alpha _3 xy + \alpha _4 xz + \alpha _5 yz \nonumber \\&\quad + \,\, \alpha _6 x + \alpha _7 y + \alpha _8 z + \alpha _9 = 0 \end{aligned}$$

(5)

where $\alpha _i$ are constants that are determined from the matrix representation of a general ellipsoid, namely

$$\begin{aligned} \textit{XAX}^T = 0 \end{aligned}$$

(6)

with

$$\begin{aligned} A = {\textit{TRSR}}^TT^T \end{aligned}$$

(7)

where $T$ and $R$ are the translational and rotational matrices, respectively. The more general form in Eq. (6) considers the ellipsoid in homogeneous coordinates.

The translational matrix is defined by

$$\begin{aligned} T= \begin{pmatrix} 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 \\ -x_0 &{}\quad -y_0 &{}\quad -z_0 &{}\quad 1 \\ \end{pmatrix} \end{aligned}$$

(8)

and defines the translation of the center of mass from the origin to the point $(x_0,y_0,z_0)$.

For the rotational matrix, instead of the common definition through trigonometric functions of the Euler angles, we use quaternions [28]. The quaternion formalism characterizes each ellipsoid by a four-dimensional vector $q=[q_0,q_1,q_2, q_3]$. In such way that the rotational matrix reads

$$\begin{aligned} R= \begin{pmatrix} 1-q_2^2-2q_3^2 &{}\quad 2 q_1 q_2 - 2 q_0 q_3 &{}\quad 2 q_1 q_3 + 2 q_0 q_2 &{}\quad 0 \\ 2 q_1 q_2 + 2 q_0 q_3 &{}\quad 1 - 2 q_1^2 - 2 q_3^2 &{}\quad 2 q_2 q_3 - 2 q_0 q_1 &{}\quad 0 \\ 2 q_1 q_3 - 2 q_0 q_2 &{}\quad 2 q_2 q_3 + 2 q_0 q_1 &{}\quad 1 - 2 q_1^2 - 2 q_2^2 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 \end{pmatrix}. \end{aligned}$$

We have followed the formulation of Ref. [26, 27], when examining the relative position of two neighboring ellipsoids. It is summarized next (see Fig. 2).

Fig. 2

Tetrahedron built with the eigenvectors $[V_0,V_1,V_2,V_3]$ of $-A^{-1}B$

Let us consider the matrix representation of two ellipsoids, $XAX^T=0$ and $XBX^T=0$. It is a fact that when $A$ and $B$ overlap, there is at least one vector $X$ that satisfies both equations at the same time. Hence, a linear combination between both equations establishes the eigenvalue problem [29],

$$\begin{aligned} \mid \lambda A + B\mid =0 \end{aligned}$$

(9)

with $\lambda$ being the eigenvalue that solves Eq. (9).

Useful properties of Eq. (9) are the following ones:

• P1 The characteristic equation Eq. (9) always has at least two negative roots.

• P2 The two ellipsoids are separated by a plane if and only if the characteristic equation Eq. (9) has two distinct positive roots.

Since the characteristic equation in Eq. (9) is a polynomial equation of degree four, we analyze the nature of the roots of a general quartic equation with real coefficients

$$\begin{aligned} ax^4+bx^3+cx^2+dx+e=0 \end{aligned}$$

(10)

which is determined by the sign of the discriminant for the quartic equation, given by

$$\begin{aligned} \begin{aligned} \Delta =&~256 a^3 e^3 - 192 a^2 b d e^2 - 128 a^2 c^2 e^2 \\&+ 144 a^2 c d^2 e - 27 a^2 d^4 + 144 a b^2 c e^2 \\&- 6 a b^2 d^2 e - 80 a b c^2 d e + 18 a b c d^3 \\&+ 16 a c^4 e - 4 a c^3 d^2 - 27 b^4 e^2 + 18 b^3 c d e \\&- 4 b^3 d^3 - 4 b^2 c^3 e + b^2 c^2 d^2. \end{aligned} \end{aligned}$$

(11)

Namely, when $\Delta <0$ the characteristic equation (Eq. (9) has two complex conjugate roots and two real roots, whereas when $\Delta >0$ one may get four real roots or two pairs of complex conjugate roots. To distinguish between the two last cases with $\Delta >0$, we inspect the auxiliary quantity for the quartic solution $P = 8ac - 3b^2$. If $P<0$ (and $\Delta >0$) all roots are real, otherwise there are two different pairs of complex conjugate roots. Therefore, we conclude that two ellipsoids are disjoint if their characteristic equation has four real roots, two real positive and two real negative roots, and this can be easily detected by evaluating $\Delta$ and $P$ solely. If $\Delta >0$ and $P<0$ the ellipsoids are disjoint, otherwise they are colliding.

According to Ref. [27], when two ellipsoids $A$ and $B$ are disjoint, the four eigenvectors of $-A^{-1}B$ form the vertices of a tetrahedron that is self-polar to both ellipsoids, see Fig. 2. Furthermore, they also proved that two eigenvectors, $V_0$ and $V_1$ are located outside of both ellipsoids while $V_2$ and $V_3$ are inside $B$ and $A$, respectively. Thus, having the four spatial positions $V_i$, the separating plane is well defined by the three (non-collinear) points, $V_0,\, V_1$ and the middle point between $V_2$ and $V_3,\, \mathbf {C}=(V_2+V_3)/2~$. Details about the computation of the contact point and the contact force for overlapping ellipsoids will be shown in Sect. 3.2.

2.2 Equations of motion

In our DEM formulation, each particle $i$ $(i=1 \ldots N)$ has three translational degrees of freedom and their rotational movements are described by the quaternion formalism [30–32]. The translational motion of the particles is governed by Newton’s Second Law of motion:

$$\begin{aligned} \sum _{j=1}^{N_c} \mathbf {F}_{ij}= & {} m \ddot{\mathbf {r}_{i}} \end{aligned}$$

(12)

with ($i = 1,\ldots ,N$) for the translation degrees of freedom. Complementarily, Euler equations describe the rotational motion,

$$\begin{aligned} \sum _{j=1}^{N_c} \tau ^x_{ij}= & {} M^x_i = I_{xx} ~ \dot{\omega }^x_{i} - (I_{yy} - I_{zz})~ \omega ^y_{i} ~ \omega ^z_{i},\nonumber \\ \sum _{j=1}^{N_c} \tau ^y_{ij}= & {} M^y_i = I_{yy} ~ \dot{\omega }^y_{i} - (I_{zz} - I_{xx})~ \omega ^z_{i} ~ \omega ^x_{i},\nonumber \\ \sum _{j=1}^{N_c} \tau ^z_{ij}= & {} M^z_i = I_{zz} ~ \dot{\omega }^z_{i} - (I_{xx} - I_{yy})~ \omega ^x_{i} ~ \omega ^y_{i} \end{aligned}$$

(13)

with $N_c$ the number of contacts of particle $i,\, I_{xx}, I_{yy},\, I_{zz}$ the eigenvalues of the moment of inertia tensor $I_{ij}$, which are given by $I_{xx}={1\over 5} m \left( b^2 + c^2\right)$, $I_{yy}={1\over 5} m \left( a^2 + c^2\right)$ and $I_{zz}={1\over 5} m \left( a^2 + b^2\right)$, respectively. For sake of simplicity, we consider homogeneous ellipsoids with $a=c$, then $I_{xx}=I_{zz}$. $\mathbf {F}_{ij}$ is the force exerted by particle $j$ on particle $i$, and $\mathbf {\tau }_{ij}$ accounts for its corresponding torque. $\mathbf {\omega }_{i}$ and $\dot{\mathbf {\omega }}_{i}$ are the angular velocity and acceleration of particle $i$, respectively. For frictionless ellipsoids there is not net torque acting on the y angular direction $\sum _{j=1}^{N_c} \tau ^y_{ij}$ = 0. Moreover, for $I_{xx}$ = $I_{zz}$ and $\omega ^y_{i}(0) = 0$ there is not momentum interchange between the angular degrees of freedom, resulting $\dot{\omega }^y_{i} = 0$. Hence, in that conditions the rotational movement of our particles are reduced to:

$$\begin{aligned} \sum _{j=1}^{N_c} \tau ^x_{ij}= & {} M^x_i= I_{xx} ~ \dot{\omega }^x_{i}, \end{aligned}$$

(14)

$$\begin{aligned} \sum _{j=1}^{N_c} \tau ^z_{ij}= & {} M^z_i= I_{zz} ~ \dot{\omega }^z_{i}. \end{aligned}$$

(15)

We have implemented a Verlet-Velocity numerical algorithm to integrate the 3D translational equations of motion (see Eq. (12)). Nevertheless, the numerical implementation of the rotational degree of freedom deserves a better description. The set of Eq. (14) are the first of two steps to simulate the evolution of the particles’ angular velocity ${\varvec{ \omega }}$, in the body frame. A second step is necessary to solve the orientation, needed for modeling frictional particles.

The rotational equations of motion are represented using quaternions. The unit quaternion $q = (q_{0},q_{1},q_{2},q_{3})$ with $q^2=1$ characterizes the particle orientation and each quaternion variable satisfies the equation of motion [30]

$$\begin{aligned} {\dot{q}} = {\frac{1}{2}}Q(q)\omega \end{aligned}$$

(16)

with

$$\begin{aligned} \dot{q} = \left( \begin{array}{l} \dot{q_{0}} \\ \dot{q_{1}} \\ \dot{q_{2}} \\ \dot{q_{3}} \end{array} \right) , \quad Q(q) = \begin{pmatrix} q_{0} &{}\quad -q_{1} &{}\quad -q_{2} &{}\quad -q_{3} \\ q_{1} &{}\quad q_{0} &{}\quad -q_{3} &{}\quad q_{2} \\ q_{2} &{}\quad q_{3} &{}\quad q_{0} &{}\quad -q_{1} \\ q_{3} &{}\quad -q_{2} &{}\quad q_{1} &{}\quad q_{0} \end{pmatrix}, \end{aligned}$$

$$\begin{aligned} \omega = \left( \begin{array}{l} 0 \\ \omega _{x} \\ \omega _{y} \\ \omega _{z} \end{array} \right) . \end{aligned}$$

Equations (13) and (16) are solved together using a Fincham’s leap-frog algorithm [33]. This algorithm considers the Taylor expansion of $q(t+dt)$ up to second order

$$\begin{aligned} q(t + dt) = q(t) + dt\,\dot{q}(t) + \frac{dt^{2}}{2}\ddot{q}(t) + O\left( dt^{3}\right) \end{aligned}$$

(17)

and since

$$\begin{aligned} q\Big (t + \frac{dt}{2}\Big ) = q(t) + \dot{q}(t){dt\over 2} \end{aligned}$$

(18)

one gets

$$\begin{aligned} q(t + dt) = q(t) + dt\,\dot{q}\Big (t + {dt\over 2}\Big ) + O\left( dt^{3}\right) . \end{aligned}$$

(19)

Here, the quaternion derivative at the mid-step, $\dot{q}(t + dt/2)$, is required and for that $q(t + dt/2)$ and $\omega (t + dt/2)$ are required. The former can be easily calculated using Eq. (19) where $\dot{q}(t)$ is obtained from Eq. (16) after computing $\omega (t)$ from Eq. (13) as

$$\begin{aligned} \begin{aligned} \omega _x(t)&= \omega _x\Big (t - {dt\over 2}\Big ) + \bigg ({M^x \over I_{xx}} \bigg ) {dt\over 2}, \\ \omega _z(t)&= \omega _z\Big (t - {dt\over 2}\Big ) + \bigg ({M^z \over I_{zz}} \bigg ) {dt\over 2}. \end{aligned} \end{aligned}$$

(20)

In the same way $\omega \Big (t + {dt\over 2}\Big )$ is determined as

$$\begin{aligned} \begin{aligned} \omega _x\Big (t + {dt\over 2}\Big )&= \omega _x\Big (t - {dt\over 2}\Big ) + \bigg ({M^x \over I_{xx}} \bigg ) dt, \\ \omega _z\Big (t + {dt\over 2}\Big )&= \omega _z\Big (t - {dt\over 2}\Big ) + \bigg ({M^z \over I_{zz}} \bigg ) dt. \end{aligned} \end{aligned}$$

(21)

To avoid buildup errors the quaternions $q(t)$ are renormalized every timestep, based on the formulation introduced by Wang [34].

3 DEM implementation of ellipsoids on GPUs

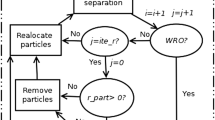
A hybrid CPU-GPU discrete element method has been implemented to compute analytically the local interaction between an arbitrary number of ellipsoids. As most of the GPGPU software some pieces of code run on the CPU and others run on the GPU. Figure 3 represents the algorithm we have developed. In this section, we will describe the implementation in details.

Fig. 3

Flowchart of our DEM algorithm. All the code runs on the CPU until the control is given to the GPU. The overlapped boxes represent different threads running in parallel. For further details about how to determine the relative position between ellipsoids and the analytical calculation of the contact distance and contact plane see Fig. 4

3.1 Overview of the CPU-GPU algorithm

As any other CUDA-software, the program begins with the initialization of the driver API, just to be able to call the functions from the API. Then, the necessary memory is allocated in both CPU and GPU, and the configuration parameters of the system are loaded. All this starting process runs on the CPU as pointed out in the first step of the flowchart of Fig. 3. The following step is the copy of all the particles data from the CPU-initialized variables to the GPU allocated memory.

Once the configuration is set up, the DEM algorithm runs in a temporal for-loop iterator. As we pointed in the previous section, a Velocity Verlet integrator algorithm is used to solve the translational equations of motion [35]. This method is divided into two steps, one at the beginning and one at the end of the loop iteration.

Both steps of the Verlet integrator are functions that run in parallel on the GPU device. In both cases, we take advantage of the powerful library of parallel algorithms and data structures, Thrust [36]. The procedure starts on the CPU, and consist in building tuples of acceleration, velocity, and position based on the particle identifier. Then a thrust-device iterator routine is launched and the control goes to the GPU. The main advantage of using Thrust library is that the number of threads (very basic element of data to be processed) and blocks (group of threads) is optimized depending on the number of tuples, and it is set up in time of execution. When the control goes to the GPU, in parallel, each thread gets a unique tuple and using the acceleration computes the corresponding velocity and position.

Fig. 4

Flowchart of the contact detection and execution for a given pair of neighboring ellipsoids. This routine runs entirely on GPU

Next we execute the collision detection method by using a neighbor list. This method consist in finding all the pairs of ellipsoids in a certain neighborhood, and that are susceptible of being in contact during a particular time-step. The collision detection is implemented using a link cell method [37] while building a list of neighbors with a given frequency. Once the collision is detected, the forces and torques exerted on each particle are calculated. The aim is to determine the total force and torque acting on each ellipsoid. Both subroutines, collision detection and execution, are implemented as traditional kernels.

3.2 Analytical deduction of the interaction force between ellipsoids

In DEM of soft particles a local inelastic deformation is assumed; thus, the interaction force between grains depends on their overlap distance. In Fig. 4 we present the flowchart of the contact detection implementation. As we have already mentioned, the collision detection has been optimized by using a link cell algorithm and a list of contacts.

First, we get a pair of neighboring ellipsoids and build individual matrix using the general representation of Eqs. (6) and (7). After that, we compute the coefficients of their characteristic equation, Eq. (10), the discriminant $\Delta$ (Eq. 11) and the auxiliary quantity $P = 8ac - 3b^2~$. When the discriminant $\Delta$ is positive and $P$ is negative, the ellipsoids are disjoint and so, there is no need to compute any interaction force. Contrary, if the discriminant is negative, the ellipsoids overlap and the contact force and torque are calculated.

As a novel contribution, we have analytically determined a common contact plane ${\mathbf {n}}$ by thoroughly tuning the scale parameter ${\mathcal {W}}$, defined in Eqs. (2) and (4). Thus, we proceed reducing the spatial scale ${\mathcal {W}}$ and shrinking both ellipsoids until they do not overlap anymore, i.e. when the discriminant $\Delta ({\mathcal {W}})= \lambda A({\mathcal {W}}) + B(\mathcal W)$ changes its sign at ${\mathcal {W}}_o$ (see Fig. 5). Remarkably, this part of the our algorithm is quite efficient because it is not necessary to build both matrices, while determining $\Delta ({\mathcal {W}})$ for each value of ${\mathcal {W}}$. Additionally, we have properly factorized the discriminant equation in terms of the parameter ${\mathcal {W}}$ and, as a result, several coefficients are computed just once. Henceforth, we will refer to the shrunk ellipsoids as $A({\mathcal {W}}_o) =A_s$ and $B({\mathcal {W}}_o)=B_s$.

Fig. 5

Determining the contact point. The fuzzy ellipsoids $A$ and $B$ are the original colliding ones. The solid ones $A_s$ and $B_s$ are the shrunk disjoint ellipsoids. The $[V_0,V_1,V_2,V_3]$ tetrahedron is also shown. Contact point is $C$ and $[x_1,x_2]$ is the overlap distance

As a second step, we analytically compute the eigenvectors $V_i$ of $-A_s^{-1}B_s$. As we pointed out above, the four eigenvectors $V_i$ define the contact plane and the contact point $\mathbf {C}=(V_2+V_3)/2$. Then, the normal vector of the contact plane is deduced by the cross product of $\mathbf {V}_0- \mathbf {C}$ and $\mathbf {V}_1-{\mathbf {C}}$ resulting,

$$\begin{aligned} {\mathbf {n}} = \frac{(\mathbf {V}_0- \mathbf {C}) \times (\mathbf {V}_1-{\mathbf {C}})}{| (\mathbf {V}_0- \mathbf {C}) \times (\mathbf {V}_1-{\mathbf {C}}) |}. \end{aligned}$$

(22)

To find the overlap distance $\delta$, we analytically derive the intersection points $x_1$ and $x_2$ between the straight line defined by $V_2$ and $V_3$ with the surface of the original ellipsoids $A$ and $B$. Thus, $\delta$ accounts for the length of the segment $[x_1~x_2]$.

Finally, the interaction force, $\mathbf {F}_{ij}$, and torque $\mathbf {\tau }_{ij}$, between two contacting particles read as:

$$\begin{aligned} {\mathbf {F}}_{ij} ^{N}= & {} -k^{N} \delta \mathbf {n} - \gamma ^{N} v_{rel}^{N} \mathbf {n}, \end{aligned}$$

(23)

$$\begin{aligned} {\mathbf {\tau }}_{ij}= & {} {\mathbf {l}}_{ij} \times {\mathbf {F}}_{ij} ^{N} \end{aligned}$$

(24)

where $k^{N}$ is the spring constant in the normal direction, $\gamma ^{N}$ is the damping coefficient in the normal direction and $v_{rel}^{N}$ is the normal relative velocity between ellipsoids $i$ and ellipsoid $j$. Vector $\mathbf {l}_{ij}$ represents the branch vector related with the contact point. For sake of simplicity, here we consider frictionless ellipsoids, and therefore we do not have any component acting on the tangential direction $\mathbf {t}$.

4 Benchmark: homogeneous cooling of frictionless ellipsoids

To validate our DEM algorithm on GPU architecture, we have implemented a benchmark that consists of a granular gas of ellipsoidal particles without friction. Hence, we have explored the cooling dynamics of a granular gas of frictionless particles. In particular, we examined the evolution of the rotational and translational temperature that are known to depend accordingly on specific laws on the geometrical and elastic properties of the ellipsoids. As we describe in this section, our data outcomes corroborate the ones presented by Villemot and co-workers in Ref. [3].

Initially, the ellipsoids are homogeneously distributed in the space following a simple cubic structure. Their initial translational and rotational velocities follow a Gaussian distribution. To minimize finite size effects, periodic boundary conditions are imposed. Moreover, to remove the sensitivity to initial conditions the system is allowed to execute several hundreds of collisions without dissipation, before starting to analyze the system temporal evolution.

We model hard particles and the maximum overlap must always be much smaller than the particle size. This have been ensured by introducing values for normal elastic constant, $k_n = 10^8$ N/m and $\rho _g = 2000 \,\mathrm{kg/m}^3$. Moreover, we use an equivalent normal dissipation parameter $\gamma _{n} = \sqrt{ {4k_{n}m_{12} \over 1 + \left( {\pi \over \ln e_n}\right) ^2 } }$, depending on the normal restitution $e_n$ and the reduced mass $m_{12}= {m_1 m_2\over m_1 + m_2}$ [38]. Hence, we estimate the contact time as $t_c = \pi \sqrt{m_{12} \over k_n}$, and accordingly a time-step of $\Delta t = {t_c \over 50}$ is set. To validate the algorithm, systems of particles with different coefficient of normal restitution have been studied, namely $e_n = 0.90, ~ 0.95, ~ 0.98$.

In all the simulations reported here, we have a fixed number of $N=4096$ particles, which are confined in a square box of size $L = 2$ m (see Fig. 6), with constant volume fraction $\eta =0.058$. Ellipsoids of several elongations ($\xi \,\in$ $[1.15,~ 3]$) have been examined. In Table 1, the geometrical dimension of the ellipsoids are given in detail.

Fig. 6

a represents an HCS of 3D homogeneous prolate ellipsoids with $\xi =a/b=2.82$ and a volume fraction of $\eta =0.058$ with coefficient of normal restitution of $e_n=0.95$. Plots (b), (c) and d show the HCS of ellipsoids of different kind of elongations of $\xi =1.15,\, \xi =2$ and $\xi =3$ respectively, keeping the same packing fraction

Table 1 Geometrical dimensions of the homogeneous ellipsoids. The elongation, $\xi = a/b$, major semi-axe $a$ and minor semi-axe $b$ are shown. In all cases, the sizes of the semi-axes correspond to a constant volume fraction $\eta =0.058$.

4.1 Homogeneous cooling state

A granular gas is a diluted set of macroscopic grains which loose their energy due to their inelastic collisions. When a granular gas evolves freely, at early stages, the dissipative nature of the collisions leads to a homogeneous cooling state (HCS). In this regime, the density and velocity fields are approximately uniform and all the time dependencies are practically controlled by the granular temperature. Analogously to the kinetic theory of gases the granular temperature can be defined from equating the kinetic energy $T \equiv {1 \over 2} m v^2$.

In the past, the HCS has been described for frictional [39, 40, 42, 43], and non-frictional spheres [44, 45], needless [46], ellipsoids [3] and non-uniform particles [47, 48]. Moreover, in the last years important experimental efforts have been made examining the macroscopic behavior of granular gases [49–52].

In our simulation, we consider a granular gas of $N$ identical ellipsoids of revolution with mass $m$ inside a closed volume $V$, with a global mass density $\rho =Nm/V$. The semi-axis $a$ and $b$ can be expressed in terms of the semi-axis $b$ and the elongation $\xi = a/b$, with $a>b$. The volume of each ellipsoid is defined as $V(\xi ) = {4\over 3}\pi a b^2= {4\over 3}\pi \xi b^3$. The eccentricity of the ellipsoid is $\zeta ^2 = 1 - {1\over \xi ^2}$. The moment of inertia is given by $I_{xx} = I_{zz} = {1\over 5} m \left( a^2 + b^2\right)$.

We can define a granular temperature for our gas of ellipsoids using the translational and rotational energies, reading as,

$$\begin{aligned} T_{tr}= & {} {2 \over 3 N} E_{tr} = {2 \over 3 N} \sum _{i=1}^{N} {1\over 2} m v_i^2, \end{aligned}$$

(25a)

$$\begin{aligned} T_{rot}= & {} {1 \over 3 N} E_{rot} = {1 \over N} \sum _{i=1}^{N} {1\over 2} I \omega _i^2 \end{aligned}$$

(25b)

where we include three translational and only two rotational degrees of freedom because the ellipsoids are frictionless. Following theses definitions Eq. (25), when full equipartition applies, $T_{tr}/T_{rot}=1$.

The total granular temperature of the gas of ellipsoids can also be defined as a weighted average of $T_{tr}$ and $T_{rot}$ by the respective degrees of freedom

$$\begin{aligned} T_{tot} = {3 \over 5} T_{tr} + {2\over 5} T_{rot}. \end{aligned}$$

(26)

Hence, when equipartition applies, $T_{tr} = T_{rot} = T_{tot}$ and a single granular temperature can be examined.

In the simple case of a gas composed by spherical particles, the energy lost can be described by a constant restitution coefficient $e_n$. In this case, it has been deduced that the evolution of the granular temperature obeys Haff’s Law [53, 54],

$$\begin{aligned} {T(t) \over T(0)}= {1 \over (1 + \alpha \Gamma _0 t)^2} = {1 \over (1 + \tau )^2} \end{aligned}$$

(27)

where $\Gamma _0$ is the equilibrium Enskog collision rate at the initial granular temperature $T(0) = { 2 \over 3} {E_{tr}(0) \over N}$ [53, 54]. The coefficient $\alpha$ is defined as a function of both the number $D$ of degrees of freedom and the effective coefficient of normal restitution $e_n$, namely $\alpha = {1-e_n^2 \over 2D}$.

Bereolos et al. [2] examined the transport properties of the hard ellipsoids fluid. Based on these results, and with the same spirit of Ref. [3] the collision rate per particle $\Gamma _0$, of 3D elliptical macroscopic bodies can be defined as,

$$\begin{aligned} \Gamma _0 = 4 \Big ({\pi T(0)\over m}\Big )^{1/2} \rho g_c S_c \langle {\mathcal {D}} \rangle _c \end{aligned}$$

(28)

where the term $\langle {\mathcal {D}} \rangle _c$ measures the average energy transfer between rotational and translational degrees of freedom over collisions and $4 \pi Sc$ accounts for the average exclusion surface in contact. Moreover, $g_c(e)$ is the isotropically averaged contact value of the pair distribution proposed by Song and Mason [55]. There, $e = {\mathcal {R}} (\xi )S(\xi )/(3V (\xi ))$ is the nonsphericity parameter and $S(\xi )$ and ${\mathcal {R}}(\xi )$ define the surface area and mean radius of the convex body, which reads as,

$$\begin{aligned} S(\xi )= & {} 2\pi b^2 \left( 1 + \xi {\frac{\arcsin \zeta }{\zeta }}\right) \end{aligned}$$

(29a)

$$\begin{aligned} {\mathcal {R}}(\xi )= & {} {a \over 2} \left[ 1 + {1\over 2\zeta \xi } \log {\left( {1 + \zeta \over 1 - \zeta }\right) }\right] . \end{aligned}$$

(29b)

Villemot and co-workers [2, 3] compute analytically the quantity $\langle {\mathcal {D}} \rangle _c$, for an homogeneous ellipsoid depending on its elongation $\xi$. Moreover, using an event-driven algorithm, a HCS of ellipsoids was identified. Their findings indicates that the cooling dynamics of a gas of ellipsoids in HCS can be also described by the mean field scheme of Eq. (27).

In the next section, we proceed exploring the kinetic evolution of a granular gas of ellipsoids, using DEM and comparing with the mean field approximation.

4.2 Numerical results

In Fig. 7 we represent the evolution of the translational $T_{tr}$ and rotational $T_{rot}$ kinetic energies for gases of ellipsoids with different elongations. In all cases the kinetic energy is monotonically decreasing, which suggests the establishment of a homogeneous cooling process for ellipsoids similar to the traditional homogeneous cooling state of spheres. Hence, after a short transient, the decay is algebraic $t^{-2}$ in agreement with the asymptotic analytic prediction of Haff’s law. Complementarily, in Fig. 8, the asymptotic value of $T_{tr}/T_{rot}$ varying the elongation and the coefficient of normal restitution is represented. Note that the coupling between degrees of freedom in a gas of ellipsoids is determined by the particle elongation $\xi$. As it was found in Ref. [3], for short ellipsoids the translational degrees of freedom cool down faster than the rotational ones. For longer ellipsoids, however, the energy equipartition $T_{tr}/T_{rot}\approx 1$ is satisfied within the numerical accuracy of the algorithm. Specifically, for ellipsoids with $\xi < 2$, at a given time the rotational kinetic energy is slightly greater than the translational one, but for $\xi >2$ the translational and rotational kinetic energy equally evolves in time. This indicates that for short ellipsoids $\xi <2$, the energy interchange between the rotational and translational degrees of freedom is notably affected, and full energy equipartition is not satisfied (see Fig.7). Although this behavior is highly non-trivial, it is still intuitive that after crossing the $\xi _c=2$, from above, a single collision of two particles may favor the translational to rotational energy transfer. Note that in collisions where the contact point is close to the center of mass of one of the particles, its translational energy diminishes, while its rotational degree of freedom is less affected. As particles get shorter, central collisions are more and more frequent, which may unbalance the energy interchange process.

Fig. 7

Translational temperatures and $T_{tr}/T_{rot}$ as function of the time for different elongations $\xi$ (from 2 to 3) and with a coefficient of normal restitution of $e_n=0.95$.

Fig. 8

Asymptotic value of $T_{tr}/T_{rot}$ as a function of the elongation, for different coefficients of normal restitution.

To compare the obtained cooling dynamics with the analytic expression Eq. (27) one needs to introduce a proper collision rate $\Gamma _0(\xi )$ and the value of $\alpha = {1-e_n^2 \over 2D}$, in which $D$ is interpreted as the number of degrees of freedom among which energy is transferred [3]. In Fig. 9, we illustrate the comparison of our numerical outcomes for the evolution of

Fig. 9

Kinetic translational energy $E_{tr}(t)/E_{tr}(0)$ as a function of the collisional time $\tau = \alpha \Gamma _0(\xi ) t$ obtained for different elongations, using as collision rate $\Gamma _0(\xi )$ Eq. (28). Note that exactly the same is obtained, when plotting $T_{tr}(t)/T_{tr}(0)$ as a function of $\tau ^* = \alpha ^* \Gamma _0(\xi ) t$, with $\alpha ^*=\sqrt{3/2}\;\alpha$

$E_{tr}(t)/N$ vs the collisional time ($\tau = \alpha \Gamma _0(\xi ) t$) with the analytical expression Eq. (27). For each case, the value of $\Gamma _0$ has been analytically deduced from Eq. (28), using Eq. (29a) and (29b), as well as the eccentricity $\xi$ of the ellipsoids. Moreover, for $\langle {\mathcal {D}} \rangle _c(\xi )$ the analytical values of Ref. [3] were used. The numerical data corresponds to particles with an effective restitution coefficients of $e_n = 0.90,\, 0.95$ and $0.98$, and results for several particle shapes $\xi$ are shown. In each case, the solid line represents the theoretical prediction of Eq. (27) using $T(0)=E_{tr}(0)/N,\, \alpha = {1-e_n^2 \over 2D}$ and setting $D=5$, that corresponds with three translational and two rotational degrees of freedom, respectively [3]. This nice scaling of the curve and the remarkable agreement with the analytic prediction validates the performance of the numerical algorithm. However, the agreement is slightly lost as we approach to the limit $\xi =1$ (spheres), as well as when the dissipation is enhanced. This seems to correlate with the fact that long ellipsoids $\xi > 2$ exhibit nearly perfect equipartition, and short ellipsoids equipartition is lacking $T_{tr}/T_{rot} \ne 1$.

As we pointed out earlier, performing even driven simulations a homogeneous cooling state in a gas of hard ellipsoids was earlier identified [3]. Thus, in Ref. [3] the cooling dynamics was also compared with Haff’s law Eq. (27), but examining the evolution of the total kinetic energy $T_{tot}(t)$ defined in Eq. (26). In Fig.10, we illustrate the kinetic evolution of the total temperature $T_{tot}$ defined by Eq. (26), for system with $\xi < 2$ i.e., where no-equipartition is found. The time scale has also been rescaled $\tau = \alpha \Gamma _0(\xi ) t$, using the analytical values of $\Gamma _0(\xi )$ and the total initial temperature $T(0)=T_{tot}(0)$. It is noticeable that Eq. (27) seems to predict the cooling dynamics during the homogeneous state in terms of $T_{tot}(t)$, for $\xi < 2$ where equipartition is lacking $T_{tr}/T_{rot} \ne 1$.

Fig. 10

Total energy as a function of the collisional time $\tau = \alpha \Gamma _0(\xi ) t$ obtained for different elongations (cases where $T_{tr}/T_{rot}\ne 1$, and several restitution coefficient. In all cases the solid line represents the analytic prediction of Eq. 27, using the collision rate $\Gamma _0(\xi )$ proposed in Ref. [3]

Although our outcomes are in good agreement with [3], they also seems to indicate that the naive mean field description of the cooling dynamics by Eq. (27) is conditioned to the existence of energy equipartition. Moreover, note the cooling dynamics predicted by Eq. (27) is based on the assumption that the restitution coefficient is constant, regardless the details of the collision event. This assumption is natural when performing event-driven simulations. Meanwhile, presupposing a constant restitution coefficient is not always valid when using DEMs of non-spherical particles, because the energy losing generally depends on the type of collision. However, the quality of the scalings obtained for the kinetic evolution of ${E_{tr}(t) \over N} = {3 \over 2} T_{tr}(t)$, (see Fig.9 results for $\xi >2$)) indicates that the particle shape can be simply accounted introducing a new characteristic time $\tau ^* = \alpha ^* \Gamma _0(\xi ) t$, which can be identified using an effective dissipation $\alpha ^* = \sqrt{3 \over 2} \; \alpha$ [47].

In addition, we have also examined the velocity statistics during the cooling process. Originally, the velocity distribution of the particles follows a Gaussian distribution then due to the low dissipation the system cools down uniformly. Consequently, the particle velocity distribution is practically governed by a single scale corresponding to the mean translational temperature $T_{tr}(t)$, and one can identify a dynamic scaling regime where the scaled velocity distribution $P(c)=P\left( {{v_i} \over {v_{ms}}}\right)$ becomes stationary (see Fig. 11). The scaled velocity distributions on the $x$ direction are illustrated at several times. The mean-square speed $v_{ms}$ has been used as scaled parameter. In all cases, the velocity distributions remain close to a Gaussian $P(c) = {1 \over \sigma _c \sqrt{2\pi }} e^{-{c^2 \over 2 \sigma _c^2}}$ featuring the expected homogeneous cooling state. Regardless of the particle anisotropy (data not shown), the scaled velocity distribution remains close to a Gaussian.

Details concerning the numerical performance of the algorithm are summarized in Table 2. We have benchmarked the algorithm computing the cooling process of ellipsoids and spheres, using different number of particles $N$ and a fixed volume fraction $\eta =0.058$. For sake of simplicity, in all cases we have used a cubic initial distribution and the system size $N$ was always multiple of $32$ [56, 57]. The control parameter was a Cundall Number ($N_C= N N_i/t_r$), where $t_r$ is the real time elapse needed to compute $N_i$ iterations. The benchmarks were executed on the same PC with an NVIDIA GeForce TITAN Black of 2280 NVIDIA cores. Note that, for small system when increasing the system size the Cundall number increases, because $N$ is smaller than the number of the GPU-cores. However, when the system size reach the GPU maximum capabilities the Cundall Number tends to a plateau, indicating $N_C \propto N$. As expected the performances of equivalent systems composed by spheres are notably better due to the simplicity of the contact interaction. Finally, it is important to remark that the reported values of $N_C$ strongly depend on the specific configuration conditions, specially the volume fraction $\eta$, which determines the collision frequency.

Fig. 11

Normalized translational velocity distribution at different times for a system of 4096 frictionless ellipsoids. Results at different times are presented. The dashed lines corresponds to a Gaussian Fit

Table 2 Values of the Cundall Number obtained computing the cooling dynamics of several number of particles $N$ during one second of simulation. For comparison results of spheres are also shown

5 Conclusion

We have presented a novel CPU-GPU implementation of an accurate DEM algorithm for a system of ellipsoids. We have implemented on GPU architecture, an analytical collision detection method and a novel method to compute the overlap distance and normal plane of contact for two colliding generalized ellipsoids. Although, sequentially, this is a really time-consuming procedure, we have taken advantage of the GPU multicore architecture.

The accuracy of the algorithm has been validated by simulating a granular gas of homogeneous prolate ellipsoids with low dissipation. We have found a uniform regime, where both the translational and rotational kinetic energy homogeneously decrease, suggesting the establishment of a homogeneous cooling process. Our findings for the collision frequency, depending on the particle eccentricity, have been validated comparing with kinetic theory for a gas of ellipsoids [3] However, the results indicate that the mean field treatment of the cooling dynamics of elongated particles is conditioned by the existence of energy equipartition. Although the results presented here are focused on frictionless ellipsoids, it is important to remark that taking advantage of the implemented kernels for rough spheres [41], the implementation of rough generalized ellipsoids is straightforward. The latter would allow us to investigate more complex processes, in granular gases of rough particles with high dissipation, where clustering and significant translation-rotation correlations are expected [42, 52]. Finally, following our findings, a detailed comparative analysis between our present framework and other parallelization strategies is now demanding. Up to authors knowledge no other analytical implementations were done that address large scales similar to the ones addressed in this paper. For comparing different performances the development of a complete new algorithm, using MPI or OPENMP is necessary. This point will be addressed elsewhere.