1 Introduction

For economic and reliable operation of power systems, it is important to forecast demand and price simultaneously over a range of time scales, from minutes to months, so that market participants can maximize their revenues [1, 2]. In the present scenario, forecasting techniques are increasingly used for proper planning and reliability of almost all deregulated power pools. However, in smart grids, demand and price forecasting has a major role due to the chance for electricity consumers to react to the market clearing price (MCP), which may affect the demand curve and result in the deviation of electricity prices from the initial forecast. In smart grids, consumers concentrate on the daily demand consumption based on electricity price changes, which in turn can help market participants to fix up appropriate bidding strategies for maximizing their revenues. For this purpose, smart grids need to employ intelligent and adaptive control mechanism, which requires accurate demand and generation forecasting for smooth operation in an optimized way [3,4,5]. Due to this fact, the importance of demand and price forecasting has been highlighted separately in two subsections below:

1.1 Demand forecasting

Several data driven approaches have been proposed by the authors for short-term demand forecasting [4]. The traditional time series models for demand forecasting include autoregressive moving average (ARMA) [6] and autoregressive integrated moving average (ARIMA) models [7], autoregressive moving average with exogenous variables (ARMAX) models [8] and generalized autoregressive conditional heteroscedastic (GARCH) models [9]. However, to overcome the deficiencies of the above statistical models in providing an accurate forecast, modern intelligent learning algorithms find more suitability as proposed by the researchers. The intelligent learning techniques include artificial neural networks (ANNs) [10, 11], support vector machines (SVMs) [12, 13], functional link network [14], rule-based systems [15], and fuzzy neural networks [16], etc. For proper planning and smooth operation of power systems, accurate demand forecasting will ensure the independent system operators (ISOs) to effectively schedule the generation and transmission resources which will be beneficial for the market participants.

1.2 Price forecasting

Because of price volatility, MCP forecasting is becoming a key issue in all the deregulated power pools taking into account the accurate bidding strategy [17,18,19,20,21,22]. The electricity price fluctuations are more erratic for which complex neural architectures are required for accurate forecasting. Although in most of the forecasting studies, both electricity demand and price are forecasted separately, there are few studies in which both lagged demand and price values are used as inputs to forecast future electricity prices. The model input comprising of both demand and price signals leads to a bi-directional approach in which reactions of the consumers to forecasting prices and subsequent changes in the demand pattern of the target day are taken into consideration, resulting in changes in the observed prices [2, 4, 23]. This mixed approach leads the consumers to manage their consumption based on the price forecasts. The dynamic framework can be realized by running alternatively the demand and price forecasting, where the forecasted demand becomes the input to the price forecasting paradigm and vice versa. The process is expected to be much faster in comparison to complex neural architectures as pointed out in the earlier researches [1,2,3,4].

To overcome the issues faced in complex neural structures, a computationally simple and adaptive ARMA-functional link neural architecture and an adaptive cubature Kalman filter (ACKF) learning approach [22, 24, 25] is presented in this work. The basis functions of the functional link block provide an expanded nonlinear transformation to the input space, thereby increasing its dimension that will be adequate to capture the nonlinearities and chaotic variations in the demand and price time series.

The cubature Kalman filter (CKF) [25] uses a third-degree spherical-radial cubature rule to provide better numerical stability and low computational overhead for mixed demand and price forecasting problem in smart grids in comparison to unscented Kalman filter (UKF), and extended Kalman filter (EKF). To validate its accuracy, the performance comparison between the ACKF and robust UKF (RUKF) [24] is presented in this paper. The proposed models provide both simultaneous and mixed demand and price forecast for the next day, considering the historical and forecasted data samples.

2 Time series data pre-processing

Keeping in view of preprocessing of the data series, in this work we have considered the single-period continuously compounded return series, known as log-return series. The return series has efficient statistical properties and is easy to handle the price and demand signals [18, 20, 21]. The single-period continuously compounded return price time series is defined as [18]:

$$R_{t} = \ln (P_{t} ) - \ln (P_{t - 1} ) = \ln \left( {\frac{{P_{t} }}{{P_{t - 1} }}} \right)$$
(1)

where Rt is the single-period log return at time t; Pt is the electricity price at time t. Similar expression is used for electricity demand return time series. For the case studies in this work, we have considered the electricity price and demand series from 1 January 2014 to 31 December 2014 of the Pennsylvania-New Jersey-Maryland (PJM) interconnection market [26]. Figure 1 shows the hourly electricity demand and price series and their corresponding returns for PJM market in 2014. It can be seen that the mean value of both demand and price return series is nearly equal to zero and the variance over the period indicates the return series to be more homogeneous.

Fig. 1
figure 1

Forward and return series of electricity demand and price of PJM market in 2014

Full size image

Thus, for forecasting 24-hour ahead electricity price, the considered return series is given by:

$$P_{t} = \psi (R_{t - 1} ,R_{t - 23} ,R_{t - 24} ,R_{t - 47} , \cdots ,R_{t - 167} ,R_{t - 168} )$$
(2)

where \(\psi\) represents a nonlinear function of the return time series inputs.

3 Electricity demand and price forecasting methodologies

The return demand or price time series is used as inputs to an ARMA and nonlinear functional expansion based low complexity neural model. The process flow of the proposed methodology is depicted in Fig. 2.

Fig. 2
figure 2

Process flow of proposed methodology

Full size image

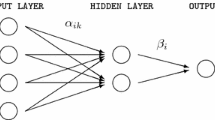
The block diagram of the combined adaptive ARMA and functional link neural network (ARMA-FLNN) architecture is shown in Fig. 3, where FEB refers to the functional expansion block of the ARMA model. This model is an adaptive pole-zero frameworks, where the ARMA model alone is described by a recursive difference equation of the form:

$$y(k) = \sum\limits_{i = 1}^{p} {a_{i} y(k - i)} + \sum\limits_{i = 1}^{n} {b_{i} x(k - i) + c_{1} \varepsilon (k - 1)}$$
(3)

where x(k) and y(k) are the input and output of the model respectively; ε(k−1)is the random white Gaussian noise of zero mean and variance of σ2; c1 is the error coefficient to be obtained from the learning algorithm; n is the total number of state variables. Besides the moving average (MA) (the second part of (3)), the first part represents the estimated past output samples y(k−i) (i=1, 2, …, p) and the price return series described in (2). The coefficients ai and bi in (3) are to be adjusted iteratively by suitable learning algorithm.

Fig. 3
figure 3

Nonlinear ARMA-FLNN

Full size image

To obtain a non-linear time series model, a nonlinear FLNN is added to the MA part of the model with activation function tanh(·), and the recursive part comprises the feedback of the delayed estimated output in the form as:

$$y(k) = \sum\limits_{i = 1}^{p} {a_{i} } y(k - i) + \tanh \left( {b_{0} + \sum\limits_{i = 1}^{m} {b_{i} }{\psi}_{i} (x(k - i)) + c_{1} \varepsilon (k - 1)} \right)$$
(4)

where m represents the total number of nonlinear expansions. The output from the FLNN is given by \(\psi_{i}\), which is expanded using three terms [xi, cosπxi, sinπxi]. However, more trigonometric expansions can be added for each variable in the form [xi, cosπxi, sinπxi, cos2πxi, sin2πxi, …, cospπxi, sinpπxi], where p is the total number of expansions. When p is chosen as 1, one expansion [xi, cosπxi, sinπxi] is adequate to produce accurate forecast. Thus, the equivalent pole-zero model of the nonlinear ARMA-FLNN is obtained as:

$$y(k) = \frac{{\sum\limits_{i = 1}^{m} {\left[ {b_{0} + b_{i} {\psi}_{i} (x(k - i))} \right] + c_{1} \varepsilon (k - 1)} }}{1 - A(k,z)}$$
(5)

where \(A(k,z) = \sum\limits_{i = 1}^{p} {a_{i} } z^{ - i}\); z is the delay operator.

The aggregated weight vector to be updated is represented as:

$$\varvec{W} = [b_{0} ,b_{1} , \cdots ,b_{i} , \cdots ,b_{m} ,a_{1} ,a_{2} , \cdots ,a_{p} ,c_{1} ]$$
(6)

The corresponding input vector associated with the weight vector W is:

$$\varvec{D} = [\psi_{1} ,\psi_{2} ,\cdots ,\psi_{m} ,y(k - 1),y(k - 2), \cdots ,y(k - p),\varepsilon (k - 1)]^{\text{T}}$$
(7)

The nonlinear ARMA-FLNN model output at the kth iteration is obtained as:

$$y(k) = \varvec{W}(k)\varvec{D}(k)$$
(8)

The error between the desired output and the estimated one is given by:

$$e(k) = d(k) - y(k)$$
(9)

For training the weights of the nonlinear ARMA, the following discrete-time equations in the matrix form, i.e., state equation (10) and output equation (11), are used:

$$\varvec{W}_{k} = \varvec{f} (\varvec{W}_{k - 1} )+\varvec{\omega}_{k} \,$$
(10)
$$\varvec{y}_{k} = \varvec{h} (\varvec{W}_{k} )+\varvec{\upsilon}_{k} \,$$
(11)

where Wk stands for all the weights associated with linear and nonlinear functional blocks, and the estimated output is yk at the kth instant, respectively; \(\varvec{\omega}_{k}\) and \(\varvec{\upsilon}_{k}\) represent the process and measurement correlated zero-mean white Gaussian noise. Further, the following relations of the process and measurement noise covariances are obtained as:

$$\varvec{E} (\varvec{\omega}_{k}\varvec{\omega}_{i}^{\text{T}} )= \left\{ {\begin{array}{*{20}l} {\varvec{Q}_{k} }\,\,\,\,\,\, \hfill & {i = k} \hfill \\ {\mathbf{0}} \,\,\,\,\,\, \hfill & {i \ne k} \hfill \\ \end{array} } \right.$$
(12)
$$\varvec{E} (\varvec{\upsilon}_{k}\varvec{\upsilon}_{i}^{\text{T}} )= \left\{ {\begin{array}{*{20}l} {\varvec{R}_{k} } \,\,\,\,\,\, \hfill & {i = k} \hfill \\ {\mathbf{0}}\,\,\,\,\,\, \hfill & { i \ne k} \hfill \\ \end{array} } \right.$$
(13)

where Qk and Rk are the model noise and measurement noise covariance matrices, respectively. For example, with only one nonlinear block, 8 past return price inputs and 5 inputs from the autoregressive (AR) block, the total number of weights to be updated is 8 × 3 + 5 + 1 = 30. Thus, the state vector at the kth instant is written as:

$$\varvec{W}_{k} = [b_{0} ,b_{1} , \cdots ,b_{24} ,a_{1} ,a_{2} , \cdots ,a_{5} ,c_{1} ]^{\text{T}}$$
(14)

The corresponding estimated output is:

$$\begin{aligned} y(k) & = \tanh (b_{0} + b_{1} \psi_{1} + \cdots + b_{24} \psi_{24} ) \\ & \quad + \,a_{1} y_{k - 1} + a_{2} y_{k - 2} + \cdots + a_{5} y_{k - 5} + c_{1} \varepsilon_{k - 1} \\ \end{aligned}$$
(15)

For estimating the parameters of the above ARMA-FLNN model, a relatively new Gaussian approximation filter known as the CKF is proposed in this paper, which uses a third-degree radial-spherical rule in generating a set of 2n cubature points weighted equally for capturing the mean and covariance. Also, it has been reported in the literature that CKF is relatively easy to tune, and results in lower computational overhead and improved numerical stability, in comparison to the UKF for parameter estimation in large systems.

Unlike the UKF, the CKF is a nonlinear Bayesian estimator that uses a third-degree spherical-radial cubature rule to generate 2n cubature points. Assuming an initial error covariance matrix P0, the computational steps are summarized as follows:

  1. 1)

    Time update

The error covariance matrix Pk−1 is factorized by using Cholesky matrix decomposition formulation as:

$$\varvec{P}_{k - 1} {\mathbf{ = }}\varvec{S}_{k - 1} \varvec{S}_{k - 1}^{\text{T}}$$
(16)

where Sk−1 is the Cholesky decomposition matrix of Pk−1. The cubature points are evaluated by:

$$\varvec{X}_{i,k - 1} = \varvec{S}_{k - 1}\varvec{\xi}_{i} + \hat{\varvec{W}}_{k - 1} \,\,\,\,\,\,\quad i = 1,2, \cdots ,2n$$
(17)

where \(\hat{\varvec{W}}_{k - 1}\) refers to the estimated value of Wk−1; \(\varvec{\xi}_{i}\) is the number of cubature points given by the following expression:

$$\varvec{\xi}_{i} = \left\{ {\begin{array}{*{20}l} {\sqrt n {\mathbf{1}}_{i} } \,\,\,\,\,\,\hfill & {i = 1,2, \cdots ,n} \hfill \\ { - \sqrt n {\mathbf{1}}_{i} } \,\,\,\,\,\,\hfill & {i = n + 1,n + 2, \cdots ,2n} \hfill \\ \end{array} } \right.$$
(18)

where 1i is the ith column vector of an \(n \times n\) identity matrix.

The cubature points are then propagated through the ARMA-FLNN state model to compute the predicted state as:

$$\varvec{X}_{{i,k |k{ - 1}}}^{p} = \varvec{f}(\varvec{X}_{i,k - 1} )$$
(19)
$$\bar{\varvec{W}}_{k|k - 1} = \frac{1}{2n}\sum\limits_{i = 1}^{2n} {\varvec{X}_{{i,k |k{ - 1}}}^{p} }$$
(20)

where \(\varvec{X}_{{i,k |k{ - 1}}}^{p}\) is the predicted state of \(\varvec{X}_{{i}, {k-1}};\)\(\bar{\varvec{W}}_{k|k - 1}\) is the average value of \({\varvec{X}_{{i,k |k{ - 1}}}^{p} }\).

The propagated covariance is calculated as:

$$\varvec{P}_{k|k - 1} = \frac{1}{2n}\sum\limits_{i = 1}^{2n} {(\varvec{X}_{{i,k|k{ - 1}}}^{p} - \bar{\varvec{W}}_{k|k - 1} )(\varvec{X}_{{i,k|k{ - 1}}}^{p} - \bar{\varvec{W}}_{k|k - 1} )^{\text{T}} } + \varvec{Q}_{k - 1}$$
(21)

where Qk−1 denotes the model noise covariance matrix at the time step k−1.

  1. 2)

    Measurement update

Use Cholesky factorization scheme to decompose the error variance matrix \(\varvec{P}_{k|k - 1}\) to obtain \(\varvec{S}_{k|k - 1}\).The cubature points are recalculated as:

$$\varvec{W}_{i,k|k - 1} = \varvec{S}_{k|k - 1}\varvec{\xi}_{i} + \hat{\varvec{W}}_{k|k - 1} \,\,\,\,\,\,\,\,\;\quad i = 1,2, \cdots ,2n$$
(22)

The forecasted measurement is then computed by propagating the cubature points through the nonlinear system as:

$$\varvec{y}_{i,k|k - 1} = \varvec{h}(\varvec{W}_{i,k|k - 1} )$$
(23)
$$\overline{\varvec{y}}_{k|k - 1} = \frac{1}{2n}\sum\limits_{i = 1}^{2n} {\varvec{y}_{i,k|k - 1} }$$
(24)

The estimated covariance is then computed as:

$$\varvec{P}_{k|k - 1}^{y} = \frac{1}{2n}\sum\limits_{i = 1}^{2n} {(\varvec{y}_{i,k|k - 1} - } \overline{\varvec{y}}_{k|k - 1} )(\varvec{y}_{i,k|k - 1} - \overline{\varvec{y}}_{k|k - 1} )^{\text{T}} + \varvec{R}_{k - 1}$$
(25)
$$\varvec{P}_{{k|k{ - 1}}}^{xy} = \frac{1}{2n}\sum\limits_{i = 1}^{2n} {(\varvec{W}_{i,k|k - 1} - } \overline{\varvec{W}}_{k|k - 1} )(\varvec{y}_{i,k|k - 1} - \overline{\varvec{y}}_{k|k - 1} )^{\text{T}}$$
(26)

where \(\varvec{P}_{k|k - 1}^{y}\) stands for the innovation covariance matrix; \(\varvec{P}_{{k|k{ - 1}}}^{xy}\) stands for cross-covariance matrix; Rk−1 is the measurement error covariance matrix at the time step k−1. Then, the Kalman gain is calculated as:

$$\varvec{K}_{k} = \varvec{P}_{{k|k{ - 1}}}^{xy} (\varvec{P}_{{k|k{ - 1}}}^{y} )^{ - 1}$$
(27)

The forecasting error and the state parameter vector are obtained as:

$$\varvec{e}_{k} = \varvec{d}_{k} - \bar{\varvec{y}}_{k|k - 1}$$
(28)
$$\hat{\varvec{W}}_{k} = \bar{\varvec{W}}_{k|k - 1} + \varvec{K}_{k} (\varvec{y}_{k} - \bar{\varvec{y}}_{k|k - 1} )$$
(29)

The error covariance matrix Pk is updated as:

$$\varvec{P}_{k} = \varvec{P}_{{k|k{ - 1}}} - \varvec{K}_{k} \varvec{P}_{{k|k{ - 1}}}^{y} \varvec{K}_{k}^{\text{T}}$$
(30)

However, when the noise statistics are not known initially or they change abruptly, it is required to update the values of Qk and Rk recursively. The formula for updating the noise covariances is given by:

$$\hat{\varvec{Q}}_{k} = (1 - \mu )\hat{\varvec{Q}}_{k - 1} + \mu (\varvec{K}_{k} \varvec{e}_{k}^{2} \varvec{K}_{k}^{\text{T}} )$$
(31)
$$\mu = (1 - \beta )/(1 - \beta^{k} )\;\;\;\;\;\;\quad 0.95 \le \beta \le 0.99$$
(32)

In a similar way, the measurement covariance matrix is updated as:

$$\hat{\varvec{R}}_{k} = \mu \hat{\varvec{R}}_{k - 1} + \varvec{e}_{k}^{2} - \frac{1}{2n}\sum\limits_{i = 1}^{2n} {(\varvec{y}_{i,k|k - 1} - } \bar{\varvec{y}}_{k|k - 1} )(\varvec{y}_{i,k|k - 1} - \bar{\varvec{y}}_{k|k - 1} )^{\text{T}}$$
(33)

Besides the process and measurement error covariances, the state estimation covariance matrix may deviate from its value \(\varvec{P}_{{k|k{ - 1}}}\)in (16) when the estimated system state is not equal to the actual system state. Thus, the propagated covariance is modified by using a fading factor \(\lambda_{k}\) as:

$$\left\{ \begin{aligned} \lambda_{k} > 1\;\;\;\;\;\;\quad {\text{when }}\frac{{tr(\eta \varvec{V}_{k} - \varepsilon \varvec{R}_{k} )}}{{tr[\varvec{P}_{{k|k{ - 1}}}^{xy} ]}}{ > 1 } \hfill \\ \lambda_{k} \le 1\;\,\,\;\;\;\;\quad {\text{when }}\frac{{tr(\eta \varvec{V}_{k} - \varepsilon \varvec{R}_{k} )}}{{tr[\varvec{P}_{{k|k{ - 1}}}^{xy} ]}} \le 1\hfill \\ \end{aligned} \right.$$
(34)
$$\varvec{V}_{k} = \left\{ {\begin{array}{*{20}l} {\varvec{w}{}_{0}\varvec{w}_{0}^{\text{T}} } \;\;\;\;\;\hfill & {k < 2} \hfill \\ {\frac{{\rho \varvec{V}_{k - 1} + \varvec{w}_{k} \varvec{w}_{k}^{\text{T}} }}{1 + \rho }} \;\;\;\;\hfill & {k \ge 2} \hfill \\ \end{array} } \right.$$
(35)

where \(tr( \cdot )\) refers to the sum of diagonal elements of the corresponding matrix; \(\eta\) is a forgetting factor whose value is taken 0.97; \(\varepsilon\) is chosen as 0.9; w0 and wk represent the process error covariances at the beginning and kth iteration; the value of ρ is chosen as 0.98. Thus, the new state error covariance matrix is rewritten as:

$$\varvec{P}_{k|k - 1} = \frac{{\lambda_{k} }}{2n}\sum\limits_{i = 1}^{2n} {(\varvec{X}_{{i,k|k{ - 1}}}^{p} - \bar{\varvec{W}}_{k|k - 1} )(\varvec{X}_{i,k|k - 1}^{p} - \bar{\varvec{W}}_{k|k - 1} )^{\text{T}} } + \varvec{Q}_{k - 1}$$
(36)

The estimated modified covariance is then computed as:

$$\varvec{P}_{{k|k{ - 1}}}^{y} = \frac{{\lambda_{k} }}{2n}\sum\limits_{i = 1}^{2n} {(\varvec{y}_{i,k|k - 1} - \bar{\varvec{y}}_{k|k - 1} } )(\varvec{y}_{i,k|k - 1} - \bar{\varvec{y}}_{k|k - 1} )^{\text{T}} + \varvec{R}_{k - 1}$$
(37)
$$\varvec{P}_{{k|k{ - 1}}}^{xy} = \frac{{\lambda_{k} }}{2n}\sum\limits_{i = 1}^{2n} {(\varvec{W}_{i,k|k - 1} - \bar{\varvec{W}}_{k|k - 1} )} (\varvec{y}_{i,k|k - 1} - \bar{\varvec{y}}_{k|k - 1} )^{\text{T}}$$
(38)

4 Differential evolution (DE) for initial learning phase

For better accuracy and convergence, the weights of the ARMA-FLNN are optimized using a differential evolution technique in the initial training phase, where only few electricity price samples or patterns are used.

Since DE [27, 28] is quite time consuming, for a real-time price forecasting, the robust CKF estimators are used for the remaining training phase. DE is a population-based meta-heuristic optimization technique that uses three steps—mutation, crossover and selection—to evolve the final solution starting from a randomly generated population with a size of Np and dimension D (number of ARMA-FLNN weights). Gmax is the maximum number of generations used in the initial phase of the training. Although there are several mutation strategies, DE/best/2/bin is used here to generate mutant vector from the target vector. From the ACKF algorithm, the objective function is obtained as:

$$f(U_{i,G} ) = \frac{1}{K}\sum\limits_{k = 1}^{K} {e_{k}^{2} }$$
(39)

where K is the iteration number used for the minimization of the objective function; ek is the error at the kth instant.

5 Model identification and performance metrics

The order of the ARMA model has been determined based on the autocorrelation function (ACF) and partial autocorrelation function (PACF) plots. The autocorrelation of lag k for the original price series is given in (40), where the subscript d signifies the day of forecast. The ACF and PACF plots for original and return price series of PJM market are shown in Fig. 4. The time lag has been considered to be 1 based on the ACF plots. After the logarithmic return, i.e. the first order difference, it is observed that ACF dies out immediately after lag 2, which signifies suitability of the model inputs considering first order difference of the price series.

$$ACF_{k} = \frac{{\sum\limits_{t = 1}^{T - k} {(P_{t,d} - \bar{P}_{d} )(P_{t + d,k} - \bar{P}_{d} )} }}{{\sum\limits_{t = 1}^{T - k} {(P_{t,d} - \bar{P}_{d} )^{2} } }}$$
(40)

where T is the study period; Pt,d is the price at time t in a particular day; \(\bar{P}_{d}\) is the mean value of price.

The mean absolute percentage error (MAPE) and root mean square error (RMSE) are considered here to measure the accuracy of the forecast results [18].

$$MAPE = \left( {\frac{1}{T}\sum\limits_{t = 1}^{T} {\frac{{\left| {F_{t} - A_{t} } \right|}}{{A_{t} }}} } \right) \times 100\%$$
(41)

where Ft is the forecasted value at time t; At is the actual quantity at time t. In a similar way, the RMSE is obtained as:

$$RMSE = \sqrt {\frac{1}{T}\sum\limits_{t = 1}^{T} {\left( {A_{t} - F_{t} } \right)^{2} } }$$
(42)

For robust forecast, another performance metric which is not very common in forecasting literature is the mean absolute scaled error (MASE) [1, 29]. The scaled MASE is defined as:

$$MASE_{T,l} = \frac{1}{T}\sum\limits_{t = 1}^{T} {\frac{{\left| {F_{t} - A_{t} } \right|}}{{\frac{1}{T - l}\sum\limits_{t = l + 1}^{T} {(A_{t} - A_{t - l} )} }}}$$
(43)

where l is the length of the cycle. In this work, hourly prices have been considered with l = 1 and T = 168 to obtain the weekly MASE. For a robust and accurate forecast, the value of MASE should be less than one. To check the model uncertainty, variance of forecast errors is also computed. If the variance becomes small, then the model is said to be less uncertain and the forecast results are more accurate. The variance of error in a time span T is defined as:

$$\sigma_{e}^{2} = \frac{1}{T}\sum\limits_{t = 1}^{T} {\left( {\frac{{\left| {F_{t} - A_{t} } \right|}}{{\frac{1}{T}\sum\limits_{t = 1}^{T} {A_{t} } }} - MAPE} \right)}^{2}$$
(44)

6 Numerical results and discussion

The proposed methodology for forecasting day-ahead demands and prices has been implemented using PJM market data from 1 January 2014 to 31 December 2014 [26]. Two types of strategies have been proposed for the forecasting models which are provided in the next two subsections. The first strategy is to forecast the electricity demand and price separately, while the second strategy is to use mixed price and demand forecasting.

6.1 Day-ahead independent forecasting of electricity demand and price

The training and testing datasets span over the years 2013 and 2014, taking into account the considered weeks of forecast. The inputs to all the proposed models comprise the return time series with the lags as observed from the ACF plots. Figure 4 shows the sample ACF and PACF of forward and return series of electricity prices of PJM market (2014). It is noted that the two blue lines in Fig. 4a-c indicate 95% confidence interval (default).

Fig. 4
figure 4

ACF and PACF plots for price forward and return series for PJM market in 2014

Full size image

The price return series indicate that the mean value of the series is nearly equal to zero. Further, the variance within each of the set of observations is observed to be equal, which reveals the price return series to be homogeneous. In Fig. 4, it is seen that there exists strong correlation of the price return series at lags 24, 48, 72 and 96, based on which the input to the proposed model is taken at the time lags of t − 23, t − 24, t − 47, t − 48, t − 71, t − 72, t − 95, and t − 96 hours, respectively. However, the time lags of 23, 47, 71, and 95 have been considered to obtain better forecasting accuracy based on the observations from the ACF plots for the weeks of forecast under consideration.

The ARMA model is identified with the orders of MA and AR based on the ACF and PACF plots, respectively excluding the effect of price spikes which are present in the month of January, 2014 in PJM market. It is clear from Fig. 4 that the ACF certainly follows damped sine wave considering 168 lags. However, after lag 96, there does not exist any significant correlation as observed from the ACF of the return price series for the whole year.

Considering the price series in the year 2014 for PJM market, it is observed that there exist seasonal variations of demands and prices based on which different periods have been chosen to evaluate the performance of the proposed models. The corresponding first and last weeks of each month in the year 2014 are taken into consideration for forecasting with the implementation of the proposed methodologies.

For initializing the weights of the ARMA-FLNN model, the DE algorithm is applied for 50 patterns of both demand and price. In this hybrid approach, the number of patterns of 8 input samples is 100; the number of population Np = 5; dimension D is equal to \(8 \times 3 + 5 + 1\) = 30 lagged terms; K = 20; and Gmax = 100. Table 1 represents the obtained weekly MAPEs by applying AUKF, ACKF, DE-AUKF, and DE-ACKF techniques respectively in the year 2014 for PJM electricity market. It is clear from the results that the ACKF technique performs better in comparison to AUKF method for demand and price forecasting. However, the average demand forecast error is observed to be nearly 1% with the implementation of all the proposed techniques, which is comparable with the demand forecasting errors in the earlier research works. Additionally, with the application of DE algorithm, it can be said that despite the improvement in demand and price forecasting accuracy, very few significant improvements in precision are achieved. However, if DE is included in the filter then the computation time will be more. It is observed that the ACKF learning approach produces MAPE very close to the DE-ACKF with a small execution time of 0.15 s in a processor, in comparison to nearly 6 min in the latter case. Thus, the ACKF algorithm has been primarily focused for the rest of the studies.

Table 1 Comparison of weekly (1st week in each month of 2014) MAPEs with proposed models for PJM market
Full size table

Table 2 represents the obtained MAPEs in the last week of each month, taking into account the demand and price forecasting by applying the ACKF algorithm. It is seen from Table 2 that the average MAPEs obtained with ACKF technique in the first and last weeks in each month of the year 2014 for price forecasting are 6.07% and 5.46% respectively. Further, the demand forecasting accuracy is observed to be around 1% in both the test weeks, which signifies good forecast performance. The best and worst price forecast results are observed to be in the last weeks of June and January 2014, which are 3.84% and 13.05%, respectively.

Table 2 Comparison of weekly (last week in each month of 2014) MAPEs with ACKF technique for PJM market
Full size table

Figure 5 represents the price forecast results of these corresponding two weeks with the implementation of ACKF model. From the obtained forecast results in the months of January, February and March 2014, it can be pointed out that during the periods of price spike, the forecasting accuracy gets decreased as depicted in Tables 1 and 2.

Fig. 5
figure 5

Weekly price forecast results of PJM market in 2014

Full size image

Huge price spikes appear in January 2014 as a result of which the forecasting accuracy becomes 11.7% and 13.05% in the first and last weeks of January respectively. In comparison to the month of January the prices series appears to be less volatile for other months in 2014. However, significant spikes around 300 and 400 $/MWh are observed in February and March as shown in Fig. 1.

However, from April to December 2014, consistent MAPE of around 4.5% is achieved in the first and last weeks of each of these months. Additionally, in the first week of July, because of volatile characteristics of price, the forecasting error becomes 8.54%. In contrast to the above analysis, it can be pointed out that the MAPEs obtained from all the models for price forecasting show a lower accuracy level in comparison to the demands considering particularly the spike periods. Further, in our proposed models, the demand forecast errors are observed to be less than 1% in most of the cases which are highly comparable with the numerous research works signifying the demand forecast accuracy in the range of 1% to 2% for the deregulated electricity markets.

In addition to the usual error metrics MAPE and MASE, another error measure RMSE is also obtained for all the periods under consideration to have a better comparison. Table 3 represents the obtained MASE and RMSE in different periods of price forecast for PJM market in the year 2014 with the inclusion of ACKF methodology. The obtained average MASE is 0.610 which signifies better forecasting accuracy keeping in view of the fact that for robust and accurate forecast, the value of MASE should be less than one as suggested by the authors in [1]. Further, the average RMSE is found to be 0.037 which signifies accurate price forecast with the proposed ACKF algorithm in comparison to the earlier research techniques.

Table 3 Comparison of weekly MASE and RMSE of price forecast in each month of 2014 for PJM market
Full size table

Additionally, two other days in January, keeping in view of the worst and the best forecasting, have been taken into consideration for comparing the prices in each hour of the corresponding day, as depicted in Table 4. It is observed from the table that huge price spikes exist on 28 January 2014 in comparison to all other days under study. As a result, high values of the performance measures MAPE, MASE and RMSE appear in the last week of January 2014 in comparison to all other test periods. However, it is clearly seen that the actual values of electricity prices in the last week of June are captured more accurately in comparison to the weekly forecast during 25-31 January. This is because of the fact that low price spikes appear in June in comparison to those in the month of January. This signifies better forecasting accuracy with the ACKF technique, thus giving the designer the choice to adopt the procedure to obtain a fast and robust forecast of prices.

Table 4 Comparison of hourly electricity prices in two different days for PJM market in 2014
Full size table

Although DE-ACKF shows slightly more significant forecasting accuracy in comparison to ACKF, keeping in view of the faster speed of operation of the models, ACKF can be chosen by the designers over DE-ACKF technique to obtain a good forecasting.

6.2 Mixed electricity demand and price forecasting

To analyze the interdependency effect of demand and price, historical demand and price values are considered as inputs to price and demand forecasting models on alternate basis. For analysis purpose, New South Wales (NSW) (2010) [30] and New England electricity market (NEM) (2009) [31] along with PJM (2014) electricity markets are taken into consideration for the proposed study. Based on the ACF, the time lagged days for demand or price as input features, along with the lagged price or demand, have been taken into consideration for forecasting, respectively. For instance, the considered sample input vectors comprise of the elements as: P(t − 23), P(t − 24), P(t − 47), P(t − 48), P(t − 71), P(t − 72), D(t − 23) and D(t − 24) for price forecasting; D(t − 23), D(t − 24), D(t − 47), D(t − 48), D(t − 71), D(t − 72), P(t − 23) and P(t − 24) for demand forecasting. P(·) and D(·) represent the price and demand at different time lags correspondingly. Based on the obtained results for individual demand and price forecasting for PJM market, ACKF methodology has been applied for joint demand and price forecasting for the NSW and NEM markets, taking into account the lower accuracy difference and fast computation time in comparison to the DE-ACKF algorithm. The obtained results are compared with those obtained in reference [4]. In addition to the test periods in [4], two other volatile weeks are also included in the case study to analyze the effect of enormous price spikes. Huge MCP spikes ranging from 200 to 6000 $/MWh are observed in the year 2010 in NSW market, whereas the annual average is indicated to be 30 $/MWh. Figure 6 indicates the price forecast result in the first week of June for NSW market in 2010. It can be observed for the MCP spike around 150 $/MWh in this week. Table 5 represents the obtained results taking into account the price forecast for these two markets in different periods. Although better forecasting accuracy is not obtained for the considered period, the obtained MAPE of 13.2% is comparable with that of 15.7% depicted in reference [4].

Fig. 6
figure 6

Weekly price forecast result of NSW market in 2010

Full size image
Table 5 Comparison of different error measures with joint demand and price forecasting for NSW (2010) and NEM (2009) markets
Full size table

Figure 7a represents the forecast results of the NSW market (2010). Huge price spike of 4065 $/MWh is observed on 22 January which shows a momentous difference in comparison to an annual average of 30 $/MWh. However, the obtained MASE of 0.95894 indicates an acceptable forecast, keeping in view of the fact that for satisfactory forecasting, MASE should be less than 1 as proposed by the researchers. Figure 7b represents the demand forecasting during the same period and the performance accuracy of 1.93% appears to be accurate in comparison to the MAPEs obtained in earlier works for load forecasting. From Table 5, it is clear that irrespective of huge price spikes in the test weeks, the obtained forecast results are within the acceptable range. The obtained average MAPEs for the weekly period of March to December is significantly comparable with the result outlined in [4]. However, in general, the classification strategy can be adopted to overcome the difficulties in forecasting, taking into account the exact value of prices at certain instances as suggested by the researchers.

Fig. 7
figure 7

Weekly forecast results of NSW market in 2010

Full size image

Additionally, it is observed for a distinct price cluster at 25 $/MWh in 1-7 September of NSW market in 2010. Figure 8a represents the weekly forecasted results in the considered period. The MAPE, MASE and RMSE are found to be 4.50%, 0.84305, and 0.037837 respectively, which indicate significant accuracy level of forecasting. For instance, Fig. 8b shows the forecasted price values on 1 September 2010 spanning over 24 hours. It can be observed that the actual prices form a group at 25 $/MWh, and are captured in an accurate manner keeping in view of the application of proposed ACKF algorithm. The same circumstances also arise for the period 2-4 September 2007, and it is observed for significant acceptable forecasting at each hour considering this period. This very specific “point-mass” non-linear effect is very difficult to model as suggested by different researchers. However, with the application of the proposed ACKF technique, the obtained error measures indicate significant forecast accuracy. This particular scenario can be considered as a possibility for future research taking into account the price forecasting strategy for different volatile markets.

Fig. 8
figure 8

Forecast results of NSW market in 2010

Full size image

Further, in comparison to individual price forecasting results depicted in Tables 1, 2 and 3 for PJM electricity market, another case study is performed keeping in view of the mixed demand and price forecasting, considering some of the test periods in the year 2014. The input vector to the proposed ACKF model is arranged considering two different scenarios S1 and S2. In S1 and S2, the input vectors are considered to be [P(t − 23), P(t − 24), P(t − 47), P(t − 48), P(t − 72), D(t − 23), D(t − 24), D(t − 48)] and [D(t − 23), D(t − 24), D(t − 47), D(t − 48), D(t − 72), P(t − 23), P(t − 24), P(t − 48)] respectively. Table 6 represents the obtained forecast results considering the price and demand data of PJM market in 2014. Based on the achieved error measures, it is observed that significant accuracy in joint demand and price forecasting is possible, which is quite comparable with the separate demand and price forecasting strategy.

Table 6 Comparison between mixed and separate price forecasting strategies (PJM market in 2014)
Full size table

Based on the average values of different error measures depicted in Table 6, it can be said that although the separate forecasting strategy shows better accuracy in comparison to mixed approach, significant difference is not achieved. Keeping in view of the smart grid environment, it is highly desired to focus primarily on the reaction of the consumers. To achieve this, both demand and price are to be considered as model inputs for acceptable forecasting as pointed out by the researchers. Thus, the mixed approach using ACKF algorithm can be used as a fast, efficient, and robust forecasting strategy.

The effectiveness of ACKF method is studied further using the worst fluctuating demand data of New York energy (NYISO) market [32] in NYC zone for the month of July 2004. The obtained results are depicted in Table 7. The obtained MAPEs are observed to be with significant accuracy and is in the acceptable range in comparison to the MAPE of 2.11% presented in [2].

Table 7 Obtained MAPEs for demand and price with proposed ACKF method for NYISO market in July 2004
Full size table

Further, the price spikes have been considered for the Queensland market of Australia to check the stability of the proposed ACKF algorithm, and the obtained forecasting results are compared with the results in [33]. The price spikes are observed to be much more than the normal price which is around 20-30 $/MWh. Such abnormal prices or price spikes are because of unanticipated incidents such as transmission network contingencies, transmission congestion and generation contingencies. These price spikes are highly unpredictable for which they have reasonable impact on usual price forecasting. However, forecasting or classification of such price spikes can reduce the effect of risk management. To test the accuracy of the proposed model, the same test periods have been taken into consideration, as depicted in [32]. Table 8 represents the obtained results of price forecast with the application of ACKF technique.

Table 8 Comparison of price forecast errors in different periods of Queensland electricity market (2003)
Full size table

The training dataset comprises the period from January to June 2003, while the period from July to October has been considered for the test dataset. It is clear from Table 8 that the price peaks are captured with greater accuracy in comparison to those obtained in [32].

To check the suitability of the proposed ACKF algorithm, the ACF of the estimated model errors as shown in Fig. 9 is examined. It is clear from Fig. 9 that there does not subsist any significant autocorrelation taking into account the residues in the considered test period. Based on the earlier researches, on time series models, it can be pointed out that the only difference between the actual and the forecasted values should be random (white) noise. If the error follows a specific pattern, the model is said to be uncertain.

Fig. 9
figure 9

Sample ACF of model errors of NSW market in 2010

Full size image

However, the ACF of residues shown in Fig. 9 for the considered test period does not show any significant autocorrelation which indicates the appropriateness of the proposed methodology.

Additionally, for forecasting strategy, day-light saving time (DST) issue must be focused while fixing up the strategy for the market participants. Typically, regions using DST adjust their clocks forward one hour close to the start of spring and adjust them backward in the autumn to standard time. In case of DST, the extra hour can be filled up with the values obtained by averaging the nearby values, thus making the data series rearranged, and the prediction results are unlikely to be sensitive to such changes. Further, in short-term forecasting strategy, the medium-term and long-term seasonality are usually disregarded, but the daily and weekly patterns are observed minutely taking into account the holidays. Based on the earlier researches, it can be said that the demand patterns on Tuesday, Wednesday, Thursday and Friday are almost matching for all the markets.

Therefore, forecast of price and demand of the holiday to be forecasted for either of these four days come from the historical data series on the same condition. The same norm has to be followed for the data series of a holiday falling on Saturday or Monday. Further, because of the interdependency characteristics of demand and price, the strategy for price forecast has to be considered based on the same rules. By following the specific patterns, accurate forecast can thus be achieved.

7 Conclusion

This paper presents a hybrid ARMA-FLNN model for short-term electricity demand and price forecasting in future smart grids. The linear ARMA and nonlinear low complexity functional link network are used jointly to capture the various aspects of nonstationary demand and price data using log-return historical time series. Instead of using normal back-propagation learning algorithm, a robust ACKF is used to tune the hybrid network parameters. To verify the forecasting ability of the filter and the hybrid ARMA-FLNN model, several case studies are used for the PJM and other electricity markets with various levels of price spikes. The forecasting results clearly proved the superiority of the robust ACKF over the robust UKF, in producing lower performance metrics during the periods of high spikes. On the other hand, the demand forecasting accuracy of nearly 1% is much better than the contemporary load forecasting techniques provided by some of the well-known neural networks. The competitiveness of the proposed approach is well analyzed in comparison to approaches in [2, 4, 32]. Additionally, the mixed approach forecasting strategy can effectively produce demand and price scheduling rules taking into account the future smart grid environment.