Abstract
With an increasing penetration of wind power in the modern electrical grid, the increasing replacement of large conventional synchronous generators by wind power plants will potentially result in deteriorated frequency regulation performance due to the reduced system inertia and primary frequency response. A series of challenging issues arise from the aspects of power system planning, operation, control and protection. Therefore, it is valuable to develop variable speed wind turbines (VSWTs) equipped with frequency regulation capabilities that allow them to effectively participate in addressing severe frequency contingencies. This paper provides a comprehensive survey on frequency regulation methods for VSWTs. It fully describes the concepts, principles and control strategies of prevailing frequency controls of VSWTs, including future development trends. It concludes with a performance comparison of frequency regulation by the four main types of wind power plants.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
With an increasing penetration of wind energy incorporated into the existing utility grid, as well as scheduled retirement of fossil-fuelled power plants, system frequency regulation capability tends to deteriorate in the event of severe frequency disturbance. This is due to absence of inertial response and ancillary frequency support by a substantial amount of variable speed wind turbines (VSWTs) [1, 2], including doubly-fed induction generators (DFIGs) and permanent magnet synchronous generators (PMSGs).
To achieve a reliable, secure and economic operation, the electrical grid is required to maintain the system frequency around the nominal value within a predetermined range at all times. As wind power plants (WPPs) gradually displace conventional synchronous generators in service, WPPs are expected to provide auxiliary frequency regulation capabilities through their fast and flexible active power control [3]. Currently, Regional Transmission Organizations (RTOs), Independent System Operator (ISOs) or equivalent entities in many countries come to realize the potential benefits of inertial response and frequency regulation from wind turbine generators (WTG) in maintaining the dynamic active power balance between power supply and demand. So, a large number of wind generators equipped with frequency regulation functions are expected to be integrated into power systems, which in turn yields extra benefits by providing various ancillary services. With a great potential demand in the power market, wind plant manufacturers are encouraged to further improve the auxiliary frequency controls for VSWTs as well. In addition, especially when wind power needs to be dispatched down in case of low load and high wind speed or due to other operational constrains, a large amount of untapped wind power can be fully utilized as spinning reserve to support temporary frequency response in the event of severe disturbances [4]. For these reasons, a win-win solution can be achieved by implementing the frequency control methods into VSWTs, providing benefits to wind power plant owners, wind turbine manufacturers and power grid operators [5,6,7,8,9,10].
The main contributions of this work is a comprehensive survey on state-of-the-art inertial response and frequency regulation methods of VSWTs is conducted based on a great number of up-to-date literatures. It systematically introduces and evaluates different types of frequency control strategies in terms of their fundamental principle and control structure. Several key future development trends are discussed. Last but not least, the advantages and disadvantages of frequency regulation performance are compared for four common types of wind power plants.
2 Wind turbine inertial control
In principle, grid frequency response can be divided into four regulation stages in terms of different time scales: inertial response, primary frequency response, secondary frequency response and tertiary frequency response as illustrated in Fig. 1 [11]. Different control methods for maximum power point tracking (MPPT) operation are implemented in the rotor-side converter of VSWTs, consisting of torque-based, active power-based and rotor speed-based converter control [10, 12,13,14,15,16]. To make VSWTs properly perform the frequency regulation function following specific frequency regulation requirements, supplementary controllers should be designed and integrated into both the existing converter power control loop and the pitch angle control loop to manipulate the corresponding reference set points of torque, active power or rotor speed [12,13,14,15,16,17,18,19].
Due to a sudden and large power supply-demand imbalance, power system frequency changes at a certain rate initially determined by the cumulative inertia of all spinning generations (synchronous generators) and composite load damping (motor, pumps etc.) [20,21,22]. The kinetic energy stored in the rotating mass of both wind turbine (WT) blades and generator rotors can be extracted through power converter control and then delivered into the power grid to arrest the rate of change of frequency (ROCOF). The typical value of wind turbine inertia is approximately 3.5 s [23]. It is worth noting that threshold value for ROCOF response is usually set in the range between 0.1 and 1.2 Hz/s for 60 Hz system or in the range between 0.1 and 1 Hz/s for 50 Hz system, and the delay time varies from 50 to 500 ms [24, 25].
Immediately following the frequency nadir, the kinetic energy extracted from rotating mass needs to be regained from currently available wind power so that the WT rotor speed and kinetic energy return to their pre-disturbance values or new optimal operation conditions. In this sense, WT inertial control is called an “energy neutral process” although the total amount of recovery energy seems larger than that of inertial response as a result of WT mechanical and electrical power losses [25]. During this recovery process, a secondary frequency drop (SFD) is likely to occur due to the reduced output power. That is to say, a large aggregated energy recovery from wind power plants performing inertial response may result in a severe SFD where the frequency drop is even lower than the initial frequency nadir in the under-frequency event [26,27,28,29,30,31,32,33,34,35,36]. With respect to the inertial recovery process, primary factors that determine its dynamic characteristics include the enabling time to reduce active power, the decreased power as a percentage of rated power (or percentage of actual power output for the inertial power recovery stage) as well as the duration of such wind power reduction [26]. A method that mitigates the SFD and assists the inertial response recovery is to extract the stored energy from the DC-link capacitors by properly reducing the DC-link voltage in proportion to the frequency deviation Δf when WTG starts to recover its rotor speed [37].
According to (1), the amount of kinetic energy ∆E for inertial response of a single wind turbine is a function of initial rotor speed ω 0; rotor speed reduction \(\Delta \omega = \omega_{0} - \omega_{1}\), \(\Delta \omega > 0\); moment of inertia of wind turbine J and inertial response duration (t 0 − t 1) [3, 38].
The inertial response performance of a WPP is typically dependent on the wind power penetration level, the number of WTGs capable of providing inertial response, the initial operation mode of individual WTGs (under full load or partial load) as well as WTGs’ physical characteristics. Relevant characteristics include upper and lower limits for rotor speed, over-loading capability of power converters, auxiliary frequency controller parameters and maximum power rate limit (dP/dt)max [4, 31, 32, 38,39,40,41,42]. To alleviate mechanical stresses on the drive train and extend a WT’s lifetime, the (dP/dt)max should not exceed 0.45 p.u./s according to several manufacturers’ datasheets [38]. Under medium and high wind conditions where WTGs are normally controlled to operate at MPP conditions, adequate kinetic energy is available to provide a useful inertial response. Under high wind speed conditions when rotor speed is constrained at the rated value, additional power provision can be fulfilled through pitch angle control to emulate an inertial response if temporary over-loading is allowed.
With the significant contribution of WTGs to enhance the system inertia, ROCOF and frequency nadir can be improved and this reduces the risks of load shedding triggered by UFLS (under frequency load shedding) and generation protection relays [43], thereby reinforcing system reliability and stability during large loss-of-supply events [44, 45]. At the same time, emulated inertial control can reinforce the system’s small signal stability due to its damping effect pn the dominant oscillation mode [46].
As of now, three typical types of inertial control are proposed to enable VSWTs to supply emulated inertial response, which can be categorized into Natural Inertial Control, Step-wise Inertial Control and Virtual Inertial Control [17, 26,27,28,29,30,31,32,33,34,35]. Each of these is discussed in detail in the remainder of this section.
2.1 Natural inertial control
For natural inertial control, a WTG’s active power output is changed following a frequency decline, in proportion to ROCOF or frequency deviation or both, in order to emulate the inertial response of a conventional synchronous generator [36, 45,46,47,48]. This is accomplished based on real-time measurements of frequency magnitude or ROCOF value. There are two main types of ROCOF dependent natural inertial control: one shot and continuous df/dt control [45, 49].
A one shot df/dt controller is designed to generate an initial power surge in proportion to the ROCOF when a severe frequency event occurs. This control scheme is implemented using a lookup table with initial df/dt value as X-coordinate and corresponding active power increment as Y-coordinate. As it is shown in Fig. 2 for an example WTG under its rated operation, the peak active power output can be achieved within 200 ms and then declines exponentially over a specified duration of T s . A short-term rotor speed restoration follows when active power declines below 1.0 p.u. (yet greater than 0.95 p.u.) [49].
A continuous df/dt controller works in real time through the entire disturbance to regulate the additional active power provision based on ROCOF. Similarly to a synchronous generator, the incremental per-unit inertial power ΔP in and per-unit inertial torque Δτ in of WTG are expressed as:
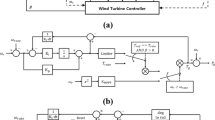
where K in is the gain of inertial controller; ω s is the per-unit synchronous generator speed; ΔP in corresponds to the portion of rotor kinetic energy extracted for additional power delivery. Usually, the dω s /dt can be replaced by df/dt in this control design, so that the magnitude of the WTG inertial response is directly proportional to the ROCOF. According to the swing equation, K in can be simply chosen as twice total inertia constant H of the wind turbine [28, 50]. Natural inertial control is also called delta power control because the shape of inertial power output resembles “delta” throughout the overall response. Figure 3 shows the control block diagram of natural inertial response. The performance of natural inertial response can be enhanced by either increasing the auxiliary controller gain K in or appropriately relaxing the limit on the power ramp rate [38].
It is noted that the measurement of df/dt is inherently a noise amplifying process. Thus, a low-pass filter is added after the derivative function block to minimize the interference from measurement noise.
Up to now, there are two types of frequency-deviation-dependent natural inertial response: fixed-droop control and variable-droop control [47, 48]. The incremental per unit inertial power ΔP in based on droop control is written as:
Figure 4 shows a typical fixed-droop controller and Fig. 5 depicts the configuration of a variable-droop controller with the droop coefficient as a function of ROCOF (df/dt) and pre-disturbance rotor speed (ω 0). A high-pass filter is applied to prevent the persistent contribution of droop control to a post-disturbance steady-state error, so the WTG can return to MPPT operation [48, 51]. Actually, variable-droop control is based on fixed-droop control by dynamically adjusting the droop gain in terms of ROCOF and ω 0. In this way, the inertial response of a WTG can be optimized by raising the frequency nadir and preventing the subsequent over-deceleration.
In general, droop-dependent inertial response can significantly boost the frequency nadir as 1/R dr increases. In contrast, ROCOF-dek lpendent inertial response can greatly mitigate the initial ROCOF as K in increases, but it cannot improve the frequency nadir. Therefore, natural inertial response that combines both ROCOF-dependent and droop-dependent loops is able to increase the frequency nadir, arrest the ROCOF and also mitigate the SFD during the rotor speed restoration [47, 48].
2.2 Step-wise inertial control
Step-wise inertial control aims to provide a certain amount of active power, which is released from kinetic energy and sustained for up to ten seconds under various wind speed conditions [34, 35, 52,53,54]. Compared with natural inertial response, the inertial power using this control can be provided in different profiles in terms of its desired magnitude and duration. Meanwhile, its inertial response tends to be much faster and stronger because a step-wise inertial response is executed without measuring real-time frequency variations. Upon detecting an event, this control method can dramatically boost the frequency nadir and alleviate the effect of kinetic energy recovery by providing a smooth and steady additional power injection [36]. The effect of step-wise inertial response is usually dependent on several factors, including step power increment, time duration, ramp rate limit, wind speed as well as inertia constant H WT.
One control method proposed to generate a constant inertial response for each step is to modify the rotor speed set point of rotor-speed-based VSWTs throughout the frequency event. The constant inertial power is derived from:
where t is the duration for constant inertial power; ω r0 is the initial rotor speed; ω rt is the rotor speed at the ending moment of inertial response. Therefore, the reference value of rotor speed is given as:
The control block diagram of constant inertial response is depicted in Fig. 6.
The other method proposed to achieve step-wise inertial control is for active-power-based VSWTs [22] to change their actual power reference by adding a temporary over-production (TOP) value ΔP op on top of the pre-event active power reference P MPPT in case of frequency disturbance. The P op is extracted from the kinetic energy stored in the rotating masses of WT. Thus, the generated electrical power output P ref is defined as:
During normal operation, a VSWT runs on the MPP corresponding to the actual wind speed. When there is an under-frequency event, a constant over-production amount of ΔP op is instantly delivered to the grid. As a result, rotor speed decelerates due to the increasing imbalance between mechanical and electromechanical torque. In Fig. 7, the basic principle of this control mechanism is illustrated. Note that the value of P ref can be constant or variable, depending on the specific strategy chosen for the overproduction period.
Once the rotor speed slows down to a low value, e.g., ω min, the overproduction process is terminated and the active power set point is reduced by a constant ΔP up , so that the electrical power output is smaller than available mechanical power. For this reason, the rotor speed is able to return to previous MPPT point for a given wind speed or another operating point corresponding to current wind speed. By increasing this ΔP up , the underproduction period tends to be shortened and meanwhile the wind turbine’s rotor speed can be restored to the MPP more rapidly. However, the SFD issue is likely to become more severe if much larger ΔP up is chosen. Thus, a TOP-based Improved Primary Frequency Response (IPFR) technique is proposed based on deloaded operation in [55] to eliminate the SFD issue and minimize the frequency deviation. Two other methods are proposed in [53,54,55,56] for DFIGs and PMSGs by adding an incremental active power based on the MPPT curve or torque limit curve to enable the rotor speed converge to a stable point when TOP ends.
2.3 Virtual inertial control
Recently, another novel inertial control strategy named virtual inertia control (VIC) is proposed to utilize the “hidden inertia” of turbine blades to provide a fast dynamic frequency support. One method is to adjust the active power output based on the system frequency deviation. This type of regulation is implemented by means of shifting the operating point upward from the MPPT curve toward the VIC power tracking curve to compensate for power imbalance, and then the rotor speed is controlled to smoothly return to the initial MPP according to (8) [57]. The upper and lower limits of the VIC power curve are defined by applying K VIC_max and K VIC_min respectively to ensure that the VSWT can operate in a steady state under various wind speed conditions. The coefficient K VIC is a function of frequency deviation:
where λ is the virtual inertia coefficient, which can be expressed as \(\lambda = \frac{{\Delta \omega_{r} }}{{\Delta \omega_{e} }} = \frac{{\omega_{r1} - \omega_{r0} }}{{\omega_{e1} - \omega_{e0} }}\). k opt is the optimal power curve coefficient. Assuming that the rotor speed of the VSWT varies from ω r0 to ω r1, so the kinetic energy to be released is equivalent to the amount of kinetic energy released from a synchronous generator with rotor speed declining from ω e0 to ω e1. A wash-out block is used to remove the steady-state dc component of frequency error. The corresponding control block diagram is illustrated in Fig. 8.
An optimal controller for VIC is proposed in [35] to emulate the inertial response with the purpose of enhancing the frequency regulation in a diesel generator dominant system. The optimal virtual inertia factor K VIC is identified using deterministic linear quadratic regulator (LQR) method. Although both VIC and natural inertial control rely on real-time frequency measurement and perform based on the MPPT operation of a VSWT, the main difference between these two control strategies lies in the fact that VIC cannot cause a SFD when a VSWT performs the inertial response according to (8).
In addition to the three classic types of inertial controls above, an alternative inertial control method was recently presented in [58] to make a DIFG provide inertial response by directly adjusting the PI control parameters in its phase locked loop (PLL). Another novel virtual synchronous control (VSynC) is proposed in [59] for a DFIG to supply inertia response when integrated into a weak ac power grid with low short-circuit ratio. Without relying on the traditional PLL technique, the VSynC enables a DFIG to synchronize with the grid directly through active power control, so that the DFIG can naturally deliver the inertial response to enhance the frequency stability like conventional synchronous generators.
In Fig. 9, comparative simulation results for a small power system with a large-scale wind farm are presented to show the frequency regulation performance for the three types of inertial control discussed above, namely, natural inertial control, step-wise inertial control and virtual inertial control. From the simulation results, it is observed that virtual inertial control’s performance is the best by mitigating the ROCOF and boosting the frequency nadir. Step-wise inertial control can reduce ROCOF, but the SFD issue arises due to the WT’s rotor speed recovery. However, this problem might be avoided by applying other inertial control methods.
3 Wind turbine frequency control
3.1 Deloaded control
To participate in primary, secondary and tertiary frequency control, a VSWT needs to be operated in a sub-optimal mode through the deloaded control so that a certain amount of spinning reserve margin or headroom is always available to supply additional active power in case of frequency contingency.
Nowadays, primary reserve is commonly achieved through either “Balance” control that reserves a constant percentage of rated power [50], or “Delta” control that reserves a fixed proportion of available maximum active power [6, 32, 60], or “Fixed reserve” control that reserves a fixed amount of active power [3]. The power references for these three types of deloaded operation are mathematically described as follows:
-
1)
Balance
$$\begin{aligned} P_{ref} = \left\{ {\begin{array}{*{20}l} {P_{de} } \hfill & {P_{de} \le P{}_{MPPT}} \hfill \\ {P{}_{MPPT}} \hfill & {P_{de} > P{}_{MPPT}} \hfill \\ \end{array} } \right. \hfill \\ P_{de} = [0, \ldots ,P_{Rated} ] \hfill \\ \end{aligned}$$(9) -
2)
Delta
$$\begin{aligned} P_{ref} = \left\{ {\begin{array}{*{20}l} {\left( {1 - K_{Reserve} } \right)P_{MPPT} } \hfill & {P_{MPPT} \le P_{Rated} } \hfill \\ {\left( {1 - K_{Reserve} } \right)P_{Rated} } \hfill & {P_{MPPT} > P_{Rated} } \hfill \\ \end{array} } \right. \hfill \\ K_{Reserve} = \left[ {0, \ldots ,1} \right] \hfill \\ \end{aligned}$$(10) -
3)
Fixed reserve
$$\begin{aligned} P_{ref} = \left\{ {\begin{array}{*{20}l} 0 \hfill & {P_{MPPT} \le \Delta P_{Reserve} } \hfill \\ \begin{aligned} P_{MPPT} - \Delta P_{Reserve} \hfill \\ P_{Rated} - \Delta P_{Reserve} \hfill \\ \end{aligned} \hfill & \begin{aligned} P_{MPPT} \le P_{Rated} \hfill \\ P_{MPPT} \ge P_{Rated} \hfill \\ \end{aligned} \hfill \\ \end{array} } \right. \hfill \\ \Delta P_{Reserve} = \left[ {0, \ldots ,\Delta P_{\hbox{max} } } \right] \hfill \\ \end{aligned}$$(11)
where P ref is the WTG active power reference; P Rated is the WTG rated power; ∆P Reserve is a fixed amount of active power serving as spinning reserve; P MPPT is the maximum wind power; K Reserve is the fixed percentage of maximum wind power; ΔP max is the maximum fixed power reserve.
Compared with the balance type, the energy efficiency of delta or fixed reserve types is higher due to their long-term stable power reserve and reduced wind power curtailment. It is shown in [61] that modern offshore wind farms are capable of maintaining 5% of rated power as spinning reserve, sustained for up to 89% of the event duration under varying wind speed conditions. In contrast, rapid variations in WPP output can be effectively smoothed by balance type control, so that the uncertainty and variability of wind power production in power system operation and dispatch are minimized [5, 32, 45, 62, 63]. Note that the reserve margin level is dependent on prevailing wind speed magnitude, wind speed forecasting accuracy and allowable upper limit of the VSWT’s rotor speed [38, 62]. One dynamic reserve allocation approach is presented in [64] to distribute the total wind farm reserve according to specific wind speed of each wind turbine. In Fig. 10, the comparative results of wind turbine steady-state power output are given for balance (P de = 0.8), delta (K Reserve = 0.2) and fixed reserve (∆P Reserve = 0.2) deloaded controls. From this figure, it can be concluded that the amount of reserve margin for the delta type tends to increase as wind speed rises. Once it exceeds the rated value (12 m/s), the power margin will be held at 0.2 p.u. For the balance type, there is no reserve margin available when active power stays below 0.8 p.u. In that case, the WT only operates in MPPT mode. For fixed reserve type, the reserve margin is fixed as 0.2 p.u. of the rated wind power over a wide range of wind speeds, provided that the optimal power output is above 0.2 p.u.
As we discussed before, the deloaded margin can reinforce the VSWT’s overall inertial response and enable primary frequency regulation by quickly delivering additional active power through power converter control [32, 64]. Meanwhile, investment in conventional spinning reserve can be reduced to a certain extent by deloaded operation of WT. Thus, deloaded control plays an essential role in supporting long-term frequency regulation from both perspectives of system stability and economics.
3.1.1 Rotor speed control
In accordance with the PMSG-WTG sub-optimum power extraction curve in Fig. 11, WTG power output is deloaded by shifting the operating point toward the left or right side of the MPPT curve while the rotor speed remains below its upper limit. The WTG output can be adjusted between P de and P max by adjusting its rotor speed between ω r,del and ω max [34, 45]. The power reference (P ref ) of the deloaded WTG at the measured rotor speed is calculated by using a simplified linear equation (12) or referring to a predefined look-up table in [62]:
where P max is the maximum power; P de is the deloaded power; ω r,max is the PMSG’s rotor speed corresponding to P max; ω r,de is the rotor speed corresponding to P de ; ω r,meas is the measured rotor speed.
The left sub-optimal operating point is unstable since it is likely to cause the wind turbine to stall under a frequency disturbance. The wind turbine should operate on the right sub-optimal curve, so as to maintain stable operation when providing frequency response over a full range of wind speeds [45]. Another advantage of right sub-optimal operation is to enable a PMSG-WTG to contribute a combination of reserved active power and greater kinetic energy to support primary frequency regulation, by allowing the rotor speed to decline from the deloaded operating point towards the maximum power point. Moreover, it can effectively reduce tear and wear losses associated with pitch angle actuation compared with using the pitch servo alone to curtail the wind power and perform primary frequency regulation. Note that this approach of right sub-optimal operation can be applicable to a DFIG-WTG as well.
Considering the fact that the rotor speed ω required for de-loaded operation may exceed the maximum value ω max for medium and high wind speeds, three wind speed modes are defined in terms of the deloaded control objective and secure operation constraints: low wind speed mode where deloaded operation is fulfilled merely by rotor speed control; medium wind speed mode where deloaded operation is conducted by combining pitch angle control and rotor speed control; and high wind speed mode where modified pitch angle control alone enables deloaded operation [12, 45, 51].
3.1.2 Pitch angle control
The original objective of pitch angle control in a WT is to prevent the generator and power converter from overloading and the rotor from being over speed [16]. To support a supplementary frequency regulation, the pitch control needs to be modified based on the wind conditions. Meanwhile, the initial pitch angle β 0 is set to maintain a certain power reserve for potential primary frequency regulation. Due to the servo time constant of the pitch controller, the response of pitch control appears to be slower than that of rotor speed control through the power converter.
3.2 Primary frequency control
Primary frequency control is an automatic governor response in proportion to the frequency deviation from the scheduled value. This response, also called frequency responsive reserve, is typically provided by a conventional generator with governor droop control to regulate its power output as a function of frequency deviation and droop setting [50, 64,65,66,67,68]. A WTG’s primary frequency regulation resembles that of a conventional generator, which is usually activated within a few tens of seconds and sustained for up to 15 min once the grid frequency deviation exceeds the allowable threshold [67]. It plays an important role in mitigating the steady-state frequency deviation after inertial response until the secondary frequency control (automatic generation control, AGC) takes over to achieve zero frequency error in the steady-state condition.
Unlike the provision of inertial response, power output needs to be curtailed beforehand by deloaded control in order to carry out primary frequency regulation in response to an under-frequency disturbance. The abilities of WTG primary frequency regulation can be evaluated from the following perspectives: delay time, ramp rate, magnitude and response speed [10].
To emulate the traditional governor response for primary frequency regulation, droop control is implemented in a VSWT to correlate the variation in grid frequency with a corresponding change in active power output through power converter control. It responds to large deviations in grid frequency by increasing or decreasing power output during the frequency event. The relationship between active power change and frequency deviation can be expressed as ∆P dr = K dr (f – f 0), where f 0 is the nominal frequency. The parameter K dr is the inverse of speed droop R as follows.
The value of R usually lies in the range between 3% and 5% for conventional generators. Larger values of K dr can further reduce the steady-state frequency deviation without obviously impacting the small signal stability of power system [32].
3.2.1 Droop curve parameters
As depicted in Fig. 12, there are several important parameters that determine the droop curve behavior, including the droop slopes (up and down), dead band and power ramp rate. These parameters should be appropriately selected to ensure that additional active power output through droop response remains within the available reserve margin [3, 11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39, 49, 69, 70]. Moreover, a droop curve with a suitable dead band can prevent the droop controller from frequent activation in response to small frequency fluctuations [4]. Note that either symmetrical droop or asymmetrical droop can be used to perform primary frequency regulation according to system operational requirements.
According to different frequency deviations in Fig. 13, the active power reference for primary droop control is calculated in accordance with the following equations:
If the frequency declines below the dead band limit f DB_lower , the active power reference of the WTG is increased based on droop-down control until it reaches P MPPT at the present wind speed. On the other hand, if the frequency rises above the dead band limit f DB_upper , the active power reference is reduced by accelerating the rotor speed. If frequency keeps going up until f switch is reached, the rotor speed ceases to rise because of its upper limit. At this moment, the pitch angle controller is enabled to further reduce the WTG’s active power output by increasing the pitch angle β. During this process, the rotor speed remains constant at the upper limit value, ω max. It is worth noting that the slope value of R 3 is mainly dependent on the allowable variation range of β [18].
3.2.2 Static droop and dynamic droop control
Static droop control is quite similar to traditional governor control, providing additional active power based on the grid frequency deviation [10]. It features a droop curve with a fixed slope and a pre-defined dead band. According to simulation tests in [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39, 49], this control can arrest system frequency decline and minimize the steady-state frequency deviation.
For dynamic droop control, the slope and dead band of droop curve are adjustable in real-time according to the ROCOF value, de-loaded level or variable wind speed conditions. Using this control method, a desirable tradeoff between improved frequency response and reduced impacts on the structural loading is attained. A study in [11] illustrates that dynamic droop curves can effectively enhance the primary response without dramatically adding extra structural loading to wind turbine components, such as the shaft and tower. Compared with the aggressive static droop curve, the frequency nadir, frequency deviation and frequency recovery process are also improved by using dynamic droop control. On the other hand, a WTG operating under low wind speed is unable to provide a strong primary frequency response due to limited reserve.
It is also beneficial to adjust the droop coefficient in real time. An overly small static droop coefficient is likely lead to WTG instability, while an overly large coefficient tends to induce noticeable oscillations in active power output during frequency recovery [4]. Variable droop control can optimize the additional active power shared among WTs, running in deloaded mode, so that the primary frequency contribution of each WT is based on its own available power reserve corresponding to the local wind speed it is experiencing. A similar variable droop control scheme is presented in [62] for DFIG wind farms to adjust their droop coefficients according to the variable power reserve, so that the total number of power output reversals in traditional units and the Root Mean Square (RMS) value of frequency deviations are dramatically diminished.
3.3 Secondary frequency control (AGC)
Secondary frequency control, also called AGC or load frequency control (LFC), is implemented during emergency frequency events as well as under normal operating conditions [50, 64]. Secondary frequency control starts within several tens of seconds and is sustained for up to several tens of minutes [67]. This control is a continuous response on the minute timescale to allocate the load change among individual WTs for the purpose of maintaining the system frequency deviation and tie line power flow deviation at zero [41]. In Fig. 14, a simplified frequency control model is applied to validate the dynamic characteristics of a power system containing conventional power plants and WPPs [71]. The specific AGC set point for each WTG depends on PI controller parameters and participation factors (PFs). The optimal method to determine PFs is presented, and takes into account the up and down ramp rates, operating reserves, dispatch limits and generation costs [72].
A secondary frequency controller based on a supervisory wind farm control system (SWFCS) fully utilizes the secondary frequency reserve to follow commands from system operator, including AGC commands (updated power set point) and power flow adjustment [50, 64]. Another novel control scheme is proposed in [73] to enable WTs to change their active power reference in accordance with a power command, so as to meet the requirement of the system operator. In [72], a coordinated AGC control strategy between WTs and combined heat and power plants (CHPs) is proposed to mitigate the real-time power imbalance by down-regulating the wind power output when CHPs are not fast enough to track power commands. Due to the rapid ramp rate of WTs, the area control error (ACE) can be significantly reduced by this means.
3.4 Tertiary frequency control
Compared with the other frequency controls mentioned above, tertiary frequency control has a relatively long decision time step ranging from the order of minutes to hours, which takes effect following the secondary control [10, 67]. This control method comprises dispatching actions from the system operator, in order to achieve the power reserve deployment and restoration for the WTG’s tertiary frequency control that enables unit commitment, economic dispatch and optimal power flow in accordance with market signals or other system requirements. As shown in Fig. 14, operational active power reference values for individual conventional generators and wind farms are equal to the sum of AGC and economic dispatch set points. Economic dispatch usually updates operational set points every 1–5 min while AGC refreshes every 0.1–1 s [74]. Nowadays, there are two types of power markets associated with tertiary frequency control, including intraday real-time market with minute-level economic dispatch and day-ahead market with daily economic unit commitment.
3.5 Coordinated frequency control
Considering a VSWT’s initial operating condition and the frequency disturbance magnitude and duration, a combination of inertial response, primary frequency control and secondary frequency control can significantly enhance the overall frequency regulation performance of power system and alleviate frequency regulation stress for conventional units [10, 34, 38, 45]. The process of coordinated down-frequency regulation can be described as follows. During the initial transient process after a frequency drop event, inertial response plays an essential part in reducing ROCOF and boosting the frequency nadir point. Once the dead-band criterion is met for a specified delay time, the primary frequency response is triggered to further enhance frequency regulation through droop control until the frequency settles into a secondary steady state. At this point, the frequency nadir is further lifted and then frequency is restored to within an acceptable range. After that, AGC control takes over to achieve zero frequency error regulation using PI controller.
Several coordinated control strategies based on pitch angle control and rotor speed control have been proposed to improve VSWTs’ frequency regulation capability over the full range of wind speed conditions and to damp frequency oscillations. Even without deloaded control, temporary frequency support can be realized by employing a coordinated strategy of pitch angle and rotor speed control [75].
The work in [50] presents a K-deviation method to perform frequency regulation in a real-time variance tracking mode. The study in [45] proposes a novel coordinated frequency regulation strategy suitable for active-power-control-oriented VSWT and perform the frequency response according to different wind speed modes. In [34], a coordinated frequency control scheme appropriate for rotor-speed-control-oriented VSWTs which perform frequency response according to different wind speed conditions. In [34], a frequency control scheme appropriate for rotor-speed-control-oriented VSWTs is proposed to coordinate rotor speed control and pitch angle control according to pre-defined wind speed zones. Another coordinated control strategy in [65] employs direct control of a DFIG-WTG’s electromagnetic torque and rotor speed to allow for additional active power delivery based on the operator’s request and allowing for varying wind conditions. In [63], Kinetic/Inertia, Proportional gain and Enhanced Pitch (KIPEP) control is presented to support both primary and secondary frequency regulation while also smoothing out the wind power output over short time frames.
In Fig. 15, comparative simulation results for a small power system with a wind power plant are provided to demonstrate the frequency regulation performance using step-wise inertial control only, static droop control only and coordinated frequency control including variable droop. Coordinated frequency control is superior to other methods in improving the overall frequency regulation performance in terms of ROCOF, frequency nadir, frequency recovery and steady-state frequency. Static droop control alone can increase the frequency nadir and reduce the steady-state frequency deviation. In contrast, step-wise inertial control can mitigate the ROCOF, but it tends to cause a SFD.
4 Frequency regulation performance comparison of different types of WTG systems
A WTG possesses a significant amount of kinetic energy in the rotating masses, which can be utilized to provide a short-term frequency support in the event of large power imbalance [76]. In general, wind turbines can be divided into two main groups: fixed-speed WTs (FSWT) and variable-speed WTs (VSWT). Each group has distinctive benefits and drawbacks in terms of their contributions to system frequency support. The FSWT can inherently provide a limited inertial response to mitigate the ROCOF. In contrast, VSWTs cannot naturally deliver any inertial power into the electrical grid due to partial or full decoupling between rotor speed and grid frequency via the power converter. Nevertheless, modern VSWTs are capable of providing an emulated inertial response that is superior to that of conventional generators, due to their faster, more accurate and flexible active power controls and the wide range over which the wind turbine rotor speed can vary [17, 23, 26, 33, 51]. Last but not least, a novel type of VSWT based on the electromagnetic coupler (WT-EMC) can provide frequency support through emulated inertial response and droop frequency regulation [19].
4.1 Type 1 and Type 2 FSWTs
Thanks to direct coupling between the rotor speed and the system frequency, a Type 1 Induction Generator with Fixed Speed can potentially provide limited inertial response. Its inertial response is a passive process, in which the kinetic energy stored in the generator, gearbox and wind blades is intrinsically released or absorbed as system frequency decreases or increases. Commercial fixed speed wind turbines (FSWT) with rated power above 1 MW have an inertial constant of 3–5 s. The stored energy in each FSWT is unrelated to wind speed, and the aggregated kinetic energy of a WPP increases with the number of turbines online [71]. However, it is difficult to tune the inertial response of Type 1 in order to meet specific grid frequency regulation requirements. Overall, the inertial response from Type 1 WTGs is restricted and uncontrollable. The Type 2 Wound-rotor Induction Generator with adjustable external rotor resistance and variable slip tends to maintain its power output at a fixed value even during an abrupt frequency decline, since the external rotor resistance maintains the power output at the target value at all times. Therefore, Type 2 WTGs hardly make any contribution to the system inertial response [6, 16].
However, it is noted that through deloading control both types can allocate a constant amount or a fixed proportion of available aerodynamic power as a reserve margin to enable primary frequency regulation with the aid of a pitch angle controller [77].
4.2 Type 3 and Type 4 VSWTs
Type 3 double fed induction generator (DFIG) and Type 4 direct drive permanent magnet synchronous generator (PMSG) VSWTs are capable of achieving rapid and accurate active power regulation by means of power converter control. These two types of VSWT act like a flywheel device to mitigate the power fluctuations resulting from variable wind conditions. In comparison with FSWTs, the inertial response of VSWTs is a proactive process where the system frequency or ROCOF is monitored and measured in a real-time manner, so it can be optimally and dynamically tuned by setting proper control parameters according to different wind speed conditions and disturbance magnitudes. To better arrest a frequency decline, allowing some headroom for the inertial power release is desirable for VSWTs to deliver additional active power within the maximum power capabilities of converters and generators [33, 34, 45].
In contrast to synchronous generators, due to their asynchronous operation, the speed variation of Type 3 WTGs is much larger than the permissible system frequency variation. Their rotor speed can be controlled between 0.7 and 1.2 using modern power converters [62]. Their emulated inertial constant can be set as large as several times their inherent inertial constant in an auxiliary control loop. The partial-scale power converter (20%–30% of full rating) in the rotor circuit of Type 3 WTGs imposes limitations on the deloaded operating level, maximum inertial response and rotational speed range (within ±20%–±30% of synchronous speed) [55]. Compared to Type 3 WTGs with the identical rated power capability and inertial constant, Type 4 WTGs are capable of providing stronger inertial response due to the wider operating range of their rotor speeds (0.5–1.2 p.u.) [34]. Moreover, the full-scale power converter allows Type 4 WTGs to possess a higher overloading capability, so that more temporary inertial power can be injected into grid for a short period [78]. In addition, Type 4 WTGs might utilize a larger amount of energy stored in the DC-link capacitor to enhance the emulated inertial response and compensate for the temporary power deficit during the rotor speed recovery [37].
5 Key technical development trends
The following trends have been identified in the literature reviewed for this paper.
5.1 Optimized coordinated frequency control between wind farms and traditional power plants
A coordinated frequency control strategy between wind farms and other power plants needs to be properly designed and implemented for an optimized and reliable frequency regulation in response to various frequency events. The sequence, duration, ramp rate and proportion of additional power provision through primary and secondary frequency responses are determined between wind farms and conventional power plants according to system requirements and targeted capital and operating costs. So, it is necessary to carry out more research to coordinate and optimize the inertial response, primary frequency regulation and secondary frequency regulation when taking into account specific types of wind turbine, the power reserve method, the active power control strategy, the wind power penetration level and stochastic wind speed conditions
5.2 Coordinated inertial response and frequency regulation for offshore wind farm through HVDC links
An HVDC line is perceived as a cost-effective technical solution to transmit large-scale wind power to a load center over a very long distance. As more and more wind farms are built offshore, HVDC links can be used effectively to mitigate wind power variability and enhance power supply reliability. However, the increasing VSWT penetration and associated HVDC interconnections can negatively impact the system ROCOF and frequency nadir due to the reduced inertia of overall power system. That is due to the fact that HVDC lines and VSWTs are insensitive to frequency changes through their power converters, which fully isolates kinetic energy stored in wind turbine and reserved wind energy from the grid frequency variations. In order to reinforce the transient frequency stability and enhance the power damping effect, it is essential to develop a coordinated control scheme for wind farms and HVDC links by taking advantage of VSWTs’ fast inertial response and HVDC links’ transient overload capability.
5.3 Advanced emulated inertial control of VSWTs
During the process of inertial response emulation, a sudden boost in active power output can lead to a sharp deceleration in rotor speed due to the imbalance between the electrical and mechanical torques. The undesirable consequence is that the turbine may stall due to taking excessive kinetic energy from the rotor as well as the intensive structural load on the mechanical components of wind turbine. Moreover, the associated recovery process following temporary overproduction results in decreased WT power output. Consequently, a SFD is likely to occur. Therefore, it is necessary to design appropriate control schemes to provide as much inertial response from VSWTs as possible, while preventing the rotor speed from over-deceleration and mitigating the impact of rotor speed recovery on the overall frequency performance.
5.4 Frequency support by energy storage to assist VSWTs’ auxiliary frequency control
In order to fully eliminate the SFD issue and compensate for inadequate frequency regulation under low wind speed conditions, the fast and precise active power control of battery energy storage systems (BESSs) can be used to assist VSWTs in providing inertial response and primary frequency regulation. As a result, the burden of frequency response on both WTs and conventional generators will be eased in terms of response time and primary reserve margin. Therefore, it becomes important to conduct further studies on optimized coordinated control algorithms for inertial response and frequency regulation shared between VSWTs, BESSs and conventional generators. The main factors to consider include starting moment, duration and ending moment of inertial response, BESS lifespan and ancillary services revenue with the purpose of improving the system dynamic frequency response while achieving an optimal balance between cost and performance.
6 Conclusion
This survey elaborates the motivation, fundamental principles and various control schemes for frequency regulation by VSWTs. A variety of frequency regulation control schemes, including inertial response, primary droop control, secondary AGC control and tertiary frequency control, are explained in detail. To assess the effectiveness of various typical inertial responses, comparative simulations were performed. This showed that coordinated frequency control including variable droop is superior to other methods.
The merits and disadvantages of frequency regulation capabilities of various types of WTGs are briefly compared. Lastly, several key technical development trends frequency regulation by VSWTs are identified.
Based on the above analysis, a variety of effective methods exist to provide effective frequency regulation by VSWTs, exceeding in some respects the services offered by conventional generators. A combination of rotor speed control, pitch angle control, and deloading can be used according to operational requirements and wind speed conditions. There is room to improve the dynamic performance of frequency regulation controllers and the distribution of frequency regulation responsibilities between VSWTs and other generators.
References
Liu Y, Liu YL, Gracia JR et al (2014) Variable-speed wind generation control for frequency regulation in the Eastern Interconnection. In: IEEE transmission and distribution conference and exposition, Chicago, 1–5 April 2014
Liu Y, Gracia JR, King TJ et al (2014) Frequency regulation and oscillation damping contributions of variable-speed wind generators in the U.S. Eastern Interconnection. IEEE Trans Sustain Energy 6(3):1–8
Tarnowski GC, Kjær PC, Dalsgaard S et al (2010) Regulation and frequency response service capability of modern wind power plants. In: IEEE PES General Meeting, Minneaplolis, 1–8 July 2010
Ruttledge L, Flynn D (2013) Co-ordination of frequency responsive wind plant in future power system. In: 2nd IET renewable power generation conference, Beijing, 1–4 September 2013
Sun YZ, Zhang ZS, Li GJ et al (2010) Review on frequency control of power systems with wind power penetration. In: International conference on power system technology, Hangzhou, 1–8 October 2010
Muljadi E, Gevorgian V, Singh M et al (2012) Understanding inertial and frequency response of wind power plants. In: IEEE power electronics and machines in wind applications conference, Golden, 1–8 July 2012
Tarnowski GC, Kjær P, Østergaard J et al (2010) Frequency control in power systems with high wind power penetration. In: 9th international workshop on large-scale integration of wind power and transmission networks for offshore wind farms, Québec, 1–8 October 2010
James C (2010) Fast simulation of wind generation for frequency stability analysis in Island power systems. In: 9th international workshop on large-scale integration of wind power and transmission networks for offshore wind farms, Québec, 1–8 October 2010
Dernbach M, Bagusche D (2010) Frequency control in Québec with DFIG wind turbine. In: 9th international workshop on large-scale integration of wind power and transmission networks for offshore wind farms, Québec, 1–8 October 2010
Ela E, Gevorgian V, Felming P et al (2014) Active power control from wind power: briding the gaps. National Renewable Energy Laboratory, Golden
Buckspan A, Aho J, Fleming P et al (2010) Combining droop curve concepts with control systems for wind turbine active power control. In: IEEE symposium on power electronics and machines in wind applications, Denver, 1–8 July 2012
Wu Z, Gao W, Yang D et al (2012) Comprehensive modeling and analysis of permanent magnet synchronous generator-wind turbine system with enhanced low voltage ride through capability. In: IEEE energy conversion congress and exposition, Raleigh, 1–8 September 2012
Kim SK, Kim ES (2007) PSCAD/EMTDC-based modeling and analysis of a gearless variable speed wind turbine. IEEE Trans Energy Convers 22(2):421–430
Miller NW, Sanchez-Gasca JJ, Price WW et al (2003) Dynamic modeling of GE 1.5 and 3.6 MW wind turbine-generators for stability simulations. In: IEEE PES general meeting, Canada, 1977–1983, July 2003
Lin L, Li XY, Wang SQ et al (2012) An active power-frequency control strategy of DFIG based on subsection control. Electric Power 45(2):49–53
Ackermann T (2012) Wind power in power systems. John Wiley Press, Chichester
Morren J, Haan SWHD, Kling WL et al (2006) Wind turbines emulating inertia and supporting primary frequency control. IEEE Trans Power Syst 21(1):433–434
Cao Z, Wang X, Tan J (2012) Control strategy of large-scale DFIG-based wind farm for power grid frequency regulation. In: 31st Chinese control conference, China, pp 6835–6840, July 2012
You R, Barahona B, Chai J et al (2015) Frequency support capability of variable speed wind turbine based on electromagnetic coupler. Renew Energy 74:681–688
Gevorgian V, Zhang Y, Ela E (2015) Investigating the impacts of wind generation participation in interconnection frequency response. IEEE Trans Sustain Energy 6(3):1004–1012
Sharma S, Huang SH, Sarma N (2011) System inertial frequency response estimation and impact of renewable resources in ERCOT interconnection. In: Proc. IEEE power eng. soc. general meeting, San Diego, USA, 1–6 July 2011
Tarnowski GC, Kjar PC, Sorensen PE et al (2009) Variable speed wind turbines capability for temporary over-production. In: IEEE power & energy society general meeting, Calgary, Canada, pp 1–7 July 2009
Žertek A, Verbič G, Pantoš M (2010) Participation of DFIG wind turbines in frequency control ancillary service by optimized rotational kinetic energy. In: 7th international conference on the European energy market, San Madrid, Spain, pp 1–6 June 2010
Arani M, Mohamed Y (2016) Analysis and mitigation of undesirable impacts of implementing frequency support controllers in wind power generation. IEEE Trans Energy Convers 31(1):174–186
Altin M, Teodorescu R, Jensen BB et al (2012) Methodology for assessment of inertial response from wind power plants. In: Proc. IEEE PES general meeting, San Diego, USA, 1–8 July 2012
Miller NW, Clark K (2010) Impact of frequency responsive wind plant controls on grid performance. In: 9th international workshop on large-scale integration of wind power and transmission networks for offshore wind farms, Québec, 1–8 October 2010
Brisebois J, Aubut N (2011) Wind farm inertia emulation to fulfill Hydro-Québec’s specific need. In: Proc. IEEE power and energy society general meeting, San Diego, USA, 1–7 July 2011
Keung PK, Li P, Banakar H et al (2009) Kinetic energy of wind-turbine generators for system frequency support. IEEE Trans Power Syst 24(1):279–287
Kayikci M, Milanovic JV (2009) Dynamic contribution of DFIG-Based wind plants to system frequency disturbances. IEEE Trans Power Syst 24(2):859–867
Kayikci M, Milanovic JV (2008) Assessing transient response of DFIG-based wind plants—the influence of model simplifications and parameters. IEEE Trans Power Syst 23(2):545–554
Ullah NR, Thiringer T, Karlsson D (2008) Temporary primary frequency control support by variable speed wind turbines—potential and applications. IEEE Trans Power Syst 23(2):601–612
Margaris ID, Papathanassiou SA, Hatziargyriou ND et al (2012) Frequency control in autonomous power systems with high wind power penetration. IEEE Trans Sustain Energy 3(2):189–199
Conroy JF, Watson R (2008) Frequency response capability of full converter wind turbine generators in comparison to conventional generation. IEEE Trans Power Syst 23(2):649–656
Wu Z, Gao W, Wang J et al (2012) A coordinated primary frequency regulation from permanent magnet synchronous wind turbine generation. In: IEEE symposium on power electronics and machines in wind applications, Denver, USA, 1–8 July 2012
Zhu X, Wang Y, Xu L et al (2011) Virtual inertia control of DFIG-based wind turbines for dynamic grid frequency support. In: IET conference on renewable power generation, Edinburgh, UK, 1–6 September 2011
Ruttledge L, Flynn D (2015) Emulated inertial response from wind turbines: gain scheduling and resource co-ordination. IEEE Trans Power Syst 31(5):3747–3755
Licari J, Ekanayake J, Moore I (2013) Inertia response from full-power converter-based permanent magnet wind generators. J Modern Power Syst Clean Energy 1(1):26–33. doi:10.1007/s40565-013-0002-6
Wang Y, Delille G, Bayem H et al (2013) High wind power penetration in isolated power systems—assessment of wind inertial and primary frequency responses. IEEE Trans Power Syst 28(3):2412–2420
Aho J, Buckspan A, Laks J et al (2012) A tutorial of wind turbine control for supporting grid frequency through active power control. In: American control conference, pp 3120–3131 June 2012
Prabha K (1994) Power system stability and control. McGraw-Hill Press, New York
Wu L, Infield DG (2013) Towards an assessment of power system frequency support from wind plant—modeling aggregate inertial response. IEEE Trans Power Syst 28(3):2283–2291
Wang H, Chen Z, Jiang Q (2015) Optimal control method for wind farm to support temporary primary frequency control with minimised wind energy cost. IET Renew Power Gener 9(4):350–359
Gonzalez-Longatt FM (2016) Impact of emulated inertia from wind power on under-frequency protection schemes of future power systems. J Modern Power Syst Clean Energy 4(2): 211–218. doi:10.1007/s40565-015-0143-x
Liu Y, Liu Y, Gracia JR et al (2014) Variable-speed wind generation control for frequency regulation in the Eastern Interconnection (EI). In: IEEE PES T&D conference and exposition, Chicago, USA, 1–5 April 2014
Zhang ZS, Sun YZ, Lin J et al (2012) Coordinated frequency regulation by doubly fed induction generator-based wind power plants. IET Renew Power Gener 6(1):38–47
Su C, Chen Z (2012) Influence of wind plant ancillary frequency control on system small signal stability. In: Proc. IEEE power and energy society general meeting, San Diego, USA, 1–8 July 2012
Min H, Muljadi E, Park JW et al (2016) Dynamic droop-based inertial control of a doubly-fed induction generator. IEEE Trans Sustain Energy 7(3):924–933
Van de Jan V, Jeroen DMD, Bart M et al (2016) Droop control as an alternative inertial response strategy for the synthetic inertia on wind turbines. IEEE Trans Power Syst 31(2):1129–1138
National grid (2011) Frequency response technical sub-group report, pp 1–34
Chang-Chien LR, Lin WT, Yin YC (2011) Enhancing frequency response control by DFIGs in the high wind penetrated power systems. IEEE Trans Power Syst 26(2):710–718
Xue Y, Tai N (2011) Review of contribution to frequency control through variable speed wind turbine. Renew Energy 36(6):1671–1677
Teninge A, Jecu C, Roye D et al (2009) Contribution to frequency control through wind turbine inertial energy storage. IET Renew Power Gener 3(3):358–370
Kang M, Kim K, Muljadi E et al (2016) Frequency control support of a doubly-fed induction generator based on the torque limit. IEEE Trans Power Syst 31(6):4575–4583
Kang M, Lee J, Hur K et al (2015) Stepwise inertial control of a doubly-fed induction generator to prevent a second frequency dip. J Electr Eng Technol 10(6):2221–2227
Gowaid IA, El-Zawawi A, El-Gammal M (2011) Improved inertia and frequency support from grid-connected DFIG wind farms. In: IEEE power systems conference and exposition, Phoenix, USA, 1–9 March 2011
Wu Z, Gao W, Zhang H et al (2016) Improved inertial control for permanent magnet synchronous generator wind turbine generators. IET Renew Power Gener. doi:10.1109/TSTE.2017.2679716
Wang Y, Meng J, Zhang X et al (2015) Control of PMSG-based wind turbines for sytem inertial response and power oscilallation damping. IEEE Trans Sustain Energy 6(2):565–574
He W, Yuan X, Hu J (2016) Inertia provision and estimation of PPL-based DFIG wind turbines. IEEE Trans Power Syst 32(1):510–521
Wang S, Hu J, Yuan X (2015) Virtual synchronous control for grid-connected DFIG-based wind turbine. IEEE J Emerg Sel Top Power Electron 3(4):932–944
Active power control in Siemens wind turbines (2016). http://www.nrel.gov/electricity/transmission/pdfs/nelson.pdf. Accessed 29 May 2016
Vos KD, Rijcke SD, Driesen J (2010) Asymmetric reserve power delivered by large wind power plants. In: Innovative smart grid technologies, Gaithersburg, USA, 1–8 Jan 2010
Vidyanandan KV, Senroy N (2013) Primary frequency regulation by deloaded wind turbines using variable droop. IEEE Trans Power Syst 28(2):837–846
Wang-Hansen M, Josefsson R, Mehmedovic H (2013) Frequency controlling wind power modeling of control strategies. IEEE Trans Sustain Energy 4(4):954–959
Chang-Chien LR, Hung CM, Yin YC (2008) Dynamic reserve allocation for system contingency by DFIG wind farms. IEEE Trans Power Syst 23(2):729–736
Almeida RGD, Lopes JAP (2007) Participation of doubly fed induction wind generators in system frequency regulation. IEEE Trans Power Syst 22(3):944–950
Ma HT, Chowdhury BH (2010) Working towards frequency regulation with wind plants: combined control approaches. IET Renew Power Gener 4(4):308–316
Zertek A, Verbic G, Pantos M (2012) A novel strategy for variable-speed wind turbines’ participation in primary frequency control. IEEE Trans Sustain Energy 3(4):791–799
Žertek A, Verbič G, Pantoš M (2012) Optimised control approach for frequency-control contribution of variable speed wind turbines. IET Renew Power Gener 6(1):17–23
Ela E, Gevorgian V, Tuohy A et al (2014) Market designs for the primary frequency response ancillary service-Part I: motivation and design. IEEE Trans Power Syst 29(1):421–431
Jalali M, Bhattacharya K (2013) Frequency regulation and AGC in isolated systems with DFIG-based wind turbines. In: Proc. power and energy society general meeting, Vancouver, Canada, 1–5 July 2013
Doherty R, Mullane A, Nolan G et al (2010) An assessment of the impact of wind generation on system frequency control. IEEE Trans Power Syst 25(1):452–460
Basit A, Hansen AD, Altin M et al (2014) Wind power integration into the automatic generation control of power system with large-scale wind power. J Eng. doi:10.1049/joe.2014.0222
Aho J, Pao L, Buckspan A (2013) A novel active power control system for wind turbines capable of AGC and primary response. In: AIAA/ASME wind symposium, USA, 2013
Feng X (2013) Dynamic balancing for low inertia power systems. In: Proc. IEEE power and energy society general meeting, Vancouver, Canada, 1–5 July 2013
Wang H, Chen Z, Jiang Q (2014) Control method for variable speed wind turbines to support temporary primary frequency control. In: IEEE PES T&D conference and exposition, Chicago, USA, 1–5 April 2014
Basit A, Hansen AD, Altin M et al (2016) Compensating active power imbalances in power system with large-scale wind power penetration. J Modern Power Syst Clean Energy 4(2):229–237. doi:10.1007/s40565-015-0135-x
Muljadi E, Singh M, Gevorgian V (2013) Fixed-speed and variable-slip wind turbines providing spinning reserves to the grid. In: Proc. IEEE power and energy society general meeting, Vancouver, Canada, 1–5 July 2013
Glover J, Overbye T, Sarma M (2015) Power system analysis and design. Cengage Learning Press, Boston
Acknowledgements
This work was supported in part by the National Natural Science Foundation of China (Nos. 61428301, 61433004 and 61627809).
Author information
Authors and Affiliations
Corresponding author
Additional information
CrossCheck date: 3 May 2017
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
WU, Z., GAO, W., GAO, T. et al. State-of-the-art review on frequency response of wind power plants in power systems. J. Mod. Power Syst. Clean Energy 6, 1–16 (2018). https://doi.org/10.1007/s40565-017-0315-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40565-017-0315-y