Stability of LCL-filtered grid-connected inverters with capacitor current feedback active damping considering controller time delays

Abstract

This paper investigates the stability of LCL-filtered grid-connected inverters with capacitor current feedback (CCF) active damping. The impact of time delays in the digital controller on active damping and its equivalent virtual impedance is analyzed. The inherent relationship between these time delays and stability is illustrated. Specially, a critical value of the CCF active damping coefficient k _{damp_c} is proposed to define three distinct regions of stability evaluation. If k _{damp_c} > 0, a sufficient but smaller damping coefficient (k _damp < k _{damp_c}) is recommended as optimum damping solution; if k _{damp_c} = 0, system will be unstable irrespective of active damping; and if k _{damp_c} < 0, active damping is not necessary to design a stable system. Necessary conditions to ensure stability are identified; guidelines for controller design are then presented to optimize the performance of active damping and dynamic response. Simulation and experimental results confirm the presented analysis.

1 Introduction

With the increasing penetration of distributed energy generation in power grids, grid-connected inverters become an indispensable component of modern power systems [1, 2]. A filter is necessary in a converter system to improve the performance of harmonic attenuation. Among filter designs, the LCL filter is attracting more attention because of its much lower weight and size, compared to single L filter. However, the LCL filter introduces substantial complexities into controller design due to the resonance phenomenon. Thus, damping solutions are needed to stabilize the converter system.

Passive damping by inserting a resistor into the filter is a direct and reliable solution. It has been proved that a resistor connected in parallel with the filter capacitor has an optimal magnitude characteristic for damping both in low and high frequency ranges, but collateral effects of high power losses are unaffordable [3]. To overcome this drawback, various active damping strategies are proposed to substitute the physical resistor by adding a feedback in the controller, which can be proportional to the capacitor current [4–6], or to the first-order differential of capacitor voltage [7], or to the second-order differential of the grid-side current [8, 9]. All of these damping strategies can be applied as a virtual resistor with the equivalently optimal performance, but proportional computation is more accurate compared with differential approximation in digital controller. Reference [10] found that an inverter-side current feedback (ICF) control loop is naturally stable, and this is equivalent to adding an inherent capacitor current feedback (CCF) term to the forward path of the direct control loop of the grid current; in other words, active damping is achieved by CCF. Therefore, in this paper, CCF active damping is adopted for its accuracy and simplicity when grid current is to be controlled directly.

Despite a vast amount of literature that has been published on the subject of LCL filter in grid-connected inverters, there is still no consensus on a stability evaluation method accounting for computation and pulse width modulation (PWM) delays [11–17]. Reference [11] presented pioneering research on active damping in discrete-time domain taking time delays into account, and concluded that discrete-time active damping is not always stable, depending on the ratio of resonance frequency to sampling frequency. Then [12] identified three distinct regions of LCL filter resonance frequency separated by one sixth of the sampling frequency (f _s/6), named the critical resonance frequency. They also proposed a design method for a digital controller in the two stable regions. Similar conclusions were also drawn in [13, 14]. However, these papers do not provide sufficient explanation of the inherent relationship between active damping and controller time delays. Reference [15] demonstrated the effect of delays on active damping performance, where the virtual impedance model consisting of a resistance paralleled with a reactance was proposed, but the conclusion is incomplete since active damping is not required when the LCL filter is operated in the high resonance frequency region. Reference [16] indicated that a single loop of grid-side current feedback without any additional active damping can be naturally stabilized by the inherent damping characteristics owing to time delays in the digital control system. Besides, [17] analyzed the relationship between time delays and stability of single loop controlled inverters, and used an intentional time delay addition method as inherent damping to improve stability of the grid-side current feedback loop.

In summary, the literature does not provide a stability evaluation method for digitally controlled LCL filtered grid-connected inverters that accounts for computation and PWM delays, nor does it provide a general guideline for selecting controller parameters to ensure stability. In this paper, Sect. 2 introduces a typical model of an LCL filtered grid-connected inverter, and the traditional method to evaluate CCF active damping is reviewed briefly. Section 3 is devoted to a theoretical explanation of the impact of time delays on active damping and the equivalent virtual impedance caused by time delays. In Sect. 4, by using a critical value of the active damping coefficient, a stability evaluation method is developed. Necessary conditions to ensure stability, and steps for designing controller parameters to optimize the performance of active damping and dynamic response, are presented in Sect. 5. Simulation and experimental results verify the presented evaluation method in Sects. 6, and 7 concludes this paper.

2 CCF active damping in continuous domain

2.1 Modeling LCL-filtered grid-connected inverter

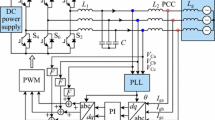
Figure 1 shows the topology of a three-phase inverter feeding the grid through an LCL filter, composed of the inverter-side inductor L ₁, filter capacitor C, and grid-side inductor L ₂. The DC-side voltage U _dc can be supplied by absorbing active current from the grid. The objective of the inverter is to regulate the grid-side current i _{2_a,b,c} as required. For this model all parameters of each phase are assumed symmetrical, including i _{2_a,b,c}, inverter-side current i _{1_a,b,c}, capacitor current i _{C_a,b,c}, grid voltage V _{g_a,b,c}, grid-side current i _{g_a,b,c}, and local load current i _{L_a,b,c}.

Fig. 1

Topology of a three-phase LCL filtered grid-connected inverter

A block diagram of the inverter and controller is given in Fig. 2. The synchronous dq frame is particularly suitable for analysing the direct control of active and reactive current in a three-phase system. However, there are three pairs of cross-coupling terms between the d-axis and the q-axis in the block diagram, so decoupling is necessary to achieve independent control. Hence, a synthesized system is implemented in the stationary αβ frame without any cross-coupling terms, while the regulation of active and reactive current remains in the synchronous dq frame [18].

Fig. 2

Synthesized system block diagram implemented in stationary αβ frame and synchronous dq frame

In Fig. 2, i _{2d_ref} and i _{2q_ref} represent the reference values of active and reactive current, regulated by G _id and G _iq respectively. i _{C_α,β} are feedback currents with active damping coefficient k _damp. Subtracting the active damping from the output of regulator, the modulation reference signal V _{mod_α,β} will be yield. This is fed to the PWM modulator after dividing by U _dc/2 to transform into a per-unit value. While bipolar sinusoidal pulse width modulation (SPWM) is used for inverter, the transfer magnitude of the inverter bridge K _pwm can be approximated by U _dc/2, since the switching frequency of inverter is assumed to be sufficiently high. G _ff is the grid voltage feed-forward function, and in most cases, it can be simplified to 1 (G _ff ≈ 1) when the grid voltage is mainly distorted by low-frequency harmonics [19].

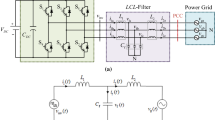
For the convenience of analysis, an equivalent circuit is used for a single-phase LCL filtered grid-connected inverter, as shown in Fig. 3. R is the virtual resistor connected in parallel with filter capacitor, representing the effect of CCF active damping. V _PCC is the voltage at the point of common coupling of the inverter and grid.

Fig. 3

Single-phase equivalent circuit of LCL filtered grid-connected inverter with virtual resistor connected in parallel with filter capacitor

2.2 Evaluation method of CCF active damping in continuous domain

Figure 4 shows a typical dual-loop control system with CCF via an active damping coefficient k _damp. The grid voltage feed-forward function G _ff(s) is ignored, since it has no relationship with stability. The open-loop transfer function T _A(s) in the s-domain can be expressed as:

$$T_{\text{A}} (s) = \frac{{G_{\text{i}} \left( s \right)}}{{s^{3} L_{1} L_{2} C + s^{2} L_{2} Ck_{\text{damp}} + s\left( {L_{1} + L_{2} } \right)}}$$

(1)

Fig. 4

Block diagram of single-phase LCL filtered grid-connected inverter with CCF active damping

To assess the relationship between active damping and the LCL filter resonance peak, it is assumed that the current regulator gain G _i(s) = 1. Typically the crossover frequency f _c is restricted to be much lower than switching frequency f _sw (f _sw is equal to sampling frequency f _s) for the effectiveness of attenuating high-frequency harmonics. Although some of the latest research suggests setting the resonance frequency f _r to be higher than the Nyquist frequency f _s/2 [20], this is not the general practice, which regards f _r < f _s/2 as necessary to ensure system controllability [21].

The frequency responses of open-loop gain are depicted in Fig. 5. The dashed curve shows the case without damping, which causes a high resonance magnitude accompanied by a sharp phase transition through −180°, and this is an unstable situation for all controller gains. In contrast, active damping can both reduce the resonance peak magnitude and smooth the phase transition, as shown in Fig. 5 for two different damping coefficients. However, increasing k _damp, results in a negative phase shift for frequencies between f _c and f _r, which means an over-damped system might lead to a poor phase margin. Therefore, the system should be stabilized by a suitable damping coefficient. Damping performance is evaluated by the ‘Q _r’-factor, related to the peak magnitude of the frequency response plot at the resonance frequency, such that the lower is the ‘Q _r’ the better is the damping performance [22].

Fig. 5

Bode diagram of CCF active damping with coefficients k _{damp_1} = 5 and k _{damp_2} = 10

3 Impacts on active damping caused by time delays

3.1 Modeling equivalent virtual impedance when taking time delays into account

The basic method of controller design for LCL filtered grid-connected inverter in continuous domain has been reviewed above. However, the controller is widely implemented by means of a digital micro-processor, and time delays shouldn’t be omitted, so the impacts on active damping and stability should be discussed.

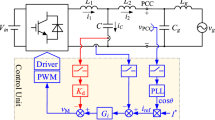
The detailed mechanism of time delays generated in a digitally controlled inverter has been analyzed in [15]. Taking into account one sample period (T _s) of computation delay and a half sample period (0.5T _s) of PWM delay, the block diagram of a digitally controlled system is introduced in Fig. 6a. Synchronous sampling is adopted in this paper, and the switching samplers are introduced into the feedback of the grid-side current, the capacitor current, and the reference value of current. The switching samplers can be represented in the s-domain by 1/T _s [23], and after a series of transformations the block diagram in the continuous domain is obtained as shown in Fig. 6b. The CCF active damping can be represented by a model of virtual impedance connected in parallel with the filter capacitor, the virtual impedance expresses as Z _eq(s):

$$Z_{\text{eq}} (s) = Re^{{1.5sT_{s} }} \triangleq R_{\text{eq}} (\omega )//jX_{\text{eq}} (\omega )$$

(2)

where

$$\left\{ {\begin{array}{*{20}l} {R_{\text{eq}} (\omega ) = \frac{R}{{\cos (1.5\omega T_{\text{s}} )}} = \frac{R}{{\cos 3\uppi\frac{f}{{f_{\text{s}} }}}}} \hfill \\ {X_{\text{eq}} (\omega ) = \frac{R}{{\sin (1.5\omega T_{\text{s}} )}} = \frac{R}{{\sin 3\uppi\frac{f}{{f_{\text{s}} }}}}} \hfill \\ \end{array} } \right.$$

(3)

Fig. 6

Block diagram of a digital controlled inverter system taking time delays into account

The virtual resistor has been changed into another form of parallel connection with a resistance R _eq and a reactance X _eq [15], shown as the dashed box in Fig. 7a. Both two components are frequency dependent and have two singular points respectively (f = f _s/6 for R _eq, and f = f _s/3 for X _eq) as shown in Fig. 7b.

Fig. 7

Model of equivalent virtual impedance taking 1.5T _s time delays into account

3.2 Impact on damping performance

The virtual reactance X _eq is inductive when f ∈ (0, f _s/3), but capacitive when f ∈ (f _s/3, f _s/2). This changes the effective value of the filter capacitor. And according to (4) the resonance frequency f _r will then be shifted to a new one f _r′.

$$f_{\text{r}} = \frac{{\omega_{\text{r}} }}{{2\uppi}} = \frac{1}{{2\uppi}}\sqrt {\frac{{L_{1} + L_{2} }}{{L_{1} L_{2} C}}}$$

(4)

For instance, in the range of (0, f _s/3), X _eq yields a higher resonance frequency f _r′ because of the effective value of filter capacitor is decreased; conversely, in the range of (f _s/3, f _s/2), X _eq yields a lower f _r′. Whether decreased or increased, f _r′ will only approach but never step over f _s/3, the singular point of X _eq.

Generally, in order to damp a resonance peak, positive R _eq is required, which occurs when f ∈ (0, f _s/6). But R _eq is negative when f ∈ (f _s/6, f _s/2), and even worse, R _eq approaches infinity when f = f _s/6, in other words, the resistance approaches an open circuit state (no damping) at the singular point of f _s/6.

Table 1 summarises the behaviour of X _eq and R _eq and their impacts on resonance frequency and active damping. These impacts mean that evaluating stability and selecting active damping parameters in a digital controller are completely different from the conventional situation in the continuous domain, due to the effect of time delays.

Table 1 Detailed analysis of impacts on virtual impedance

4 Evaluation method of stability regarding time delays

4.1 Descriptions of Nyquist stability criterion

The Nyquist stability criterion is widely used for designing and analyzing linear and time-invariant systems with feedback, and it is adopted in this paper. Before evaluating stability, the significance of −180° phase crossings within the frequency ranges that have magnitudes above 0 dB in bode diagram, and their relationship with open-loop unstable poles, should be reviewed as follows:

• 1) A −180° crossing where phase increases with frequency is defined as positive crossing; a −180° crossing where phase decreases with frequency is defined as negative crossing. The numbers of positive and negative crossings are denoted by C ⁺ and C ⁻ respectively.

• 2) The value of 2(C ⁺–C ⁻) must be equal to the number of open-loop unstable poles to ensure stability. If no open-loop unstable pole exists, that means the value of 2(C ⁺–C ⁻) must be equal to zero to ensure stability, so the value of C ⁺ also should be equal to zero, since C ⁻ is restricted to zero by the Nyquist criterion; if a pair of open-loop unstable poles exists, that means the value of 2(C ⁺–C ⁻) must be equal to 2 to ensure stability, so the value C ⁺ should be equal to 1.

4.2 Location of unstable open-loop poles

Based on the equivalent block diagram of the system in continuous domain shown in Fig. 6b, the open-loop gain with time delays can be easily derived, and is shown in (5). The denominator of T _{A_Delay}(s) contains a nonlinear element $e^{{ - 1.5sT_{\text{s}} }}$, a transcendental function with open-loop poles that cannot be solved directly in the s-domain. On the other hand, T _D(z) can be derived from Fig. 6a as the discrete representation of open-loop gain, an expression without any nonlinear element in the denominator part as shown in (6), and this form is preferred for determining poles. Thus, unstable open-loop poles can be comprehensively explored in the z-plane.

$$T_{{{\text{A}}\_{\text{Delay}}}} (s) = \frac{{G_{\text{i}} (s){\text{e}}^{{ - 1.5sT_{\text{s}} }} }}{{s^{3} L_{1} L_{2} C + s^{2} L_{2} Ck_{\text{damp}} {\text{e}}^{{ - 1.5sT_{\text{s}} }} + s(L_{1} + L_{2} )}}$$

(5)

$$\begin{aligned} T_{\text{D}} (z) & = \frac{{G_{\text{i}} (z)}}{{\omega_{\text{r}} (L_{1} + L_{2} )}} \cdot \\ & \quad \frac{{\omega_{\text{r}} T_{\text{s}} \left( {z^{2} - 2z\cos (\omega_{\text{r}} T_{\text{s}} ) + 1} \right) - (z - 1)^{2} \sin (\omega_{\text{r}} T_{\text{s}} )}}{{(z - 1)\left[ {z\left( {z^{2} - 2z\cos (\omega_{\text{r}} T_{\text{s}} ) + 1} \right) + (z - 1)\frac{{k_{\text{damp}} \sin (\omega_{\text{r}} T_{\text{s}} )}}{{\omega_{\text{r}} L_{1} }}} \right]}} \\ \end{aligned}$$

(6)

A critical value of the active damping coefficient k _{damp_c} is proposed as shown in (7). The relationship between k _{damp_c}, the ratio of resonance frequency to sampling frequency f _r/f _s, and the sampling frequency f _s is depicted by Fig. 8. Parameters f _s = 10 kHz and L ₁ = 2.3 mH are used as a typical example. The resonance frequency can be divided into three regions depending on k _{damp_c} > 0, k _{damp_c} = 0, and k _{damp_c} < 0, defined as low resonance frequency region, critical resonance frequency, and high resonance frequency region.

$$k_{{{\text{damp}}\_{\text{c}}}} = \frac{{\left[ {2\cos \left( {2\uppi\frac{{f_{\text{r}} }}{{f_{\text{s}} }}} \right) - 1} \right]2\uppi\,f_{\text{r}} L_{1} }}{{\sin \left( {2\uppi\frac{{f_{\text{r}} }}{{f_{\text{s}} }}} \right)}}$$

(7)

Fig. 8

Variation of critical value k _{damp_c} with sampling frequency f _s and resonance frequency f _r

The location of unstable open-loop poles can be easily concluded by means of k _{damp_c:}

• 1) If k _damp > k _{damp_c}, there is a pair of unstable open-loop poles, and when k _damp < k _{damp_c}, no unstable open-loop poles exist. Substituting k _damp = k _{damp_c} into T _D(z) allows a pair of critical open-loop poles z _1,2 = (1 ± j$\sqrt 3$)/2 to be calculated, located on the unit circle of z-plane. Their unique mapping poles s _1,2 = ±jπf _s/3 (related to the frequency f _s/6) on the imaginary axis of s-plane can also be exactly derived.

• 2) The magnitude of T _D(z)|| ^−jπ/3 _z=e tends towards infinity, yielding a new resonance frequency of f _s/6. This is defined as the critical resonance frequency, where the −180° crossing definitely will occur in bode diagram.

4.3 Stability evaluation method

Based on the previous analysis, the stability evaluation can be focused on the relationship between k _damp and k _{damp_c}. When the value of k _{damp_c} is different from the resonance frequency, the problem should be divided into three regions, and each region has sub-cases as listed in Table 2. Each sub-case will now be discussed.

Table 2 Regions and sub-cases in stability analysis

Case 1.1: If k _damp > k _{damp_c} > 0, the resonance frequency is located in the low region (f _r < f _s/6), and k _{damp_c} > 0 is satisfied, so a pair of open-loop unstable poles is produced. Hence, to ensure stability, the value of 2(C ⁺–C ⁻) must be equal to 2, i.e., C ⁺ = 1 and C ⁻ = 0, which means the positive −180° crossing should be at f _s/6. Consequently, the magnitude margin at f _r defined as GM ₁ must be greater than 0 dB to prevent the negative crossing, i.e. C ⁻ = 0; and the magnitude margin at f _s/6 defined as GM ₂ must be smaller than 0 dB to ensure the positive crossing, i.e. C ⁺ = 1. The bode diagram for this case is shown in Fig. 9a.

Fig. 9

Bode diagram of sub-cases of stability analysis

The resonance frequency is shifted to a higher one (f _r′ > f _s/6), and as discussed in Sect. 3.2 the virtual resistance R _eq is negative and has adverse effect on active damping when f _r′∈(f _s/6, f _s/2). The stringent constraint on overall stability margins is an adverse effect of negative R _eq.

Case 1.2: If k _damp = k _{damp_c} > 0 while f _r < f _s/6, k _{damp_c} > 0 is satisfied and a pair of open-loop poles arises on the imaginary axis of s-plane. According to the previous analysis, the critical resonance peak is shifted to f _s/6 (f _r′ = f _s/6). Although active damping fails to suppress the resonance peak, the system can remain stable when the value of 2(C ⁺–C ⁻) remains 0, i.e. when C ⁺ = 0 and GM ₁ is greater than 0 dB. The bode diagram is shown in Fig. 9b.

A critical resonance peak is produced but cannot be damped when k _damp = k _{damp_c}, and the virtual resistance R _eq approaches an open-circuit state at the singular point of f _s/6, which means R _eq makes no contribution to suppression when the resonance peak is located at critical resonance frequency.

Case 1.3: If 0 < k _damp < k _{damp_c} while f _r < f _s/6, k _{damp_c} > 0 is satisfied, and no unstable pole exists. Hence, GM ₁ greater than 0 dB and C ⁻ = 0 is enough for ensuring stability. The bode diagram is shown in Fig. 9c.

The resonance frequency f _r′ ∈ (0, f _s/6) so the virtual resistance R _eq is positive and has beneficial effect on active damping. The relaxed stability condition is seemed as the beneficial effect from positive R _eq.

Case 2.1: If k _damp > k _{damp_c} = 0 and the resonance frequency is located at the critical point (f _r = f _s/6), k _{damp_c} = 0 is satisfied, and a pair of open-loop unstable poles is produced. Similarly to the Case 1.1, negative and positive crossings should occur at f _r and f _s/6 respectively, which causes the phase-frequency curve to touch the scale line of −180° in the bode diagram, i.e. C ⁺ = 0.5. The system cannot be stable irrespective of active damping. The bode diagram is shown in Fig. 9d.

Case 2.2: If k _damp = k _{damp_c} = 0 and f _r = f _s/6, k _{damp_c} = 0 is satisfied. The system is unstable with no damping supplied for the resonance peak and the negative crossing occurs at the critical resonance frequency.

Case 3.1: If k _damp > 0>k _{damp_c} while the resonance frequency is located in the high region (f _s/6 < f _r < f _s/2), k _{damp_c} < 0 is satisfied and a pair of open-loop unstable poles is produced, similarly to Case 1.1. It should be noted that the frequency of positive crossing is changed to f _r, so the necessary magnitude margins are GM ₂ > 0 dB to prevent the negative crossing at f _s/6, i.e. C ⁻ = 0, and GM ₁ < 0 dB to ensure the positive crossing, i.e. C ⁺ = 1. The bode diagram is shown in Fig. 9e.

Case 3.2: If k _damp = 0>k _{damp_c} while f _s/6 < f _r < f _s/2, k _{damp_c} < 0 is satisfied, and this case is shown by the dashed curve (no damping) in Fig. 9e. Here it can be seen that the phase transits below −180° at f _s/6 (well before the resonance frequency), which means, even though there is no damping to supress the resonance peak, the system is naturally stabilized by selecting a suitable gain for the current regulator, because the magnitude response crosses 0 dB prior to f _s/6. An updated bode diagram with no damping is shown in Fig. 9f, where the current regulator gain of G_i1 is larger than G_i2. The magnitude margin at f _s/6 defined as GM2_Nodamping must be greater than 0 dB to ensure stability.

This analysis leads to a generalized stability evaluation method accounting for digital controller time delays, as follows:

• 1) If k _{damp_c} > 0, which is equivalent to the condition that the LCL resonance frequency is in the low region (f _r < f _s/6), k _damp > 0 is necessary for stability so active damping is applied. A sufficient but smaller damping coefficient (k _damp < k _{damp_c}) is recommended as an optimal solution because the virtual resistance R _eq makes a contribution to active damping. In contrast, over damping (k _damp > k _{damp_c}) leads to an adverse effect, and the conditions of overall stability would be compromised. The critical damping (k _damp = k _{damp_c}) solution should be avoided because it leads to a new resonance frequency (f _s/6), where R _eq makes no contribution to damping the resonance peak.

• 2) If k _{damp_c} = 0, which is equivalent to the condition that the LCL resonant frequency is equal to the critical frequency (f _s/6), the system will be unstable irrespective of active damping, unless additional modifications are implemented to the controller time delays [15].

• 3) If k _{damp_c} < 0, which is equivalent to the condition that LCL resonant frequency is above the critical frequency (f _s/6 < f _r < f _s/2), and even if k _damp = 0 a single loop of grid-side current feedback is naturally stabilized by a proper current regulator gain. Certainly, system is also stable when a redundant damping solution (k _damp > 0) is applied.

Therefore, k _{damp_c} is an important measure of stability and k _{damp_c} = 0 will cause instability.

5 Design method for controller parameters

5.1 Phase and magnitude margins

High-performance LCL filtered grid-connected converters should have fast dynamic response, sufficient switching frequency attenuation, and good damping performance while preserving stability. This section provides guidelines for selecting controller parameters. A proportional integral (PI) current regulator is adopted in this paper, which expresses as G _i(s) = K _p + K _i/s.

Dynamic response is mainly evaluated by the phase margin (PM) at the unity-gain crossover frequency f _c, and as discussed above, to guarantee the robust stability of system, sufficient magnitude margins GM1 and GM2 also should be assured. PM, GM1 and GM2 are deduced and presented from (8) to (10). PM _Nodamping and GM2_Nodamping can be derived by substituting k _damp = 0 into (8) and (10). Typically, PM $\in$ (30°, 60°), and 3 < |GM| < 6 are recommended to ensure satisfactory dynamic response and robust stability [24].

$$PM = 180^\circ + \angle T_{{{\text{A}}\_{\text{Delay}}}} \left( s \right)\left| {_{{s = {\text{j}}2\uppi\,f_{\text{c}} }} } \right. = { \arctan }\frac{{2\uppi\,f_{\text{c}} K_{\text{p}} }}{{K_{\text{i}} }} - 3\uppi\frac{{f_{\text{c}} }}{{f_{\text{s}} }} - { \arctan }\frac{{f_{\text{c}} k_{\text{damp}} { \cos }\left( {3\uppi\frac{{f_{\text{c}} }}{{f_{\text{s}} }}} \right)}}{{f_{\text{c}} k_{\text{damp}} { \sin }\left( {3\uppi\frac{{f_{\text{c}} }}{{f_{\text{s}} }}} \right) + 2\uppi\,L_{1} \left( {f_{\text{r}}^{2} - f_{\text{c}}^{2} } \right)}}$$

(8)

$$GM1 = - 20{ \lg }\left| {T_{{{\text{A}}\_{\text{Delay}}}} (s )} \right|\left| {_{{s = {\text{j}}2\uppi\,f_{\text{r}} }} } \right. = - 20{ \lg }\left| {\frac{{K_{\text{p}} L_{1} }}{{k_{\text{damp}} \left( {L_{1} + L_{2} } \right)}}} \right|$$

(9)

$$GM2 = - 20{ \lg }\left| {T_{{{\text{A}}\_{\text{Delay}}}} (s )} \right|\left| {_{{s = {\text{j}}2\uppi\frac{{f_{\text{s}} }}{6}}} } \right. = - 20{ \lg }\left| {\frac{{K_{\text{p}} }}{{\frac{\uppi}{3}f_{\text{s}} L_{1} L_{2} C\left[ {\left( {2\uppi\,f_{\text{r}} } \right)^{2} - \left( {\frac{\uppi}{3}f_{\text{s}} } \right)^{2} + \frac{\uppi}{3}f_{\text{s}} \frac{{k_{\text{damp}} }}{{L_{1} }}} \right]}}} \right|$$

(10)

5.2 Selection of optimum damping parameters

The selection of k _damp directly impacts the performance of active damping. In order to demonstrate the selection of optimum damping parameters, two typical design examples with different LCL filters are given in Table 3. For these two designs, Fig. 10 shows the variation of ‘Q _r’-factor with different k _damp.

Table 3 Parameter list of typical examples

Fig. 10

Variation of ‘Q _r’-factor with different k _damp

For example filter 1, k _{damp_c} > 0, while the resonance frequency is located in the low region (f _r = 1.40 kHz). As seen in Fig. 10a, the value of Q _r is high if active damping is not supplied (k _damp = 0), or if the damping coefficient is equal to the critical value (k _damp = k _{damp_c} = 7.2), so that active damping fails to suppress the resonance peak. In contrast, Q _r approaches 0 dB by selecting a damping coefficient higher than 4, and thus optimum damping performance could be achieved by k _damp = 4. Similarly, k _damp = 10 could be chosen for an over-damped solution, and then Q _r is less than 0 dB.

For example filter 2, k _{damp_c} < 0, while the resonance frequency is located in the high region (f _r = 2.34 kHz). As mentioned at the end of Sect. 4.3, a single loop of grid-side current feedback without damping can sometimes be stabilized, but, as seen in Fig. 10b, the high Q _r when k _damp = 0 indicates that the resonance peak still exists. Moreover, Q _r does not show any significant improvement beyond k _damp = 2, so k _damp = 2 is considered as the redundant damping solution.

The optimized controller parameters for these two examples, including PI regulators, active damping parameters and stability margins, are presented in Table 4.

Table 4 Optimized controller parameters of typical examples

5.3 Root loci

After exploring stability margins using bode diagram to ensure all the parameters above are selected correctly, it is also necessary to investigate the movement of closed-loop transfer function poles by root loci to verify the stable operating region.

For example filter 1, Fig. 11a shows the root loci of variation in active damping parameter for the PI regulator. By increasing k _damp from zero, the dominant poles will be forced to track back inside the unit circle, and the overall system becomes stable. However, the over-damping (k _damp > k _{damp_c}) solution will make the poles track back outside the unit circle, thus, stability will deteriorate. The part of the root loci within the unit circle boundary region determines the upper and lower limit of k _damp, so the observation of root loci verifies the value of k _damp calculated for filter 1 in Table 4.

Fig. 11

Root loci

For example filter 2, Fig. 11b shows the root loci of variation in proportional gain for the single-loop system without active damping. The dominant poles track well inside the unit circle, hence, the system remains stable until K _p becomes larger than the upper limit. The observation of root loci also verifies the result of K _p calculated for filter 2 in Table 4.

Figure 11c shows the root loci of variation in k _damp when k _{damp_c} = 0, while the resonance frequency is close to the critical resonance frequency. As can be seen, the system will be unstable irrespective of active damping.

6 Verification of evaluation method

6.1 Verification by simulation

Using the parameters in Table 4, both simulations and experiments were performed on a three-phase distribution static compensator (D-STATCOM). Simulations were implemented to verify the stability evaluation method and the guidelines for controller design, examining the effect of harmonic attenuation, the dynamic response, and the performance of active damping.

The primary objective of the D-STATCOM is to regulate the grid-side current i ₂ as the reactive load requires. The control algorithm is implemented in a synthesized scheme including a stationary αβ frame and a synchronous dq frame. Reference values of reactive current i _2q stepping from 30 to 15 A were examined to evaluate the transient response.

Simulation results with example filter 1 are shown in Fig. 12a–c.

Fig. 12

Transient response of regulated reactive current and FFT of grid-side current with filter 1 (k _{damp_c} > 0)

The reference current steps down at 0.1 s, and the converter operates without oscillation with active damping is enabled. Active damping is disabled at 0.2 s, and immediately a large resonant current arises for all three cases. It is clear that active damping is necessary to maintain stability when k _{damp_c} > 0. Moreover, a fast Fourier transform (FFT) of the grid-side current demonstrates the effectiveness of the filter. Compared with the over-damping solution in Fig. 12a, a sufficient but smaller active damping (k _damp < k _{damp_c}), i.e. an optimum solution in Fig. 12c, possesses the same total harmonic distortion (THD) and equivalent damping performance at the new resonance frequency f _r′, but also achieves a faster transient response because of the enhanced phase margin. As to critical damping (k _damp = k _{damp_c}), a significant resonant component is observed at f _s/6 in Fig. 12b, due to the matching condition of k _damp, that results in active damping being ineffective on the resonance peak.

Simulation results with filter 2 are shown in Fig. 12a–b, and both the transient response and THD are acceptable. Even without active damping, the system is still quite stable, that means active damping is not a necessary condition for LCL filtered converters when k _{damp_c} < 0.

It should be noted that an abundant resonant component can be observed when there is no damping. In contrast, the redundant adoption of active damping leads to a reduced resonant component. Furthermore, comparison stability tests with different regulator gains were conducted to validate the understanding of root loci for single-loop grid-side current feedback without active damping, shown in Fig. 11b. It was discussed earlier that very high loop gain is difficult to achieve because system becomes unstable beyond a certain stage, and this is verified by Fig. 13c which shows that without active damping the stability degrades for a higher K _p close to upper limit (K _p = 7.1).

Fig. 13

Transient response of regulated reactive current and FFT of grid-side current with filter 2 (k _{damp_c} < 0), and test of stability margin for different regulator gain when using no damping

6.2 Experimental verification

The experimental verification was carried out in three steps: ① testing the current tracking capability of the over damping solution and the optimum damping solution when using filter 1; ② testing the current tracking capability of the redundant damping solution and without damping when using filter 2; ③ testing the stability of un-damped converter with the different K _p when using filter 2.

As seen in Fig. 14a, b, the experimental results verified that active damping solutions with both larger and smaller k _damp possess the equivalent effect of harmonic attenuation and damping performance with example filter 1. Faster current tracking capability was obtained with the optimum damping solution (k _damp < k _{damp_c}).

Fig. 14

Experimental results for inverter with filter 1 (k _{damp_c} > 0)

Compared with the experimental result for the redundant damping inverter with filter 2, shown in Fig. 15a, the inverter without damping can be naturally stabilized by a suitable loop gain, and faster tracking capability can be obtained, as shown in Fig. 15b. However, the resonance oscillation is barely suppressed when k _damp = 0, and in fact the LCL filter with a high resonant frequency approaches the performance of a single L filter, hence, the benefit of having a three-order filter is lost to a large extent.

Fig. 15

Experimental results for inverter with filter 2 (k _{damp_c} < 0)

Figure 15c demonstrates that with the undamped solution it is difficult to achieve both very high loop gain and sufficient stability margins. The stability deteriorates when K _p = 7. Generally, it is preferable for the controller to have wider stability margins rather than a large K _p.

Finally, both of simulation and experimental results show an evident steady-state error. This paper is focussed on the stability evaluation method considering the stability margins and the performance of active damping, and not on minimising steady-state error, which might be effectively compensated by a fundamental proportional resonant (PR) regulator [25].

7 Conclusion

In this paper, a critical value of the CCF active damping coefficient k _{damp_c} is proposed to construct a stability evaluation method for LCL filtered grid-connected converters. This value is based on analysis of the inherent relationship between time delays in the digital controller and stability. If k _{damp_c} > 0, while the resonance frequency is located in the low region (f _r < f _s/6), active damping is identified as an essential factor for stability, furthermore, a sufficient but smaller damping coefficient (k _damp < k _{damp_c}) is recommended as optimum solution. In contrast, over damping (k _damp > k _{damp_c}) leads to a stringent constraint on overall stability margins, and selection of critical damping (k _damp = k _{damp_c}) should be avoided, because it results in a new resonance peak at the critical frequency (f _s/6) which cannot be damped. If k _{damp_c} = 0, while the resonance frequency meets the critical frequency, system will be unstable irrespective of active damping. If k _{damp_c} < 0, active damping is not required, and by adopting a suitable regulator gain, a single-loop controller without any additional damping is sufficient to design a stable system. Both simulation and experimental results have confirmed the stability evaluation method and verified the guidelines for selecting controller parameters to improve the stability margins and the performance of active damping.