Abstract
Energy management is facing new challenges due to the increasing supply and demand uncertainties, which is caused by the integration of variable generation resources, inaccurate load forecasts and non-linear efficiency curves. To meet these challenges, a robust optimization method incorporating piecewise linear thermal and electrical efficiency curve is proposed to accommodate the uncertainties of cooling, thermal and electrical load, as well as photovoltaic (PV) output power. Case study results demonstrate that the robust optimization model performs better than the deterministic optimization model in terms of the expected operation cost. The fluctuation of net electrical load has greater effect on the dispatching results of the combined cooling, heating and power (CCHP) microgrid than the fluctuation of the cooling and thermal load. The day-ahead schedule is greatly affected by the uncertainty budget of the load demand. The economy of the optimal decision could be achieved by adjusting different uncertainty budget levels according to control the conservatism of the model.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The energy crisis and rising air pollution have led to a greater worldwide focus on energy efficiency methods. A promising approach for domestic power generation is a combined cooling, heating and power (CCHP) system [1,2,3], that can simultaneously provide cooling, heating and power energy. CCHP systems have also been referred to as tri-generation systems, and have been widely applied in hospitals, supermarkets, and schools [4,5,6,7]. CCHP microgrid is a complex system with many operation conditions, a variety of structures, and highly coupled characteristics caused by the physical connections among components. The optimal control strategy relies on the load profile and RES generation, which might show different patterns in the terms of different time scales, such as daily/weekly/monthly/seasonal patterns. It is also difficult to characterize the performance of the components because of the nonlinearity of their efficiency curves, which cannot be expressed as deterministic values. Considering these obstacles, energy management of a CCHP microgrid is challenging.
Many researches have been carried out about optimizing CCHP microgrid operation using different strategies and optimization methods. The performance of CCHP systems following a hybrid electric-thermal load (FHL) is compared with the performance of a CCHP following the electric load (FEL) and the thermal load (FTL) [8]. To compensate prediction error, an online optimal operation approach for CCHP microgrids based on model predictive control with feedback correction was proposed in [9]. A comparison between the CCHP systems and traditional systems was carried out in [10], in terms of the energy-saving ratio and the cost-saving ratio. Chance constrained programming and particle swarm optimization were used in [11] to optimize economic dispatch of combined heat and power (CHP) system. The optimization model for planning operation of CCHP systems was presented in [12,13,14], and the mixed integer nonlinear programming model was then converted into a linear programming model by appropriate piecewise linear approximation of the nonlinear performance curve.
Any solution must address the impacts of uncertainties on optimal CCHP system operation. Stochastic optimization [15,16,17,18], chance-constrained stochastic optimization [11, 19, 20], fuzzy programs [21], and quantitative uncertainty analysis [22,23,24] have been applied in power generation and irrigation systems. However, the computational solutions to the stochastic optimization problem are intractable and only an approximate model can be used. Moreover, the probabilistic distribution or precise data parameters of the uncertainty parameters must be given, which is problematic in real-world applications.
Recently, the robust optimization has received significant attention in [25, 26] as a modelling framework for optimization under parameter uncertainty. The robust optimization seeks the commitment and dispatch of generation resources for immunizing against all possible uncertain situations. In [27], a robust optimization approach was proposed to accommodate the uncertainties of wind power and provide a robust unit commitment schedule for thermal generators under the worst wind power output scenario. Hajimiragha et al. [28] applied a robust model to analyze the electricity and transport sectors by considering the most relevant planning uncertainties and determining the impact of estimation errors on the parameters of the planning model. In considering the worst-case amount of harvested RES, [29] introduced a robust optimization approach to maintain the supply demand balance arising from intermittent RES. In [30], an inexact two-stage stochastic robust programming was proposed for residential micro-grid management-based on random demand. In [31, 32], a robust optimization method was introduced to determine the optimum capacity of distributed generation technologies for buildings under uncertain energy demands. The work in [33] used a robust optimization model for managing combined heat and power systems via linear decision rules. In [34,35,36], a utilized robust optimization model was utilized to manage building energy system with CHP systems considering the randomness of electrical and thermal load, as well as solar power production. However, [30, 34,35,36] did not consider battery cost, piecewise linear approximate the non-linear efficiency curves of the MT and their influence on dispatching results. Ramp limits and component operational and maintenance cost were also not considered. In addition, few research considered the situation that the fluctuation of different load have effect on the dispatching results of a CCHP microgrid under different robustness budget.
To deal with these problem, we employ the robust optimization approach incorporating a piecewise linear thermal and electrical efficiency curve to hedge the uncertainties of the power (cooling load, thermal load, electric load, and PV outputs) in this paper. Specifically, the uncertainties of the load and output PV in each period are within an interval defined by their lower and upper bounds and can be obtained based on the historical data or estimated with a confidence interval. This problem can be formulated as a min-max problem with the objective of minimizing the total cost under the worst scenario. We apply a tractable solution approach to solve robust optimization problem and verify the effectiveness of the proposed approach with computational results in this paper.
The remainder of this paper is organized as follows. Section 2 formulates the deterministic optimization model for energy management of a CCHP microgrid. Section 3 presents a detailed expression of the worst-case optimization model and the proposed robust interval optimization model for energy management of CCHP Microgrid. Section 4 presents numerical case study results, and conclusions are drawn in Section 5.
2 Deterministic optimal dispatching model for a CCHP microgrid
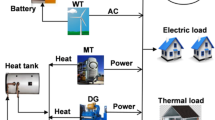
A schematic of the energy flows for the CCHP microgrid is shown in Fig. 1. This paper considers a CCHP microgrid that includes a PV cell, a battery, an MT, a gas boiler, an absorption chiller, an electric chiller, and heat exchanger, along with cooling, heating and power load.
-
1.
Optimization objective: The objective function contains cost and incomes:
$$\hbox{min}\,C = \sum\limits_{t = 1}^{T} {C_{grid} { + }C_{ng} + C_{bt} + C_{rm} }$$(1)-
a)
Cost of interacting with the grid:
$$C_{grid}^{t} { = }(R_{grid}^{t} P_{grid}^{t} - R_{excess}^{t} P_{excess}^{t} )\Delta t$$(2) -
b)
Aging Cost of the battery [34]:
$$C_{bt}^{t} = R_{bt} (U_{bt,dis*}^{t} + U_{bt,chr*}^{t} )\Delta t$$(3) -
c)
Natural gas cost:
$$C_{ng}^{t} = R_{ng}^{t} (F_{mt}^{t} + F_{b}^{t} )\Delta t$$(4) -
d)
Running and maintenance cost:
$$C_{rm}^{t} = \left[ \begin{aligned} P_{mt}^{t} R_{mt,rm} \text{ + }H_{b}^{t} R_{b,rm} \text{ + }H_{h}^{t} \text{/}\eta_{he} R_{he,rm} \text{ + } \hfill \\ \begin{array}{*{20}l} {\begin{array}{*{20}l} {} \hfill \\ \end{array} } \hfill \\ \end{array} \begin{array}{*{20}l} {} \hfill \\ \end{array} H_{ac}^{t} R_{ac,rm} \text{ + }P_{ec}^{t} R_{ec,rm} \text{ + }P_{pv}^{t} R_{pv,rm} \text{ + } \hfill \\ (P_{bt,chr}^{t} + P_{bt,dis}^{t} \text{)}R_{bt,rm} \text{ + }(H_{tst,chr}^{t} + H_{tst,dis}^{t} \text{)}R_{tst,rm} \hfill \\ \end{aligned} \right]\Delta t$$(5)
where C t ng , C t grid , C t bt , C t rm are the natural gas cost, the cost of interacting with the grid, the aging cost function of the battery, and the running and maintenance cost of the system in time period t, respectively; R t ng is the tariff for natural gas; F t mt , F t b are the fuel consumption of the MT and the boiler in period t, respectively; R t grid is the tariff for purchasing power from the main grid; R t excess is the tariff for selling power to the main grid; P t grid , P t excess are power provided by the main grid and sold to the main grid in period t, respectively; R t bt is charge/discharge of battery cycles cost; U t c,bt* , U t disc,bt* are the status flag transferring from charging to discharging and from discharging to charging of the battery in period t; P t mt , H t mt are the power and heat produced by the MT in period t; P t bt,chr , P t bt,dis are the charge/discharge power of BT in period t; H t tst,chr , H t tst,dis are the thermal power stored/released by TST in period t; H t ac is the heat required by the absorption chiller when handling the users’ cooling requirements in period t; P t ec is the electricity demand of the electric chiller when handling the users’ cooling requirements in period t; P t pv is the PV output in period t; and R rm is the running and maintenance cost of the unit.
-
a)
-
2.
Constraints on the system: constraints include cooling balances, heating balances, electricity balances and operational constraints for each device.
-
a)
Cooling balance:
$$COP_{ac} \cdot H_{ac}^{t} + COP_{ec} \cdot P_{ec}^{t} - Q_{c}^{t} = 0$$(6) -
b)
Thermal balance:
$$H_{re}^{t} + H_{b}^{t} - H_{ac}^{t} - H_{tst,dis}^{t} + H_{tst,chr}^{t} = H_{h}^{t} /\eta_{he}$$(7)where the recovered thermal energy H t re from the MT can be estimated as:
$$H_{re}^{t} = H_{mt}^{t} \eta_{re}$$(8) -
c)
Electric power balance:
$$P_{mt}^{t} + P_{grid}^{t} + P_{ec}^{t} + P_{bt,dich}^{t} - P_{bt,chr}^{t} - P_{excess}^{t} = P_{l}^{t} - P_{pv}^{t}$$(9) -
d)
Micro gas turbine:
The relationship between the fuel energy (F t mt ) and the power output (P t mt ) can be modeled using a straight line [1].
$$F_{mt}^{t} = \alpha P_{mt}^{t} + \beta U_{mt}^{t}$$(10)where α, β are fuel-to-electric-energy conversion parameter, respectively; and U t mt is the binary variable that is equal to 1 if the MT is on in period t and 0 otherwise. The capacity and ramp rate constraints are define by (9)–(11):
$$U_{mt}^{t} P_{mt}^{\hbox{min} } \le P_{mt}^{t} \le U_{mt}^{t} P_{mt}^{\hbox{max} }$$(11)$$U_{mt}^{t} P_{mt}^{down} \le P_{mt}^{t} - P_{mt}^{t - 1} \le U_{mt}^{t} P_{mt}^{up}$$(12)For each unit in the system, the input variables (consumed fuel and electricity) are related to the output variables (generated heat, electricity, cooling) by means of the nonlinear performance curves. Usually, low load results in low efficiency. As shown in Fig. 2, the thermal and electrical efficiency of the MT is defined in (13)–(16) through piecewise linearization [12]. Because the nonlinear efficiency curve is changed to several line segments, the control problem can be modelled as a MILP:
$$P_{mt}^{t} = U_{mt}^{t} B_{mt}^{1} + \sum\limits_{k = 1}^{{L_{mt} }} {D_{mt}^{t,k} }$$(13)$$U_{mt}^{t} = \sum\limits_{k = 1}^{{L_{mt} }} {v_{mt}^{t,k} }$$(14)$$\sum\limits_{j = k + 1}^{{L_{mt} }} {v_{mt}^{t,k} } \le \frac{{D_{mt}^{t,k} }}{{B_{mt}^{k + 1} - B_{mt}^{k} }} \le \sum\limits_{j = k}^{{L_{mt} }} {v_{mt}^{t,k} }$$(15)$$H_{mt}^{t} = U_{mt}^{t} A_{mt}^{1} + \sum\limits_{k = 1}^{{L_{mt} }} {g_{mt}^{k} } D_{mt}^{t,k}$$(16)where H t mt is the heat produced by the MT; A k mt is the coefficient of the thermal and electrical efficiency curve; B k mt is the block limit of the thermal and electrical efficiency curve; g k mt is the slope of block k of the thermal and electrical efficiency curve; v t,k mt is the binary variable encoding the thermal and electrical efficiency curve of the MT; and L mt is the index set of the piecewise linear thermal and electrical efficiency curve.
-
e)
Storage battery: The MIP formulation of the battery energy model is represented by:
$$\left\{ \begin{aligned} U_{bt,chr}^{t} P_{bt,chr}^{\hbox{min} } \le P_{bt,chr}^{t} \le U_{bt,chr}^{t} P_{bt,chr}^{\hbox{max} } \hfill \\ U_{bt,dis}^{t} P_{bt,dis}^{\hbox{min} } \le P_{bt,dis}^{t} \le U_{bt,dis}^{t} P_{bt,dis}^{\hbox{max} } \hfill \\ U_{bt,dis}^{t} + U_{bt,chr}^{t} \le 1 \hfill \\ W_{bt}^{t} = W_{bt}^{t - 1} (1 - \sigma_{bt} ) + (\eta_{bt}^{chr} P_{bt,chr}^{t} - P_{bt,dis}^{t} /\eta_{bt}^{dis} )\Delta t \hfill \\ W_{bt}^{\hbox{min} } \le W_{bt}^{t + 1} \le W_{bt}^{\hbox{max} } \hfill \\ \end{aligned} \right.$$(17)Equations (14)–(15) represent the ramp rate constraints of the charging/discharging battery:
$$P_{bt,chr}^{down} \le P_{bt,chr}^{t + 1} - P_{bt,chr}^{t - 1} \le P_{bt,chr}^{up}$$(18)$$P_{bt,dis}^{down} \le P_{bt,dis}^{t + 1} - P_{bt,dis}^{t} \le P_{bt,dis}^{up}$$(19)Equations (16)–(17) represent the status-transfer flag of the charging/discharging battery:
$$U_{bt,chr}^{t + 1} - U_{bt,chr}^{t} \le U_{bt,chr*}^{t}$$(20)$$U_{bt,dis}^{t + 1} - U_{bt,dis}^{t} \le U_{bt,dis*}^{t}$$(21) -
f)
Thermal storage tank (TST):
$$\left\{ \begin{aligned} U_{tst,dis}^{t} H_{tst,dis}^{\hbox{min} } \le H_{tst,dis}^{t} \le U_{tst,dis}^{t} H_{tst,dis}^{\hbox{max} } \hfill \\ U_{tst,chr}^{t} H_{tst,chr}^{\hbox{min} } \le H_{tst,chr}^{t} \le U_{tst,chr}^{t} H_{tst,chr}^{\hbox{max} } \hfill \\ U_{tst,chr}^{t} + U_{tst,dis}^{t} \le 1 \hfill \\ H_{ts}^{t} = H_{ts}^{t - 1} \left( {1 - \sigma_{tst} } \right) + (\eta_{tst}^{chr} H_{tst,chr}^{t} - H_{tst,dis}^{t} /\eta_{tst}^{dis} )\Delta t \hfill \\ H_{tst}^{\hbox{min} } \le H_{tst}^{t} \le H_{{_{tst} }}^{\hbox{max} } \hfill \\ \end{aligned} \right.$$(22) -
g)
Power exchange between the main grid and microgrid:
$$\left\{\begin{array}{l} 0 \le P_{grid}^{t} \le U_{grid}^{t} P_{grid}^{\hbox{max} } \hfill \\ 0 \le P_{excess}^{t} \le U_{excess}^{t} P_{grid}^{\hbox{max} } \hfill \\ \end{array} \right.$$(23)Mutual exclusion of status:
$$U_{grid}^{t} + U_{excess}^{t} \le 1$$(24)
-
a)
3 Solution methodology
3.1 Robust decision-making model
A typical MILP model is defined in the following form:
The uncertainty may reside in the coefficient a ij , the objective function c or the right-hand side b. If these coefficients are unknown constants within known bounds, a meaningful robust MILP can be formulated. Unlike the modeling of uncertainty in stochastic programming, the uncertainty model in robust optimization is typically depicted as an uncertainty range. Each coefficient a ij in the constraints of the constraints of the formulation (i.e., the coefficient of the j th variable in the i th constraint) is an independent, symmetrical and bounded random variable that can assume a value from the interval \([\bar{a}_{ij} - \hat{a}_{ij} ,\bar{a}_{ij} + \hat{a}_{ij} ]\), where \(\bar{a}_{ij}\) is the nominal value and \(\hat{a}_{ij}\) is the maximum deviation from the nominal value. The scaled deviation of a ij can be denoted by \(\eta_{ij} = (\bar{a}_{ij} - \hat{a}_{ij} )/\bar{a}_{ij}\) or \(\eta_{ij} = (\bar{a}_{ij} + \hat{a}_{ij} )/\bar{a}_{ij}\), which is defined as the relative value of the forecast error and the realization of the uncertainty. In addition, when formulating a robust MILP problem [26], it is necessary to define an integer control parameter denoted by Γ i with values in the interval [0, |J i |]; this is called the budget of uncertainty. Γ i = 0 yields the nominal problem and thus does not incorporate uncertainty, whereas Γ i = |J i | corresponds to interval-based uncertainty sets and leads to the most conservative case. The η ij value is constrained as:
A robust optimization formulation seeks for optimal solutions that optimize the objective function and meet the problem requirements for all possible uncertainties in constraint coefficients. As a result, the variables are independent of the uncertain parameters. In a worst-case analysis that accounts for uncertainty, we consider the following problem (30)–(33):
For the i th constraint, the auxiliary problem (34)–(36) is shown as follows:
Accordingly, the dual of problem (34)–(36) is shown as problem (37)–(40):
where z i and p ij are the dual decision variables for constraints (35)–(36) of the auxiliary problem. When incorporating model (37)–(40) into the original problem (30)–(33), the robust linear counterpart is formulated as:
3.2 Uncertain energy output formulation
In general, the optimal operation of a CCHP microgrid is associated with uncertainties from cooling, thermal and electrical load, and the PV output. The randomness of cooling and thermal load is affected by the weather surrounding the buildings; the electrical load in the buildings are influenced by the level of consumer activities, and the power output of a PV unit can be impacted by the radiation of the sun and the ambient weather. Because of these factors, it is difficult to precisely characterise their power value. In this paper, we assume that these power values fall within the intervals of Q t c,u ∈ [Q t c − Q ld c , Q t c + Q ud c ], H t h,u ∈ [H t h − H ld h , H t h + H ud h ], P t l,u ∈ [P t l − P ld l , P t l + P ud l ], and P t pv,u ∈ [P t pv − P ld pv , P t pv + P ud pv ], with Q t c , H t h , P t l and P t pv representing the predicted value in period t and Q t c,u , H t h,u , P t l,u and P t pv,u representing sets of possible cooling, thermal and electrical load and the output PV. Q ld c , Q ud c , H ld h , H ud h , P ld l , P ud l , P ld pv and P ud pv representing the allowed maximum deviations above and below Q t c , H t h , P t l and P t pv , respectively, which can take any values with their uncertain interval. For this approach, Γ t c , Γ t h , Γ t nl represent cardinality budgets [26] introduced to adjust the ranges of uncertainty for the cooling, thermal and net electricity load (P t l − P t pv ) in period t by the system operators, respectively; these affect the robustness of the problem against the level of conservatism of the solution.
The worst-case scenario is the key aspect of the robust interval optimization model; it is a set of parameter values such that the security for any other scenarios can be guaranteed if and only if there is a feasible solution under this scenario [32,33,34,35]. Therefore, the expressions in (48), (51) and (54), can be interpreted as the security requirements of the CCHP microgrid under the worst-case scenarios of uncertain parameters (cooling, thermal, electrical load and PV output):
where η ld c , η ud c are the scaled deviations for the random cooling load; η ld h , η ud h are the scaled deviations for the random thermal load. Similarly, η ld l , η ud l , η ld pv , η ud pv are the scaled deviations for the random electrical load and the PV output.
Identifying the worst-case scenarios when cooling, thermal, and electric load and PV vary within their uncertain intervals requires transforming (21), (22) and (24) into an equivalent max optimization problem (48), (51) and (53) for calculating the worst-case scenarios.
Thus, a CCHP microgrid economic dispatch model is a min-max optimization problem. To make the above problem tractable, (57), (63) and (69) must be converted into corresponding dual problems (60), (66) and (72) by introducing dual variables λ t c , π t+ c1 , π t− c1 , λ t h , π t+ h1 , π t− h1 , λ t nl , π t+ l1 , π t− l1 , π t+ pv2 , and π t− pv2 .
Finally, a tractable robust model can be formulated as:
along with (1)–(20), (23), (60)–(62), and (66)–(68), (73)–(75).
4 Case study
To verify the performance of the proposed algorithm, a CCHP building in Shanghai, China, was used in a case study. The building has twelve floors with a total square footage of 6000 m2 and an average floor height of 3.8 m. Figure 3 shows the hourly PV output and the cooling, heating, and power load for representative days during the summer.
The CCHP system consists of a photovoltaic system (80 kW), a battery (200 kWh), a gas micro turbine (200 kW), a boiler (258 kW), an electric chiller (100 kW), an absorption chiller (200 kW), a heat exchanger (200 kW), and a thermal storage tank (150 kWh), as shown in Fig. 1. Table 1 is the peak-valley price of the double system electricity price in summer and selling prices at different times of the day [37, 38]. The fuel we chose here is a widely used fuel, which is natural gas, and its price is 0.4561 $/m3. Table 2 lists the remaining parameters used in this study as referenced by [1, 9, 39].
Based on the observation of historical data, it has been shown that hourly PV power and cooling, heating, and power load follow a normal distribution with a mean value μ and standard deviation σ during for representative days in summer,as shown in Fig. 2 and Table 11. To estimate the uncertainties of PV power and the cooling, heating, and power load, the fluctuation of the uncertainties are defined as:
where Δθ i,t is the fluctuation range of the i-th uncertainty (including the PV output and the cooling, heating, and power load). The upper fluctuation of each uncertainty is expressed as Δθ i,t (i.e., Q ud c = Δθ c,t , H ud h = Δθ h,t , P ud l = Δθ l,t and P ud pv = Δθ pv,t ), whereas the lower fluctuation of the each uncertainty is modelled as −Δθ i,t (i.e., Q ld c = −Δθ c,t, H ld h = −Δθ h,t , P ld l = −Δθ l,t , P ld pv = −Δθ pv,t ). The fluctuation interval can be controlled effectively by adjusting the parameter value of ρ it .
To demonstrate the effectiveness of the uncertain set in the robust optimization model, a Monte-Carlo simulation was adopted to sample the cooling, heating and electrical power randomly. We then determined the probability of each interval that fell into the uncertain interval and calculated the average probability of each interval.
It can be seen from Table 3 that with the decrease of ρ, the probability that the cooling, heating and electrical power and PV output are included in the uncertain set also decreases. When the value of ρ reaches 0.9, it can be guaranteed that the probability will reach 97%; however, when the value decreases to 0.1, the probability decreases to 67%. Therefore, the conservativeness of robust optimization model can be controlled effectively by adjusting the parameter value of ρ.
To analyze the effectiveness of the proposed model, five cases are studied and simulated as shown in Table 4, in which ‘✓’ means that source is in the CCHP microgrid. The MILP robust optimization model is solved by Cplex [40]. The PSO approach was applied to solve the case 5, which used nonlinear efficiency curves [11].
4.1 Comparison of three efficiency models under deterministic optimization
Table 5 summarizes the operating cost and computing times of the three aforementioned approaches when an optimality parameter was specified. The three methods yield similar solutions in terms of total operating cost, though Case 3 obtained a lower operating cost than Case 1 and 5 because a global optimization result was guaranteed for the MILP. Meanwhile, Case 3 achieved a more accurate system operating status than Case 1 and 5, without sacrificing computational advantage.
As shown in Fig. 4, compared with Case 3, there were different MT optimization results for the CCHP microgrid in Cases 1 and 5. In Case 1, the MT provided its rated power in periods 12 to 19 but operated at rated power during periods 14 to 18 in Case 3. In all time periods, the scheduling curves of the MT were extremely similar for both Case 3 and Case 5. In Case 5, the power generated by the MT was greater than Case 3 in periods 7 to 13 and 19 to 24, which could not determine global optimization results through comparing the optimization results for both deterministic and robust cases when considering the piecewise linear efficiency curve model in detail.
4.2 Comparison of constant efficiency model and piecewise linear efficiency curve model under robust optimization
Table 6 provides the simulated running cost under different load and PV uncertainties, using constant and piecewise linear efficiency curves, respectively. It shows that when the fluctuation interval of the uncertainties increases, the running cost of the robust case increases.
Figure 5 shows the operating conditions of the MT, the exchange power with the main grid, the electric chiller power, and the gas boiler power during the entire scheduling horizon at different uncertainty levels during the summer when ρ = 0.9. When coping with the fluctuation of load and PV output, the power generated by the MT in the robust case was always greater than in the corresponding deterministic case due to the response of the MT to the uncertainty of the cooling, thermal and electrical energy requests. Meanwhile, the CCHP microgrid sold less extra power to the main grid, and coordinated the power of the electric chiller and absorption chiller. In considering the aging cost, the scheduling curves of the battery were extremely similar for both the deterministic and robust cases in all time periods.
Compared with the constant efficiency model, there were different dispatching results for the CCHP microgrid in the piecewise linear efficiency model. In Case 2, the MT provided rated power during periods 11 to 19 but operated at rated power during periods 13 to 19 in Case 4. In Cases 3 and 4, the CCHP microgrid sold almost no extra power to the main grid during periods 9 to 11; however, it sold more extra power to the main grid during these periods in Cases 1 and 2. The TST charged more heating power during periods 1 to 6 and 22 to 24, charged less heating power during periods 9 to 12 and discharged more heating power during periods 18 to 21 than in the constant efficiency model. In all time periods, the scheduling curves of the electric chiller were extremely similar for both Case 1 and Case 2, but the power of the electric chiller was greater than in the piecewise linear efficiency model during periods 11 to 18. In addition, the power of the absorption chiller provided more cooling power during periods 12 to 18 in piecewise linear efficiency model.
To show the effectiveness of robust optimization and its applicability in a real-time environment, Monte Carlo simulation is applied to generate different realizations of load and RES generation. The size of the sample is set to be 1000. The expected intra-day operation cost of the robust optimization and the deterministic optimization can be calculated under the day-ahead schedule. The expected operation cost of two optimization models are shown in Table 7. It can be seen from Table 7 that with the increase of ρ, compared with robust optimization, the operating cost of deterministic optimization was increasing. When ρ equals to 0.1/0.3, the expected cost of deterministic approach is almost the same with robust optimization approach, only increased by 0.18%/0.27%, respectively. When ρ equals to 0.5/0.7/0.9, expected cost of the deterministic approach is more than robust optimization approach, increased by 1.85%/2.54%/3.25%, respectively. The economy of the optimal decision could be achieved by adjusting the fluctuation interval of uncertainty set to control the conservatism of the model.
4.3 Influence of uncertainty budget levels on the system fluctuation (ρ = 0.9)
Compared with no fluctuation of the cooling, thermal and net electrical load, Figs. 6, 7 and 8 shows the adjusted power of the MT and the exchange power with the main grid in different robustness budgets in controlling the uncertain ranges of cooling, thermal and net electricity load when ρ = 0.9. In Fig. 6, Γ h and Γ nl are fixed at 1 and 2, respectively, to ensure the worst-case thermal and net electrical load. Γ c is adjusted from 0 to 1. Γ c =0 denotes there are no cooling load fluctuation; Γ c = 1 denotes the worst-case cooling load. Table 8 shows the change of operating cost with the increase of robustness budget Γ c .
In Fig. 7, Γ c and Γ nl are fixed at 1 and 2, respectively, to ensure the worst-case cooling and net electricity load; the uncertainty set of the thermal load is enlarged by increasing the robustness Γ h from 0 to 1. Table 9 shows the change of operating cost as the robustness budget Γ h increase.
In Fig. 8, Γ c and Γ h are fixed at 1 and 1, respectively, to ensure the worst-case cooling and thermal load; the uncertainty set of the net electrical load are enlarged by increasing the robustness Γ nl from 0 to 2. Table 10 shows the change of operating cost as the robustness budget Γ nl increase.
Tables 8, 9 and 10 show that with the increase of the robustness budget Γ (Γ c , Γ h and Γ nl ), the operating cost of the robust case increases. When Γ c is adjusted from 0 to 1 (Γ h = 1 and Γ nl = 2), the operating cost increases by 2.33%. When Γ h is adjusted from 0 to 1 (Γ c = 1 and Γ nl = 2), the operating cost increases by 0.07%. When Γ nl is adjusted from 0 to 2 (Γ c = 1 and Γ h = 1), the operating cost increases by 5.94%. The differences in the operating cost show that the fluctuation of net electrical load has the more significantly effect on the operating cost of the CCHP microgrid than the fluctuation of the cooling or thermal.
Figures 6, 7 and 8 show that with the increase of the robustness budget Γ (Γ c , Γ h and Γ nl ), there are different dispatching results for the CCHP microgrid under different uncertainty budget levels of different energy (cooling, thermal and electrical). The fluctuation of net electrical load have the greater effect on the dispatching results of the CCHP microgrid than the fluctuation of the cooling or thermal.
In general, these dispatching results demonstrate that uncertainties in the load and PV outputs are mitigated by the MT, the exchange power with the main grid, and other components.The thermal fluctuation during the summer subtly change the dispatching results, which reduce the impact on the superior power grid. When the fluctuation in cooling load, electrical load and PV become increase, the exchange power with the main grid will change with the system electric power fluctuation, which have impacts on the superior grid. These fluctuation can be suppressed not only by adjusting the MT but also coordinating other equipment.
5 Conclusion
This paper presented a robust optimization method that considered piecewise linear thermal and electrical efficiency curves to hedge the uncertainties of the cooling, thermal, and electrical load and solar power generation for the energy management of a CCHP microgrid. A worst-case security-constrained economic optimization model was developed and a strong duality theory was used to transform the problem into a MILP formulation. The robustness could also be adjusted to control the conservativeness of the proposed model.
By characterizing a piecewise linear thermal and electrical efficiency curve model instead of constant efficiencies or non-fixed efficiency models, the operating status of the system could be reflected exactly without sacrificing problem linearity.
The simulation results showed that fluctuation of the system have less effect on the dispatching results of the battery when considering the aging cost. Meanwhile, the robust optimization approach performs better than the deterministic optimization mode, and decreases the expected operation cost. Furthermore, compared with fluctuation of the cooling and thermal load, fluctuation of net electrical load has a greater influence on the operating cost and conditions of the system.
The demand response can mitigate the variability of renewable resources and partial user demand by allowing user demand to be controllable. Thus, future research should be focus on combining the robust optimization method with demand response to address the uncertainties of the CCHP microgrid.
References
Cho H, Mago PJ, Luck R et al (2009) Evaluation of CCHP systems performance based on operational cost, primary energy consumption, and carbon dioxide emission by utilizing an optimal operation scheme. Appl Energy 86(12):2540–2549
Liu M, Shi Y, Fang F (2014) Combined cooling, heating and power systems: a survey. Renew Sustain Energy Rev 35:1–22
Gu W, Wu Z, Bo R et al (2014) Modeling, planning and optimal energy management of combined cooling, heating and power microgrid: a review. Int J Electr Power Energy Syst 54(1):26–37
Arcuri P, Florio G, Fragiacomo P (2007) A mixed integer programming model for optimal design of trigeneration in a hospital complex. Energy 32(8):1430–1447
Ge YT, Tassou SA, Chaer I et al (2009) Performance evaluation of a tri-generation system with simulation and experiment. Appl Energy 86(11):2317–2326
Guo L, Liu W, Cai J et al (2013) A two-stage optimal planning and design method for combined cooling, heat and power microgrid system. Energy Convers Manag 74(10):433–445
Zhao B, Zhang X, Li P et al (2014) Optimal sizing, operating strategy and operational experience of a stand-alone microgrid on Dongfushan Island. Appl Energy 113(2):1656–1666
Mago PJ, Chamra LM, Ramsay J (2010) Micro-combined cooling, heating and power systems hybrid electric-thermal load following operation. Appl Therm Eng 30(8–9):800–806
Gu W, Wang Z, Wu Z et al (2016) An online optimal dispatch schedule for CCHP microgrids based on model predictive control. IEEE Trans Smart Grid. doi:10.1109/TSG.2016.2523504
Gang H, You S, Ye T et al (2014) Analysis of combined cooling, heating, and power systems under a compromised electric–thermal load strategy. Energy Build 84:586–594
Wu Z, Gu W, Wang R et al (2011) Economic optimal schedule of CHP microgrid system using chance constrained programming and particle swarm optimization. In: Proceedings of the 2011 IEEE power and energy society general meeting, vol 35(8), San Diego CA, 24–29 July 2011, pp 1–11
Bischi A, Taccari L, Martelli E et al (2014) A detailed MILP optimization model for combined cooling, heat and power system operation planning. Energy 74(5):12–26
Milan C, Stadler M, Cardoso G et al (2015) Modeling of non-linear CHP efficiency curves in distributed energy systems. Appl Energy 148:334–347
Wang H, Yin W, Abdollahi E et al (2015) Modelling and optimization of CHP based district heating system with renewable energy production and energy storage. Appl Energy 159(1):401–421
Wang L, Singh C (2008) Stochastic combined heat and power dispatch based on multi-objective particle swarm optimization. Int J Electr Power Energy Syst 30(3):226–234
Piperagkas GS, Anastasiadis AG, Hatziargyriou ND (2011) Stochastic PSO-based heat and power dispatch under environmental constraints incorporating CHP and wind power units. Electr Power Syst Res 81(1):209–218
Liu X (2012) Optimization of a combined heat and power system with wind turbines. Int J Electr Power Energy Syst 43(1):1421–1426
Marquez AC, Heguedas AS, Iung B (2005) Monte Carlo-based assessment of system availability. A case study for cogeneration plants. Reliab Eng Syst Saf 88(3):273–289
Wu J, Zhu J, Chen G et al (2008) A hybrid method for optimal scheduling of short-term electric power generation of cascaded hydroelectric plants based on particle swarm optimization and chance-constrained programming. IEEE Trans Power Syst 23(4):1570–1579
Liu Z, Wen F, Ledwich G (2011) Optimal siting and sizing of distributed generators in distribution systems considering uncertainties. IEEE Trans Power Deliv 26(4):2541–2551
Moradi MH, Hajinazari M, Jamasb S et al (2013) An energy management system (EMS) strategy for combined heat and power (CHP) systems based on a hybrid optimization method employing fuzzy programming. Energy 49(1):86–101
Smith A, Luck R, Mago PJ (2010) Analysis of a combined cooling, heating, and power system model under different operating strategies with input and model data uncertainty. Energy Build 42(11):2231–2240
Valipour M (2015) Optimization of neural networks for precipitation analysis in a humid region to detect drought and wet year alarms. Meteorol Appl 23(1):91–100
Khasraghi MM, Sefidkouhi MA, Valipour M (2015) Simulation of open- and closed-end border irrigation systems using SIRMOD. Arch Agron Soil Sci 61(7):929–941
Ben-Tal A, Nemirovski A (2000) Robust solutions of linear programming problems contaminated with uncertain data. Math Program 88(3):411–421
Li Z, Ding R, Floudas CA (2011) A comparative theoretical and computational study on robust counterpart optimization: I. Robust linear optimization and robust mixed integer linear optimization. Ind Eng Chem Res 50(18):10567–10603
Jiang R, Wang J, Guan Y (2012) Robust unit commitment with wind power and pumped storage hydro. IEEE Trans Power Syst 27(2):800–810
Hajimiragha AH, Canizares CA, Fowler MW et al (2011) A robust optimization approach for planning transition to plug-in hybrid electric vehicles. IEEE Trans Power Syst 26(4):2264–2274
Zhang Y, Gatsis N, Giannakis G (2013) Robust energy management for microgrids with high-penetration renewables. IEEE Trans Sustain Energy 4(4):944–953
Ji L, Niu DX, Huang GH (2014) An inexact two-stage stochastic robust programming for residential micro-grid management-based on random demand. Energy 67:186–199
Rezvan AT, Gharneh NS, Gharehpetian GB (2014) Robust optimization of distributed generation investment in buildings. Energy 67:186–199
Akbari K, Nasiri MM, Jolai F et al (2014) Optimal investment and unit sizing of distributed energy systems under uncertainty: a robust optimization approach. Energy Build 85(85):275–286
Zugno M, Morales JM, Madsen H (2014) Robust management of combined heat and power systems via linear decision rules. In: 2014 International IEEE energy conference (ENERGYCON), Cavta, Italian, 13–16 May 2014, pp 479–486
Liu P, Fu Y (2013) Optimal operation of energy-efficiency building: a robust optimization approach. In: Proceedings of the 2013 IEEE power and energy society general meeting, Vancouver, BC 21–25 July 2013, pp 1–5
Wang R, Wang P, Xiao G (2015) A robust optimization approach for energy generation scheduling in microgrids. Energy Convers Manag 106(5):597–607
Wang C, Jiao B, Guo L et al (2016) Robust scheduling of building energy system under uncertainty. Appl Energy 167:366–376
Shanghai Municipal Development & Reform Commission http://www.shdrc.gov.cn/gk/xxgkml/zcwj/jgl/20805.htm. Accessed 6 Jan 2016
Shanghai Municipal Development & Reform Commission http://www.shdrc.gov.cn/xxgk/cxxxgk/15073.htm. Accessed 4 Dec 2015
Miao Y, Jiang Q, Cao Y (2012) Battery switch station modeling and its economic evaluation in microgrid. In: Proceedings of the 2012 IEEE power and energy society general meeting, San Diego CA, 22–26 July 2012, pp 1–11
IBM ILOG CPLEX V12.1 User’s manual for CPLEX. ftp://public.dhe.ibm.com/software/websphere/ilog/docs/optimizati
Acknowledgments
This work was supported by the National Science Foundation of China (No. 51277027), the National Science and Technology Support Program of China (No. 2015BAA01B01) and the State Grid Corporation of China (SGTYHT/14-JS-188).
Author information
Authors and Affiliations
Corresponding author
Additional information
CrossCheck date: 30 November 2016
Appendix A
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
LUO, Z., GU, W., WU, Z. et al. A robust optimization method for energy management of CCHP microgrid. J. Mod. Power Syst. Clean Energy 6, 132–144 (2018). https://doi.org/10.1007/s40565-017-0290-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40565-017-0290-3