Abstract
To utilize heat and electricity in a clean and integrated manner, a zero-carbon-emission micro Energy Internet (ZCE-MEI) architecture is proposed by incorporating non-supplementary fired compressed air energy storage (NSF-CAES) hub. A typical ZCE-MEI combining power distribution network (PDN) and district heating network (DHN) with NSF-CAES is considered in this paper. NSF-CAES hub is formulated to take the thermal dynamic and pressure behavior into account to enhance dispatch flexibility. A modified DistFlow model is utilized to allow several discrete and continuous reactive power compensators to maintain voltage quality of PDN. Optimal operation of the ZCE-MEI is firstly modeled as a mixed integer nonlinear programming (MINLP). Several transformations and simplifications are taken to convert the problem as a mixed integer linear programming (MILP) which can be effectively solved by CPLEX. A typical test system composed of a NSF-CAES hub, a 33-bus PDN, and an 8-node DHN is adopted to verify the effectiveness of the proposed ZCE-MEI in terms of reducing operation cost and wind curtailment.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The dual-pressure from global energy crisis and environment pollution, has led to the reformation of energy utilization behaviors. Exploiting renewable energies is a world-wide consensus to address energy and environment issues. Renewable energies, such as wind power and solar power, have gained a rapid development both in concentrated and distributed manner in the last decades [1]. However, most available wind and solar power are greatly curtailed in the recent years, especially in Northeast and Northwest China, which prevents the stable development of renewable energy industry [2].
Utilizing multiple energy carriers including electricity, heat, cold, and natural gas in an integrated way is a trend to reduce the waste of wind and solar power. Integrated energy system (IES) is a symbolic system incorporating multiple energy carriers by connecting several energy networks with a few energy hubs (EH) capable of the transmission, conversion, and storage among different energy carriers [3, 4]. Through IES and EH, different energy networks can be co-optimized and managed to improve the utilization ratio of wind and solar power and increase dispatch flexibility of the whole energy supply system [5–8].
CHP unit is a kind of EH capable of supplying heat and electricity simultaneously, i.e., co-generation. In this respect, CHP is utilized to co-optimize heating network and electrical network to increase the flexibility and reduce curtailed wind and solar power [5–7]. Unfortunately, CHP needs natural gas backup to generate electricity, which breaks the original intention to release environment issue due to carbon emission caused by burning fossil fuel. Compressed air energy storage (CAES), a promising energy storage technique, also uses natural gas combustion to produce electricity and leads to environment issues similar to CHP. By incorporating thermal energy storage system (TES) into CAES, advanced adiabatic compressed air energy storage system (AA-CAES) and non-supplementary fired compressed air energy storage system (NSF-CAES) are capable of storing the thermal generated during air compression process in an air storage tank, and releasing it to heat the compressed air during electricity generation process [9, 10]. Thus, no gas combustion is needed in such advanced CAES systems. Similar with CHP, NSF-CAES is a class of EH capable of combined cooling, heating, and power generation. Owing to the zero-carbon-emission character, NSF-CAES hub can be adopted to construct a zero-carbon IES. On that basis, a zero-carbon-emission micro Energy Internet (ZCE-MEI) architecture is proposed by developing NSF-CAES as a clean EH to encompass the power distribution network (PDN) and district heating network (DHN) in this paper. The feasibility of using NSF-CAES as a clean energy hub in Energy Internet has been analyzed in [11], while more emphasis has been put on the scheduling of ZCE-MEI in this paper.
The studies that are suitable for modeling CAES has been available in [12–16]. CAES system and NSF-CAES system are formulated and implemented to power network dispatch operation in [12, 13] respectively. The optimal scheduling of wind power integrated with CAES in transmission system is studied in [14]. Meanwhile, by considering wind power generation and CAES, a low-carbon-emission micro grid architecture and corresponding thermal-wind-storage joint operation dispatch method are proposed respectively in [15, 16]. Optimal operation strategies of CAES on electricity spot markets with fluctuating prices are reported in [17]. On the other hand, the combined operation of electricity and heating system has been investigated in several literatures as [5–8, 18, 19]. Optimal operation strategies have been developed in [5] to accommodate wind power. Dispatch problem of combined heat and power, and transmission-constrained unit commitment by co-optimize PDN and DHN are investigated in [6, 7] respectively. Two combined analysis methods have been developed in [8] to analysis the operation of heating and electricity network. Optimal power flow of integrated electrical and heating system is studied in [18]. Besides, coordinated scheduling of energy resources for distributed district heating and cooling systems in an integrated energy grid has been investigated in [19].
Although some existing references are dedicated to explore the operation of CAES and combined operation of integrated electricity and heating systems, most of them establish a simplified efficiency based power block model to formulate CAES, without modeling the pressure and temperature dynamic of CAES. CAES is a natural EH capable of co-generation of cool, heat and power. It is necessary to consider the pressure behaviors and temperature dynamic to enhance dispatch flexibility. On the other hand, with the high penetration of renewable energies, voltage management of PDN is more difficult and important compared with traditional PDN. Thus, voltage, reactive power, and corresponding reactive compensators need to be formulated to maintain reactive power balance and voltage quality in the optimal operation of PDN. Besides, most exist combined heat and electricity systems use CHP as the interface between PDN and DHN, which undoubtedly opposites the requirement of zero-carbon-emission. In this regard, we intend to develop a short-term day-ahead scheduling model for the proposed ZCE-MEI integrated NSF-CAES to reduce wind power curtailment and save system operation cost.
The contribution of this paper mainly includes the following three parts. Firstly, a micro Energy Internet architecture is proposed, NSF-CAES is utilized as a clean EH to achieve zero-carbon-emission. Secondly, detailed dispatch model of NSF-CAES hub is constructed by considering the pressure behaviors and thermal dynamics. DistFlow model of the radial PDN is also formulated by incorporating discrete and continuous reactive power compensators, and on load tap changer (OLTC). Thirdly, operation of the proposed ZCE-MEI is optimized to reduce curtailed wind power and operation cost compared with traditional PDN and DHN.
The rest of this paper is organized as follows. Micro Energy Internet and ZCE-MEI architecture are proposed in Section 2, operation mechanism and detailed dispatch model of NSF-CAES hub are also formulated to incorporate the pressure behaviors and temperature dynamics. In Section 3, optimal operation of ZCE-MEI incorporating PDN and DHN with NSF-CAES hub is modeled to reduce operation cost and wind curtailment. The effectiveness of the proposed architecture and dispatch model is verified through a typical ZCE-MEI composed of a NSF-CAES hub, an 8-node DHN, and a 33-bus PDN in Section 4. Conclusions and further research directions are drawn in Section 5.
2 Zero-carbon emission micro Energy Internet
2.1 Micro Energy Internet
Micro Energy Internet (MEI) is a system composed of distributed energy sources, energy storage units, multi-carrier energy sources, multi-carrier loads, and distribution networks [20]. MEI can be operated independently or connected to public energy networks. Urban and rural community, hospital, industrial park, and school are representatives of MEI. MEI aims at realizing an integrated optimization and dispatch of multiple energy sources to save costs and reduce emissions through the conversion and storage among different energy carriers.
Except for MEI, a few solutions including micro gird (MG), virtual power plant (VPP) have been proposed to handle the energy supply issues. MG is a system consists of at least one clean energy generation unit and energy storage unit, mainly supplying personal power load demand in specific geographical areas [21]. MG connected to the PDN could operate in an isolated mode or a grid connection mode [21]. VPP is a system composed of several distributed generation units, can usually be regarded as a traditional power plant. VPP puts more emphasis on the comprehensive generation and trading characters of the whole virtual plant, and usually used in the electricity market [22]. MG and VPP only focus on the power supply without considering other energy forms such as thermal energy considered in CHP. CHP can supply thermal and power energy simultaneously, which could be viewed as a generation unit in MEI. Besides, MEI could accommodate the flow distribution of both power and other energy carriers. Undoubtedly, MG is the basis of the MEI, which puts more emphasis on the coordinated management and operation of multiple energy carriers.
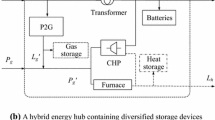
The architecture of a typical MEI is illustrated in Fig. 1 [20]. Several networks including power network, heat network, cold network, and natural gas network are connected with each other through energy conversion and storage devices, i.e., energy hubs, such as CHP, CAES, heat storage system, and refrigerator. The main focus of this paper is the combined heat and power scheduling of a MEI with PDN and DHN. It is worth mentioning that a zero-carbon-emission NSF-CAES is used as the hub between PDN and DHN in proposed ZCE-MEI, rather than CHP which discharges carbon.
2.2 NSF-CAES hub
As mentioned above, NSF-CAES can be viewed as a clean EH capable of co-generation of cool, heat and power. The diagram of a common NSF-CAES hub with two-stage compression and two-stage expansion is shown in Fig. 2. The whole system is composed of air compression unit, air storage tank, air turbine, and heat regeneration system. During charging, the air compressor utilizes off-peak electricity, curtailed wind power and solar power to drive compressor to compress air to a high pressure one, and store the high pressure air into air storage tank. Different from CAES, the thermal energy along air compression is stored in a heat regeneration system to improve operation efficiency in NSF-CAES. When the electricity is needed, high pressure air stored in air storage tank can be released and preheated by the stored thermal energy to the turbine to drive generator. Thus, the decoupling storage of thermal energy and molecular potential energy is realized. Multi-stage air compressor and multi-stage air turbine structure are often employed in actual NSF-CAES hubs to improve the whole energy storage and conversion efficiency [10, 23]. For simplicity, a NSF-CAES hub with 2-stage compressor and 2-stage turbine is considered in this paper.
Motivated by [18], the interface of NSF-CAES with PDN and DHN is shown in Fig. 3. Thermal energy stored in regeneration system and generated by immersion heater or heat pump plays the role of heating source for DHN. From another aspect, wind power and off-peak electricity act as the input of NSF-CAES hub, i.e., compressor is the electrical interface of NSF-CAES with grid. Besides, NSF-CAES hub can provide electricity power for the PDN, i.e., generator is the interface of NSF-CAES with grid.
2.3 NSF-CAES formulation
The following assumptions are made before modeling NSF-CAES.
-
1)
The air is considered as an ideal one, and meets ideal gas equation.
-
2)
Air storage tank adopts the isothermal model, i.e., temperature of stored air equals to that of ambient [24].
-
3)
Air storage tank employs the constant volume model, i.e., volume of air storage tank keeps no change [24].
-
4)
Compressor and turbine use the adiabatic model.
-
5)
Heat loss of thermal energy storage tank is neglected.
-
6)
Power consumption of circulating pump is neglected.
-
7)
Pressure loss of high pressure air and water through the heat exchanger is neglected.
2.3.1 Compressor
According to [10, 20, 23], power consumption of r th stage compressor during charging satisfies:
where \(p_{j,r,t}^{c}\) is the power demand of r th stage compressor at time t; \(\eta_{j,r}^{c}\) is the adiabatic efficiency of r th stage compressor; κ is the adiabatic exponent of air; R g is the gas constant; \(qm_{j,t}^{c}\) is the mass flow rate of air of compressor j at time t; \(\tau_{j,r,t}^{c,in}\) is the inlet temperature of r th stage compressor at time period t; \(pr_{j,r,t}^{c,in}\) and \(pr_{j,r,t}^{c,out}\) are the inlet and outlet air pressure of r th stage compressor at time period t.
Equation (1) defines the bounds of consumed power of each stage compressor.
where \(u_{j,t}^{c}\) is the binary variable that is equal to 1 if compressor is working; \(p_{j,r}^{c,l}\) and \(p_{j,r}^{c,u}\) are the lower bound and upper bound of power demand of r th stage compressor.
Total power demand of compressor is given by
where n c is the number of compressor stage; \(A_{j,t}^{c}\) is the total power consumption of compressor.
Air mass flow rate of each stage compressor should be kept within the limits.
where \(qm_{j}^{c,l}\) and \(qm_{j}^{c,u}\) are the lower and upper bound of mass flow rate of air of compressor j.
The relationship between air temperature of inlet and outlet r th stage compressor is given by [10, 20, 23]
where \(\tau_{j,r,t}^{c,out}\) is the outlet temperature of r th stage compressor at time period t.
Air pressure in each stage compressor is constrained by
where \(pr_{j,1,t}^{c,in}\) and \(pr_{j,r,t}^{c,in}\) are the inlet air pressure of 1-stage and r th stage compressor at time period t; pr am is the ambient pressure; \(pr_{j,r}^{c,in,l}\) and \(pr_{j,r}^{c,in,u}\) are lower and upper bound of inlet air pressure of r th stage compressor; \(pr_{j,r,t}^{c,out}\) and \(pr_{{j,n_{c} ,t}}^{c,out}\) are the outlet air pressure of r th stage compressor; \(pr_{j,r}^{c,out,l}\) and \(pr_{j,r}^{c,out,u}\) are the lower and upper bound of outlet air pressure of r th stage compressor; β j,r is the compression ratio of r th stage compressor.
Equation (6) denotes the inlet air pressure of 1-stage compressor. Equations (7) and (8) depict the bound of inlet and outlet air pressure of r th stage compressor. The relationship between inlet air pressure of (r + 1)th stage and outlet air pressure of r th stage is given by (9). Equation (10) describes the link between outlet air pressure of the last stage and air pressure of air storage tank. Correlations of inlet air pressure and outlet air pressure of r th stage compressor are shown in (10) and (12).
2.3.2 Turbine
To some extent, the operation mechanism of turbine can be regarded as an inverse process of compressor. Thus, the formulations for turbine can be easily inferred from that of compressor.
For NSF-CAES j, power generated by s th stage turbine can be calculated by
where \(p_{j,s,t}^{g}\) is the power generation of s th stage turbine at time t; \(\eta_{j,s}^{g}\) is the adiabatic efficiency of s th stage turbine; \(qm_{j,t}^{g}\) is the mass flow rate of air of turbine j; \(\tau_{j,s,t}^{g,in}\) is the inlet temperature of s th turbine; \(pr_{j,s,t}^{g,in}\) and \(pr_{j,s,t}^{g,out}\) are the inlet and outlet air pressure of s th stage turbine.
Power generated by each stage of turbine should be keep in the bounds.
where \(u_{j,t}^{g}\) is the binary variable that is equal to 1 if turbine is working; \(p_{j,s}^{g,l}\) and \(p_{j,s}^{g,u}\) are the lower bound and upper bound of power generation of s th stage turbine.
Correspondingly, we have the total power generation:
where n e is the number of turbine stage; \(A_{j,t}^{g}\) is the total power generation of NSF-CAES turbine.
Air mass flow rate of each stage turbine should be kept within the range:
where \(qm_{j}^{g,l}\) and \(qm_{j}^{g,u}\) are the lower and upper bound of mass flow rate of air of turbine j.
Similar to (5), the connection between inlet and outlet air temperature of s th stage turbine at each time period t can be formulated as
where \(\tau_{j,s,t}^{g,out}\) is the outlet temperature of s th stage turbine at time period t.
Air pressure in each stage turbine is constrained by
where \(pr_{j,1,t}^{g,in}\) and \(pr_{j,s,t}^{g,in}\) are inlet air pressure of 1-stage and s th stage turbine at time period t; pr st is the pressure of air storage tank; \(pr_{j,s}^{g,in,l}\) and \(pr_{j,s}^{c,in,u}\) are lower and upper bound of inlet air pressure of s th stage turbine; \(pr_{j,s,t}^{g,out}\) and \(pr_{{j,n_{e} ,t}}^{g,out}\) are outlet air pressure of s th and n e stage turbine; \(pr_{j,s}^{g,out,l}\) and \(pr_{j,s}^{g,out,u}\) are lower and upper bound of outlet air pressure of s th stage turbine; γ j,s is the expansion ratio of s th stage turbine.
The meanings of (18)–(24) can be concluded according to (6)–(12).
2.3.3 Air storage tank
Pressure of high pressure air in storage tank at time period t + 1 can be calculated by
where \(pr_{j,t}^{st}\) is the pressure of air storage tank at time period t; V is the volume of air storage tank; \(\tau_{t}^{st}\) is the temperature of air storage tank.
Equation (25) is a measure for the state of charge (SOC) of NSF-CAES hub.
In the light of the operation requirements of NSF-CAES, air pressure in the air storage tank should be kept in the limits:
where \(pr_{j}^{l}\) and \(pr_{j}^{u}\) are the lower and upper bound of pressure of air storage tank.
2.3.4 Regenerative system
Based on the heat exchange theory, thermal energy collected by cooler equipped after r th stage compressor at time period t during charging can be depicted by [20, 23, 25]:
where \(h_{j,r,t}^{g}\) and \(h_{{j,n_{c} ,t}}^{g}\) are the collected heat by r th stage cooler; c a is the constant pressure specific heat of air.
Accordingly, the total thermal energy collected during charging is the sum of that of each cooler, i.e.,
Similarly, thermal energy consumed by heater equipped before s th stage turbine during discharging can be calculated by
where \(h_{j,1,t}^{c}\) and \(h_{j,s,t}^{c}\) are the consumed heat by the first and s th stage heater.
Also, we have the total consumed thermal energy given by
The SOC of thermal energy storage system of NSF-CAES can be illustrated as
where \(H_{j,t}^{st}\) is the heat of heat regeneration system at time period t; \(H_{j}^{st,l}\) and \(H_{j}^{st,u}\) are the lower and upper bound of heat can be stored in the heat regeneration system.
Noting that, heat power recycled by the heat exchanger with water as cooling medium as in Fig. 2, i.e., 1-stage water cooling and 2-stage water cooling, is ignored in this part. The modeling process is similar to that of heat exchanger with conduction oil.
3 Operation of zero-carbon-emission micro Energy Internet
It is worth mentioning that wind power is considered as a class of scheduled generation source, i.e., allowing curtailment during the operation of ZCE-MEI in this paper. The errors between day-ahead forecasting and the real-time situation are neglected. Besides, wind power is regarded as free so that it will be consumed as much as possible [26].
3.1 Objective function
It is assumed that NSF-CAES hub and heat pump are the heat sources of DHN in the proposed ZCE-MEI, while heat pump is the main heat source. In this regard, we assume that heat pump buy electricity directly from power grid not some buses in the PDN. Thus, NSF-CAES hub is the only coupling point between DHN and PDN in the proposed ZCE-MEI. We consider the objective of reducing scheduling cost of ZCE-MEI over the whole dispatch periods:
where b t and θ t are the electricity price and power bought from grid at time period t; \(d_{j,t}^{hp}\) is the power demand of heat pump in DHN; n hp is the number of equipped heat pump.
The first term in (35) is the cost of electricity bought from gird for PDN while the second term is the electricity cost for heat pump in DHN. Objective function (35) is subjected to the following constraints.
3.2 Constraints
-
1)
Heat pump and circulating water pump
Similar to (27) and (28), total thermal energy supplied by the NSF-CAES hub and heat pump equipped at node i can be calculated by:
where \(h_{i,t}^{hp}\) and \(h_{i,t}^{g}\) are the heat generated by NSF-CAES hub and heat pump at time period t; c w is the constant pressure specific heat of recycle water; \(m_{i,t}^{g}\) is the mass flow rate of recycle water at node i; \(\tau_{i,t}^{S}\) and \(\tau_{i,t}^{R}\) are the temperature of supply water system and return water system at node i.
Temperature of the water at each heat pump should be kept in the range:
where \(\tau_{i}^{S,l}\) and \(\tau_{i}^{S,u}\) are the lower and upper bound of temperature of supply water at node i.
Power consumed by circulating water pump equipped at node i satisfies [18]:
where \(pr_{i,t}^{S}\) and \(pr_{i,t}^{R}\) are pressure of supply water and return water of node i at time period t; \(d_{i,t}^{cp}\) is the power demand of circulating water pump at node i; ρ is the density of recycle water; \(\eta_{i}^{cp}\) is the efficiency of circulating water pump.
The power consumption of heat pump and circulating water should be limited by:
where \(d_{i}^{hp,l},d_{i}^{cp,l}\) and \(d_{i}^{hp,u},d_{i}^{cp,u}\) are the lower and upper bound of power consumption of heat pump and circulating water pump equipped at node i.
-
2)
Heat load
Heat load at node i of DHN in ZCE-MEI can be calculated by [8, 25]:
where \(m_{i,t}^{d}\) is the mass flow rate of recycle water of head load at node i at time period t; \(h_{i,t}^{d}\) is heat load demand.
There exist a minimum supply pressure and return pressure for circulating water pump in each NSF-CAES connected to node i, i.e.,
Accordingly, temperature of return water at heat load i is constrained by:
where \(\tau_{i}^{R,l}\) and \(\tau_{i}^{R,u}\) are the lower and upper bound of temperature of return water.
-
3)
Heat network
According to the continuity of flow [6, 8, 25], for each node i ∊ H(N), the following equations are satisfied:
where F(i) and T(i) are the set of pipes with node i as ‘from’ or ‘to’ node; \(m_{b,t}^{S}\) and \(m_{b,t}^{R}\) are the mass flow rate of recycle water of supply and return water system of pipe b at time t; \(m_{i,t}^{g}\) and \(m_{i,t}^{d}\) are the mass flow rate of recycle water of heat generation unit and heat load at node i.
The relationship between temperature of node i ∊ H(N) and temperature of pipe b ∊ H(P) can be depicted as:
where \(\tau_{b,t}^{S,out}\) and \(\tau_{b,t}^{R,out}\) are outlet temperature of pipe b of supply system and return system at time t.
The relationship between node temperature and temperature of pipe is illustrated as:
where \(\tau_{b,t}^{S,in}\) and \(\tau_{b,t}^{R,in}\) are inlet temperature of pipe b of supply system and return system at time t.
Mass flow of each pipe b of supply network and return network should be limited according the physical character of pipe, i.e.,
where \(m_{b}^{u}\) is the upper bound of mass flow rate of recycle water through pipe b.
The pressure between inlet and outlet of pipe b can be illustrated as [18, 25]:
where μ b is the pressure loss coefficient of pipe.
The temperature drops exponentially during recycle water flow in pipes [18]. The outlet temperature of pipe b is an exponential function of inlet temperature of pipe b.
where λ b is temperature loss coefficient of pipe; L b is the length of pipe b; \(\tau_{t}^{am}\) is the ambient temperature at time period t.
-
4)
Power distribution network
Different from the power transmission network, PDN usually has a radial topology as shown in Fig. 4.
The power flow in such a radial PDN can be described by DistFlow model or Branch flow as in [27–29] and can be illustrated as:
where P ij and Q ij are the active power and reactive power flow of line l(i,j); \(p_{j}^{g}\) and \(q_{j}^{g}\) are the active power and reactive power generation of generation unit at bus j; \(p_{j}^{d}\) and \(q_{j}^{d}\) are the active power and reactive power demand of load at bus j; i ij is square of current through line l(i,j), while \(i_{ij}^{u}\) is the upper bound; r ij and x ij are the resistance and reactance of line l(i,j), while z ij is the impedance of line l(i,j); U i is the square of voltage amplitude of bus i; V sl is the voltage of slack bus; \(p_{i}^{l}\) and \(p_{i}^{u}\) are the upper and lower bound of active power output of generation unit; \(q_{i}^{l}\) and \(q_{i}^{u}\) are the upper and lower bound of reactive power output of generation unit.
Equations (53) and (54) model the active power and reactive power balance of PDN, respectively. Voltage drops along the distribution line l(i,j) is depicted in (55). Equation (56) describes the connection between power, square of voltage, and square of current. The limits of square of current, square of voltage, active power, and reactive power are respectively shown in (57)–(59).
DistFlow model (53)–(59) is only for radial PDNs. Some modifications are needed when it comes to other PDNs. The main advantages of DistFlow model are listed as follows: ① The reactive power balance and node voltage are considered in the power flow equations; ② The equations can be converted to linear ones or SOCP ones and the optimal solution can be easily obtained as in [29, 30], which is similar with DC flow model of transmission line that ignores reactive power. The linearized DistFlow can be illustrated as follows [30]:
It is assumed that PDN of MEI is a radial one, DistFlow model and Branch flow can be implemented to formulate PDN of MEI. The renewable energy sources, continuous and discrete reactive power compensators can be incorporated in the improved DistFlow model [31, 32]. Thus, the PDN of MEI can be formulated based on linearized DistFlow model as:
where \(W_{j,t}^{g}\) and \(A_{j,t}^{g}\) are the power output of wind generator and NSF-CAES hub equipped at bus j at time period t; \(A_{j,t}^{c}\) is the power demand of NSF-CAES hub; C j,t is the value of shunt capacitors/reactors; Q cj,t is the supplemented reactive power of continuous compensator; K ij,t is the tap ratio of OLTC on line l(i,j); \(W_{i}^{g,l}\) and \(W_{i}^{g,u}\) are the lower and upper bound of available wind power output.
Active power distribution of line l(i,j) is formulated as (65). Equations (66) and (67) depict the reactive power distribution for line l(i,j) with and without reactive power compensator equipped on bus j, respectively. Equations (68) and (69) denote the voltage of bus j for line l(i,j) with or without OLTC. (70) is similar to (58). The available wind power is constrained by (71).
3.3 Model simplifications
Aggregating the objective and constraints, dispatch model of ZCE-MEI in terms of reducing system operation cost can be formulated as:
Dispatch model (72) is actually a large scale mixed integer nonlinear programming (MINLP) problem, which is hard to be effectively solved. In this section, each part of this model, including NSF-CAES hub, PDN, and DHN are linearized to yield a mixed integer linear programming (MILP) which can be easily solved by CPLEX.
-
1)
Linearization of NSF-CAES hub
Air pressure pr, temperature τ, and mass flow rate qm are the adjustable variables of a NSF-CAES hub. It is difficult to adjusting them simultaneously owing to the complexity of hydraulic–thermal dynamics. Fortunately, a practical NSF-CAES hub often operates at a constant pressure and constant temperature (CP–CT) mode [10, 23]. Thus, (1) and (13) reduces to
respectively.
Similarly, (5) and (17) reduce to
respectively.
Besides, under CP–CT operation mode, (6)–(12) and (18)–(24) are eliminated.
-
2)
Linearization of PDN
As for PDN, (66) and (68) are nonlinear equations. The term U j,t C j,t in (66) is a nonlinear one, to linearize this term, the discrete variable C can be formulated as [31–33],
where \(g_{j,0} ,\;g_{j,1} , \ldots ,g_{{j,v^{j} }}\) are binary variables; E D is set of buses for shunt capacitors/reactors; s j is the step size of shunt capacitors/reactors; \(C_{j}^{l}\) and \(C_{j}^{u}\) are the lower and upper bound of shunt capacitors/reactors; v j is a integer which can be decided by:
Thus, the term U j,t C j,t in (66) is transformed to
Usually, (80) can be linearized by utilizing big M method, i.e.,
where \(\delta_{j,0} ,\;\delta_{j,1} , \ldots ,\delta_{{j,v^{j} }}\) are binary variables; M is a big number.
As for the OLTC branch l(i,j), the term of left side of (68) can be expanded as:
where K ij,1, K ij,2,…,\(K_{{ij,n_{ij} }}^{{}}\) are the available value of tap of OLTC; n ij is the number of available OLTC tap value. In this regard, (68) can be linearized as [31–33]:
where h j,k,t are dummy variable; b ij,1,t and \(b_{{ij,n_{ij} ,t}}\) are binary variables, with \(\sum\limits_{k = 1}^{{n_{ij} }} {b_{j,k,t} } = 1.\)
-
3)
Linearization of DHN
As for DHN, there exists four different operating strategies, including constant flow and constant supply temperature (CF–CT), constant flow and variable supply temperature (CF–VT), variable flow and constant supply temperature (VF–CT), variable flow and variable supply temperature (VF–VT) [25, 34]. Under the VF–VT and VF–CT modes, the temperature dynamics (49) and (50) are nonlinear, which made the dispatch problem difficult to be solved. Fortunately, in an actual DHN, CF–VT has more flexibility than CF–CT, and CF–VT yields a linear DHN model.
For simplicity, the widely used CF–VT mode is implemented in this paper, thus, (43), (44), (49) and (50) are unnecessary.
Through above transformations and simplifications, the original MINLP (72) is reduced to a MILP problem, which can be effectively solved by commercial solvers.
4 Case study
4.1 System settings
The configuration of the test ZCE-MEI is shown in Fig. 5. The designed ZCE-MEI is composed of a 33-bus PDN, an 8-node DHN, a NSF-CAES hub, 4 wind generators, 1 heat pump, and several reactive power compensators both discrete and continuous including OLTC, SVG, shunt capacitor and reactor. A 3 MW wind generator is equipped with NSF-CAES hub at Bus 2, the other three 0.5 MW wind generators are employed at Bus 7, 19, 26 respectively. This configuration is valued in [35]. Heat pump is equipped at node N1. It is worth mentioning that heat pump buy electricity directly from power grid not some buses in the PDN. Thus, NSF-CAES hub is the only coupling point between DHN and PDN in this test system.
Time-of-use power price is shown in Fig. 6. The power demand, heat demand, and available wind power of the ZCE-MEI are shown in Fig. 7. Power ratio of each bus in ZCE-MEI can be generated by each load divide system load of the standard matpower data. Heat load ratio, and mass flow rate of each node are shown in Table 1.
To maintain voltage quality of PDN in the designed ZCE-MEI, several kinds of reactive power compensator are equipped at key buses of PDN. Several OLTCs with a minimum tap changer 0.95, maximum tap changer 1.05, and tap step 0.01 are equipped on Line #1, #18, #22, #25 respectively. Meanwhile, shunt capacitors/reactors with a minimum value 0 and maximum value 0.2, and step 0.05 are located on Bus #5, #10, #13, #17, #20, #23, #30 respectively. Besides, SVG are equipped on Bus #4, #9, #14 to provide continuous reactive power.
4.2 Simulation of NSF-CAES
In this section, operation of a 1 MW NSF-CAES hub is simulated to verify the effectiveness of the proposed formulation. The rated parameters of each stage compressor and turbine are depicted in Table 2 and Table 3, respectively. Besides, the rated mass flow rate of each compressor and turbine are 0.64, 2.46 kg/s, respectively. The volume of air storage tank of the designed NSF-CAES is 2000 m3.
The round trip energy flow of the designed 1 MW NSF-CAES hub is illustrated in Fig. 8. The electricity efficiency η e = 1.46/2.8 = 52.14%, the round trip energy efficiency η CAES = (1.46 + 0.4193)/1.3867 = 67.12%. These efficiencies are acceptable for commercial applications to realize return of investment at commercial scale.
4.3 Simulation results
All simulations are implemented on a laptop with Intel i5-4210M CPU and 16 GB RAM. The operation of NSF-CAES hub, system operation cost and wind curtailment are analyzed consequently in the following subsections.
-
1)
Operation of NSF-CAES hub
The SOC of NSF-CAES and that of TES of NSF-CAES hub are shown in Fig. 9 and Fig. 10, respectively. Figure 11 illustrates the heat power output of heat pump and NSF-CAES hub.
We can learn from above two figures that NSF-CAES utilizes free wind power and cheap electricity at off-peak periods, such as from t = 1 to t = 6, to charge the air into air storage tank to store the energy in two forms, i.e., thermal energy in TES and molecular potential energy in air storage tank. The molecular potential energy can be used to drive turbine to generate electricity during on-peak periods, such as from t = 13 to t = 14, under the condition of consuming certain thermal energy stored in TES. Although most heat load are supplied by heat pump in the DHN, some of the thermal energy stored in TES during energy charging process can be directly used to supply heat power for heat load to save cost, such as at time periods t = 10, t = 16. Similar conclusions can be drawn by analyzing Fig. 9, Fig. 10, and Fig. 11 simultaneously.
-
2)
Operation cost and wind curtailment
Power output of wind generator, power bought from grid, and wind curtailment of wind generator #1 under the designed ZCE-MEI and separate operation modes are comparatively studied in Fig. 12 and Fig. 13.
Comparing Fig. 12 and Fig. 13, we draw the conclusion that by utilizing NSF-CAES hub in MEI, curtailed wind power during off-peak time can be reduced by storing the available free wind power in NSF-CAES and using the stored energy to supply power demand during on-peak periods. Thus, the power brought from grid can also be reduced in the proposed MEI, also the system operation cost. Through co-optimize PDN and DHN in the proposed ZCE-MEI, wind power curtailment of the whole system is reduced from 5.2347 to 2.0452 MWh as shown in the red shadow in Fig. 12 and Fig. 13. System operation cost of MEI and separate operation of PDN and DHN is compared in Table 4. By co-optimize PDN and DHN through NSF-CAES hub, the operation cost of the whole system is reduced 3.32% compared with optimize DHN and PDN separately.
Besides, we can also learn from the two figures that, during period from t = 8 to t = 22, all the available wind power has been utilized to supply the power load demand.
-
3)
Optimal power flow
Optimal temperature distribution of DHN of the designed ZCE-MEI at the on-peak heat load period (t = 5) and off-peak heat load period (t = 15) are shown in Fig. 14.
It is shown in Fig. 14 that the different heat load at on-peak period (t = 15) and off-peak period (t = 5) can be supplied by adjusting the return water temperature. Under the condition of the same supply water temperature, the smaller the return water is, the larger the heat power can be supplied. Besides, the temperature of outlet of supply and return water system usually lower than that of inlet of supply and return water system which is similar to the common sense.
Optimal power flow of PDN at on-peak time period (t = 11) and off-peak time period (t = 5) are depicted in Fig. 15. Voltage of each bus during off-peak power load and on-peak power load and corresponding states of OLTCs are shown in Fig. 16 and Fig. 17.
We can learn from above figures that node voltage and reactive power balance are maintained and supplied in the required limits by adjusting the OLTC and shunt capacitors/reactors at on-peak and off-peak time periods.
5 Conclusion
This paper proposes a zero-carbon-emission micro Energy Internet architecture to utilize power and heat in an integrated manner. NSF-CAES hub is a clean energy hub accommodating DHN and PDN. A detailed NSF-CAES dispatch model is constructed to consider the pressure behaviors and temperature dynamics. To maintain the voltage quality of PDN in the proposed ZCE-MEI, an improved linearized DistFlow model is utilized to take OLTC and capacitor and reactor shunt compensator into account. Optimal operation of the ZCE-MEI is realized in terms of reducing operation cost. A typical 1 MW NSF-CAES hub is designed to show the effectiveness of the proposed NSF-CAES formulation. Simulation results verified the advantages of the proposed ZCE-MEI in reducing operation cost and wind curtailment.
Noting that, we assume there is no uncertainty in the system parameter, thus the method cannot adapt to situations with parameter uncertainties which is more common in actual system. Our further work will focus on the optimal dispatch of MEI with uncertainty, the robust optimization and stochastic optimization methods would be adopted to handle this kind of problem.
References
Brunekreeft G, Buchmann M, Dänekas C et al (2015) Regulatory pathways for smart grid development in China. Springer Fachmedien Wiesbaden, Wiesbaden, pp 119–138
Global wind report: annual market update 2015 (2016). Global Wind Energy Council (GWEC), Brussels
Geidl M, Andersson G (2007) Optimal power flow of multiple energy carriers. IEEE Trans Power Syst 22(1):145–155
Shabanpour-Haghighi A, Seifi AR (2015) Energy flow optimization in multicarrier systems. IEEE Trans Ind Inform 11(5):1067–1077
Li JH, Fang JK, Zeng Q et al (2016) Optimal operation of the integrated electrical and heating systems to accommodate the intermittent renewable sources. Appl Energy 167:244–254
Li ZG, Wu WC, Shahidehpour M et al (2016) Combined heat and power dispatch considering pipeline energy storage of district heating network. IEEE Trans Sustain Energy 7(1):12–22
Li ZG, Wu WC, Wang JH et al (2016) Transmission-constrained unit commitment considering combined electricity and district heating networks. IEEE Trans Sustain Energy 7(2):480–492
Liu XZ, Wu JZ, Jenkins N et al (2016) Combined analysis of electricity and heat networks. Appl Energy 15:1238–1250
Jakiel C, Zunft S, Nowi A (2007) Adiabatic compressed air energy storage plants for efficient peak load power supply from wind energy: the European project AA-CAES. Int J Energy Technol Policy 5(3):296–306
Mei SW, Wang JJ, Tian F et al (2015) Design and engineering implementation of non-supplementary fired compressed air energy storage system: TICC-500. Sci China Technol Sci 58(4):600–611
Xue XD, Mei SW, Lin QY et al (2016) Energy Internet oriented non-supplementary fired compressed air energy storage and prospective of application. Power Syst Technol 40(1):164–171
Daneshi H, Srivastava AK, Daneshi A (2010) Generation scheduling with integration of wind power and compressed air energy storage. In: Proceedings of the 2010 IEEE PES transmission and distribution conference and exposition, New Orleans, LA, USA, 19–22 April 2010, 6 pp
Liu B, Chen LJ, Zhang Y et al (2014) Modeling and analysis of unit commitment considering RCAES system. In: Proceedings of the 33rd Chinese control conference (CCC’14), Nanjing, China, 28–30 July 2014, pp. 7478–7482
Abbaspour M, Satkin M, Mohammadi-Ivatloo B et al (2013) Optimal operation scheduling of wind power integrated with compressed air energy storage (CAES). Renew Energy 51:53–59
Fang C, Chen LJ, Zhang Y et al (2014) Operation of low-carbon-emission microgrid considering wind power generation and compressed air energy storage. In: Proceedings of the 33rd Chinese control conference (CCC’14), Nanjing, China, 28–30 July 2014, pp. 7472–7477
Wang C, Chen LJ, Liu F et al (2014) Thermal–wind-storage joint operation of power system considering pumped storage and distributed compressed air energy storage. In: Proceedings of the 2014 power systems computation conference (PSCC’14), Wroclaw, Poland, 8–22 August 2014, 7 pp
Lund H, Salgi G, Elmegaard B et al (2009) Optimal operation strategies of compressed air energy storage (CAES) on electricity spot markets with fluctuating prices. Appl Therm Eng 29(5/6):799–806
Awad B, Chaudry M, Wu JZ et al (2009) Integrated optimal power flow for electric power and heat in a microgrid. In: Proceedings of the 20th international conference and exhibition on electricity distribution (CIRED ‘09), Part 2, Prague, Czech, 8–11 June 2009, 1 pp
Wu QH, Zheng JH, Jing ZX (2015) Coordinated scheduling of energy resources for distributed DHCs in an integrated energy grid. CSEE J Power Energy Syst 1(1):95–103
Hwang T, Choi M, Kang S et al (2012) Design of application-level reference models for micro energy grid in IT perspective. In: Proceedings of the 8th international conference on computing and networking technology (ICCNT’12), Gyeongju, Republic of Korea, 27–29 August 2012, pp. 180–183
Xue XD, Liu BH, Wang YC et al (2016) Micro energy network design for community based on compressed air energy storage. Proc CSEE 36(12):1–7
Katiraei F, Iravani MR, Lehn PW (2005) Micro-grid autonomous operation during and subsequent to islanding process. IEEE Trans Power Deliv 20(1):248–257
Dielmann K, van der Velden A (2003) Virtual power plants (VPP): a new perspective for energy generation? In: Modern techniques and technologies: proceedings of the 9th international scientific and practical conference of students, post-graduates and young scientists (MTT’03), Tomsk, Russia, 7–11 April 2003, pp. 18–20
Wang SX, Zhang XL, Yang LW et al (2016) Experimental study of compressed air energy storage system with thermal energy storage. Energy 103:182–191
Budt M, Wolf D, Span R et al (2016) A review on compressed air energy storage: basic principles, past milestones and recent developments. Appl Energy 15:250–268
Zhao H (1995) Analysis, modelling and operational optimization of district heating systems. PhD Thesis, Technical University of Denmark, Copenhagen
Ji Z, Kang CQ, Chen QX et al (2013) Low-carbon power system dispatch incorporating carbon capture power plants. IEEE Trans Power Syst 28(4):4615–4623
Baran ME, Wu FF (1989) Network reconfiguration in distribution systems for loss reduction and load balancing. IEEE Trans Power Deliv 4(2):1401–1407
Farivar M, Low SH (2013) Branch flow model: relaxations and convexification—Part I. IEEE Trans Power Syst 28(3):2554–2564
Wei W, Mei SW, Wu L, Wang J, Fang Y (2016) Robust operation of distribution networks coupled with urban transportation infrastructures. IEEE Trans Power Syst. doi:10.1109/TPWRS.2016.2595523
Wang ZY, Chen B, Wang JH et al (2015) Coordinated energy management of networked microgrids in distribution systems. IEEE Trans Smart Grid 6(1):45–53
Liu B, Liu F, Mei SW et al (2015) AC-constrained economic dispatch in radial power networks considering both continuous and discrete controllable devices. In: Proceedings of the 27th Chinese control and decision conference (CCDC’15), Qingdao, China, 23–25 May 2015, pp. 6249–6254
Ding T, Liu SY, Yuan W et al (2016) A two-stage robust reactive power optimization considering uncertain wind power integration in active distribution networks. IEEE Trans Sustain Energy 7(1):301–311
Ferreira RS, Borges CLT, Pereira MVF (2014) A flexible mixed-integer linear programming approach to the AC optimal power flow in distribution systems. IEEE Trans Power Syst 29(5):2447–2459
Pirouti M, Bagdanavicius A, Ekanayake J et al (2013) Energy consumption and economic analyses of a district heating network. Energy 57(8):149–159
Denholm P, Sioshansi R (2009) The value of compressed air energy storage with wind in transmission-constrained electric power systems. Energy Policy 37(8):3149–3158
Acknowledgment
This work was supported in part by the National Natural Science Foundation of China (No. 51321005, No. 51377092, No. 51577163), and Opening Foundation of the Qinghai Province Key Laboratory of Photovoltaic Power Generation and Grid-connected Technology.
Author information
Authors and Affiliations
Corresponding author
Additional information
CrossCheck date: 12 September 2016
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
LI, R., CHEN, L., YUAN, T. et al. Optimal dispatch of zero-carbon-emission micro Energy Internet integrated with non-supplementary fired compressed air energy storage system. J. Mod. Power Syst. Clean Energy 4, 566–580 (2016). https://doi.org/10.1007/s40565-016-0241-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40565-016-0241-4