1 Introduction

In the past decades, renewable energy becomes ever-increasingly important in generation system planning. Biomass, wind, photovoltaic, hydropower, geothermal and ocean energy technologies have been significantly developed [1–3]. For a remote coastal or island area, only a stand-alone tidal or wind system cannot provide a continuous supply of energy due to random variations of tidal current and wind speed in different periods and seasons. In order to satisfy the continuous load demand in remote locations, a hybrid energy system with mixed tidal power, wind power and battery storage is an essential option. Such a system may widely exist in coastal areas and islands across the world in the future. It is necessary to investigate a hybrid generation system of wind and tidal powers. Tidal current offers energy by harnessing the daily rise and fall of tidal currents. Although many tidal power projects have been developed or planned worldwide [4–6], little work has been done for tidal power modeling. On one hand, tidal current has daily regularity, which wind power does not have; on the other hand, similar to wind speed, tidal current speed has random features in individual hours.

A lot of researches have been devoted to the reliability evaluation of power system with wind power [7–10]. The generation unit sizing and cost analysis for stand-alone wind, photovoltaic (PV) and hybrid PV/wind system is conducted in [11]. A size optimization method of a PV/wind integrated hybrid energy system with battery storage using simulated annealing is introduced in [12]. However, very little or no work has been done on the reliability evaluation of power system with both tidal and wind power generations as well as battery energy storage. The main contributions of this paper include the following.

  1. 1)

    A reliability model of tidal power generation system (TPGS) considering both forced outage rate (FOR) of TPGS and random nature of tidal current speed is presented.

  2. 2)

    In order to integrate tidal or wind generation into a power system, a power electronic converter must be used. Therefore, the analysis of the reliability behavior of the power electronic converter plays a vital role in the reliability assessment of power system with tidal and wind generations. A reliability model of the power electronic converter, which considers operating temperature impacts on the failure rates of electronic components, is incorporated into the reliability analysis of power system with TPGS and wind power generation system (WPGS) in this paper. In most previous work for reliability evaluation of power system with wind or tidal power, the failure model of power electronic converter has been missed.

  3. 3)

    A battery energy storage system should be considered to deal with the intermittent nature of wind and tidal power, particularly for a remote coastal power supply system. Some efforts on the reliability assessment of wind power system with battery energy storage have been carried [13–15]. However, the reported studies did not consider the FOR of power generation system and chronological features of battery bank charging and discharging powers. In addition to incorporating the FOR of TPGS and WPGS, a chronological power output model of battery energy storage system (BESS) is derived.

The paper is organized as follows. The probabilistic multiple states and chronological model of TPGS is developed in Section 2. The chronological time series model of wind power is also briefly summarized in this section. In Section 3, the reliability models of TPGS and WPGS are presented with a focus on the derivation of FOR of power electronic converter. The chronological power output model of BESS is presented in Section 4. The calculations of two reliability indices, the loss of load expectation (LOLE) and expected energy not supply (EENS), are given in Section 5. Case studies and analysis are conducted in Section 6, followed by conclusions in Section 7.

2 Probabilistic models of tidal and wind power generation systems

In order to take the random nature of tidal current speed into consideration, a probability distribution of tidal current speed is modeled first. Then, this probability distribution is combined with the power output model of tidal current generator to develop a chronological multiple state model of tidal power. The chronological time series model of wind power is briefly discussed. Note that power output models of tidal and wind generations are necessary not only for calculating load curtailments required in system reliability indices but also for estimating the failure rates of power electronic converter, which will be discussed in Section 3.

2.1 Probability distribution model of tidal current speed

An appropriate probability distribution for tidal current speed is the first step for establishing the probabilistic multi-state model of TPGS. As reported in our previous work [16], Wakeby distribution and other nine popular distributions were investigated and compared for appropriateness to model tidal current speed. By using four years of tidal current speed data at ten different sites located in North America, the Kolmogorov-Smirnov test (K-S test) and the root-mean-square error (RMSE) index for both posteriori and priori tests indicated that the Wakeby distribution not only has the best statistical performance but also is the only one out of ten selected distributions that passed the K-S test. The five-parameter Wakeby distribution, which is used for modeling tidal current speed, is defined by the following quantile function [16].

$$V_{\text{t}} (F) = \xi + \frac{\alpha }{\beta }\left[ {1 - \left( {1 - F} \right)^{\beta } } \right] - \frac{\gamma }{\sigma }\left[ {1 - \left( {1 - F} \right)^{ - \sigma } } \right]$$
(1)

where V t(F) is the tidal current speed where “t” represents “tidal” and is not a subscript index; F = F(V) = p(V t ≤ V) the cumulative distribution function of the Wakeby distribution; and α, β, γ, σ, ξ the five parameters of the Wakeby distribution. These parameters can be estimated by using historical tidal current speed records and an L-moment estimation (LME) method. The basic idea is to estimate the parameters by calculating the first five linear moments from sample data and let each of them be equal to the corresponding moment expression that can be derived from the definition of L-moment. The details of this method can be found in [16]. In order to consider the variations of tidal current speeds in different seasons, historical records are divided into four seasons. The historical tidal current speeds at each hour of each day in the same seasonal period are gathered together into a group in each season, i.e. 24 groups per season and 96 groups per year. The parameters of 96 Wakeby distributions representing each typical hour in each season can be estimated by using the historical records for the 96 groups. Once the five parameters in each group are obtained, the probability of tidal current speed falls in a specific interval [V t,i , V t,i+1] can be calculated by

$$p\left( {V_{{{\text{t}},i}} \le V_{\text{t}} \le V_{{{\text{t}},i + 1}} } \right) = F_{i + 1} - F_{i}$$
(2)

The F i+1 and F i are calculated from (1). Together with the FOR and power output characteristic of TPGS, a probabilistic multi-state model of TPGS in each group can be constructed. The power output model of TPGS is discussed in Section 2.2, whereas the details of the chronological multi-state probability model will be given in Section 2.3.

2.2 Power output model of TPGS

With a cut-in speed (V cutin) and a rated speed (V rated), the output power of a TPGS (P out) can be calculated by [17]:

$$P_{\text{out}} = \left\{ {\begin{array}{*{20}l} 0 \hfill & {0 < V_{\text{t}} < V_{\text{cutin}} } \hfill \\ {0.5C_{\text{p}} \rho AV_{\text{t}}^{3} } \hfill & {V_{\text{cutin}} \le V_{\text{t}} < V_{\text{rated}} } \hfill \\ {P_{\text{rated}} } \hfill & {V_{\text{rated}} \le V_{\text{t}} } \hfill \\ \end{array} } \right.$$
(3)

where V cutin, V rated, P rated are the cut-in speed, rated speed and rated power of the TPGS, respectively; C p the power capture coefficient and its value for a typical design is in the range of 0.4~0.5 [18]; \(\rho\) the seawater density; A the area swept out by the tidal turbine rotor; and V t the tidal current speed.

According to (3), a TPGS starts to deliver electric power when the tidal current speed exceeds the cut-in speed and reaches its rated power (P rated) when the tidal current speed is at V rated. Therefore, the electrical power output characteristic curve of a TPGS can be divided into three regions as shown in Fig. 1. In region 1, the tidal current speed is lower than cut-in speed and the TPGS has no power output. As tidal current speed increases, the TPGS will get into region 2 and delivers electric power which is proportional to the seawater density \(\rho\) and the cube of the tidal current speed V t for a given cross-sectional area A. In region 3, the power output of the TPGS will remain at its rated power when the tidal current speed reaches or exceeds the rated speed.

Fig. 1
figure 1

Power output characteristic curve of the TPGS

Full size image

2.3 Chronological multi-state probability model of TPGS

For each interval of time, the power output of a TPGS, as formulated by (3), depends not only on the probabilistic characteristic of tidal current speed but also on the FOR of the TPGS because the TPGS can fail with a probability of FOR at any interval of time. FOR (F OR) is defined as the probability of a component or system being unavailable due to out of service [19, 20], i.e., unavailability. The availability is equal to 1 − F OR. Therefore, the probability of a TPGS staying in a power output state is equal to the probability of tidal current speed within a certain range to generate the power output multiplied by the availability (1 − F OR) of the TPGS in that state. The FOR of a TPGS relies on failure and repair rates of all components in the TPGS. One important component is a power electronic converter which is composed of many electronic subcomponents. The failure rates of electronic components are related to the operating temperature, which depends on the power flowing through them. The calculation method for the FOR of a TPGS is developed in Section 3. The output power of a TPGS varies from zero to the rated power (P rated) when the tidal current speed varies from cut-in speed to rated speed. The tidal current speed’s range V cutin ≤ V t < V rated can be divided into multiple intervals. In general, more intervals lead to more accurate results but require more computing efforts. A compromise between the number of intervals and computing time should be considered. As an illustrative example, the states, probabilities of each state and corresponding power outputs of a TPGS for 7 intervals are listed in Table 1.

Table 1 State probabilities and corresponding power output for a TPGS
Full size table

In Table 1, P j represents the average power output of the TPGS when the tidal current speed is within the interval [V t,j , V t,j−1]. Let V t,1 = V rated and V t,6 = V cutin, the P j can be calculated by

$$\begin{aligned} P_{j} &= \frac{1}{{V_{{{\text{t}},j - 1}} - V_{{{\text{t}},j}} }}\int_{{V_{{{\text{t}},j}} }}^{{V_{{{\text{t}},j - 1}} }} {0.5C_{\text{p}} \rho AV_{\text{t}}^{3} {\text{d}}V_{\text{t}} } \\ &= \frac{{0.125C_{\text{p}} \rho A\left( {V_{{{\text{t}},j - 1}}^{4} - V_{{{\text{t}},j}}^{4} } \right)}}{{V_{{{\text{t}},j - 1}} - V_{{{\text{t}},j}} }},\quad j = 2,3, \cdots ,6 \hfill \\ \end{aligned}$$
(4)

For each hour and in each state, the tidal power output of a TPGS can be calculated using (4). The probability of each state, which is used for reliability index calculations in Section 5, includes the FOR for that state and in that hour. As will be seen in Section 3, the FOR is different in each hour since it depends on the junction temperatures of electronic components that vary with the hourly power output.

A chronological model of TPGS with each hour having multiple states must be developed. First, as mentioned earlier, the FOR of a TPGS varies with time. Second, BESS needs to be modeled using a chronological power output model to catch up its charging and discharging processes since its discharging capacity is related to its charging states in previous hours. This model will be presented in Section 4. Third, the power output of WPGS is modeled using a chronological time series model, as discussed in Section 2.4 below. As mentioned before, the historical tidal current speeds are divided into 96 groups (4 seasons and 24 hours per day) and each group corresponds to a Wakeby distribution with different parameters. In other words, each hour of each day in the same season is represented using their common Wakeby distribution. 24 Wakeby distributions for 24 hours per day in the same season are arranged by time order and then repeat D times (the number of days in each season) to form the hourly probability distribution in each season. In the end, the chronological multiple state model for 8760 hours considering both daily and seasonal variations are constructed. Each hour has its Wakeby distribution of tidal current speed. With the hourly power output characteristic and hourly FOR of a TPGS, the 7-state model of the TPGS based on its Wakeby distribution is applied.

2.4 Power output model of WPGS

The most widely used time series model for simulating the hourly wind speed is an auto regressive and moving average (ARMA) model [7, 9]. Wind speed (W k ) for a selected wind farm site at any given time can be estimated by [7]

$$W_{k} = \mu_{k} + \sigma_{k} y_{k}$$
(5)

where μ k , σ k are the historical hourly mean wind speed and stand deviation for a specific site, respectively; and y k the time series value within k th time interval and can be obtained sequentially using the following equation:

$$\begin{aligned} y_{k} = \phi_{1} y_{k - 1} + \phi_{2} y_{k - 2} + \cdots + \phi_{n} y_{k - n} + \\ \alpha_{k} - \theta_{1} \alpha_{k - 1} - \cdots - \theta_{m} \alpha_{k - m} \hfill \\ \end{aligned}$$
(6)

where \(\phi_{i} \left( {i = 1,2, \cdots ,n} \right),\) and \(\theta_{j} (j = 1,2, \cdots ,m)\) are the auto-regressive and moving average parameters of the model, respectively; and \(\alpha_{k}\) the white noise with zero mean and a variance of \(\sigma_{\alpha }^{2}\). All the parameters can be estimated by a non-linear least-squares method [9].

The hourly power output of a WPGS system can be determined at any given hourly wind speed by [7, 8]:

$$P_{\text{W}} (k) = \left\{ {\begin{array}{*{20}l} 0 \hfill & {0 < W_{k} < V_{\text{ci}} } \hfill \\ {(A + B \times W_{k} + C \times W_{k}^{2} )P_{\text{r}} } \hfill & {V_{\text{ci}} \le W_{k} < V_{\text{r}} } \hfill \\ {P_{\text{r}} } \hfill & {V_{\text{r}} \le W_{k} < V_{\text{co}} } \hfill \\ \text{0} \hfill & {W_{k} \text{ } \ge V_{\text{co}} } \hfill \\ \end{array} } \right.$$
(7)

where V ci, V r, V co are the cut-in, rated and cut-out wind speed, respectively; P r the rated power output of the WPGS; and A, B, C three constants and can be determined by V ci and V r [8]. Similar to TPGS, if a WPGS fails in a specific hour, the WPGS cannot have any wind power output. Therefore, the expected hourly wind power output when the WPGS does not fail should be the power calculated using (7) multiplied by its availability (1 − F OR), whereas the wind power output is zero when the WPGS fails with the unavailability FOR.

3 FOR evaluation of TPGS and WPGS

As seen in Section 2, the FOR of a TPGS or WPGS is needed to calculate the expected tidal or wind power output in their chronological model. As mentioned in Introduction, a TPGS or WPGS includes a power electronic converter in addition to a generator and other components. The mean FOR values of generators and other mechanical or electrical components can be easily estimated from statistical records and do not change over time. However, the failure rates of the power electronic components depend on its voltage, junction temperature and other factors [21, 22]. The junction temperature, as the main factor affecting the failure rate of the power electronic components, is related to its power loss, which is determined by the electric current flowing through the component. The electric current is determined by the power output of the generator unit (wind or tidal), which varies with time. A reliability model of power electronic components associated with junction temperature, power loss and voltage is presented in this section. By calculating the power loss of power electronic components, the junction temperature can be estimated. Therefore, the junction temperature related failure rates of the power electronic component can be estimated.

The back-to-back (BTB) power electronic converter is the most popular converter used in both tidal power and wind power generation system. In this paper, both TPGS and WPGS are based on a fully controllable BTB converter with doubly-fed induction generator (DFIG) configuration.

3.1 Power losses of electronic components

The BTB converter consists of a rotor side converter (RSC) and a grid side converter (GSC) connected with a common DC bus. The RSC is directly connected to the rotor windings of the DFIG and the GSC is directly connected to the power grid through a transformer. The power losses of the BTB converter are the power losses in semiconductor switches (insulated gate bipolar transistors-IGBTs and diodes) and the power flowing through the BTB converter is the rotor power. The power losses of an IGBT or a diode can be divided into conduction loss and switching loss. The calculation of the power losses of an IGBT or a diode can be estimated by [17, 21]

$$\begin{aligned} P_{\text{I}} &= P_{\text{I,con}} + P_{\text{I,sw}} = \frac{1}{2}\left( {U_{\text{ce0}} \frac{I}{\pi } + r_{\text{ce}} \frac{{I^{2} }}{4}} \right) \hfill \\ \text{ } &\,\,\,\,\pm \cos \phi \left( {\frac{{mU_{\text{ce0}} I}}{8} + \frac{{mr_{\text{ce}} I^{2} }}{3\pi }} \right) + \frac{{f_{\text{sw}} U_{\text{DC}} I}}{{\pi U_{\text{ref,I}} I_{\text{ref,I}} }}\left( {E_{\text{on}} + E_{\text{off}} } \right) \hfill \\ \end{aligned}$$
(8)
$$\begin{aligned} P_{\text{D}} &= P_{\text{D,con}} + P_{\text{D,rec}} = \frac{1}{2}\left( {U_{\text{d0}} \frac{I}{\pi } + r_{\text{T}} \frac{{I^{2} }}{4}} \right)\\ \text{ } &\,\,\,\,\pm \cos \phi \left( {U_{\text{d0}} \frac{mI}{8} + r_{\text{T}} \frac{{mI^{2} }}{ 3\pi }} \right) + \frac{{f_{\text{sw}} U_{\text{DC}} IE_{\text{rec}} }}{{\pi U_{\text{ref,D}} I_{\text{ref,D}} }} \hfill \\ \end{aligned}$$
(9)

where P I, P D are the power loss of an IGBT and a diode, respectively; subscripts “con”, “sw”, “rec” represent the conduction, switch and recovery, respectively; subscripts “I”, “D” represent IGBT and diode, respectively; U ce0,U d0 the voltage drops on the IGBT and diode, respectively; r ce, r T the resistances of IGBT and diode, respectively; E on, E off the power losses of an IGBT in its on-state and off-state, respectively; E rec the reverse recovery energy loss of a diode; U DC the DC bus voltage; U ref,I, U ref,D the reference commutation voltage of the IGBT and diode, respectively; I ref,I, I ref,D the reference commutation current of the IGBT and diode, respectively; f sw the switch frequency; m the modulation index; φ the angle between voltage and current; and I the peak phase current at the AC side interface and can be calculated by [17]:

$$I_{\text{rsc}} = \frac{{\sqrt 2 \left| {P_{\text{r}} } \right|}}{{\sqrt 3 U_{\text{rl}} }} = \frac{{\sqrt 2 \left| { - n_{\text{s}} P_{\text{out}} \left( {1 - n_{\text{s}} } \right)} \right|}}{{\sqrt 3 U_{\text{rl}} }}$$
(10)
$$I_{\text{gsc}} = \frac{{\sqrt 2 \left| {P_{\text{r}} } \right|}}{{\sqrt 3 U_{\text{gl}} }} = \frac{{\sqrt 2 \left| { - n_{\text{s}} P_{\text{out}} /\left( {1 - n_{\text{s}} } \right)} \right|}}{{\sqrt 3 U_{\text{rl}} }}$$
(11)

where I rsc, I gsc are the peak phase current through RSC and GSC, respectively; U rl, U gl the rotor line-to-line voltage and grid line-to-line voltage, respectively; n s the slip of the DFIG; and P out the power output of generator unit, which is calculated by (3) or (7) depending on if it a tidal power unit or a wind power unit. It should be noted that (8) and (9) contain ± and ∓, where the upper sign is used when the RSC (or GSC) works as an inverter and the lower sign is used when the RSC (or GSC) works as a rectifier.

3.2 Junction temperature of semiconductor switch

Both the IGBTs and diodes are mounted on a heat sink and dissipate heat to it. Therefore, each module’s junction temperature is the sum of the temperature rise in the interface (\(\Delta\) T ri) and the heat sink temperature (T hs) itself. The junction temperature (T jc) can be calculated by

$$T_{\text{jc}} = T_{\text{hs}} + \Delta T_{\text{ri}}$$
(12)

where

$$\Delta T_{\text{ri}} = P_{\text{I/D}} R_{\text{ji}}$$
(13)
$$T_{\text{hs}} = T_{\text{a}} + n\left( {P_{\text{I}} + P_{\text{D}} } \right)R_{\text{ha}}$$
(14)

where P I/D represents the power loss of an IGBT or a diode, which is calculated using (8) or (9); T a the ambient temperature; n the number of modules mounted on the heat sink; and R ji, R ha the thermal resistances from the junction to the interface case of an IGBT or diode and from the heat sink to the ambient environment, respectively.

3.3 Failure rate of power electronic components

The failure rate of a power electronic component, which takes junction temperature and other factors into consideration, can be estimated by [17, 21].

$$\lambda_{\text{pec}} = \pi_{\text{gr}} \left( {\lambda_{\text{b}} \pi_{\text{odc}} \pi_{\text{ot}} + \lambda_{\text{nb}} \pi_{\text{ndc}} \pi_{\text{nt}} + \lambda_{\text{tcb}} \pi_{\text{tca}} \pi_{\text{dtc}} } \right) + \lambda_{\text{sj}} + \lambda_{\text{eos}}$$
(15)

where λ pec is the predicted failure rate of a power electronic component; λ b, λ nb, λ tcb the operation-related, non-operation-related (environmental) and temperature cycling base failure rate, respectively; λ sj, λ eos the solder joint failure rate contribution and electrical overstress failure rate contribution, respectively; π gr the growth rate factor, which reflects improvements in device manufacturing over time; π odc,π ndc the operation-related and non-operation-related duty cycle factor, respectively; π ot, π nt the operating and non-operating temperature acceleration factor, respectively; π tca, π dtc the temperature cycling rate acceleration factor and temperature cycling delta temperature acceleration factor, respectively; The definitions of all the base failure rates can be found in [23]. It should be emphasized that the parameters π ot, π nt, π tca, π dtc are related to junction temperatures. Their calculation formulas are given in Appendix. More information of the Pi-factors can be found in [17].

3.4 Failure rate of the BTB converter

The BTB converter includes a RSC, a GSC and a DC bus in series. Each RSC or GSC consists of six IGBTs and six diodes. Those components are also in series from a reliability point of view. Therefore, the failure rate of BTB converter can be calculated by

$$\lambda_{\text{BTB}} = 6\left( {\lambda_{\text{I,rsc}} + \lambda_{\text{D,rsc}} } \right) + \lambda_{\text{DC}} + 6\left( {\lambda_{\text{I,gsc}} + \lambda_{\text{D,gsc}} } \right)$$
(16)

where λ BTB is the failure rate of BTB converter; λ I,rsc, λ D,rsc the failure rate of an IGBT and a diode in the RSC, respectively; λ I,gsc, λ D,gsc the failure rate of an IGBT and a diode in the GSC, respectively; and λ DC the failure rate of DC bus. The failure rates of all electronic components can be calculated by using (15).

3.5 FOR calculation of TPGS and WPGS

In a TPGS or WPGS, there are three subsystems: BTB converter, control system and kinetic energy conversion device. The failure rate of the BTB converter is calculated by (16). The kinetic energy conversion device (KECD) consists of blades, driven shaft, gearbox, DFIG generator, transformer and other parts. If any of those components fails, the subsystem fails. Thus, the failure rate of the KECD subsystem is the sum of failure rates of all these components, which can be estimated from historical records. The failure rate of the control subsystem can be also estimated from historical data.

Each subsystem can be repaired by replacing failed components. The repair rate can be assumed to be the reciprocal of the replacement time. The repair rate of a TPGS or WPGS can be approximately estimated by

$$\mu_{\text{ps}} = \frac{{\prod\nolimits_{j = 1}^{n} {\mu_{j} \times \sum\nolimits_{j = 1}^{n} {\lambda_{j} } } }}{{\sum\nolimits_{j = 1}^{n} {\left( {\lambda_{j} \prod\nolimits_{i = 1,i \ne j}^{n} {\mu_{i} } } \right)} }}$$
(17)

where μ j , λ j are the repair and failure rates of subsystem j, respectively; and n the number of subsystem. The forced outage rate (F OR) (or unavailability) of a TPGS or WPGS can be calculated by

$${\text{Unavailability}} = F_{\text{OR}} = \frac{{\lambda_{\text{ps}} }}{{\lambda_{\text{ps}} + \mu_{\text{ps}} }}$$
(18)

where μ ps, λ ps are the repair and failure rates of TPGS or WPGS, respectively.

4 Power output model of BESS

In a power system composed of tidal and wind generations, a BESS is often required to compensate power imbalance in dealing with the random natures of tidal current speeds, wind speeds and loads. This is particularly true for a power system located at a remote coastal area and when it does not have a connection to a power grid. In the normal operating states, the excessive output power from TPGS and WPGS can be charged and stored in a BESS. The stored energy can be discharged from the BESS to avoid or reduce load losses when the total generation capacity of TPGS and WPGS is inadequate. The power that can be given by the system (charged) to a BESS or is needed by the system (discharged) from a BESS in the s th state of the TPGS within the k th time interval can be expressed as follows:

$$\begin{aligned} &P_{{{\text{diff}},s}} (k) \equiv P_{\text{L}} (k) - P_{{{\text{T}},s}} (k) - P_{\text{W}} (k) \hfill \\ &P_{{{\text{bat}},s}} (k) = \left\{ {\begin{array}{*{20}l} {P_{\text{dismax}} } &\quad {P_{{{\text{diff}},s}} (k) \ge P_{\text{dismax}} } \\ {P_{\text{diff,s}} (k)} &\quad {\text{0 < }P_{{{\text{diff}},s}} (k) \le P_{\text{dismax}} } \\ 0 &\quad {P_{{{\text{diff}},s}} (k) = 0} \\ {P_{{{\text{diff}},s}} (k)} &\quad {\text{0} \ge P_{{{\text{diff,}}s}} (k) \ge P_{\text{chamax}} } \hfill \\ {P_{\text{chamax}} } & \quad {P_{{{\text{diff}},s}} (k) \le P_{\text{chamax}} }\\ \end{array} } \right. \\ \end{aligned}$$
(19)

where P L(k) the load power within the k th time interval; P T,s (k) the power output of the TPGS in its s th state within the k th time interval; P W(k) the power output of the WPGS within the k th time interval; and P dismax,P chamax the maximum discharge (represented by a positive number) and charge power (represented by a negative number) of the BESS, respectively.

Eq. (19) includes the limit constraints of maximum discharge and charge power of the BESS. However, the lower and upper limit constraints of the storage capacity of the BESS have not been included in (19) yet. The minimum and maximum energy storage capacity limits Q min and Q max can be converted into the additional equivalent power output constraints within k th time interval. The equivalent discharge power output constraint is defined by:

$$P_{\text{edismax}} \left( k \right) \triangleq \left\{ {\begin{array}{*{20}l} {P_{\text{dismax}} } \hfill & {{\text{if}}\left( {Q_{\text{bat}} \left( k \right) - Q_{ \hbox{min} } } \right)/t \ge P_{\text{dismax}} } \hfill \\ {\left( {Q_{\text{bat}} \left( k \right) - Q_{ \hbox{min} } } \right)/t} \hfill & {{\text{if}}\left( {Q_{\text{bat}} \left( k \right) - Q_{ \hbox{min} } } \right)/t < P_{\text{dismax}} } \hfill \\ \end{array} } \right.$$
(20)

where P edismax(k) is the equivalent discharge power output limit corresponding to the minimum energy storage capacity limit Q min in the k th interval; Q bat(k) the stored energy in the k th interval; and t the length of the time interval k. The equivalent charge power output constraint is defined by:

$$P_{\text{echmax}} \left( k \right) \triangleq \left\{ {\begin{array}{*{20}l} {P_{\text{chmax}} } \hfill & {{\text{if}}\left( {Q_{ \hbox{max} } - Q_{\text{bat}} \left( k \right)} \right)/t \ge \left| {P_{\text{chmax}} } \right|} \hfill \\ {\left( {Q_{\text{bat}} \left( k \right) - Q_{ \hbox{max} } } \right)/t} \hfill & {{\text{if}}\left( {Q_{ \hbox{max} } - Q_{\text{bat}} \left( k \right)} \right)/t < \left| {P_{\text{chmax}} } \right|} \hfill \\ \end{array} } \right.$$
(21)

where P echmax(k) is the equivalent charge power output limit corresponding to the maximum energy storage capacity limit Q max in the k th interval. Note that like P chmax(k), P echmax(k) is also a negative value, which indicates the charging mode.

P bat,s (k) calculated in (19) is the power that can be potentially given by the system (charged) to the BESS or is needed by the system (discharged) from the BESS in the s th state of the TPGS within the k th time interval. The actual discharge or charge power must be constrained by (20) or (21) corresponding to energy storage capacity limits. In other words, the actual discharge power of the BESS should be the lesser between P bat,s (k) > 0 and P edismax(k). Similarly, the actual charge power of the BESS should be the larger one between P bat,s (k) < 0 and P echmax(k), where the larger one represents a smaller absolute value since both P bat,s (k) and P echmax(k) are negative values in the charging mode of the BESS. The above ideas can be expressed mathematically as follows:

$$P_{{{\text{bout}},s}} (k) = \left\{ {\begin{array}{*{20}l} {\hbox{min} \left\{ {P_{{{\text{bat}},s}} (k),P_{\text{edismax}} (k)} \right\}} \hfill & {{\text{if}}\;P_{{{\text{bat,}}s}} (k) \ge 0} \hfill \\ {\hbox{max} \left\{ {P_{{{\text{bat}},s}} (k),P_{\text{echmax}} (k)} \right\}} \hfill & {{\text{if}}\;P_{{{\text{bat,}}s}} (k) < 0} \hfill \\ \end{array} } \right.$$
(22)

The actual discharge or charge power in the s th state of the TPGS within the k th interval can be calculated in two cases when the WPGS is in service and out-of-service, respectively. Therefore, the average charge/discharge power P bout(k) of the BESS within the k th time interval can be calculated by

$$P_{\text{bout}} (k) = \sum\limits_{s = 1}^{7} {\left[ {P_{{{\text{bout}},s}} (k) \times p_{s} (k) + P^{\prime}_{{{\text{bout}},s}} (k) \times p^{\prime}_{s} (k)} \right]}$$
(23)

where P bout,s (k), \(P^{\prime}_{{{\text{bout}},s}} (k)\) are the actual discharge or charge power in the s th state of the TPGS within the k th interval when the WPGS is in service and out-of-service, respectively; \(p_{s} (k)\) is equal to the probability of the k th state of the TPGS multiplied by the availability of the WPGS, whereas \(p^{\prime}_{s} (k)\) is equal to the probability of the k th state of the TPGS multiplied by the unavailability of the WPGS; P bout(k) > 0 means that the BESS is delivering power to the system and can be treated as a generator; P bout(k) = 0 means the BESS is in its standby mode; P bout(k) < 0 means that the BESS is being charged from the system and can be treated as a load.

The stored energy of the BESS in the next (k + 1) interval can be calculated by:

$$Q_{\text{bat}} (k + 1 )= Q_{\text{bat}} (k) - P_{\text{bout}} (k)t$$
(24)

where t is the length of the time interval k and is often considered to be one hour.

5 Reliability indices

The following two reliability indices are used in the paper: loss of load expectation (LOLE) and expected energy not supplied (EENS).

5.1 Loss of load expectation index

In any state of the TPGS within the k th interval, if the total load is larger than the total generation output of both TPGS and WPGS, i.e., P diff,s (k) > 0, then the BESS is running in the discharge mode. However, the actual discharged power from the BESS may not cover the power shortage P diff,s (k) > 0. In this situation, a load curtailment occurs. Note that the load curtailments are calculated in different combinations of events when the WPGS is in service and out-of-service and when the BESS is available and unavailable. The loss of load expectation index (LOLE) is defined as the expected duration within a certain period of time (such as 1 year) over which the load demand exceeds the total generated power [18]. Mathematically, the LOLE (I LOLE) for the model presented in the paper can be expressed by:

$$I_{\text{LOLE}} = \sum\limits_{k = 1}^{8760} {\sum\limits_{s = 1}^{7} {\left[ \begin{aligned} &p_{{{\text{bu}},s}} (k) \times A_{\text{B}} + \\ &p^{\prime}_{{{\text{bu}},s}} (k) \times A_{\text{B}} + \\ &p_{{{\text{bd}},s}} (k) \times (1 - A_{\text{B}} )+ \\ &p^{\prime}_{{{\text{bd}},s}} (k) \times (1 - A_{\text{B}} )\\ \end{aligned} \right]} }$$
(25)

where p bu,s (k), p bd,s (k) are the probabilities of load curtailments in the s th state of the TPGS within the k th time interval when the WPGS is in service and when the BESS is available and unavailable, respectively, whereas \(p^{\prime}_{{{\text{bu}},s}} (k)\) and \(p^{\prime}_{{{\text{bd}},s}} (k)\) are the probabilities of load curtailments in the s th state of the TPGS within the k th time interval when the WPGS is out-of-service and when the BESS is available and unavailable, respectively; and A B the availability of the battery energy storage system.

5.2 Expected energy not supplied index

The expected energy not supplied (EENS, represents by I EENS)) can be calculated by

$$I_{\text{EENS}} = \sum\limits_{k = 1}^{8760} {\left( {\sum\limits_{s = 1}^{7} {\left( \begin{aligned} &C_{{{\text{BU}},s}} \left( k \right) \times p_{{{\text{bu}},s}} \left( k \right) \times A_{\text{B}} +\\ &C_{{{\text{BU}},s}}^{{\prime }} \left( k \right) \times p_{{{\text{bu}},s}}^{{\prime }} \left( k \right) \times A_{\text{B}} +\\ &C_{{{\text{BD}},s}} \left( k \right) \times p_{{{\text{bd}},s}} \left( k \right) \times \left( {1 - A_{\text{B}} } \right) + \\ &C_{{{\text{BD}},s}}^{{\prime }} \left( k \right) \times p_{{{\text{bd}},s}}^{{\prime }} \left( k \right) \times \left( {1 - A_{\text{B}} } \right)\\ \end{aligned} \right)} } \right)} \times t$$
(26)

where C BU,s (k), C BD,s (k) are the load curtailments in the s th state of the TPGS within the k th time interval when the WPGS is in service and when the BESS is available and unavailable, respectively; p bu,s (k), p bd,s (k) the corresponding probabilities of load curtailment as defined in (25); \(C^{\prime}_{{{\text{BU}},s}} (k)\), \(C_{{{\text{BD}},s}} (k)\) the load curtailments in the s th state of the TPGS within the k th time interval when the WPGS system is out of service and when the BESS is available and unavailable, respectively; and \(p^{\prime}_{{{\text{bu,}}s}} (k)\), \(p^{\prime}_{{{\text{bd,}}s}} (k)\) the corresponding probabilities of load curtailment as defined in (25).

6 Case studies

6.1 System and data sources

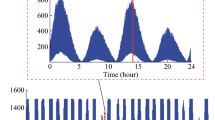
It was assumed that the studied power system is a remote local area and consists of a tidal power generation system (TPGS), a wind power generation system (WPGS) and a battery energy storage system (BESS) with an aggregated annual load curve. Both the TPGS and WPGS are based on a DFIG configuration, in which the stator windings are directly connected to a power grid through a transformer and the rotor windings are connected to the grid via a bidirectional BTB converter and a transformer. The rated power output of the TPGS (P T,rate) is 1.5 MW and its cut-in and rated tidal current speeds are 1.2 and 3.5 knots, respectively. The rated power output of the WPGS (P W,rate) is 1 MW. The cut-in, rated and cut out wind speeds are 4, 12 and 25 m/s, respectively. The IGBT and diode modules are those from the ABB Hipack (5SNA 1800E170100) and all the parameters used in (8), (9) and (12)-(14) can be found in the data sheets of the ABB website [22, 24]. The tidal current speeds used in this paper were obtained from the National Ocean Service (NOS) of National Oceanic and Atmospheric Administration (NOAA) in the USA. The site is located at Golden Gate Bridge, the west coast of North America. The four years’ tidal current speed data in 2011-2014 at 10 minutes intervals (6 data per hour) were used in this paper. A tidal power output curve for one week (Jan. 01–07, 2011) is shown in Figure 2. It can be seen from Fig. 2 that the tidal power generator has four power output periods per day (regularity) and the power outputs are different at the same time of different days (randomness). The wind speeds used in this paper were obtained from the Iowa Environmental Mesonet (IEM) [25], which collects environmental data from cooperating members with observing networks. The wind speed data around the Golden Gate Bridge can be found from the website [25]. The four years’ wind speed data in 2011–2014 at one-hour interval (24 data per day) were used in this paper. The shape of the annual load curve is represented by the IEEE-RTS load model, which demonstrates the seasonal behaviors of load changes.

Fig. 2
figure 2

Tidal power output curve from 01, Jan. to 07, Jan. 2011

Full size image

6.2 Reliability parameters and basic reliability indices

By using the actual tidal current speed data, the parameters for 96 groups of Wakeby distributions were estimated. Using (4) and Table 1, the 7-state model of the TPGS was constructed. The parameters of the ARMA model for the WPSG were estimated by using the actual wind speed data and its order was identified as ARMA (3, 2) using an ARMA parameter recognition method. The time series power output model of the WPGS was established using (7). The tidal power output curve is shown in Figure 2. The failure rates of the BTB converter and the FORs of the TPGS and WPGS were obtained by using the proposed models. The repair times of the BTB converter and KECD in the TPGS were assumed to be 192 and 240 hours per repair, respectively. The repair times of the BTB converter and KECD in the WPGS were assumed to be 120 and 200 hours per repair, respectively. The control subsystem was assumed to be 100% reliable. The failure rates of each power generation system component are summarized in Table 2. In Table 2, BD, SH, GB, TS and GE represent blades, shaft, gearbox, transformer and generator, respectively. The λ ps represents the total failure rate of the entire power generation system. Note that the failure rates of RSC, DC, GSC, λ ps and F OR listed in Table 2 are the annual average values. These parameters are different from one state of the TPGS to another in each hour depending on the power output of TPGS and WPGS in each state in each hour. The parameters of the BESS are as follows: P dismax = 600 kW, P chamax = −600 kW, Q max = 1800 kWh, Q min = 0.1Q max, A B = 0.99. The yearly peak load P max is assumed to be 600 kW. The basic reliability indices of the studied system are calculated using the proposed method and summarized in Table 3. Note that in Table 3, the units of I LOLE and I EENS in each season are hours/season and kWh/season, respectively, whereas the units of I LOLE and I EENS in the last column (yearly) are hours/year and kWh/year, respectively.

Table 2 Average failure rates (failures/year) and FOR of the TPGS and WPGS
Full size table
Table 3 Reliability indices of the studied system
Full size table

It can be seen in Table 3 that the reliability indices of the studied hybrid power system are the lowest in spring, higher in summer and fall, and the highest in winter. This is not a general conclusion but specific to the studied system since it depends on the composition of random behaviors of wind and tidal speeds.

6.3 Effects of the installed capacity ratio of TPGS and WPGS on the system EENS index

The TPGS and WPGS are the generation power sources in the studied system, whereas the BESS stores energy when the generation capacity exceeds the load demand and delivers power to the system when the generation capacity is inadequate. The wind speed and tidal current speed behave differently in randomness and intermittence. The installed capacity ratio of the TPGS and WPGS has a significant impact on the reliability indices of the studied hybrid generation system. In this section, the total generation capacity (2.5 MW), the parameters of the BESS (the capacity and other parameters) and the load profile (the annual peak and load curve shape) remain same as those in the basic case in Section 6.2 but the installed capacity ratio of the TPGS and WPGS varies. The EENS indices for different installed capacity ratios of the TPGS and WPGS are plotted in Fig. 3. It can be seen from Fig. 3 that the EENS basically remains unchanged after the ratio is larger than 1.38, whereas it dramatically jumps when the ratio is smaller than 1.38. This suggests that the effects of increased tidal generation capacity and decreased wind generation capacity by the same amount are offset after their ratio is beyond 1.38. On the other hand, once the ratio is smaller than 1.38, the negative effect due to the decreased tidal generation capacity dramatically exceeds the positive effect due to the increased wind generation capacity by the same amount. Therefore, the ratio 1.38 of the TPGS and WPGS is a critical point to keep the hybrid system reliability level. In other words, the tidal generation capacity should not be lower than 1.45 MW, which corresponds to this critical point if the total capacity of the TPGS and WPGS is kept at 2.5 MW. This is very useful information for selecting relative tidal and wind generation capacities in the hybrid generation system.

Fig. 3
figure 3

EENS index for different installed capacity ratios of the TPGS and WPGS

Full size image

6.4 Effects of variation in the installed capacity of TPGS or WPGS on the system EENS index

In Section 6.3, the effect of generation capacity ratio of the TPGS and WPGS on the EENS index was investigated under the condition the total generation capacity remains unchanged. In this section, the effect of increasing either tidal or wind generation capacity on the EENS index is investigated by assuming that all other parameters (the wind or tidal generation capacity, the parameters of the BESS and the load profile) are the same as those in the basic case in Section 6.2. In the first scenario, only the installed capacity of the TPGS is increased from 1.5 MW (the original value in the basic case) to 2 MW, whereas in the second scenario, only the installed capacity of the WPGS is increased from 1 MW (the original value in the basic case) to 1.5 MW. The EENS index against the increased installed capacity of the TPGS or WPGS is plotted in Fig. 4.

Fig. 4
figure 4

EENS index against the increased installed capacity of TPGS or WPGS

Full size image

It can be seen from the Fig. 4 that the EENS index decreases as the installed capacity of the TPGS or WPGS increases. However, the impact of increasing installed capacity of the TPGS is larger than that of increasing installed capacity of the WPGS. The difference becomes more significant as the increased installed capacity is larger. It is reasonable to judge that the reliability of the hybrid generation system is more sensitive to the TPGS than the WPGS. This is because the power system can obtain more power from the TPGS than the WPGS on the average when they have the same increased installed capacity since in general, tidal power has less randomness than wind power.

6.5 Effects of the maximum charge/discharge power of the BESS on the system EENS index

In order to investigate the effects of the maximum charge/discharge power of the BESS on the EENS index, either the maximum charge power is changed from −400 to −800 kW or the discharge power is changed from 400 to 800 kW. Note the negative sign represents the charging mode. All other parameters of the BESS remain unchanged. The variations of EENS index with the maximum charge or discharge power of the BESS are plotted in Figs. 5 and 6, respectively. It can be seen from Figs. 5 and 6 that the EENS index dramatically decreases as the maximum charge or discharge power increases from 400 to 500 kW. However, the EENS index almost remains unchanged after the maximum charge or discharge power reaches 500 or 550 kW and beyond. This phenomenon can be explained as follows. A higher maximum charge power ensures that more electric energy can be stored in the BESS, which is needed to deliver later when the system generation is inadequate. A higher maximum discharge power represents that the stored energy can be more and faster drawn from the BESS when the load demand exceeds the system generation. Therefore, in general, increasing the maximum charge or discharge power of the BESS can improve the reliability of the hybrid power system with tidal and wind generations. However, this effect is limited at and beyond a critical point. Such a critical point is different for different systems, depending on the balance degree between the total tidal and wind generation capacity and the system load profile. This critical point is 550 kW in the studied system, indicating that 550~600 kW should be selected as the maximum charge/discharge capacity of the BESS. A higher maximum charge/discharge capacity will not lead to any further improvement in the system reliability but requires higher costs, whereas a lower maximum charge/discharge capacity will result in quickly-increasing system risks.

Fig. 5
figure 5

EENS index against the maximum charge power of the BESS

Full size image
Fig. 6
figure 6

EENS index against the maximum discharge power of the BESS

Full size image

7 Conclusions

A reliability evaluation method for hybrid tidal and wind power systems with battery energy storage is presented. Such hybrid systems with co-existence of both tidal and wind energy sources may most likely occur in coastal areas or islands. A chronological multiple state probability model of tidal power generation system (TPGS) is developed. In this model, both force outage rate (FOR) of TPGS and random nature of tidal current speed are considered. A TPGS or WPGS (wind power generation system) includes a power electronic converter in which the failure rates of electronic components are sensitive to their junction temperatures, whereas the junction temperatures depend on delivered powers of a TPGS or WPGS. The delivered power state related failure rates of the power electronic converters are incorporated into the evaluation of the FORs of TPGS and WPGS. In addition, a chronological power output model of battery energy storage system (BESS) is derived and its failure probability is considered.

The proposed method was applied to a hybrid generation system of tidal and wind powers with BESS. The seasonal and annual reliability indices are evaluated. The studied system has different reliability levels in different seasons. Various sensitivity studies are conducted. These include the effects on the EENS index of the installed capacity ratio of the TPGS and WPGS, variations of installed capacity of the TPGS or WPGS and maximum charge or discharge capacity of the BESS. The results indicated that there exists a critical turning point for the effects of all these parameters on the studied hybrid generation system reliability. When a parameter exceeds the critical turning point, the effect becomes weak or disappearing. In general, the values of the critical points are varied for different system compositions. Identifying the critical point values is important for selecting the installed capacity ratio of TPGS and WPGS, their installed capacities, maximum charge or discharge capacity of BESS and other parameters in the design of a power system with hybrid tidal and wind generation sources and battery storage.