1 Introduction

Distributed inverters have been widely implemented in many applications, such as photovoltaic (PV) plant, wind plant and microgrid, to connect distributed sources to the power grid [1–5], where distributed inverters are generally controlled by pulse width modulation (PWM) methods. For three-phase inverters, sinusoidal pulse width modulation (SPWM) with the triplen harmonic added and the space vector pulse width modulation (SVPWM) can effectively increase the maximum modulation index to 1.15 [6–8]. Compared with SPWM, the discontinuous pulse width modulation (DPWM) can clamp the associated phase to the positive or negative DC rail, and then significantly reduce the switching losses [9–13]. But DPWM will introduce more high frequency harmonics than SPWM. Ref. [12] presented that when DPWM and SPWM produce the same switching losses by increasing the switching frequency of DPWM, the total harmonic distortion (THD) of DPWM is still larger than that of SPWM when the modulation index is low.

To reduce the high frequency harmonics, LC, LCL or other high order filters can be employed [14–16]. However, LC or LCL resonance peak will decline the inverter performance. Active or passive damping method can be employed to eliminate the resonance peak. But these methods will increase the complexity of the control system. What’s more, the high order filter may bring serious resonance problems when many distributed inverters are connected to PCC [17]. Alternatively, the interleaved PWM can reduce the high frequency harmonics [18]. But it cannot be directly applied to multiple distributed inverters because they are not connected in parallel at the DC side.

Reference [19] proposed the global synchronous pulse width modulation (GSPWM) method, where global synchronous unit (GSU) was employed to realize the basic functions of GSPWM and the high frequency harmonics can be eliminated at PCC. Ref. [20] proposed the method to reduce the switching frequency and the filter size when using GSPWM. When calculating the harmonics of inverters controlled by DPWM, GSPWM will cost much time to calculate the harmonics of discontinuous modulation waveforms. And it is hard to implement these complicated calculations in digital signal processor (DSP) or other digital controllers. Besides, the conventional GSPWM method adopts a particle swarm optimization (PSO) method with many particles and iteration steps to find the optimal phase shift angles and the synchronization frequency. Together with the harmonic calculation procedure, it will definitely increase the operation burden of GSU.

This paper therefore proposes a new method to fast calculate the high frequency harmonics of three-phase inverters when the modulation waveforms are discontinuous. Then, a new processing method to fast calculate the important optimal phase shift angles and the frequency of sending synchronization signals is introduced. Finally, MATLAB simulations and experimental results verify the performance of the proposed method.

2 Basic principle of three-phase PWM

For the three-phase three-wire inverters, any zero-sequence signal can be injected into the modulation [9]. There are 6 kinds of DPWMs generated by adopting different zero-sequence components, which are DPWM0, DWPM1, DPWM2, DPWM3, DPWMMIN, and DPWMMAX [9, 10, 13]. In general, the modulation reference values can be listed as

$$u_{s}^{*} = u_{s} + u_{0} \quad s = {\text{a,b,c}}$$
(1)
$$u_{\text{a}} = D\sin (\omega t)$$
(2)

where u s is the modulation reference value of SPWM; \(u_{s}^{*}\) the modulation reference value of DPWM; u 0 the zero-sequence component; and D the modulation index.

Figure 1 shows the normalized waveforms of u a, \(u_{\text{a}}^{*}\), u 0 for 6 kinds of DPWM methods when D = 0.9. The main difference among these DPWM methods is u 0 [9, 10].

Fig. 1
figure 1

DPWM modulation waveforms of phase a when D = 0.9

Full size image

In addition, the modulation waveform of triplen harmonic PWM consists of both fundamental component and a third-harmonic component [12, 13] as shown in Fig. 2. Given that the modulation waveforms of these modulation methods are discontinuous or non-sinusoidal, the piecewise integration can be employed to calculate the high frequency harmonics [13]. And the only difference is the outer and inner double Fourier integral limits. So DPWMMIN is taken as an example in the following analysis and verification.

Fig. 2
figure 2

Modulation waveforms of phase a for the triplen harmonic PWM

Full size image

3 Principles and realization of global synchronous discontinuous pulse width modulation (GSDPWM)

When three-phase inverters are connected in parallel, the THD of total current will change periodically as same as that analyzed in [19]. For simplicity, this subsection takes two identical three-phase inverters as an example for analysis, and their parameters are listed in Table 1. MATLAB is used to simulate this phenomenon. Assuming the frequency of these two inverters are 10.0001 kHz and 9.9999 kHz due to the unavoidably variable oscillation frequency of crystal inside the digital controller and DPWMMIN is employed, Fig. 3 shows the THD trajectories of currents in 5 s. It is obvious that the THD of total current changes with time progresses and the minimal THD only appears once. Therefore, it is superior to fix the THD of total current to be as small as possible during the operation. GSU and the corresponding carrier phase angle adjustment method can be employed to achieve this objective [19], whose basic structure is shown in Fig. 4.

Table 1 Parameters of two inverters
Full size table
Fig. 3
figure 3

THD trajectories of the three-phase total currents and output currents of two inverters in 5 s

Full size image
Fig. 4
figure 4

Basic structure of GSDPWM

Full size image

The primary functions of GSU are to:

  1. 1)

    receive parameters and the PWM type of each inverter, and calculate the high frequency harmonics of total current by using the proposed fast calculation method;

  2. 2)

    calculate φ PWMMbest and f syn with the fast intelligent method. Where φ PWMMbest is the optimal phase shift angle and f syn is the sending frequency of synchronous signals.

However, DPWM will produce different harmonic characteristics compared with SPWM. Therefore, next section will discuss the fast calculation methods for realizing the expected synchronous operation of three-phase inverters.

4 Fast calculation method of current harmonics

This section proposes a new method to fast calculate the high frequency harmonics of three-phase inverters. A look-up table is developed to help fast calculate the voltage harmonics of each inverter, and then a simplified equivalent harmonic circuit is proposed to calculate current harmonics of the three-phase inverter. Doing so, the total current harmonics can be further derived to get the relationships between total current harmonics and the phase shift angle of each inverter. The current harmonics of three-phase inverter can be analyzed by using the double Fourier method. Assuming u a *, u b * and u c * are symmetrical under steady state, only a few parts of harmonics in u a * need to be calculated. Specifically, since the phase shift angle of φ PWMM generates the equal effect on three-phase currents, it is reasonable to only calculate the current harmonics of one phase. The calculation method of total current harmonics will be presented below.

4.1 Voltage harmonic calculation

Figure 5a shows the general illustration of three-phase inverter M, where u Ma, u Mb and u Mc are the three-phase output voltages; and Z M refers to the output filter impedance of inverter M. Assuming the grid voltage is purely sinusoidal, the equivalent circuit harmonics can be drawn as Fig. 5b, where u hMa, u hMb and u hMc are the voltage harmonics of u Ma, u Mb, u Mc, respectively.

Fig. 5
figure 5

Illustration of three-phase inverter M

Full size image

By using the double Fourier method [13], voltage harmonics can be expressed as:

$$\begin{aligned} u_{{{\text{h}}Ms}} &= \sum\limits_{m = 1}^{\infty } {\Big[A_{m0}\,{\text{cos}}(m(\omega_{\text{c}} t + \varphi_{{{\text{PWM}}M}} ))} \\ &\quad+\, B_{m0}\,{\text{sin}}(m(\omega_{\text{c}} t + \varphi_{{{\text{PWM}}M}} ))\Big] \\ &\quad+\, \sum\limits_{m = 1}^{\infty } {\sum\limits_{\begin{subarray}{l} n = - \infty \\ (n \ne 0) \end{subarray} }^{\infty } {\Big[A_{mn}\,{\text{cos}}(m(\omega_{\text{c}} t + \varphi_{{{\text{PWM}}M}} )} } \\ &\quad +\, n(\omega_{0} t + \theta_{s} + \theta_{0} )) + B_{mn}\,{\text{sin}} (m(\omega_{\text{c}} t \\ &\quad+\, \varphi_{{{\text{PWM}}M}} ) + n(\omega_{0} t + \theta_{s} + \theta_{0} ))\Big] \\ s &= {\text{a}}:\theta_{s} = 0; \, s = {\text{b}}:\theta_{s} = - \frac{ 2\uppi }{3}; \, s = {\text{c}}:\theta_{s} = - \frac{ 4\uppi }{3} \\ \end{aligned}$$
(3)

where m and n are the carrier multiple index and the fundamental multiple index, respectively; A m0 and B m0 the parameters of carrier multiple harmonics; A mn and B mn the parameters of sideband harmonics.

Compared with SPWM, the modulation reference values of DPWM are discontinuous. So the piecewise integration method is employed here. For DPWMMIN type:

$$A_{mn} + {\text{j}}B_{mn} = \frac{1}{{2\uppi^{2} }}\sum\limits_{i = 1}^{4} {\int_{{y_{1} \left( i \right)}}^{{y_{2} \left( i \right)}} {\int_{{x_{1} \left( i \right)}}^{{x_{2} \left( i \right)}} {2V_{\text{dc}} \exp ({\text{j}}(mx + ny))} } } {\text{d}}x{\text{d}}y$$
(4)

where i is the number of each piece; x 1(i), x 2(i), y 1(i), and y 2(i) are the inner or outer integral limits which are listed in Table 2.

Table 2 Outer and inner integral limit for DPWMMIN
Full size table

Equation (3) can also be expressed as

$$u_{{{\text{h}}Ms}} = \mathop \sum \limits_{{f = f_{1M} + 1}}^{\infty } u_{{{\text{h}}Mfs}} \quad s = {\text{a,b,c}}$$
(5)

u hMo is the voltage harmonics of point o in Fig. 5b.

$$u_{{{\text{h}}Mo}} = \frac{{u_{{{\text{h}}M{\text{a}}}} + u_{{{\text{h}}M{\text{b}}}} + u_{{{\text{h}}M{\text{c}}}} }}{3}$$
(6)

u hMo can also be expressed as

$$u_{{\text{h}}Mo} = \mathop \sum \limits_{{f = f_{1M} + 1}}^{\infty } u_{{\text{h}}Mfo}$$
(7)

The voltage across Z M of phase a is

$$\Delta u_{{{\text{h}}M{\text{a}}}} = u_{{{\text{h}}M{\text{a}}}} - u_{{{\text{h}}Mo}} = u_{{{\text{h}}M{\text{a}}}} - \frac{{u_{{{\text{h}}M{\text{a}}}} + u_{{{\text{h}}M{\text{b}}}} + u_{{{\text{h}}M{\text{c}}}} }}{3}$$
(8)

According to (3) and (8), ∆u hMa can be expressed as

$$\begin{aligned} \Delta u_{{{\text{h}}M{\text{a}}}} & = u_{{{\text{h}}M{\text{a}}}} - u_{{{\text{h}}Mn}} \\ &= \sum\limits_{m = 1}^{\infty } {\Big[A_{m0} \,{\text{cos}}(m(\omega_{\text{c}} t + \varphi_{{{\text{PWM}}M}} ))} \\ & \qquad \quad +\, B_{m0}\,{\text{sin}}(m(\omega_{\text{c}} t + \varphi_{{{\text{PWM}}M}} ))\Big] \\ & \quad + \sum\limits_{m = 1}^{\infty } {\sum\limits_{\begin{subarray}{l} n = - \infty \\ (n \ne 0) \end{subarray} }^{\infty } {\Big[A_{mn}\,{\text{cos}}(m(\omega_{\text{c}} t + \varphi_{{{\text{PWM}}M}} )} } \\ & \qquad \qquad \qquad +\, n(\omega_{0} t + \theta_{s} + \theta_{0} )) + B_{mn}\,{\text{sin}} (m(\omega_{\text{c}} t + \varphi_{{{\text{PWM}}M}} ) \\ & \qquad \qquad \qquad +\,n(\omega_{0} t + \theta_{s} + \theta_{0} ))\Big] \quad n \ne 3,6,9 \ldots \\ \end{aligned}$$
(9)

Equation (9) explains that ∆u hMa can be calculated from (3). ∆u hMa can also be expressed as

$$\Delta u_{{{\text{h}}M{\text{a}}}} = \mathop \sum \limits_{{f = f_{1M} + 1}}^{\infty } \Delta u_{{{\text{h}}Mf{\text{a}}}}$$
(10)

It is impractical to calculate all harmonics in (9), so only the dominant high frequency harmonics are taken into consideration. In this paper, only harmonics with following multiple indices and fundamental multiple indices are involved in calculation: m = 1 (n = 0,1,2,4,5), m = 2 (n = 0,1,2,4,5). Even so, it still costs much time to calculate A mn and B mn . For easily calculating the current harmonics, C mn can be defined as (11), which is a complex value.

$$\left\{ {\begin{array}{*{20}l} {C_{{mn}} = \frac{{A_{{mn}} + {\text{j}}B_{{mn}} }}{{V_{{{\text{dc}}}} }}} \\ {{\text{ }}A_{{mn}} + {\text{j}}B_{{mn}} = C_{{mn}} V_{{{\text{dc}}}} } \\ \end{array} } \right.$$
(11)

Since A mn and B mn are the functions of modulation index D and V dc, the look-up table method can be employed to calculate C mn according to D. Then, A mn and B mn can be calculated with C mn and V dc. D ranges from 0 to 1.15 for DPWMMIN. The step resolution of D is 0.01 in the look-up table. So, the size of the table is 115 × 10. Table 3 shows an example of the look-up table. Then, ∆u hMfa can be calculated according to C mn in the look-up table. The look-up tables of other modulation methods can also be developed by using the above method.

Table 3 Example of the look-up table
Full size table

4.2 Calculation of current harmonics

Figure 5c shows the equivalent circuit for harmonic with frequency f, where the phasor can be employed to calculate the harmonic current with the specific frequency f of phase a in inverter M:

$$\dot{I}_{{{\text{h}}Mf{\text{a}}}} = \frac{{\Delta \dot{U}_{{{\text{h}}Mf{\text{a}}}} }}{{Z_{Mf} }}$$
(12)

Then, the total current harmonic with frequency f can be derived as:

$$\begin{aligned} \dot{I}_{{{\text{hsum}}f{\text{a}}}} =\,& I_{{{\text{hsum}}f{\text{a}}}} \exp ({\text{j}}\varphi_{{{\text{hsum}}f{\text{a}}}} ) = \mathop \sum \limits_{M = 1}^{N} I_{{{\text{h}}Mf{\text{a}}}} \exp ({\text{j}}\varphi_{{i{\text{h}}Mf{\text{a}}}} ) \\ = & \mathop \sum \limits_{M = 1}^{N} I_{{{\text{h}}Mf{\text{a}}}} \exp ({\text{j}}\varPhi_{{i{\text{h}}Mf{\text{a}}}} (\varphi_{{{\text{PWM}}M}} )) \\ =\,& W_{f} (\varphi_{{{\text{PWM}}1}} ,\varphi_{\text{PWM2}} , \ldots ,\varphi_{{{\text{PWM}}N}} ) \\ \end{aligned}$$
(13)

The amplitude and phase angle are

$$I_{{{\text{hsum}}f{\text{a}}}} = \left| {W_{f} } \right| = W_{1f} \left( {\varphi_{{{\text{PWM}}1}} ,\varphi_{\text{PWM2}} , \ldots ,\varphi_{{{\text{PWM}}N}} } \right)$$
(14)
$$\varphi_{{{\text{hsum}}f{\text{a}}}} = {\text{angle(}}W_{f} ) = W_{2f} \left( {\varphi_{{{\text{PWM}}1}} ,\varphi_{\text{PWM2}} , \ldots ,\varphi_{{{\text{PWM}}N}} } \right)$$
(15)

where W f , W 1f and W 2f are functions of φ PWMM .

The purpose of this section is to get the relationship between phase shift angle of φ PWMM and the total harmonic current of phase a:

$$I_{\text{hsuma}} = \sqrt {\mathop \sum \limits_{{f = f_{1M} + 1}}^{\infty } I_{{{\text{hsum}}f{\text{a}}}}^{2} } = F\left( {\varphi_{{{\text{PWM}}1}} ,\varphi_{\text{PWM2}} , \ldots ,\varphi_{{{\text{PWM}}N}} } \right)$$
(16)

where F is the function of φ PWMM .

So, the THD of total current is

$$H_{\text{suma}} = \sqrt {\frac{{I_{\text{hsuma}}^{2} }}{{I_{{1{\text{suma}}}}^{2} }}}$$
(17)

where I 1suma is the root mean square (RMS) value of total fundamental current of phase a, which can be written as

$$I_{{1{\text{suma}}}} = \sqrt {\mathop \sum \limits_{M = 1}^{N} I_{{1M{\text{a}}}}^{2} }$$
(18)

where I 1Ma is the RMS value of output fundamental current of inverter M.

5 Fast intelligent method to calculate φ PWMMbest and f synmin

Reference [19] has proposed a PSO method to calculate φ PWMMbest and f synmin. But it costs too much time because the initial positions of particles are random. Given that the DC-link voltage and power factor of distributed inverters will not change rapidly, the difference between two adjacent calculation results is almost invariable. This section therefore proposes a fast intelligent method to calculate φ PWMMbest and f synmin. In detail, when calculating φ PWMMbest in every iteration process, the initial position of each particle is set as φ PWMMbest of the last iteration. But when calculating f synmin at the first iteration process, the intermediate calculation results of φ PWMMbest can be employed to choose the initial value of f synmin unlike that in [19], and then the initial f syn during every iteration is set as the obtained value of the last calculation. Doing so, the calculation speed can be improved up to 5 to 10 times due to the first initial value of f syn is not far from the final result of f synmin.

5.1 Calculation of φ PWMMbest

To calculate φ PWMMbest, Eq. (16) should be minimized as (19), which is actually an optimization problem.

$$\left\{ {\begin{array}{*{20}c} {\hbox{min} } & {I_{\text{hsuma}} = F(\varphi_{\text{PWM1}} ,\varphi_{\text{PWM2}} , \ldots ,\varphi_{\text{PWM}N} )} \\ {{\text{s}} . {\text{t}} .} & {0^{ \circ } < \varphi_{\text{PWM}M} < 360^{ \circ } \quad M = 1,2, \ldots ,N} \\ \end{array} } \right.$$
(19)

This paper adopts the PSO method [21, 22] to solve (19). Specifically, the optimization method should initialize the position and the velocity of each particle and then find the optimal phase shift angle. Two parts of calculating φ PWMMbest are elaborated in the following.

5.1.1 Part A

For the first calculation of φ PWMMbest, the initial position and the velocity of particle x are defined as φ x (0) and v x (0) (x = 1, 2,…, X max), respectively. φ x (0) and v x (0) could be derived as (20) and (21), respectively.

$$\left\{ \begin{aligned} & \varvec{\varphi }_{x} \left( 0 \right) = \left[ {\varphi_{{{\text{PWM}}1x}} \left( 0 \right),\varphi_{{{\text{PWM}}2x}} \left( 0 \right), \ldots ,\varphi_{{{\text{PWM}}Nx}} \left( 0 \right)} \right] \\ & \varphi_{{{\text{PWM}}1x}} \left( 0 \right) = 0 \\ & \varphi_{{{\text{PWM}}Mx}} \left( 0 \right) = {\text{rand}}\left( {\left[ {0^\circ ,360^\circ } \right]} \right) \quad M = 2, 3, \ldots ,N \\ \end{aligned} \right.$$
(20)
$$\left\{ \begin{aligned} & \varvec{v}_{x} \left( 0 \right) = \left[ {v_{{{\text{PWM}}1x}} \left( 0 \right),v_{{{\text{PWM}}2x}} \left( 0 \right), \ldots ,v_{{{\text{PWM}}Nx}} \left( 0 \right)} \right] \\ & v_{{{\text{PWM}}1x}} \left( 0 \right) = 0 \\ & v_{{{\text{PWM}}Mx}} \left( 0 \right) = v_{ \hbox{max} } {\text{rand}}\left( {\left[ { - 1,1} \right]} \right) \quad M = 2,3, \ldots ,N \\ \end{aligned} \right.$$
(21)

After the first calculation of φ PWMMbest, the initial velocity is still expressed with (21). But the initial position of particle x will employ the result of the last calculation:

$$\varvec{\varphi }_{x} (0) = [\varphi_{\text{PWM1best}} ,\varphi_{\text{PWM2best}} , \ldots ,\varphi_{{{\text{PWM}}N{\text{best}}}} ]$$
(22)

5.1.2 Part B

During the calculation, the PSO method should first initialize c as 0 and then calculate the I hsumax of each particle by using (23).

$$I_{\text{hsumax}} \left( c \right) = F\left( {\varvec{\varphi }_{\varvec{x}} \left( c \right)} \right) \quad x = 1,2, \ldots ,X_{ \hbox{max} }$$
(23)

After one iteration, the GSU should save the historical best position of particle x as φ xbest, and save the historical best positions of all particles as φ gbest. Then PSO method increases c by 1 and updates the position and the velocity of particle x by using the method presented in Part A:

$$\left\{ \begin{array}{l} {\varvec{v}}_{x} (c) = \{ {\varvec{v}}_{x} (c - 1) + a_{1} {\text{ rand}}_{1} \,([0,1])[{\varvec{\varphi}}_{{x{\text{best}}}} - {\varvec{\varphi}}_{x} (c - 1)] + a_{2} {\text{ rand}}_{2}\, \left( {\left[ {0,1} \right]} \right)[{\varvec{\varphi}}_{\text{gbest}} - {\varvec{\varphi}}_{x} (c - 1)]\} \hfill \\ {\varvec{\varphi}}_{x} \left( c \right) = {\varvec{\varphi}}_{x} \left( {c - 1} \right) + {\varvec{v}}_{x} \left( c \right) \hfill \\ \end{array} \right.$$
(24)

The PSO method will repeat the above calculation method until c > c max, where c max is the max iteration times.

Finally, the PSO method could find the optimal phase shift angle of φ gbest.

$$\varvec{\varphi }_{\text{gbest}} \left( 0 \right) = \left[ {\varphi_{\text{PWM1best}} ,\varphi_{\text{PWM2best}} , \ldots ,\varphi_{{{\text{PWM}}N{\text{best}}}} } \right]$$
(25)

5.2 Calculation of f synmin

There are also two main parts to calculate f synmin.

5.2.1 Part A

For the first calculation of f synmin, GSU initializes f synmin by using the following processes.

  1. 1)

    Selecting all the positions whose I hsumax are larger than the allowable THD value H allow in subsection 5.1;

  2. 2)

    Finding the position φ bound, which is the nearest one from φ gbest among all the selected positions in process 1) above;

  3. 3)

    Calculating:

    $$\Delta \varvec{\varphi }_{\text{bb}} = \left| {\varvec{\varphi }_{\text{gbest}} - \varvec{\varphi }_{\text{bound}} } \right| = [\Delta \varphi_{{{\text{bb}}1}} ,\Delta \varphi_{\text{bb2}} , \ldots ,\Delta \varphi_{{{\text{bb}}N}} ]$$
    (26)
    $$\Delta \varvec{\varphi }_{\text{bbmax}} = { \hbox{max} }(\Delta \varphi_{{{\text{bb}}1}} ,\Delta \varphi_{\text{bb2}} , \ldots ,\Delta \varphi_{{{\text{bb}}N}} )$$
    (27)
  4. 4)

    Initializing f synmin as

    $$f_{\text{synmin}} = \frac{{\Delta \varphi_{{ 1 {\text{s}}}} }}{{\Delta \varphi_{\text{bbmax}} }}$$
    (28)

    where ∆φ 1s is the maximum deviation of φ PWMM per second.

After the first calculation, GSU will then initialize f synmin as the f syn of the last calculation process during the next iteration.

5.2.2 Part B

With the known f synmin, the maximum THD of total current, H max, at PCC can be calculated by using (29).

$$\left\{ {\begin{array}{*{20}l} {{\text{max}}\;I_{{{\text{hsumax}}}} = F\left( {\varphi _{{{\text{PWM1}}}} ,\varphi _{{{\text{PWM2}}}} , \ldots ,\varphi _{{{\text{PWM}}N}} } \right)} \\ {{\text{s}}.{\text{t}}.\;\;\;\varphi _{{{\text{PWM}}M{\text{best}}}} - \Delta \varphi _{{M{\text{max}}}} < \varphi _{{{\text{PWM}}M}} < \varphi _{{{\text{PWM}}M{\text{best}}}} + \Delta \varphi _{{M{\text{max}}}} \quad M = 1,2, \ldots ,N{\text{ }}} \\ \end{array} } \right.$$
(29)

where ∆φ Mmax is the maximum deviation of φ PWMM between two synchronization signals. When H max is lower than H allow, f synmin could be treated as the final calculation result. On the other hand, when H max is higher than H allow, GSU will increase f synmin and recalculate (29). The corresponding flow chart is shown in Fig. 6.

Fig. 6
figure 6

Flow chart of calculating f synmin

Full size image

6 Simulation verification

MATLAB/Simulink is used to verify the performance of GSDPWM for three-phase inverters. Firstly, the two inverters with parameters shown in Table 1 are used to verify GSDPWM. f syn is set to be 2 Hz. Figure 7 shows the THD trajectories with or without GSDPWM. The THD of total current will change between the minimum value and the maximum value without GSDPWM. And the THD of total current is obviously lowered down by using GSDPWM. Figure 8a shows the waveforms of total current without GSDPWM. Figure 8b shows the waveform of total current with GSDPWM. Figure 9a, b show the fast Fourier transform (FFT) spectrums of currents in Fig. 8a, b, respectively. It is obvious that the total current has smaller current ripple and its THD is low when GSDPWM is employed.

Fig. 7
figure 7

THD trajectories of the total current and the output currents of two inverters with or without GSDPWM

Full size image
Fig. 8
figure 8

Simulation waveforms of i suma, i sumb and i sumc

Full size image
Fig. 9
figure 9

FFT spectrum of i suma

Full size image

Next, six inverters with different parameters and different types of DPWM are used to verify the general performance of GSDPWM. The parameters of six inverters are listed in Table 4. When using GSDPWM method to calculate the φ PWMMbest, the corresponding calculation results are listed in Table 4 too. And the calculation result of f synmin is 20 Hz. Figure 10a shows the THD trajectories of total current with or without GSDPWM, where the THD of i suma changes with time progresses when not adopting GSDPWM. Figure 10b shows the FFT spectrum of i suma at point A of Fig. 10a. And the FFT spectrum of i suma when using GSDPWM is shown in Fig. 10c.

Table 4 Parameters of six three-phase inverters
Full size table
Fig. 10
figure 10

Simulation results of 6 inverters with or without GSDPWM

Full size image

In [19], the initial value of f synmin in the first iteration process is set as the maximum frequency of communication. Considering that the synchronization frequency cannot be higher than the switching frequency, the initial value is 5 kHz, which is far from the final result 20 Hz. When employing the fast intelligent method, φ bound is [0°, 210°, 129°, 244°, 31°, 75°]. So ∆φ bb is [0°, 6°, 3°, 8°, 5°, 3°]. ∆φ bbmax = 8°. And f synmin = 72°/8° = 9 Hz. The initial value of f synmin is close to the final result 20 Hz. So it costs less time to find the final result.

7 Experimental verification

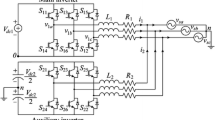
The experimental prototype was constructed by using two three-phase voltage source inverters. Each inverter has its own independent DC source, conversion circuit, first order filter, and digital controller. The parameters of two inverters are listed in Table 5. These two inverters are connected to a programmable AC voltage source AMETEK-CI-4500LS, whose RMS value of phase voltage is 110 V and the output frequency is 50 Hz.

Table 5 Parameters of two experimental inverters
Full size table

Firstly, two three-phase inverters are connected in parallel without using GSDPWM. Considering that the THD of i suma, i sumb and i sumc are the same under steady-state condition, only i suma was recorded to calculate the THD trajectory. LECROY oscilloscope was used to continuously record 400 waveforms of i suma in 200 s. The length of each waveform is 0.05 s. Then, MATLAB/Simulink was used to calculate the THD of each waveform. Finally, these 400 THD values were drawn in figures. The THD of i suma is shown by the red line in Fig. 11a, which is similar as the simulation result.

Fig. 11
figure 11

Experimental results of two inverters with or without GSDPWM

Full size image

Then, GSDPWM is employed and the THD trajectory of i suma is shown by the green line in Fig. 11a, which is almost constant during the operation. Figure 11b shows the experimental waveforms without GSDPWM, and the THD of output current is up to 9.3 %. Figure 11c shows the experimental waveforms with GSDPWM, and the THD of output current is reduced to 4.8 %. In addition, W a is the PWM sequence signals of the upper IGBT in phase a, and it is discontinuous by adopting the DPWMMIN method. Figure 12a shows the waveforms of W 1a, W 2a and the synchronization signals. W 1a and W 2a are the PWM sequence signals of inverter 1 and 2, respectively. The frequency of synchronization signals is 20 Hz. Figure 12b is the zoomed view of Fig. 12a, where the phase shift between W 1a and W 2a is 180°.

Fig. 12
figure 12

Experimental results of pulse waveforms and synchronization signals

Full size image

8 Conclusion

This paper proposes a fast global synchronous discontinuous pulse width modulation (GSDPWM) method, which can reduce the total high frequency current harmonics when many inverters with DPWM, third-harmonic PWM and SVPWM are connected to the same PCC. The look-up table method is employed to greatly improve the current harmonic calculation speed. Then, a new fast processing method to calculate the important optimal phase shift angles and the frequency of sending synchronization signals is introduced. GSDPWM can be employed among inverters with different PWM types and parameters. Finally, MATLAB simulation and experimental results verified the performance of GSDPWM.