1 Introduction

The microgrid as a new concept has been brought about due to the development of renewable energy systems, storage devices and coordinate converter control scheme. It has been an important role in electric industry restructure due to the increasing attentions on environmental, economical, and social interests [1–4]. With the increasing penetration of DG units and rapid growth of distributed loads, the single bus microgrid to some extent cannot satisfy the demand of power supply system construction. The multi-bus microgrid consisted of several buses is a practical solution to connect the wide area distributed DG units and loads, which can realize the objective of optimizing network operation, minimizing the distribution network losses and maintaining the voltage profiles [5–7]. The proliferation of nonlinear loads in power systems has been increasing in an unprecedented pace in recent years due to the advance of power electronics technologies. As a result, the power quality issue, induced by the nonlinear loads, has become a crucial factor that may affect the normal operation of both customer devices and power systems [8, 9]. As a conventional approach, ancillary devices, such as passive filters and active power filters (APF), can be installed in the grid to overcome the distribution network harmonic problems. These ancillary devices, however, are undesirable because of their high installation costs.

In the multi-bus microgrid, the DG interfacing converters can be considered as active cells for control and management purposes [10, 11]. Although the DG interfacing converters may introduce harmonics into the power network, and cause power quality issues, they are also able to improve system efficiency and power quality if designed and controlled properly. Thus, DG units have the ability to enhance the power quality as well as the reliability of microgrids. Using DG units as harmonics compensators can reduce the need for adding extra devices in multi-bus microgrids. This leads to the result that a significant growth of DG penetration in multi-bus microgrids will require new control scheme in order to exploit the power quality improvement capability of DG units. Therefore, a merging concept is to use these power electronic interfaced DG systems to simultaneously realize real power generation and harmonic compensation functions.

A shunt resistive active power filter (R-APF) control scheme based on voltage detection for the purpose of harmonic compensation has been proposed in [12, 13]. The APF was controlled as a small virtual resistance at selected harmonic frequencies, and therefore it is possible to damp out harmonic propagation. But this control scheme is affected by the location of APF, the detection point and the network characteristics. Therefore, the value of the virtual resistance should be chosen carefully, otherwise, other buses’ voltage distortion may be deteriorated. Further, a cooperative control of two APFs with communication was proposed in [14] to damp out harmonic propagation within the power distribution system, where a central controller regulates the virtual resistance value according to the voltage distortions at each APF installation position. However, the mutual communication increases the investment cost and reduces the operational reliability. In [15], the compensation approach for PCC harmonics is derived by setting the DG unit to work as an R-APF. The DG system works as a small resistance at selected harmonic frequencies. Therefore, the harmonic currents of nonlinear loads installed at the PCC can be absorbed by DG system, resulting in an improved PCC voltage and line current quality with low total harmonic distortion (THD). Nevertheless, the prerequisite of implementing this control function is that additional measurement devices, e.g. voltage and current transducers and communication channels, are required to provide the PCC distortion information since the DG units normally locate far away from PCC. Similarly, the virtual resistance should be chosen carefully to attenuate the harmonic distortion. In [16], a harmonic impedance synthesis technique was presented for voltage-controlled distributed generation inverters in order to damp harmonic voltage distortion in a distribution network. Negative harmonic inductances and positive harmonic resistances are synthesized at the dominant harmonic frequencies. Thus, the harmonic voltage drop on the grid-side inductance can be effectively attenuated. Nevertheless, the synthesized harmonic impedance should be designed carefully, which will affect the harmonic damping performance and the operational stability. Also in [17], a selective virtual impedance loop is considered to improve the sharing accuracy of load harmonic currents among the DG units, which however needs low-bandwidth data communication signals among individual distributed generation systems. Unfortunately, the communication among DG units will increase the system complexity and reduce the operational reliability in a multi-bus microgrid.

In order to improve the power quality regulation capability and operational reliability of wide area distributed multi-bus microgrids, this paper proposes a novel approach to compensate bus voltage and current harmonics, which only requires the local information of DG units, i.e., the converter output voltage and current. The proposed controller has a cascaded structure, whose outer loop voltage controller regulates the distorted bus voltage without using the directly measured bus information and the accompanied long distance communication. An inner loop harmonic current compensator regulates the current harmonics. This control scheme enables the DG unit to absorb the harmonic currents introduced by the nonlinear loads, so that the current quality injected into the main bus is improved, and the sub-bus voltage distortion can be mitigated. Therefore, the burden of the power quality regulator installed at per level bus is relieved. The detailed illustration of the proposed control scheme will be elaborated in the following Sections. Matlab simulations and experimental prototype have verified the performance of the proposed power quality control approach in a multi-bus microgrid.

2 General illustration of power quality in a multi-bus microgrid

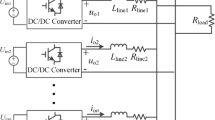
The single-line diagram of a general multi-bus microgrid is shown in Fig. 1 as an example for illustration. The multi-bus microgrid comprises one 10 kV bus, two 380 V buses and three feeders. Two 380 V buses are connected to the 10 kV bus through step-up transformers. Three combinations of linear and nonlinear loads are supplied by the multi-bus microgrid. Two DG units are equipped with a grid-interfacing converter and a hybrid energy resource which contains energy sources and energy storage system. Each DG unit is able to supply any amount of real power within the pre-specified limits. Z Linen (n = 1,2,…, i) represents the line impedance which cannot be neglected in the multi-bus microgrid. As shown in Fig. 1, a static switch is inserted between the utility grid and the multi-bus microgrid to connect/disconnect the multi-bus microgrid during the online/offline operation. With the increasing applications of nonlinear loads, the power quality of the multi-bus microgrid would be significantly deteriorated due to the harmonics propagation. A unified power quality conditioner (UPQC) can be installed at the main bus to compensate harmonics.

Fig. 1
figure 1

General illustration of a multi-bus microgrid with power electronics interfaced DG systems

Full size image

However, the complex structure of the multi-bus microgrid increases the difficulty of harmonics compensation. For example, the UPQC installed at Bus 1 as shown in Fig. 1 can improve the current and voltage quality of Bus 1, however, it cannot restraint the harmonic propagation within the multi-bus microgrid and guarantee the power quality of sub-buses (e.g. Bus 2 and Bus 3), which directly supply the distributed loads. With the harmonic current flowing in the multi-bus microgrid, the voltage of sub buses will be distorted due to the voltage drop on the line impedance. The distorted bus voltage will seriously affect the normal operation of distributed loads.

In order to illustrate the harmonic propagation within the microgrid, a two-bus network interconnected through an isolation transformer is shown in Fig. 2 as a simple example. The DG unit and distributed loads are connected to the sub-bus, and a diode rectifier with an RC load is considered as the nonlinear load to produce harmonic currents.

Fig. 2
figure 2

Comparison of harmonic currents flow

Full size image

For the conventional control method, the DG unit is controlled to generate real power and its output current i DG injected to the sub-bus is sinusoidal, as shown in Fig. 2a. Hence, the harmonic currents introduced by the nonlinear load mainly flow to the main bus due to the lower impedance of the utility grid. The harmonic propagation within the multi-bus network will unavoidably generate the voltage harmonics as expressed below:

$$\dot{V}_{Line} = Z_{Line\_h} \cdot \dot{I}_{h}$$
(1)

where \(\dot{V}_{Line}\) is the harmonic voltage matrix; \(\dot{I}_{h}\) is the harmonic current matrix and Z Line_h is the corresponding order harmonic impedance matrix, respectively. The harmonic voltage will lead to the sub-bus voltage distortion within the multi-bus microgrid.

When the main bus is connected to many sub-buses with distributed nonlinear loads, as shown in Fig. 1, the current flowing to the utility grid is the sum of currents flowing from the sub-buses to the main bus, which can be expressed as:

$$i_{G} = \sum\limits_{k = 1}^{m} {i_{k} }$$
(2)

where i k is the current flowing from k th sub-bus to the main bus and m is the total number of sub-buses.

Due to the nonlinear loads, the currents flowing to the main bus contain harmonics, and (2) can be rewritten as:

$$i_{G} = \sum\limits_{h = 1}^{n} {i_{Gh} } = \sum\limits_{k = 1}^{m} {\sum\limits_{h = 1}^{n} {i_{kh} } }$$
(3)

where i kh is the h th order component of the current flowing from k th sub-bus to the main bus.

The total harmonic distortion of the current injected to the utility grid from the multi-bus microgrid can be expressed as:

$$THD_{i} = \frac{{\sqrt {\sum\limits_{h = 2}^{n} {I_{{Gh}^{2}} } } }}{{I_{G 1} }} \times 100\%$$
(4)

where I G1 and I Gh are the rms values of the fundamental and h th harmonic components of the current injected to the utility grid, respectively.

When the multi-bus microgrid contains many nonlinear loads, the harmonics propagation will lead to serious power quality problems within the multi-bus microgrid. Meanwhile, the harmonic currents flowing to the utility grid will aggravate the THD of the grid current. In other words, the main bus handles all burdens of the harmonic currents introduced by the distributed nonlinear loads. This will increase the burden of the UPQC installed at the main bus.

In contrast, the current i DG can be controlled to contain harmonics according to the distortion information of the bus voltage, and the DG unit can absorb the harmonic currents introduced by the nonlinear load as shown in Fig. 2b. Therefore, this can help compensate the harmonic currents flowing from the sub-bus to the main bus by dispatching the harmonic currents introduced by the nonlinear load. With the decreasing distortion of the current flowing to the main bus, the voltage quality of sub buses will be improved, and the burden of the harmonic compensation devices installed at the main bus can be relieved. This will benefit the customer devices, the multi-bus microgrid and the utility grid simultaneously. However, a reliable approach to acquire the information of voltage and current harmonics at any level buses is not straightforward. The communication between the bus and the DG will reduce the operational reliability of the whole system and increase investment to guarantee the bandwidth of communication channels. Especially, relying on communication is not practical when the communication distance is long. This paper thus proposes a new method to indirectly acquire the distortion information of the bus voltage without communication, and the DG units could accurately compensate current harmonics. The details will be presented in the next Section.

3 Proposed control principle

In order to illustrate the control principle, a two-bus network is derived from Fig. 1. In specific, the configuration of two buses network and its control block diagram are shown in Fig. 3. It can be seen that Bus 2 is connected to Bus 1 through a step-up transformer. The DG unit 1 and the distributed loads 2 composed of linear and nonlinear loads are connected to Bus 2. The nonlinear load represented by a rectifier circuit with an RC load could introduce current harmonics. The DG unit 1 connects to Bus 2 through a distribution line represented by Z Line3. When properly controlled, the DG unit can compensate the harmonic currents, and in consequence, improve the voltage quality of Bus 2, as shown in Fig. 2b. The main control blocks include bus voltage calculation, phase locked loop (PLL) and cascaded voltage and current controller, which will be next illustrated in detail.

Fig. 3
figure 3

Overall illustration of the circuit configuration and control diagram

Full size image

3.1 Bus voltage calculation

It should be noted that the proposed control scheme is to deal with power quality issues in a multi-bus microgrid, where the DG converter is installed far away from the ac bus. To well illustrate this scenario, a single line representation is drawn in Fig. 4, where Z Line3 represents the impedance between DG unit 1 and its adjacent Bus 2, whose value can be easily obtained by calculating the known cable or line parameters. In practice, the DG units and distributed loads will at times locate far apart, and then the line impedance cannot be neglected. As a result, the harmonic propagation in the multi-bus microgrid will lead to the Bus 2 voltage distortion, which is definitely unwanted for both loads supplied by Bus 2 and the multi-bus microgrid. Compared with the traditional control scheme that directly measures the Bus 2 voltage and delivers the distortion information to the DG units via a communication system, the proposed approach indirectly obtain the Bus 2 voltage by only measuring the DG unit 1 line current injected into the ac bus and the converter output voltage. The Bus 2 voltage depicted in Fig. 4 can then be calculated as:

$$\left[ \begin{array}{c} \dot{V}_{Bus 2\_1} \hfill \\ \dot{V}_{Bus 2\_5} \hfill \\ \dot{V}_{Bus 2\_7} \hfill \\ \, \quad \vdots \hfill \\ \dot{V}_{Bus 2\_n} \hfill \\ \end{array} \right] = \left[ \begin{array}{c} \dot{V}_{{{\text{DG1}}\_1}} \hfill \\ \dot{V}_{{{\text{DG1}}\_5}} \hfill \\ \dot{V}_{{{\text{DG1}}\_7}} \hfill \\ \, \quad\vdots \hfill \\ \dot{V}_{{{\text{DG1}}\_n}} \hfill \\ \end{array} \right] - \left[ {\begin{array}{*{20}c} {Z_{Line 3\_1} } & 0 & 0 & \cdots & 0 \\ 0 & {Z_{Line 3\_5} } & 0 & \cdots & 0 \\ 0 & 0 & {Z_{Line 3\_7} } & \cdots & 0 \\ \vdots & \vdots & \vdots & {} & \vdots \\ 0 & 0 & 0 & \cdots & {Z_{Line 3\_n} } \\ \end{array} } \right]\text{ }\left[ \begin{array}{c} \dot{I}_{{{\text{DG1}}\_1}} \hfill \\ \dot{I}_{{{\text{DG1}}\_5}} \hfill \\ \dot{I}_{{{\text{DG1}}\_7}} \hfill \\ \, \quad \vdots \hfill \\ \dot{I}_{{{\text{DG1}}\_n}} \hfill \\ \end{array} \right]$$
(5)

where \(\dot{V}_{Bus2}\) is the Bus 2 voltage vector; \(\dot{V}_{DG1}\) is the converter output voltage vector; Z Line3 is the line impedance vector; \(\dot{I}_{\text{DG1}}\) is the output current vector of DG unit 1; n is the highest harmonic order, respectively.

Fig. 4
figure 4

Single-line illustration of the DG system in the multi-bus microgrid

Full size image

The information of line impedance between the DG and the Bus can be obtained through the following methods. The first one is that the line information can be obtained from the power network design and construction parameters. The line impedance value is generally designed in accordance with the requirement of microgrid stability and the requirement of power sharing. The parameters of the line impedance can be relatively accurate. Other methods discussed in literature [18–20], inject a perturbation into the grid and then measure the PCC voltage and current to analyze and calculate line impedance at each frequency, these methods can accurately and rapidly measure the line impedance at each frequency, and it is suitable for the applications which need to measure harmonic impedance rapidly. For instance, the real resistance and inductance of feeder in [20] are 1 Ω and 6.1 mH, meanwhile, the measured values are 1.05 Ω and 6.01 mH. The measurement error is below 5%. It can be seen that the estimated values are very close to the real values of the feeder impedance. Further discussion on detailed line impedance estimation schemes is out of the scope of this paper.

It is noted that both voltage and current are the sum of weighted fundamental and harmonic components. Hence, the Bus 2 voltage can be rewritten as (6).

$$v_{Bus 2} = \sum\limits_{h = 1}^{n} {v_{Bus 2\_h} }$$
(6)

where h = 1,2,…,n, represents the harmonic order. The Bus 2 voltage calculated by (6) will be next used for PLL calculation as shown in Fig. 5.

Fig. 5
figure 5

Block diagram of the SRF-PLL

Full size image

3.2 Phase locked loop

In the proposed approach, the voltage and current controller are designed in the rotating dq reference frame. The estimation of ac voltage parameters, such as voltage amplitude and phase angle, will act as a crucial role in the overall performance of the synchronization algorithm. With a low pass filter used to eliminate the harmonics, a synchronous reference frame phase locked loop (SRF-PLL) [21–23] as shown in Fig. 5 is used in the proposed control strategy. In spite of the good behavior of the SRF-PLL under sinusoidal conditions, its performance is deteriorated when the three phase input signal becomes distorted. When the three-phase instantaneous voltage waveforms are transformed from the abc reference frame into the rotating dq reference frame by means of the Park transformation [24, 25], the fundamental and (6n±1)th harmonics in the abc reference frame are represented by DC component and 6n th harmonics in the rotating dq reference frame. In the rotating dq reference frame, two low pass filters (LPFs) with high cutoff frequency, e.g. 150 Hz, implemented in the control scheme can easily eliminate the 6th and higher order harmonics to obtain the DC components of v d and v q. The LPFs have few affects to the DC components of the v d and v q . Therefore, the SRF-PLL with LPFs in the rotating dq reference frame can provide a good performance of the phase angle and magnitude estimation under distorted condition. In the rotating dq reference frame, the DC component of the v d represents the amplitude of the fundamental component of Bus 2 voltage, which is subsequently set as the voltage reference in the next subsection. A feedback control loop is used to control the angular position by forcing the v q component to be zero. As depicted in Fig. 5, the estimated grid frequency is ω. As a feed forward signal, the nominal angular frequency is conventionally adopted to improve the dynamics of the phase estimation θ derived by integrating ω.

3.3 Control scheme based on bus voltage calculation

After obtaining the phase angle of Bus 2 voltage from the SRF-PLL, the three-phase instantaneous Bus 2 voltage calculated in the above subsection can be transformed from the abc reference frame into the rotating dq reference frame by means of the Park transformation. The d- and q-axis components of Bus 2 voltage should be incorporated into a voltage control loop to achieve proper harmonic voltage tracking performance as depicted in Fig. 3. In order to provide voltage harmonic compensation, the d-axis voltage component should be subtracted from the amplitude of fundamental voltage derived from the SRF-PLL and the q-axis voltage reference should be set to zero simply, as illustrated in (7).

$$\left\{ \begin{aligned} & v_{Bus 2\_h\_d} = v_{Bus 2\_d} - v_{Bus 2\_f} \\ & v_{Bus 2\_h\_q} = v_{Bus 2\_q} - 0 \\ \end{aligned} \right.$$
(7)

where v Bus2_h_d and v Bus2_h_q are the d- and q-axis harmonic components of the Bus 2 voltage; v Bus2_d and v Bus2_q are the measured d- and q-axis components of the Bus 2 voltage and v Bus2_f is the amplitude of the fundamental component of Bus 2 voltage, respectively.

The voltage control loop uses a proportional controller plus multiple paralleled resonant controllers to achieve proper harmonic voltage tracking performance as expressed in (8).

$$G_{uh} (s )\;{ = }\;K_{up} + \sum\limits_{n = 1}^{k} {\frac{{K_{uh} s}}{{s^{2} + (6n\omega_{ 0} )^{2} }}}$$
(8)

where K up is the proportional gain; k is the highest harmonics order selected for compensation; K uh is the resonant gain and ω 0 is the nominal angular frequency, respectively. It should be noted that the resonant controller in the synchronous reference frame is more effective than that in the stationary frame, since it represents two equivalent resonant terms in the stationary frame for compensating two adjacent odd harmonics [26–28].

Similarly, the three-phase instantaneous DG line current injected to Bus 2 can also be transformed from the abc reference frame into the rotating dq reference frame. The current reference can be obtained by combining the harmonic current reference and the fundamental current reference as illustrated in (9).

$$i_{{{\text{DG1}}\_ref}} = i_{{{\text{DG1}}\_f}} + i_{h}$$
(9)

where i DG1_ref is the current reference; i DG1_f is the fundamental current command and i h is the current harmonics reference to compensate. From (7), (8) and (9), the current reference i DG1_ref can be derived as:

$$i_{{{\text{DG1}}\_ref}} (s) = i_{{{\text{DG1}}\_f}} (s) + G_{uh} (s )v_{Bus 2\_h} (s)$$
(10)

For the inner current control loop, a proportional integral (PI) controller plus multiple paralleled resonant controllers as shown in Fig. 3 are used in the synchronous dq frame in order to force the DG line current to track the reference [29, 30], as expressed in (11).

$$G_{i} (s ) = K_{pi} \left( 1 { + }\frac{1}{{T_{i} s}} \right) + \sum\limits_{n = 1}^{k} {\frac{{K_{ih} s}}{{s^{2} + (6n\omega_{ 0} )^{2} }}}$$
(11)

where K pi is the proportional gain; T i is the integral time constant; K ih is the resonant gain and ω 0 is the nominal angular frequency, respectively.

4 Analysis of harmonic compensation capability in a multi-bus microgrid

In order to briefly illustrate the compensation capability of the proposed control method in a multi-bus microgrid, a comparison for three different scenarios is presented below. In detail, for the first scenario, the multi-bus microgrid only has one UPQC installed at the main bus to compensate harmonics. For the second scenario, additional APFs are installed at all sub-bus to compensate the current harmonics raised by the local nonlinear loads. For the third scenario, the distributed converters could perform as the active power filters to compensate the current harmonics by using the proposed method in this paper, while eliminating the APF installed at each sub-bus.

For clear illustration, this section assumes that there are only 5th and 7th harmonic currents in the multi-bus microgrid as shown in Fig. 1, where, the 5th harmonic currents introduced by the distributed loads 1 to 3 are 0.02, 0.02 and 0.01 in per unit, and the 7th harmonic currents introduced by the distributed loads 1 to 3 are 0.01, 0.01 and 0.005 in per unit, respectively.

In the first scenario, the DGs are controlled to inject real power, and only the UPQC installed at the main bus can compensate the harmonics introduced by all nonlinear loads. The maximum rms value of APF part compensation current can be calculated as:

$$I_{{{\text{APF}}\_\hbox{max} }} = \sqrt {\sum\limits_{h = 2}^{n} {\left( {I_{{{\text{APF}}\_h\_\hbox{max} }} } \right)^{2} } } = \sqrt {\sum\limits_{h = 2}^{n} {\left( {\sum\limits_{k = 1}^{m} {I_{kh} } } \right)^{2} } } = \;0.0557({\text{p}} . {\text{u}} .)$$
(12)

where I kh is the rms value of h th harmonic current introduced by the k th distributed load; m is the total number of distributed loads and n is the highest harmonics order, respectively. In this scenario, the APF part of UPQC can guarantee the quality of current injected into the utility grid and the main bus voltage. However, it cannot attenuate the harmonic propagation within the multi-bus microgrid and guarantee the power quality of sub-buses.

In order to improve the power quality within the multi-bus microgrid, the second scenario can be assumed, where the additional APF′ and APF″ are installed at Bus 2 and Bus 3, respectively. In this scenario, APF′ and APF″ compensate the harmonics introduced by the distributed loads connected to Bus 2 and Bus 3, respectively. The maximum rms value of APF′ and APF″ compensation current can respectively be calculated as:

$$\left\{ \begin{array}{l} I_{{{\text{APF}}^{\prime }\_\max }} = \sqrt {\sum\limits_{{h = 2}}^{n} {\left( {I_{{{\text{APF}}^{\prime }\_h}} } \right)^{2} } } = 0.0224({\text{p}}{\text{.u}}{\text{.}}) \hfill \\ I_{{{\text{APF}}^{\prime \prime }\_\max }} = \sqrt {\sum\limits_{{h = 2}}^{n} {\left( {I_{{{\text{APF}}^{\prime \prime }\_h}} } \right)^{2} } } = 0.0112({\text{p}}{\text{.u}}{\text{.}}) \end{array} \right.$$
(13)

Because of the compensation capability of APF′ and APF″, the APF part of the UPQC at the main bus only needs to compensate the current harmonics introduced by the distributed load 1, and the maximum rms value of APF part compensation current reduces to 0.0224 p.u.. Compared to the first scenario, the power quality within the multi-bus microgrid can be significantly improved and the burden of the APF part is relieved. However, this scenario needs additional APF installed at each sub-bus, which would definitely increase the installation investment.

In the last scenario, the DGs are controlled to realize real power generation and harmonic compensation functions. Being different from the above two scenarios, DG 1 and DG 2 are controlled to absorb the current harmonics introduced by the distributed loads. Therefore, they can perform like APF′ and APF″ to compensate the current harmonics at Bus 2 and Bus 3. The maximum rms value of APF part compensation current is the same as the second scenario. Therefore, the last scenario can guarantee the power quality within the multi-bus as well but reduce the investment for additional power quality devices. The comparison among these three scenarios is summarized in Table 1.

Table 1 Comparison of compensation capability of three scenarios
Full size table

When the grid voltage is distorted, a UPQC installed at the main bus can help guarantee the microgrid power quality. The dynamic voltage restorer (DVR) part is used to compensate the harmonic voltages of the main bus voltage. Meanwhile, the APF part is used to compensate the harmonic currents injected to the grid. Doing so, the proposed control scheme can provide a good performance under the distorted gird voltage condition.

In microgrid, the line impedance can be classified into three categories: resistive impedance, inductive impedance and capacitive impedance, respectively. In the proposed control scheme, the calculation accuracy of bus voltage and the harmonic compensation performance are not affected by the impedance type. However, the large error between the real line impedance value and estimated value will affect the accuracy of the harmonic voltage calculation, and the complete compensation cannot be achieved. But when considering the closed control loop can achieve proper fundamental and harmonic current tracking performance and the estimated values are very close to the real values of the feeder impedance [18–20], the proposed harmonic compensation scheme can still significantly improve the power quality of the microgrid.

5 Simulation and experimental verifications

To verify the performance of the proposed power quality control approach in a multi-bus microgrid, Matlab simulations were first conducted according to the configuration of multi-bus microgrid shown in Fig. 1. The detailed circuit and control parameters of the simulated multi-bus microgrid are listed in Table A1 of Appendix A.

In simulation, the fundamental current commands of DG unit 1 and DG unit 2 are 30 A and 50 A, respectively. When the DG units are first controlled to inject real power and do not carry out the function of harmonics compensation, the simulation results are shown in Fig. 6. From Fig. 6c and f, it can be seen that the currents injected to the multi-bus microgrid from the DG units are sinusoidal. The current harmonics introduced by the nonlinear loads now flow to the main bus. Therefore, the Bus 2 and Bus 3 voltages as shown in Fig. 6a, d and the currents injected into the Bus 1 from sub-buses as shown in Fig. 6b, e are all distorted, where the THD of v Bus2 and v Bus3 are 2.45% and 2.95%, the THD of i Bus2 and i Bus3 are 23.88% and 14.64%, respectively. In order to guarantee the power quality of the main bus, the compensated current of the APF part installed at Bus 1 is large, as shown in Fig. 6g. However, this UPQC cannot improve the power quality of sub-buses as analyzed in Section 4. Figure 7 shows the simulated results with the proposed harmonic compensation strategy. In this case, the current harmonics introduced by the nonlinear loads are compensated by the controlled DG units, leading to improved power quality of Bus 2 and Bus 3 currents injected to the Bus 1, as shown in Fig. 7b and e respectively. Meanwhile, the voltage distortions of Bus 2 and Bus 3 are mitigated as shown in Fig. 7a and d, respectively. The THDs of Bus 2 and Bus 3 voltages are now reduced to 0.94% and 1.25%, and the THDs of Bus 2 and Bus 3 currents are reduced to 1.62% and 1.24%, respectively. The currents spectrum of APF part operated under both conditions are shown in Fig. 8. It can be seen that the currents compensated by the APF part of UPQC installed at Bus 1 are reduced significantly as analyzed when the DG units carry out the function of harmonics compensation. Therefore, the power quality within the multi-bus microgrid can be significantly improved, while the burden of the APF part at the main bus is relieved without using any communication between DG units and buses. It is noted that the UPQC installed the main bus can compensate the harmonics introduced by the distorted grid voltage, and maintain the main bus voltage quality. The harmonic compensation performance under distorted voltage condition is almost the same as the simulation results shown in Fig. 7. Therefore, the simulation results under distorted grid voltage condition are not shown here.

Fig. 6
figure 6

Performance of the DGs without compensation

Full size image
Fig. 7
figure 7

Performance of the DGs with compensation

Full size image
Fig. 8
figure 8

Current spectrum comparison of the APF part

Full size image

Another simulation was conducted to verify the performance of the proposed power quality control approach under the inaccurate line impedance condition, In the simulation, the error of the line impedance was selected higher than the usual error of the estimated and the real impedance value, where the impedance value used in the Bus 2 voltage calculation is 10% higher than its real value, and the impedance value used in the Bus 3 voltage calculation is 10% lower than its real value. The simulation results are shown in Fig. 9. In this case, the THDs of Bus 2 and Bus 3 voltages are 1.02% and 1.36%, and the THDs of Bus 2 and Bus 3 currents are 2.86% and 1.76%, respectively. Figure 10 shows the currents spectrum of APF part operated with the accurate and inaccurate line impedance value. It can be seen that the harmonics compensation shown in Fig. 9 is deteriorated a little compared to the accurate line impedance condition shown in Fig. 7. But the harmonic compensation can still improve the power quality of the microgrid.

Fig. 9
figure 9

DGs compensation performance with inaccurate impedance

Full size image
Fig. 10
figure 10

Currents spectrum comparison of APF part

Full size image

To validate the performance of the proposed compensation scheme in experiments, a hardware prototype was implemented in the laboratory based on the circuit configuration shown in Fig. 3 and the parameters listed in Table A2 of Appendix A. For the experimental system, a programmable DC source was used to represent the DG and connected to the microgrid through a three-phase converter. The developed control algorithm was executed on a dSPACE1103 real-time platform.

The steady-state experimental results without harmonic compensation are shown in Fig. 11, where the DG is controlled to only inject real current, which is commanded to 4.2 A. It can be seen that the bus voltage and bus current injected into the main bus are severely distorted because of the large current harmonics induced by the nonlinear load and the non-negligible line impedance. As a result, the THD of v Bus2 and i Bus2 are found to be 5.26% and 28.76%, respectively. In contrast, when the harmonic compensation function is implemented, the DG will simultaneously inject real power to the microgrid and absorb most of the harmonics introduced by the nonlinear load. The corresponding experimental results are shown in Fig. 12. It can be seen that the power quality of both bus voltage and bus current are improved significantly, and the THD of v Bus2 and i Bus2 are now reduced to 2.41% and 4.63%, respectively. Figure 13 shows the spectrum analysis of Bus 2 voltage and Bus 2 current operated under both conditions.

Fig. 11
figure 11

Experimental waveforms without compensation

Full size image
Fig. 12
figure 12

Experimental waveforms with compensation

Full size image
Fig. 13
figure 13

Comparison of spectrum operated under both above conditions

Full size image

6 Conclusion

This paper has proposed a novel control approach of DG interfacing converter for harmonic compensation in a multi-bus microgrid. The proposed control approach can simultaneously enable the DG units to deliver real power into the multi-bus microgrid and compensate the harmonics appeared in the bus voltages and currents introduced by nonlinear loads within the multi-bus microgrid without communication. It only requires local information of the DG unit, such as the converter output voltage and current and the line impedance, to derive the distortion information of its adjacent bus. As a consequence, the traditional measurement devices installed at the bus as well as the long distance communication between the bus and the converter can be eliminated. An outer voltage control loop and an inner current control loop are designed to guarantee the DG real power generation and harmonics compensation functions. The proposed approach is suitable for a multi-bus microgrid since the DG units can compensate the current harmonics, mitigate the buses voltage distortion, and ensure the customer devices in normal operations within the multi-bus microgrid, while significantly relieve the burden of the power quality regulators installed at the PCC. Matlab simulations and experimental verifications are presented to show the performance of the proposed control approach.