Derivation and conformity measurement of a popular explicit analytic Borowy 2C PV module model

Abstract

A popular explicit analytic Borowy 2C PV module model is proposed for power generation prediction. The maximum power point and the open-circuit point which are calculated in this model cannot be equal to the data given by manufacturers under standard test condition (STC). The derivation of this model has never been mentioned in any literatures. The parameter forms of 2C model in this paper are more simplified, and the model is decomposed into a STC sub-model and an incremental sub-model. The STC model is derived successfully from an ideal single-diode circuit model. Relative error estimations are developed to do the conformity error measurements. The analysis results showed that though the biases at those critical points are very small, the conformity will depend on both of the two ratio values I_m/I_sc and V_m/V_oc, which can be used to verify whether 2C model is applicable for the PV module produced by a particular manufacturer.

1 Introduction

Analytic photovoltaic module modeling with the parameters provided by PV module manufacturer is critical for PV plant sizing [1, 2], simulation [3], testing [4], PV plant monitoring [5, 6], dispatching [7], and energy management [8]. A very popular PV module model introduced by Borowy & Salameh [2] named 2C model proposed in this paper, has been heavily cited by 229 papers from Google and 66 papers from IEEE-Xplore database, with no derivation process. [3–6] have used 2C model in their works. All known that the awareness of strong theoretic based or data well driven modeling process is necessary for a user, therefore, this paper aims to fill the blank and present not only a detailed derivation but also a conformity study of 2C model.

In Sect. 2, the 2C model is introduced, which can be decomposed into a sub-model under standard test condition (STC) and an incremental sub-model. Two new parameter sets $({\gamma _{{I_{{\text{m}}} }} ,\gamma _{{V_{{\text{m}}} }} })$ and $(\sigma _{{I_{m} }} ,\sigma _{{V_{{\text{m}}} }})$ are introduced to simplify the model and help the further derivation and conformity study. The contradictions of 2C model with manufacturer’s datasheet have been explored in Sect. 3. In Sect. 4, 2C model under STC is derived from a single-diode circuit model. The conformity error measurements of 2C model with manufacturer’s datasheet have been developed in Sect. 5. Finally conclusions are made in Sect. 6.

2 2C model and its decomposition

2.1 Basic formula

$$ I = I_{{{\text{SC}}}} \left[ {1 - C_{1} \left( {\exp \left( {\frac{{V - \Delta V}}{{C_{2} V_{{{\text{OC}}}} }}} \right) - 1} \right)} \right] + \Delta I $$

(1)

$$ C_{1} = \left( {1 - \frac{{I_{\text{m}} }}{{I_{\text{SC}} }}} \right)\exp \left( { - \frac{{V_{\text{m}} }}{{C_{2} V_{\text{OC}} }}} \right) $$

(2)

$$ C_{2} = \left( {\frac{{V_{\text{m}} }}{{V_{\text{OC}} }} - 1} \right)/\ln \left( {1 - \frac{{I_{\text{m}} }}{{I_{\text{SC}} }}} \right) $$

(3)

$$ \Delta I = \alpha \frac{R}{{R_{\text{ref}} }}\Delta T + \left( {\frac{R}{{R_{\text{ref}} }} - 1} \right)I_{\text{SC}} $$

(4)

$$ \Delta V = - \beta \Delta T - R_{\text{s}} \Delta I $$

(5)

$$ \Delta T = T_{\text{C}} - T_{\text{ref}} $$

(6)

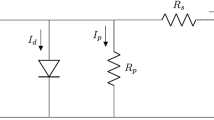
where R and T_c are the solar irradiance and module temperature, respectively. C₁, C₂, ΔI, ΔV and ΔT are intermediate variables; I_sc is the short circuit current; V_oc is the open circuit voltage; I_m is the current at maximum power; V_m is the voltage at maximum power; α is the short circuit current temperature correlation (%/°C or A/°C); β is the open circuit voltage temperature correlation (%/°C or V/°C); R_ref and T_ref are the references of solar irradiance and ambient temperature and R_ref = 1 kW/m², T_ref = 25 °C, respectively; R_s is internal series resistance.

2.2 New direct forms of C₁ and C₂

Assuming two parameter sets:

$$ \left\{\!\!{\begin{array}{ll} {\frac{{I_{\text{m} }}}{{I_{{{\text{SC}}}} }}\,=\,\gamma _{{I_{\text{m}} }} ,} & {\frac{{V_{{\text{m}}} }}{{V_{{{\text{OC}}}} }}\,=\,\gamma _{{V_{{\text{m}}} }} } \\ {1 - \frac{{I_{\text{m}} }}{{I_{{{\text{SC}}}} }}\,=\,\sigma _{{I_{{\text{m}}} }} ,} & {1 - \frac{{V_{{\text{m}}} }}{{V_{{{\text{OC}}}} }}\,=\,\sigma _{{V_{{\text{m}}} }} } \\ \end{array} } \right. $$

(7)

From (7), the equation is obtained as follows:

$$ C_{1} = \left( {\sigma_{{I_{\rm{m}} }} } \right)^{{\frac{1}{{\sigma_{{V_{\text{m}} }} }}}} $$

(8)

$$ C_{2} = - \frac{{\sigma_{{V_{\text{m}} }}}}{{\ln \sigma_{{I_{\rm{m}} }} }} $$

(9)

It can be proved that:

$$ C_{2} = - \frac{1}{{\ln C_{1} }} $$

(10)

$$ 0 < \sigma_{{I_{\rm m} }}\,<\,1,\;\;0 < \sigma_{{V_{\rm m} }}\,<\,1 $$

(11)

$$ 0\,<\,C_{1}\,<\,1 $$

(12)

2.3 Decompose 2C model into two sub-models

2C model can be decomposed into two sub-models, one is the model under STC, the other one is the incremental model

1) Under STC, R = R_ref, T_c = T_ref, ΔI = 0, ΔV = 0, ΔT = 0. (1) will be written as follows:

$$ I(V) = I_{\text{SC}} \left[ {1 - C_{1} \left( {\exp \left( {\frac{V}{{V_{\text{OC}} C_{2} }}} \right) - 1} \right)} \right] $$

(13)

$$ V(I) = C_{2} V_{\text{OC}} \ln \left[ {\left. {1 + \frac{1}{{C_{1} }}\left( {1 - \frac{I}{{I_{\text{SC}} }}} \right)} \right]} \right. $$

(14)

2) With R and T_c changing in time, ΔI, ΔV and ΔT will also change according to (4)–(6).

$$ \left\{ \begin{array}{l} I^{ * } = I - \Delta I \hfill \\ V^{ * } = V - \Delta V \hfill \\ \end{array} \right. $$

(15)

(1) will become as follows:

$$ I^{*} = I_{\text{SC}} \left. {\left[ {1 - C_{1} \left( {\exp \left( {\frac{{V^{*} }}{{C_{2} V_{\text{OC}} }}} \right) - 1} \right)} \right.} \right] $$

(16)

Even if R and T_c are not the reference values, the characteristic curves of I and V are still the same under STC, since the pattern of (13) is same with (16). (15) is a coordinate shift operation to transform (V, I) into (V*, I*). (13) and (16) are both determined by I_sc, V_oc and C₁, C₂. Therefore, the parameter forms of C₁ and C₂ will determine 2C model not only for its STC model, but also for its incremental model.

3 Contradictions of 2C model under STC

3.1 2C model at V = 0 under STC

Assuming $I\,= \,I_{\text{SC}}^{\prime\prime}$ at V = 0, (16) can be written as:

$$ I_{\text{SC}}^{\prime\prime} = I_{\text{SC}} $$

(17)

which means the short circuit point in model is exactly at the assumed short circuit point.

3.2 2C model at V = V_m under STC

Assuming $I = I_{\text{m}}^{\prime\prime}$ at V = V_m, (16) can be written from (7, 8, 10) as:

$$ I_{\text{m}}^{\prime\prime} = I_{\text{m}} + I_{\text{SC}} C_{1} $$

(18)

From (18), the bias between $I = I_{\text{m}}^{\prime\prime}$ and I_m can be derived as:

$$ \Delta I_{\text{m}}^{\prime\prime} = I_{\text{m}}^{\prime\prime} - I_{\text{m}} = I_{\text{SC}} C_{1}\,>\,0 $$

(19)

which means that the power point of the model (V_m, $I_{\text{m}}^{\prime\prime}$) always locates at the upper side of the maximum power point (V_m, I_m) provided by manufactory.

3.3 2C model at I = I_m under STC

Assuming V = $V_{\text{m}}^{\prime\prime}$ at I = I_m, from (14), $V_{\text{m}}^{\prime\prime}$ is given as:

$$ V_{\text{m}}^{\prime\prime} = C_{2} V_{\text{OC}} \ln \;\left[ {1 + \frac{1}{{C_{1} }}\left( {1 - \frac{{I_{\text{m}} }}{{I_{\text{SC}} }}} \right)} \right] $$

(20)

Defining:

$$ Z_{ 2} = V_{\text{m}}^{\prime\prime} /V_{\text{m}} $$

(21)

From (8) and (9), (20) can be written as:

$$ Z_{2} = \ln \left( {1 + \sigma_{{I_{\rm m} }}^{{1 - \frac{1}{{\sigma_{{V_{\rm m} }} }}}} } \right)/\ln \left( {\sigma_{{\text{I}_{\rm m} }}^{{1 - \frac{1}{{\sigma_{{V_{\rm m} }} }}}} } \right) $$

(22)

Defining:

$$ x_{3} = \sigma_{{I_{\text{m}} }}^{{1 - \frac{1}{{\sigma_{{V_{\text{m}} }} }}}} $$

(23)

Thus:

$$ z_{2} = \ln \left( {1 + x_{3} } \right)/\ln \left( {x_{3} } \right) $$

(24)

(23) can be derived as:

$$ \ln (x_{3} ) = \left( {1 - \frac{1}{{\sigma_{{V_{\text{m}} }} }}} \right)\ln (\sigma_{{I_{\text{m}} }} ) $$

(25)

From (11), it can be derived that

$$ \left( {1 - \frac{1}{{\sigma_{{V_{\text{m}} }} }}} \right) < 0,\quad {\rm ln}(\sigma_{{\text{I}_{\text{m}} }} ) < 0 $$

(26)

$$ \ln (x_{3} ) > 0 $$

(27)

which means X₃ > 1, (1 + X₃)/X₃ > 1, so that ln[(1 + X₃)/X₃] > 0, ln(1 + X₃) − ln (X₃) > 0. Finally, it can be derived that

$$ \ln \left( {1 + x_{3} } \right) > \ln \left( {x_{3} } \right) $$

(28)

(28) can be expressed as:

$$ \ln \left( {1 + x_{3} } \right)/\ln \left( {x_{3} } \right) > 1 $$

(29)

Substituting (29) into (24), it is shown that Z₂ > 1, so that $V_{\text{m}}^{\prime\prime} > V_{\text{m}}$ at I = I_m, i.e., the power point ($V_{\text{m}}^{\prime\prime}$, I_m) of the model always locates at the right side of the maximum power point (V_m, I_m) provided by manufactory.

3.4 2C model at V =  V_oc under STC

Assuming I = $I_{ 0}^{\prime\prime}$ at V = V_oc, (13) can be written from (8) and (9) as:

$$ I_{0}^{\prime\prime} = I_{\text{SC}} \;\left[ {1 - \sigma_{{I_{\rm m} }}^{{\frac{1}{{\sigma_{{V_{\text{ m}} }} }}}} \;\left( {\sigma_{{I_{\rm m} }}^{{\frac{{ - V_{\text{OC}} }}{{V_{\text{oc}} \sigma_{{V_{\text{m}} }} }}}} - 1} \right)} \right] = I_{\text{SC}} \sigma_{{I_{\text{ m}} }}^{{\frac{1}{{\sigma_{{V_{\text{ m}} }} }}}} = I_{\text{SC}} C_{1} > 0 $$

(30)

which means the current at V = V_oc is greater than 0, with a constant error I_scC₁.

4 A derivation of C₁ and C₂ from an ideal single-diode PV circuit model

4.1 PV circuit model with an ideal single-diode

The circuit model based on semiconductor theory with a single diode is given by (1) [9].

$$ I = I_{\text{ph}} - I_{\text{s}} \left[ {\exp \left( {\frac{{q(V + R_{\text{s}} I)}}{nkT}} \right) - 1} \right] - \frac{{V + R_{\text{s}} I}}{{R_{\text{sh}} }} $$

(31)

where I_ph is the photonic current (principally depends on the solar irradiance); I_s1 and I_s2 are the reverse saturation currents of diode 1 and 2, respectively; q is the electron charge and q = 1.60,217,646×10⁻¹⁹ C; k is the Boltzmann constant and k = 1.3,806,503×10⁻²³ J/K; T is the cell temperature in Kelvin; n is the diode ideality factors; R_s is the series resistance; R_sh is the shunt resistance. (31) is a complex equation without any explicit solutions for both voltage V and current I.

If neglecting R_s and R_sh, (1) will become:

$$ I(V) = I_{\text{ph}} - I_{\text{s}} = I_{\begin{subarray}{l} {\text{ph}} \\ \end{subarray} } - I_{0} \left[ {\exp \left( {\frac{V}{{V_{\text{T}} }}} \right) - 1} \right] $$

(32)

where I₀ is the reverse saturation current; V_T is the energy equivalent [9].

At the short circuit point under STC, (32) becomes:

$$ I(V)\left| {_{V = 0} } \right. = I_{\text{ph}} = I_{\text{SC}} $$

(33)

Thus:

$$ I(V) = I_{\text{SC}} - I_{0} \left[ {\exp \left( {\frac{V}{{V_{\text{T}} }}} \right) - 1} \right] $$

(34)

(14) can be expressed as:

$$ V(I) = V_{\text{T}} \ln \left[ {1 + \left( {\frac{{I_{\text{SC}} - I}}{{I_{0} }}} \right)} \right] $$

(35)

It is known that when $I = I_{\text{SC}} - I_{ 0} ({\text{e}} - 1)$, the observed voltage is equal to V_T, which can be expressed as follows:

$$ V_{\text{T}} = V(I)\left| {_{{I = I_{\text{SC}} - I_{0} ({\text{e}} - 1)}} } \right. $$

(36)

4.2 A single-diode PV circuit model expressed by C₁ and C₂

Substituting (34) into the following form:

$$ I(V) = I_{\text{SC}} \left\{ {1 - \frac{{I_{0} }}{{I_{\text{SC}} }}\left[ {\exp \left( {\frac{{V_{\text{OC}} }}{{V_{\text{T}} }} \cdot \frac{V}{{V_{\text{OC}} }}} \right) - 1} \right]} \right\} $$

(37)

Assuming there are two new parameters C₁* and C₂*, which are expressed as:

$$ C_{1}^{*} = \frac{{I_{0} }}{{I_{\text{SC}} }},\quad \quad C_{2}^{*} = \frac{{V_{\text{T}} }}{{V_{\text{OC}} }} $$

(38)

(37) can be derived as:

$$ I(V) = I_{\text{SC}} \left\{ {1 - C_{1}^{*} \left[ {\exp \left( {\frac{V}{{C_{2}^{*} V_{\text{OC}} }}} \right) - 1} \right]} \right\} $$

(39)

4.3 Key equation to solve C₁* and C₂*

C₁* and C₂* can be derived by (39) at the open circuit point and MPP points.

1) At the open circuit point, assuming V = V_oc, I = 0, (39) can be derived as:

$$ \exp \left( {\frac{1}{{C_{2}^{*} }}} \right) = 1 + \frac{1}{{C_{1}^{*} }} $$

(40)

For simplifying, defining

$$ \left\{ {\begin{array}{*{20}c} {C_{3} = 1/C_{1}^{*} } \\ {C_{4} = 1/C_{2}^{*} } \\ \end{array} } \right. $$

(41)

(40) can be expressed as:

$$ \exp \left( {C_{4} } \right) = 1 + C_{3} $$

(42)

2) At the MPP point, assuming V = V_m, I = I_m,(38) can be derived as:

$$ 1 + (1 - \gamma_{{I_{\text{m}} }} )C_{3} = \left( {1 + C_{3} } \right)^{{\gamma_{{V_{\text{m}} }} }} $$

(43)

Defining

$$ y = 1 + (1 - \gamma_{{I_{\text{m}} }} )C_{3} - \left( {1 + C_{3} } \right)^{{\gamma_{{V_{\text{m}} }} }} $$

(44)

which is the key equation to get the solution of C₃ when y = 0. The curve of (44) is shown in Fig. 1.

Fig. 1

Curve of (44)

4.4 Solution of C₁* and C₂*

Normally, C₃ >> 1 when $\gamma_{{I_{\text{m}} }} \in [0.85,0.99];\;\;\;\gamma_{{V_{\text{m}} }} \in [0. 7 5,0. 8 5 ]$ [10]. Thus:

$$ 1 + C_{3} \cong C_{3} $$

(45)

(43) can be expressed by C₁* according to (41) as:

$$ C_{1}^{*} \left[ {C_{1}^{*} - \left( {1 - \frac{{I_{\text{m}} }}{{I_{\text{SC}} }}} \right)^{{\frac{1}{{\left( {1 - \frac{{V_{\text{m}} }}{{V_{\text{OC}} }}} \right)}}}} } \right] = 0 $$

(46)

Since C₃ >> 1, C ^*₁ ≠ 0, the final solution is given by

$$ C_{1}^{*} = \left( {1 - \frac{{I_{\text{m}} }}{{I_{\text{SC}} }}} \right)^{{\frac{1}{{\left( {1 - \frac{{V_{\text{m}} }}{{V_{\text{OC}} }}} \right)}}}} $$

(47)

which is same with C₁ in direct form given by (8), proving the indirect form given by (2). From (45), (42) can be written as:

$$ \exp (C_{4} ) = C_{3} $$

(48)

Thus

$$ C_{2}^{*} = \left( {C_{4}^{*} } \right)^{ - 1} = \left( {\ln C_{3}^{*} } \right)^{ - 1} = \left( {\frac{{V_{\text{m}} }}{{V_{\text{OC}} }} - 1} \right)/\ln \left( {1 - \frac{{I_{\text{m}} }}{{I_{\text{SC}} }}} \right) $$

(49)

which is also exactly the same with (3).

4.5 I₀ and V_T in generic single-diode PV circuit model

According to (39) and (7), I₀ and V_T are given by

$$ I_{0} = C_{1}^{*} I_{\text{sc}} = I_{\text{sc}} \left( {\sigma_{{I_{\rm m} }} } \right)^{{\frac{1}{{\sigma_{{V_{\text{m}}}}}}}} $$

(50)

$$ V_{\text{T}} = C_{2}^{*} V_{\text{oc}} = - V_{\text{oc}} \left( {\sigma_{{_{{V_{\text{m}} }} }} } \right)/\left( {\ln \sigma_{{_{{I_{\text{m}} }} }} } \right) $$

(51)

5 The conformity measurement of STC sub-model calculated data with manufacturer’s datasheet

5.1 The error of the calculated maximum voltage in model and the provided maximum voltage

According to (20), the relative error is defined as:

$$ \delta_{{V_{\text{oc}} }} = \frac{{V_{\text{oc}}^{\prime\prime} - V_{\text{OC}} }}{{V_{\text{OC}} }} = \frac{{V_{\text{oc}}^{\prime\prime} }}{{V_{\text{OC}} }} - 1 = C_{2} \ln \left( {1 + \frac{1}{{C_{1} }}} \right) - 1 $$

(52)

$$ = - \left( {\ln C_{1} } \right)^{ - 1} \ln \left( {1 + C_{1}^{ - 1} } \right) - 1 $$

(53)

It is known that $\delta_{{V_{oc} }}$ is greater than 0 since C₁ is great than 0 from Fig. 2.

Fig. 2

Curve of (53)

At the open-circuit point, V_oc calculated in 2C STC sub-model is greater than the the assumed value one, and the bias $\delta_{{V_{\text{oc}} }}$ greatly depends on the value of C₁. The bias will increase if C₁ increases.

Replacing C₁ by $\gamma_{{I_{\rm m} }}$ and $\gamma_{{V_{\text{m}} }}$ into (53),

$$ \delta_{{V_{\text{oc}} }} = - (1 - \gamma_{{V_{\text{m}} }} )\ln \left( {1 + 1/\left( {1 - \gamma_{{I_{\rm m} }} } \right)^{{1/(1 - \gamma_{{V_{\text{m}} }} )}} } \right)/\ln \left( {1 - \gamma_{{I_{\rm m} }} } \right) - 1 $$

(54)

Fig. 3 shows that $\delta_{{V_{\text{oc}} }} \in \left[ { 1. 7 8 {\text{e}}^{ - 1 5} , 6. 6 7 {\text{e}}^{ - 5} } \right]$ when $\gamma_{{I_{\rm{m}} }} \in \left[ { 0. 8 5, \, 0.99 \, } \right],\quad \quad \gamma_{{V_{\text{m}} }} \in \left[ { 0. 7 5, \, 0.85 \, } \right]$. The error of the maximum voltage $V_{\text{oc}}^{\prime}$ which is calculated with the maximum voltage V_oc provided by manufactory is very small though $V_{\text{oc}}^{\prime} > V_{\text{oc}}$.

Fig. 3

Relative error $\delta_{{V_{\text{oc}} }}$with $\gamma_{{I_{\rm m} }}$ and $\gamma_{{V_{\text{m}} }}$ in (54)

5.2 The error of between $I_{\text{m}}^{\prime\prime}$ and I_m at V = V_m under STC

From (18) and (12), the relative error is given as:

$$ \delta_{{I_{\rm{m}} }} = \frac{{\Delta I_{\text{m}}^{\prime\prime} }}{{I_{\text{m}} }} = \frac{{I_{\text{m}}^{\prime\prime} - I_{\text{m}} }}{{I_{\text{m}} }} = \frac{{I_{\text{SC}} }}{{I_{\text{m}} }}C_{1} > 0 $$

(55)

$$ = \frac{1}{{\gamma_{{I_{\rm m} }} }}\left( {1 - \gamma_{{I_{\rm m} }} } \right)^{{1/\left( {1 - \gamma_{{_{{V_{\rm m} }} }} } \right)}} $$

(56)

From Fig. 4, it is shown that $\delta_{{I_{\rm{m}} }} \in \left[ { 4. 6 9 {\text{e}}^{ - 1 4} , 5. 9 6 {\text{e}}^{ - 4} } \right]$ when $\gamma_{{I_{\rm{m}} }} \in \left[ { 0. 8 5, \, 0.99 \, } \right],\;\;\;\;\gamma_{{V_{\text{m}} }} \in \left[ { 0. 7 5, \, 0.85 \, } \right]$. The error of $I_{\text{m}}^{\prime\prime}$ at $V = V_{\text{m}}$ and $I_{\text{m}}$ at the MPP point is very small though $I_{\text{m}}^{\prime\prime} > I_{\text{m}}$

Fig. 4

Relative error $\delta_{{I_{\rm{m}} }}$with $\gamma_{{I_{m} }}$ and $\gamma_{{V_{\text{m}} }}$in (56)

5.3 The error between $V_{\text{m}}^{\prime\prime}$ and $V_{\text{m}}$ at $I = I_{\text{m}}$ under STC

From (20) and (7), it can be obtained that:

$$ \delta_{{V_{\text{m}} }} = - \frac{{(1 - \gamma_{{V_{\text{m}} }} )}}{{\gamma_{{V_{\text{m}} }} \ln (1 - \gamma_{{I_{\text{m}} }} )}}\ln \left[ {1 + (1 - \gamma_{{I_{\rm{m}} }} )^{{\left( {\frac{{\gamma_{{V_{\text{m}} }} }}{{1 - \gamma_{{V_{\text{m}} }} }}} \right)}} } \right] $$

(57)

In Fig. 5, $\delta_{{V_{\text{m}} }} \in \left[ { 1. 7 8 {\text{e}}^{ - 1 3} , 5. 9 2 {\text{e}}^{ - 4} } \right]$ when $\gamma_{{I_{\rm{m}} }} \in \left[ { 0. 8 5, \, 0.99 \, } \right],\;\;\;\gamma_{{V_{\text{m}} }} \in \left[ { 0. 7 5, \, 0.85 \, } \right],$ which means the error between $V_{\text{m}}^{\prime\prime}$ and $V_{\text{m}}$ at the MPP point is very small though $V_{\text{m}}^{\prime\prime} > V_{\text{m}}$_.

Fig. 5

Relative error $\delta_{{V_{\text{m}} }}$with $\gamma_{{I_{\rm{m}} }}$$\gamma_{{V_{\text{m}} }}$ and in (57)

5.4 Prove of $V_{\text{m}} < V_{\text{m}}^{\prime} < V_{\text{m}}^{\prime\prime} \;{\text{and}}\;I_{\text{m}} < I_{\text{m}}^{\prime} < I_{\text{m}}^{\prime\prime}$

dP/dV is decreasing monotonously and it is 0 at point ($V_{\text{m}}^{\prime}$, $I_{\text{m}}^{\prime}$). If dP/dV at point (V_m, $I_{\text{m}}^{\prime\prime}$) is greater than 0, and dP/dV at (V ^″ _m , I _m ) is smaller than 0, the above non-equality can be proved.

$$ \frac{{{\text{d}}P}}{{{\text{d}}V}} = I_{\text{SC}} \left[ {\frac{I}{{I_{\text{SC}} }} - \frac{V}{{C_{2} V_{\text{OC}} }}\left( {1 + C_{1} - \frac{I}{{I_{\text{SC}} }}} \right)} \right] $$

(58)

At point (V _m , I ^″ _m ),

$$ \begin{aligned} \left. {\frac{{{\text{d}}P}}{{{\text{d}}V}}} \right|_{{(V_{\text{m}} ,I_{\text{m}}^{\prime\prime} )}} = I_{\text{SC}} \left[ {\left( {C_{1} + \frac{{I_{\text{m}}^{{}} }}{{I_{\text{SC}} }}} \right) - \frac{{V_{\text{m}} }}{{C_{2} V_{\text{OC}} }}\left( {1 - \frac{{I_{\text{m}}^{{}} }}{{I_{\text{SC}} }}} \right)} \right] \\ = I_{\text{SC}} \left\{ {1 + (1 - \gamma_{{I_{\rm{m}} }} )\left[ {\left( {1 - \gamma_{{I_{\text{m}} }} } \right)^{{\left( {\frac{{\gamma_{{V_{\text{m}} }} }}{{1 - \gamma_{{V_{\text{m}} }} }}} \right)}} - 1 - \frac{{\gamma_{{V_{\text{m}} }} }}{{1 - \gamma_{{V_{\text{m}} }} }}\ln \left( {1 - \gamma_{{I_{\text{m}} }} } \right)} \right]} \right\} \\ \end{aligned} $$

(59)

From Fig. 6, dP/dV is greater than 0 when $\gamma_{{I_{\text{m}} }} \in \left[ { 0. 8 5, \, 0.99 \, } \right],\quad\,\gamma_{{V_{\text{m}} }} \in \left[ { 0. 7 5, \, 0.85 \, } \right]$.

Fig. 6

Curve of dP/dV at point (V _m , $I_{{\text{m}}}^{\prime\prime}$) in (59)

From (17), it can be derived that

$$ V_{\text{m}}^{\prime\prime} = C_{2} V_{\text{OC}} \ln \left[ {1 + \frac{1}{{C_{1} }}\left( {1 - \frac{{I_{\text{m}} }}{{I_{\text{SC}} }}} \right)} \right] = C_{2} V_{\text{OC}} \ln \left[ {1 + \frac{1}{{C_{1} }}(1 - \gamma_{{I_{\rm{m}} }} )} \right] $$

(60)

Then (58) can be expressed as:

$$ \left. {\frac{{{\text{d}}P}}{{{\text{d}}V}}} \right|_{{\left( {V_{{\text{m}}}^{{\prime \prime }} ,I_{{\text{m}}} } \right)}} = I_{{{\text{SC}}}} \left \{ 1 - (1 - \gamma _{{I_{{\text{m}}} }} )\left \{1 + \left[ {1 + \left( {1 + (1 - \gamma _{{I_{{\text{m}}} }} )^{{\frac{{\gamma _{{V_{{\text{m}}} }} }}{{1 - \gamma _{{V_{{\text{m}}} }} }}}} } \right)} \right] \right \} \times \ln \left( {1 + \left( {1 - \gamma _{{I_{{\text{m}}} }} } \right)^{{\frac{{ - \gamma _{{V_{{\text{m}}} }} }}{{1 - \gamma _{{V_{{\text{m}}} }} }}}} } \right) \right \} $$

(61)

The value of dP/dV at point ($V_{{\text{m}}}^{\prime\prime}$, I _m ) is smaller than 0 when when $\gamma_{{I_{\text{m}} }} \in \left[ { 0. 8 5, \, 0.99 \, } \right],\;\;\;\;\gamma_{{V_{\text{m}} }} \in \left[ { 0. 7 5, \, 0.85 \, } \right]$ in Fig. 7.

Fig. 7

Curve of dP/dV at point ($V_{{\text{m}}}^{\prime\prime}$, I _m ) in (61)

5.5 The error between the maximum power calculated in model and provided by manufactory

Defining the voltage and current at the MPP point are V ^′_m and I ^′_m P_m = V_mI_m, the error can be given as:

$$ \delta_{{P_{\text{m}} }} = \frac{\Delta P}{{P_{\text{m}} }} = \frac{{P_{\text{m}}^{\prime} - P_{\text{m}} }}{{P_{\text{m}} }} = (1 + C_{1} )\frac{{I_{\text{SC}} }}{{I_{\text{m}} }}\frac{{V_{\text{m}}^{\prime} }}{{V_{\text{m}} }} - C_{2} \frac{{I_{\text{m}}^{\prime} }}{{I_{\text{m}} }}\frac{{V_{\text{OC}} }}{{V_{\text{m}} }} - 1 $$

(62)

It is difficult to have an explicit expression of $\delta_{{P_{\text{m}} }}$. It is proved above that

$$ V_{\text{m}} < V_{\text{m}}^{\prime\prime} < V_{\text{m}}^{\prime\prime} \;,\;I_{\text{m}} < I_{\text{m}}^{\prime\prime} < I_{\text{m}}^{\prime\prime} $$

(63)

From (56) and (57), it is derived that

$$ \frac{{I_{\text{m}}^{\prime\prime} }}{{I_{\text{m}} }} = \delta_{{I_{m} }} + 1 < \hbox{max} \left( {\delta_{{I_{\rm{m}} }} } \right) + 1 = 1.000{,}596 $$

(64)

$$ \frac{{V_{\text{m}}^{\prime\prime} }}{{V_{\text{m}} }} = \delta_{{V_{\text{m}} }} + 1 < \hbox{max} \left( {\delta_{{V_{\text{m}} }} } \right) + 1 = 1.000{,}592 $$

(65)

Thus:

$$ \begin{aligned} \delta_{{P_{\text{m}} }} = \frac{\Delta P}{{P_{\text{m}} }} = \frac{{P_{\text{m}}^{\prime\prime} }}{{P_{\text{m}} }} - 1 = \frac{{I_{\text{m}}^{\prime} V_{\text{m}}^{\prime} }}{{I_{\text{m}} V_{\text{m}} }} - 1 < \frac{{I_{\text{m}}^{\prime\prime} V_{\text{m}}^{\prime\prime} }}{{I_{\text{m}} V_{\text{m}} }} - 1 \\ < (\hbox{max} (\delta_{{V_{\text{m}} }} ) + 1)(\hbox{max} (\delta_{{I_{\rm{m}} }} ) + 1) - 1 \\ = 1.000{,}596*1.000{,}592 - 1 = 0.001{,}19 = 0.119\% \\ \end{aligned} $$

(66)

which means the model relative error of the calculated maximum power is small and negligible.

6 Conclusion

1) 2C model is a single-diode circuit model, since it can be derived to a single-diode circuit model theoretically. (39) defines the original physical parameters of 2C, i.e., C₁ is the ratio of reverse saturation current I₀ to the short circuit current I_sc, C₂ is the ratio of energy equivalent V_T to the open circuit voltage V_oc.

2) The expressions of C₁ and C₂ in manufacturer’s datasheet of 2C model are mostly correct under a reasonable approximation assumption for almost manufacturer’s PV modules.

3) Though there are contradictions of 2C model with manufacturer’s datasheet, the relative errors are very small, which can be negligible in engineering application.

4) The conformity error measurement method by 3D curves gives a systematic method for power community users to be aware of the conformity errors of their own PV modules by using 2C model in real application.

Therefore, the calculate data in 2C model is almost the same with the manufacturer’s datasheet under STC. If applying 2C model in a real application, it is necessary to find other PV module models.