1 Introduction

By 2022, the length of China’s high-speed railways (HSRs) in operation exceeded 40,000 km, and the total length of China's railways in operation exceeded 150,000 km [1]. In China, bridges play an important role in HSRs. Take the Beijing–Shanghai HSR line as an example, the ratio of the total length of bridges to the length of the entire line is more than 80%. With the large-scale construction and development of China’s HSRs, the running safety has become one of the major issues confronted by the high-speed trains during operation in complex environments [2]. The China’s HSR network is expanding to southeast coastal and southwest mountainous areas where geological conditions are hostile and complex. The maritime railway bridges face a high risk of excessive wind and waves loads, which threaten the safety of bridges and railways. In addition, the severity of vessel–bridge collisions on bridges across the sea and river is becoming increasingly prominent. Different from the coastal or plain areas, the mountainous areas are more prone to earthquakes, rockfalls, and other types of mountainous disasters due to complex topography and terrain, which also pose a significant threat to the running safety of the high-speed railways. Meanwhile, higher speeds of trains result in more complex coupled vibrations of the train–bridge system under external excitations [3]. The number of long-span bridges which are characterized by high flexibility and low structural damping are increasing, which makes the bridges more vulnerable to vibrations due to the external excitation. For the above reasons, train derailment and overturning accidents caused by external excitation occur from time to time around the world. It is vitally meaningful to conduct studies on coupling vibrations of the train–bridge system under external excitations.

As the train passes a bridge at a certain speed, the movement of train mass along the bridge will change the natural vibration characteristics of the bridge. Because of the track irregularity, manufacturing deviations and wheel–rail defects, the train and bridge have characteristics of self-excitation, probably causing the coupling vibration between the moving train and the bridge [4]. When trains pass through the bridge, the dynamic characteristics of trains could be directly or indirectly affected by the external excitation. The direct effects are mainly induced by the wind and earthquake loads, while the indirect effects are mainly caused by waves and collision loads. Usually, direct effects act on the both trains and bridges; in contrast, indirect effects firstly affect the vibration of the bridge, which in turn affects the vibration of the train. The external excitations will cause the bridge displacement, which is equivalent to changing the track irregularity, will also affect the vibration of the train. With the gradual improvement of vehicle–track coupled dynamics theory [5, 6] as well as the test technology of external excitations of train–bridge systems, the analytical method based on the coupling vibration of train–bridge systems under external excitations has gradually become the main way to evaluate the running safety of the trains and bridges [7].

Through focusing on the research progress in the past 10 years, this work first reviews and introduces the train–bridge coupling system, followed by the review and analysis on the research status of the influence of winds, waves, impact loads and seismic loads on the train–bridge coupling system.

2 Train–bridge coupling vibration model

In general, the train–bridge coupling vibration refers to the train–bridge system without considering the influence of rail, while train–track–bridge (TTB) coupling vibration includes the additional influence of the rail. As a matter of fact, trains operate on the track structures, and track structures are laid on bridge decks. That means the track ties the train and bridge together. When trains running on different track structures, the wheel–rail forces are different, resulting in different vibrations of tracks and bridges [8]. There are a lot of studies focusing on the coupling vibration of train–bridge systems [2, 9], and this paper only gives a brief review. In the train–bridge system, the finite element model is generally used to establish the bridge model; the vehicle model can be simplified to a mass–spring–damper system, which typically includes one body, two bogies and four wheelsets (see Fig. 1). Both the body and bogie have 5 degrees of freedom (DOFs). When different DOFs are selected for wheelsets, vehicle models with 23, 27, 31 and 35 DOFs can be obtained, respectively. The motion equations of vehicle models can be derived in D’Alembert’s principle. The specific expressions of vehicle equations are available in the literature [5, 6, 10], which are thus not introduced in details in this paper. It is also noted that more refined train models [11, 12] can also be obtained by commercial code, such as SIMPACK.

There is also plentiful research on the coupling vibration model of train–track–bridge systems [13] (see Fig. 2), and some of the commonly-used models are introduced herein. A TTB model typically consists of a wheel–rail dynamic interaction model and a track–bridge dynamic interaction model. Zhai et al. [14] started to investigate the train–track–bridge system dynamics in 1995, which is an extension of the vehicle–track coupled dynamics. In 1997, Zhai et al. [8] established a train–track–bridge dynamic interaction model (TTBDIM) by including a detailed track submodel. The model could be a two-dimensional model (2D model) or a three-dimensional model (3D model). Based on that, the goal to provide an analytical methodology for simulating trains passing bridges in high-speed operation has been achieved, and TTBDIM is becoming more refined [8].

Fig. 1
figure 1

Mass–spring–damper model of vehicles [15]

Full size image
Fig. 2
figure 2

Train–track–bridge dynamic interaction model [13]

Full size image

For convenience, the train–bridge coupling vibration and the train–track–bridge coupling vibration are unified as train–bridge coupling vibration in this paper.

In terms of wheel–rail contact theory, there are mainly two models: one is to consider wheel–rail interaction with spring force and damping force, and the other is to solve the normal and tangential contact forces between wheel and rail using the wheel–rail contact theory. Generally, three methods are commonly used to solve for the wheel–rail normal force, i.e., the spring method, the constraint equation method and the Hertz contact theory. The creep force analysis theory mainly includes Kalker linear theory, Shen theory, and so on [5, 6].

Numerical methods proposed for solving the governing equations of the dynamic system [9] include the direct coupling method, the in-time-step iteration method, the intersystem iteration method, the explicit integration method (Zhai method) [16], and the Park method [17]. Train and bridge are often regarded as two subsystems, and the Newmark-β method is often used to solve the equation through separate iteration. In addition, the Ruge–Kutta method is also employed in some studies to solve the equation.

Although the time-domain method can consider the effect of various factors comprehensively, it is still difficult to evaluate the reliability of the train–bridge system. Therefore, an increasing number of random vibration methods are proposed recently, which includes the probability density evolution method (PDEM) [18], pseudo-excitation method (PEM) [19,20,21], statistical linearization [22], surrogate model approach [23, 24], subset simulation [25], new point estimation method [26] and other theories or methods [27, 28].

3 Effect of crosswinds

During the past several decades, significant efforts have been devoted by many researchers to studying wind–train–bridge coupling vibrations, and huge improvements have been achieved in this regard. Li et al. [15] and Cai et al. [29] summarized the development and achievement of wind–train–bridge systems. This section presents a review of the research status in terms of wind loads, wind–train–bridge coupling vibration and its application, during the past decade.

3.1 Wind load of train–bridge system

Wind loads acting on train–bridge system are usually divided into three parts: static wind loads, buffeting loads and self-excited loads [15]. Usually, the incoming wind speed of the train in the running process is relatively small, and the vibration displacements of the train and the bridge are relatively small as well. In addition, the self-excited load of the bridge and train is also relatively small, which is not discussed in this paper. In fact, the sudden-change effect of wind load is one of the controlling factors of the wind–vehicle–bridge (WVB) system and has received great attention. In view of this, the wind loads of the train–bridge system are reviewed from the following three aspects: static wind loads, buffeting loads, and wind load sudden-change effect.

3.1.1 Static wind loads

There are mainly three methods proposed to study the aerodynamic coefficients of the train–bridge system: the wind tunnel test, numerical simulation and field measurement. The field measurement is costly, and it is difficult to obtain the aerodynamic coefficients of moving trains. Therefore, the wind tunnel test and numerical simulation are most used among the aforementioned three methods. For the train–bridge system, the bridge is usually in a static state, and therefore, it is convenient to obtain its aerodynamic coefficient through wind tunnel test or numerical simulation. Different from the bridge that is in static state, the train is in a moving state, which requires more sophisticated test facilities or advanced simulation techniques to obtain the aerodynamic coefficients. The aerodynamic coefficients of trains are defined as [15]:

$$C_{\text{D}} \left( \alpha \right) = \frac{{F_{\text{D}} \left( \alpha \right)}}{{\frac{1}{2}\rho U^{2} HL}},\;C_{\text{L}} \left( \alpha \right) = \frac{{F_\text{L} \left( \alpha \right)}}{{\frac{1}{2}\rho U^{2} BL}},\;C_{\text{M}} \left( \alpha \right) = \frac{{M_{Z} \left( \alpha \right)}}{{\frac{1}{2}\rho U^{2} B^{2} L}},$$
(1)

where \(C_{\text{D}}\), \(C_{\text{L}}\) and \(C_{\text{M}}\) are drag coefficient, lift coefficient and moment coefficient, respectively; \(F_{\text{D}}\), \(F_{\text{L}}\) and \(M_{Z}\) are drag force, lift force and moment, respectively; \(\alpha\) is the angle of attack of the incoming wind; \(\rho\) is the air density; \(U\) is the incoming wind speed; \(H\), \(B\) and \(L\) are the height, width and length of the model, respectively; the aerodynamic coefficients of bridges can also be defined in a similar way.

The wind tunnel test methods for aerodynamic characteristics of train–bridge systems include static and moving train model tests. The force sensor and pressure sensor can be used to test the aerodynamic forces and moments. The traditional test method mainly adopts the static vehicle model wind tunnel test, in which the force is measured by the balance. Recently, the moving train model test was used in several studies [30, 31] to compare with the static train model test. The results show that the aerodynamic coefficients obtained by the two test methods are different. However, the method of static train model test is still used in practical engineering applications due to its convenience.

For the static train model wind tunnel test, He et al. [32] and Guo et al. [33], respectively, used the pressure measurement method to test the aerodynamic characteristics of the train model on a simply supported box girder. The static test ignores the relative motion of train and bridge deck [34], which could lead to inaccurate prediction of aerodynamic characteristics of train–bridge system. To overcome this problem, the moving train model wind tunnel test is proposed, which can be divided into two categories according to the moving speed of the train model: high-speed experiments and low-speed experiments.

A high-speed moving train in model experiments requires a long sliding track, which makes it difficult to conduct such experiments with the conventional wind tunnel. Li et al. [35] proposed a moving train model test device with a length of 164 m for the high-speed train, and the drag coefficients of train in the direction of movements is determined by machine vision technology. In addition, the test speed can reach up to 55 m/s. However, it is difficult to consider the effect of crosswinds using the proposed device. Usually, the low-speed moving train model test is carried out in a conventional wind tunnel, and the moving speed and time for acceleration and deceleration of the train model are constrained by the section size of the wind tunnel. Li et al. [36] proposed a 1/45-scaled moving train model device for wind tunnel test. The track length is 18 m, the maximum speed is 10 m/s, and the train is a three-car model (see Fig. 3). The device is driven by servo motor and drives the vehicle through steel wire rope. The sliding track of the train model is located above the bridge deck. The deceleration of the moving train model needs special treatment.

Fig. 3
figure 3

Schematic diagram of the moving vehicle model device [36]

Full size image

If the train model moves on a guideway, the rail irregularity is inevitable, which could induce vehicle inertia force, affecting the accuracy of force measurements. Therefore, the aerodynamic force testing method and the smoothness of moving guide rail for the train model are two important aspects to improve the accuracy of test results. Dorigatti et al. [37] tested the aerodynamic characteristics under crosswinds of a moving vehicle model by pressure measurement. He et al. [38] arranged 200 measuring points on the vehicle model. To improve the track of moving train model, Xiang et al. [39] adopted a linear module as the sliding track, where a servo motor drives the train model via synchronous belt (see Fig. 4a and b). The speed range is 0.5–10 m/s. It not only accounts for the influence of wind attack angle and wind direction angle, but also realizes the bidirectional movement of the train model. The maximum acceleration of the train can reach to 50 m/s2, and the minimum acceleration distance is 1.0 m to reach the maximum speed of 10 m/s. The force balance measurement results show that the device can obtain relatively stable aerodynamic time history. When both the wind speed and train speed are different, the test data of vehicle drag coefficient CFy have good repeatability under same yaw angle β (see Fig. 4c). Li et al. [34] proposed a new aerodynamic test system for trains, which uses servo motor synchronous drive system and wireless sensor module to measure the aerodynamic force on high-speed trains. The maximum speed of the train model can reach to 15 m/s, and the effective acquisition time is 0.7 s. In addition, due to the independent arrangement between the bridge model and the driving system, the replacement of the bridge model can be realized and the adaptability of the system is improved.

Fig. 4
figure 4

The device of moving vehicle model in wind tunnel tests and experimental results (units: m): a vertical view; b lateral view; c result validation [34, 39]

Full size image

He et al. [40] proposed an experimental facility in the low-speed wind tunnel to study the aerodynamic characteristics of moving trains on the bridge. The train model is driven by the gravity because the train model is moving on a big U-shaped slide rail guide with two huge arch guide rails, and the maximum speed of train can reach up to 6 m/s. A wireless data acquisition system is installed on the train carriages to measure the pressure during the test. The aerodynamic characteristics of the train–bridge system are studied comprehensively through surface wind pressure distributions. Hu et al. [41]. proposed a wind tunnel device (see Fig. 5) which has two moving tracks to test the aerodynamic characteristics of moving vehicles under crosswinds.

Fig. 5
figure 5

The device with two moving tracks [41]

Full size image

Due to the limitation of current experiment technology, the Reynolds number of wind tunnel test is still relatively low. To overcome this issue, the numerical simulation method is often adopted. There are four methods to simulate the relative movement of trains, i.e., the moving wall method [42], multi-reference system method, sliding grid method [43] and moving grid method [30]. The former two methods are suitable for the simulation of steady aerodynamic characteristics, while the latter two methods can be used for the simulation of unsteady aerodynamic characteristics, for instance, two trains passing each other, train passing bridge tower and so on.

Meanwhile, the simple bridge sections [44, 45], such as box girder, are usually selected for the numerical simulation. However, most long-span high-speed railway bridges adopt plate-truss structure as the main girder, which has a very complex aerodynamic shape that the current numerical simulation techniques are usually incapable of yielding accurate prediction results [46].

3.1.2 Buffeting loads

The buffeting loads of bridges and trains are usually determined using the analytical model in structural wind engineering. According to Scanlan’s quasi-steady aerodynamic force expression, the buffeting loads on the bridge and vehicle per unit length can be expressed as follows [15]:

$$\begin{array}{*{20}l} {D_{\text{bu}} \left( {x,t} \right) = \frac{1}{2}\rho U^{2} B\left[ {2\frac{H}{B}C_{\text{D}} \left( {\alpha_{0} } \right)\frac{{v\left( {x,t} \right)}}{U}\gamma_{1} \left( t \right)} \right],} \hfill \\ {L_{\text{bu}} \left( {x,t} \right) = - \frac{1}{2}\rho U^{2} B\left\{ {2C_{\text{L}} \left( {\alpha_{0} } \right)\frac{{v\left( {x,t} \right)}}{U}\gamma_{2} \left( t \right) + \left[ {C^{\prime}_{\text{L}} \left( {\alpha_{0} } \right) + \frac{H}{B}C_{\text{D}} \left( {\alpha_{0} } \right)} \right]\frac{{w\left( {x,t} \right)}}{U}\gamma_{3} \left( t \right)} \right\}} \hfill \\ {M_{\text{bu}} \left( {x,t} \right) = \frac{1}{2}\rho U^{2} B^{2} \left[ {2C_{\text{M}} \left( {\alpha_{0} } \right)\frac{{v\left( {x,t} \right)}}{U}\gamma_{4} \left( t \right) + C^{\prime}_{\text{M}} \left( {\alpha_{0} } \right)\frac{{w\left( {x,t} \right)}}{U}\gamma_{5} \left( t \right)} \right],} \hfill \\ \end{array} ,$$
(2)

where \(D_{{\text{bu}}}\), \(L_{\rm bu}\) and \(M_{{\text{bu}}}\) are the buffeting drag load, buffeting lift load and buffeting moment, respectively; \(C^{\prime}_{\text{L}}\) and \(C^{\prime}_{\text{M}}\) are the slope of lift coefficient and moment coefficient, respectively; \(v\left( {x,t} \right)\) and \(w\left( {x,t} \right)\) are the transverse and vertical fluctuating wind speeds at position x along the main beam, respectively; \(\gamma_{i} \left( t \right)\) (i = 1,2,…,5) is the aerodynamic admittance function in time domain; \(\alpha_{0}\) is wind attack angle.

In Eq. (2), the aerodynamic coefficients, fluctuating wind speeds and aerodynamic admittances are three important classes of parameters for calculating the buffeting loads. The acquisition method of aerodynamic coefficient has been discussed above and thus are not repeated herein.

For the continuous fluctuating wind field, it can be discretized into spatially related multiple wind speed points by the common method in wind engineering. However, for moving trains, two kinds of wind spectra are often used for the simulation of fluctuating wind: one is the dynamic wind spectrum, and the other is the static point wind spectrum. The dynamic wind spectrum is related to train speed [47], while the static wind spectrum is not affected by train speed. To ensure calculation efficiency, the number of simulation points in most simulation methods is limited. The distance between wind field simulation points of long-span bridges is usually large (generally 10 m), and the wind speed varies greatly when transiting from one wind speed point to another, resulting in certain differences when used for the calculation of train buffeting loads. The simulation method of moving wind spectrum is to convert multi-point wind field simulation into single-point simulation, which can effectively avoid the error of multi-point dispersion of wind field. Based on Taylor’s freezing assumption, the moving wind spectrum is derived from Kaimal spectrum [47] and Simu spectrum [48]. Yan et al. [49] proposed a spectral analysis framework for analyzing the overturning risk of high-speed trains based on Kaimal spectrum, and Wu et al. [50] also derived the formula for calculating the power spectrum and the correlation coefficient function of wind turbulence relative to moving trains based on Kaimal spectrum. The dynamic wind spectrum aims at the fluctuating wind load of moving trains, which cannot ensure the synchronous coordination of wind spectrum between trains and bridges, while static moving wind field can ensure that bridges and trains are in the same fluctuating wind field.

Aerodynamic admittance is an important parameter reflecting the buffeting loads of train, and the aerodynamic force of train would be overestimated if the effect of aerodynamic admittance is neglected. The aerodynamic admittance is mainly obtained from wind tunnel tests [51, 52], numerical simulation [53,54,55] and field measurement. At present, wind tunnel test is still the most important way, and the numerical solution of aerodynamic admittance mainly includes two-dimensional and three-dimensional simulations. So far, two kinds of train aerodynamic admittance expressions have been proposed, namely, the theoretical calculation formula and the fitted formula. After the aerodynamic admittance is determined, there are also two ways to simulate the pulse force of trains. One is using the aerodynamic weight function [56, 57] to get the pulse force by integrating in the time domain, and the other is using the aerodynamic admittance to correct the wind spectrum. Based on this, much research has been made, aiming at a more convenient, practical and accurate calculation formula or function.

3.1.3 Sudden change effect of winds

The sudden change of wind loads, which is a phenomenon caused by the wind shielding effect of pylons and also typically observed from two trains passing each other, is a controlling factor for a WVB system. In case of sudden change of wind loads, the wind loads acting on the train will experience a sudden decrease or increase, which is extremely unfavorable to the running safety.

Two methods are commonly used to study the wind shielding effect of bridge tower: one is wind tunnel test [58,59,60], and the other is computational fluid dynamics [61,62,63]. The wind tunnel test involves the static train model and the moving train model. In the static train model, the train is manually relocated in different positions to test the aerodynamic characteristics and obtain the aerodynamic curve when trains cross the bridge tower [64]. In the moving train model, the experiment is conducted with moving trains [58]. The two kinds of wind tunnel tests will produce different test results (see Fig. 6). The aerodynamic coefficients will increase when the train directly enters the tail of the tower. Since the length of the train model is greater than the width of the bridge tower, when the train speed is low, the sudden change effect of wind load has relatively little impact on the safety of the train. The numerical simulation mainly aims to simulate aerodynamic characteristics and evaluate the impact of train speed. Wang et al. [65] computed the dynamic aerodynamic coefficients through the simulation of moving vehicles passing by the bridge tower using the dynamic mesh method. The results show that the bridge tower has significant shielding effect on the aerodynamic forces of the vehicles, and the simulated aerodynamic coefficients are larger than those measured from the wind tunnel tests.

Fig. 6
figure 6

Drag coefficient of vehicles crossing pylons [58]

Full size image

Three types of methods are usually adopted to investigate the sudden change effect of wind loads for two trains passing by each other in wind tunnel tests. First, for the intersection of stationary trains, the aerodynamic curve of the train is “concave” or “convex”, which is a commonly used method at present [66]. The final curve can also be synthesized by testing the aerodynamic coefficients of train at different positions. Second, static-dynamic intersection, usually the train on the windward side or leeward side is in a stationary state [31]. Third, dynamic intersection, both trains on the windward side and leeward side are in motion [41]. The results of the three test methods are different (see Fig. 7).

Fig. 7
figure 7

Drag coefficient of two trains passing by each other [41]

Full size image

Numerical methods can simulate well the relative motion between trains. Huang et al. [67] used the sliding grid method to simulate the process of double-vehicle intersection. In addition, the fluid structure coupling method can be used to address the effect of train and bridge displacement on the aerodynamic characteristics of two trains passing by each other on the bridge.

3.2 Analytical model

After the wind loads of the train–bridge system is defined, the governing equations of motion of the WVB system (see Fig. 8) can be obtained on the basis of the train–bridge coupling model [15]:

$$\begin{gathered} {\varvec{M}}_{\text{b}} {\ddot{\varvec u}}_{\text{b}} + {\varvec{C}}_{\text{b}} \dot{\varvec{u}}_{\text{b}} + {\varvec{K}}_{\text{b}} {\varvec{u}}_{\text{b}} = {\varvec{F}}_{\text{stb}} + {\varvec{F}}_{\text{bub}} + {\varvec{F}}_{\text{seb}} + {\varvec{F}}_{\text{vb}} , \hfill \\ {\varvec{M}}_{\text{v}} {\ddot{\varvec u}}_{\text{v}} + {\varvec{C}}_{\text{v}} \dot{\varvec{u}}_{\text{v}} + {\varvec{K}}_{\text{v}} {\varvec{u}}_{\text{v}} = {\varvec{F}}_{\text{stv}} + {\varvec{F}}_{\text{buv}} + {\varvec{F}}_{\text{bv}} , \hfill \\ \end{gathered}$$
(3)

where the subscripts ‘b’ and ‘v’ stand for bridge and train, respectively; \({\varvec{M}}\), \({\varvec{C}}\) and \({\varvec{K}}\) are mass, damping and stiffness matrices, respectively; \({\varvec{F}}_{\text{st}}\), \({\varvec{F}}_{\text{bu}}\) and \({\varvec{F}}_{\text{se}}\) are static wind loads, buffeting wind loads and self-excited wind loads, respectively (specific expressions of the static wind loads and buffeting loads are shown in Eqs. (1) and (2), respectively); \({\varvec{F}}_{\text{vb}}\) and \({\varvec{F}}_{\text{bv}}\) are the interaction force between train and bridge; \({\varvec{u}}\) represents the displacement vector.

Fig. 8
figure 8

Schematic diagram of train–bridge system subjected to wind load

Full size image

The wind load parameters of the train–bridge system are required to facilitate the analysis. The static wind force coefficient of the train–bridge system needs to be obtained by wind tunnel test or numerical simulation. The aerodynamic admittances of trains and bridges are often set as 1.0 for conservative purpose. Flutter derivatives of bridges can be obtained through wind tunnel tests, and for its identification methods one can refer to the relevant literature [15]. The rail irregularities and fluctuating wind fields can be simulated by spectral methods. Finally, separated iteration and whole-process iteration can be used to solve Eq. (3).

3.3 Effect of crosswinds on train–bridge system

There are many factors affecting the WVB system, including the aerodynamic coefficients, average wind speed, fluctuating wind, rail irregularities, train and bridge parameters, and sudden change of wind loads. To reveal the influence laws of these parameters, we need to conduct sensitivity analysis on various parameters of the WVB system.

For a specific train–bridge system, the response of the train increases with the wind speed [68]. When other conditions except wind load are kept the same, the vertical acceleration of the train under the average wind load is higher than that under both the mean wind load and fluctuating wind load. The average wind speed has a relatively small effect on the acceleration of train, but it has a significant effect on the wheel unloading rate of the train. Fluctuating winds will increase the response of trains and bridges, and the response of trains and bridges will increase if the correlation of fluctuating wind field is neglected. The lateral wheelset force of trains mainly depends on the geometric irregularity of rail. Generally, for long-span bridges, its displacement under wind load and train load is equivalent to the long-wave irregularity, whose influences on the response of trains are relatively limited (see Fig. 9).

Fig. 9
figure 9

The effect of crosswinds on the vertical acceleration av of train body: a under mean wind; b under average wind and fluctuating wind (modified after [68])

Full size image

When the average wind speed, fluctuating wind speed and rail irregularities are fixed, there is a significant correlation between the aerodynamic coefficients of the train and its various responses, such as the lateral acceleration and drag coefficient of the train body, vertical acceleration and lift coefficient of the train body, derailment coefficient, wheel unloading rate, and overturning moment coefficient [69]. A typical example is that when different wind barrier heights are set, the aerodynamic parameters of the train will change, and the response of train also changes, showing a certain correlation. In most of the existing WVB coupling vibration studies, the aerodynamic coefficients of trains under different wind deflection angles are described by the sinusoidal criterion, which is essentially the aerodynamic coefficients of stationary trains under train incoming flow. Due to the long length of the train, the criterion is basically applicable to the middle car. However, the aerodynamic coefficients of the head car and the tail car in motion are obviously different from those of other cars.

When considering the effect of train movement, crosswinds have a great impact on train safety, but their impact on bridge vibration can be basically ignored. Different bridge sections have different flow patterns. Different aerodynamic coefficients will be obtained when trains are combined with different bridge sections. Trains will also have different aerodynamic coefficients at different positions on the bridge deck, which will also affect the coupling vibration performance of the WVB system.

The crosswind plays a dominant role in the transverse response of a bridge [68]. The lateral displacement and acceleration of the bridge increase with the increasing wind speed. The stiffness of the bridge has a certain impact on its acceleration, but the lateral vibration of trains has little impact on the lateral displacement of the bridge. In contrast, the spatial correlation of bridge buffeting force has a significant impact on the bridge dynamic response. The geometric nonlinearity of the bridge will affect the extreme value of bridge vibration, but will not affect the change trend of bridge vibration. Nonlinear factors, for instance, the cable sag effect, beam column effect and structural configuration change caused by large displacement, and the nonlinear self-excited loads, and the angle of attack effect caused by torsional angle displacement of the main beam have little effect on the train response.

In addition to time-domain analysis, some research results are obtained by frequency-domain analysis [70, 71]. The results of frequency-domain analysis are different due to the diversity of trains and bridges. Train speed has little effect on the main frequency of bridges. By studying the train–bridge system without wind, researchers [70] found that the main frequencies are dependent on the fundamental frequencies of trains and bridges. The effect of wind was then evaluated by comparison with the case without wind, and the obtained results can be summarized as follows. For suspended monorail vehicle and bridge, the dominant frequencies of bridge acceleration excited by the wind are force mainly concentrated in the range from 2 to 10 Hz, but some differences exist between the lateral and vertical effect of bridges. However, for suspended monorail vehicles, the dominant frequencies of the lateral and vertical acceleration of vehicles under different wind excitations are the same, which all are 0.24 Hz. For road truck, the main frequencies range from 1 to 10 Hz. Overall, there are few studies on the WVB coupling vibration in frequency domain in recent years, and more relevant studies are needed in the future.

The WVB coupling vibration analysis has been investigated in various aspects, including the determination of proper bridge stiffness [72], the wind barrier performance evaluation and optimization [69, 73,74,75,76,77,78] and the safety assessment of train passing the pylons [79].

4 Effect of wave loads

With the long span bridges extending to the coastal area, the running safety of trains under the action of wind, wave and flow has received increasing attention recently. Zhu et.al [80], Fang et.al [81] and Kong et.al [82] have carried out researches on this issue. This section reviews research progress from the aspects of wave loads, coupling model of wind–wave–train–bridge (WWVB) system, coupling vibration of WWVB system and so on.

4.1 Simulation of wave load

Wave load is caused by the relative motion between wave water point and structure, which is random in nature and is difficult to be described accurately in mathematical form. Offshore structures are generally classified as small-scale structures or large-scale structures. Their wave forces are usually estimated by Morison equation [83, 84] and diffraction/radiation theories, respectively [85]. To be specific, Morison equation is a semi-theoretical and semi-empirical formula, which assumes that the wave force as the sum of the resistance caused by the wave velocity and the inertial force caused by the acceleration of wave. According to diffraction theories, when the wave encounters a large-scale pier of bridges, the wave field will form an outward-scattered wave, and the incident wave and scattered wave will be superimposed to form a new wave field. Assuming that the incident and scattered waves obey the potential motion, the horizontal wave force acting on the pier per unit height can be derived from Laplace equation. Then, it is necessary to analyze the effect of correlation between wind and wave by measuring the empirical correlation of wind–wave data. The measured data should include significant wave height, average wind speed and wave period. The following formula of significant wave height and average wind speed is proposed in [81]:

$$H_{\text{S}} = aU(z_{10} )^{{^{b} }} + c,$$
(4)

where \(a\), \(b\) and \(c\) are coefficients obtained by fitting; \(H_{\text{S}}\) is significant wave height; \(U(z_{10} )\) is average wind speed.

4.2 Analytical model

By extending the WVB model mentioned above, a WWVB model (see Fig. 10) for crossing sea railway bridges is established by inclusion of the wave load [81]. The whole model includes four parts: wind field, wave field, train subsystem and bridge subsystem. The modeling of train subsystem and bridge subsystem has been already discussed in Sect. 1, while the wind field has been already described in Sect. 2. In addition, the random unidirectional wave field is adopted in the WWVB model and the associated wave load is generated through the liner irregular wave kinematic (velocity and acceleration) theory.

Fig. 10
figure 10

Schematic diagram of train–bridge system subjected to wind and wave [81]

Full size image

Five interaction relationships including train–bridge coupling, aerodynamic coupling, wind–train interaction, pier–water interaction and the combination of wind and wave are considered. To simplify the model, it is assumed that the dead weight of the structure, wave load and wind load act on the centroid of the corresponding structural element. Besides, assuming that wind and wave are unidirectional and act on the bridge along the transverse bridge, the governing equations of motion of the WWVB model can be expressed as [81]:

$$\begin{gathered} {\varvec{M}}_{\text{b}} {\ddot{\varvec u}}_{\text{b}} + {\varvec{C}}_{\text{b}} \dot{\varvec{u}}_{{\text{b}}} + {\varvec{K}}_{\text{b}} {\varvec{u}}_{\text{b}} = {\varvec{F}}_{\text{vb}} + {\varvec{F}}_{\text{wb}} + {\varvec{F}}_{\text{stb}} + {\varvec{F}}_{{\text{bub}}} + {\varvec{F}}_{{\text{seb}}} , \hfill \\ {\varvec{M}}_{\text{v}} {\ddot{\varvec u}}_{\text{v}} + {\varvec{C}}_{\text{v}} \dot{\varvec{u}}_{\text{v}} + {\varvec{K}}_{\text{v}} {\varvec{u}}_{\text{v}} = {\varvec{F}}_{{\text{bv}}} + {\varvec{F}}_{{\text{stv}}} + {\varvec{F}}_{{\text{buv}}} , \hfill \\ \end{gathered}$$
(5)

where \({\varvec{F}}_{\text{wb}}\) is the wave fore acting on the bridge; \({\varvec{F}}_{{\text{stv}}}\) and \({\varvec{F}}_{{\text{buv}}}\) are the static wind loads and buffeting force acting on the train, respectively; \({\varvec{F}}_{\text{stb}}\), \({\varvec{F}}_{{\text{bub}}}\) and \({\varvec{F}}_{{\text{seb}}}\) are the static wind loads, buffeting force and self-excited force acting on the bridge, respectively; the definitions of other terms in Eq. (2) are the same as those in Eq. (3).

4.3 Effect of wave on train–bridge system

The effect of wave load on the dynamic responses of bridge and train could be evaluated by comparing the numerical results obtained from the WVB and WWVB models. The results show that the dynamic responses of the train–bridge system increase significantly under wave loads, especially the lateral response of the bridge and train, as shown in Fig. 11.

Fig. 11
figure 11

Lateral response of train–bridge system under wave loads: a acceleration; b displacement [81]

Full size image

When wind speed and wave height are small, the lateral response of bridge is affected by the fundamental frequency of both bridge and wind or wave spectrum. However, when both the wind speed and wave height are high, the bridge response is mainly controlled by the fundamental frequency of bridge. The dynamic response of bridges and trains increase with the increase in wind speed and wave height. High wind speed and high wave height may increase the lateral displacement in the middle of bridge span and lateral acceleration of train excessively, threatening the safety of structure and the running comfort of trains. When the wave is small, the train speed is the important factor affecting the safety and comfort of the train. With the increase in wave loads, the influence of speed on the train decreases gradually [86]. Since wind–wave has an impact on the dynamic response of the train–bridge system, from another perspective, we can use the response of the train–bridge system under the joint action of wind and wave to study the scour action of wind–wave loads. Kong et al. [82] found that waves can cause significant lateral vibrations of the bridge, and therefore, the response of the bridge deck and moving vehicles can be employed to detect the erosion damage of the bridge foundation.

5 Effect of impact loads

When the train runs on the bridge, the coupled train–bridge system may be affected by impact loads. In Ref. [87], the dynamic responses of the bridge and the running safety indices of the train on the bridge under three types of collision loads are analyzed. In this section, rockfall, vessel–bridge collision, truck-bridge collision and ice–bridge collision are taken as the main impact loads affecting the coupled train–bridge model. The simulation of impact loads, the establishment of impact loads–train–bridge model, and the dynamic response of the train–bridge system under the action of impact loads are reviewed.

5.1 Simulation of impact loads

5.1.1 Rockfall load

Rockfall movement is quite complex which is influenced by many factors [88]. For example, the starting position of rockfall, topographic conditions, stratigraphic geology and vegetation coverage of hillside, and the size and shape of rockfall will affect the movement track of rockfall. The terrain conditions of hillside also play a leading role in the rockfall movement. Some simplifications and assumptions are usually made during the analysis. For example, the slope shape is assumed to be composed of several straight slope sections, the rolling stone is simplified into a sphere, and the mass distribution is uniform. In addition to the theoretical calculation of the falling track and speed of falling rocks, the professional falling rock calculation program can also be used to simulate the falling track and speed of falling rocks. The commonly used nonlinear finite element software for collision simulation and analysis is used to simulate the whole collision process and to obtain the impact forces in different stages of collision in [89].

5.1.2 Vessel–bridge collision load

Ship–bridge collision is a complicated nonlinear dynamic process with huge energy exchange taking place in a very short duration. Experiments [90] and numerical simulations [91] are usually adopted to simulate the whole collision process, in order to obtain the impact forces in different stages of collision [92]. The characteristic of the collision of bow structure is critical to study the ship–pier collision process [90]. The collision process can be divided into three stages, during which the collision force has two peak values [93]. The collision force exerted on bridge pier depends on various factors such as the collision angle, collision speed, vessel type, size and tonnage. In addition, other factors including the material and structural characteristics of the vessel and the bridge, the involved boundary conditions, and nonlinear-inelastic properties of materials [94] could also affect the collision force.

5.1.3 Truck–bridge collision load

In general, there are two types of truck–bridge collision loads depending on the collision location of the bridge, i.e., truck–pier collision that takes place at the bridge pier [95, 96], and the collision between over-height trucks and bridge superstructures [97, 98]. Experimentation [96] and numerical simulation [95, 97,98,99] are the two common approaches adopted to assess behaviors of the bridge pier subjected to the vehicular impact. There are two main ways to calculate the vehicle–bridge impact force: the equivalent static force (ESF) approach [100] and the peak impact force (PIF) approach [101]. Related studies show that the calculation results of the ESF approach are not conservative, and the PIF can better reflect the actual situation of bridge under impact [99]. Truck mass, impact velocity, and impact angle have a great influence on the truck–bridge collision load, meanwhile, impact velocity plays a dominant role in the collision force [96]. The impact process by a heavy truck was divided into four stages according to the dynamic behavior of the truck [96], namely, head affecting stage, engine affecting stage, cab crushing stage and trailer affecting stage. Similarly, Wu et al. [95] found that when the vehicle impact speed is 100 km/h, the time history curve of the impact force can be divided into three peak forces, which are vehicle’s bumper collides with the pier, vehicle’s engine impact and vehicle’s cargo impact, respectively.

5.1.4 Ice–bridge collision load

Generally, two approaches, i.e., field experiment [87, 102] and numerical simulation [103], are commonly adopted to acquire the dynamic ice collision load. The major parameters affecting the impact due to ice floe include the magnitude, duration time and frequency component of the collision force. Xia et al. [102] carried out a field experiment to obtain the time history curve of the drifting-floe collision force. These parameters are determined by the factors such as the size, mass and floating speed of the floe, and the contact manner between the floe and the pier body. Direct measurement for all these factors is quite difficult, but the major parameters can be directly identified from the time history curves of the collision force. The ice pier interaction could be grouped into three different phases, including the loading phase, extrusion phase and separation phase [103]. The ice impact loads increase continuously in the loading stage and may reach a peak in the extrusion stage.

5.2 Analytical model

Based on the train–bridge system model, the coupling vibration model of train–bridge system under impact load can be established conveniently, as illustrated in Fig. 12. The governing equations of motion of the train–bridge system subjected to impact load can be expressed as [93]

$$\begin{gathered} {\varvec{M}}_{\text{b}} {\ddot{\varvec u}}_{\text{b}} + {\varvec{C}}_{\text{b}} \dot{\varvec{u}}_{\text{b}} + {\varvec{K}}_{\text{b}} {\varvec{u}}_{\text{b}} = {\varvec{F}}_{\text{vb}} , \hfill \\ {\varvec{M}}_{\text{v}} {\ddot{\varvec u}}_{\text{v}} + {\varvec{C}}_{\text{v}} \dot{\varvec{u}}_{\text{v}} + {\varvec{K}}_{\text{v}} {\varvec{u}}_{\text{v}} = {\varvec{F}}_{{\text{bv}}} + {\varvec{F}}_{{\text{ib}}} , \hfill \\ \end{gathered}$$
(6)

where \({\varvec{F}}_{{\text{ib}}}\) is the impact load acting on the bridge; the definitions of the other terms in Eq. (6) are the same as those in Eq. (3).

Fig. 12
figure 12

Schematic diagram of train–bridge system subjected to impact load [93]

Full size image

5.3 Effect of impact loads on train–bridge system

In this section, four collision loads are taken as the representative of impact loads. Accordingly, the impact loads–train–bridge model is established and presented. Subsequently, the effect of impact loads on the train–bridge system is introduced.

The impact load is similar to the dynamic response of trains and bridges. Collision loads have an obvious effect on the dynamic responses of the bridge. Vibration of the bridge induced by collision loads has a great effect on the dynamic responses of high-speed trains [87]. The collision loads have a great influence on the lateral response of trains and bridges, while the influence becomes small with regard to the vertical response. The lateral displacements and accelerations of the bridge subjected to the collision load are much greater than those without collision. The lateral acceleration, lateral wheelset force, wheel unloading rate, and derailment coefficient of the train are significantly affected by collision loads (see Figs. 13 and 14).

The effect of impact on dynamic characteristics of the train–bridge system is also related to the position where the collision occurs. The closer to the impact point, the greater the dynamic response of the train–bridge system. Besides, the impact effect of the bridge is also related to the size of the impact force. The collision loads have time effect, which have an impact on the train–bridge system in a short period of time [89]. Additionally, the train speed, the size of the impact force and impact angle can be considered to research the effect of collision loads, and the running safety of trains is ensured by limiting train speed.

Response-spectrum analysis (RSA) [104, 105] is also used to study the effect of collision loads on the train–bridge system to avoid the limitation of the equivalent static analysis. Some RSA procedures specifically tailored to barge–bridge collisions are proposed for dynamically analyzing the bridge response to collision loads, but the response spectrums used in these studies cannot be applied accurately to the conditions in the moderate- and high-frequency ranges.

Fig. 13
figure 13

Effect of falling rock on train–bridge system [106]

Full size image
Fig. 14
figure 14

Effect of vessel–bridge collision on train–bridge system (modified after [93])

Full size image

6 Effect of seismic loads

The damage caused by earthquakes is much worse than the other natural disasters. Since high-speed railway bridges account for 50%–80% of the total length of a typical railway, earthquakes are likely to occur when trains travel on the bridges. Therefore, it is necessary to evaluate the safety of trains running on bridges under seismic load.

6.1 Analytical model

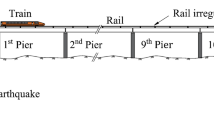
Seismic load is a kind of sudden load. Strong earthquakes release huge energy in a short time; at the same time, earthquakes have continuity, and will cause aftershock and other secondary disasters. In 2006, Xia et al. [107] established a dynamic model of coupled train–bridge systems subjected to earthquakes (see Fig. 15) in which the nonuniform characteristics of the seismic waves from different foundations are considered. Later on, Xu et al. [3] developed a new comprehensive model to fully investigate the dynamic performance of train–track systems under coupling effects of lateral earthquakes and track random irregularities. For the analysis of the lateral stability of the train crossing a bridge during the earthquake, a general analytical framework was established [108].

Fig. 15
figure 15

Schematic diagram of train–bridge system subjected to earthquake [107]

Full size image

Two methods are commonly employed to study the effect of seismic load acting on train–bridge systems, i.e., the numerical simulation [109] and the hybrid simulation [110]. The numerical simulation is usually involved with a three-dimensional seismic load–train–bridge model [111], which uses rail irregularity as the internal excitation and seismic load as the external excitation. The hybrid simulation usually combines advanced finite element analysis with sub-structure testing to simulate the nonlinear dynamic responses of a complex structure subjected to seismic loads [110]. The advantage of hybrid simulation is that the experimental costs can be reduced significantly. Seismic input methods also have certain influence on the research results of train–bridge systems, and the main seismic input methods include the direct solution method, the relative motion method, the large mass method and the large stiffness method [112]. By adopting the relative motion method, the governing equations of motion of the seismic load–train–bridge system is shown in Eq. (7) [109]:

$$\begin{gathered} {\varvec{M}}_{\text{b}} {\ddot{\varvec u}}_{\text{b}} + {\varvec{C}}_{\text{b}} \dot{\varvec{u}}_{\text{b}} + {\varvec{K}}_{\text{b}} {\varvec{u}}_{\text{b}} = {\varvec{F}}_{{\text{vb}}} + {\varvec{F}}_{{\text{gb}}} , \hfill \\ {\varvec{M}}_{\text{v}} {\ddot{\varvec u}}_{\text{v}} + {\varvec{C}}_{\text{v}} \dot{\varvec{u}}_{\text{v}} + {\varvec{K}}_{\text{v}} {\varvec{u}}_{\text{v}} = {\varvec{F}}_{{\text{bv}}} + {\varvec{F}}_{\text{gv}} , \hfill \\ \end{gathered}$$
(7)

where \({\varvec{F}}_{{\text{gb}}}\) and \({\varvec{F}}_{\text{gv}}\) are the seismic loads acting on the bridge and the train, respectively; the other terms have the same meaning as defined in Eq. (3).

6.2 Effect of earthquake excitation

To study the effect of earthquake excitation, the first step is to choose an appropriate ground motion power spectrum and generate random ground motion samples [113]. When the earthquake occurs, the earthquake excitation plays a leading role in the vibration of the train–bridge system. The impact of earthquake on train response is greater than that of rail irregularity. Seismic motions include lateral and vertical ground motions. The lateral seismic waves have a great influence on the lateral vibrations of the railway vehicles and tracks, but with relatively slight impacts on the vertical vibrations of the train–bridge systems [3]. Vertical seismic excitation has little lateral response, but it results in the slight increase of the vertical response, as shown in Fig. 16. Besides, the time of occurrence and incident direction angle of earthquake are found to be the key indexes affecting the safety of train running. Topography also plays a role in the earthquake effect results. Zhu et al. [114] found neglecting the effect of V-shaped canyon leads to the inappropriate assessment of the maximum seismic response of the irregular high-speed railway. It is well known that both track irregularities and seismic motions are random in nature. It is therefore reasonable to employ random vibration theory to analyze the dynamic responses of the train–track/bridge interaction system [115]. When analyzing the effect of earthquake on bridge vibration, the influence of train speed can be ignored, but train speed should be considered when analyzing the effect of earthquake on the train [115].

Fig. 16
figure 16

Effect of earthquake excitation on train–bridge system (modified after [109])

Full size image

The traveling wave effect should be considered for the large bearing distance of long-span bridges; PEM [115], PDEM [116] and other random vibration methods are used to study the effect of travelling waves. Zeng et al. [115] investigated the influence of traveling seismic waves on the random vibration responses of the system by employing twelve types of seismic wave propagation velocities. Tian and Lou [116] found that the responses of bridge taking into consideration the traveling wave effect significantly differ from those under uniform support motions [117]. In general, traveling waves have both positive and negative effect on structural response, which should be analyzed according to specific conditions.

Generally, frequent-domain methods are widely used in seismic research. The characteristic frequencies or frequency ranges governed by earthquakes are different greatly from those governed by track random irregularities. The lateral seismic waves dominate the characteristic frequencies of system responses of some lateral dynamic indices at low frequency [3]. RSA [118, 119] can also be used to address seismic responses of train–bridge systems. Spectrum characteristic analysis results indicated that the characteristics of earthquake motions have significant influence on the seismic acceleration responses of trains and bridges. Between the single bridge model and train–bridge coupling model, there are some differences of the period corresponding to the peak value of curves in deck acceleration spectra [120]. For the safety of the train running on the bridge subjected to earthquake, Zeng and Dimitrakopoulos [121] studied train derailment under earthquakes of various predominant frequencies; they found that the earthquake of low predominant frequency mainly affects the train derailment, while the earthquake of relatively high predominant frequency has negligible influence on the train derailment even with high acceleration amplitudes.

7 Conclusions and challenges

7.1 Conclusions

In recent years, many scholars have conducted plentiful explorations and research on the vibration performance of train–bridge systems under external excitations, and obtained many useful conclusions, which promoted the development of high-speed railway and ensured the safe operation of high-speed railway bridges in complex environments. The coupling vibration of train–bridge systems under four typical external excitations, i.e., wind, wave, impact load and earthquake excitation are reviewed in this work. The external excitations of wind and earthquake directly act on the train, while the wave and impact load indirectly affect the running of the train by acting on the bridge. The external excitations play an important role in the operation safety of the train on bridge.

7.2 Challenges

There still remain lots of interesting and challenging issues in the research of the coupling vibration of train–bridge systems under external excitations. Some key problems and challenges in analytical theory, experimental technology and applications are summarized as follows:

  1. (1)

    The train–bridge system is subjected to the random action of track geometry irregularities and external excitations such as wind, earthquake and wave. Meanwhile, the average wind speed and wind direction, vehicle body mass, earthquake intensity and other parameters are also random. It is necessary to develop a stochastic vibration method for nonstationary and nonlinear systems. Probabilistic-based framework is of critical importance for evaluation of the vehicle running safety on long-span bridges under multiple random excitations.

  2. (2)

    More refined models of the train–bridge system under external excitations are needed. First, it is important to establish a refined train–bridge coupling vibration model for new rail transit systems, such as high-speed maglev system, and evaluation on the effect of external excitations draw increasing attention. Second, it is necessary to consider the plastic deformation of bridge model under earthquake, rock fall or ship collision.

  3. (3)

    For high-speed trains, the yaw angle synthesized by lateral wind and vehicle speed is small. The current wind tunnel test of moving train model usually has a small Reynolds number, a low train speed and a large yaw angle. Therefore, it is necessary to develop the wind tunnel test technology of moving train model under the condition of small yaw angle.

  4. (4)

    The running safety and comfort of trains are the key to the dynamic design of long-span railway bridges. Considering the randomness and other factors, the (wind) train–bridge coupling vibration analysis needs to determine the bridge stiffness, bridge deck track line and other parameters by probability method, so as to improve the safety and economy of bridge structure.

  5. (5)

    In recent years, frequent extreme disasters, such as strong wind, earthquake and flood, will seriously threaten the safety of train–bridge systems. It is worth paying attention to the running safety of trains under extreme disasters.