1 Introduction

The viaduct bridges are widely used in high-speed railway systems, in order to control the foundation settlement and to reduce the workload in railway maintenance. As a critical problem in bridge design, the dynamic effects of live loads must be considered, which include the moving effects of the train and the track irregularity. The vehicle–bridge interaction system is a popular model to optimise the design parameters of the vehicle and the bridge. However, since the parameters used in calculations usually differ from the actual values [1], probabilistic analysis is necessary for the vehicle–bridge interaction system. As a deterministic and time-variant system subject to random excitations, it is important to better understand the random responses of the running safety indices, including the derailment coefficient, the wheel unloading rate, and the lateral wheel axle force, so as to ensure the running safety and to enhance the reliability and cost-effectiveness of bridge design.

Parameters of the vehicle, bridge and track structure can be regarded as certain deterministic factors, while the track irregularity, as one of the system excitations, is a random factor and expressed by known power spectrum formulas in most cases. Traditionally, the track irregularity is input into the interaction system model as a spatial sample, which is numerically simulated, such as the harmony superposition method (HSM) [2, 3]. The spatial sample is necessarily random; thus, the dynamic response of the vehicle–bridge interaction system is also a stochastic process and the maximum value of the factors calculated from spatial irregularity samples has inevitable variability. Some attempt for statistical parameters of the dynamic response is carried out by simulating many times with different random phase angles in HSM. The work improved the reliability of calculation but its error is still difficult to estimate.

The problem of random response of the vehicle–bridge interaction system has attracted attention of many researches. Perrin et al. [4] established a nonstationary four-dimensional random field model of track irregularities and obtained the probability density function of responses. Wetzel et al. [5] studied the random dynamic responses of trains under wind load by a subset simulation method. Majka et al. [6] evaluated the safety of the vehicle–bridge interaction system under random track irregularities considering bridge skewness. Wu et al. [7] described the bridge using non-Gaussian uncertainty model and investigated the dynamic criteria by the method of polynomial chaos. Lombaert et al. [8] solved the interaction problem in the frequency domain and studied the effect of the constant moving load under road surface unevenness by decomposing the vehicle–bridge interaction force using the Fourier transform. For other types of excitations present in the interaction system, Kiureghian et al. [9] adopted random structural vibrations produced by multi-point seismic excitation, and Alduse et al. [10] considered the uncertainty of wind speed and direction to study the fatigue damage in long-span bridges.

The classical random vibration theory usually adopts traditional sampling methods, which without exception require a large size of samples and are therefore computationally ineffective. Therefore, other mathematical methods are used to obtain the power spectra of the dynamic responses directly from the input power spectrum of track irregularity. In recent years, the pseudo-excitation method (PEM) [11] has become the most popular of these methods. Zhang et al. [12] improved the train riding comfort condition by optimising the vehicle suspension parameters with the min–max approach. Zhu et al. [13] proposed an approach for predicting the train-induced ground vibrations considering random track unevenness. Li et al. [14] and Zhu et al. [15] proved that the bridge responses follow Gaussian distributions and established a framework to calculate the upper and lower limits of vehicle–bridge system responses from the auto-spectra and the cross-spectra of bridge vibrations.

The multiple-excitation analysis of vehicle–bridge interaction system can be established by considering the spectrum of the wind load and the seismic load. Zhang et al. [16] analysed the nonstationary random responses of interaction systems subjected to lateral horizontal earthquakes by PEM and the precise integration method (PIM) and obtained the time-dependent power spectral density (PSD) functions and standard deviations of the responses. He et al. [17] proposed an efficient analysis framework for the interaction system subjected to wind loads and studied the nonstationary effects on the vibration responses. The methods presented in [10,11,12,13,14,15,16] were all validated by Monte Carlo simulations. By the above-mentioned studies, the statistic characteristics of response in frequency domain can be fully obtained, free of the accidental effect; also the dynamic behaviour in each frequency band of the system movements and forces can be obtained. The work improves the objectivity of bridge dynamic analysis.

The relative position of the vehicle with respect to bridge subsystems is ever-changing when the train is running over the bridge, and thus, the interaction system is time variant. However, PEM requires each subsystem and their interactions to be linear. For solving the problem, Zhai et al. [1] defined different time steps for the subsystems of the vehicle, the track, and the bridge, in order to meet the accuracy requirements. Lei et al. [18] proposed an iterative procedure in time and avoided solving the nonlinear equations when a nonlinear wheel–rail interaction model was adopted. Zhang et al. [19] established an inter-history iteration method by which the two subsystems were solved separately. The iterative process was interposed for faster convergence. Liu et al. [20] developed an easier iteration method, in which the wheel–rail interaction force is defined by the system response from the previous time step. Zhu et al. [13] divided the vehicle–track–bridge system into the vehicle–track subsystem and the bridge subsystem and improved the accuracy by using a much lower interface stiffness between the two subsystems. Mohammdzadeh et al. [21] simulated the wheel–train interaction with SIMPACK software and assembled the two subsystems using the importance sampling and response surface methods. It should be noted that the calculation efficiency was suboptimal in the former research; for example, it is reported by He et al. [17] that a single case of PEM analysis required 900 s of computation time, which is much longer than that of the traditional vehicle–bridge–wind interaction analysis.

It is known that a train has high risk of derailment while passing over a bridge if the stiffness of the bridge is insufficient, with which the safety factors defined in the design code TB 10002–2017 (Code on Design of Railway Bridges and Culverts) are concerned. Clearly, the safety factors are random with certain probability density functions, and it is required that the maximum values of the safety factors are below the limits stipulated in the code. A safer and more effective framework for vehicle–bridge interaction system assessment is proposed in this paper, in which the dynamic responses are calculated by PEM, the probability of the safety factors exceeding the given limits can be calculated, and the vehicle–bridge interaction system performance can be evaluated. The Monte Carlo method is used to validate the proposed method using a case study of a bridge with five simply supported spans.

2 Theoretical analysis method for vehicle–bridge interaction system based on PEM

The load acting on the vehicle–bridge interaction system has two parts: the deterministic one and the random one. The deterministic load is the moving load of the train, for which the system response can be found by the existing methods [19] without considering the track irregularities. The random load is induced by the dynamic effects of the track irregularity, for which PEM can be adopted. PEM is a popular method in random vibration analysis [11], by which the power spectrum of system response can be obtained directly from the power spectrum of excitation.

The track irregularity is a zero-mean Gaussian process; thus, the dynamic response due to track irregularity must be another zero-mean Gaussian process, too. In other words, the mean value of the response is determined by the moving load of the train and the standard deviation of the response is determined by the track irregularity. It can be proved that the standard deviation, σi, of response for the ith degree of freedom of the system can be obtained from the auto-power spectrum Sii(ω, t) as follows:

$$\sigma_{i}^{2} \left( t \right) = \int\limits_{0}^{\infty } {S_{ii} \left( {\omega ,t} \right){\text{d}}\omega } ,$$
(1)

where ω is frequency and t is time.

Then, the probabilistic characteristics of the system response can also be obtained. The flowchart of the solution procedure is shown in Fig. 1.

Fig. 1
figure 1

Flowchart of solution procedure

Full size image

The following assumptions [19] are adopted in the modelling of the vehicle–bridge interaction system:

  1. A1:

    The vehicle and bridge subsystems are linear.

  2. A2:

    The vertical wheel–rail interaction force is derived from the assumption that the wheel and the rail have the same vertical displacement at any time.

  3. A3:

    The lateral wheel–rail interaction force is derived from the simplified Kalker creep theory, i.e. the lateral wheel–rail interaction force is proportional to the wheel–rail relative velocity, and the proportionality coefficient is defined in [19].

  4. A4:

    The wheel–rail interaction force is distributed to the two neighbouring bridge nodes inversely proportional to the wheel-node distances.

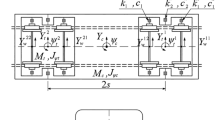
The vehicle–bridge interaction system is illustrated in Fig. 2. The equations of motion for the two interacting subsystems can be expressed as follows:

$$\left[ {\begin{array}{*{20}c} {{\varvec{M}}_{{\text{v}}} } & 0 \\ 0 & {{\varvec{M}}_{{\text{b}}} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\ddot{\varvec{X}}} {}_{{\text{v}}}} \\ {{\ddot{\varvec{X}}} {}_{{\text{b}}}} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {{\varvec{C}}_{{\text{v}}} } & 0 \\ 0 & {{\varvec{C}}_{{\text{b}}} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\dot{\varvec{X}}}{}_{{\text{v}}}} \\ {{\dot{\varvec{X}}}{}_{{\text{b}}}} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {{\varvec{K}}_{{\text{v}}} } & 0 \\ 0 & {{\varvec{K}}_{{\text{b}}} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\varvec{X}}{}_{{\text{v}}}} \\ {{\varvec{X}}{}_{{\text{b}}}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{\varvec{F}}{}_{{\text{v}}}} \\ {{\varvec{F}}{}_{{\text{b}}}} \\ \end{array} } \right],$$
(2)

where M, C, and K are the mass, damping, and stiffness matrices, respectively; X and F are the displacement and force vectors; the subscripts ‘v’ and ‘b’ refer to the vehicle and the bridge, respectively. The dynamic matrices of the vehicle and the bridge are derived, respectively, from the rigid body dynamics method and finite element method (FEM) [19], where the damping matrix of the bridge subsystem Cb is formed by the Rayleigh damping, and the proportional factors are calculated by the first two frequencies of the bridge model.

Fig. 2
figure 2

Vehicle–bridge interaction system

Full size image

As an interaction system, the right-hand side terms, Fv and Fb, in Eq. (2) are functions of Xv and Xb of the wheel sets, as expressed in Eq. (3):

$$\left[ {\begin{array}{*{20}c} {{\varvec{F}}_{{\text{v}}} } \\ {{\varvec{F}}_{{\text{b}}} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\sum {\left( {{\varvec{m}}{}_{{{\text{vv}}}}{\ddot{\varvec{X}}} _{{\text{v}}} + {\varvec{c}}{}_{{{\text{vv}}}}{\dot{\varvec{X}}}_{{\text{v}}} + {\varvec{k}}{}_{{{\text{vv}}}}{\dot{\varvec{X}}}_{{\text{v}}} + {\varvec{m}}{}_{{{\text{vb}}}}{\ddot{\varvec{X}}} _{{\text{b}}} + {\varvec{c}}{}_{{{\text{vb}}}}{\dot{\varvec{X}}}_{{\text{b}}} + {\varvec{k}}{}_{{{\text{vb}}}}{\varvec{X}}_{{\text{b}}} + {\varvec{f}}_{{{\text{v}}i}} } \right)} } \\ {\sum {\left( {{\varvec{m}}{}_{{{\text{bv}}}}{\ddot{\varvec{X}}} _{{\text{v}}} + {\varvec{c}}{}_{{{\text{bv}}}}{\dot{\varvec{X}}}_{{\text{v}}} + {\varvec{k}}{}_{{{\text{bv}}}}X_{{\text{v}}} + {\varvec{m}}{}_{{{\text{bb}}}}{\ddot{\varvec{X}}} _{{\text{b}}} + {\varvec{c}}{}_{{{\text{bb}}}}{\dot{\varvec{X}}}_{{\text{b}}} + {\varvec{k}}{}_{{{\text{bb}}}}{\varvec{X}}_{{\text{b}}} + {\varvec{f}}_{{{\text{b}}i}} } \right)} } \\ \end{array} } \right],$$
(3)

where Σ stands for summation over the wheel sets; m, c, k, and f stand for the mass, damping, stiffness and irregularity-induced forces, respectively, of a single wheel set; quantities with subscripts ‘vv’ and ‘bb’ are for the vehicle and bridge only, respectively; quantities with subscripts ‘vb’ and ‘bv’ are attributed to the interaction between the vehicle and bridge; subscripts ‘vi’ and ‘bi’ stand for the vehicle and bridge subsystems related to vehicle i, respectively. Then, the dynamic equilibrium equations of the vehicle–bridge interaction system can be formed by moving the right-hand side terms in Eq. (2) to the left-hand side as in Eq. (4).

$$\left[ {\begin{array}{*{20}c} {{\varvec{M}}_{{{\text{vv}}}} } & {{\varvec{M}}_{{{\text{vb}}}} } \\ {{\varvec{M}}_{{{\text{bv}}}} } & {{\varvec{M}}_{{{\text{bb}}}} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\ddot{\varvec{X}}} {}_{{\text{v}}}} \\ {{\ddot{\varvec{X}}} {}_{{\text{b}}}} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {{\varvec{C}}_{{{\text{vv}}}} } & {{\varvec{C}}_{{{\text{vb}}}} } \\ {{\varvec{C}}_{{{\text{bv}}}} } & {{\varvec{C}}_{{{\text{bb}}}} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\dot{\varvec{X}}}{}_{{\text{v}}}} \\ {{\dot{\varvec{X}}}{}_{{\text{b}}}} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {{\varvec{K}}_{\rm vv} } & {{\varvec{K}}_{{{\text{vb}}}} } \\ {{\varvec{K}}_{\rm bv} } & {{\varvec{K}}_{{{\text{bb}}}} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\varvec{X}}{}_{{\text{v}}}} \\ {{\varvec{X}}{}_{{\text{b}}}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{\varvec{F}}{}_{{{\text{v}}i}}} \\ {{\varvec{F}}{}_{{{\text{b}}i}}} \\ \end{array} } \right].$$
(4)

For a given wheel set, its lateral (y) displacement is denoted as y1; the relative vertical (z) displacement, and pitch (about axis y) and yaw (about axis x) angles of the vehicle bogie are denoted as z1, u1, and v1, respectively; for the neighbouring nodes I and J, their lateral displacements are denoted as y2 and y3, respectively, vertical displacements as z2 and z3, respectively, and torsional rotations as u2 and u3, respectively. The wheel–rail interaction force is distributed to the two neighbouring bridge nodes inversely proportional to the wheel-node distances, where the weighting factors are denoted as p for node I and q for node J, respectively. For a given wheel set, the equilibrium equations of the interaction system subjected to pseudo-excitation are expressed as follows:

$$\left[ {\begin{array}{*{20}c} {\tilde{F}_{{z_{1} }} } \\ {\tilde{F}_{{v_{1} }} } \\ {\tilde{F}_{{z_{2} }} } \\ {\tilde{F}_{{u_{2} }} } \\ {\tilde{F}_{{z_{3} }} } \\ {\tilde{F}_{{u_{3} }} } \\ \end{array} } \right] = - 2\left[ {\begin{array}{*{20}c} 1 & {d_{1} } & { - p} & { - pe} & { - q} & { - qe} \\ {d_{1} } & {d_{1}^{2} } & { - pd_{1} } & { - pd_{1} e} & { - qd_{1} } & { - qd_{1} e} \\ { - p} & { - pd_{1} } & {p^{2} } & {p^{2} e} & {pq} & {pqe} \\ { - pe} & { - pd_{1} e} & {p^{2} e} & {p^{2} e^{2} } & {pqe} & {pqe^{2} } \\ { - q} & { - qd_{1} } & {pq} & {pqe} & {q^{2} } & {q^{2} e} \\ { - qe} & { - qd_{1} e} & {pqe} & {pqe^{2} } & {q^{2} e} & {q^{2} e^{2} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {k_{1} z_{1} + c_{1} \dot{z}_{1} } \\ {k_{1} v_{1} + c_{1} \dot{v}_{1} } \\ {k_{1} z_{2} + c_{1} \dot{z}_{2} } \\ {k_{1} u_{2} + c_{1} \dot{u}_{2} } \\ {k_{1} z_{3} + c_{1} \dot{z}_{3} } \\ {k_{1} u_{3} + c_{1} \dot{u}_{3} } \\ \end{array} } \right] + 2\left( {k_{1} \tilde{\delta } + c_{1} \dot{\tilde{\delta }}} \right)\left[ {\begin{array}{*{20}c} 1 \\ {d_{1} } \\ { - p} \\ { - pe} \\ { - q} \\ { - qe} \\ \end{array} } \right] = - {\varvec{K}}_{{\text{F}}} {\varvec{X}}_{{\text{F}}} - {\varvec{C}}_{{\text{F}}} \dot{\user2{X}}_{{\text{F}}} + 2\left( {k_{1} \tilde{\delta } + c_{1} \dot{\tilde{\delta }}} \right){\varvec{T}}_{{\text{F}}} ,$$
(5)
$$\left[ {\begin{array}{*{20}c} {\tilde{M}_{{u_{{1}} }} } \\ {\tilde{M}_{{u_{2} }} } \\ {\tilde{M}_{{u_{3} }} } \\ \end{array} } \right] = - 2k_{1} b_{1}^{2} \left[ {\begin{array}{*{20}c} 1 & { - p} & { - q} \\ { - p} & {p^{2} } & {pq} \\ { - q} & {pq} & {q^{2} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {u_{1} } \\ {u_{2} } \\ {u_{3} } \\ \end{array} } \right] - 2c_{1} b_{1}^{2} \left[ {\begin{array}{*{20}c} 1 & { - p} & { - q} \\ { - p} & {p^{2} } & {pq} \\ { - q} & {pq} & {q^{2} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\dot{u}_{1} } \\ {\dot{u}_{2} } \\ {\dot{u}_{3} } \\ \end{array} } \right] + 2b_{1}^{2} \left( {k_{1} \tilde{\beta } + c_{1} \dot{\tilde{\beta }}} \right)\left[ {\begin{array}{*{20}c} 1 \\ { - p} \\ { - q} \\ \end{array} } \right] = - {\varvec{K}}_{{\text{M}}} {\varvec{X}}_{{\text{M}}} - {\varvec{C}}_{{\text{M}}} \dot{\user2{X}}_{{\text{M}}} + 2b_{1}^{2} \left( {k_{1} \tilde{\beta } + c_{1} \dot{\tilde{\beta }}} \right){\varvec{T}}_{{\text{M}}} ,$$
(6)
$$\left[ {\begin{array}{*{20}c} {\tilde{H}_{y1} } \\ {\tilde{H}_{y2} } \\ {\tilde{H}_{u2} } \\ {\tilde{H}_{y3} } \\ {\tilde{H}_{u3} } \\ \end{array} } \right] = - 2c_{c} \left[ {\begin{array}{*{20}c} 1 & { - p} & { - ph} & { - q} & { - qh} \\ { - p} & {p^{2} } & {p^{2} h} & {pq} & {pqh} \\ { - ph} & {p^{2} h} & {p^{2} h^{2} } & {pqh} & {pqh^{2} } \\ { - q} & {pq} & {pqh} & {q^{2} } & {q^{2} h} \\ { - qh} & {pqh} & {pqh^{2} } & {q^{2} h} & {q^{2} h^{2} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\dot{y}_{1} } \\ {\dot{y}_{2} } \\ {\dot{u}_{2} } \\ {\dot{y}_{3} } \\ {\dot{u}_{3} } \\ \end{array} } \right] + 2c_{c} \dot{\tilde{\varepsilon }}\left[ {\begin{array}{*{20}c} 1 \\ { - p} \\ { - ph} \\ { - q} \\ { - qh} \\ \end{array} } \right] = - {\varvec{C}}_{{\text{H}}} \dot{\user2{X}}_{{\text{H}}} + 2c_{{\text{c}}} \dot{\tilde{\varepsilon }}{\varvec{T}}_{{\text{H}}} ,$$
(7)
$$\left[ {\begin{array}{*{20}c} {\tilde{P}_{{z_{2} }} } \\ {\tilde{P}_{{u_{2} }} } \\ {\tilde{P}_{{z_{3} }} } \\ {\tilde{P}_{{u_{3} }} } \\ \end{array} } \right] = - m_{0} \left[ {\begin{array}{*{20}c} {p^{2} } & {p^{2} e} & {pq} & {pqe} \\ {p^{2} e} & {p^{2} e^{2} } & {pqe} & {pqe^{2} } \\ {pq} & {pqe} & {q^{2} } & {q^{2} e} \\ {pqe} & {pqe^{2} } & {q^{2} e} & {q^{2} e^{2} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\ddot{z}_{2} } \\ {\ddot{u}_{2} } \\ {\ddot{z}_{3} } \\ {\ddot{u}_{2} } \\ \end{array} } \right] - I_{0} \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 \\ 0 & {p^{2} } & 0 & {pq} \\ 0 & 0 & 0 & 0 \\ 0 & {pq} & 0 & {q^{2} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\ddot{z}_{2} } \\ {\ddot{u}_{2} } \\ {\ddot{z}_{3} } \\ {\ddot{u}_{2} } \\ \end{array} } \right] - m_{0} \ddot{\tilde{\delta }}\left[ {\begin{array}{*{20}c} p \\ {pe} \\ q \\ {qe} \\ \end{array} } \right] - I_{0} \ddot{\tilde{\beta }}\left[ {\begin{array}{*{20}c} 0 \\ p \\ 0 \\ q \\ \end{array} } \right] = - {\varvec{M}}_{{\text{P}}} {\ddot{\user2{X}}}_{{\text{P}}} - m_{0} \ddot{\tilde{\delta }}{\varvec{T}}_{{{\text{P}}1}} - I_{0} \ddot{\tilde{\beta }}{\varvec{T}}_{{{\text{P}}2}} ,$$
(8)

where Eq. (5) describes the vertical pseudo-excitation, Eq. (6) the torsional pseudo-excitation, Eq. (7) the lateral pseudo-excitation, and Eq. (8) the pseudo-inertia excitation, respectively; definitions of the symbols used in these interaction equations are listed in Table 1.

Table 1 Definitions of symbols used in Eqs. (3)–(8)
Full size table

The power spectra of the vertical, lateral, and torsional pseudo-excitations are as follows:

$$S_{\delta \delta } \left( \omega \right) = S_{zz} \left( {\frac{\omega }{V}} \right)/V = S_{zz} \left( \varOmega \right)/V,$$
(9)
$$S_{\varepsilon \varepsilon } \left( \omega \right) = S_{yy} \left( {\frac{\omega }{V}} \right)/V = S_{yy} \left( \varOmega \right)/V,$$
(10)
$$S_{\beta \beta } \left( \omega \right) = S_{uu} \left( {\frac{\omega }{V}} \right)/V = S_{uu} \left( \varOmega \right)/V,$$
(11)

where V is the train speed; Sδδ(ω), Sεε(ω), and Sββ(ω) are the vertical, lateral, and torsional power spectra of excitations; Ω is the spatial frequency of track irregularity; Szz(Ω), Syy(Ω), and Suu(Ω) are the power spectra of track irregularity in the vertical, lateral, and torsional directions [14, 15].

From Eqs. (3–11), the additional loads of a single wheel set related to the pseudo-excitations caused by irregularities δ, ε, and β are respectively as follows:

$$\begin{aligned} \tilde{\varvec F}_{\delta } \left( \omega \right) & = 2k_{1} \tilde{\delta }{\varvec T}_{{\text{F}}} + 2c_{1} \dot{\tilde{\delta }}{\varvec T}_{{\text{F}}} + m_{0} \ddot{\tilde{\delta }}{\varvec T}_{{{\text{P}}1}} \\ & = \left( {2k_{1} {\varvec T}_{{\text{F}}} + 2c_{1} {\text{i}}\omega {\varvec T}_{{\text{F}}} - m_{0} \omega^{2} {\varvec T}_{{{\text{P}}1}} } \right){\text{e}}^{{{\text{i}}\omega \left( {t - {\Delta }t} \right)}} \sqrt {S_{\delta \delta } \left( \omega \right)} \\ & = \left( {2k_{1} {\varvec T}_{{\text{F}}} + 2c_{1} {\text{i}}\omega {\varvec T}_{{\text{F}}} - m_{0} \omega^{2} {\varvec T}_{{{\text{P}}1}} } \right){\text{e}}^{{ - {\text{i}}\omega {\Delta }t}} \sqrt {S_{\delta \delta } \left( \omega \right)} {\text{e}}^{{{\text{i}}\omega t}} , \\ \end{aligned}$$
(12)
$$\tilde{\varvec F}_{\varepsilon } \left( \omega \right) = 2c_{{\text{c}}} {\text{i}}\omega {\varvec T}_{{\text{H}}} \sqrt {S_{\varepsilon \varepsilon } \left( \omega \right)} {\text{e}}^{{{\text{i}}\omega \left( {t - \Delta t} \right)}} = 2c_{{\text{c}}} {\text{i}}\omega {\varvec T}_{{\text{H}}} {\text{e}}^{{ - {\text{i}}\omega \Delta t}} \sqrt {S_{\varepsilon \varepsilon } \left( \omega \right)} {\text{e}}^{{{\text{i}}\omega t}} ,$$
(13)
$$\begin{aligned} \tilde{\varvec F}_{\beta } \left( \omega \right) & = 2k_{1} b_{1}^{2} \tilde{\beta }{\varvec T}_{{\text{M}}} + 2c_{1} b_{1}^{2} \dot{\tilde{\beta }}{\varvec T}_{{\text{M}}} + I_{0} \ddot{\tilde{\beta }}{\varvec T}_{{{\text{P}}2}} \\ & = \left( {2k_{1} b_{1}^{2} {\varvec T}_{{\text{M}}} + 2c_{1} b_{1}^{2} {\text{i}}\omega {\varvec T}_{{\text{M}}} - I_{0} \omega^{2} {\varvec T}_{{{\text{P}}2}} } \right){\text{e}}^{{{\text{i}}\omega \left( {t - \Delta t} \right)}} \sqrt {S_{\beta \beta } \left( \omega \right)} \\ & = \left( {2k_{1} b_{1}^{2} {\varvec T}_{{\text{M}}} + 2c_{1} b_{1}^{2} {\text{i}}\omega {\varvec T}_{{\text{M}}} - I_{0} \omega^{2} {\varvec T}_{{{\text{P}}2}} } \right){\text{e}}^{{ - {\text{i}}\omega \Delta t}} \sqrt {S_{\beta \beta } \left( \omega \right)} {\text{e}}^{{{\text{i}}\omega t}} , \\ \end{aligned}$$
(14)

where Δt is the time difference between the concerned wheel set and the first wheel set passing over the same point, i is the imaginary unit and equal to the square root of −1. The pseudo-excitation of irregularities can be obtained by adding the pseudo-excitations for all the wheel sets. Based on the fundamental assumption of PEM, the track irregularities related to vertical direction, δ, torsional angle, β, and lateral direction, ε, must be analysed independently. In this way, the power spectra of vehicle–bridge interaction system can be calculated.

For a single wheel set, the force of the primary suspension system under pseudo-excitation related to directions y and z, and rotation u (about axis x) are as follows:

$$F_{{{\text{w}}y}} = 2c_{{\text{c}}} \left( {p\dot{y}_{2} + ph\dot{u}_{2} + q\dot{y}_{3} + qh\dot{u}_{3} - \dot{y}_{1} } \right),$$
(15)
$$\begin{aligned} F_{{{\text{w}}z}} & = 2k_{1} \left( {pz_{2} + qz_{3} + peu_{2} + qeu_{3} - z_{1} - d_{1} v_{1} } \right) \\ & \quad + 2c_{1} \left( {p\dot{z}_{2} + q\dot{z}_{3} + pe\dot{u}_{2} + qe\dot{u}_{3} - \dot{z}_{1} - d_{1} \dot{v}_{1} } \right), \\ \end{aligned}$$
(16)
$$F_{{{\text{w}}u}} = 2k_{1} b_{1}^{2} \left( {pu_{2} + qu_{3} - u_{1} } \right) + 2c_{1} b_{1}^{2} \left( {p\dot{u}_{2} + q\dot{u}_{3} - \dot{u}_{1} } \right).$$
(17)

The vertical acceleration, aw, and angular acceleration about axis x, βw, are as follows:

$$\left\{ {\begin{array}{*{20}l} {a_{{\text{w}}} = p\ddot{z}_{2} + q\ddot{z}_{3} + \ddot{\delta }} \hfill \\ {\beta_{{\text{w}}} = p\ddot{u}_{2} + q\ddot{u}_{3} + \ddot{\beta }} \hfill \\ \end{array} } \right..$$
(18)

Thus, the interaction forces at the left- and right-hand side wheel–rail contact points are as follows:

$$F_{{{\text{w}}y1}} = F_{{{\text{w}}y2}} = \frac{1}{2}F_{{{\text{w}}y}} = c_{{\text{c}}} \left( {p\dot{y}_{2} + ph\dot{u}_{2} + q\dot{y}_{3} + qh\dot{u}_{3} - \dot{y}_{1} } \right),$$
(19)
$$F_{{{\text{w}}z1}} = \frac{1}{2}\left( {m_{0} a_{{\text{w}}} + F_{{{\text{w}}z}} + G} \right) + \frac{{I_{0} \beta_{{\text{w}}} + F_{{{\text{w}}u}} }}{{g_{0} }},$$
(20)
$$F_{{{\text{w}}z2}} = \frac{1}{2}\left( {m_{0} a_{{\text{w}}} + F_{{{\text{w}}z}} + G} \right) - \frac{{I_{0} \beta_{{\text{w}}} + F_{{{{\rm w}u}}} }}{{g_{0} }},$$
(21)

where Fwy1 and Fwy2 are the lateral contact forces at the left- and right-hand sides, respectively; Fwz1 and Fwz2 are the lateral contact forces at the left- and right-hand sides, respectively; G is the static load of wheel set; and g0 is the gauge.

The maximum values of the derailment coefficient, XDR, the wheel unloading rate, XOL, and the lateral wheel axle force, FAY, are required to be evaluated as safety factors in the designing codes [2]. They are functions of the wheel–rail forces as follows:

$$X_{{{\text{DR}}}} \left( t \right) = \frac{Q\left( t \right)}{{P\left( t \right)}},$$
(22)
$$X_{{{\text{OL}}}} \left( t \right) = 1 - \frac{P\left( t \right)}{{P_{0} }},$$
(23)
$$F_{{{\text{AY}}}} \left( t \right) = 2Q\left( t \right),$$
(24)

where P0 is the static wheel load, which is a constant; P(t) and Q(t) are the vertical and lateral wheel–rail forces at a single side of the wheel set, respectively. It can be proved by Eqs. (5–8) that Q(t) and P(t) are both an independent random process.

As a random process, the probability of a factor exceeding its limit can be calculated from its probability density function. The mean values of the wheel–rail vertical and lateral forces, µP and µQ, can be obtained using the deterministic loads and the standard deviation can be calculated by Eq. (1). Then, it can be proved by the central limit theorem that the wheel–rail vertical and lateral forces follow Gaussian distributions when the number of samples is large enough.

The wheel unloading rates and the lateral wheel axle forces are functions of the wheel–rail vertical and lateral forces; thus, they will also follow Gaussian distributions with the following mean values and standard deviations:

$$\left\{ {\begin{array}{*{20}l} {\mu_{{{\text{OL}}}} = 1 - \frac{{\mu_{P} }}{{P_{0} }}} \hfill \\ {\sigma_{{{\text{OL}}}} = \frac{{\sigma_{P} }}{{P_{0} }}} \hfill \\ \end{array} } \right.,$$
(25)
$$\left\{ {\begin{array}{*{20}c} {\mu_{{{\text{FAY}}}} = 2\mu_{Q} } \\ {\sigma_{{{\text{FAY}}}} = 2\sigma_{Q} } \\ \end{array} } \right.,$$
(26)

where µOL and σOL are the mean value and standard deviation of the wheel unloading rate, respectively; µFAY and σFAY are the mean value are standard deviation of the lateral wheel axle force, respectively.

The derailment coefficient is the ratio of two random variables, P(t) and Q(t), both following Gaussian distributions with known mean values and standard deviations. Thus, the probability density function of the derailment coefficient is as follows:

$$f\left( x \right) = \frac{{b_{x} d_{x} }}{{a_{x}^{{3}} }}\frac{1}{{\sqrt {2{\uppi }} \sigma_{Q} \sigma_{P} }}\left[ {\varPhi \left( {b_{x} /a_{x} } \right) - \varPhi \left( { - b_{x} /a_{x} } \right)} \right] + \frac{1}{{a_{x}^{2} {\uppi }\sigma_{Q} \sigma_{P} }}{\text{exp }}\left( {\frac{ - c}{2}} \right),$$
(27)

where \(\varPhi \left( \cdot \right)\) is the cumulative distribution function of the standard Gaussian distribution, and

$$a_{x} = \sqrt {\frac{{x^{2} }}{{\sigma_{Q}^{{2}} }} + \frac{1}{{\sigma_{P}^{{2}} }}} ,\quad b_{x} = \frac{{x\mu_{Q} }}{{\sigma_{Q}^{2} }} + \frac{{\mu_{P} }}{{\sigma_{P}^{{2}} }},\quad c = \frac{{\mu_{Q}^{{2}} }}{{\sigma_{Q}^{2} }} + \frac{{\mu_{P}^{2} }}{{\sigma_{P}^{2} }},\quad d_{x} = \exp \left( {\frac{{b_{x}^{2} - ca_{x}^{2} }}{{2a_{x}^{2} }}} \right).$$

Then, the probability of the concerned factor exceeding its limit can be calculated by integrating the probability density function.

3 Case study

In this case study, a typical high-speed train runs over a bridge with four column piers and five pre-stressed concrete simply supported spans. A mass density per metre and frequencies are assigned to the span beams instead of a specified cross section. The nodes at the abutments and pier bottoms are fixed in the model. The train comprises eight vehicles, each 25 m in length, and runs at speeds of 250, 300, and 350 km/h. To reduce the effect of sudden load application, the first wheel set of the train is assumed to be 100 m from the bridge end when the simulations starts, i.e. the train is on the bridge between 1.03 and 3.03 s for 350 km/h. The bridge is shown in Fig. 3, and a complete list of the vehicle and bridge parameters are provided in Tables 2 and 3, respectively.

Fig. 3
figure 3

Bridge used in case study

Full size image
Table 2 Parameters of vehicle
Full size table
Table 3 Parameters of bridge
Full size table

The power spectra of track irregularity, S(f), are adopted from TB/T 3352-2014 (PSD of Ballastless Track Irregularities of High-Speed Railway) in the directions of profile (z direction), alignment (y direction), and cross-lever (about x axis) as follows:

$$S\left( f \right) = \frac{A}{{f^{k} }},$$
(28)

where S(f) is in mm2/m−1; f is spatial frequency in m−1; A and k are coefficients. The values of coefficients A and k and spatial frequency f are listed in Table 4 and Table 5, respectively. The cross-lever is the height difference of the two rails, which is the product of the torsional irregularity and the gauge.

Table 4 Fitting formula coefficients for mean spectra
Full size table
Table 5 Spatial frequencies at segment division points
Full size table

To validate the proposed method, 100 Monte Carlo simulations were carried out with track irregularity samples generated by HSM. A comparison of the PEM and Monte Carlo simulation results for the train speed of 350 km/h is shown in Figs. 4–11, where the black lines represent the results of PEM, and the red lines represent the mean values or standard deviations of the Monte Carlo simulations. (In graphs throughout the paper, abbreviations Disp., Acc., and AA stand for the displacement, acceleration, and angular acceleration, respectively.) It is found that the two methods agree well for all the concerned factors.

Fig. 4
figure 4

Mean values of a vertical, b lateral, and c torsional mid-span displacements (black line: PEM; red line: Monte Carlo)

Full size image
Fig. 5
figure 5

Standard deviations of a vertical, b lateral, and c torsional mid-span displacements (black line: PEM; red line: Monte Carlo)

Full size image
Fig. 6
figure 6

Mean values of a vertical, b lateral, and c torsional mid-span accelerations (black line: PEM; red line: Monte Carlo)

Full size image
Fig. 7
figure 7

Standard deviations of a vertical, b lateral, and c torsional mid-span accelerations (black line: PEM; red line: Monte Carlo)

Full size image
Fig. 8
figure 8

Mean values of a vertical, b lateral, and c torsional car body accelerations (black line: PEM; red line: Monte Carlo)

Full size image
Fig. 9
figure 9

Standard deviations of a vertical, b lateral, and c torsional car body accelerations (black line: PEM; red line: Monte Carlo)

Full size image
Fig. 10
figure 10

Mean values of a vertical left-hand side, b vertical right-hand side, and c lateral wheel–rail forces (black line: PEM; red line: Monte Carlo)

Full size image
Fig. 11
figure 11

Standard deviations of a vertical left-hand side, b vertical right-hand side, and c lateral wheel–rail forces (black line: PEM; red line: Monte Carlo)

Full size image

However, some noticeable differences are also found between the PEM and Monte Carlo results, especially for the factors with zero-mean value. This is due to the limited sample numbers used in the Monte Carlo simulations. Larger sample numbers were tried and it was found that the differences were reduced with the increase in sample number.

The power spectra densities (PSDs) of bridge mid-span displacements and accelerations, the car body accelerations, and the wheel–rail forces of the first wheel set are calculated and shown in Figs. 12–15, where DPSD, APSD, and FPSD stand for displacement PSD, acceleration PSD, and force PSD, respectively.

Fig. 12
figure 12

PSDs of a vertical, b lateral, and c torsional mid-span displacements

Full size image
Fig. 13
figure 13

PSDs of a vertical, b lateral, and c torsional mid-span accelerations

Full size image
Fig. 14
figure 14

PSDs of a vertical, b lateral, and c torsional car body accelerations

Full size image
Fig. 15
figure 15

PSDs of a vertical left-hand side, b vertical right-hand side, and c lateral wheel–rail forces

Full size image

It can be observed in the figures that the dominant frequencies of the bridge are the lateral natural frequency of 25 Hz and the torsional natural frequency of 15 Hz. For vertical direction, the dominant frequency of bridge is the loading frequency of 3.9 Hz, which is determined by the train speed (350 km/h) divided by train length (25 m). The vertical inertia force of the wheel set is proportional to the second derivative of track irregularity by assumption A2 and Eq. (12); thus, there is a much stronger high-frequency component in bridge accelerations compared to displacements.

For a similar reason, much stronger high-frequency components due to the inertia force of the wheel set exist in the vertical wheel–rail forces. On the other hand, the lateral wheel–rail force has a peak in the frequency range 10–20 Hz, which is related to the lateral local resonant of the two subsystems. The irregularity is a wideband excitation, i.e. between 1.2 and 97.2 Hz, considering the train speed of 350 km/h. So the dominant frequency of the vehicle response is around the first-order natural frequency due to resonance, which is much lower than that of the bridge subsystem.

In order to analyse the distribution of the safety factors, the results produced by the proposed method were compared to those by the Monte Carlo method, as illustrated in Table 6 and Figs. 16–18, where the numbers of samples in corresponding ranges are shown at the top of the bars. There were 100 simulations and 3000 time steps in each simulation; thus, the theoretical number of samples in a given range can be calculated from the corresponding probability multiplied by 300,000.

Table 6 Ranges of safety factors
Full size table
Fig. 16
figure 16

Distributions of safety factors for train speed of 250 km/h

Full size image
Fig. 17
figure 17

Distributions of safety factors for train speed of 300 km/h

Full size image
Fig. 18
figure 18

Distributions of safety factors for train speed of 350 km/h

Full size image

It can be seen that the numbers of samples from the Monte Carlo simulations in the given ranges are similar to the theoretical ones calculated by the proposed method in all the considered cases.

The results can also be analysed by examining the time histories of the safety factors. A “common range” is defined by the “three-sigma rule”, by which outlying observations can be highlighted. The upper and lower limit comparison of the PEM and Monte Carlo simulation are shown in Figs. 19–23, where the black lines represent the confidence intervals and mean values of PEM, the blue lines represent the upper and lower limits of Monte Carlo simulations, and the red lines represent the mean value of Monte Carlo results and the confidence intervals related to the criteria defined by the “three-sigma rule”. It can be seen in the figures that most of the simulated data are in the “common range”.

Fig. 19
figure 19

Limits of derailment coefficient of left wheel for a 250 km/h, b 300 km/h, and c 350 km/h (black lines: PEM; blue lines: upper and lower limits of Monte Carlo; red lines: mean value of Monte Carlo)

Full size image
Fig. 20
figure 20

Limits of derailment coefficient of right wheel for a 250 km/h, b 300 km/h, and c 350 km/h (black lines: PEM; blue lines: upper and lower limits of Monte Carlo; red lines: mean value of Monte Carlo)

Full size image
Fig. 21
figure 21

Limits of wheel unloading rate of left wheel for a 250 km/h, b 300 km/h, and c 350 km/h (black lines: PEM; blue lines: upper and lower limits of Monte Carlo; red lines: mean value of Monte Carlo)

Full size image
Fig. 22
figure 22

Limits of wheel unloading rate of right wheel for a 250 km/h, b 300 km/h, and c 350 km/h (black lines: PEM; blue lines: upper and lower limits of Monte Carlo; red lines: mean value of Monte Carlo)

Full size image
Fig. 23
figure 23

Limits of lateral wheel axle force of right wheel for a 250 km/h, b 300 km/h, and c 350 km/h (black lines: PEM; blue lines: upper and lower limits of Monte Carlo; red lines: mean value of Monte Carlo)

Full size image

It is clear that the probability of the safety factors exceeding the limits increased with the analysis duration, which may lead to loss of objectivity. The limits concerned in this paper are from the codes for evaluating the safety performance based on the maximum values measured in a single experiment or calculation. Thus, it is not the original intention of the code to ensure that the safety factors are less than the limits for every train over the entire service life of the bridge. The probability density functions of the three safety factors are studied in this paper, based on which reasonable limits can be probabilistically established in future work.

4 Conclusions

  1. (1)

    Despite its time variety and randomness, the vehicle–bridge interaction problem can be solved by the method proposed in the paper based on PEM, by which the power spectrum densities of vehicle–bridge interaction system responses can be obtained directly from the power spectrum density of the track irregularity. The proposed method has been validated by Monte Carlo simulations.

  2. (2)

    A typical Chinese high-speed railway bridge has been adopted as a case study, in which the dynamic responses of the vehicle, the bridge, and wheel–rail interaction forces were calculated by the proposed method. It has been found that the dominant frequency of bridge vertical response is the load frequency of train, while the dominant frequencies of bridge lateral responses are the natural frequencies of bridge.

  3. (3)

    The wheel unloading rate and the lateral wheel axle force follow Gaussian distributions, while the derailment coefficient follows the probability density function shown in Eq. (27), using which the probability of the safety factors exceeding the given limits can be calculated for the duration of time when the train runs over the bridge.