1 Introduction

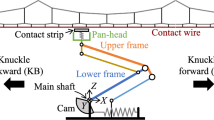
In electrified railway systems, the catenary constructed along the railroad is used to power the electric train. The electric current is transmitted to the train through a sliding contact with a pantograph mounted on the vehicle roof, as illustrated in Fig. 1. The catenary’s contact wire serves mechanically as the electrical path for the pantograph and the electrical current. The current collection quality is dominated by the mechanical interaction performance between the contact wire and the pantograph collectors.

Fig. 1
figure 1

Schematics of pantograph–catenary system

Full size image

Usually, the contact wire is hanged by several droppers to keep it as flat as possible or to have a certain amount of pre-sag, which has been proven beneficial to keep a stable contact with pantographs [1]. However, the installation error, temperature variance, insufficient maintenance and multiple impacts in long-term operation may result in the deviation of the catenary geometry with respect to its design position [2, 3], which affects the sliding contact of the pantograph–catenary. As shown in Fig. 2, the deviation happens in longitudinal and vertical directions, which have been proven by the measurement data in our previous work [4]. Similar to the track irregularity [5], the catenary geometry deviation also has a stochastic nature, resulting in an indeterministic response of pantograph–catenary interaction. Therefore, the realistic geometry deviation is desired to be measured and properly included in the numerical tools to evaluate the dispersion of pantograph–catenary behaviour, which is the main topic of this paper.

Fig. 2
figure 2

Illustration of geometry deviation

Full size image

As the most vulnerable part of the traction power system, the pantograph–catenary system has been a common research objective that attracts ever-increasing attention of scholars from the scientific community and the industry [6]. Due to the high cost and limited access of field tests, numerical modelling has been a mainstream approach to study the pantograph–catenary dynamics and has experienced an advanced development in the last several decades [7]. In the early stage of research, the catenary is normally assumed to be a mass-spring system [8], in which only the stiffness and mass distributions are considered without the contribution of wave propagation. With the increase of train speed, the catenary nonlinearity significantly affects the response [9]. That is why the finite element method has been the most popular approach to model the catenary. To achieve convincing numerical results, the measurement data from field tests are utilised to modify and validate numerical models, which has prompted new measurement and identification techniques [10, 11]. Another state of the art is to digitalise the external disturbance from vehicle-track [12, 13], wind load [14] and other experimental factors and adequately include them in the numerical model. In order to improve the numerical efficiency, some scholars have devoted their attention to developing fast simulation techniques, such as the moving mesh [15], moving window [16] and offline integration method [17]. Commonly, the numerical models are used in the design phase to check the acceptance of the design strategy. Recently, the modelling of degradation has been an emerging technique to utilise the numerical model to predict service performance [18]. Based on this idea, the defective droppers [19, 20], irregularity [21], contact wire wear [22] and the tension variation [23] are correctly modelled and included in the assessment of pantograph–catenary interaction. It is worthwhile to mention the works of Van et al. [24] and Gregori et al. [25]. The geometry deviation is considered in these two works when modelling the catenary, and the results indicate that the geometry deviation leads to a particular dispersion of the response. The geometry data from measurement can further support and validate the main conclusion of these two works.

From the above literature review, it is seen that most numerical simulations of pantograph–catenary interaction are performed based on design data without any geometry imperfections. Some works that attempt to include a random geometry deviation in the catenary model lack the support of measured geometry data. This paper presents a filed measurement of the catenary geometry based on a laser rangefinder, which can provide realistic contact wire geometry for the numerical simulation. Based on the Monte Carlo method, many contact wire geometry samples are generated, with the same distribution and frequency characteristics as the measurement data. The random geometry deviation is included in a catenary model built by the finite element method (FEM). In combination with a pantograph model with flexible collectors, the dispersion of response caused by the random geometry deviation is investigated with different cut-off frequencies and operating speeds.

The rest of this paper is organised as follows: Sect. 2 describes the measurement of catenary geometry. The catenary model with geometry deviation is built in Sect. 3. The stochastic analysis of the contact force is performed in Sect. 4, and Sect. 5 states the conclusions.

2 Measurement of catenary geometry

To provide a realistic catenary geometry data for the numerical simulation, the geometry of an existing catenary on the Gardemobanen line from the Norwegian railway network was measured. The main purpose of this paper is to find out the effect of geometrical deviations on the interaction performance of the pantograph–catenary system, namely the vertical contact quality. Therefore, only the geometrical deviations in vertical and longitudinal directions were measured. Obviously, the former directly impacts the sliding contact between the pantograph strip and contact wire. The latter may affect the frequency characteristics of the contact force. A laser rangefinder (Leica DISTO™ D8) was used to measure the height of critical points, including upper and lower joints of droppers, steady arm points and joints of stitch wires. The height was measured as the relative vertical height with respect to the rail. The vertical measurement is illustrated in Fig. 3, and the height H of the catenary wires can be estimated by

$$H = H_{\text{r}} + H_{\text{w}} = L_{\text{r}} \cdot \sin \alpha + L_{\text{w}} \cdot \sin \beta ,$$
(1)

where Hw is the vertical height between the critical point and the laser rangefinder, and Hr is the vertical height between the rail and the laser rangefinder; Lw and β are respectively the distance and the corresponding pitch angle from the laser rangefinder to the contact wire; Lr and α are respectively the distance and the corresponding pitch angle of the rail.

Fig. 3
figure 3

The measurement of vertical geometry with the aid of a laser rangefinder

Full size image

The longitudinal distance Dl of each critical point was also measured using the method illustrated in Fig. 4. To estimate the longitudinal distance Dl, the yaw angle γ between the pole and rail is necessary. However, due to the limitation of the 6-axis inertial measurement unit (IMU) installed in the laser rangefinder, the yaw angle γ is not convenient to measure. An alternative method is to measure the distances from the laser rangefinder to the pole Lp and to the rail Lhr and the pole-rail distance Lpr. Then, the yaw angle γ and the longitudinal distance Dl can be estimated by

$$\begin{aligned} & \gamma = \arccos \left[ {(L_{\text{hr}} - L_{\text{pr}} )/L_{\text{p}} } \right], \\ & D_1 = L_{\text{p}} \cdot \sin \gamma = L_{\text{p}} \cdot \sin \left[ {\arccos \left[ {(L_{\text{hr}} - L_{\text{pr}} )/L_{\text{p}} } \right]} \right]. \\ \end{aligned}$$
(2)
Fig. 4
figure 4

The measurement of longitudinal geometry

Full size image

Therefore, seven parameters Lr, Lw, α, β, Lp, Lhr and Lpr need to be measured using the laser rangefinder. The accuracy of measurement in the range of 10–30 m can be controlled within 0.1 mm. Moreover, the measurement accuracy of the pitch angles α and β is controlled within 0.1°. Hence, the effect of any measurement errors for these two parameters on the measurement accuracy is small enough to be neglected.

Figure 5 shows the comparison of contact wire geometry within one span between the measurement and design data. The sag between two critical points is calculated based on the tension and gravity in the contact wire. It is seen that the measured geometry has a significant difference from the designed one. Especially in the vertical direction, the measured geometry shows a significant irregularity. The dropper points also show distinct deviation in the longitudinal direction. The following two approaches are utilised to describe the stochastics of deviations in each direction.

Fig. 5
figure 5

Comparison of contact wire geometry between measurements and design data

Full size image

As illustrated in Fig. 6, the standard deviation of the critical point deviation against the design data is calculated for the longitudinal direction. The Gaussian distribution is employed to characterise the dispersion of longitudinal deviation, of which the probability density function (PDF) can be written as follows:

$$f\left( x \right) = \frac{1}{{\sigma_{\text{g}} \sqrt {2{\uppi} } }}\exp \left[ { - \frac{1}{2}\left( {\frac{{x - \mu_{\text{g}} }}{{\sigma_{\text{g}} }}} \right)^{2} } \right],$$
(3)

where \(\sigma_{{\text{g}}}\) is the longitudinal standard deviation of critical points, which takes the value of 0.23 m; \(\mu_{{\text{g}}}\) is the corresponding mean value, which is close to zero. Following the Gaussian distribution, many samples of random longitudinal deviations are generated for all the critical points. Then, the longitudinal coordinate of each critical point can be obtained by the summation of the original position and the longitudinal deviation.

Fig. 6
figure 6

Procedure to characterise stochastics of catenary geometry deviations

Full size image

For the vertical direction, a smoothing spline is used to connect all the critical points, of which the PSD is estimated using the Yule–Walker AR method. Then, the inverse Fourier transform is implemented to generate many samples of vertical deviation from the measured PSD (Fig. 7a). The generated PSDs show good agreement with the measured one (Fig. 7b). The vertical deviations of all critical points can be obtained by the interpolation according to their longitudinal coordinates. The vertical and longitudinal coordinates of critical points are input in the catenary model to compute the initial configuration. The details of the shape-finding method are described in the next section.

Fig. 7
figure 7

a Generated deviation signal from the measured PSD; b comparison of generated and measured PSD

Full size image

3 Modelling of pantograph–catenary system with geometry deviation

The absolute nodal coordinate formulation (ANCF) is utilised to model the catenary in this paper, which has been proven capable of accurately describing the initial configuration [26] and addressing the geometrical nonlinearity [27]. The pantograph is represented by a developed lumped mass model with two flexible collectors to reproduce the high-frequency modes.

3.1 ANCF beam and cable elements

The catenary comprises a number of complex components, but its dynamic behaviour with a pantograph is normally determined by five main components: the contact wire, the messenger wire, the dropper, the stitch wire and the steady arm, as illustrated in Fig. 8. The ANCF beam element is employed here to describe the geometrical nonlinearity of messenger, contact and stitch wires. The dropper is modelled by an ANCF cable element with a nonlinear stiffness to describe different working conditions in tension and compression. The steady arm is modelled by a linear truss element, which can rotate around the support point. The claws on clamps are assumed as lumped masses.

Fig. 8
figure 8

The catenary model with ANCF beam and cable elements

Full size image

In this work, the ANCF beam with 12 degrees of freedom (DOFs) is adopted to discretise the contact, messenger, and stitch wires. The elastic force vector \({\varvec{Q}}_{\text{e}}\) for each element can be expressed as the product of the secant stiffness matrix \({\varvec{K}}_{{\text{e}}}\) and the DOF vector e as follows:

$${\varvec{Q}}_{{\text{e}}} = {\varvec{K}}_{{\text{e}}} {\varvec{e}},$$
(4)

where the derivation of the secant stiffness matrix \({\varvec{K}}_{{\text{e}}}\) can be found in [26]. In the shape-finding procedure, the tangent stiffness matrices are primarily used to calculate the incremental DOF vector \(\Delta {\varvec{e}}\) and the incremental unstrained length \(\Delta L_{0}\). The corresponding tangent stiffness matrices \({\varvec{K}}_{{\text{T}}}\) and \({\varvec{K}}_{{\text{L}}}\) can be obtained by taking partial of Eq. (4) against e and L0 as follows:

$$\Delta {\varvec{F}} = \frac{{\partial {\varvec{Q}}}}{{\partial {\varvec{e}}}}\Delta {\varvec{e}} + \frac{{\partial {\varvec{Q}}}}{{\partial L_{0} }}\Delta L_{0} = {\varvec{K}}_{{\text{T}}} \Delta {\varvec{e}} + {\varvec{K}}_{{\text{L}}} \Delta L_{0} ,$$
(5)

where F is the internal force vector. A similar derivation can also be used to derive the tangent stiffness matrices of the ANCF cable element. It should be noted that when the dropper works in slackness, the axial stiffness changes to zero. Assembling the stiffness matrix of each element yields the global incremental equilibrium equation for the whole catenary as follows:

$$\Delta {\varvec{F}}^{{\text{G}}} = {\varvec{K}}_{{\text{T}}}^{{\text{G}}} \Delta {\varvec{U}}_{{\text{C}}} + {\varvec{K}}_{{\text{L}}}^{{\text{G}}} \Delta {\varvec{L}}_{0} ,$$
(6)

where \(\Delta {\varvec{F}}^{{\text{G}}}\) is the global unbalanced force vector. \({\varvec{K}}_{{\text{T}}}^{{\text{G}}}\) and \({\varvec{K}}_{{\text{L}}}^{{\text{G}}}\) are the global stiffness matrices related to the incremental nodal displacement vector \(\Delta {\varvec{U}}_{{\text{C}}}\) and the incremental unstrained length vector \(\Delta {\varvec{L}}_{{0}}^{{}}\), respectively. The initial configuration of the catenary can be calculated by solving Eq. (6). The details of the initialisation procedure are discussed in the following section.

3.2 Computation of initial configuration with contact line height variability

It can be seen that Eq. (6) cannot be solved directly because \(\left[ {\begin{array}{*{20}c} {{\varvec{K}}_{{\text{T}}}^{{\text{G}}} } & {{\varvec{K}}_{{\text{L}}}^{{\text{G}}} } \\ \end{array} } \right]\) is not a square matrix. The total number of unknowns exceeds the total number of equations, which leads to undetermined solutions. Therefore, additional constraint conditions should be provided to reduce the number of unknowns and ensures that Eq. (6) has unique solutions. These additional constraint conditions are determined by the design specification and the measurement geometry data. In this work, three types of additional constraints are defined, illustrated in Fig. 9.

  • The vertical positions of all dropper points in the contact wire are restricted according to the geometry data.

  • The longitudinal direction of each node is restricted to suppress the longitudinal movement.

  • The designing tensions are imposed on the endpoints of messenger, contact and stitch lines.

Fig. 9
figure 9

Illustration of additional constraints in the shape-finding of catenary

Full size image

These constraint conditions reduce \(\left[ {\begin{array}{*{20}c} {{\varvec{K}}_{{\text{T}}}^{{\text{G}}} } & {{\varvec{K}}_{{\text{L}}}^{{\text{G}}} } \\ \end{array} } \right]\) in Eq. (6) to be a square matrix, which ensures the equality between the numbers of equations and unknowns. The steady arm points are fixed tentatively in the iterative procedure to place the steady arm points at their correct positions. The inclination of each steady arm can be calculated by the resistance forces in the fixed point, which is replaced by a rigid truss element without rotation DOFs to reproduce the realistic behaviour of a steady arm. It should be noted that these additional constraints are only used in the shape-finding procedure. They are removed after the equilibrium state is achieved.

An example is presented here using the parameters of the measured catenary in Sect. 2. The main property parameters of the catenary are collected in Table 1. Firstly, each dropper’s longitudinal position and steady arm point are modified by the random longitudinal deviation generated from \(N\left( {u_{{\text{g}}} ,\delta_{{\text{g}}}^{2} } \right)\). Using one sample of vertical deviation in Fig. 8a, the dropper’s heights and steady arm point can be extracted by interpolation according to their longitudinal positions. The convergence condition is defined as follows:

$$\max \left( {\left| {\left[ {\begin{array}{*{20}c} {\Delta {\varvec{U}}_{{\text{C}}} } \\ {\Delta {\varvec{L}}_{{0}}^{{}} } \\ \end{array} } \right]} \right|} \right) < 10^{ - 9} {\kern 1pt} {\text{m}}{.}$$
(7)
Table 1 Catenary property parameters
Full size table

The maximum absolute residual versus the cycle index is presented in Fig. 10. It is seen that the convergence condition can be satisfied after 18 cycles of iteration. The results of catenary geometry are presented in Fig. 11. It is seen that the deviated configuration has a distinct difference from the original one. In the next section, a pantograph model is included to investigate the contact force’s dispersion with the effect of geometry deviation. The central nine spans are chosen as the contact force analysis range to eliminate the boundary effect interference.

Fig. 10
figure 10

Absolute residual in shape-finding procedure

Full size image
Fig. 11
figure 11

Results of catenary geometry: a full geometry; b locally enlarged view of one span

Full size image

3.3 Pantographs–catenary interaction formulation

To evaluate the response at high frequencies, the pantograph is assumed to be a lumped mass model with flexible collectors, as shown in Fig. 12. Each collector is discretised into a few 2D beam elements. The stiffness matrix can be written as follows:

$${\varvec{k}}_{{{\text{pe}}}} = \frac{{EI_{{{\text{pe}}}} }}{{l_{{{\text{pe}}}}^{3} }}\left[ {\begin{array}{*{20}c} {12} & {6l_{{{\text{pe}}}} } & { - 12} & {6l_{{{\text{pe}}}} } \\ {6l_{{{\text{pe}}}} } & {4l_{{{\text{pe}}}}^{2} } & { - 6l_{{{\text{pe}}}} } & {2l_{{{\text{pe}}}}^{2} } \\ { - 12} & { - 6l_{{{\text{pe}}}} } & {12} & { - 6l_{{{\text{pe}}}} } \\ {6l_{{{\text{pe}}}} } & {2l_{{{\text{pe}}}}^{2} } & { - 6l_{{{\text{pe}}}} } & {4l_{{{\text{pe}}}}^{2} } \\ \end{array} } \right],$$
(8)

where \(l_{{{\text{pe}}}}\) is the element length and \(EI_{{{\text{pe}}}}\) is the bending stiffness of the collector. Usually, the collector is made of two types of materials, namely graphite and aluminium. The bending stiffness of the collector is calculated by the mixture theory [28]. As the flexibility of the pantograph framework is very low [29], it is treated as a rigid lumped mass here. A penalty function method is employed to couple the contact wire and the collector. Therefore, the contact force \(f_{\text{c}}\) can be calculated by

$$f_{\text{c}} = \left\{ {\begin{array}{*{20}l} {k_{{\text{s}}} (z_{{\text{p}}} - z_{{\text{c}}} )} \hfill & {{\text{if}}\quad {\kern 1pt} z_{{\text{p}}} - z_{{\text{c}}} > 0} \hfill \\ 0 \hfill & {{\text{if}}\quad {\kern 1pt} z_{{\text{p}}} - z_{{\text{c}}} \le 0} \hfill \\ \end{array} } \right.,$$
(9)

in which \(z_{{\text{p}}}\) is the pantograph head uplift, and \(z_{{\text{c}}}\) is the vertical displacement of the contact wire in the contact point. Using Eq. (9), the equation of motion for the pantograph–catenary system is written as

$${\varvec{M}}_{{\text{G}}}^{{}} {\ddot{\varvec{U}}}\left( t \right){\varvec{ + C}}_{{\text{G}}}^{{}} {\dot{\varvec{U}}}\left( t \right){\varvec{ + K}}_{{\text{G}}}^{{}} \left( t \right){\varvec{U}}\left( t \right){\varvec{ = F}}_{{\text{G}}}^{{}} \left( t \right),$$
(10)

where \({\varvec{M}}_{{\text{G}}}^{{}}\), \({\varvec{C}}_{{\text{G}}}^{{}}\) and \({\varvec{K}}_{{\text{G}}}^{{}} \left( t \right)\) are the mass, damping and stiffness matrices for the whole system, respectively; \({\varvec{F}}_{{\text{G}}}^{{}} \left( t \right)\) is the external force vector. A Newmark integration scheme is adopted to solve Eq. (10). The stiffness matrix \({\varvec{K}}_{{\text{G}}}^{{}} \left( t \right)\) is updated according to the catenary deformation in each time step to describe the geometrical nonlinearity and dropper slackness [15].

Fig. 12
figure 12

Lumped mass model of pantograph with flexible collectors

Full size image

4 Effect of geometry deviation on contact forces

This section investigates the effect of catenary geometry deviation on the contact force through a series of numerical simulations. The measured contact forces collected by an inspection vehicle regularly running in the Norwegian network are compared with the simulation results. Then, the effect of the cut-off frequency on the simulation results is investigated. Finally, probabilistic analyses are performed on the simulated data to assess the interaction performance of the pantograph–catenary system. In Sect. 4.1, the train speed is set as 160 km/h, consistent with the inspection vehicle’s speed. In Sects. 4.2 and 4.3, the train speed changes from 160 to 280 km/h to investigate the dynamic performance at different speeds. It should be noted that 280 km/h is the catenary top speed, which is defined as 0.7 times the wave propagation speed according to En 50119 [30].

4.1 Comparison with measurement data

Based on the idea of the Monte Carlos method, 400 numerical simulations are performed to describe the dispersion of dynamic responses. According to En 50367 [31], the contact force standard deviation filtered within 0–20 Hz is the most critical assessment indicator to describe the comprehensive current collection quality. Therefore, the histogram of the contact force standard deviation obtained by 400 simulations is presented in Fig. 13. The standard deviation of the simulated contact force generally follows a symmetric distribution with a standard deviation of 0.59 N and a mean of 11.82 N. The measured contact force standard deviations from five independent field tests are denoted by dash lines in Fig. 13. The measured contact forces are obtained by the inspection vehicle regularly running in the Norwegian network. The average time interval between two adjacent measurements is six months. All these measured contact force standard deviations are within the scope of the simulation results. However, all the measurement results are in the ‘left part’ of the distribution, which can be explained from two aspects. The first one is that the bad performance in the right part is not likely to happen in the field test due to the appropriate maintenance of the railway operator. The second explanation is that the average of the simulation results cannot accurately represent the actual condition, and the simulation results are expected to be calibrated according to the measurement data. However, both explanations cannot be fully verified at present because only a very limited amount of measurement data are available. The actual distribution of contact force statistics deserves to be revealed with abundant measurement data in the future.

Fig. 13
figure 13

Histogram of simulated contact force standard deviation. Dash lines denote the measured contact force standard deviations from five times of field tests

Full size image

4.2 Analysis with different cut-off frequencies

The current standard En 50367 specifies a frequency range of interest within 0–20 Hz. This low-frequency range is expected to be improved to capture more high-frequency behaviour of the pantograph–catenary interaction. It should be noted that the high-frequency measurement data cannot be provided to validate the simulation results, which is beyond the frequency range of the current measurement equipment. The work in this section only conducts a qualitative analysis to point out the expected impact of the geometry deviation on the contact force when the cut-off frequency moves up to 200 Hz. In this numerical simulation, a small element size of the contact wire and a pantograph model with flexible collectors are adopted to ensure numerical accuracy at high frequencies. The train speed is chosen from 160 to 280 km/h with an interval of 40 km/h. For each speed, 400 simulations are performed to ensure that the dispersion can be reflected. Figure 14 shows the root mean square (RMS) of the contact force standard deviation with different cut-off frequencies. It is seen that the RMS undergoes a significant increase with the cut-off frequency increasing and then becomes stable after the cut-off frequency reaches a critical value. Generally, the critical value increases with the improvement of the speed. At 160 km/h, the RMS becomes stable after the cut-off frequency is larger than 90 Hz. The critical cut-off frequencies are about 105, 125 and 150 Hz at the speed of 200, 240 and 280 km/h, respectively. The corresponding spatial wavelength is around 0.5 m, about 1/16 of the interval between two adjacent droppers. According to the analysis in [26], the cut-off frequency should cover the 1/4 of dropper interval to fully describe the catenary’s geometry effect in the contact force. However, the geometry deviation is not considered in [26]. Thus, this critical cut-off frequency should be improved to cover the 1/16 of the dropper interval to describe the effect of the catenary geometry deviation fully. The boxplots of contact force standard deviation with different cut-off frequencies at 160 and 280 km/h are presented in Fig. 15. It is seen that the fluctuating range of the contact force standard deviation does not show a significant change when the cut-off frequency increases over the critical value.

Fig. 14
figure 14

RMS of contact force standard deviation with different cut-off frequencies

Full size image
Fig. 15
figure 15

Boxplots of contact force standard deviation with different cut-off frequencies at a 160 km/h and b 280 km/h

Full size image

4.3 Probability analysis

In assessing current collection quality, the statistical minimum contact force is a critical index and should be positive to restrict the occurrence of contact loss, which is calculated by

$$F_{{{\text{smin}}}}^{{}} = F_{{{\text{mean}}}} - 3\delta ,$$
(11)

where \(F_{{{\text{mean}}}}\) is the mean contact force and \(\delta\) is the contact force standard deviation. The coefficient ‘3’ is determined by the 99.73% confidence level. In this section, the statistical minimum contact force at each speed is calculated to check the interaction performance with random geometry deviation of catenary. Figure 16a, b presents the boxplots of statistical minimum contact force at different operating speeds with the cut-off frequencies of 20 and 200 Hz, respectively. At 200 km/h, the statistical minimum contact forces are always positive with 20 and 200 Hz cut-off frequencies, which satisfies the assessment standard. Actually, 200 km/h is the operating speed for the analysed catenary system. When the speed moves up to 240 km/h, some negative statistical minimum contact forces can be observed with the 200 Hz cut-off frequency. At 280 km/h, the negative statistical minimum contact force can be observed with the 20 Hz cut-off frequency. Almost all statistical minimum contact forces are smaller than 0 N with 200 Hz cut-off frequency at 280 km/h. According to En 50119 [30], 280 km/h is very close to the catenary’s top speed, which is defined as 0.7 times the wave propagation speed. When the train speed is close to the top speed, unsatisfactory current collection quality can be expected. But it should be noted that not all the contact loss at 200 Hz cut-off frequency is unacceptable. According to the experience of railway operators, a certain amount of contact loss is tolerant at high frequency. Thus, the definition of the statistical minimum contact force should be modified. Assuming that 1% contact loss is acceptable at 200 Hz, the modified statistical minimum contact force can be calculated by

$$F_{{{\text{smin}}}}^{{}} = F_{{{\text{mean}}}} - 2.326\delta ,$$
(12)
Fig. 16
figure 16

Boxplots of statistical minimum contact force at different operating speeds with cut-off frequencies of a 20 Hz and b 200 Hz

Full size image

where the coefficient ‘2.326’ is determined by the 98% confidence level, which means that 1% negative contact force can be tolerant. The boxplots of modified statistical minimum contact force at different operating speeds with 200 Hz cut-off frequency are presented in Fig. 17. It is seen that all the modified statistical minimum contact forces are above zero at speeds of 200 and 240 km/h. At 280 km/h, most results are no longer acceptable.

Fig. 17
figure 17

Boxplots of modified statistical minimum contact force at different operating speeds with 200 Hz cut-off frequency

Full size image

Figure 18 presents the probability densities of statistical minimum contact force at different operating speeds with the cut-off frequencies of 20 Hz. The statistical minimum contact forces with 20 Hz cut-off frequency are always larger than the threshold 0 N at 200 and 240 km/h. At 280 km/h, the statistical minimum contact force has a 0.68% possibility to be negative. When the cut-off frequency moves up to 200 Hz, the probability densities of modified statistical minimum contact force at different operating speeds are presented in Fig. 19. It is seen that the modified statistical minimum contact force has an 85.58% possibility to be negative at 280 km/h. If fewer contact losses are preferred, the pantograph has to be uplifted to have a higher mean contact force. It should be noted that the threshold of 1% for the contact loss is just an example here to demonstrate the probability analysis. The railway operator should give a more reasonable value according to actual conditions.

Fig. 18
figure 18

Probability density of statistical minimum contact force at different operating speeds with 20 Hz cut-off frequency

Full size image
Fig. 19
figure 19

Probability density of modified statistical minimum contact force at different operating speeds with 200 Hz cut-off frequency

Full size image

5 Conclusions

This paper presents a field measurement of the catenary geometry from the Norwegian railway network, providing realistic catenary geometry data for the numerical simulation. Based on the Monte Carlo method, many contact wire geometry samples are generated and included in the catenary model. Employing a pantograph model with flexible collectors, the effect of random geometry deviation on the contact force is investigated. The main conclusions are drawn as follows:

  1. (1)

    The catenary geometry deviation causes a significant dispersion of the response of pantograph–catenary interaction. The measured contact forces by the inspection vehicle from the field tests are within the scope of the simulation results.

  2. (2)

    The critical cut-off frequency should be improved to cover 1/16 of the dropper interval, which can fully describe the effect of the catenary’s geometry deviation on the contact force.

  3. (3)

    The statistical minimum contact force can be modified according to the tolerant contact loss rate at high frequency. The probability analysis indicates that modified statistical minimum contact force has an 85.58% possibility to be negative at 280 km/h. The pantograph–catenary system has an unpleasant interaction performance at the catenary top speed when the random catenary geometry deviation is included.