Abstract
We study cooperation between the airline and high-speed rail (HSR) sectors by formulating their joint profit as a maximization problem using a multinomial logit choice model in a three-node setting. We allow the non-purchase option as an outside option available to consumers. The demand for each choice is not only a function of the price but also the service quality, such as the total trip time, frequency of service, and ease of connecting from the hub to a nearby HSR station. As a result, the following findings are presented. First, regardless of the service quality of either sector and the non-purchase option, cooperation decreases the total volume of the domestic market of a country. Second, when the attractiveness of the outside option is high, the HSR and air sectors can prevent a large reduction in the total volume by cooperation in the connecting market. However, this is not the case in the domestic market. Third, if the non-purchase quality in the domestic market is high, then cooperation increases the social welfare of the whole market. If the non-purchase quality is low, then cooperation increases the welfare of the whole market only in cases where the number of potential customers in the connecting market is relatively large. We also show the effect of improving air–rail service quality on each market share and on the total profit.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Traditionally, high-speed rail (HSR) has been one of most efficient ways to travel between an origin and destination which are less than 1000 km apart, or when the travel time is less than 1.5 h [1,2,3]. Therefore, HSR is a de facto competitor of the air sector as it provides a service which otherwise would be provided by an airline. For example, with the introduction of an HSR in Taiwan in 2007 linking the two largest cities, Taipei and Kaohsiung (248 km apart), the domestic airline industry experienced a significant drop in market share and a decrease in profit [4]. However, as alluded to by Givoni and Banister [5], the relationship between airlines and HSR is far from that of pure competitors. In particular, they argue that the existence of HSR can complement the airline industry by providing services from a node within an airline network to nearby cities. In fact, this HSR–airline “cooperation” is especially economically desirable for hub–spoke-type networks which are common in most countries. With most airports located outside of city centers, the integration of HSR with local train networks can further enhance the benefits associated with HSR–airline cooperation. Another often cited advantage of HSR–airline cooperation is the environmental benefit associated with a reduction in CO\(_2\) emissions [6].
As HSR–airline cooperation is a relatively new concept, there are only a limited number of cases/routes where such cooperation has been implemented, most of which can be found in Europe. One example is the air–rail services provided by Lufthansa and Deutsche Bahn that link the airline hub in Frankfurt to nearby cities, including Stuttgart, Cologne, and Bonn. These three cities are located between 130 and 150 km from Frankfurt with commuting times of 38–65 min. Daily, the numbers of trains running from Frankfurt to Stuttgart, Cologne, and Bonne are 23, 43, and 27, respectively. Passengers traveling via Frankfurt to one of these three cities are provided with a combo ticket comprising an airline ticket to Frankfurt and an HSR ticket from Frankfurt to their final destination. Such cooperation provides two obvious benefits. First, luggage will be delivered directly to the final destination, and passengers can avoid the inconvenience of retrieving luggage at the airport and then carrying it during transit. This could also limit the possible time delay caused by luggage transit when the airport crew need to handle large volumes of luggage during rush hours. Second, HSR in these three cities is integrated with the local train networks, therefore eliminating the need for connections involving other forms of ground transportation.
While HSR–airline cooperation is appealing, its implementation is subject to a number of challenges. Perhaps, the most important one is the fact that airlines and HSR are owned by separate entities, who are operated under different objectives and by different institutions. Traditionally, they see each other as rivals and compete for the same consumers. After Tokyo’s successful bid to host the 2020 summer Olympics, discussions have begun on the use of Shizuoka Airport as a hub through which passengers from other countries could visit Tokyo and Osaka during the Olympics. The discussions have included two key issues. One is that the two major airports serving the Tokyo area, Narita and Haneda, are already operating at close to their maximum capacity during busy seasons. Any increase in demand during the Olympics would likely push these airports over their maximum flight capacities, leading to delays and other problems. Second, in the event of disruptions caused by earthquakes or other natural hazards, HSR–airline cooperation would provide a much-needed alternative to ensure reliable transportation during the Olympics. However, even during initial discussions, there have been a number of issues raised by the two main entities involved: the Japan Railway Company (JR) and Shizuoka prefecture. In particular, JR has argued that it presents a major engineering challenge and is technically impossible to construct an underground facility under the current location of Shizuoka Airport to link the airport to the HSR network. This suggests the Japanese government should not rely on the two parties to voluntarily engage in the discussion and implementation of HSR–airline cooperation.
Another possible explanation of why there is little HSR–airline cooperation in practice is that the benefit and trade-offs of such cooperation are not well understood. Competition between the airline and HSR industries has been an active research area for years [7,8,9,10,11,12]. In particular, two papers concluded that the introduction of a new HSR network would have a negative impact on the airline industry by decreasing its market share [7, 11]. Adler et al. [8] developed an almost complete game engineering model and concluded that the European Union (EU) could benefit from HSR–airline cooperation. Yang and Zhang [9] studied the competition between these two sectors by formulating the objective of HSR as a weighted sum of its profit and social surplus. Their paper shows that increasing the weight on social surplus would lower the price of both HSR and airlines, thereby benefitting consumers. This is not a surprising result, as the HSR sector includes consumer surplus in its objectives. The paper then conducts a comparative statistical analysis of the airport access time, rail speed, and other factors. An empirical study by Behrens and Pels [10] focuses on the London–Paris market and finds that there was intense competition between airlines and HSR. Their paper further identifies that the frequency, travel time, and ease to connect to other networks are the factors which determine travelers’ preference. On the other hand, there is relatively little literature on the cooperation between these two sectors [5, 13,14,15,16]. The two papers which are most relevant to our present study are by Socorro and Viecens [15] and Jiang and Zhang [13]. Both papers use a simplified three-node network in which a non-domestic origin city is linked to a final domestic destination through a domestic hub and consider the cases of whether the airport is capacity constrained or not. However, Socorro and Viecens [15] applied a prescribed rule to ration airport capacity when there is a shortage of capacity. In contrast, Jiang and Zhang [13] endogenize the decision of allocating scarce airport capacity between different markets. Their paper further analyzes the impact of traffic frequency, vertical differentiation between nodes, price elasticity, and heterogeneous passenger types on the market outcomes. In this respect, the framework developed by Jiang and Zhang [13] is more complete and allows for the consideration of more factors which have practical relevance to consumers’ preference.
Our paper also relies on a simple three-node network to examine the market outcomes of HSR–airline cooperation with consideration of airport capacity. However, our work differs from Jiang and Zhang [13] and Socorro and Viecens [15] in a number of ways. First, we deploy a multinomial logit model (MNL) to represent consumers’ travel demand. Thus, in contrast to Jiang and Zhang [13], we consider factors that are crucial for determining the demand for different transportation modes, such as frequency, travel time, cost, time to airport or HSR station, and conformability, and allow them to be related to the demand nonlinearly. In other words, our approach does not require the marginal effect of these factors on the demand to be constant. Second, our approach to modeling the demand allows “non-purchase” as an outside option available to consumers. That is, when their maximum willingness to pay is less than the cheapest ticket prices, they can decide to cancel the trip. Therefore, our model can more realistically reflect the decision-making process of consumers. Without the “non-purchase” option, an analysis might overestimate the market shares of both transportation modes.
Recently, Xia and Zhang [16] also considered competition and cooperation between HSR and airlines in a three-node setting. There are some differences with our model. They assume that (1) the air transport and HSR are vertically differentiated, (2) the demand function is a function of both fares and the total travel time, (3) there are two airlines operating in the international market, and (4) the hub airport capacity is constrained. Unlike their model, we assume that the demand function is defined as an MNL model, so that air transport and HSR are horizontally differentiated. The MNL model is widely used in estimating travel demand (see [17]). The popularity of MNL stems from the fact that it is analytically tractable, reasonably accurate, and easily estimable using standard statistical techniques [18]. Since the service quality for each mode and non-purchase option is incorporated as a linear function in the MNL demand, we can also analyze the effect of travel time on HSR–airline cooperation through a sensitivity analysis of service quality. Moreover, in our model, the operating cost changes depending on the service quality. This is a more realistic assumption than in the above papers. However, the present paper does not consider competition in the international market and capacity constraint. Although these are important issues in practice, we focus on the analysis of the effect of service quality and the non-purchase option on the transport operator’s profits, consumer surplus, and social welfare.
Our contributions are summarized as follows. First, in an HSR-accessible market, we show that rail fare increases as the service quality of HSR increases (Proposition 3.2), which agrees with the results of previous papers (e.g., [9, 16]). However, airfare is not affected by the service quality of HSR, which differs from the conclusions of the existing literature (e.g., [9, 16]). This is due to the independence of irrelevant alternatives (IIA) in the MNL. Second, we find that when air transport and HSR cooperate, transport operators charge a higher fare in HSR-accessible markets and the air–air connection market increases (Proposition 4.2), which has also been shown in Xia and Zhang [16]. However, airfare in HSR-inaccessible markets is not affected by cooperation, while Xia and Zhang [16] show that when air transport and HSR compete, the network carrier may charge excessively high airfares. The difference between the result of the present study and Xia and Zhang may be due to the choice of available transport alternatives in the connecting market. Xia and Zhang [16] assume that both air–rail and air–air connections are available in the HSR–airline competition case. However, we assume that the air–air transfer is the only available option, which is the same as in Socorro and Viecens [15] and Jiang and Zhang [13]. We separate the air–rail transfer demand into the HSR-inaccessible and HSR-accessible cases. Finally, we show that when the non-purchase quality in HSR-accessible markets is relatively high, social welfare increases with HSR–airline cooperation (Proposition 4.7). This result has not been shown in previous studies. Following Xia and Zhang [16], the comparison of results is summarized in Table 1.
The remainder of the paper is organized as follows. In Sect. 2, we introduce the notation and assumptions used in this paper. In Sect. 3, we formulate an air and rail model for the competition and cooperation cases, and derive the optimal prices for both sectors. In Sect. 4, we study the effect of cooperation on the total market volume and social welfare for each market by comparing the competition and cooperation cases. In Sect. 5, we present numerical results to evaluate the effect of coordination on the whole market. Finally, Sect. 6 concludes the paper with further comments.
2 Notations
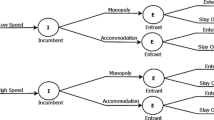
Following Jiang and Zhang [13], we consider a network structure in which there are three cities (A, B, and H) with inter-city transport services, AH and HB, being connected by only two links (Fig. 1). The AH route is operated only by the air sector, while HB is served by both airline and HSR operators. In addition, an airline serves the AB market using a hub-and-spoke strategy with H as its hub. That is, there is no direct flight service in the AB market.Footnote 1
Let \(M_i>0\) be the number of potential customers in market i where \(i=1,2,3\) indicate the markets AH, HB, and AB, respectively. The sizes of these markets are determined from the city’s population or annual number of passengers from the city. We define the set of fare classes offered by the air and HSR operators in market i as \({\mathcal {A}}_i\) and \({\mathcal {R}}_i\), respectively. The set of all services in market i is denoted by \({\mathcal {N}}_i={\mathcal {A}}_i\cup {\mathcal {R}}_i\).
We use an MNL model to calculate the probability of a consumer selecting a particular travel mode. The desirability of a particular travel mode under our model settings can be determined from the fare price, travel time, frequency, and other attributes. Let \(f_{i,j}\) be the price of service j in market i, and \(\varvec{f}_i=\{f_{i,j}\}_{j\in {\mathcal {N}}_i}\) be the vector of prices for all services in market i. The consumer utility function for service j in market i is defined by
where \(b_{i,j}\) characterizes the quality of the service, \(\beta _i>0\) represents the price sensitivity parameter, \(\epsilon _j\) is a mean-zero random component, and \(u_{i,0}\) is the utility associated with an outside alternative. The quality of service \(b_{i,j}\) is typically modeled as a linear function of its attributes, i.e., \(b_{i,j}=\varvec{\alpha }^{\rm T }\varvec{x}_{i,j}\), where \(\varvec{\alpha }\) is a vector of parameters, and \(\varvec{x}_{i,j}\) is a vector of attribute values for option j in market i. The service quality of the air sector in market 3 is assumed to also be affected by the connection time at the airport. The term \(\epsilon _{j}\) is assumed to be an independent identically distributed (i.i.d.) random variable with a Gumbel distribution that has cumulative density function \(F(x)=\exp \{-\exp \{-(\frac{x}{\mu }+\gamma )\}\}\), where \(\gamma\) is Euler’s constant, and \(\mu\) is the scale parameter. The mean and variance of \(\epsilon _{j}\) are 0 and \(\mu ^2\pi ^2/6\), \(\mu >0\), respectively. The probability that customers in market i select a service j is given by
and the probability of non-purchase is given by
Using the probability of selecting option j defined in Eqs. (3) and (4), the expected demand for mode of transport j in market i, \(d_{i,j}\), is calculated as the product of the number of potential customers and the probability of selection. That is, \(d_{i,j}\equiv M_ip_{i,j}\).
We now consider the cost function. The cost function \(C_{i,j}(\cdot )\) is defined as a function of the demand and consists of the variable and fixed costs:
where \(c_{i,j}(b_{i,j})\) is variable cost, and \(I_{i,j}(b_{i,j})\) is fixed cost. Note that the variable and fixed costs are also a function of the service quality \(b_{i,j}\). We assume that \(c_{i,j}(b_{i,j})\) is increasing with service quality \(b_{i,j}\). For simplicity of notation, we write \(c_{i,j}\) and \(I_{i,j}\) instead of \(c_{i,j}(b_{i,j})\) and \(I_{i,j}(b_{i,j})\), respectively.
3 High-speed rail and airline model
In this section, we first consider an air and rail competition problem (followed by the cooperation cases) and derive the optimal prices for both sectors.
3.1 Competition case
In the competition case, the air and HSR sectors compete for the route HB, and the air sector acts as a monopoly in markets \(i=1\) (AH) and \(i=3\) (AB).Footnote 2 Thus, the set of available transportation modes in the markets is \({\mathcal {N}}_1={\mathcal {A}}_1\), \({\mathcal {N}}_2={\mathcal {A}}_2\cup {\mathcal {R}}_2\) and \({\mathcal {N}}_3={\mathcal {A}}_3\), and \({\mathcal {R}}_1={\mathcal {R}}_3=\emptyset\). With the above cost and demand information, the maximization problem of the air sector is as follows:
where \(V_a\) denotes the maximum expected profit of the air sector at equilibrium, \(\varvec{f}=\{f_{i,j}\}\) for all \(i=1,2,3, j\in {\mathcal {N}}_i\) is the vector of ticket prices for all markets, and \(\varvec{f}_a=\{f_{i,j}\}\) for all \(i=1,2,3, j\in {\mathcal {A}}_i\) is the vector of air prices. The optimal price and expected demand for service j in market i in the competition case are denoted by \(f^*_{i,j}\) and \(d^*_{i,j}=M_ip^*_{i,j}\), respectively.
The maximization problem for HSR is given by
where \(V_r\) denotes the maximum expected profit of the HSR sector at equilibrium, \(\varvec{f}_2=\{f_{2,j}\}\) for all \(j\in {\mathcal {A}}_2\cup {\mathcal {R}}_2\), and \(\varvec{f}_{2,r}=\{f_{2,j}\}\) for all \(j\in {\mathcal {R}}_2\).
The profit functions \(v_a\) and \(v_r\) are not concave in \(\varvec{f}_a\) and \(\varvec{f}_{2,r}\) (see [20]), and this poses problems when finding numeric solutions for the models. However, as suggested by Dong et al. [21], a one-to-one relationship between the price and market share allows us to reformulate the problem by using the market share as the decision variable. In particular, the ratio of the market shares \(p_{i,j}/p_{i,0}\) can be expressed as a function of the attributes as well as the utility of the outside alternative, \(p_{i,j}/p_{i,0}=\exp \{(b_{i,j}-\beta _if_{i,j}-u_{i,0})/\mu \}\). Thus, we obtain the price as a function of the ratio of market shares:
Here we define a vector of probabilities as \(\varvec{p}=\{p_{i,j}\}\) for all \(i=1,2,3,\, j\in \bigcup _i({\mathcal {A}}_i\cup {\mathcal {R}}_i)\), \(\varvec{p}_a=\{p_{i,j}\}\) for all \(i=1,2,3, j\in \bigcup _i{\mathcal {A}}_i\) and \(\varvec{p}_2=\{p_{2,j}\}\) for all \(j\in {\mathcal {A}}_2\cup {\mathcal {R}}_2\).
With this reformulation, we obtain the following lemma.
Lemma 3.1
-
(i)
The total profit of the airline \(v_a(\varvec{p})\) is jointly concave in \(\varvec{p}_a\).
-
(ii)
The total profit of the HSR \(v_r(\varvec{p})\) is jointly concave in \(\varvec{p}_{2,r}\).
Then, the profit functions are concave in the market share (see “Appendix” for details). Next, we use the Lambert W function [22] to obtain a closed-form expression for the market share as follows (see “Appendix” for details).
Proposition 3.1
-
(i)
The market share of air transport for class \(j\in {\mathcal {A}}_i\) in market \(i=1,2,3\) is given by
$$\begin{aligned} p^*_{i,j}=\frac{W[\sum _{k\in {\mathcal {A}}_i}A_{i,k}]}{1+W[\sum _{k\in {\mathcal {A}}_i}A_{i,k}]+W[\sum _{k\in {\mathcal {R}}_i}A_{i,k}]}\frac{A_{i,j}}{\sum _{k\in {\mathcal {A}}_i}A_{i,k}}, \end{aligned}$$(8)and the market share for HSR for class \(j\in {\mathcal {R}}_2\) in market \(i=2\) is given by
$$\begin{aligned} p^*_{2,j}=\frac{W[\sum _{k\in {\mathcal {R}}_2}A_{2,k}]}{1+W[\sum _{k\in {\mathcal {A}}_2}A_{2,k}]+W[\sum _{k\in {\mathcal {R}}_2}A_{2,k}]}\frac{A_{2,j}}{\sum _{k\in {\mathcal {R}}_2}A_{2,k}}, \end{aligned}$$(9)where
$$\begin{aligned} A_{i,j}=\exp \left\{ \frac{1}{\mu }(b_{i,j}-u_{i,0}-\mu -\beta _ic_{i,j})\right\} . \end{aligned}$$(10) -
(ii)
The optimal price of air travel for class \(j\in {\mathcal {A}}_i\) in market \(i=1,2,3\) is given by
$$\begin{aligned} f^*_{i,j}=\frac{\mu }{\beta _i}\left( 1+W\left[ \sum _{k\in {\mathcal {A}}_i}A_{i,k}\right] \right) +c_{i,j}. \end{aligned}$$(11)The optimal price of HSR for class \(j\in {\mathcal {R}}_2\) in market \(i=2\) is given by
$$\begin{aligned} f^*_{2,j}=\frac{\mu }{\beta _2}\left( 1+W\left[ \sum _{k\in {\mathcal {R}}_2}A_{i,k}\right] \right) +c_{2,j}. \end{aligned}$$(12)
From Eqs. (11) and (12), we note that the optimal fare for each sector depends only on the utility of all fare classes provided by its own sector and the non-purchase option. In other words, the HSR (or air) price is not affected by the characteristics of the air (or HSR) sector in a competitive market. We also note that the price difference between the fare classes depends only on the operating cost, because the first term of Eq. (11) is the same for each price. However, in practice, fare classes are differentiated by the advance purchase time and other conditions (e.g., cancellation and refund policies), rather than by differences in the operating costs. Thus, the optimal price does not fully express the characteristics of fare class. The above observations are due to the independence of irrelevant alternatives (IIA) property of the multinomial logit (MNL) model.Footnote 3 Although the MNL model has these drawbacks, it enables us to obtain the market shares and prices as a simple closed-form expression. In the rest of this paper, we focus on the analysis of the market shares rather than the prices and analyze the competition and cooperation problems when each sector provides a single fare class in each market. Thus, we redefine the set of services in each market as follows: \({\mathcal {N}}_1=\{a\}\), \({\mathcal {N}}_2=\{a,r\}\), and \({\mathcal {N}}_3=\{a\}\). Note that “a” and “r” represent the air service and the HSR service, respectively.
Now, we analyze the effect of the service quality on the market share and optimal price. We define the difference between the service quality and the variable cost as the cost-adjusted service quality, \({\hat{b}}_{i,j}\equiv b_{i,j}-\beta _ic_{i,j}\). The cost-adjusted service quality \({\hat{b}}_{i,j}\) allows us to measure the service quality with consideration of the variable cost. A high value of \({\hat{b}}_{i,j}\) implies that a firm provides good service for passengers at a low cost.
Proposition 3.2
For each market \(i=1,2,3\) and sector \(j\in {\mathcal {N}}_i\), the market share \(p^*_{i,j}\) and optimal price \(f^*_{i,j}\) are increasing in service quality \({\hat{b}}_{i,j}\). In market 2, the market share \(p^*_{2,j}\) is decreasing with increasing quality of the competitor’s service \({\hat{b}}_{2,k}\), \(k\ne j\in {\mathcal {N}}_2\).
The interpretation of the model is mostly intuitive, but we also provide some further explanation. An increase in the service quality of the sector in each market increases its market share. As customers value service quality, an increase in service quality also implies that they are willing to pay more, leading to higher optimal prices. In addition, this proposition implies that the market share of the air (or HSR) sector decreases as the service quality provided by the HSR (or air) increases in market 2. Since the air (or HSR) sector does not respond to changes in the rival’s service quality according to the IIA property, its market share decreases with increases in the rival’s market share. Related to this result, we can also show the effect of the HSR entities on the air sector share in the HSR-accessible market (i.e., market 2). From Eq. (8), the air sector share with consideration of the HSR entity is given by \(p^{*}_{2,a}=W[A_{2,a}]/(1+W[A_{2,a}]+W[A_{2,r}])\). When \(b_{2,r}\rightarrow -\infty\), the air sector share without consideration of the HSR entity can be obtained as \(p^{**}_{2,a}=W[A_{2,a}]/(1+W[A_{2,a}])\). Thus, the HSR entity has a negative impact on the air sector market share, and the better the service quality of the HSR is, the more the air sector market share decreases. Similar results have been found in empirical research. Wan et al. [26] used a difference–indifference approach and investigated the impact of the commencement of HSR services on airlines’ number of available seats for domestic flights and the frequency on the affected routes in China, Japan, and South Korea in the sampling period 1994–2012. They found that China’s HSR services with a maximum speed of about 200 km/h (300 km/h) can cause a significant reduction in airline seat capacity on medium-haul (or long-haul) routes. Since the reduction in available seats can be considered as a decrease in the market share, their results are consistent with our findings.
Based on the optimal prices and the corresponding market shares, we obtain the maximum total profits for both sectors.
Proposition 3.3
The maximum total profits of the air and HSR sectors are given by
and
We next derive expressions for the social surplus by first defining \(S(\varvec{f})\) as the consumer surplus from the multinomial logit model (3) and (4). Following Small and Rosen [27], the consumer surplus can be expressed as follows:
We define the consumer surplus in the competition case as \(S_{\text{C}}\equiv S(\varvec{f}^*)\), where \(\varvec{f}^*\) represents the vector of optimal prices. The social welfare is defined as the sum of the total consumer surplus and total profits from the air and HSR operators:
3.2 Cooperation case
In the cooperation case, the air and HSR sectors make decisions jointly to maximize their total profit. The HSR sector not only operates in market \(i=2\) (HB) but also in market \(i=3\) (AB). Thus, customers who travel from A to B can then choose between air (\(j=a\)) and HSR (\(j=ar\)) transport for the route HB, \({\mathcal {N}}_3=\{a,ar\}\). We refer to the air–rail service as “ar.” Thus, in the cooperation case, the HSR (air) is an alternative itinerary for the air (HSR) in market 2. Similarly, the air–rail (connecting flights) service can be considered as an alternative itinerary for the connecting flights (air–rail) in market 3. The service quality of the air–rail service \(b_{3,ar}\) is affected not only by the travel time and the frequency for each sector, but also by the accessibility between the airport and the HSR station. Customers in market \(i=1\) face the same decisions as in the competition case.
The joint maximization problem of the sectors is given by
where \({\mathcal {N}}_1=\{a\}\), \({\mathcal {N}}_2=\{a,r\}\), \({\mathcal {N}}_3=\{a,ar\}\) and \(\tilde{\varvec{f}}=(f_{1,a},f_{2,a},f_{3,a},f_{2,r},f_{3,ar})\). The optimal price and its expected demand for sector j in market i are denoted by \({\tilde{f}}^*_{i,j}\) and \({\tilde{d}}^*_{i,j}=M_i{\tilde{p}}^*_{i,j}\), respectively.
We follow the same procedure as in Sect. 3.1 and prove in “Appendix” that the profit as a function of the market share is concave.
Lemma 3.2
The total profit \(v_{ar}(\varvec{p}_{ar})\) is jointly concave in \(\varvec{p}_{ar}\).
Closed forms of the optimal prices and market shares are also obtained (see “Appendix” for details).
Proposition 3.4
-
(i)
The market share of sector \(j\in {\mathcal {N}}_i\) in markets \(i=1,2,3\) is given by
$$\begin{aligned} {\tilde{p}}^*_{i,j}=\frac{A_{i,j}}{\sum _{j\in {\mathcal {N}}_i}A_{i,j}}\frac{W[\sum _{j\in {\mathcal {N}}_i}A_{i,j}]}{1+W[\sum _{j\in {\mathcal {N}}_i}A_{i,j}]}, \end{aligned}$$(18)where \(A_{i,j}\) is given in Eq. (10).
-
(ii)
The optimal price of sector \(j\in {\mathcal {N}}_i\) in market \(i=1,2,3\) is given by
$$\begin{aligned} {\tilde{f}}^*_{i,j}=\frac{\mu }{\beta _i}\left( 1+W\left[ \sum _{j\in {\mathcal {N}}_i}A_{i,j}\right] \right) +c_{i,j}. \end{aligned}$$(19) -
(iii)
The maximum total profit is given by
$$\begin{aligned} V_{ar}=\sum ^3_{i=1}\left\{ M_i\frac{\mu }{\beta _i}W\left[ \sum _{j\in {\mathcal {N}}_i}A_{i,j}\right] -\sum _{j\in {\mathcal {N}}_i}I_{i,j}\right\} . \end{aligned}$$(20)
We do not assume that the fare \({\tilde{f}}^*_{3,a}\) (\({\tilde{f}}^*_{3,ar}\)) fulfills the non-arbitrage condition; that is, \({\tilde{f}}^*_{3,a}\) (\({\tilde{f}}^*_{3,ar}\)) is less than or equal to \({\tilde{f}}^*_{1,a}+{\tilde{f}}^*_{2,a}\) (\({\tilde{f}}^*_{1,a}+{\tilde{f}}^*_{2,r}\)). In practice, the non-arbitrage condition does not hold in a specific market; that is, an itinerary with a connection at an intermediate city is less expensive than a ticket from the origin to the intermediate city. This phenomenon is called hidden-city ticketing. Wang and Ye [28] formulate a flight network revenue management model to analyze the cause of hidden-city ticketing and its impact on both airlines’ revenues and consumers’ welfare. They show that the hidden-city opportunity may arise when there is a large difference in the price elasticity of demand for related itineraries. In our model, there is a possibility of this opportunity occurring because the price sensitivity parameter \(\beta _i\), the non-purchase quality \(u_{i,0}\), and the service quality \(b_{i,j}\) differ from market to market. However, as we show in the next corollary, if the price sensitivity parameter is homogeneous in \(\beta _i=\beta\) for all \(i=1,2,3\) and the non-purchase quality is normalized to zero \(u_{i,0}=0\) for all i, then the non-arbitrage condition holds.
Corollary 3.1
Suppose that \(\mu =1\), \(\beta _i=\beta\) and \(u_{i,0}=0\) for \(i=1,2,3\). If the operating cost of the connecting itinerary is lower than the sum of the operating cost for the air sector in market 1 and the HSR or air sector in market 2, that is, \(c_{3,a}\le c_{1,a}+c_{2,a}\) (\(c_{3,ar}\le c_{1,a}+c_{2,r}\)) and the cost-adjusted service quality of the connecting flight is lower than the sum of the cost-adjusted service quality of the air sector in markets 1 and 2, that is, \({\hat{b}}_{3,a}\le {\hat{b}}_{1,a}+{\hat{b}}_{2,a}\), and \({\hat{b}}_{1,a}\le 2\), then we have \({\tilde{f}}^*_{3,a}\le {\tilde{f}}^*_{1,a}+{\tilde{f}}^*_{2,a}\) (\({\tilde{f}}^*_{3,ar}\le {\tilde{f}}^*_{1,a}+{\tilde{f}}^*_{2,r}\)).
This assumption for the operating costs implies that it is too expensive for passengers to purchase air tickets separately or to switch between modes of transport in terms of the ticketing service fee, connection time, timetable incompatibilities, baggage transportation, etc. Therefore, in the absence of HSR–airline cooperation, it is not worthwhile for any passenger on route AB to use the route AH by air and the route HB by HSR or air.
The consumer surplus in the cooperation case is given by \(S_{\text{I}}\equiv S(\tilde{\varvec{f}}^*)\), where \(S(\cdot )\) is given in Eq. (15) and \(\tilde{\varvec{f}}^*\) is the vector of the optimal prices for the cooperation case. The social welfare is defined as the sum of the consumer surplus and the total profit:
4 Analysis of the competition and cooperation cases
With the closed-form solutions we derived in Sects. 3.1 and 3.2, we compare the competition and cooperation cases. First, we investigate the relationship between the market share and optimal price between the sectors in a market where the two sectors operate in the same market: market 2 in the competition case and markets 2 and 3 in the cooperation case.
Proposition 4.1
In both the competition and cooperation cases, the cost-adjusted service quality is positively associated with the market share in market 2. This is also applicable to market 3 in the cooperation case but not the competition case, because the HSR service is not provided in market 3. Finally, in the cooperation case, if the variable cost \(c_{2,r}\le c_{2,a}\), then the optimal price of HSR is less than that of the air sector in market 2. The air–rail itinerary in market 3 is preferable to air only, if \(c_{3,ar}\le c_{3,a}\). Furthermore, the difference in the optimal price between air and rail in market 2 and air and air–rail in market 3 is equal to the difference in the variable cost between the two sectors.
This proposition implies that the relationship between the market shares of both sectors depends not only on the service quality but also on their variable costs, as the variable cost affects the optimal price. Given that the operating cost of air–rail is lower than that of the connecting flights, the practical implication is that enhancing the accessibility between the airport and HSR station (or \(b_{3,ar}\) increases) could increase the market share of the air–rail itinerary. Finally, since the air–rail price is lower than the air price in market 3 in the cooperation case, marginal users will change from air to the air–rail itinerary.
Next, we formalize the effect of improving the service quality of the combined air–rail transport \(b_{3,ar}\) (e.g., baggage integration, access time to destination, and accessibility between the airport and HSR stationFootnote 4) on the optimal price, market share, total profit, and consumer surplus in the following tables. Since the fixed and variable costs, \(I_{3,ar}\) and \(c_{3,ar}\), are affected by the service quality, the operator faces a trade-off between the operating cost and service quality. We assume that the cost-adjusted service quality of the air–rail service is increasing with service quality, that is, \(\partial {\hat{b}}_{3,ar}/\partial b_{3,ar}\ge 0\). In other words, the value of improving the service quality exceeds the additional variable cost.
We focus on market 3, as it is the most relevant. The three choices are listed in the columns of Table 2, and the impacts on their market share, optimal price, and total profit are summarized by the rows. Several observations can be made from the table. First, an increase in the service quality increases the air–rail market share and reduces that of its alternative (connecting flights). This conclusion is supported by empirical evidence. For example, a survey-based stated preference analysis by Roman and Martin [30] on passengers at the Madrid Barajas airport showed that one of the main factors for HSR–airline cooperation to be successful is the connection time. Thus, one way to promote “air–rail” options is to increase the number of HSR trains departing from the hub to make the hub more accessible to final destinations. This result also has an indirect impact on air pollution as an increase in the air–rail market leads to (1) the substitution of high-pollution air travel with low-pollution HSR and (2) reducing airport congestion, thereby reducing unnecessary fuel consumption while aircrafts wait at runways for takeoff or circling in the air while waiting for landing (HB). Second, Table 2 also indicates a decline in the probability of the “non-purchase” option (column 3) for market 3 (AB), implying that the total demand increases with improvement in the service quality. The increase in travel demand is mostly due to the improvements in the air–rail option. As rail infrastructure is already in place in most big cities, the IATA [31] suggests that increasing the frequency of trains, and therefore passengers, would incur little additional operating costs. Third, due to the additional demand (owing to a decline in the non-purchase decision), the prices of both sectors serving market 3 increase. However, consumer surplus also increases. The decline in consumer surplus for the air–rail itinerary due to increased prices could be more than offset by the increase from improved service quality, leading to a net increase in the consumer surplus. The impact on the total revenue is not clear. Total revenue increases when the incremental revenue is greater than the incurred fixed cost associated with service quality improvements. Therefore, social welfare increases with improvement in the service quality when the increase in the total profit is relatively large. These results are consistent with Xia and Zhang [32], who also use a three-node model to analyze the co-location of airports and HSR stations as a form of HSR–airline integration and its impact on air and rail operator’s profits, consumer surplus, and social welfare. Xia and Zhang [32] show numerically that both social welfare and the overall profit of the air and rail operators decrease with the air–rail connection time when the marginal cost of reducing the air–rail connection time is not sufficiently large. In other words, a reduction in the air–rail connection time may improve social welfare and increase the combined profit.
We next turn our attention to the comparison of the impacts on the optimal prices and the market share for two cases (competition versus cooperation) in Table 3, with each row reporting the impact on each of the three markets.
Proposition 4.2
The relationship between the competition and cooperation cases with respect to the optimal price and the market share is given in Table 3.
Since the route AH for market 1 in this instance has the same settings as in the competition case, market 1 is not affected by cooperation. As shown in the second column, the optimal prices in markets 2 and 3 increase compared to the competition case, mainly because the joint operation of the air and the HSR sectors gives the firms a greater market power. However, even if the airfare or the optimal prices increase, the effect of cooperation on the air sector share in market 2 is ambiguous and depends on the comparison of the cost-adjusted service quality between the air and HSR sectors. We show in “Appendix” that the conditions under which the air sector market share decreases as a result of the cooperation, \({\tilde{p}}^*_{2,a}< p_{2,a}^*\), include 1) the cost-adjusted service quality of the air option being lower than that of HSR (\({\hat{b}}_{2,a}\le {\hat{b}}_{2,r}\)), and 2) the substitutability between the air and the HSR sectors being sufficiently high (i.e., \({\hat{b}}_{2,a}\approx {\hat{b}}_{2,r}\)). Thus, when a domestic route is subject to a high level of competition, that is, (2) holds, cooperation leads to a decrease in passengers to the final destination B due to a decrease in the air sector market share in market 2. This conclusion is supported by some empirical evidences for the reduction in the air sector market share following the opening of the air–rail service at Frankfurt Airport. During 1998–2006, the numbers of passengers on the routes between Frankfurt and four other major cities, Cologne, Dusseldorf, Stuttgart, and Hanover, are reported to have declined by 74.2\(\%\), 24.8\(\%\), 29.4\(\%\), and 23\(\%\), respectively [33]. In addition, as we can see in Table 3, the air sector market share in market 3 also decreases as a result of cooperation, regardless of the competition level as measured by the substitutability between the air and HSR sectors. This is contrary to the case in market 2 where market shares are affected by the substitutability between the two sectors. Therefore, in the planning stage when considering cooperation between the air and HSR sectors, authorities need to carefully evaluate the effect of cooperation on the domestic and connecting air demand to avoid negative consequences for the regional airports. In terms of the total volume, Table 2 indicates that cooperation leads to a decline in both sectors in market 2, mainly due to the higher prices experienced by the passengers in both sectors. For market 3, while the air sector market share decreases with cooperation, the total volume of both itineraries actually increases, suggesting that the air–rail service can increase the size of the market. Thus, cooperation effectively increases the use of HSR in the domestic market, which is consistent with Jiang and Zhang [13]. Next, we further examine the change in the market share in market 2 for the competition and cooperation cases.
Proposition 4.3
If the HSR market share is greater (less) than the air sector market share in the competition case \(p^*_{2,r}\ge (\le ) p^*_{2,a}\), then the HSR share is also greater (less) than the air sector share in the cooperation case \({\tilde{p}}^*_{2,r}\ge (\le ) {\tilde{p}}^*_{2,a}\). In addition, the difference in market share between the HSR and air sectors increases compared to the competition case.
In the short–medium-distance journey market, the market share of HSR is typically larger than that of the air sector. An example is the market between Tokyo and Osaka, the two largest cities in Japan. The HSR sector is larger than the air sector by a margin of 53\(\%\) (MLIT [34]). This result suggests that if the sectors cooperate in such a market, then the HSR share is further increased at the expense of the air sector. Conversely, in a long-distance journey market, the air sector market share is typically larger than the HSR share. Proposition 4.3 implies that even if cooperation were to take place in the long-distance market, the HSR share would not likely increase to a large extent. Therefore, cooperation should be implemented in the short–medium-range market to reduce airport congestion. This conclusion is supported by empirical evidence. In particular, analysis by Givoni and Banister [5] for Heathrow Airport found that HSR–airline cooperation for destinations of less than 600 km is beneficial to airlines, passengers, and the environment.
Next, we report the results of the analysis of the robustness of cooperation with respect to changes in market conditions. More specifically, we study the relation between the total market volume and the attractiveness of outside alternatives \(u_{i,0}\), \(i=1,2,3\) under changes in market conditions. For both the competition and cooperation cases, we conclude that the total volume for each market is reduced with increasing attractiveness of the no-purchase alternative. However, the decrease in the total volume for the cooperation case is lower than for the competition case.
Proposition 4.4
When the cost-adjusted service quality of HSR and/or the air sector is greater than that of the non-purchase quality, if both sectors cooperate, then the decrease in the total volume associated with an increase in the non-purchase attractiveness is reduced in market 3. However, this is not the case for market 2.
An increase in the attractiveness of the outside option could also be due to an increase in the competitors’ service quality. One such instance is the entry of low-cost carriers (LCCs) into the market or a reduction in the toll for expressways connecting a hub. In fact, the HSR share for journeys between Kansai (Kyoto, Osaka, and Hyogo) and Fukuoka decreased 2.2\(\%\) from 2011 to 2012 after LCCs began operating (MLIT [35]). In such situations, the HSR and air sectors can prevent a large reduction in their total market share by cooperating in the connecting market (market 3) because cooperation increases the total volume in market 3 (Proposition 4.2) by enhancing the service quality. However, since the total volume in market 2 decreases the result of cooperation, cooperation cannot avoid a reduction in profits in this situation.
The final set of results focuses on the impact of cooperation on the service providers’ profit and the consumer surplus. Since the number of potential customers \(M_i\) and service quality \({\hat{b}}_{i,j}\) differ from market to market, directly comparing the profits and surpluses for all markets for the competition and the cooperation cases might be misleading. We therefore compare these values separately in each of the markets. Let \(V_{i}\) and \({\tilde{V}}_i\) be the profit in market i for the competition and cooperation cases, respectively. Note that, by default, the profit in market 2 for the competition case is the sum of the profits of the air and HSR sectors: \(V_2=V_{2,a}+V_{2,r}\). Let \(S_{i}\) and \(W_i\) denote the consumer surplus and social welfare, respectively, in market i for the competition case. We use the variables \({\tilde{S}}_i\) and \({\tilde{W}}_i\) to represent the consumer surplus and social welfare in the cooperation case.
Proposition 4.5
The relationship between the competition and cooperation cases with respect to the total profit and consumer surplus for each market is given in Table 4.
Table 4 reports the distribution of social surplus for the competition and cooperation cases in the three markets, including the producers’ surplus for the air and rail sectors (1), consumers surplus (2), and the total surplus (3), where the number in parentheses corresponds to the column number. We discuss each market in a sequence by comparing it to Table 3. Because the optimal prices and market share in market 1 remained unchanged as reported in Table 3, the distribution of the social, producers’ (the air and rail sectors) and consumers’ surplus is equivalent between the two cases. For market 2, together with the lower travel demand (reported in Table 3) and higher optimal prices, consumers become worse off under the cooperation case. Moreover, the effect on both the market share (Table 3), and on the profits earned by the air and rail sectors is unclear. The total profit in market 2 increases with cooperation only if the increase in the total profit resulting from the loss of competition between the HSR and air sectors exceeds the reduction in the total profit due to the decrease in total volume under cooperation (see proof of Proposition 4.5(v) in “Appendix”). In the next proposition, we further consider the effect of cooperation on the total profit in market 2.
Finally, in market 3, even with higher optimal prices, the impact on the consumers is outweighed by the benefit of the increase in travel demand, leading to a higher consumer surplus. A combination of higher optimal prices and travel demand results in an increase in the producers’ total revenue. However, the effect on producers’ surplus (total profit) is unclear. If the total revenue exceeds the fixed cost of air–rail transport, then the producer’s surplus increases under cooperation. Although the fixed cost is not considered, this result agrees with Proposition 1 in Socorro and Viecens [15]. In the above study, when both sectors are assumed to cooperate, the air sector stops operating in market 2 (route HB). That is, the HSR or rail sector operates as a monopolist in the market, and the air and rail jointly earn a higher level of profit by raising the price of their services. However, in our setting, the air sector continues to provide a service in market 2 even under the cooperation setting. We argue that our results and setting are more realistic, as there is a risk of losing passengers to other airlines that operate short-haul flights, as some passengers could still prefer to connect to a hub via short-haul flights. This also reflects the operation strategies that many airlines use for short-haul flights within routes where they have made intermodal agreements with the HSR sector. For example, in the case of Frankfurt Airport, the train service does not fully replace the air services as exemplified by the fact that Lufthansa still operates air services on the route from Frankfurt to Dusseldorf. On the other hand, there is no flight offered by the air sector providing a service between Cologne/Bonn Airport and Frankfurt Airport [36]. Another example is the TGV Air service. Despite the services offered by the rail sector, a large percentage of daily passenger services and of the total services run between Paris-CDG and Nantes Airport are still provided by the air sector (European Regions Airline Association ERAA2011). The above examples support our findings.
In addition to the continuation of the service operated by the air sector, we consider the availability of outside alternatives in each market. Outside alternatives lead to the ambiguity in the results for market 2. In the next proposition, we show the effect of outside alternatives in market 2 on the social surplus in market 2 and for the whole market.
Proposition 4.6
The effect of the service quality of outside alternatives in market 2 on the social welfare is summarized in Table 5.
If the service quality of the outside options is low, then customers have little incentive to choose the outside options. This implies that there will be limited changes in the total volume, even if the prices of the services increase under cooperation. Thus, the reduction in the total profit due to a decrease in the total market volume under cooperation is low. In such a case, as in Table 4, the producers’ surplus increases with cooperation because the increase in the total profit resulting from the removal of competition between the HSR and air sectors exceeds the reduction in the total profits due to the decreased total market volume. However, the social welfare would also decrease due to an increase in the consumer surplus. For the special case in which the non-purchase quality has a value \(u_{2,0}={\hat{b}}_{2,j}-\mu \le {\hat{b}}_{2,j}\), we can show that the social welfare in market 2 strictly decreases with cooperation (see the proof of Proposition 4.6(iii) in “Appendix”). When the service quality of the outside alternative is higher than the service quality of both sectors, cooperation does not impact the consumer surplus, producers’ surplus, and social surplus. In a sense, the availability of outside options upsets the market equilibrium, and the air sector abandons its service entirely.
Furthermore, as we reported in Table 3, the total profit in the connecting market (market 3) is increased with cooperation in the case where the fixed cost of the air–rail mode is relatively low. In this case, the total profit for the whole market under cooperation is never lower than under competition, and so the airline and the HSR have incentives to cooperate.
Proposition 4.7
For lower fixed costs for the air–rail mode, if the non-purchase quality in market 2 is high, then cooperation increases the social welfare of the whole market. If not, then cooperation increases the welfare of the whole market only in the case where a gain in the welfare in market 3 exceeds a loss in market 2.
From this proposition, the fixed cost of the air–rail mode and non-purchase quality in market 2 play an important role in determining the effectiveness of cooperation on social welfare for the whole market. When the non-purchase quality in market 2 is high, the effect of cooperation on social welfare for the whole market depends on the welfare in market 3, because cooperation does not impact the welfare in market 2 by Proposition 4.6. Thus, in this case, the fixed cost of the air–rail mode affects the social welfare for the whole market. When the non-purchase quality in market 2 is relatively low, we need to consider the balance between the decrease in social welfare in market 2 and the increase in social welfare in market 3. Since the amount of social welfare in each market depends largely on the number of potential customers, the social welfare will be increased by cooperation if the amount of social welfare in the connecting market is relatively large. We will demonstrate this with numerical examples.
5 Numerical examples
In this section, a numerical example is used to illustrate the impact of different parameters on the performance of the optimal price, market share, and profit in each market. Table 6 displays the parameters used in the numeric example. Figure 2 reports the market shares in competition and cooperation cases.
We summarize the main findings as follows. First, we compare the optimal prices and market shares between the two cases in each market. The overall observation concerning the changes in the air sector in each market is consistent with Proposition 4.2. In particular, since the parameters in Table 6 imply that the cost-adjusted service qualities of the air sector are greater than those of the rail sector in the market 2, \({\hat{b}}_{2,a}=9.5<{\hat{b}}_{2,r}=10.75\), the air share is reduced by 23% (0.43 to 0.2) as a result of introducing cooperation between the two sectors. In the market 3, the total volume is increased (marked in Fig. 2 with “air”) by the cooperation because the air–rail takes a large share of the market partially due to increase in service quality resulting from air–HSR integration. Figure 3 shows the optimal prices for the both cases, where from left to right corresponds to markets 1, 2, and 3, respectively. Within each market, two bars are depicted for the competition (left) and cooperation (right), respectively. The main observation is that the prices of both the air and HSR sectors increase in the market 2 (HB), while the air–rail price is lower than its counterpart of competition case marked by the “Air–Air” in the market 3 (AB). Thus, these results are consistent with Propositions 4.1 and 4.2.
As existence of the outside options might impact the passengers’ choice of transportation modes as well as overall demand, we next explore the sensitivity of its service quality on market equilibrium. Figures 4 and 5 plot the air market shares in competition and cooperation cases against the different values of the non-purchase quality \(u_{2,0}\) with dash and sold lines representing cooperation and competition, respectively. For the case \({\hat{b}}_{2,a}<{\hat{b}}_{2,r}\), in which the service quality of the HSR sector is greater than that of the air sector, the air share of the market is always reduced by the cooperation. However, when \({\hat{b}}_{2,a}>{\hat{b}}_{2,r}\) or the reversed relationship of the service quality holds, the changes in the air sector in the market depend on the value of the non-purchase quality \(u_{2,0}\). For small value \(u_{2,0}\), Fig. 5 indicates that the air share would rise when the cooperation is introduced, mainly because the outside (or non-purchase) options remain insufficiently desirable so that the passengers choose the air as the travel model even if its price is raised by the cooperation.
As alluded to in Table 4 that the impacts of air–HSR cooperation on the producers’ surplus and social surplus in market 2 are ambiguous, we then investigate how the desirability of non-purchase quality impacts the market equilibrium. Figures 6, 7 and 8 plot the producers’ surplus, consumer surplus, and social welfare of cooperation case and competition case in market 2 against various levels of the “non-purchase quality.” In addition, Fig. 9 plots the difference subtracting the each value of competition from that of cooperation against various levels of non-purchase quality. When the non-purchase quality \(u_{2,0}\) is lower than that of the service quality offered by both air and rail sectors (\(b_{2,a}=10\) and \(b_{2,r}=11\)), the total profit decreases by the cooperation, and higher optimal prices and lower quantity are demanded. This leads to a decline of the consumer surplus as well as the social surplus. In other words, the increases in the producers’ surplus are more than offset by the decreases in consumers’ surplus when quality of the non-purchase is low. In a sense, passengers are “forced” by the low quality of the non-purchase option or the high reward/utility of the trips to engage in the market, even the prices are high. However, when the parameter \(u_{2,0}\) is large, the cooperation has little impact on the market outcomes in market 2, owing to the fact that the passengers can shield the impact of higher prices by choosing the outside alternative. These results are consistent with Proposition 4.6.
Finally, Figs. 10 and 11 show the difference of social welfare in whole market \(W_{\text{I}}-W_{\text{C}}\) plotted against the non-purchase quality \(u_{2,0}\) and the fixed cost of air–rail mode \(I_{3,ar}\) for three distinct values of the number of potential customers \(M_3\), respectively. In both Figs. 10 and 11, one can see the difference increases as \(M_3\) increases. In Fig. 10, the difference increases with \(u_{2,0}\), and thus the cooperation increases social welfare for large value of \(u_{2,0}\). For low value of \(u_{2,0}\), the cooperation increases social welfare only if \(M_3\) is relatively large. In Fig. 11, the difference decreases with \(I_{3,ar}\), and the cooperation is effective to social welfare for low value of the fixed cost and high value of the number of potential customers. The effect of cooperation on social welfare is consistent with the result in Proposition 4.7.
6 Conclusions
There is a growing interest in the transportation research community as well as from governments in the benefits of HSR–airline cooperation or integration. This is partially due to an expansion of the HSR sector in many countries. This paper studies the effect of HSR–airline cooperation using multinomial logit models to represent the market share or consumer demand for different transportation modes. Our methodological contribution is twofold. First, using a multinomial logit approach allows the relationship between passengers’ demand and the factors that affect passengers’ or travelers’ choices to be nonlinear. This is different from previous studies, which tend to model travelers’ choices using a linear demand function. Second, our approach explicitly considers the impact of the availability of an outside or non-purchase option on the market equilibrium.
The main findings of our paper are as follows. First, improving air–rail service quality (e.g., increasing the accessibility of transfers from airports to rail networks between a hub and the final destination) would lead to an increase in the market share of the combined air–rail sector in conjunction with a lower travel demand (or market share) for the connecting flight, as well as the non-purchase options. Consumers switching from the non-purchase option to either the connecting flight or the air–rail option results in an increase in the optimal prices at equilibrium. The decrease in consumer surplus for the air–rail itinerary due to increased prices could be more than offset by the increase in the service quality, leading to an overall increase in the consumer surplus. Second, when the two sectors cooperate, the decrease in total demand due to higher optimal prices in market 3 is more than compensated for by the transfer of the traveler’s demand from the non-purchase options to the air–rail option, leading to an increase in the overall travel demand. However, since cooperation does not impact the service quality in market 2, the higher prices lead to a lower overall travel demand. Finally, we show that the fixed cost of the air–rail itinerary and the non-purchase quality in the domestic market play an important role in determining the effectiveness of cooperation on social welfare for the whole market. When the non-purchase quality in market 2 is high, cooperation does not have much effect on the social welfare in the domestic market, because customers have little incentive to switch to an outside option and the change in the total volume is limited. Thus, the social welfare of the whole market increases with cooperation if the gain in social welfare in the connecting market exceeds the fixed cost of the air–rail mode. When the non-purchase quality in market 2 is relatively low, we show that cooperation increases the welfare in market 3 under the lower value of the air–rail fixed cost and decreases the welfare in market 2. Thus, cooperation increases social welfare for the whole market when the number of potential customers in market 3 is relatively large.
The current paper is subject to a number of limitations. First, we do not consider airport capacity constraints. As reported in previous papers, the airport capacity could have a large effect on the change in welfare. Some of the results in this paper might be sensitive to this assumption of unlimited airport capacity. Second, for the combined air–rail service to be successful, it is important to optimize the profits and other benefits of not only the passengers, airlines, and rail operators, but also the operators of the airports and railway infrastructure companies. For airports’ operators, one possible benefit is that if the “freed” slots or legs, due to the HSR–airline integration, are used for serving long-haul flights, the airport can obtain additional landing fees and possibly increase the total number of passengers. Thus, cooperation could increase the profits of the airport operators as well. On the other hand, the parking revenue might decrease if private car trips to the airport are substituted by rail transportation. However, parking revenue only represents a small fraction of the total revenue of the airport operators. In addition, the reallocation of the freed slots to long-haul flights will lead to an increase in the global environmental impacts (air pollution and CO\(_2\) emissions) for the aviation sector, if these trips represent additional ones. This might be worth further attention when considering associated externalities in HSR–airline cooperation. Finally, since the air and rail companies are subject to different business cultures, operating practices, and regulations, consideration of the division of revenue between these two entities is also an important consideration. Our implicit assumption is that there will be “side payments” agreed between the two parties to facilitate their cooperation. However, more strategic consideration based on Nash-bargaining game theory would also be appropriate for analyzing this situation, but is beyond the scope of the current paper as we are mainly interested in determining the overall or aggregated impact by modeling them jointly as an optimization problem. We leave the above considerations for our future research.
Notes
When there is a direct flight service in the AB market, the network structure is called a “fully connected” (point-to-point) network. Recently, Jiang and Zhang [19] showed theoretically that HSR entry would affect airlines’ network structure such that they move from a point-to-point to a hub–spoke network. Their results provide a rationale for our model set-up using a hub–spoke structure.
In the absence of HSR–airline cooperation, although there are some consumers who are willing to travel from A to B using the route HB by HSR and the route AH by air (we refer to this as itinerary “ar”), we assume that the air sector acts as a monopoly in the connecting market. This assumption is valid because of the following: (1) When a customer is searching for airline tickets for route AB using a travel search engine, the itinerary “ar” rarely appears in the search results, especially when the HSR station is not located in the airport. Thus, most customers choose the itinerary with connecting flights and earn air miles or points. (2) The itinerary “ar” seems to be preferred by customers who travel from A to B through the connecting city H and want to stay for a couple of days at city H. However, travel search engines (e.g., Skyscanner or Kayak) offer stopovers or multi-city flight options to customers. Thus, customers can reduce their costs by using this option, and the demand for the itinerary “ar” would be very low. For these reasons, we regard the demand for HSR along route AH and the demand for air along route HB separately.
Chiambaretto et al. [29] measure the willingness to pay of intermodal passengers for some intermodal service attributes using a conjoint analysis.
References
Janic M (1993) A model of competition between high speed rail and air transport. Transp Plan Technol 17(1):1–23
Rothengatter W (2011) Competition between airlines and high-speed rail. In: Macario R, van de Voorde E (eds) Critical Issues in air transport economics and business. Routledge, Oxford
Givoni M (2005) Aircraft and high speed train substitution: the case for airline and railway integration, Unpublished Ph.D. thesis. University College, London
Jeng CR, Su CH (2013) The predicament of domestic airline service after the introduction of Taiwan high-speed rail. Transp J 52(1):134–143
Givoni M, Banister D (2006) Airline and railway integration. Transp Policy 13(5):386–397
Givoni M (2007) Environmental benefits from mode substitution: comparison of the environmental impact from aircraft and high-speed train operations. Int J Sustain Transp 1(4):209–230
Park Y, Ha HK (2006) Analysis of the impact of high-speed railroad service on air transport demand. Transp Res Part E 42(2):95–104
Adler N, Pels E, Nash C (2010) High-speed rail and air transport competition: game engineering as tool for cost-benefit analysis. Transp Res Part B 44:812–833
Yang H, Zhang A (2012) Effects of high-speed rail and air transport competition on prices, profits and welfare. Transp Res Part B 46:1322–1333
Behrens C, Pels E (2012) Intermodal competition in the London-Paris passenger market: high-speed rail and air transport. J Urban Econ 71(3):278–288
Gonzalez-Savignat M (2004) Competition in air transport: the case of the high speed train. J Transp Econ Policy 38(1):77–108
Adler N, Fu X, Oum TH, Yu C (2014) Air transport liberalization and airport slot allocation: the case of the Northeast Asian transport market. Transp Res Part A 62:3–19
Jiang C, Zhang A (2014) Effects of high-speed rail and airline cooperation under hub airport capacity constraint. Transp Res Part B 60:33–49
Cokasova A (2006) Analysis of passenger viewpoints and of the practical shift in air rail intermodal transport. Ph.D. dissertation, University of Zilina
Socorro MP, Viecens MF (2013) The effects of airline and high speed train integration. Transp Res Part A 49:160–177
Xia W, Zhang A (2016) High-speed rail and air transport competition and cooperation: a vertical differentiation approach. Transp Res Part B 94:456–481
Ben-Akiva M, Lerman S (1985) Discrete-choice analysis: theory and application to travel demand. MIT Press, Cambridge, p 308
Talluri KT, van Ryzin GJ (2004) The theory and practice of revenue management. Kluwer, Dordrecht
Jiang C, Zhang A (2016) Airline network choice and market coverage under high-speed rail competition. Transp Res Part A 92:248–260
Hanson W, Martin K (1996) Optimizing multinomial logit profit functions. Manag Sci 42(1):992–1003
Dong L, Kouvelis P, Tian Z (2009) Dynamic pricing and inventory control of substitute products. Manuf Ser Oper Manag 11(2):317–339
Corless RM, Gonnet GH, Hare DEG, Jeffrey DJ, Knuth DE (1996) On the Lambert \(W\) function. Adv Comput Math 5(4):329–359
Cascetta E, Papola A, Pagliara F, Marzano V (2011) Analysis of mobility impacts of the high speed Rome–Naples rail link using within day dynamic mode service choice models. J Transp Geogr 19(4):635–643
Clever R, Hansen M (2008) Interaction of air and high-speed rail in Japan. Transp Res Rec J Transp Res Board 2043:1–12
Roman C, Espino R, Martin JC (2007) Competition of high-speed train with air transport: the case of Madrid-Barcelona. J Air Transp Manag 13:277–284
Wan Y, Ha HK, Yoshida Y, Zhang A (2016) Airlines’ reaction to high-speed rail entries: empirical study of the Northeast Asian market. Transp Res Part A 94:532–557
Small KA, Rosen HS (1981) Applied welfare economics with discrete choice models. Econ 49(1):105–130
Wang Z, Ye Y (2015) Hidden-city ticketing: the cause and impact. Transp Sci 50(1):288–305
Chiambaretto P, Baudelaire C, Lavril T (2013) Measuring the willingness-to-pay of air–rail intermodal passengers. J Air Transp Manag 26:50–54
Roman C, Martin JC (2014) Integration of HSR and air transport: understanding passengers’ preferences. Transp Res Part E 71:129–141
IATA (2003) Air/rail intermodality study. Prepared by IATA Air Transport Consultancy Services for the European Commission, Airports Council International, Air Transport Action Group, the Community of European Railway and Infrastructure Companies (CER) and the International Union of Railways. http://ec.europa.eu/transport/rail/studies/doc/2003_air_rail.pdf. Accessed 30 Aug 2017
Xia W, Zhang A (2017) Air and high-speed rail transport integration on profits and welfare: effects of air–rail connecting time. J Air Transp Manag 65:181–190
Vespermann J, Wald A (2011) Intermodal integration in air transportation: status quo, motives and future developments. J Transp Geogr 19:1187–1197
MLIT (2010) 2010 Inter-regional travel survey in Japan. Ministry of Land, Infrastructure, Transport and Tourism movement of Japan. http://www.mlit.go.jp/common/001005632.pdf. Accessed 30 Aug 2017 (in Japanese)
MLIT (2014) The impacts of low-cost carriers on Japanese aviation market (Report No.118), Ministry of land, infrastructure, transport and tourism movement of Japan. http://www.mlit.go.jp/pri/houkoku/gaiyou/pdf/kkk118.pdf. Accessed 30 Aug 2017 (in Japanese)
Grimme W (2007) Experiences with advanced air–rail passenger intermodality—the case of Germany. Paper presented at the air transport research society (ATRS) world conference
Sato K, Chen Y (2014) High-speed rail and airline cooperation under the multinomial logit model: model and properties. In: Proceedings of the 7th international forum on shipping, ports and airports, pp 84–92
Acknowledgements
Sato acknowledges funding support from a JSPS Grant-in-Aid for Young Scientists (B) (26870643). Chen acknowledges funding support from a JSPS fellowship in 2013–2014 during his sabbatical at the National Graduate Institute for Policy Studies, Japan. An earlier version of this paper was presented at the International Forum on Shipping, Ports and Airports (IFSPA) 2014 [37].
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
1.1 Proof of Sect. 3
Proof of Lemma 3.1
(i) It is known that the form of the function \(v_a\) is not quasi-concave in \(\varvec{f}_{a}\) (see [20]), we reformulate the problem as finding an inverse function. The ratio of the market shares \(p_{i,j}/p_{i,0}=\exp ((b_{i,j}-\beta _if_{i,j}-u_{i,0})/\mu )\) yields
Then, the airline’s problem (5) can be rewritten as
where
\(\varvec{p}=\{p_{i,j}\}\) for all \(i=1,2,3, j\in \bigcup _i({\mathcal {A}}_i\cup {\mathcal {R}}_i)\) and \(\varvec{p}_a=\{p_{i,j}\}\) for all \(i=1,2,3, j\in \bigcup _i{\mathcal {A}}_i\).
Similar to the airline’s case, the HSR’s profit in terms of the market share \(\varvec{p}_{2,r}\) is given by
where \(\varvec{p}_2=\{p_{2,j}\}\) for all \(j\in {\mathcal {A}}_2\cup {\mathcal {R}}_2\) and
Differentiating \(v_a\) with respect to \(p_{i,j}\) for \(i=1,2,3, j\in \bigcup _i{\mathcal {A}}_i\), we have
Moreover, the second derivatives of \(v_a\) are given by
Let \(\#_c\) be the number of fare classes provided by airline for all market, that is, \(\#_c=\sum ^3_{i=1}|{\mathcal {A}}_i|\). For any vector \(\varvec{y}\in {\mathbb {R}}^{\#_c}\), we have \(\varvec{y}{\mathcal {H}}_{-v_a}\varvec{y}^{\text T}\ge 0\), where \({\mathcal {H}}_{-v_a}\) is Hessian of \(-v_a\). Hence, \(v_a\) is concave in \(\varvec{p}_a\).
(ii) The first and second derivatives of Eq. (26) with respect to \(\varvec{p}_{2,r}\) are given by
Since the structure of the above equation is similar to the air case (27), we can show that \(v_r(\varvec{p}_{2})\) is concave in \(\varvec{p}_{2,r}\). \(\square\)
Proof of Proposition 3.1
From Proposition 3.1, there exists an optimal share for each of the air and HSR sector. To characterize the equilibrium prices and market shares at the equilibrium in market 2, we introduce the Lambert W function [22]. For any nonnegative z, the function W[z] is the solution w satisfying
It is known that the W function is positive, increasing and concave in \(z\in [0,\infty ]\).
(i) We derive the share of airline for fare class j in the market i, \(p^*_{i,j}\). Using Eq. (27), the first-order condition \(\partial v_a/\partial p_{i,j}=0\) gives
Exponentiating the above equation and taking summation both sides, we obtain
where
By the definition of the W function, we have \(W[\sum _{j\in {\mathcal {A}}_i}A_{i,j}]=(1/p^*_{i,0})\sum _{j\in {\mathcal {A}}_i}p^*_{i,j}\). Thus, we obtain
Similarly, from Eq. (32), we obtain
Since \(\sum _{j\in {\mathcal {A}}_i}p^*_{i,j}+\sum _{j\in {\mathcal {R}}_i}p^*_{i,j}+p^*_{i,0}=1\), by substituting the above equations, we obtain \(p^*_{i,0}=1/(1+W[\sum _{j\in {\mathcal {A}}_i}A_{i,j}]+W[\sum _{j\in {\mathcal {R}}_i}A_{i,j}])\). It gives
By substituting the above equation into Eq. (27), we have
Since \({\mathrm {e}}^{-W[\sum _{j\in {\mathcal {A}}_i}A_{i,j}]}=W[\sum _{j\in {\mathcal {A}}_i}A_{i,j}]/\sum _{j\in {\mathcal {A}}_i}A_{i,j}\), we obtain
(ii) From Eq. (34), we have
By Eq. (22), the left-hand side of the above equation is equal to the optimal price \(f^*_{i,j}\). Substituting \(p^*_{i,0}=1/(1+W[\sum _{j\in {\mathcal {A}}_i}A_{i,j}]+W[\sum _{j\in {\mathcal {R}}_i}A_{i,j}])\) and Eq. (37) into the right-hand side of Eq. (42), we obtain \(f^*_{i,j}=\frac{\mu }{\beta _i}(1+W[\sum _{j\in {\mathcal {A}}_i}A_{i,j}])+c_{i,j}\) for \(j\in {\mathcal {A}}_i\). Similarly, by using Eq. (38), we obtain \(f^*_{2,j}\) for \(j\in {\mathcal {R}}_2\). \(\square\)
Proof of Proposition 3.2
For any \(x\ge 0\), it is well-known that \(W(x)\ge 0\) and
Thus, we have
Differentiate \(p^*_{i,a}\), \(i=1,3\), with respect to \({\hat{b}}_{i,a}\), we have
Differentiate \(p^*_{2,j}\), \(j=a,r\), with respect to \({\hat{b}}_{2,j}\), we have
Hence, \(p^*_{i,j}\) are increasing in \(b_{i,j}\). Since \(W[A_{i,j}]\) is increasing in \({\hat{b}}_{i,j}\), \(f^*_{i,j}\) is also increasing in \({\hat{b}}_{i,j}\).
Differentiate \(p^*_{2,j}\) with respect to \({\hat{b}}_{2,k}\), \(k\ne j\), we obtain
Hence, \(p^*_{2,j}\) is decreasing in \({\hat{b}}_{2,k}\), \(k\ne j\). \(\square\)
Proof of Proposition 3.3
By substituting \(p^*_{i,j}\) and \(f^*_{i,j}\), \(i=1,2,3\), \(j\in {\mathcal {N}}_i\), into Eq. (24), we obtain
The maximum total profit of HSR is given by
\(\square\)
Proof of Lemma 3.2
Using Eq. (22), the problem can be rewritten as
where
and \(\varvec{p}_{ar}=(p_{1,a},\,p_{2,a},\,p_{3,a},\,p_{2,r},\,p_{3,ar})\).
Differentiating \(v_{ar}\) with respect to \(p_{i,j}\) for i and \(j\in {\mathcal {N}}_i\), we obtain
Moreover, we get
For any vector \(\varvec{y}\in {\mathbb {R}}^5\), we have \(\varvec{y}{\mathcal {H}}_{-v_{ar}}\varvec{y}^{\text T}\ge 0\), where \({\mathcal {H}}_{-v_{ar}}\) is Hessian of \(-v_{ar}\). Hence, \(v_{ar}\) is jointly concave in \(\varvec{p}_{ar}\). \(\square\)
Proof of Proposition 3.4
(i) For service j in the market i, the first-order condition is given in Eq. (46): \(\partial v_{ar}/\partial p_{i,j}=0\). Subtracting the equation \(\partial v_{ar}/\partial p_{i,j}=0\) from the equation \(\partial v_{ar}/\partial p_{i,k}=0\), we obtain
where \(B_i(j,k)=\exp \{(b_{i,k}-b_{i,j}-\beta _i(c_{i,k}-c_{i,j}))/\mu \}\). The first-order condition \(\partial v_{ar}/\partial p_{i,j}=0\) can be rewritten as
Since \(\sum _{j\in {\mathcal {N}}_i}{\tilde{p}}^*_{i,j}+{\tilde{p}}^*_{i,0}=1\), we have
Substituting the above equation into Eq. (51) and multiplying both sides by \(1+\sum _{k\in {\mathcal {N}}_i, k\ne j}B_i(j,k)\), we get
Since \(\sum _{j\in {\mathcal {N}}_i}{\tilde{p}}^*_{i,j}+{\tilde{p}}^*_{i,0}=1\), we have
Substituting Eq. (53) into the above equation, we obtain
Therefore, by \(B_i(j,k)=A_{i,k}/A_{i,j}\) and Eq. (53), we have
(ii) By the first-order condition \(\partial v_{ar}/\partial p_{2,a}=0\), we have
(iii) Substituting \({\tilde{p}}^*_{i,j}\) and \({\tilde{f}}^*_{i,j}\) for \(i=1,2,3\) and \(j\in {\mathcal {N}}_i\) into Eq. (17), we have
where the last equation follows from Eq. (55).
The next lemma is useful to show some properties of optimal price and market share. \(\square\)
Lemma 7.1
For any \(x, y\ge 0\), \(W[x+y]\le W[x]+W[y]\).
Proof
By the definition of Lambert W function, we have
Thus, we have
Substituting \(x=W[x]\mathrm {e}^{W[x]}\) and \(y=W[y]\mathrm {e}^{W[y]}\) into the above equation, we get
For \(0\le x\le y\), since W[x] is increaseing in x, we obtain
So, we obtain
It implies that \((W[x]+W[y])/W[x+y]\ge 1\). Hence, we have \(W[x+y]\le W[x]+W[y]\). \(\square\)
Proof of Corollary 3.1
Suppose that \(\mu =1\), \(\beta _i=\beta\) and \(u_{i,0}=0\) for \(i=1,2,3\). Then, from Proposition 3.4(ii), we have \({\tilde{f}}_{3,ar}=(1/\beta )(1+{\tilde{W}}_{3})+c_{3,ar}\), \({\tilde{f}}_{1,a}=(1/\beta )(1+W[A_{1,a}])+c_{1,a}\) and \({\tilde{f}}_{2,r}=(1/\beta )(1+{\tilde{W}}_{2})+c_{2,r}\), where \({\tilde{W}}_2=W[A_{2,a}+A_{2,r}]\) and \({\tilde{W}}_3=W[A_{3,a}+A_{3,ar}]\). It implies that
Since we assume that \(c_{3,ar}\le c_{1,a}+c_{2,r}\), it is sufficient to show that \({\tilde{W}}_3\le 1+W[A_{1,a}]+{\tilde{W}}_2\). Here we have
Thus, we obtain
where the last inequality follows from an assumption that \({\hat{b}}_{2,a}\le 2\). Thus, we have \(A_{3,ar}\le \mathrm {e}+A_{2,r}\). Similarly, we can show that \(A_{3,a}\le A_{1,a}+A_{2,a}\). Hence, from Lemma 7.1, we have
This gives \({\tilde{f}}_{3,ar}\le {\tilde{f}}_{1,a}+{\tilde{f}}_{2,r}\).
Similarly, we have
From \(c_{3,a}\le c_{1,a}+c_{2,a}\) and inequality (65), we obtain \({\tilde{f}}_{3,a}\le {\tilde{f}}_{1,a}+{\tilde{f}}_{2,a}\). \(\square\)
1.2 Proof of properties in Sect. 4
Proof of Proposition 4.1
In competition case, by Eq. (8), we have
Hence, if \(b_{2,r}-\beta _2c_{2,r}\le (\ge ) b_{2,a}-\beta _2c_{2,a}\), we have \(p^*_{2,r}\le (\ge ) p^*_{2,a}\).
In cooperation case, we give the proof only for the case of \(i=2\). If \(b_{2,r}-\beta _2c_{2,r}\le (\ge ) b_{2,a}-\beta _2c_{2,a}\), then \(A_{2,r}\le (\ge )A_{2,a}\). Since \({\tilde{p}}^*_{2,r}/{\tilde{p}}^*_{2,a}=A_{2,r}/A_{2,a}\), we have \({\tilde{p}}^*_{2,r}\le (\ge ){\tilde{p}}^*_{2,a}\) if \(b_{2,r}-\beta _2c_{2,r}\le (\ge ) b_{2,a}-\beta _2c_{2,a}\).
Next, we show the relationship of optimal prices of both sectors. We show only the case of \(i=2\). Since \(c_{2,r}\le c_{2,a}\) and \({\tilde{f}}^*_{2,r}={\tilde{f}}^*_{2,a}-c_{2,a}+c_{2,r}\), we have \({\tilde{f}}^*_{2,r}\le {\tilde{f}}^*_{2,a}\). Moreover, the difference between the air and HSR prices is given by \({\tilde{f}}^*_{2,a}-{\tilde{f}}^*_{2,r}=c_{2,a}-c_{2,r}\). \(\square\)
Lemma 7.2
The consumer surplus in market i, \(i=1,2,3\), is given by
Proof
Let \(S_{i}\) be the consumer surplus in market i, and it follows from Eq. (15) that
The consumer surplus under the optimal prices in competition and cooperation cases is obtained by substituting Eqs. (11) and (19), respectively. Here, we only show that the case for \(i=2\) in cooperation case. We have
where \({\tilde{W}}_2=W[A_{2,a}+A_{2,r}]\). Since \(A_{2,a}+A_{2,r}={\tilde{W}}_2\exp \{{\tilde{W}}_2\}\), we obtain
Similarly, we have
Thus, for \(i=2\), the value in parentheses in Eq. (69) can be rewritten as
Thus, we obtain Eq. (69). \(\square\)
1.3 Proof of Properties in Table 2
Suppose that \({\hat{b}}_{3,ar}\) is increasing in \(b_{3,ar}\). Then, we have
-
(i)
The market share of air–rail \({\tilde{p}}^*_{3,ar}\) is increasing in its service quality \(b_{3,ar}\), and the market share of alternative itinerary \({\tilde{p}}^*_{3,a}\) is decreasing in the service quality \(b_{3,ar}\). Moreover, the non-purchase probability \({\tilde{p}}^*_{3,0}\) is decreasing in \(b_{3,ar}\).
-
(ii)
The optimal price of air–rail \({\tilde{f}}^*_{3,ar}\) is increasing in its own service quality \(b_{3,ar}\), and the optimal price of alternative itinerary \({\tilde{f}}^*_{3,a}\) is also increasing in the service quality \(b_{3,ar}\).
-
(iii)
The maximum total revenue \(V_{ar}-\sum ^3_{i=1}\sum _{j\in {\mathcal {N}}_i}I_{i,j}\) is increasing in the service quality \(b_{3,ar}\). However, the maximum total profit \(V_{ar}\) is ambiguous with respect to the service quality \(b_{3,ar}\).
-
(iv)
The consumer surplus \(S_I\) is increasing in the service quality \(b_{3,ar}\).
Proof
Define \({\tilde{W}}=W[A_{3,a}+A_{3,ar}]\). Since \({\hat{b}}_{3,ar}\) is increasing in \(b_{3,ar}\), we have
(i) For any \(x\ge 0\), it is known that \(W[x]\ge 0\) and
By Eq. (18), we obtain
Thus, we obtain the part (i).
(ii) Since \(A_{3,ar}\) is increasing in \(b_{3,ar}\) and W[x] is increasing in x, the proof is straightforward. Similarly, from Eq. (20), we obtain part (iii).
(iv) From Lemma 7.2, we obtain
The partial differential of \(S_I\equiv S(\tilde{\varvec{f}}^*)\) with respect to \(b_{3,ar}\) is given by
The last inequality follows from Eq. (77). Hence, the consumer surplus is increasing in \(b_{3,ar}\). \(\square\)
Proof of Proposition 4.2
-
(i)
In markets 2 and 3, the optimal price in the cooperation case \({\tilde{f}}^*_{i,j}\), \(j\in {\mathcal {N}}_i\), is higher than that in the competition case \(f^*_{i,j}\).
-
(ii)
In market 2, the effect of cooperation on the market share for each sector is ambiguous. However, if the cost-adjusted service quality of the HSR is greater than that of the air, \({\hat{b}}_{2,r}\ge {\hat{b}}_{2,a}\) or the substitutability between the air and the HSR sectors is sufficiently high, then the market share of the air sector in market 2 decreases when compared to the competition case \({\tilde{p}}^*_{2,a}< p^*_{2,a}\).
-
(iii)
In market 3, the market share of the airline in cooperation case is lower than that in competition case, \({\tilde{p}}^*_{3,a}< p^*_{3,a}\).
-
(iv)
Compared with the competition case, the total volume in cooperation case is low in market 2 and is high in market 3.
Proof
(i) Since \(W[A_{i,j}]<W[\sum _{j\in {\mathcal {N}}_i}A_{i,j}]\) for \(i=2,3\), it follows from Eqs. (11) and (19) that \(f^*_{i,j}<{\tilde{f}}^*_{i,j}\).
(ii) For simplicity of notation, we write \(W_a\), \(W_r\) and \({\tilde{W}}\) instead of \(W[A_{2,a}]\), \(W[A_{2,r}]\) and \(W[A_{2,a}+A_{2,r}]\), respectively. Subtracting \({\tilde{p}}_{2,a}^*\) from \(p_{2,a}^*\), we obtain
Set \(\zeta \equiv (A_{2,a}+A_{2,r})W_a\) and \(\eta \equiv A_{2,a}{\tilde{W}}\). The definition of Lambert W function gives \((\zeta /(A_{2,a}+A_{2,r}))\exp \{\zeta /(A_{2,a}+A_{2,r})\}=A_{2,a}\) and \((\eta /A_{2,a})\exp \{\eta /A_{2,a}\}=A_{2,a}+A_{2,r}\). Thus, we have
Since the function \(x\exp \{x\}\) is increasing in x, we have \(\zeta \ge \eta\), so \((A_{2,a}+A_{2,r})W_a>A_{2,a}{\tilde{W}}\).
If the substitutability between the air and the HSR sectors is sufficiently high, i.e., \(A_{2,r}\approx A_{2,a}\), then we obtain \(A_{2,r}W_a-A_{2,a}W_r\approx 0\). Hence, we have \({\tilde{p}}^*_{2,a}<p^*_{2,a}\).
Next, we show the part (ii) under the different assumption. We define \({\bar{\zeta }}\equiv A_{2,r}W_a\) and \({\bar{\eta }}\equiv A_{2,a}W_r\). We obtain
The last inequality follows from \(b_{2,r}-\beta _2c_{2,r}\ge b_{2,a}-\beta _2c_{2,a}\). Thus, we have \({\bar{\zeta }}\ge {\bar{\eta }}\), so \(A_{2,r}W_a\ge A_{2,a}W_r\). Therefore, by Eq. (80), we have \({\tilde{p}}_{2,a}^*<p_{2,a}^*\).
(iii) Set \(W_a\equiv W[A_{3,a}]\) and \({\tilde{W}}\equiv W[A_{3,a}+A_{3,ar}]\). Subtracting \({\tilde{p}}_{3,a}^*\) from \(p_{3,a}^*\), we obtain
In the same manner with part (ii), we can show that \(W_a(A_{3,a}+A_{3,ar})>A_{3,a}{\tilde{W}}\). Hence, we have \(p_{3,a}^*>{\tilde{p}}_{3,a}^*\).
(iv) By Lemma 7.1, we have \(W[A_{2,a}+A_{2,r}]<W[A_{2,a}]+W[A_{2,r}]\). From Eqs. (8) and (18), the non-purchase probabilities of both cases in market 2 are given by
Thus, we obtain \(p^*_{2,0}<{\tilde{p}}^*_{2,0}\), so \(p^*_{2,a}+p^*_{2,r}>{\tilde{p}}^*_{2,a}+{\tilde{p}}^*_{2,r}\). In market 3, since we have \(W[A_{3,a}]<W[A_{3,a}+A_{3,ar}]\), the relation of total volumes is given by \(p^*_{3,a}<{\tilde{p}}^*_{3,a}+{\tilde{p}}^*_{3,ar}\). \(\square\)
Proof of Proposition 4.3
Proof Define \(\zeta \equiv W[A_{2,r}]\) and \(\eta \equiv W[A_{2,a}]\). Then, we obtain \(\zeta {\mathrm {e}}^\zeta =A_{2,r}\) and \(\eta {\mathrm {e}}^\eta =A_{2,a}\). Thus, \(\zeta /\eta =(A_{2,r}/A_{2,a}){\mathrm {e}}^{\eta -\zeta }\). By Eq. (8), we have \(p^*_{2,r}/p^*_{2,a}=W[A_{2,r}]/W[A_{2,a}]\). Moreover, Eq. (18) gives \({\tilde{p}}^*_{2,r}/{\tilde{p}}^*_{2,a}=A_{2,r}/A_{2,a}\). Hence, we obtain
If \(p^*_{2,a}\le p^*_{2,r}\), then \(W[A_{2,a}]\le W[A_{2,r}]\). So, we have
If \(p^*_{2,a}\ge p^*_{2,r}\), then \(W[A_{2,a}]\ge W[A_{2,r}]\). Thus, by Eq. (81), we obtain
\(\square\)
Proof of Proposition 4.4
-
(i)
In market 2, if \(u_{2,0}\le {\bar{b}}_{2,a}-\mu (3/2-\log 2(1+\exp \{({\bar{b}}_{2,r}-{\bar{b}}_{2,a})/\mu \}))\), then we have \(\partial ( {\tilde{p}}_{2,a}+{\tilde{p}}_{2,r})/\partial u_{2,0}\le \partial (p_{2,a}+p_{2,r})/\partial u_{2,0}\le 0\).
-
(ii)
In market 3, if \(u_{3,0}+\mu (3/2-\log 2)\le {\bar{b}}_{3,a}\), then we have \(\partial p_{3,a}/\partial u_{3,0}\le \partial ({\tilde{p}}_{3,a}+{\tilde{p}}_{3,ar})/\partial u_{3,0}\le 0\).
Proof
Suppose that the total volume for competition and cooperation cases in market 2 are given by
It is easy to see that \(\partial T_2/\partial u_{2,0}<0\) and \(\partial {\tilde{T}}_2/\partial u_{2,0}<0\). Thus, the total volumes are decreasing in the attractiveness of the outside option \(u_{2,0}\). Let \(\varDelta _2\) be the difference of the total volume between the both cases, that is, \(\varDelta _2=T_2-{\tilde{T}}_2\). Then, we have
Here the function \(f(x)=(1-x)x^2\) is increasing in \(0\le x\le 2/3\) and decreasing in \(2/3\le x\le 1\). In addition, by Proposition 4.2, we have \(p_{2,0}\le {\tilde{p}}_{2,0}\). Thus, if \(p_{2,0}\le {\tilde{p}}_{2,0}\le 2/3\), then we obtain \((1-p_{2,0})p_{2,0}^2\le (1-{\tilde{p}}_{2,0}){\tilde{p}}^2_{2,0}\), and \(\partial \varDelta _2/\partial u_{2,0}\ge 0\). This implies that \(\partial {\tilde{T}}_2/\partial u_{2,0}\le \partial T_2/\partial u_{2,0}\le 0\). By the assumption \(u_{2,0}\le {\bar{b}}_{2,a}-\mu (3/2-\log 2(1+\exp \{({\bar{b}}_{2,r}-{\bar{b}}_{2,a})/\mu \}))\), the relation \({\tilde{p}}_{2,0}\le 2/3\) holds.
Similarly, we set \(\varDelta _3=p_{3,a}-({\tilde{p}}_{3,a}+{\tilde{p}}_{3,ar})\). Then, we have
By Proposition 4.2, we have \({\tilde{p}}_{3,0}\le p_{3,0}\). In addition, the assumption \(u_{3,0}+\mu (3/2-\log 2)\le {\bar{b}}_{3,a}\) implies that \(p_{3,0}\le 2/3\). Thus, we have \(\partial \varDelta _3/\partial u_{3,0}\le 0\) for \({\tilde{p}}_{3,0}\le p_{3,0}\le 2/3\). Hence, we obtain \(\partial p_{3,a}/\partial u_{3,0}\le \partial ({\tilde{p}}_{3,a}+{\tilde{p}}_{3,ar})/\partial u_{3,0}\le 0\). \(\square\)
Remark 7.1
In the above proposition, the right-hand side of the condition \(u_{2,0}\le {\bar{b}}_{2,a}-\mu (3/2-\log 2(1+\exp \{({\bar{b}}_{2,r}-{\bar{b}}_{2,a})/\mu \}))\) can be approximated as
Thus, Proposition 4.3 holds when the service quality of outside alternative is almost same or lower than that of the HSR.
Proof of Proposition 4.5
-
(i)
In market 1, the consumer surplus in competition case is equal to that in cooperation case.
-
(ii)
In market 2, the consumer surplus in cooperation case is lower than that in competition case.
-
(iii)
In market 3, the consumer surplus in cooperation case is greater than that in the competition case.
-
(iv)
In market 1, the profit in competition case is equal to that in cooperation case.
-
(v)
In market 2, the profit in cooperation is greater(lower) than that in competition case if the loss of total profit caused by competition between HSR and air is greater(lower) than the reduction in total profit due to the decrease in total volume by cooperation.
-
(vi)
In market 3, the revenue in cooperation case is greater than that in competition case. However, the profit in cooperation case is greater than that in competition case if the gain in revenue exceeds the fixed cost of air–rail mode.
Proof
(i) Since the optimal prices for both cases are equivalent in market 1, the consumer surplus in competition case is equal to that of the cooperation case.
(ii) From Proposition 4.2, we have \(f^*_{2,j}\le {\tilde{f}}^*_{2,j}\) for each \(j=a,r\). Hence, by Lemma 7.2, \({\tilde{S}}_2(\tilde{\varvec{f}}^*_{2})\le S_2(\varvec{f}^*_{2})\).
(iii) Since \({\mathcal {N}}_3=\{a\}\) for the competition case and \({\mathcal {N}}_3=\{a,ar\}\) for the cooperation case, the proof is straightforward by comparing Eqs. (67) and (68) in Lemma 7.2.
(iv) In market 1, the profit for the competition case is provided by the air sector. The profit is given by the first term of Eq. (13). For the cooperation case, the profit is also provided by the air sector which represents the first term of Eq. (20). Hence, the profit for both cases are equivalent.
(v) From Proposition 3.3, we have
where \(W_a=W[A_{2,a}]\) and \(W_r=W[A_{2,r}]\). In the above equation, \(M_2(\mu /\beta _2)(2W_aW_r/(1+W_a+W_r))\) represents the loss of total profit due to the competition. In the cooperation case, the profit in market 2 is given by \({\tilde{V}}_{2}=M_2(\mu /\beta _2){\tilde{W}}_2-I_{2,a}-I_{2,r}\) where \({\tilde{W}}_2=W[A_{2,a}+A_{2,r}]\). By comparing the total profits of competition and cooperation case in market 2, we have
Since the difference of the non-purchase probability between both cases is given by
Eq. (88) can be rewritten as follows:
The value \(M_2(\mu /\beta _2)(1/p_{2,0}-1/{\tilde{p}}_{2,0})\) in the first term in Eq. (90) is positive because \(p_{2,0}\le {\tilde{p}} _{2,0}\) and it represents the reduction in total profit due to the decrease in total volume by cooperation. Thus, we have \(V_2\le (\ge ){\tilde{V}}_2\), if \(1/p_{2,0}-1/{\tilde{p}}_{2,0}\le (\ge )2W_aW_r/(1+W_a+W_r)\).
(vi) Since we have \(V_{3,a}=M_3(\mu /\beta _3)W[A_{3,a}]-I_{3,a}\) and \({\tilde{V}}_3=M_3(\mu /\beta _3)W[A_{3,a}+A_{3,ar}]-I_{3,a}-I_{3,ar}\), the difference is given by
The first term represents the gain in total revenue and it takes positive value. Thus, the revenue in cooperation case is greater than that in competition case. If the gain exceeds the fixed cost of air–rail mode, then we have \(V_{3,a}\le {\tilde{V}}_{3}\). \(\square\)
Lemma 7.3
In the competition case, let \(V_2\) be the total profit for the air and the HSR in market 2, \(V_2=V_{2,a}+V_r\). Then, we have
-
(i)
\(V_2\) and \({\tilde{V}}_2\) are decreasing in \(u_{2,0}\).
-
(ii)
\(V_2-{\tilde{V}}_2\rightarrow 0\) as \(u_{2,0}\rightarrow \infty\).
-
(iii)
\(S_2\) and \({\tilde{S}}_2\) are increasing in \(u_{2,0}\).
-
(iv)
\(S_2-{\tilde{S}}_2\rightarrow 0\) as \(u_{2,0}\rightarrow \infty\).
Proof
The proofs of parts (i) and (iii) directly follow from the partial differential of \(V_2\), \({\tilde{V}}_2\), \(S_2\) and \({\tilde{S}}_2\) with respect to \(u_{2,0}\). Thus, we omit the proofs. For parts (ii) and (iv), we have \(W[A_{2,a}]\rightarrow 0\) and \(W[A_{2,r}]\rightarrow 0\) as \(u_{2,0}\rightarrow \infty\). Thus, \(V_2\rightarrow 0\) and \({\tilde{V}}\rightarrow 0\). In addition, the difference between the consumer surplus of competition and cooperation cases in market 2 is given by
Thus, we have \(S_2-{\tilde{S}}_2\rightarrow 0\) as \(u_{2,0}\rightarrow \infty\). \(\square\)
Proof of Proposition 4.6
-
(i)
If \(u_{2,0}\) is relatively small, then we have \(W_2\ge {\tilde{W}}_2\).
-
(ii)
If \(u_{2,0}\) is relatively large, then we have \(W_2\approx {\tilde{W}}_2\).
-
(iii)
If \(u_{2,0}={\hat{b}}_{2,j}-\mu\) for \(j=a,r\), then we have \(W_2>{\tilde{W}}_2\).
Proof
By Eq. (92), the difference of the consumer surplus in market 2 can be rewritten as \(S_2-\tilde{S_2}=M_2(\mu /\beta _2)\log ({\tilde{p}}_{2,0}/p_{2,0})\). Thus, the difference of the social welfare is given by
where \(m(x)=\log (x)-1/x\). From the proof of Proposition 4.2(iv), we have \(p_{2,0}\le {\tilde{p}}_{2,0}\). Since m(x) is increasing in \(x>0\), we have \(m(p_{2,0})\le m({\tilde{p}}_{2,0})\). In the proof of Proposition 4.4, we show that \(\varDelta _2={\tilde{p}}_{2,0}-p_{2,0}\) is increasing in \(u_{2,0}\). Thus, for small value of \(u_{2,0}\), the difference between the \({\tilde{p}}_{2,0}\) and \(p_{2,0}\) is small, and so \(m({\tilde{p}}_{2,0})-m(p_{2,0})\) is relatively small. On the other hand, we can show that the function \(2W_aW_r/(1+W_a+W_r)\) of the last term in Eq. (93) is decreasing in \(u_{2,0}\). Therefore, for small value of \(u_{2,0}\), we have \(W_2\ge {\tilde{W}}_2\).
From Lemma 7.3, part (ii) holds. For part (iii), since \({\hat{b}}_{2,a}=b_{2,r}\) and \(u_{2,0}=b_{2,j}-\mu\) for \(j=a,r\), we have \(A_{2,j}=1\) for \(j=a,r\). Thus, the difference of profit and consumer surplus is given by
where \(\varOmega \approx 0.5671\) is Omega constant. Thus, the difference of the social welfare is given by \(W_2-{\tilde{W}}_2\approx 0.1218\times M_2(\mu /\beta _2)>0\). Hence, we obtain \(W_2>{\tilde{W}}_2\). \(\square\)
Rights and permissions
This article is published under an open access license. Please check the 'Copyright Information' section either on this page or in the PDF for details of this license and what re-use is permitted. If your intended use exceeds what is permitted by the license or if you are unable to locate the licence and re-use information, please contact the Rights and Permissions team.
About this article
Cite this article
Sato, K., Chen, Y. Analysis of high-speed rail and airline transport cooperation in presence of non-purchase option. J. Mod. Transport. 26, 231–254 (2018). https://doi.org/10.1007/s40534-018-0172-z
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40534-018-0172-z